Development of Various Types of Independent Phase Based Pulsewidth Modulation Techniques for Three-Phase Voltage Source Inverters
Abstract
:1. Introduction
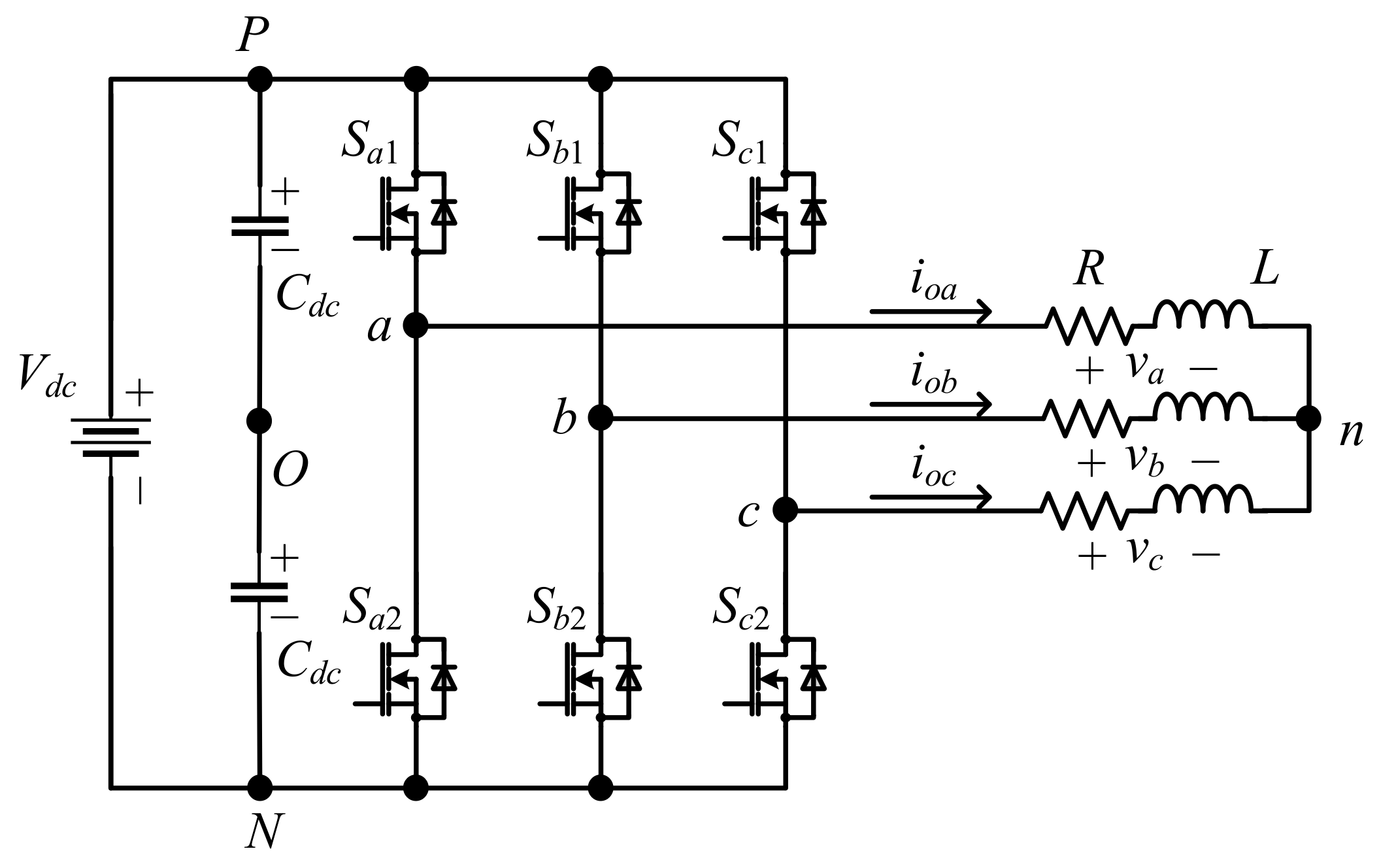
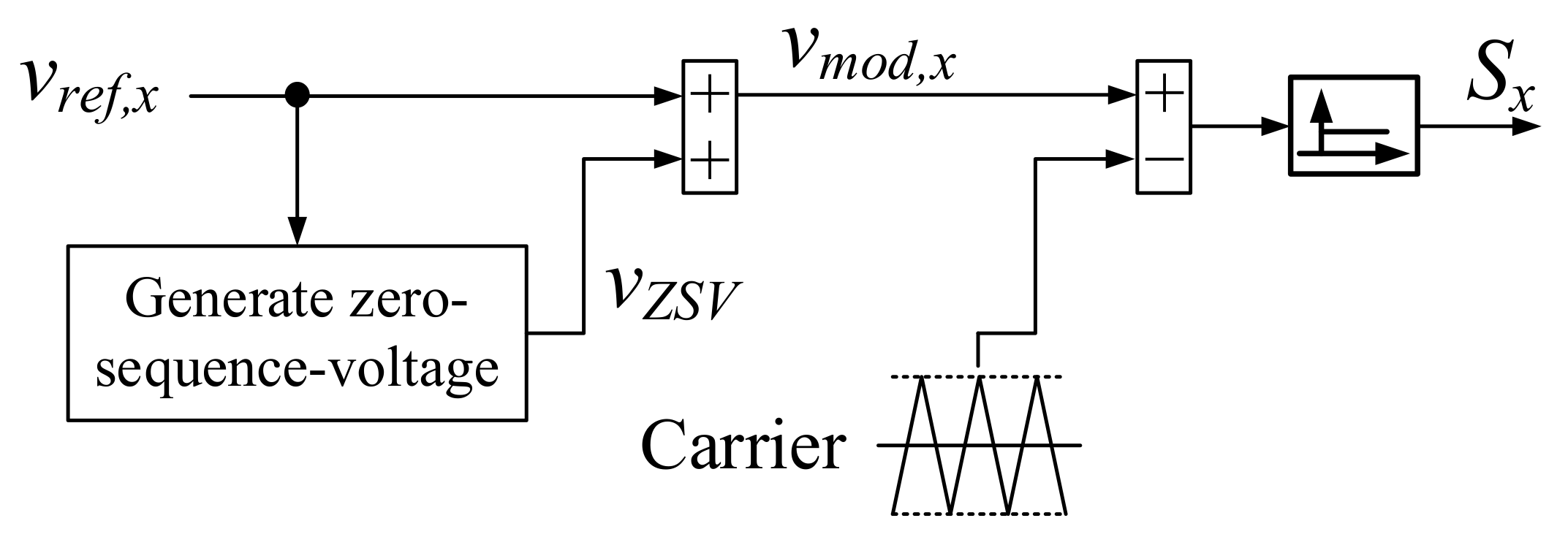
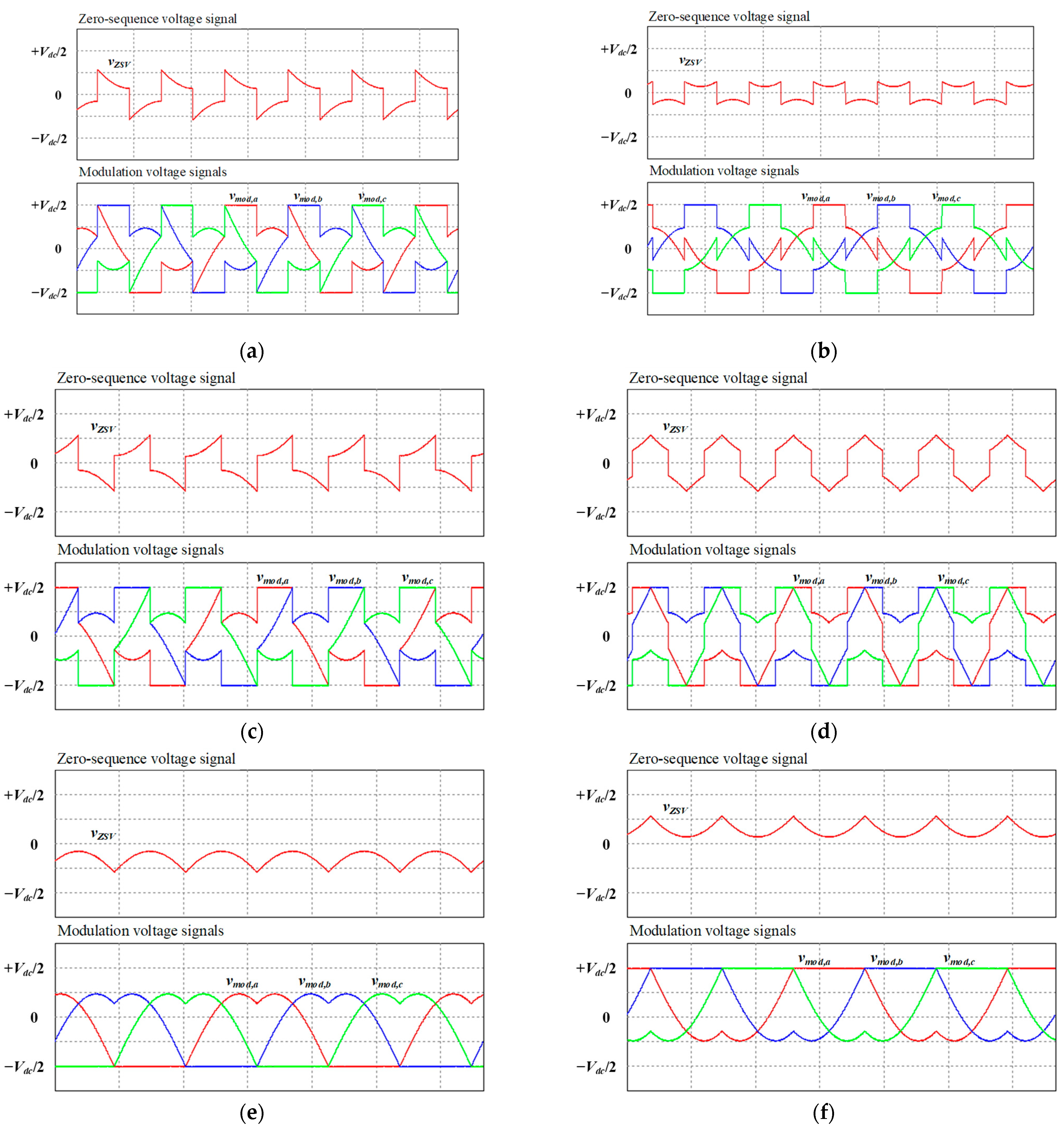
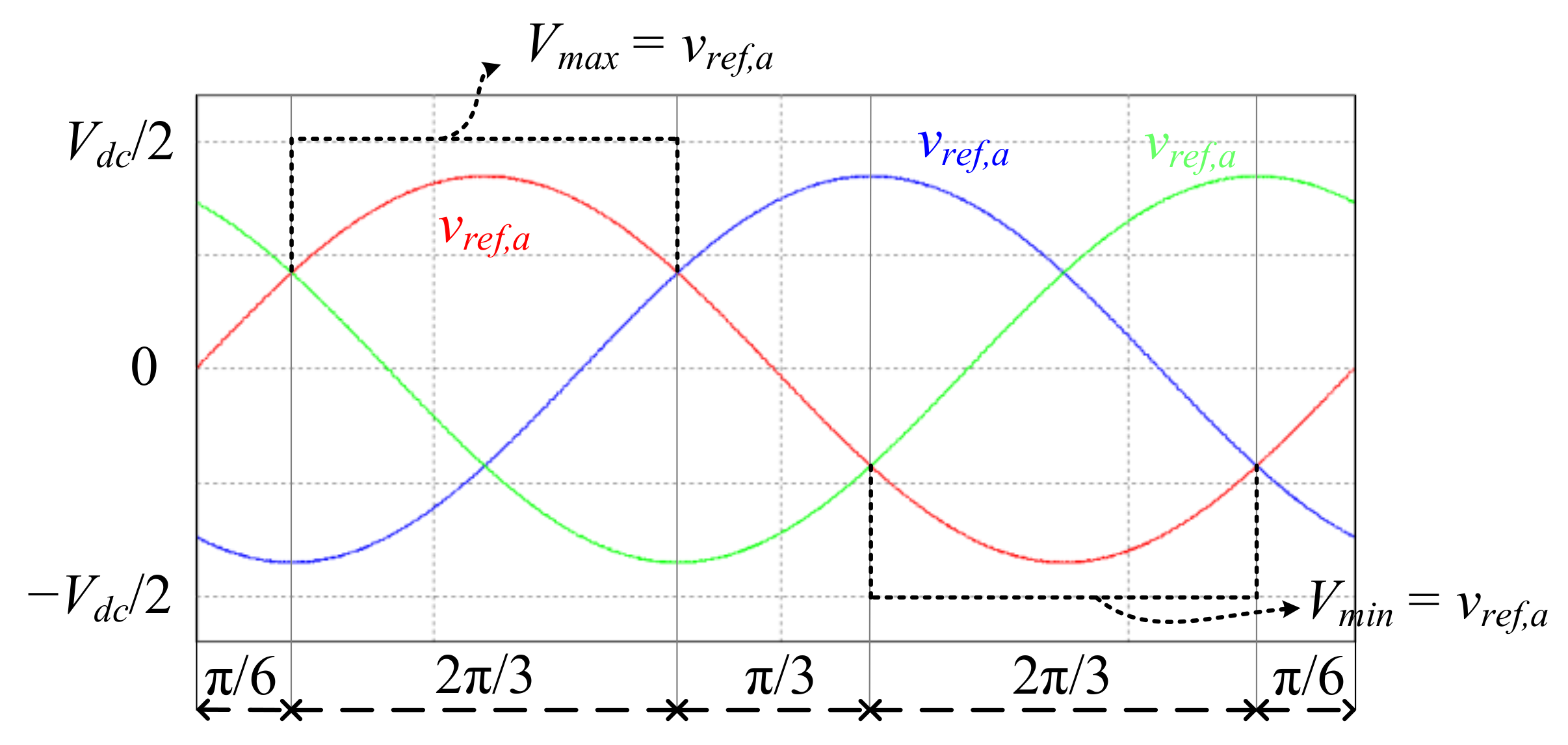
2. Three-Phase DPWM Techniques
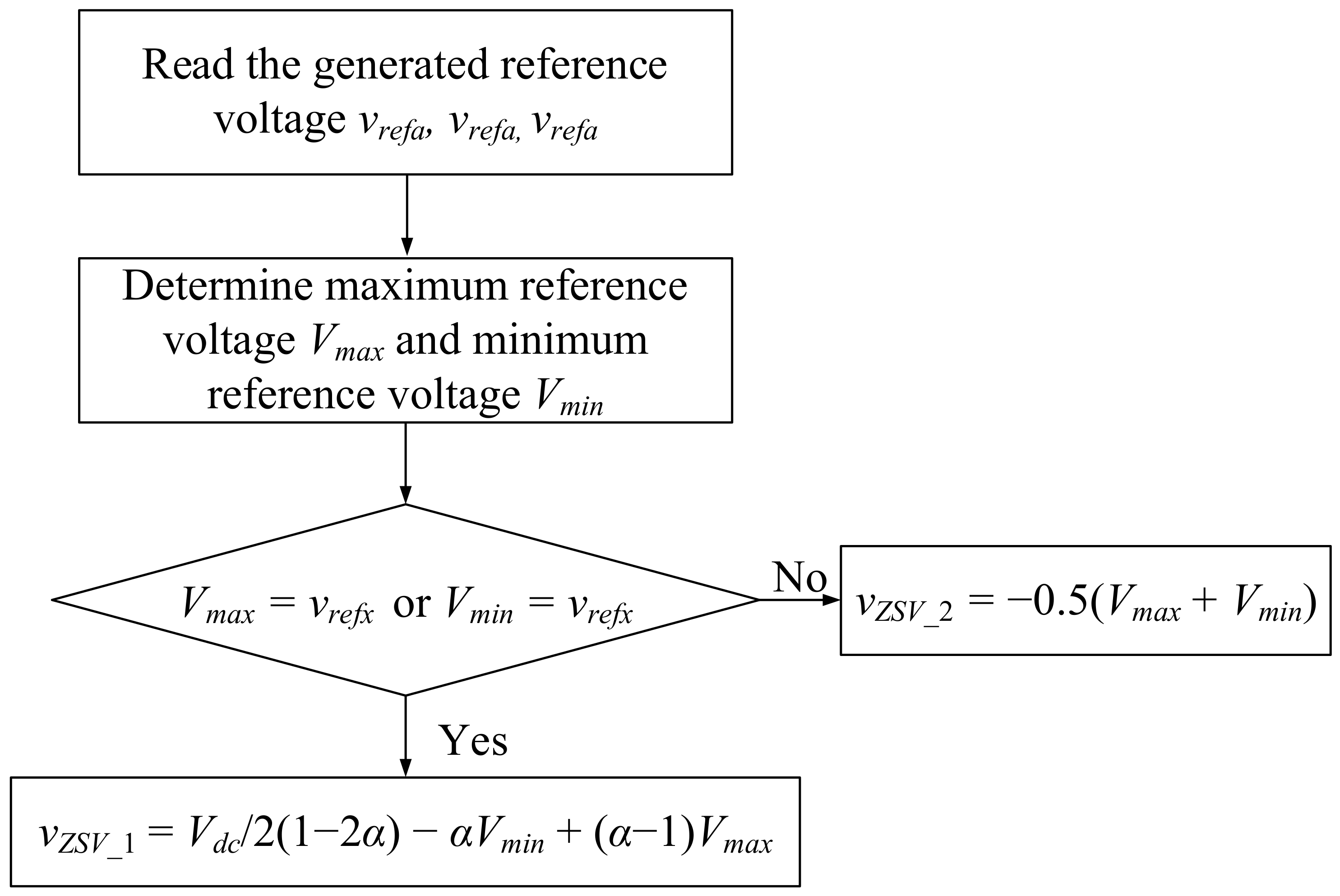
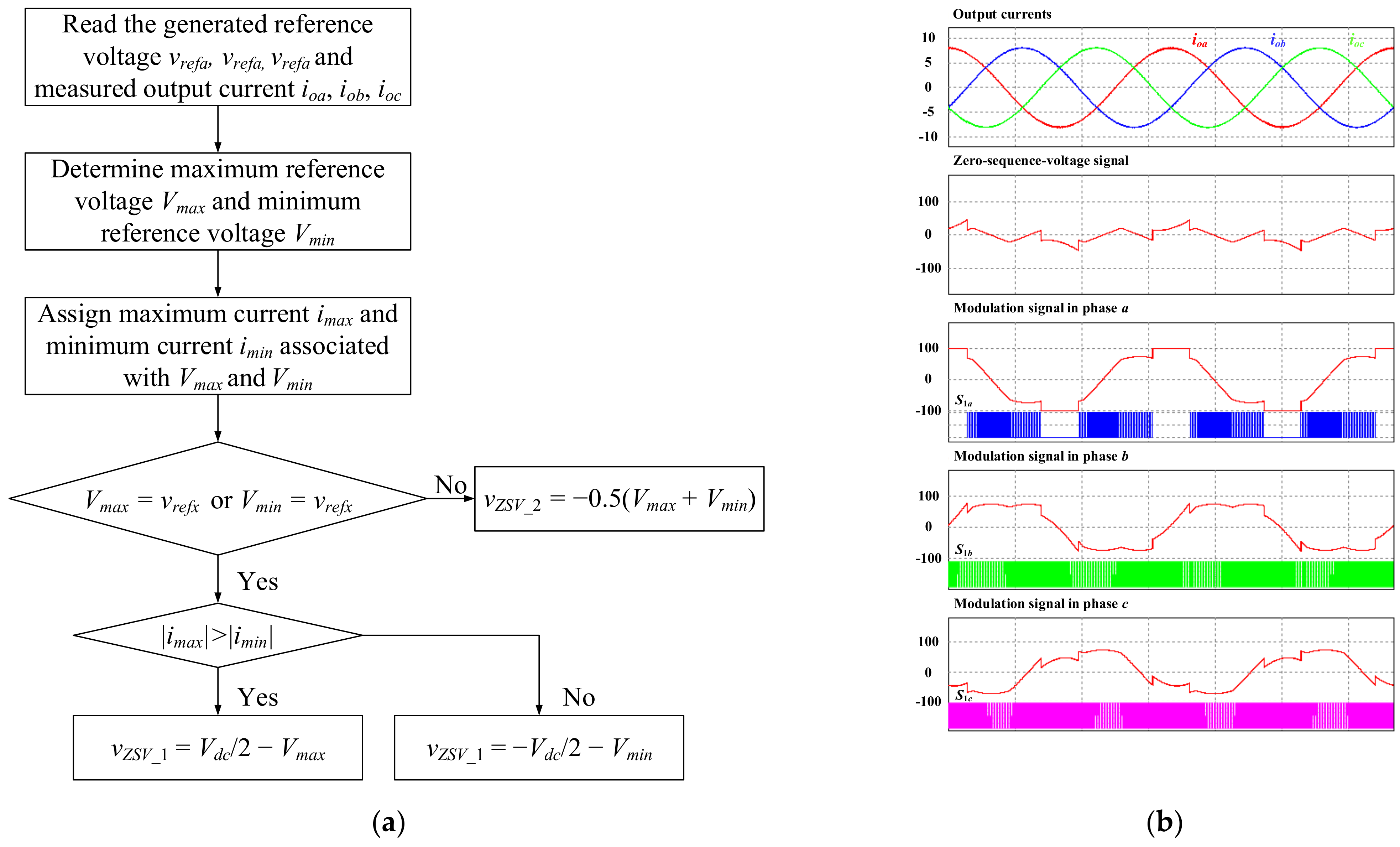
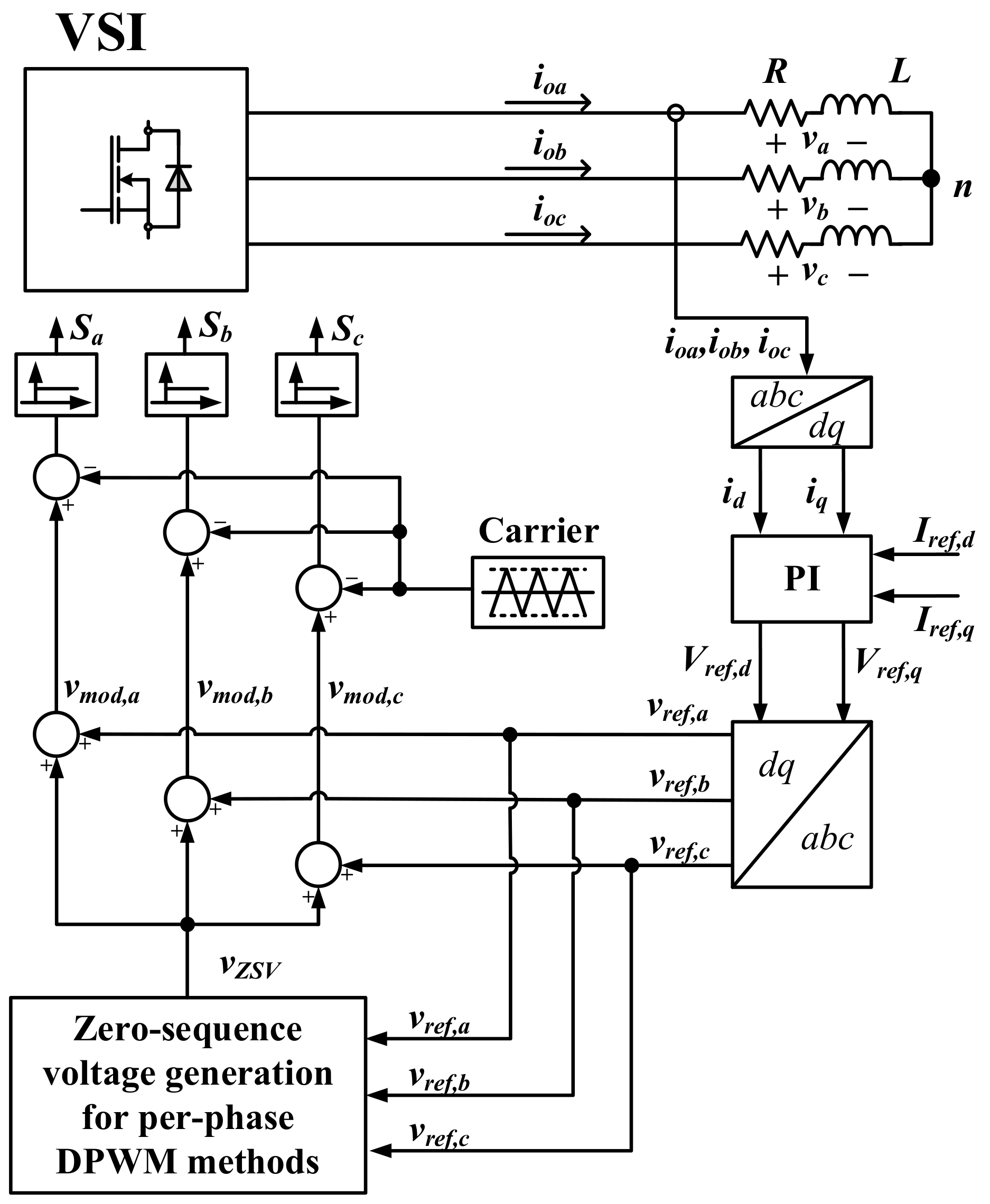
3. Per-Phase DPWM Technique for Independent Control of Switching Loss
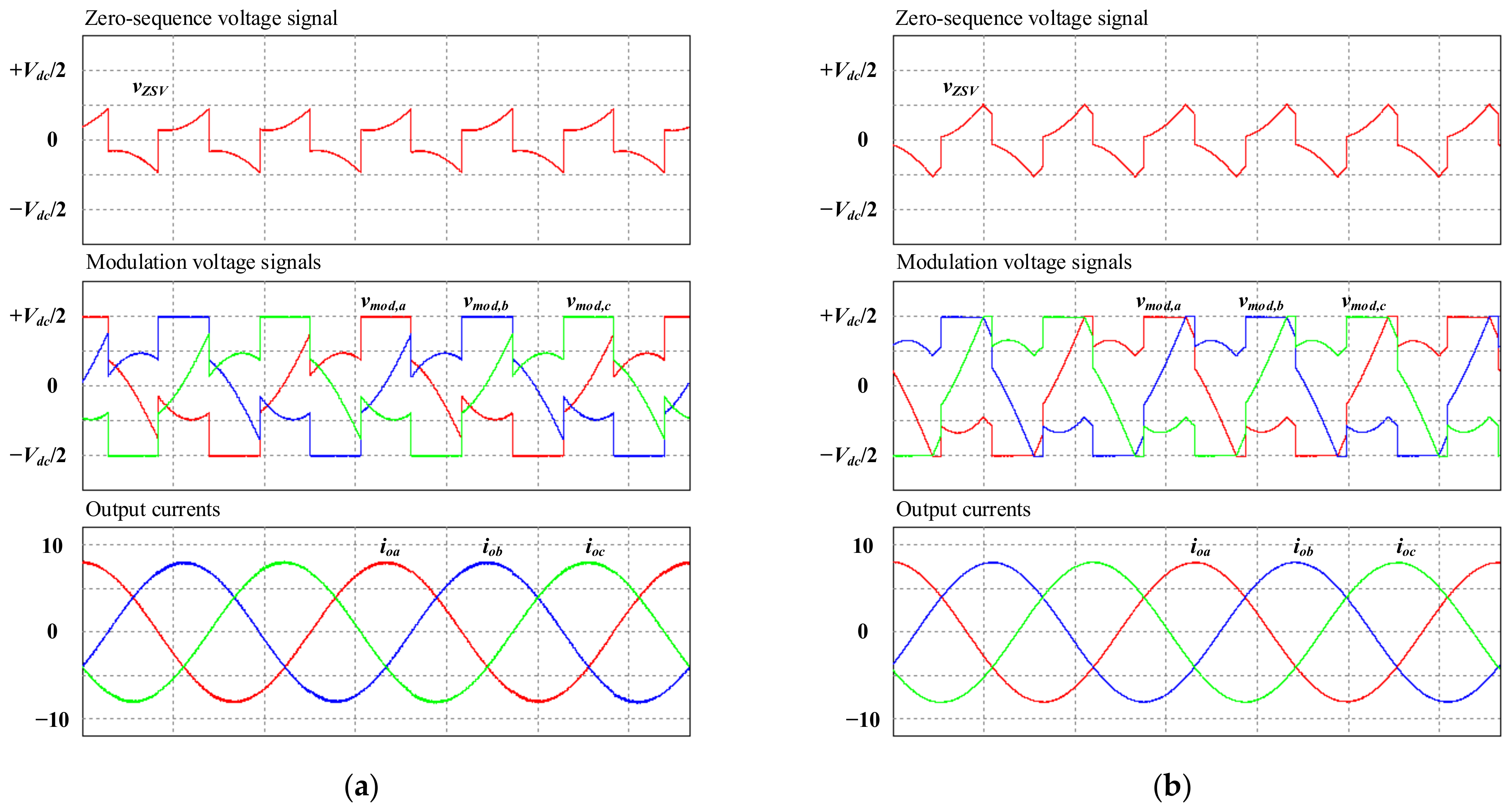
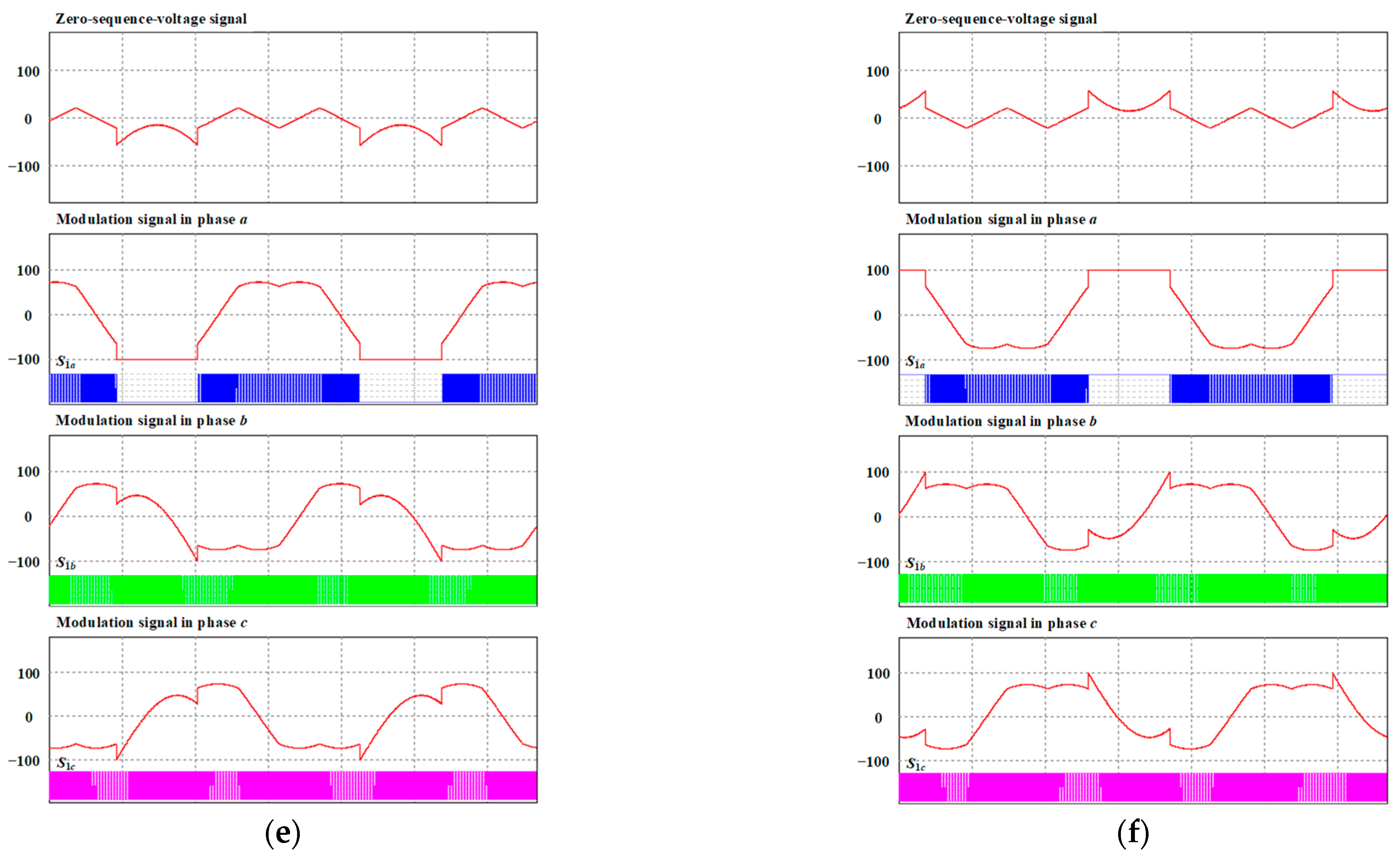
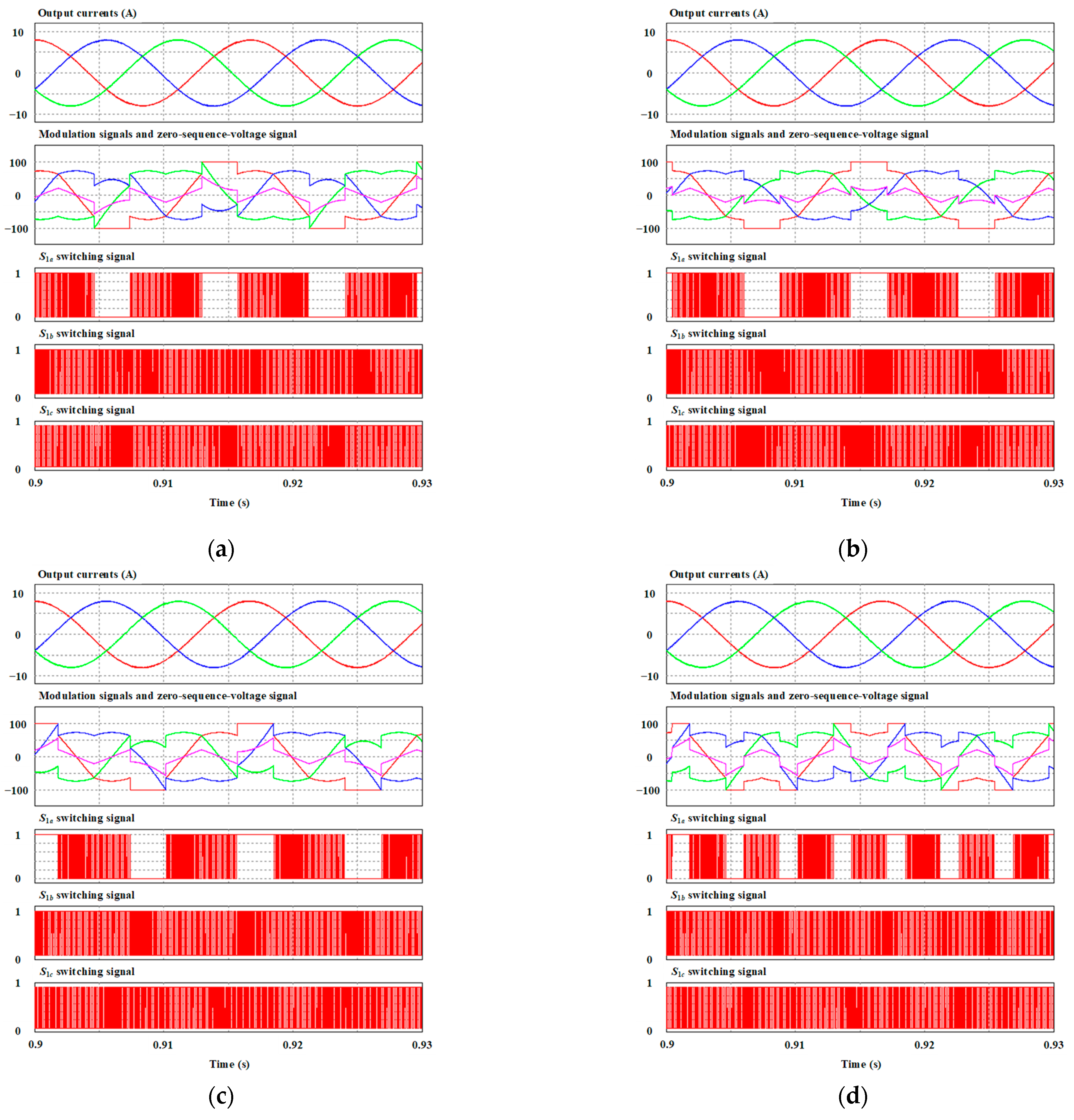
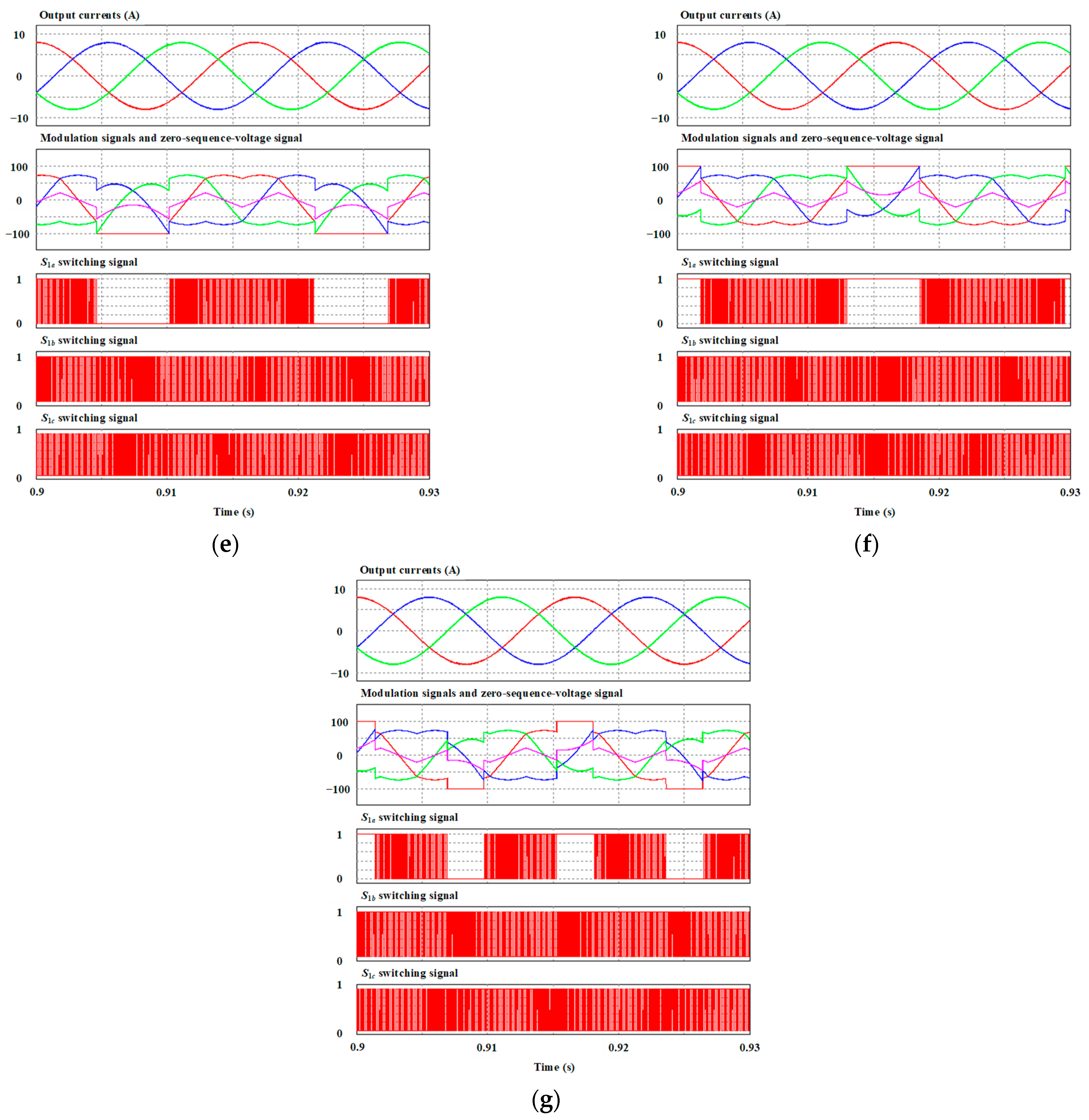
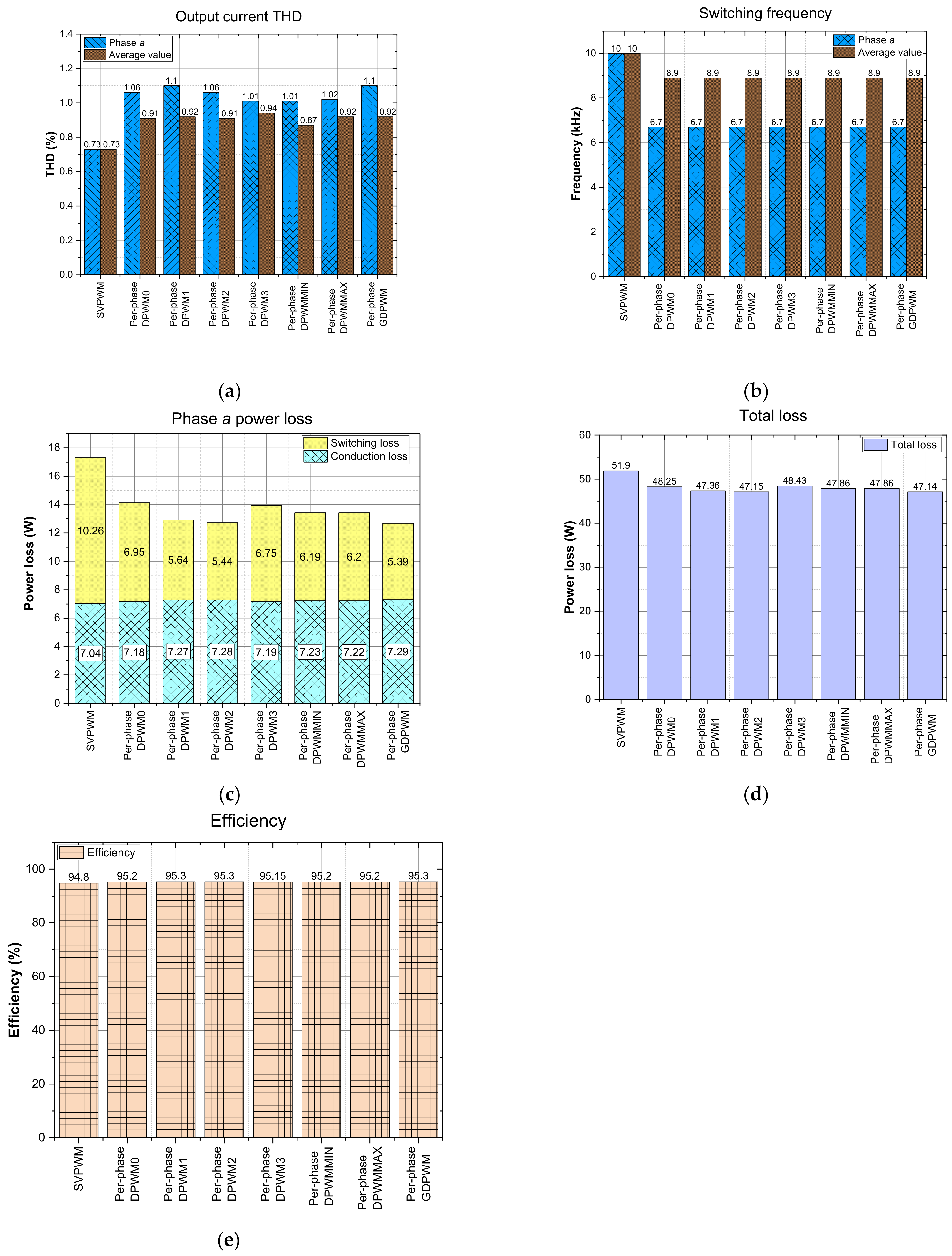
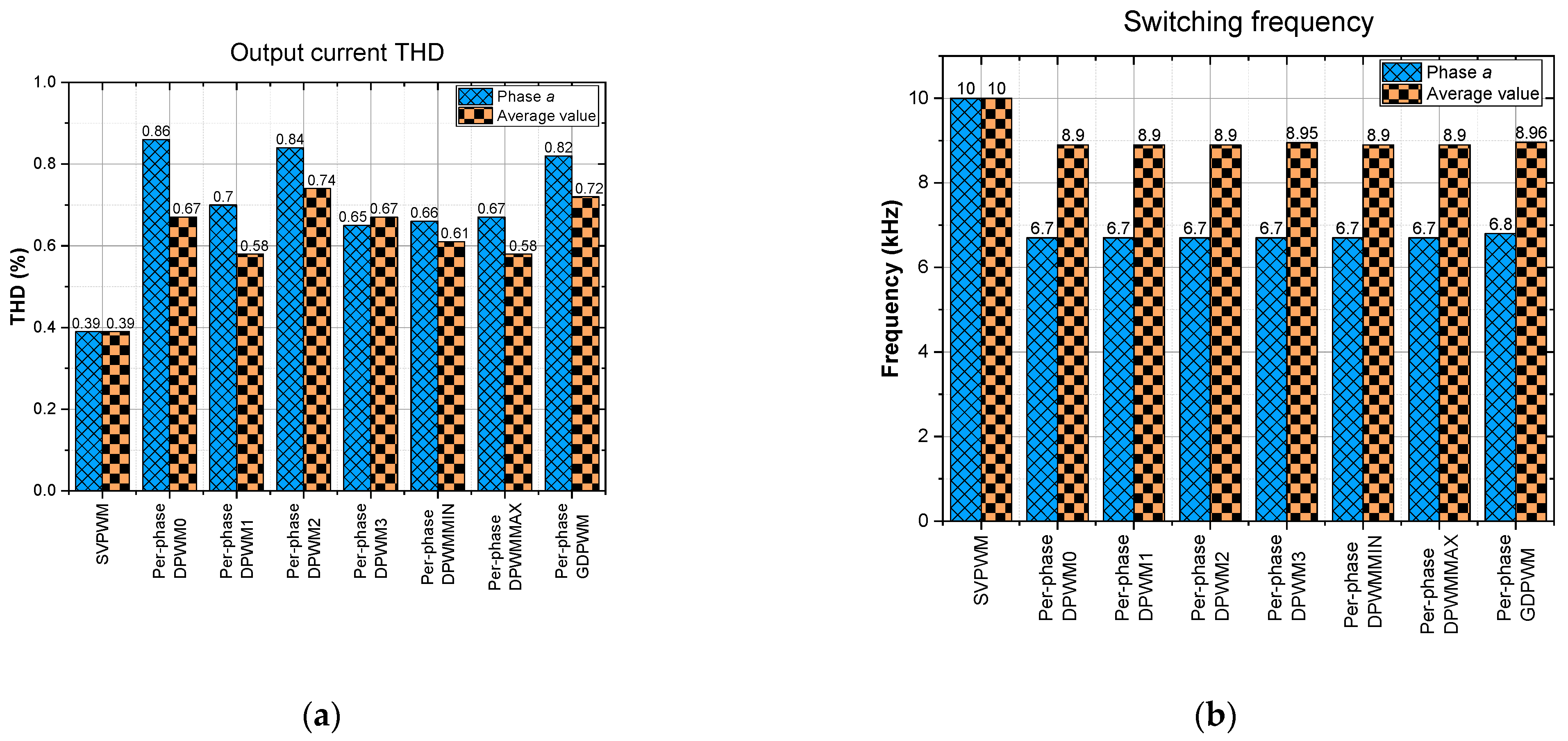
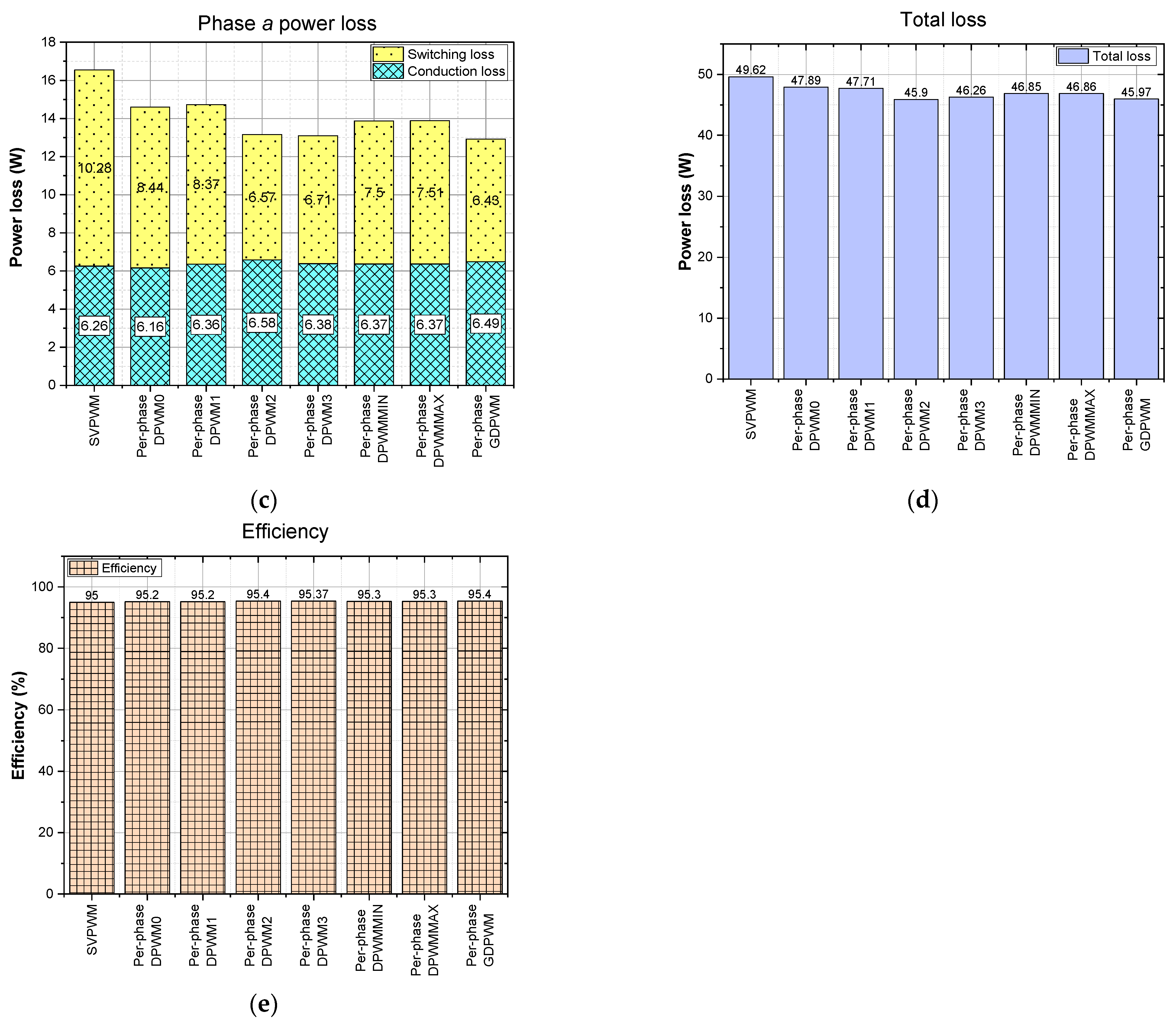
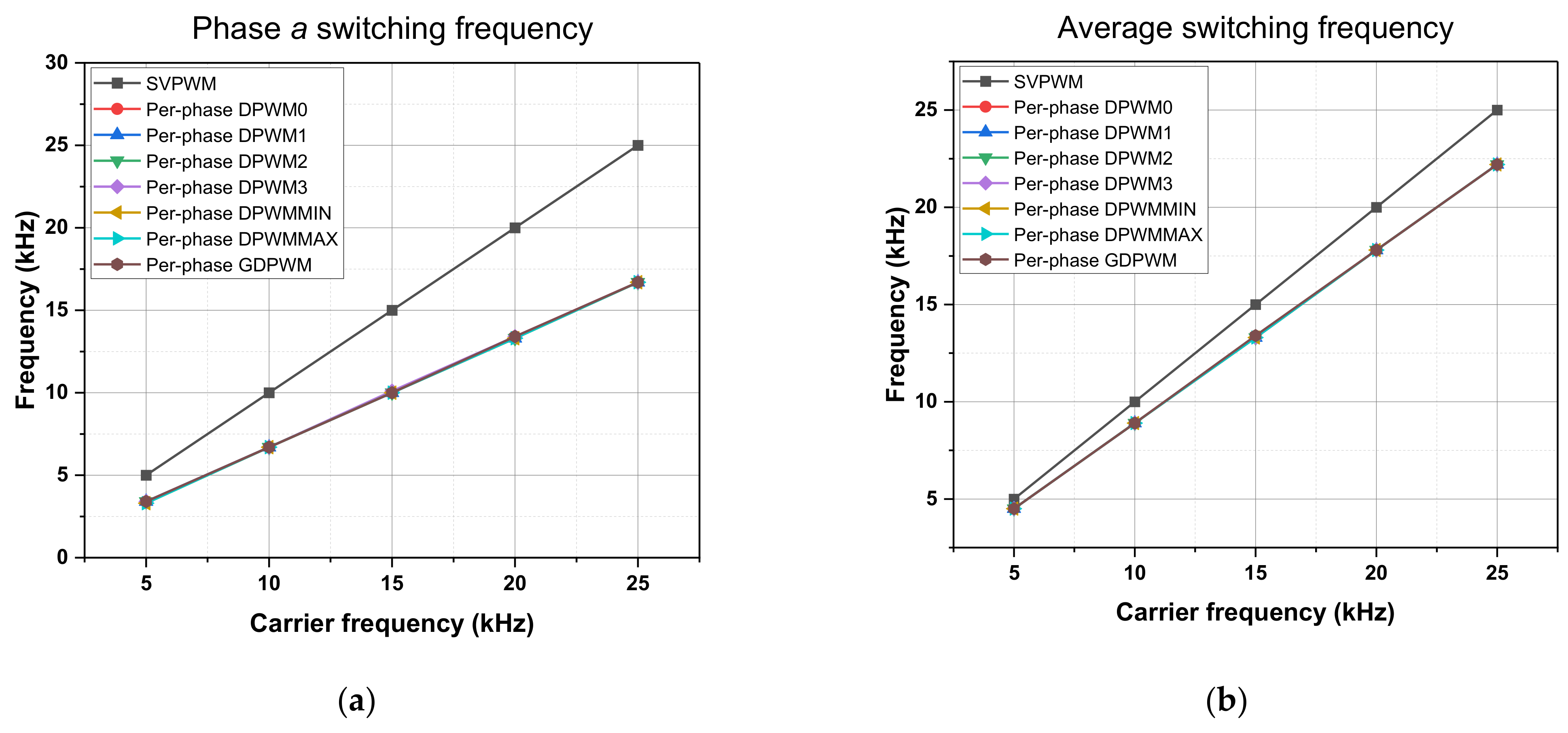
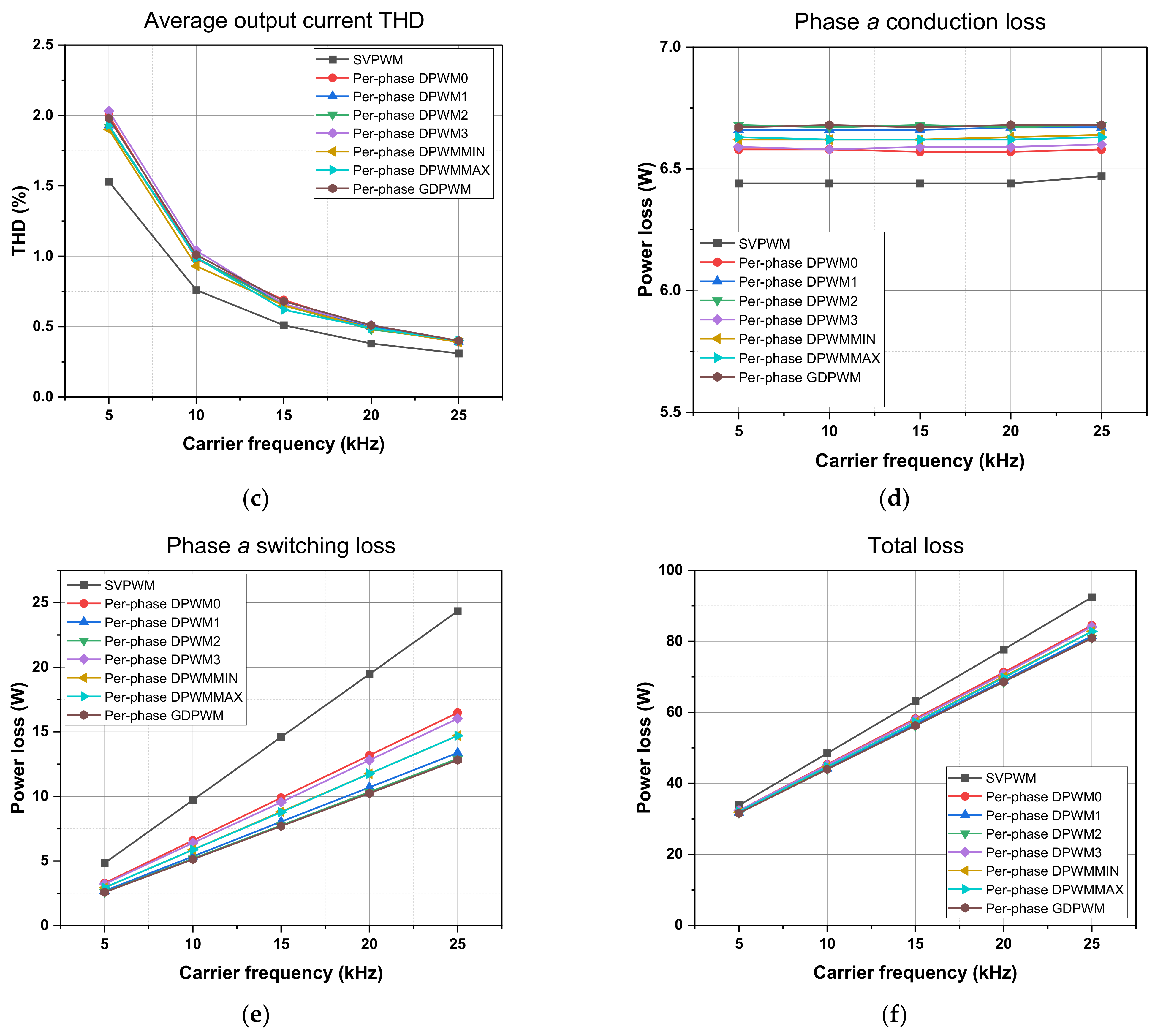
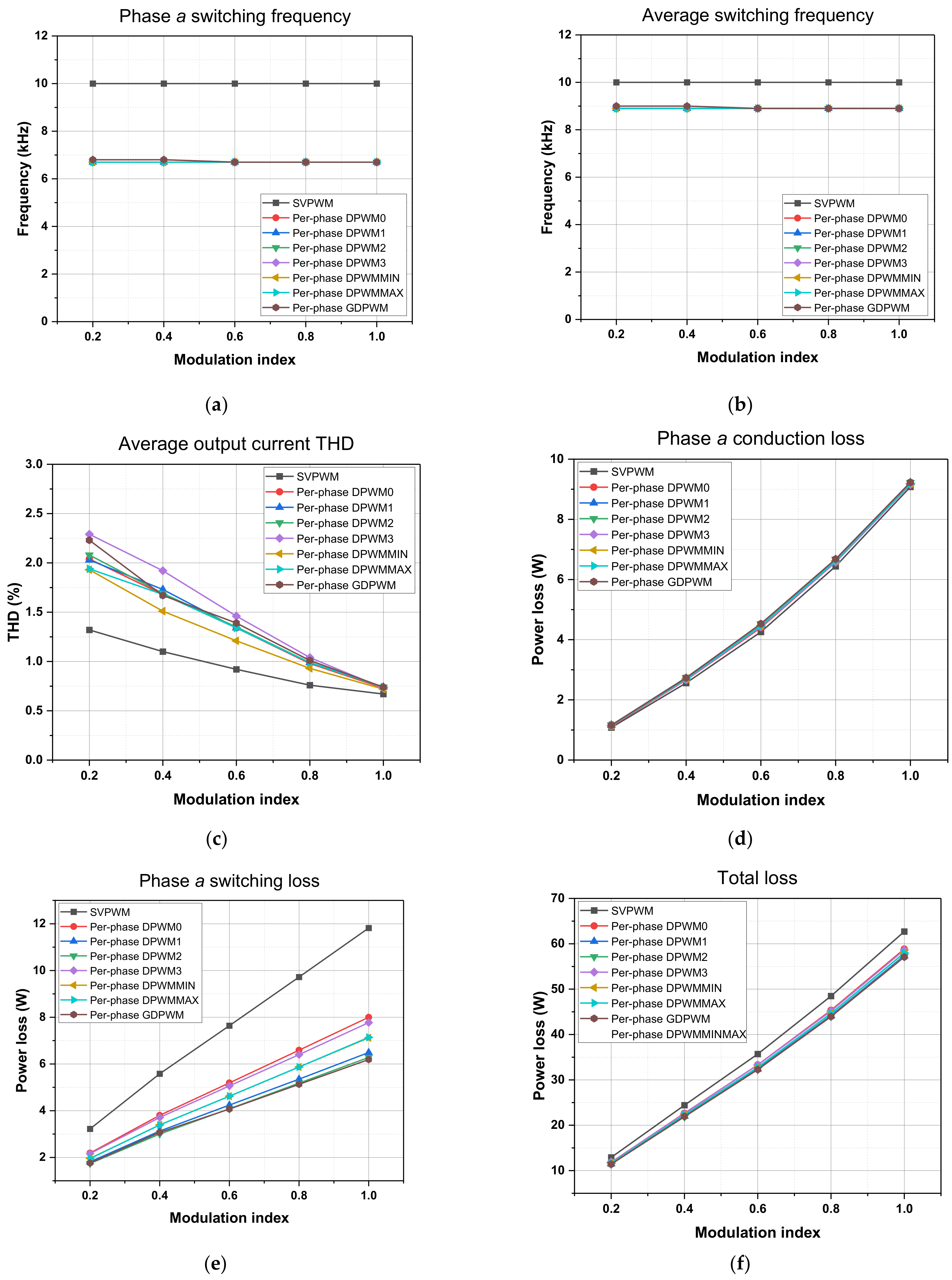
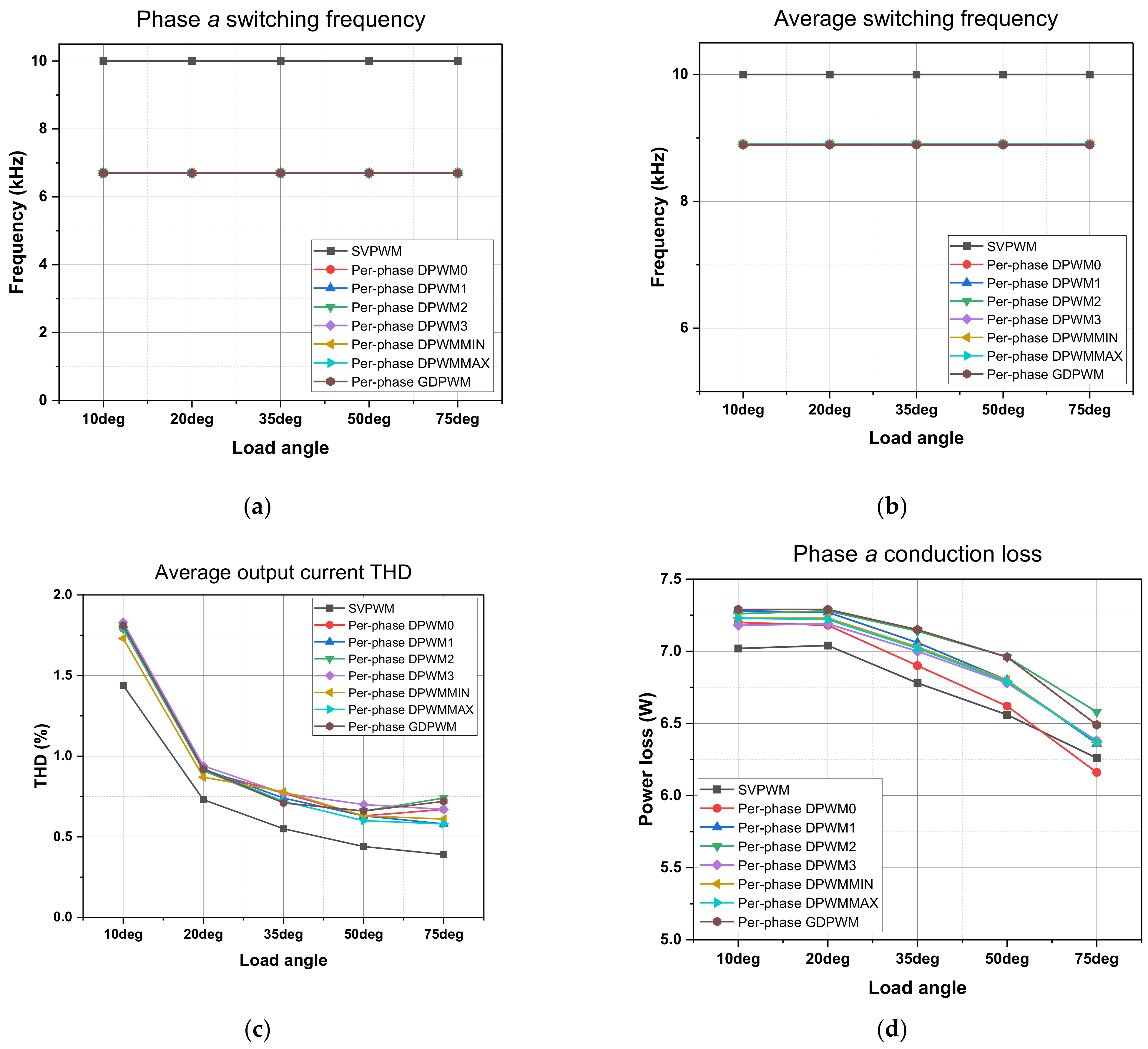
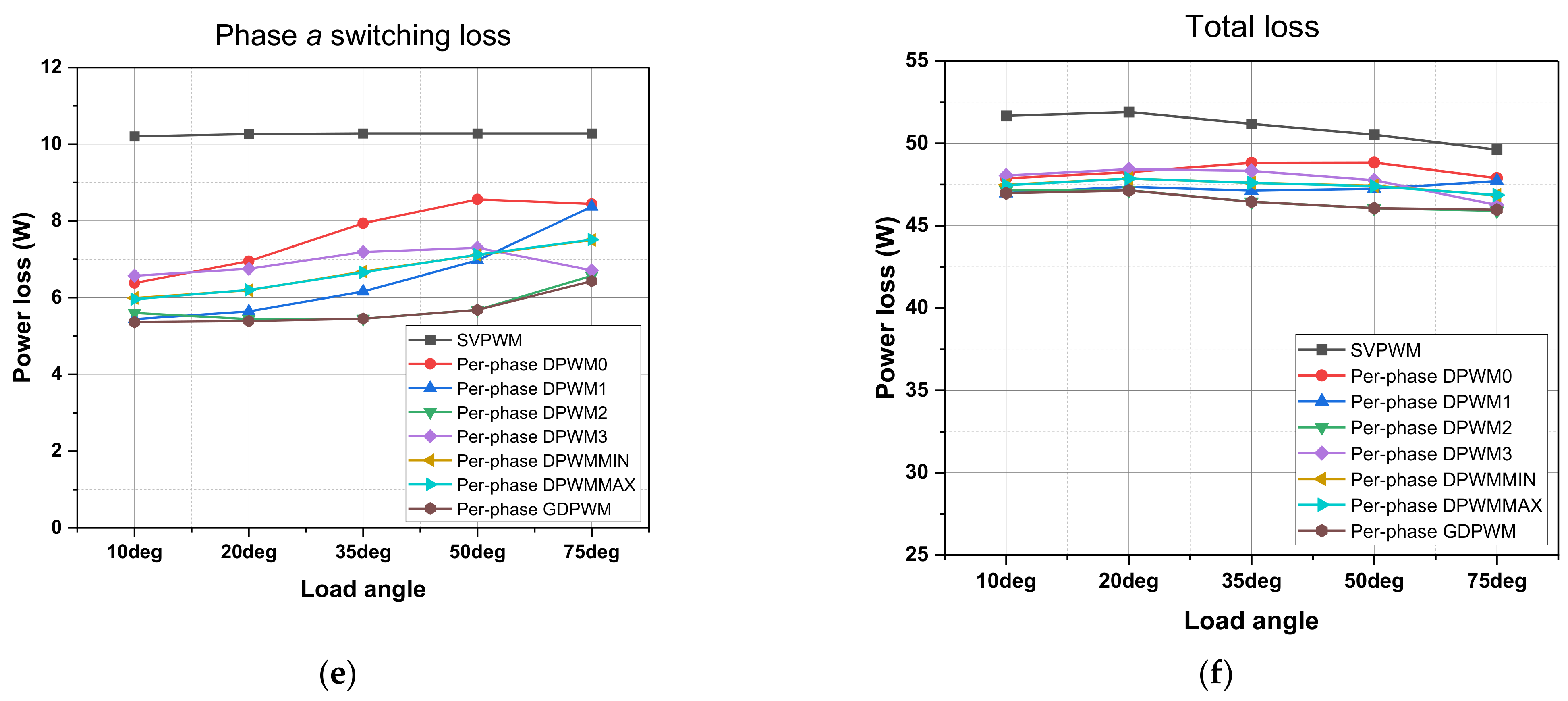
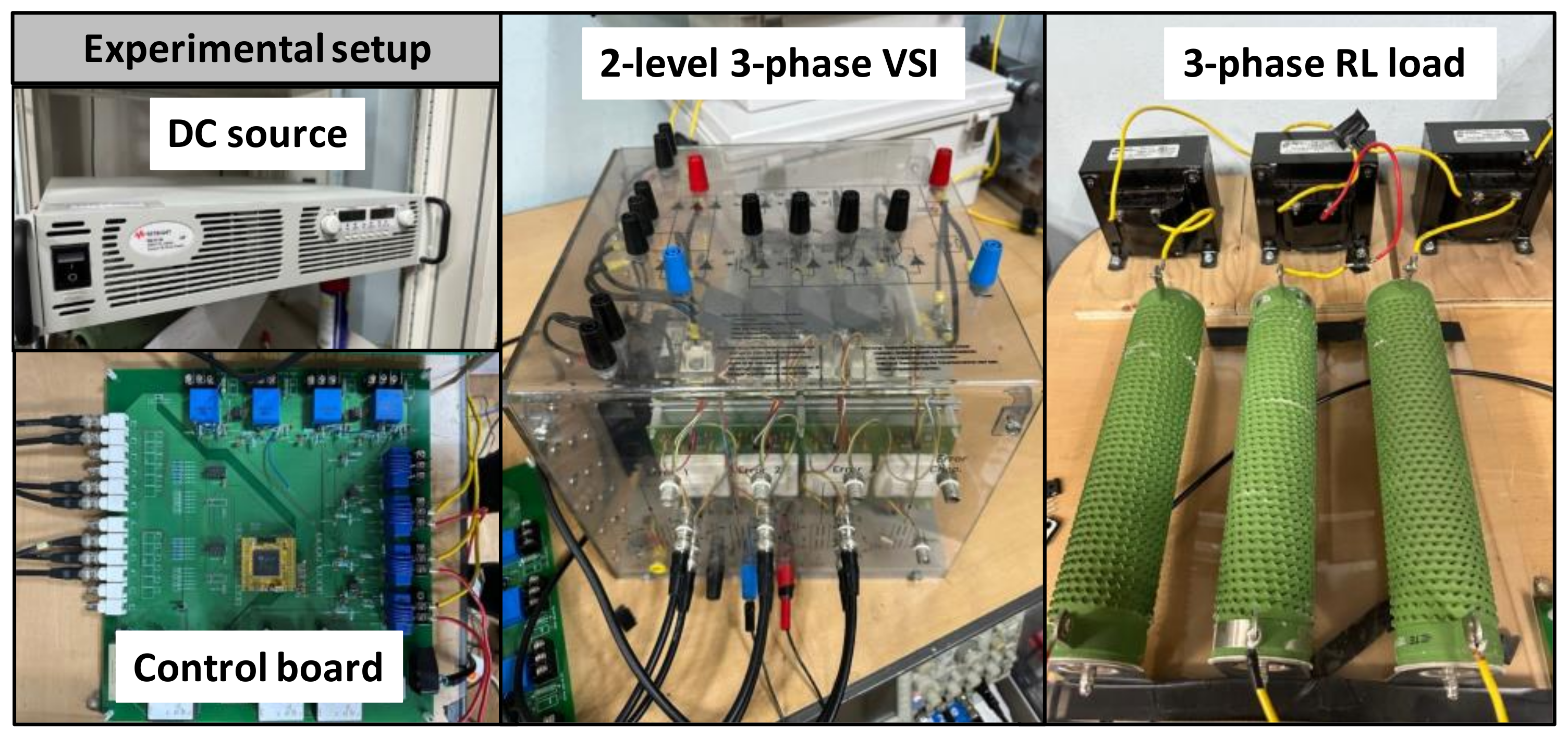
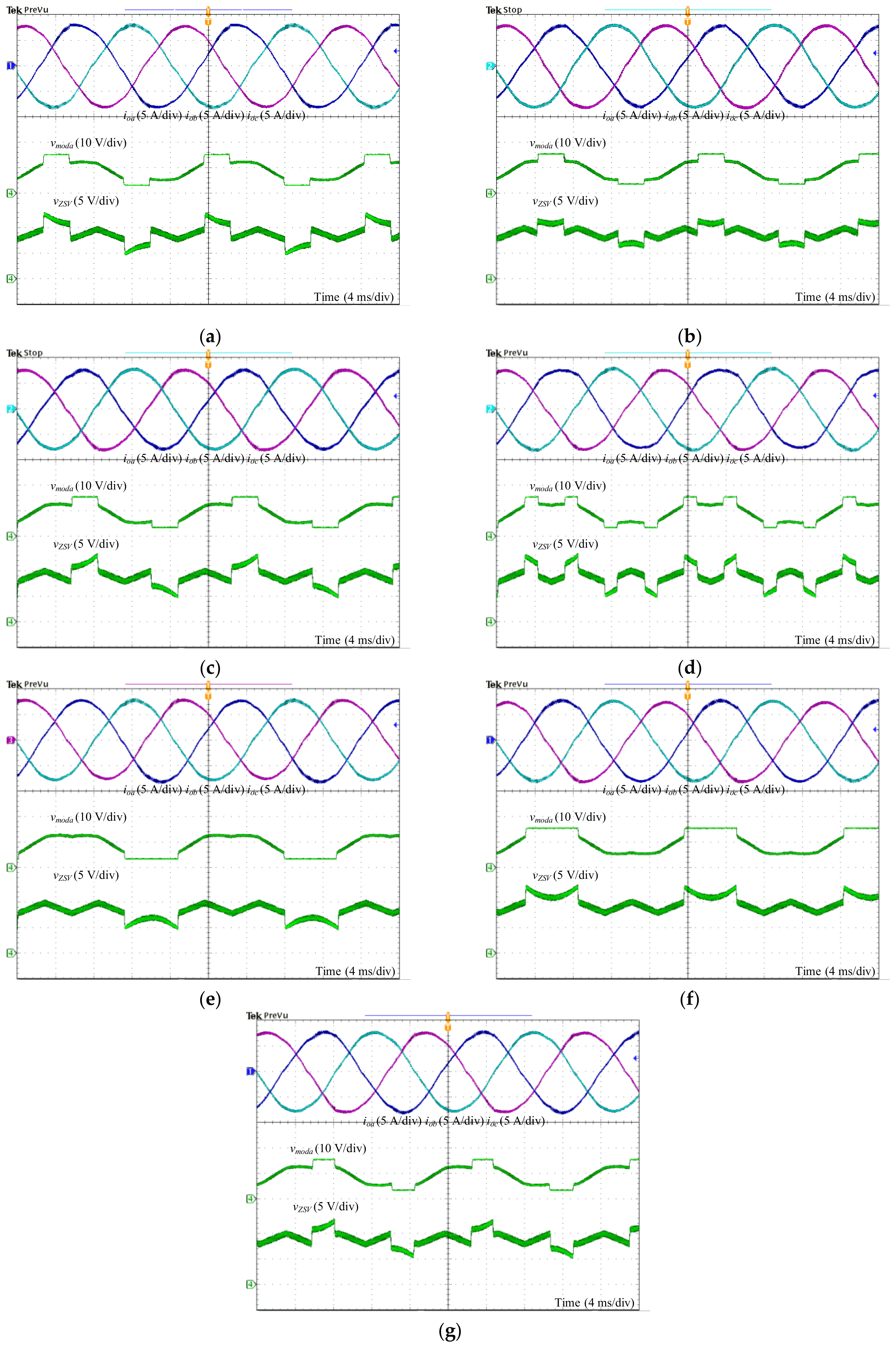
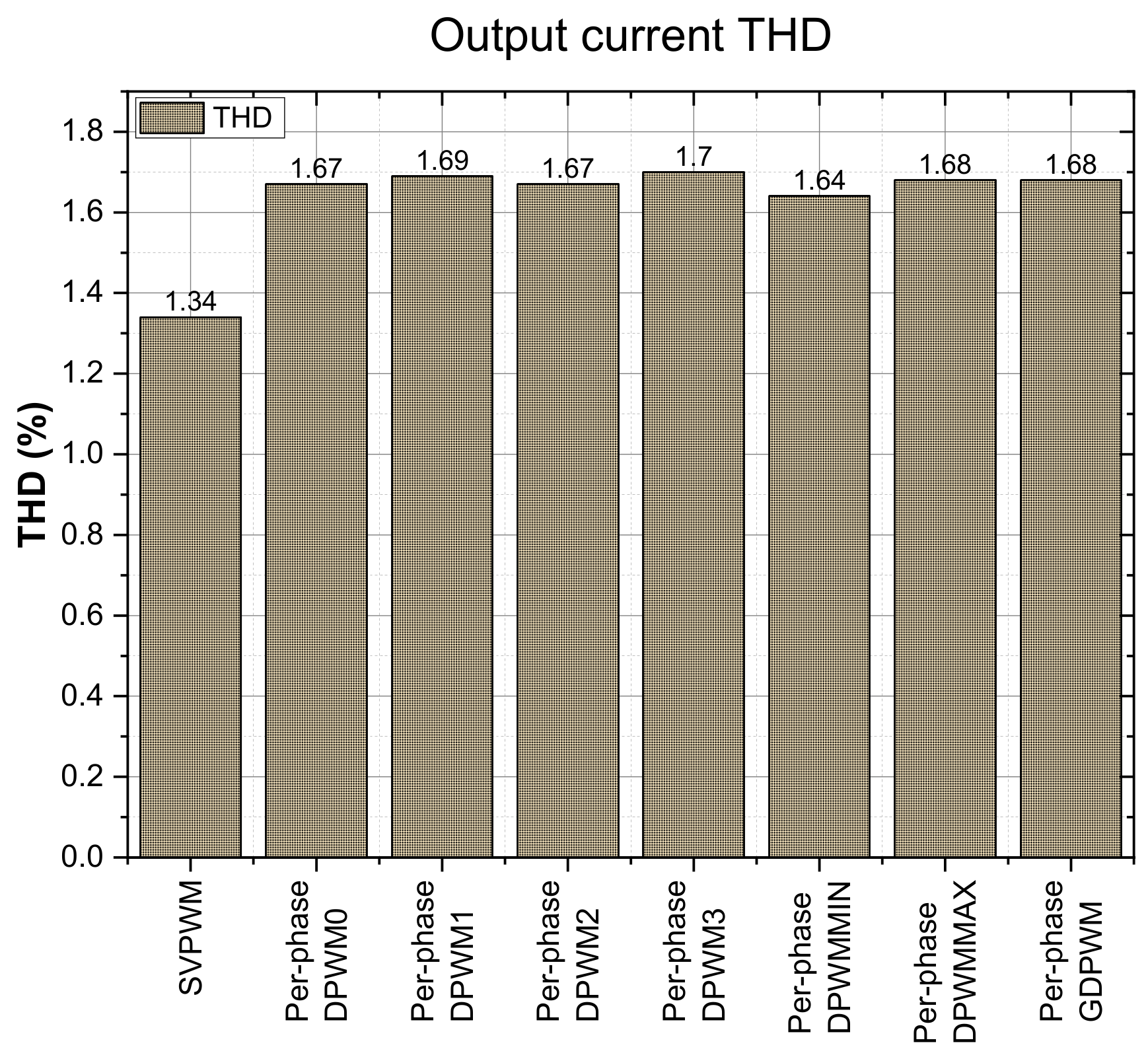
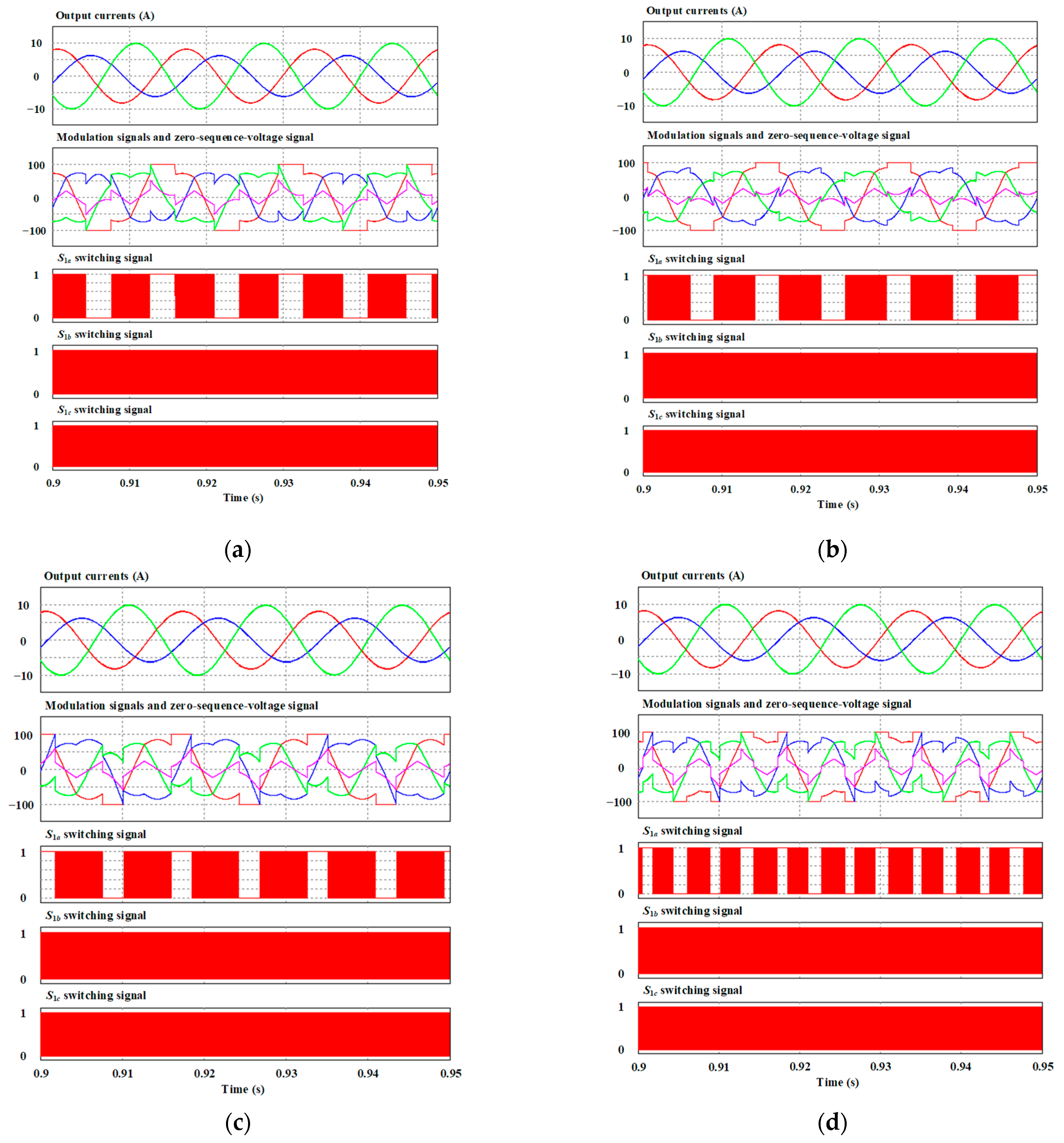
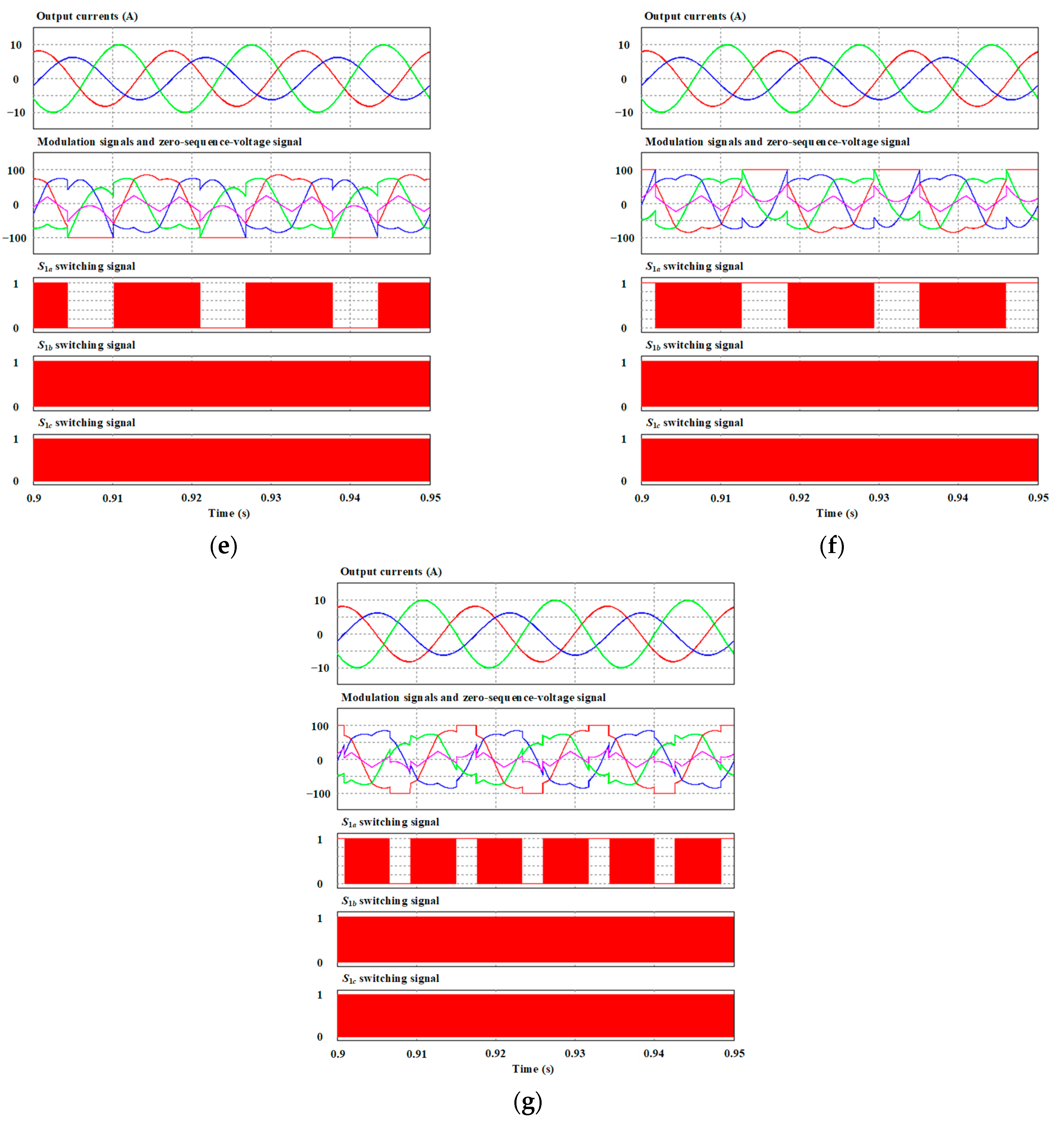
4. Verification and Evaluation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2L3P | 2-level 3-phase |
| VSI | Voltage source inverter |
| THD | Total harmonic distortion |
| CPWM | Continuous pulse-width-modulation |
| DPWM | Discontinuous pulse-width-modulation |
| SPWM | Sinusoidal pulse-width-modulation |
| SVPWM | Space vector pulse-width-modulation |
| CBPWM | Carrier-based pulse-width modulation |
| GDPWM | Generalized discontinuous pulse-width-modulation |
References
- Falck, J.; Felgemacher, C.; Rojko, A.; Liserre, M.; Zacharias, P. Reliability of Power Electronic Systems: An Industry Perspective. IEEE Ind. Electron. Mag. 2018, 12, 24–35. [Google Scholar] [CrossRef]
- Wang, H.; Liserre, M.; Blaabjerg, F. Toward Reliable Power Electronics: Challenges, Design Tools, and Opportunities. IEEE Ind. Electron. Mag. 2013, 7, 17–26. [Google Scholar] [CrossRef]
- Wang, H.; Liserre, M.; Blaabjerg, F.; Rimmen, P.d.P.; Jacobsen, J.B.; Kvisgaard, T.; Landkildehus, J. Transitioning to Physics-of-Failure as a Reliability Driver in Power Electronics. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 97–114. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An industry-based survey of reliability in power electronic converters. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3151–3157. [Google Scholar]
- Baker, N.; Liserre, M.; Dupont, L.; Avenas, Y. Improved Reliability of Power Modules: A Review of Online Junction Temperature Measurement Methods. IEEE Ind. Electron. Mag. 2014, 8, 17–27. [Google Scholar] [CrossRef]
- Held, M.; Jacob, P.; Nicoletti, G.; Scacco, P.; Poech, M.H. Fast power cycling test of IGBT modules in traction application. In Proceedings of the Second International Conference on Power Electronics and Drive Systems, Singapore, 26–29 May 1997; Volume 421, pp. 425–430. [Google Scholar]
- Sathik, M.; Jet, T.K.; Gajanayake, C.J.; Simanjorang, R.; Gupta, A.K. Comparison of power cycling and thermal cycling effects on the thermal impedance degradation in IGBT modules. In Proceedings of the IECON 2015–41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 1170–1175. [Google Scholar]
- Moeini, R.; Tricoli, P.; Hemida, H.; Baniotopoulos, C. Increasing the reliability of wind turbines using condition monitoring of semiconductor devices: A review. In Proceedings of the 5th IET International Conference on Renewable Power Generation (RPG) 2016, London, UK, 21–23 September 2016; pp. 1–6. [Google Scholar]
- Andresen, M.; Ma, K.; Buticchi, G.; Falck, J.; Blaabjerg, F.; Liserre, M. Junction Temperature Control for More Reliable Power Electronics. IEEE Trans. Power Electron. 2018, 33, 765–776. [Google Scholar] [CrossRef]
- Chen, G.; Cai, X. Adaptive Control Strategy for Improving the Efficiency and Reliability of Parallel Wind Power Converters by Optimizing Power Allocation. IEEE Access 2018, 6, 6138–6148. [Google Scholar] [CrossRef]
- Peyghami, S.; Davari, P.; Blaabjerg, F. System-Level Reliability-Oriented Power Sharing Strategy for DC Power Systems. IEEE Trans. Ind. Appl. 2019, 55, 4865–4875. [Google Scholar] [CrossRef]
- Song, Y.; Wang, B. Evaluation Methodology and Control Strategies for Improving Reliability of HEV Power Electronic System. IEEE Trans. Veh. Technol. 2014, 63, 3661–3676. [Google Scholar] [CrossRef]
- Andresen, M.; Buticchi, G.; Falck, J.; Liserre, M.; Muehlfeld, O. Active thermal management for a single-phase H-Bridge inverter employing switching frequency control. In Proceedings of the PCIM Europe 2015 International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 19–20 May 2015; pp. 1–8. [Google Scholar]
- Wei, L.; McGuire, J.; Lukaszewski, R.A. Analysis of PWM Frequency Control to Improve the Lifetime of PWM Inverter. IEEE Trans. Ind. Appl. 2011, 47, 922–929. [Google Scholar] [CrossRef]
- Ko, Y.; Andresen, M.; Buticchi, G.; Liserre, M. Discontinuous-Modulation-Based Active Thermal Control of Power Electronic Modules in Wind Farms. IEEE Trans. Power Electron. 2019, 34, 301–310. [Google Scholar] [CrossRef]
- Kaczorowski, D.; Mittelstedt, M.; Mertens, A. Investigation of discontinuous PWM as additional optimization parameter in an active thermal control. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar]
- Valentine, N.; Das, D.; Sood Phd, B.; Pecht, M. Failure Analyses of Modern Power Semiconductor Switching Devices. Int. Symp. Microelectron. 2015, 2015, 000690–000695. [Google Scholar] [CrossRef]
- Sintamarean, C.; Wang, H.; Blaabjerg, F.; Iannuzzo, F. The impact of gate-driver parameters variation and device degradation in the PV-inverter lifetime. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 2257–2264. [Google Scholar]
- Liang, W.; Castellazzi, A. Temperature adaptive driving of power semiconductor devices. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 1110–1114. [Google Scholar]
- Minh Hoang, N.; Sangshin, K. Active Thermal Control Algorithm with Independent Power Control Based on Three-phase Four-wire Converter. Trans. Korean Inst. Electr. Eng. 2022, 71, 967–978. [Google Scholar] [CrossRef]
- Kim, J.; Nguyen, M.-H.; Kwak, S.; Choi, S. Lifetime Extension Method for Three-Phase Voltage Source Converters Using Discontinuous PWM Scheme with Hybrid Offset Voltage. Machines 2023, 11, 612. [Google Scholar] [CrossRef]
- Nguyen, M.-H.; Kwak, S.; Choi, S. Individual Loss Reduction Technique for Each Phase in Three-Phase Voltage Source Rectifier Based on Carrier-Based Pulse-Width Modulation. J. Electr. Eng. Technol. 2023, 1–10. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Simple analytical and graphical methods for carrier-based PWM-VSI drives. IEEE Trans. Power Electron. 1999, 14, 49–61. [Google Scholar] [CrossRef]
- Keliang, Z.; Danwei, W. Relationship between space-vector modulation and three-phase carrier-based PWM: A comprehensive analysis [three-phase inverters]. IEEE Trans. Ind. Electron. 2002, 49, 186–196. [Google Scholar] [CrossRef]
- Ojo, O. The generalized discontinuous PWM scheme for three-phase voltage source inverters. IEEE Trans. Ind. Electron. 2004, 51, 1280–1289. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. A high-performance generalized discontinuous PWM algorithm. IEEE Trans. Ind. Appl. 1998, 34, 1059–1071. [Google Scholar] [CrossRef]
- Kolar, J.W.; Ertl, H.; Zach, F.C. Influence of the modulation method on the conduction and switching losses of a PWM converter system. In Proceedings of the Conference Record of the 1990 IEEE Industry Applications Society Annual Meeting, Seattle, WA, USA, 7–12 October 1990; Volume 501, pp. 502–512. [Google Scholar]
- Ogasawara, S.; Akagi, H.; Nabae, A. A novel PWM scheme of voltage source inverters based on space vector theory. Arch. Für Elektrotechnik 1990, 74, 33–41. [Google Scholar] [CrossRef]
- Taniguchi, K.; Ogino, Y.; Irie, H. PWM technique for power MOSFET inverter. IEEE Trans. Power Electron. 1988, 3, 328–334. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Rodriguez, P.; Blaabjerg, F.; Malinowski, M. Reduction of Switching Losses in Active Power Filters with a New Generalized Discontinuous-PWM Strategy. IEEE Trans. Ind. Electron. 2008, 55, 467–471. [Google Scholar] [CrossRef]


| SVPWM | 0.5 | x |
| DPWM0 | ||
| DPWM1 | ||
| DPWM2 | ||
| DPWM3 | ||
| DPWMMIN | 1 | x |
| DPWMMAX | 0 | x |
| Parameter | Value |
|---|---|
| (V) | 200 |
| dc-link capacitance (μF) | 680 |
| (Ω) | 10 |
| (mH) | 10 |
| Carrier frequency (kHz) | 10 |
| Fundamental frequency (Hz) | 60 |
| P gain | 5 |
| I gain | 100 |
| Sampling frequency (kHz) | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, M.H.; Kwak, S.; Choi, S. Development of Various Types of Independent Phase Based Pulsewidth Modulation Techniques for Three-Phase Voltage Source Inverters. Machines 2023, 11, 1054. https://doi.org/10.3390/machines11121054
Nguyen MH, Kwak S, Choi S. Development of Various Types of Independent Phase Based Pulsewidth Modulation Techniques for Three-Phase Voltage Source Inverters. Machines. 2023; 11(12):1054. https://doi.org/10.3390/machines11121054
Chicago/Turabian StyleNguyen, Minh Hoang, Sangshin Kwak, and Seungdeog Choi. 2023. "Development of Various Types of Independent Phase Based Pulsewidth Modulation Techniques for Three-Phase Voltage Source Inverters" Machines 11, no. 12: 1054. https://doi.org/10.3390/machines11121054
APA StyleNguyen, M. H., Kwak, S., & Choi, S. (2023). Development of Various Types of Independent Phase Based Pulsewidth Modulation Techniques for Three-Phase Voltage Source Inverters. Machines, 11(12), 1054. https://doi.org/10.3390/machines11121054







