The LESGIRgram: A New Method to Select the Optimal Demodulation Frequency Band for Rolling Bearing Faults
Abstract
:1. Introduction
2. Theoretical Background
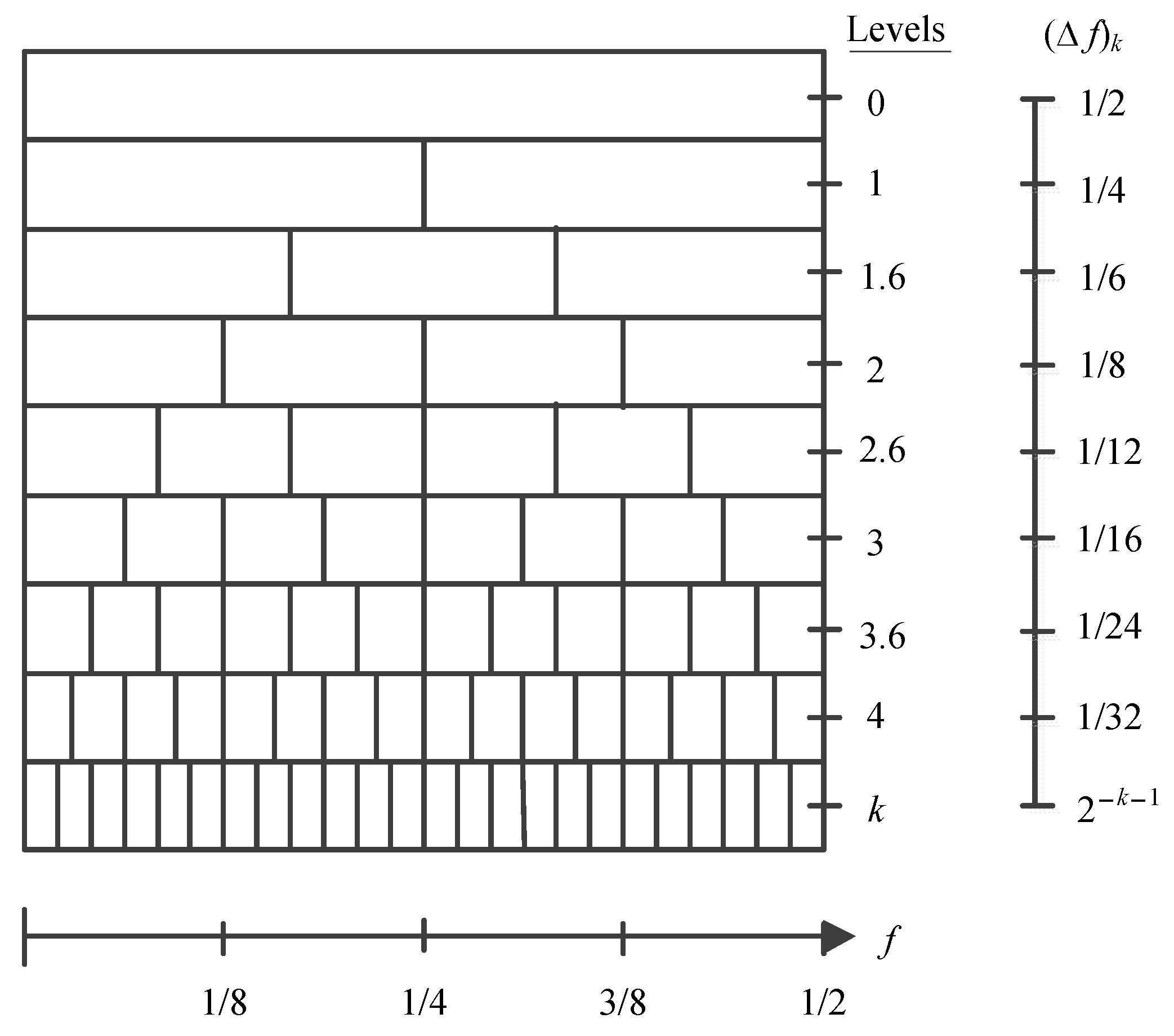
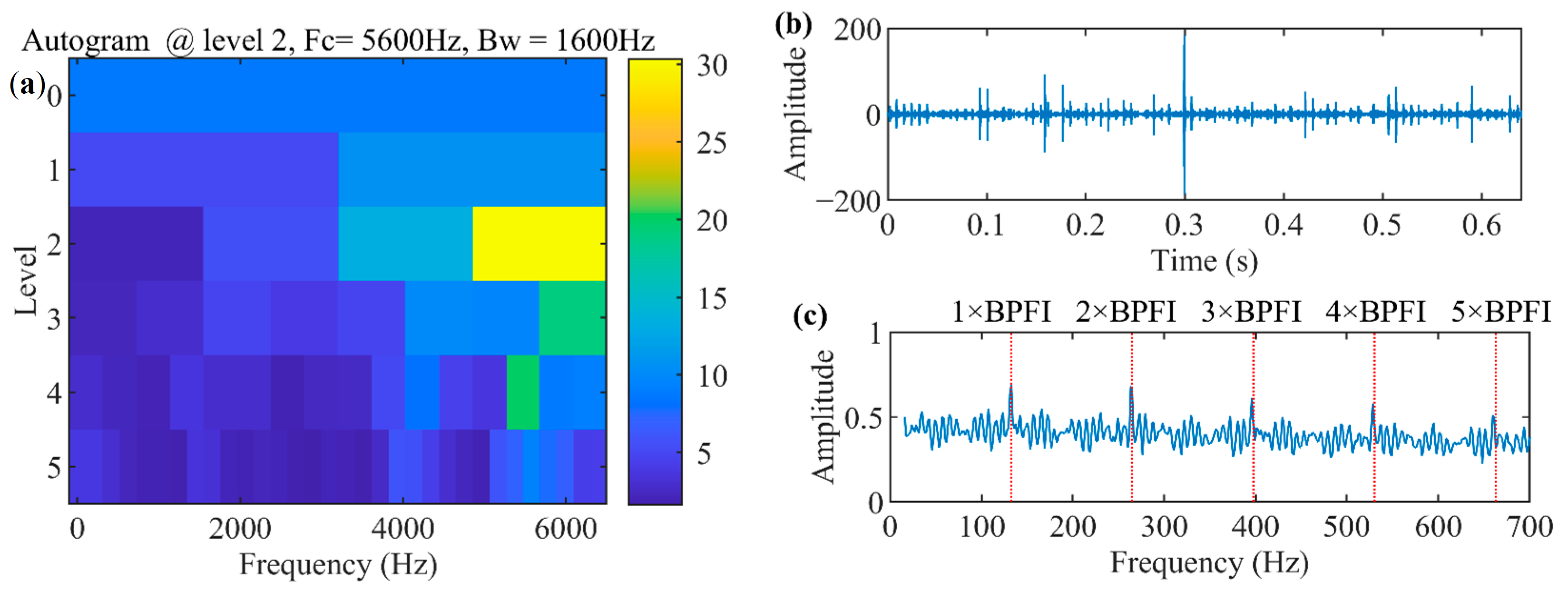
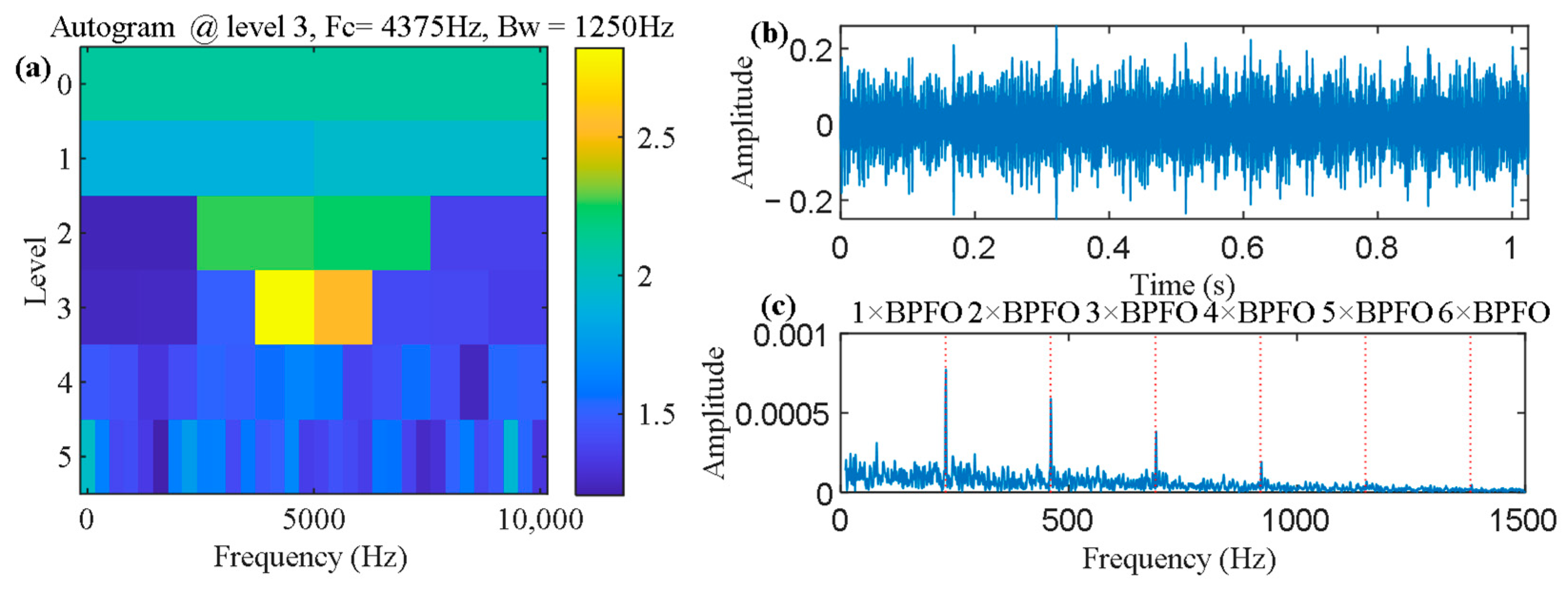
2.1. Fast Kurtogram and Autogram
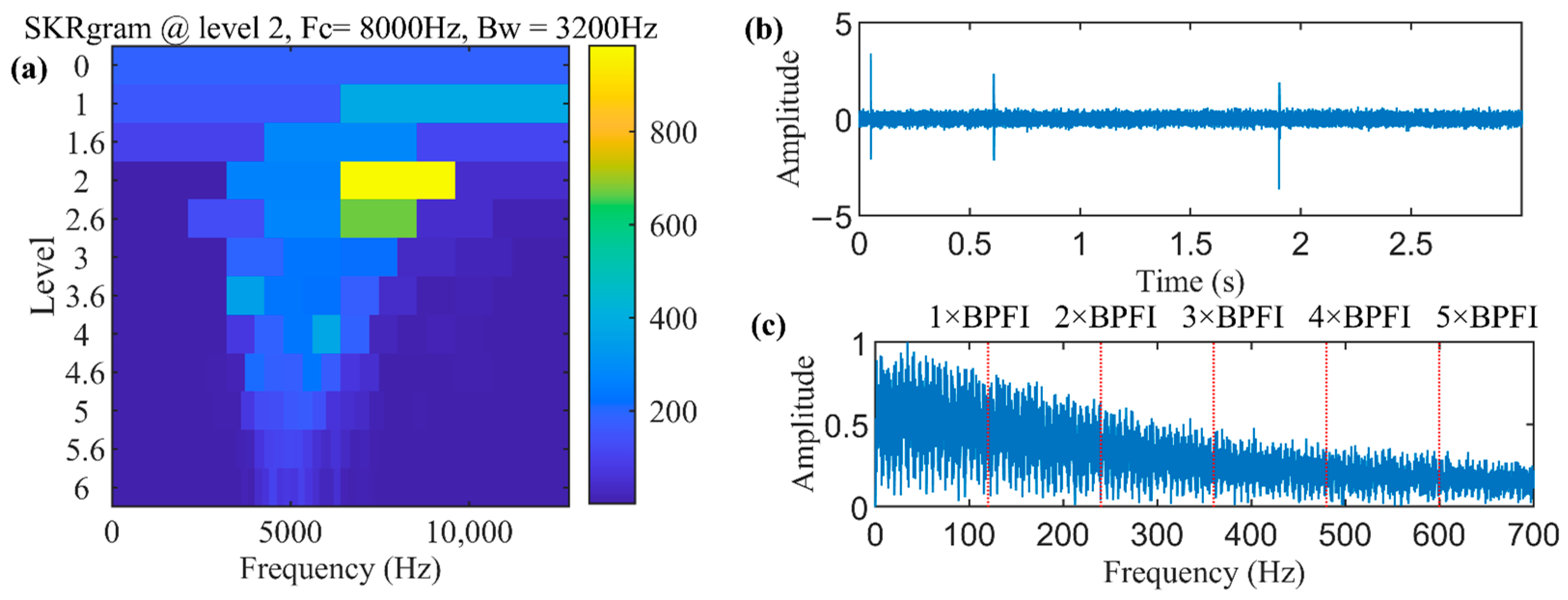
2.2. SKRgram
- Obtain the SK matrix of the health planetary gearbox as a baseline by using FK, named SKbaseline.
- Calculate the SK matrix of the measured signal using FK to obtain an SK matrix of the same size as the SKbaseline, labeled SKmeasured.
- Divide each value in the SKmeasured matrix by the corresponding value of SKbaseline to obtain the spectral kurtosis ratio matrix SKR.
- Represent the SKR matrix as a Kurtogram. In the SKRgram, the concentrated area with higher SKR values is the part where the planet bearing failure is prominent.
- Select the three most concentrated regions from the SKRgram, and then regard the corresponding regions in the Kurtogram of the measured signals as potential filtering regions.
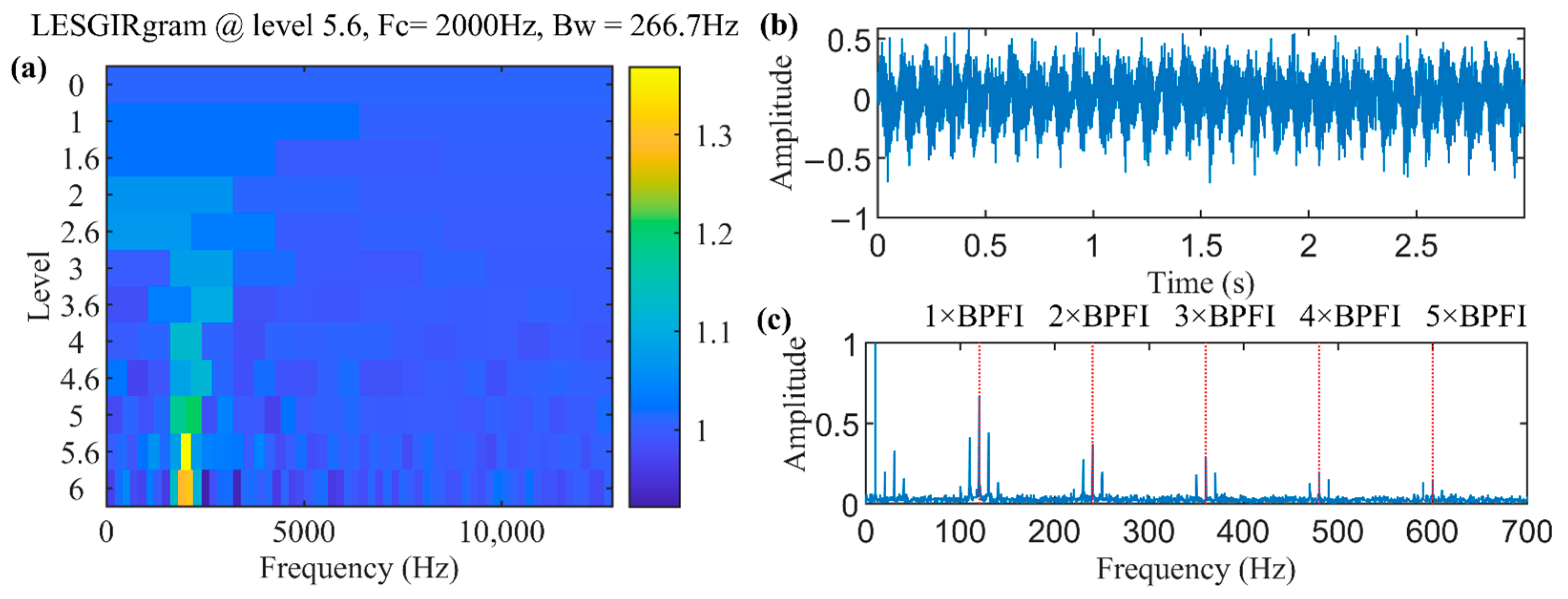
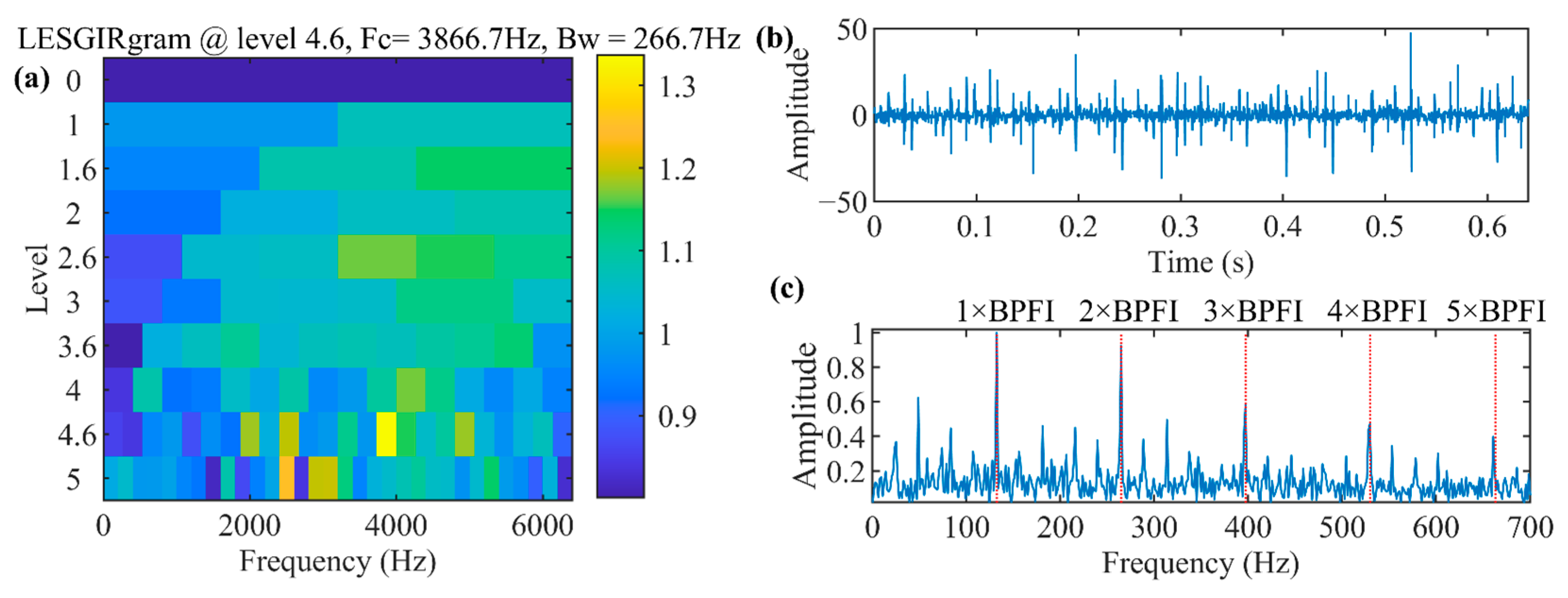
2.3. The Proposed Method: LESGIRgram
3. Simulation Evaluation
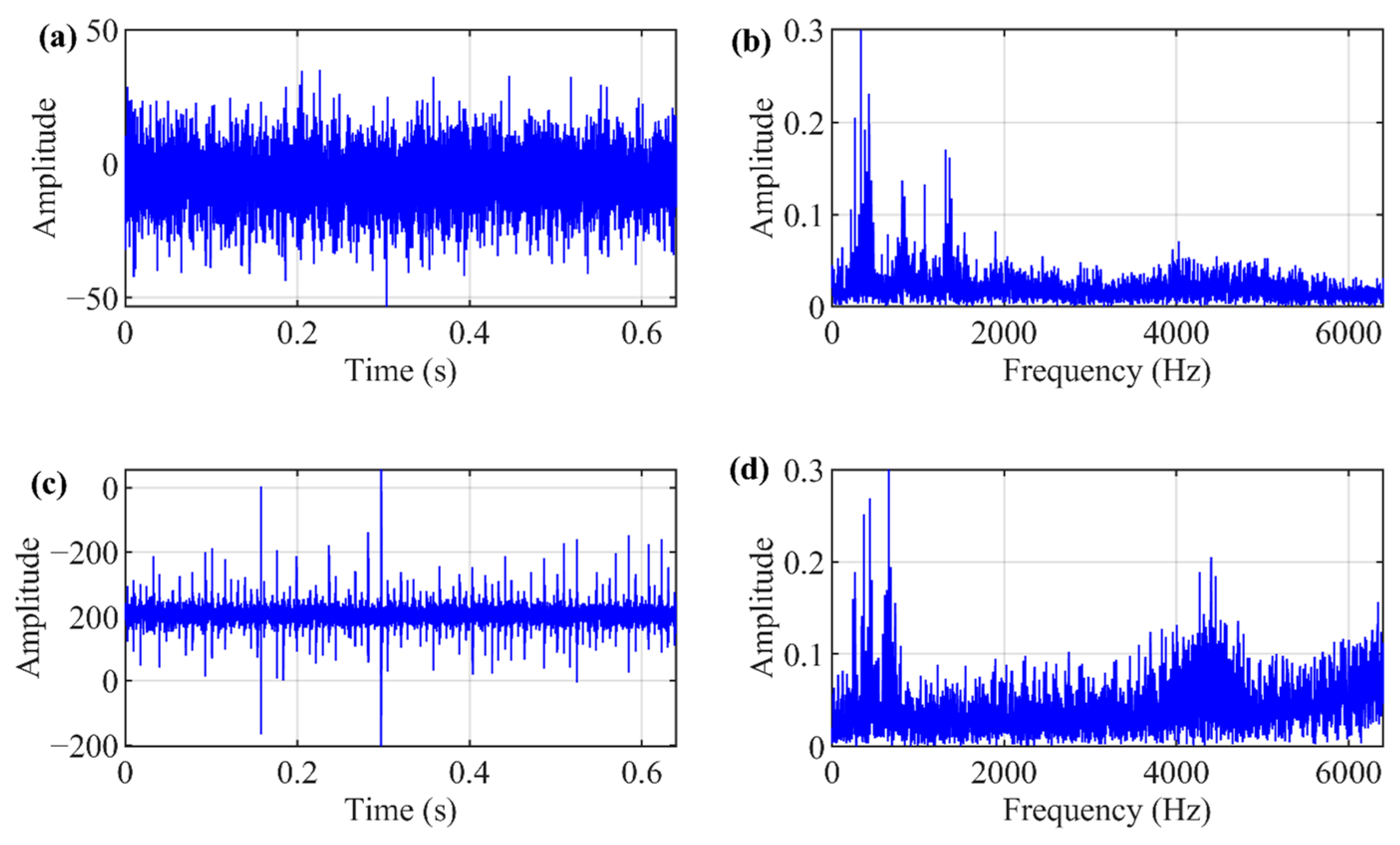
3.1. Simulation Model of Bearing Failure Data
3.2. Results on Simulated Bearing Inner Fault Signal
3.3. Results on Simulated Bearing Inner Fault Signals under Various Conditions
3.3.1. Results on Bearing Inner Fault Signals with Different GAUSSIAN White Noise Levels
3.3.2. Results on Bearing Inner Fault Signals with Different Amplitude of Harmonic Interference
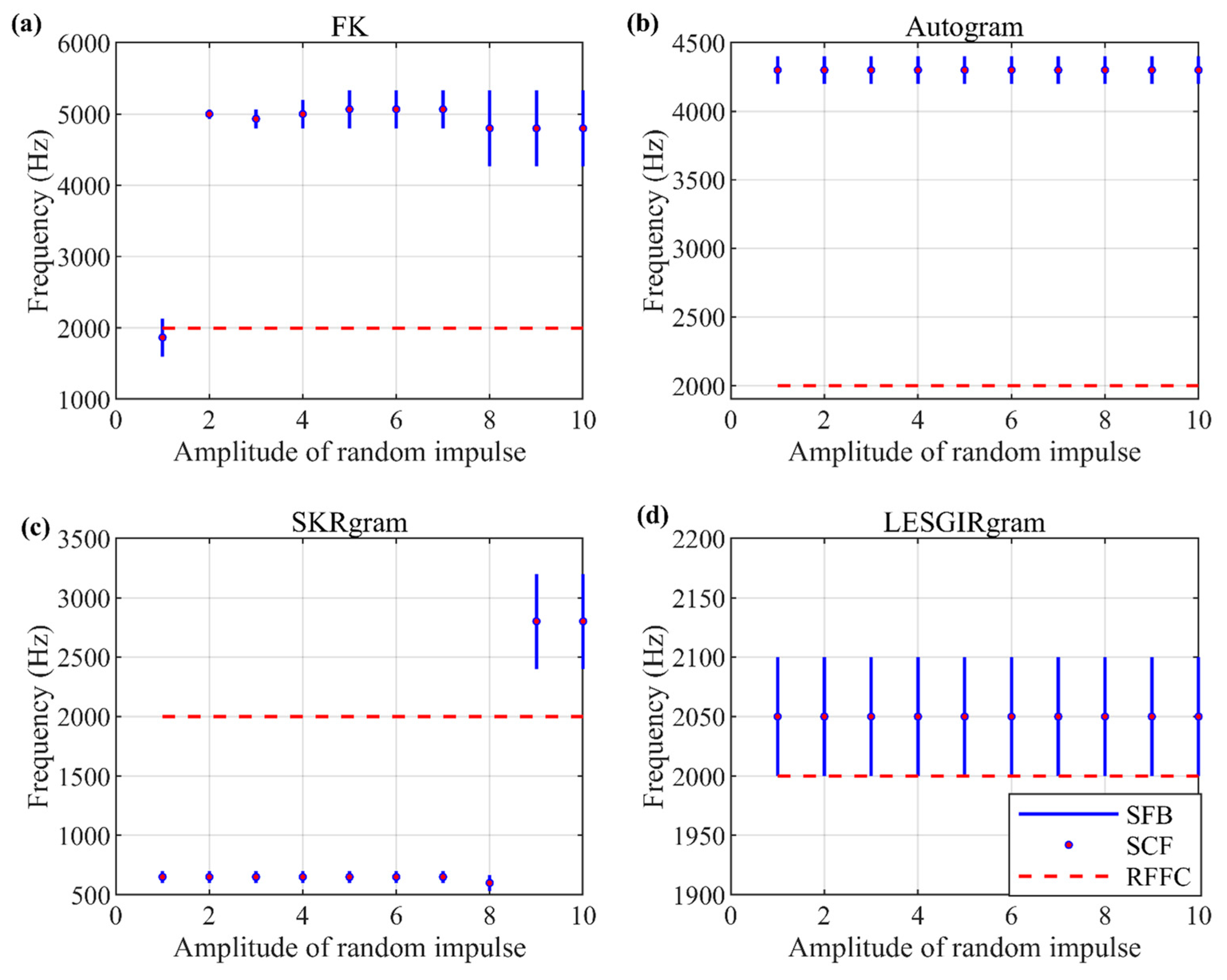
3.3.3. Results on Bearing Inner Fault Signals with Different Amplitude of Random Impulse
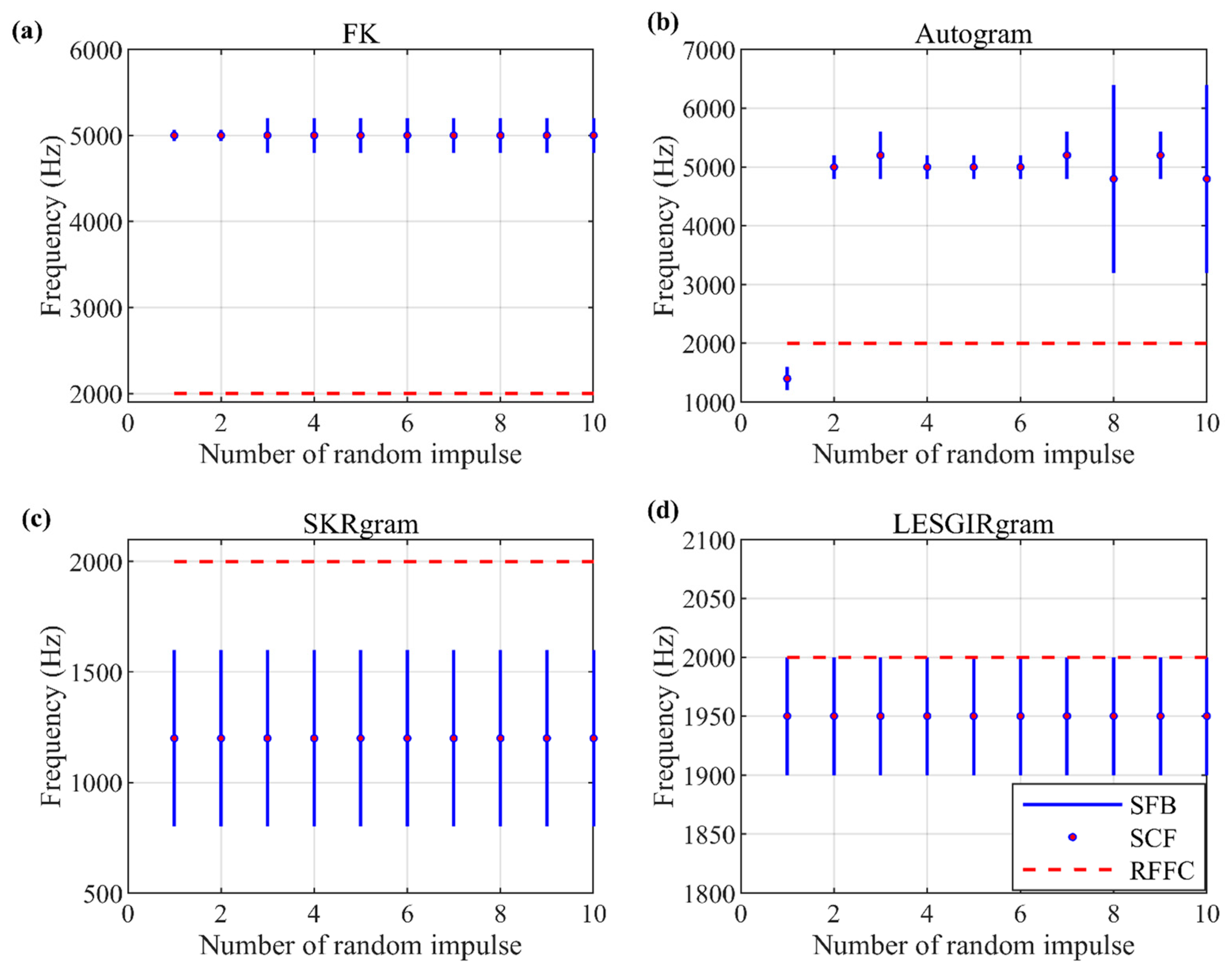
3.3.4. Results on Bearing Inner Fault Signals with Different Number of Random Impulses
3.4. Summary of Comparison Results on Simulated Signals
4. Experimental Evaluation
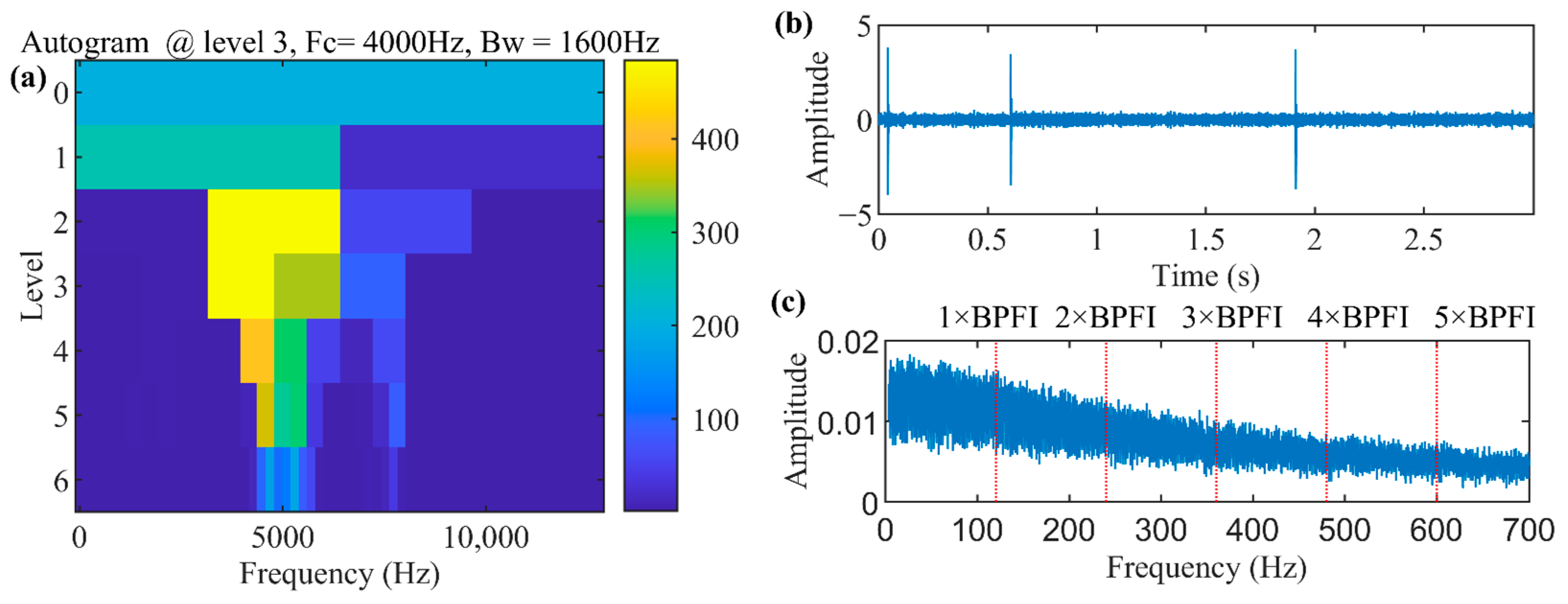
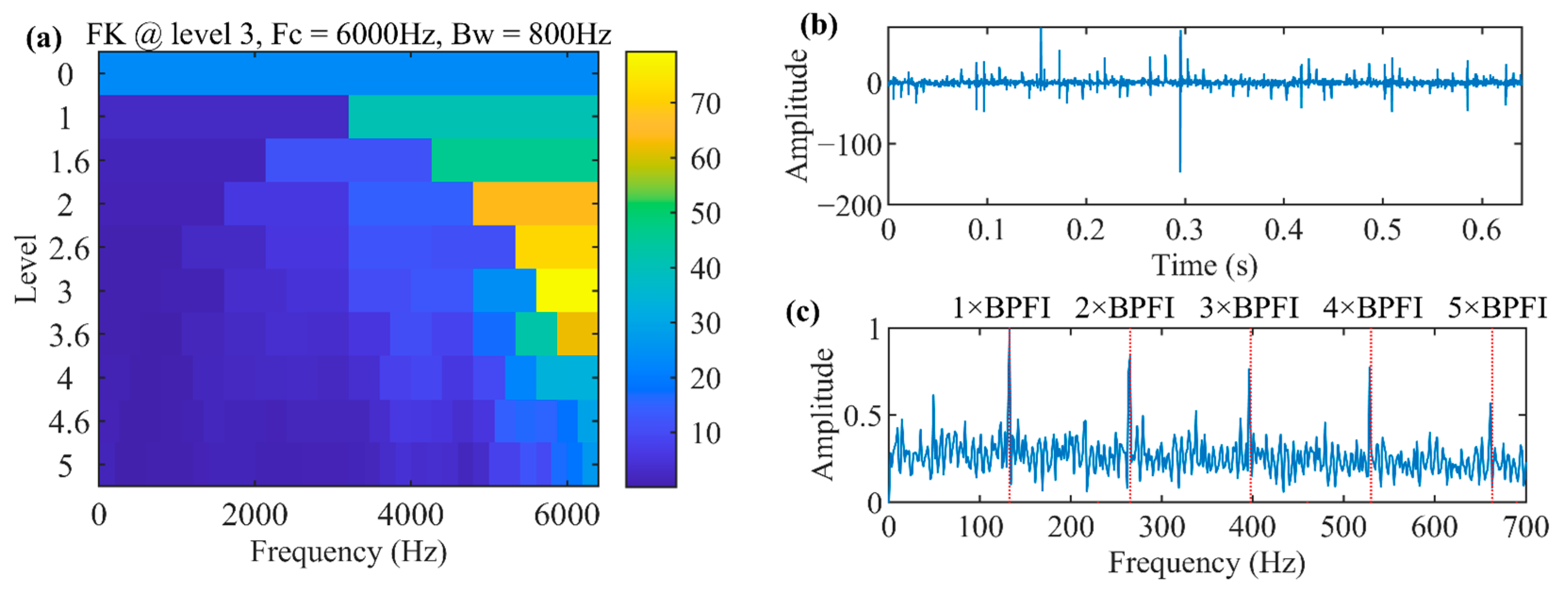
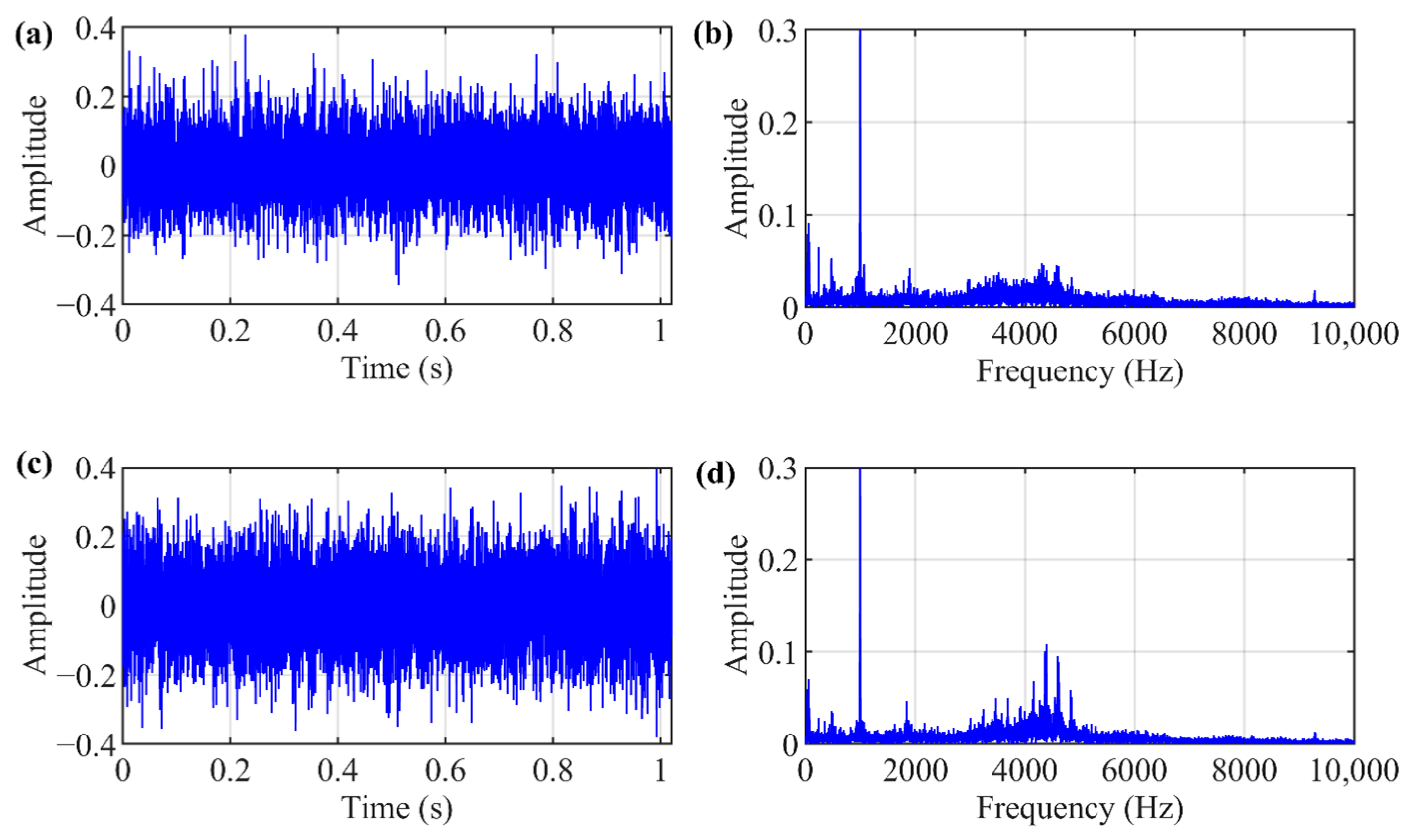
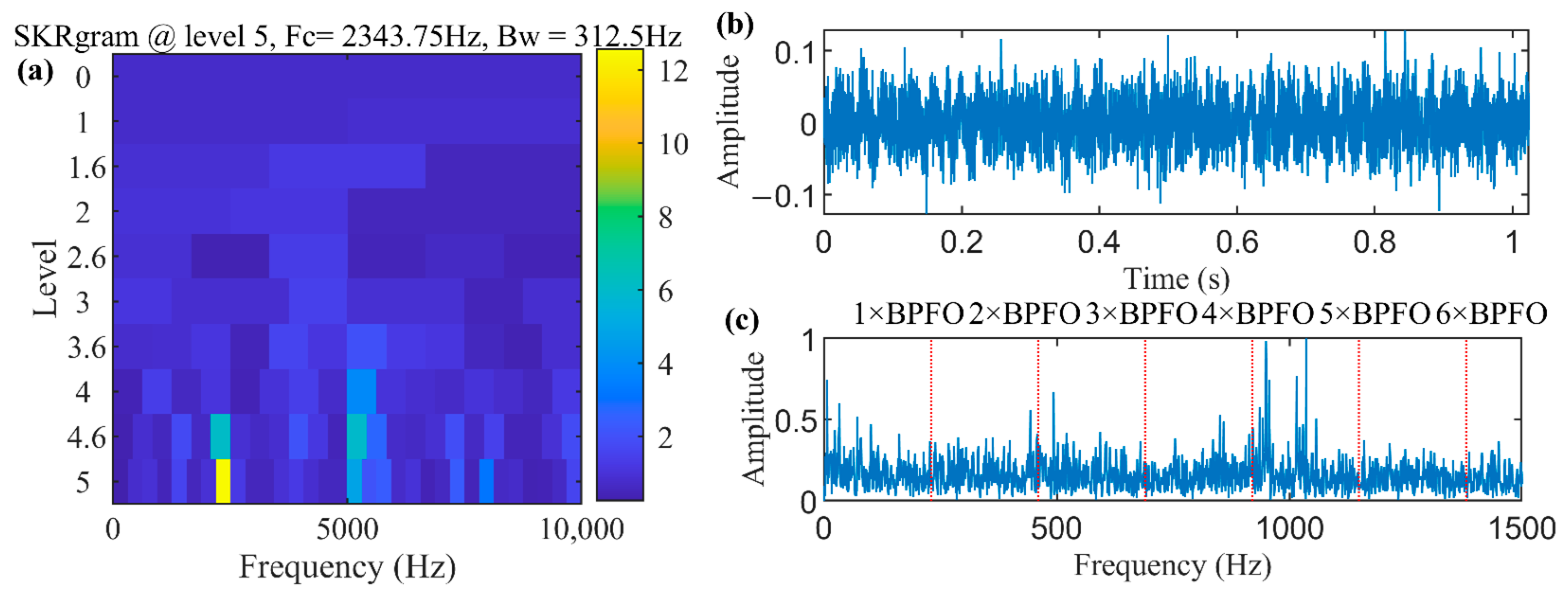
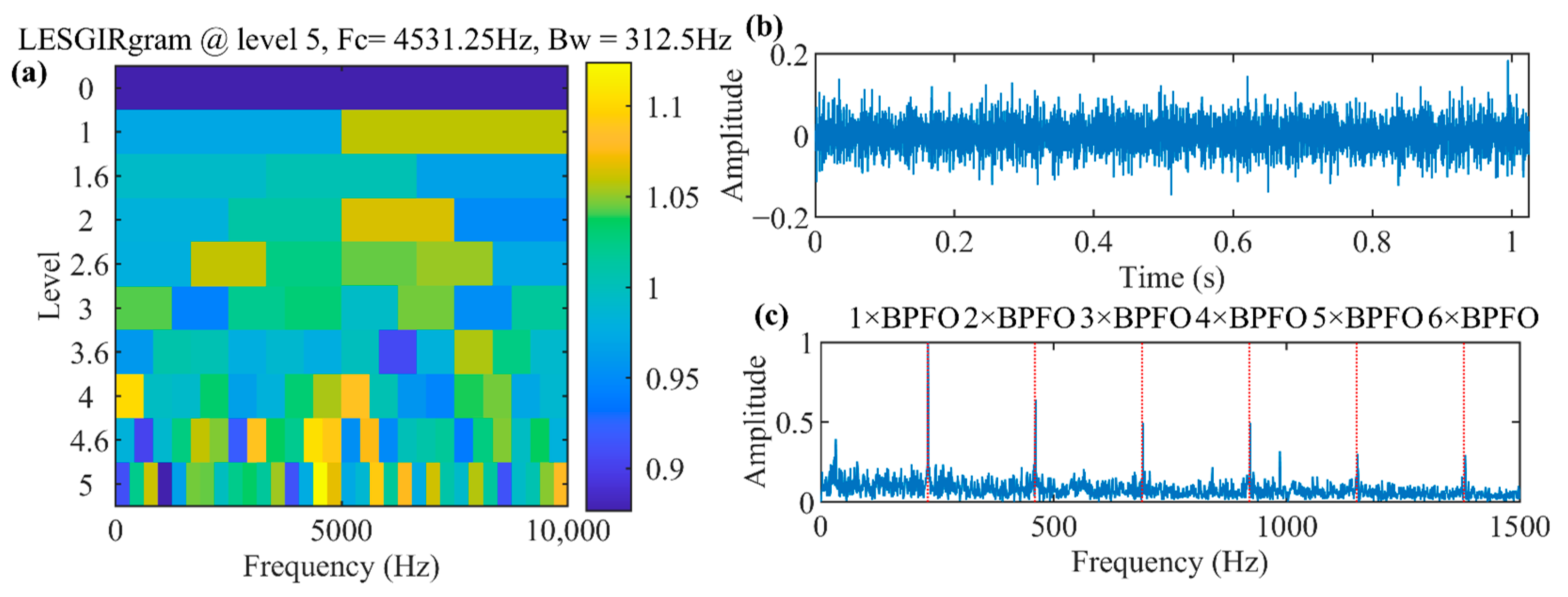
4.1. Rolling Bearing Inner Race Defect Detection of QPZZ Test Bench Bearing Dataset
4.2. Rolling Bearing Outer Race Defect Detection from IMS Bearing Dataset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Huang, D.; Zhou, D.; Liu, H. Optimal IMF Selection and Unknown Fault Feature Extraction for Rolling Bearings with Different Defect Modes. Measurement 2020, 157, 107660. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, K.; Xiang, L.; Xu, Y. Differential Spectral Amplitude Modulation and Its Applications in Rolling Bearing Fault Diagnosis. Measurement 2022, 201, 111755. [Google Scholar] [CrossRef]
- Dwyer, R.F. A Technique for Improving Detection and Estimation of Signals Contaminated by under Ice Noise. J. Acoust. Soc.Am. 1983, 74, 124–130. [Google Scholar] [CrossRef]
- Antoni, J. The Spectral Kurtosis: A Useful Tool for Characterising Non-Stationary Signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. The Spectral Kurtosis: Application to the Vibratory Surveillance and Diagnostics of Rotating Machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Antoni, J. Fast Computation of the Kurtogram for the Detection of Transient Faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an Improved Kurtogram Method for Fault Diagnosis of Rolling Element Bearings. Mech. Syst. Signal Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Tsui, K.L. An Enhanced Kurtogram Method for Fault Diagnosis of Rolling Element Bearings. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Barszcz, T.; JabŁoński, A. A Novel Method for the Optimal Band Selection for Vibration Signal Demodulation and Comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The Autogram: An Effective Approach for Selecting the Optimal Demodulation Band in Rolling Element Bearings Diagnosis. Mech. Syst. Signal Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Antoni, J. The Infogram: Entropic Evidence of the Signature of Repetitive Transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Liao, Z.; Song, L.; Chen, P. A Novel Fast Entrogram and Its Applications in Rolling Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2021, 154, 107582. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, J.; Zhang, J. A Novel Optimal Demodulation Frequency Band Extraction Method of Fault Bearing Based on Power Spectrum Screening Combination-Gram. Mech. Syst. Signal Process. 2022, 174, 109104. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Z.; Wang, J.; Han, B.; Bao, H.; Liu, Z.; Li, S. Fast Nonlinear Hoyergram for Bearings Fault Diagnosis under Random Impact Interference. Meas. Sci. Technol. 2022, 33, 075112. [Google Scholar] [CrossRef]
- Liang, L.; Liu, C.; Wang, J. Periodicity Measure of Cyclo-Stationary Impulses Based on Low Sparsity of Gini Index and Its Application to Bearing Diagnosis. ISA Trans. 2023, 138, 611–627. [Google Scholar] [CrossRef]
- Wang, T.; Han, Q.; Chu, F.; Feng, Z. A New SKRgram Based Demodulation Technique for Planet Bearing Fault Detection. J. Sound Vib. 2016, 385, 330–349. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of Kurtosis-Guided-Grams via Gini Index for Bearing Fault Feature Identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Borghesani, P.; Antoni, J. CS2 Analysis in Presence of Non-Gaussian Background Noise—Effect on Traditional Estimators and Resilience of Log-Envelope Indicators. Mech. Syst. Signal Process. 2017, 90, 378–398. [Google Scholar] [CrossRef]
- Smith, W.A.; Borghesani, P.; Ni, Q.; Wang, K.; Peng, Z. Optimal Demodulation-Band Selection for Envelope-Based Diagnostics: A Comparative Study of Traditional and Novel Tools. Mech. Syst. Signal Process. 2019, 134, 106303. [Google Scholar] [CrossRef]
- Hurley, N.; Rickard, S. Comparing Measures of Sparsity. IEEE Trans. Inform. Theory 2009, 55, 4723–4741. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, W.; Gu, J.X.; Song, D.; Cheng, Y.; Zhou, Z.; Gu, F.; Ball, A.D. Product Envelope Spectrum Optimization-Gram: An Enhanced Envelope Analysis for Rolling Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2023, 193, 110270. [Google Scholar] [CrossRef]
- Chen, B.; Cheng, Y.; Zhang, W.; Gu, F. Enhanced Bearing Fault Diagnosis Using Integral Envelope Spectrum from Spectral Coherence Normalized with Feature Energy. Measurement 2022, 189, 110448. [Google Scholar] [CrossRef]
- Su, H.; Xiang, L.; Hu, A.; Xu, Y.; Yang, X. A Novel Method Based on Meta-Learning for Bearing Fault Diagnosis with Small Sample Learning under Different Working Conditions. Mech. Syst. Signal Process. 2022, 169, 108765. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet Filter-Based Weak Signature Detection Method and Its Application on Rolling Element Bearing Prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Hou, B.; Wang, D.; Wang, Y.; Yan, T.; Peng, Z.; Tsui, K.-L. Adaptive Weighted Signal Preprocessing Technique for Machine Health Monitoring. IEEE Trans. Instrum. Meas. 2021, 70, 3504411. [Google Scholar] [CrossRef]










| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Sampling frequency fs | 25.6 kHz | f1 | 10 Hz |
| duration | 3 s | φ1 | π/6 |
| M1 | 360 | B2 | 0.1 |
| fm | 120 Hz | f2 | 20 Hz |
| fr | 10 Hz | φ2 | −π/3 |
| fn1 | 2000 Hz | M3 | 3 |
| ξ1 | 0.02 | fn2 | 5000 Hz |
| M2 | 2 | ξ2 | 0.02 |
| B1 | 0.1 | SNR | −5 dB |
| Parameters | LYC6205E |
|---|---|
| Pitch diameter | 38.5 mm |
| Bearing width | 15 mm |
| Bearing roller diameter | 7.94 mm |
| The number of the roller | 9 |
| Contact angle | 0 rad |
| Inter-race defect | 1.5 × 0.2 mm |
| BPFI | 132.55 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, T.; Tang, G.; Wang, X. The LESGIRgram: A New Method to Select the Optimal Demodulation Frequency Band for Rolling Bearing Faults. Machines 2023, 11, 1052. https://doi.org/10.3390/machines11121052
Tian T, Tang G, Wang X. The LESGIRgram: A New Method to Select the Optimal Demodulation Frequency Band for Rolling Bearing Faults. Machines. 2023; 11(12):1052. https://doi.org/10.3390/machines11121052
Chicago/Turabian StyleTian, Tian, Guiji Tang, and Xiaolong Wang. 2023. "The LESGIRgram: A New Method to Select the Optimal Demodulation Frequency Band for Rolling Bearing Faults" Machines 11, no. 12: 1052. https://doi.org/10.3390/machines11121052
APA StyleTian, T., Tang, G., & Wang, X. (2023). The LESGIRgram: A New Method to Select the Optimal Demodulation Frequency Band for Rolling Bearing Faults. Machines, 11(12), 1052. https://doi.org/10.3390/machines11121052






