Efficient Navigation and Motion Control for Autonomous Forklifts in Smart Warehouses: LSPB Trajectory Planning and MPC Implementation
Abstract
:1. Introduction
2. Problem Statement
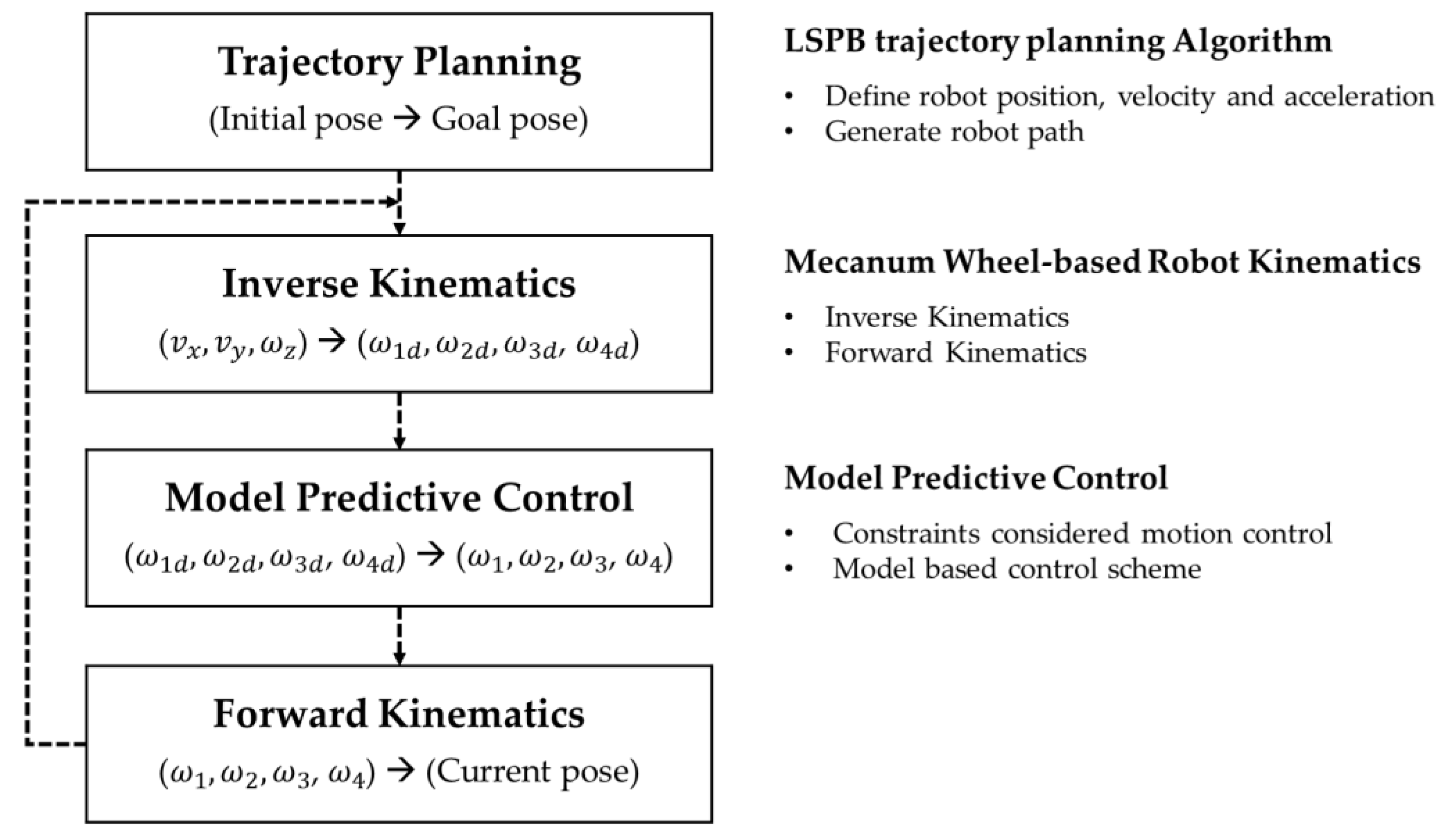
3. Mecanum Wheel-Based Robot Kinematics
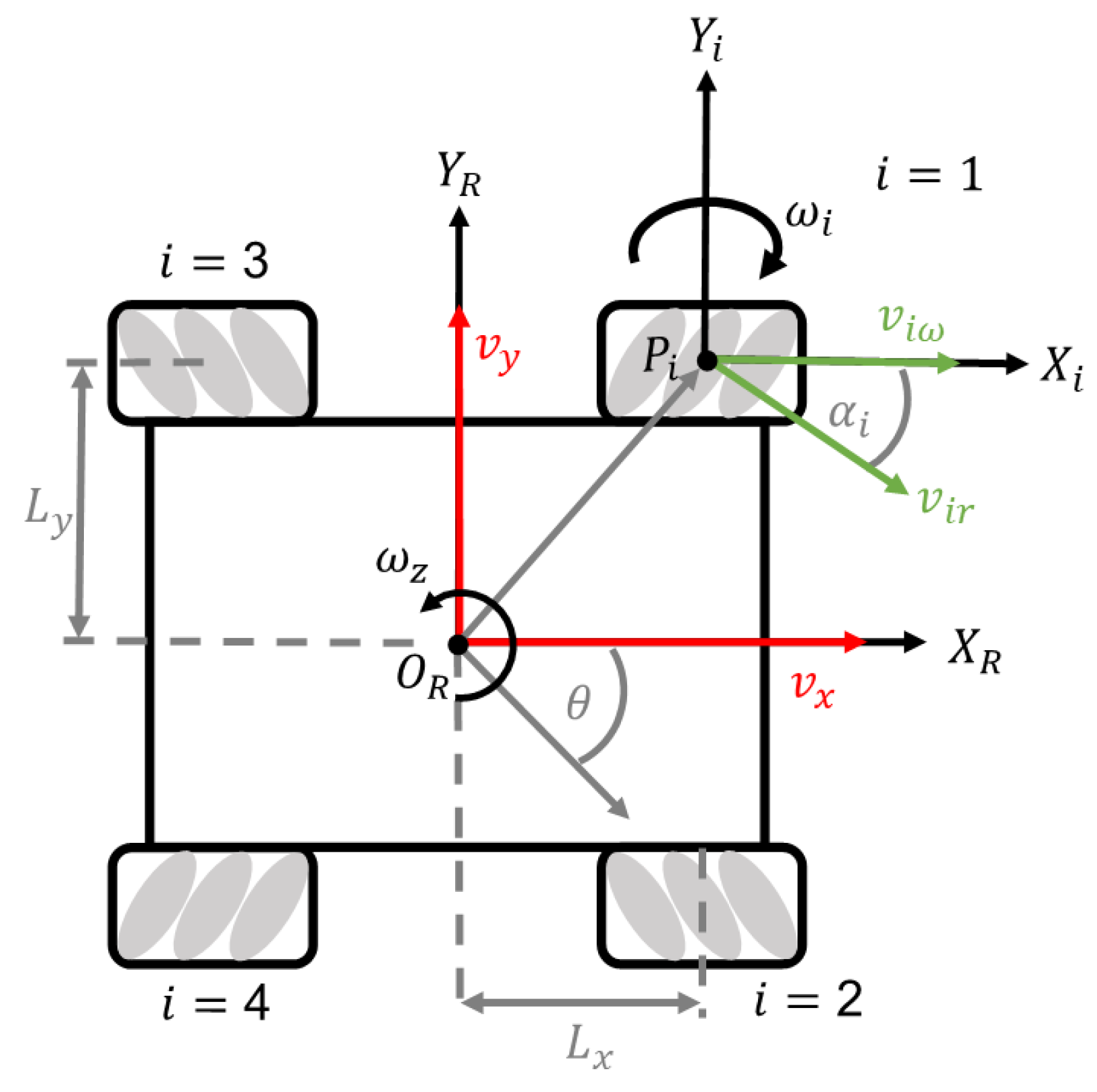
3.1. Robot Configuration
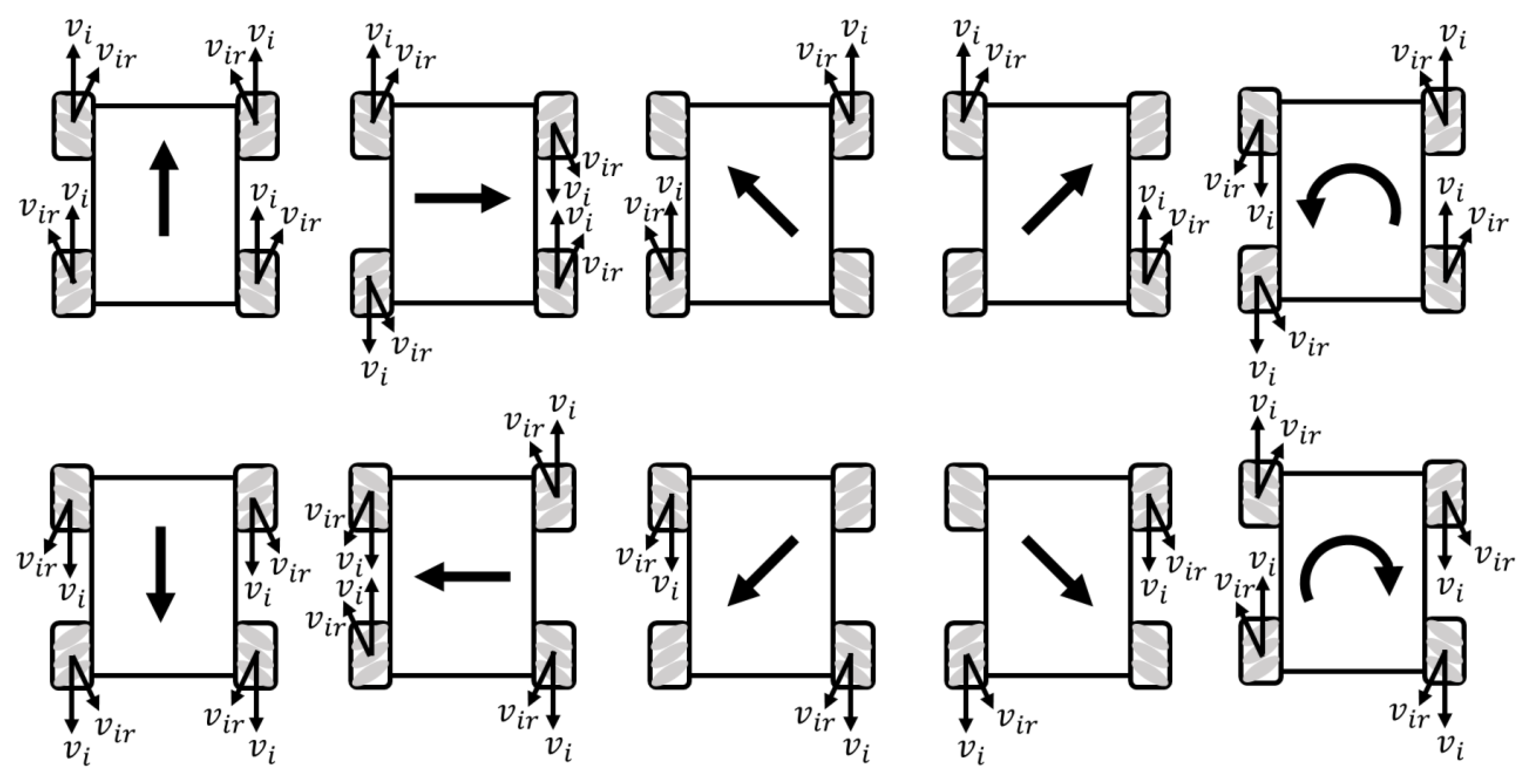
3.2. Inverse Kinematics and Forward Kinematics
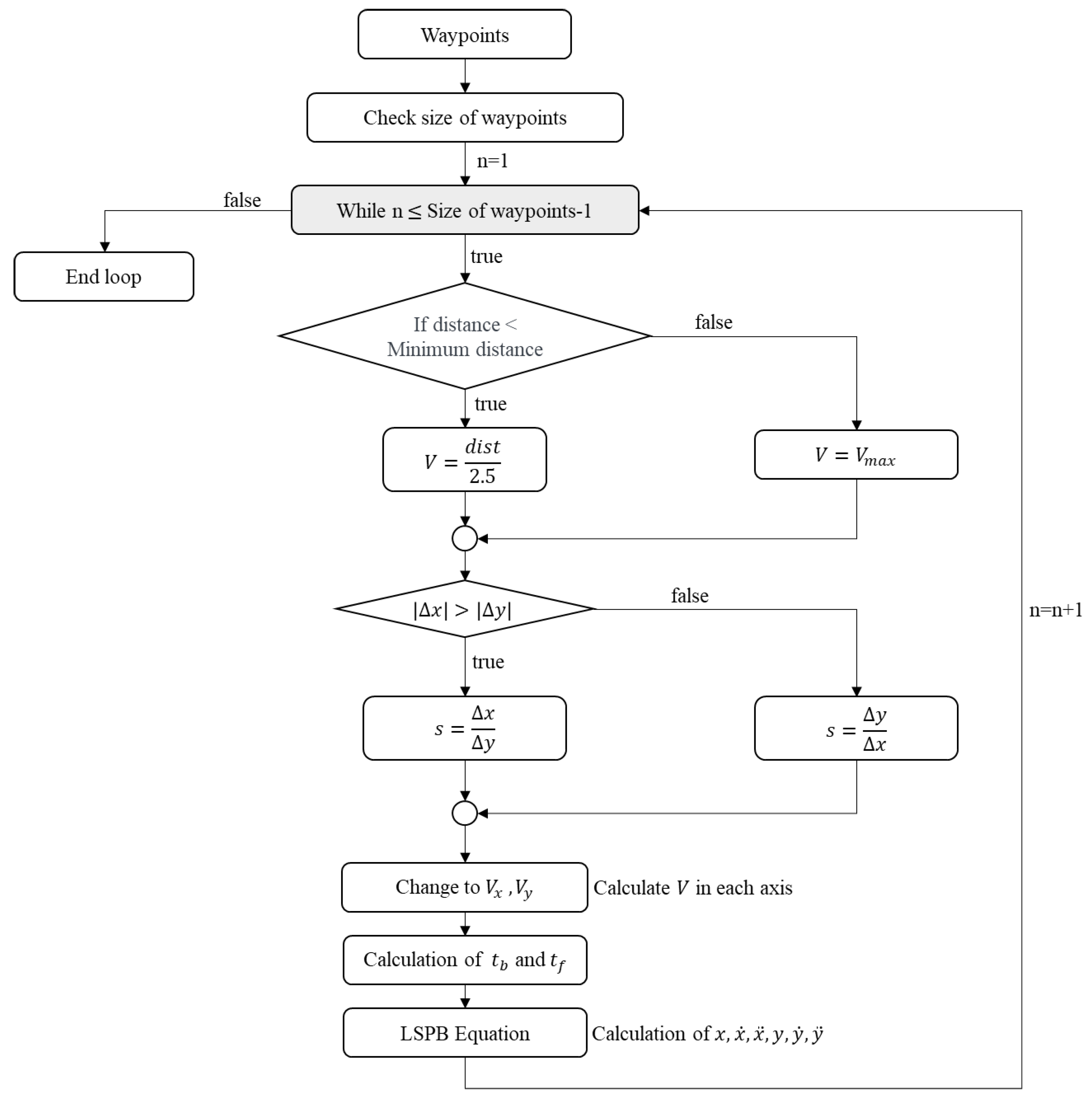
4. Trajectory Planning
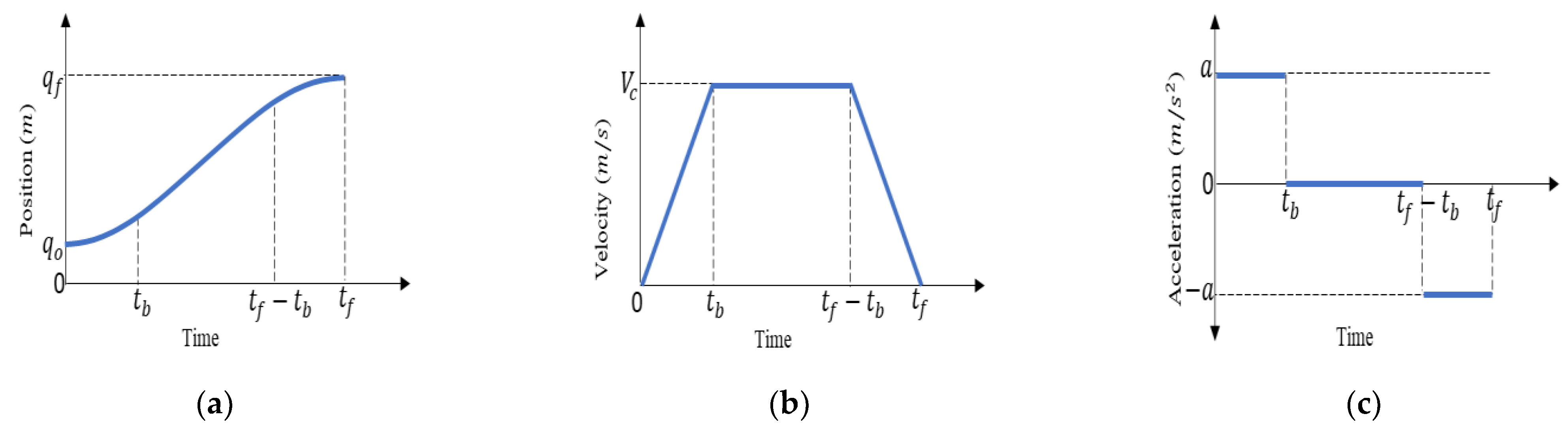
4.1. Linear Segments with Parabolic Blends (LSPB) Theory
4.2. Modified LSPB-Based Trajectory Planning
5. Robot Motion Controller
- Maximum velocity (forward and backward):
- Maximum acceleration (acceleration and deceleration):
- Maximum rotational velocity:
6. Simulation and Results
6.1. Simulink Model
6.2. Simulation Results
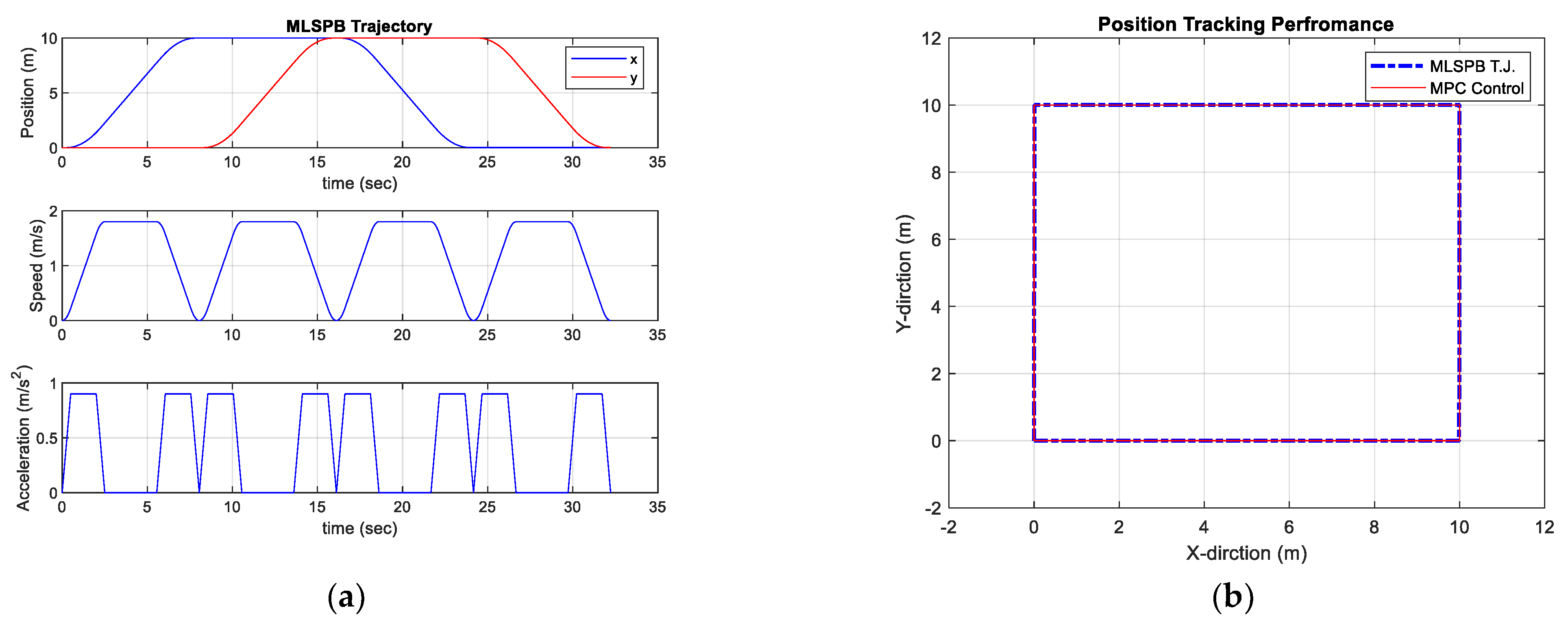
6.2.1. The Key Parameters (Rectangular Shape Path)
6.2.2. Rectangular Shape Path: LSPB vs. MLSPB
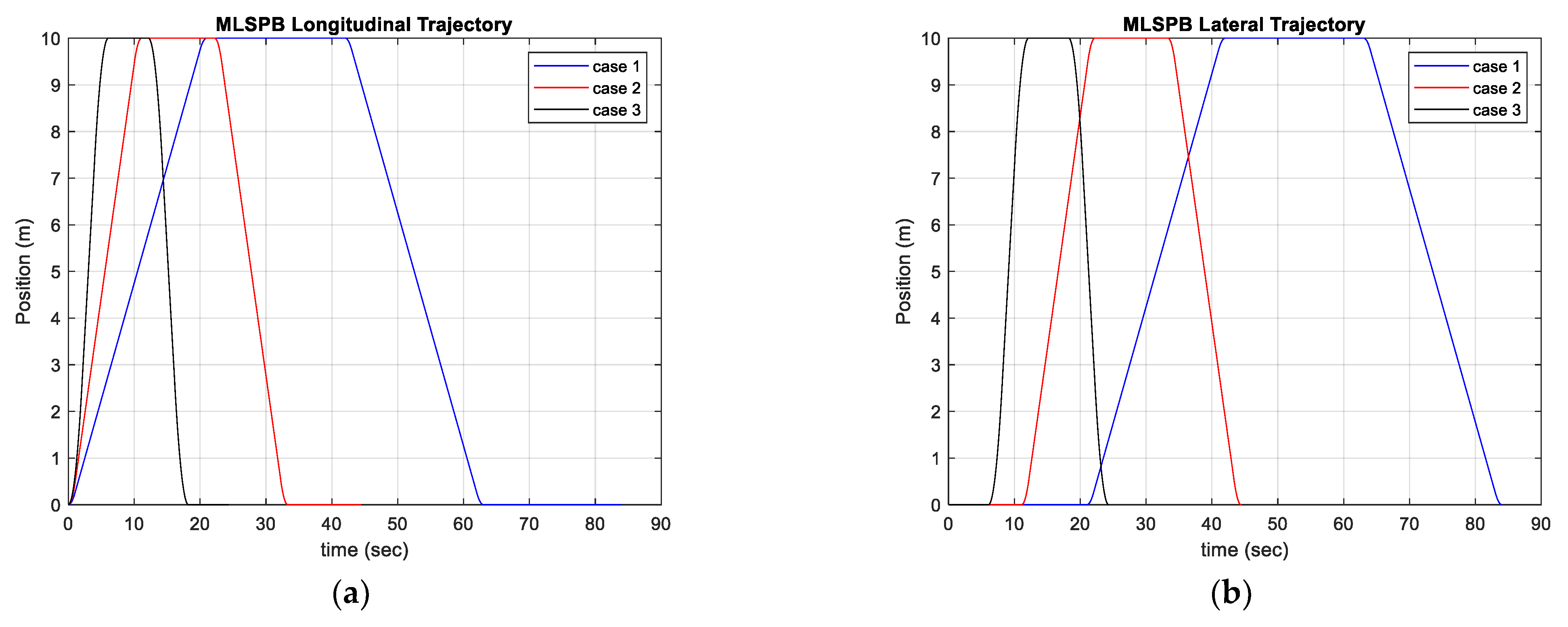
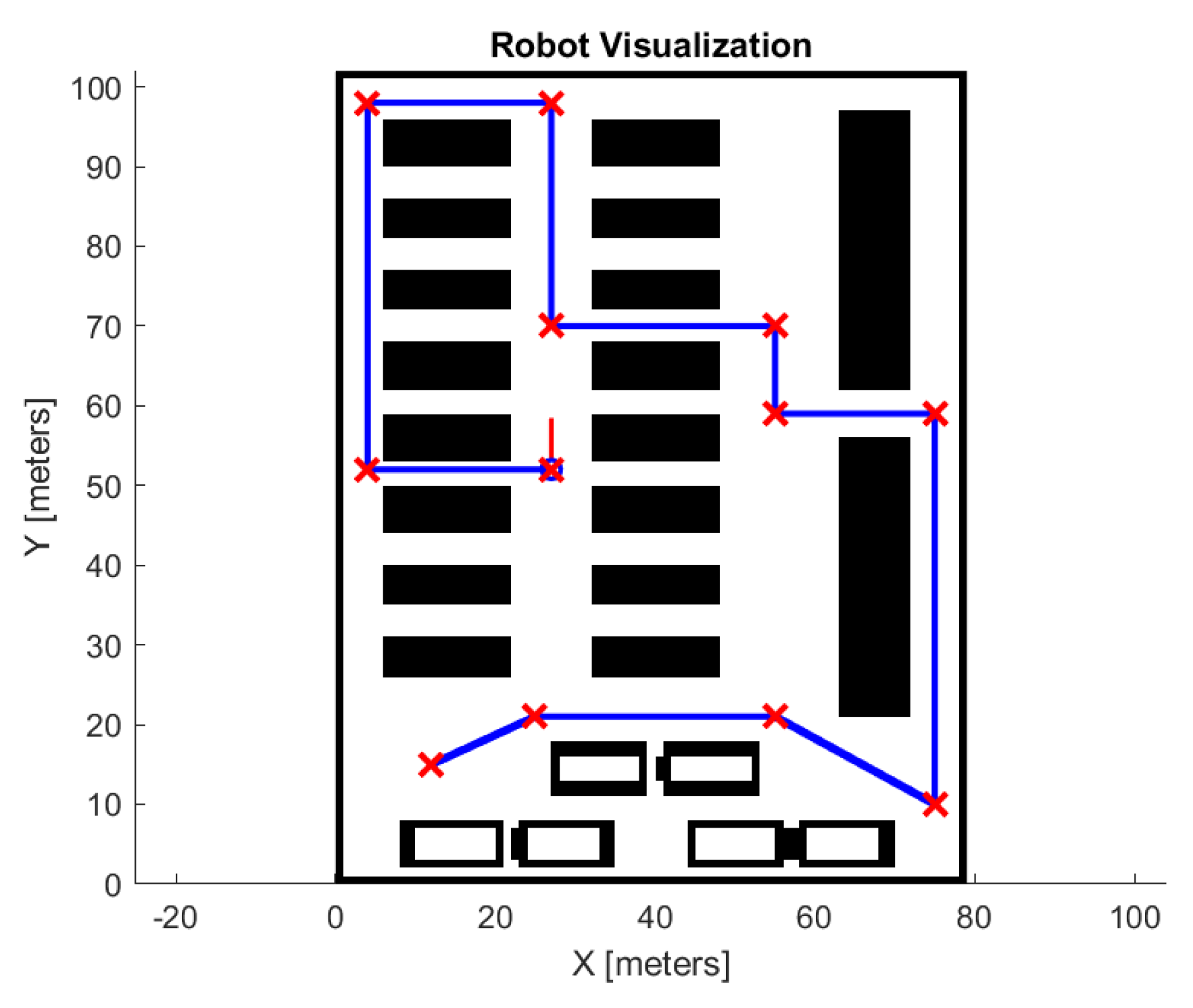
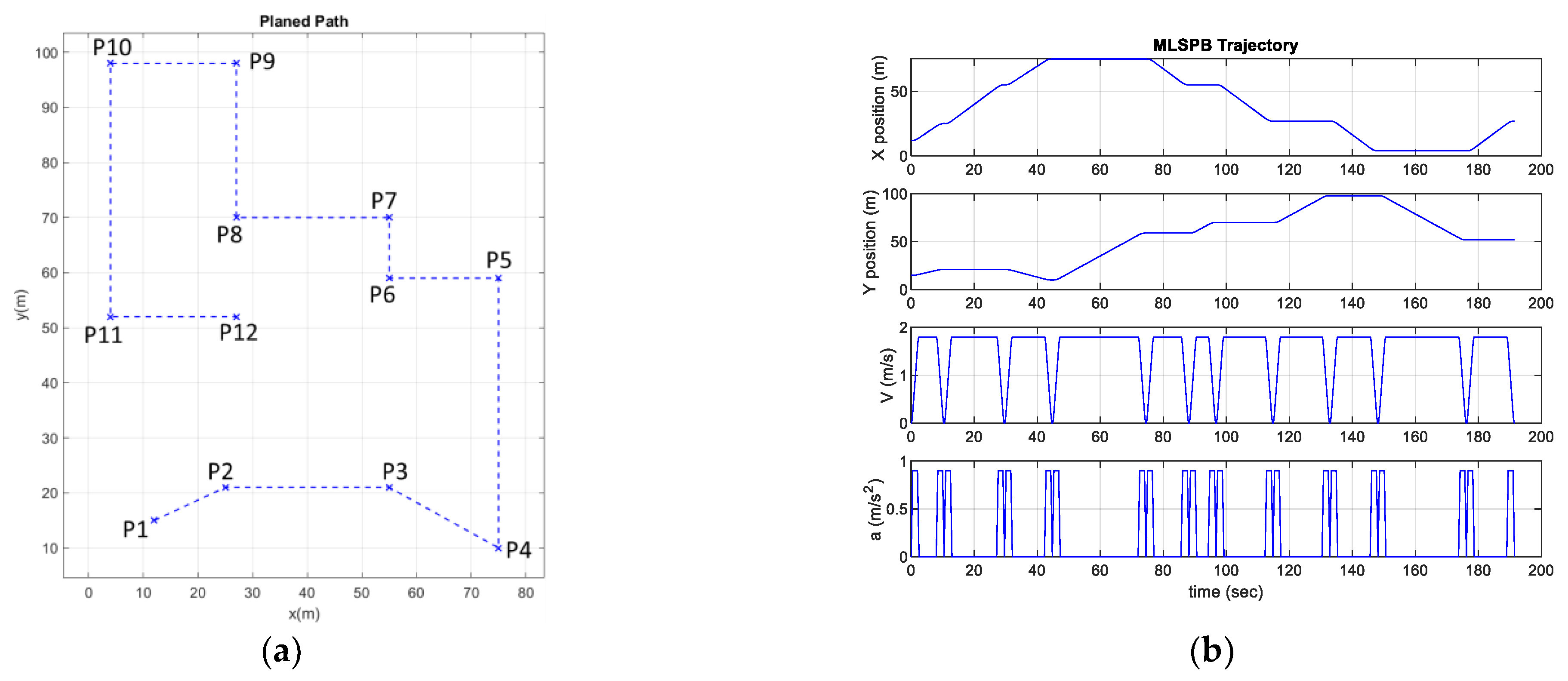
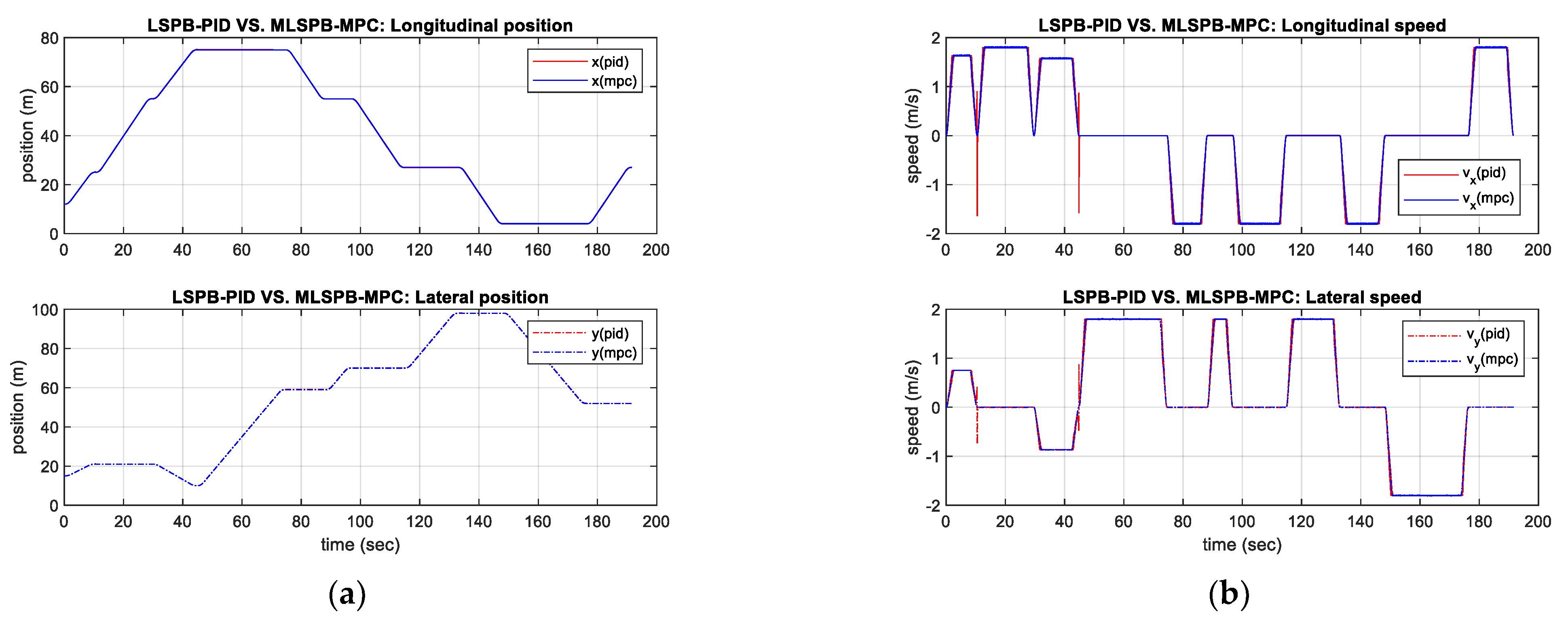
6.2.3. Warehouse-like Environment: LSPB vs. MLSPB
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bourne, D.; Choset, H.; Hu, H.; Kantor, G.; Niessl, C.; Rubinstein, Z.; Simmons, R.; Smith, S. Mobile manufacturing of large structures. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, DC, USA, 26–30 May 2015; p. 1565. [Google Scholar]
- Shneier, M.; Bostelman, R. Literature Review of Mobile Robots for Manufacturing; NIST: Gaithersburg, MD, USA, 2015. [Google Scholar] [CrossRef]
- Polaris. Autonomous Forklift Market Share, Size, Trends, Industry Analysis Report. Available online: https://polarismarketresearchscoop.wordpress.com/2022/07/18/autonomous-forklift-market-business-status-growth-industry-trends-and-outlook-2022-to-2030/ (accessed on 24 October 2023).
- Qian, J.; Zi, B.; Wang, D.; Ma, Y.; Zhang, D. The Design and Development of an Omni-Directional Mobile Robot Oriented to an Intelligent Manufacturing System. Sensors 2017, 17, 2073. [Google Scholar] [CrossRef] [PubMed]
- Taher, H.; Zhao, C.X. Omnidirectional mobile robots, mechanisms and navigation approaches. Mech. Mach. Theory 2020, 153, 103958. [Google Scholar] [CrossRef]
- Kanjanawanishkul, K. Omnidirectional wheeled mobile robots: Wheel types and practical applications. Int. J. Adv. Mechatron. Syst. 2015, 6, 74788. [Google Scholar] [CrossRef]
- Adăscăliţei, F.; Doroftei, I. Practical applications for mobile robots based on Mecanum wheels—A systematic survey. Rom. Rev. Precis. Mech. Opt. Mechatron. 2011, 40, 21–29. [Google Scholar]
- Kumar, N.V.; Kumar, C.S. Development of collision free path planning algorithm for warehouse mobile robot. Procedia Comput. Sci. 2018, 133, 456–463. [Google Scholar] [CrossRef]
- Massoud, M.M.; Abdellatif, A.; Atia, M.R.A. Different Path Planning Techniques for an Indoor Omni-Wheeled Mobile Robot: Experimental Implementation, Comparison and Optimization. Appl. Sci. 2022, 12, 12951. [Google Scholar] [CrossRef]
- Karur, K.; Sharma, N.; Dharmatti, C.; Siegel, J.E. A Survey of Path Planning Algorithms for Mobile Robots. Vehicles 2021, 3, 448–468. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Kim, D.-H.; Kim, S.-R. On-line minimum-time trajectory planning for industrial manipulators. In Proceedings of the 2007 International Conference on Control, Automation and Systems, Seoul, Republic of Korea, 17–20 October 2007; pp. 36–40. [Google Scholar]
- Kim, J.; Kim, S.R.; Kim, S.J.; Kim, D.H. A practical approach for minimum-time trajectory planning for industrial robots. Ind. Robot Int. J. 2010, 37, 51–61. [Google Scholar] [CrossRef]
- Davies, T.; Jnifene, A. Multiple Waypoint Path Planning for a Mobile Robot using Genetic Algorithms. In Proceedings of the CIMSA 2006 IEEE International Conference on Virtual Environments, Human-Computer Interfaces, and Measurement Systems, La Coruna, Spain, 12–14 July 2006; pp. 21–26. [Google Scholar]
- Samad, T.; Bauer, M.; Bortoffc, S.; Cairano, S.D.; Fagiano, L.; Odgaard, P.F.; Rhinehart, R.R.; Sánchez-Peña, R.; Serbezov, A.; Ankersen, F.; et al. Industry engagement with control research: Perspective and messages. Annu. Rev. Control 2020, 49, 1–14. [Google Scholar] [CrossRef]
- Qina, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Umar, A.A.; Kim, J.-S. Nonlinear Model Predictive Path-Following for Mecanum-Wheeled Omnidirectional Mobile Robot. Trans. Korean Inst. Electr. Eng. 2021, 70, 1946–1952. [Google Scholar] [CrossRef]
- Moreno-Caireta, I.; Celaya, E.; Ros, L. Model Predictive Control for a Mecanum-wheeled Robot Navigating among Obstacles. IFAC Pap. 2021, 54, 119–125. [Google Scholar] [CrossRef]
- Tamba, T.A.; Hong, B.; Hong, K.-S. A path following control of an unmanned autonomous forklift. Int. J. Control Autom. Syst. 2009, 7, 113–122. [Google Scholar] [CrossRef]
- Affia, I.; Aamer, A. An internet of things-based smart warehouse infrastructure: Design and application. J. Sci. Technol. Policy Manag. 2021, 13, 90–109. [Google Scholar] [CrossRef]
- Hao, J.; Shi, H.; Shi, V.; Yang, C. Adoption of automatic warehousing systems in logistics firms: A technology–organization–environment framework. Sustainability 2020, 12, 5185. [Google Scholar] [CrossRef]
- Macfarlane, S.; Croft, E.A. Jerk-bounded manipulator trajectory planning: Design for real-time applications. IEEE Trans. Robot. Autom. 2003, 19, 42–52. [Google Scholar] [CrossRef]
- Walch, A.; Eitzinger, C.; Zambal, S.; Palfinger, W. LSPB Trajectory Planning Using Quadratic Splines. In Proceedings of the 3rd International Conference on Mechatronics and Robotics Engineering, Paris, France, 8–13 February 2017; pp. 81–87. [Google Scholar] [CrossRef]
- Nurallah, G.; Bing, Q.; Hamid, T. Kinematic Model of a Four Mecanum Wheeled Mobile Robot. Int. J. Comput. Appl. 2015, 113, 6–9. [Google Scholar] [CrossRef]
- Li, Y.; Dai, S.; Zheng, Y.; Tian, F.; Yan, X. Modeling and Kinematics Simulation of a Mecanum Wheel Platform in RecurDyn. J. Robot. 2018, 2018, 9373580. [Google Scholar] [CrossRef]
- Jia, Y.; Song, X.; Xu, S.S.-D. Modeling and Motion Analysis of Four-Mecanum Wheel Omni-directional Mobile Platform. In Proceedings of the International Automatic Control Conference (CACS), Sun Moon Lake, Taiwan, 2–4 December 2013. [Google Scholar]
- Al-Dahhan MR, H.; Schmidt, K.W. Safe and Efficient Path Planning for Omni-directional Robots using an Inflated Voronoi Boundary. C¸Ankaya Univ. J. Sci. Eng. 2019, 16, 46–69. [Google Scholar]
- Kim, J.-C.; Pae, D.-S.; Lim, M.-T. Obstacle Avoidance Path Planning based on Output Constrained Model Predictive Control. Int. J. Control Autom. Syst. 2019, 17, 2850–2861. [Google Scholar] [CrossRef]
- Klančar, G.; Zdešar, A.; Blazic, S.; Škrjanc, I. Path Planning. In Wheeled Mobile Robotics; Butterworth-Heinemann: Cambridge, MA, USA, 2017; pp. 161–206. [Google Scholar]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots, 2nd ed.; MIT Press: Cambridge, MA, USA, 2011; p. 369. [Google Scholar]
- Craig, J.J. Introduction to Robotics Mechanics and Control, 3rd ed.; Dworkin, A., Ed.; Pearson Education International: Upper Saddle River, NJ, USA, 2005; p. 385. [Google Scholar]
- Khatamianfar, A. Advanced Discrete-Time Control Methods for Industrial Applications. Ph.D. Thesis, University of New South Wales, Sydney, NSW, Australia, 2015. [Google Scholar]
- Abdul-Lateef, W.E.; Huayier, A.F.; Farhood, N.H. Design of planning Trajectory for the planar Robot Manipulator using Linear Segments method with Parabolic Blends (LSPB). J. Mech. Eng. Res. Dev. 2021, 44, 159–171. [Google Scholar]
- Li, X.; Tan, S.; Feng, X.; Rong, H. LSPB Trajectory Planning: Design for the Modular Robot Arm Applications. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009; pp. 1–4. [Google Scholar]
- Lei, J.; Luo, Z.; Li, C. Multi-Robot Systems—New Advances [Working Title]; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Ioana, I.; Blejan, M.; Blejan, R. S-curve motion profiles generator for hydraulic actuators. In Proceedings of the 2019 International Conference on Hydraulics and Pneumatics—HERVEX, Baile Govora, Romania, 13–15 November 2019; pp. 124–127. [Google Scholar]
- OMRON. HD-1500 Series Autonomous Mobile Robot. Available online: https://automation.omron.com/en/us/products/family/hd (accessed on 24 September 2023).
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Fiedler, F.; Karg, B.; Lüken, L.; Brandner, D.; Heinlein, M.; Brabender, F.; Lucia, S. do-mpc: Towards FAIR nonlinear and robust model predictive control. Control Eng. Pract. 2023, 140, 105676. [Google Scholar] [CrossRef]
- RoboMate. Omni-Directional Mobility Platform. Available online: http://www.vetexinc.com/vehicles/robomate.html (accessed on 14 November 2023).





| Symbol | Parameter | Unit |
|---|---|---|
| Mecanum wheel radius | m | |
| The distance between the wheel and the robot’s center in the x (longitudinal) axis | m | |
| The distance between the wheel and the robot’s center in the y (lateral) axis | m | |
| The robot’s linear velocity in the x-axis | m/s | |
| The robot’s linear velocity in the y-axis | m/s | |
| The robot’s angular velocity along the z-axis at the center point | rad/s | |
| i = (1, 2, 3, 4) | Wheel numbers | - |
| Linear velocity of each wheel | m/s | |
| Velocity of Mecanum roller direction of each wheel | m/s | |
| Mecanum roller angle | rad |
| Parameter | Symbol | Value |
|---|---|---|
| Prediction horizon | P | 10 |
| Control horizon | m | 5 |
| Sampling time | Ts | 0.01 (s) |
| Maximum speed | 1.8 (m/s) | |
| Speed constraint | 1.8 (m/s) | |
| Maximum acceleration | 0.9 () | |
| Acceleration constraint | ||
| Maximum angular speed | (m/s) | |
| Angular speed constraint | (m/s) | |
| Wheel radius 1 | 0.133 (m) | |
| Wheel base 1 | 0.762 (m) | |
| Wheel track 1 | 0.610 (m) |
| Speed (m/s) | Acceleration ) | Position RSME (m) | Working Time (s) | Average Jerk |
|---|---|---|---|---|
| 0.5 | 0.5 | 0.0210 | 84.03 | 0.5837 |
| 1.0 | 0.9 | 0.0409 | 44.43 | 1.1830 |
| 2.5 | 1.2 | 0.0835 | 24.31 | 2.5928 |
| Method | Position RSME (m) | Working Time (s) | Average Jerk ) |
|---|---|---|---|
| LSPB−PID | 0.0751 | 30.23 | 30,424 |
| MLSPB−MPC | 0.0604 | 32.23 | 1.8115 |
| Method | Position RSME (m) | Working Time (s) | Average Jerk |
|---|---|---|---|
| LSPB−PID | 0.0795 | 191.468 | 14,097 |
| MLSPB−MPC | 0.0705 | 191.520 | 3.7184 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vorasawad, K.; Park, M.; Kim, C. Efficient Navigation and Motion Control for Autonomous Forklifts in Smart Warehouses: LSPB Trajectory Planning and MPC Implementation. Machines 2023, 11, 1050. https://doi.org/10.3390/machines11121050
Vorasawad K, Park M, Kim C. Efficient Navigation and Motion Control for Autonomous Forklifts in Smart Warehouses: LSPB Trajectory Planning and MPC Implementation. Machines. 2023; 11(12):1050. https://doi.org/10.3390/machines11121050
Chicago/Turabian StyleVorasawad, Konchanok, Myoungkuk Park, and Changwon Kim. 2023. "Efficient Navigation and Motion Control for Autonomous Forklifts in Smart Warehouses: LSPB Trajectory Planning and MPC Implementation" Machines 11, no. 12: 1050. https://doi.org/10.3390/machines11121050
APA StyleVorasawad, K., Park, M., & Kim, C. (2023). Efficient Navigation and Motion Control for Autonomous Forklifts in Smart Warehouses: LSPB Trajectory Planning and MPC Implementation. Machines, 11(12), 1050. https://doi.org/10.3390/machines11121050






