An Open-Circuit Fault Diagnosis Method Based on Adjacent Trend Line Relationship of Current Vector Trajectory for Motor Drive Inverter
Abstract
:1. Introduction
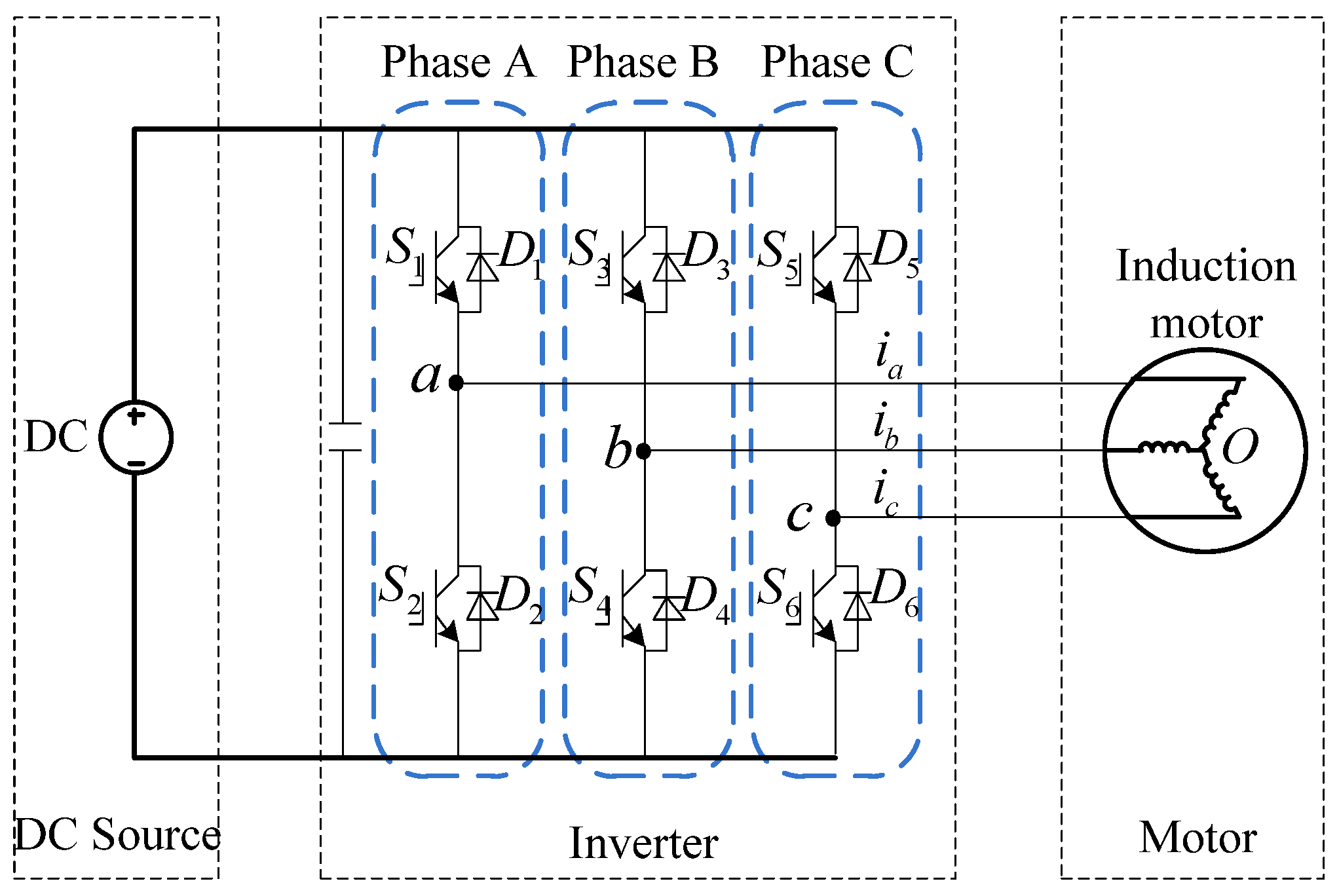
2. The OC Fault Analysis for Motor Drive Inverter System
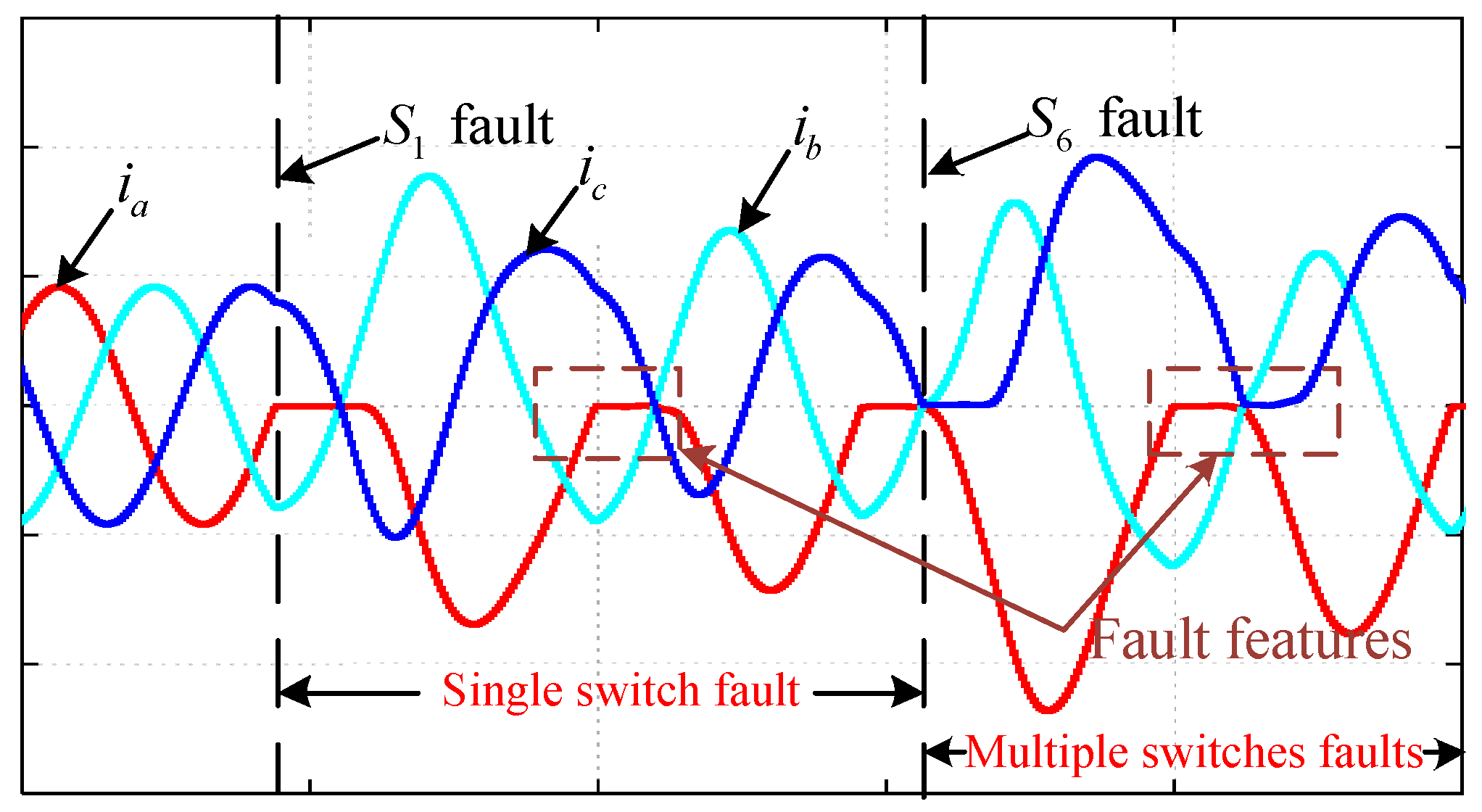
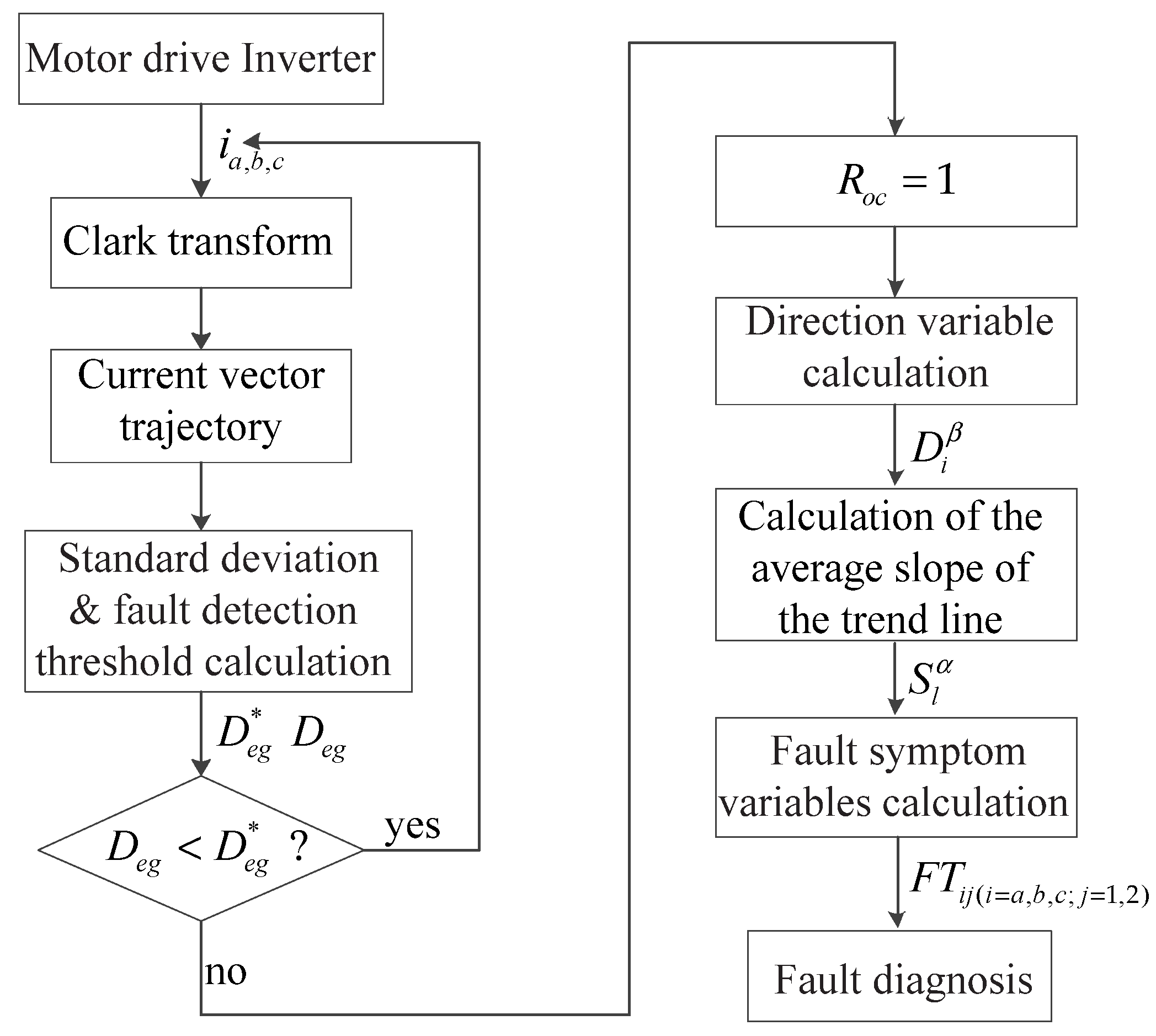
3. Fault Diagnosis Analysis of the Proposed Method
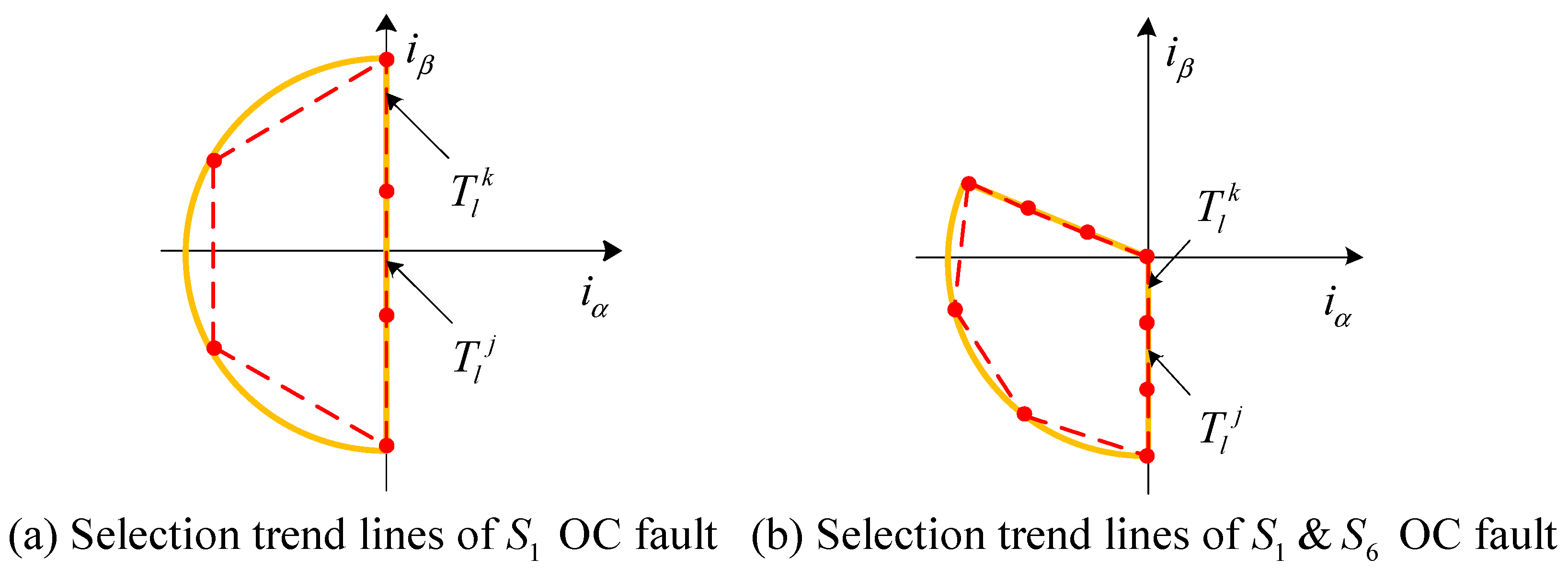
3.1. Fault Feature Extraction of Adjacent Trend Lines
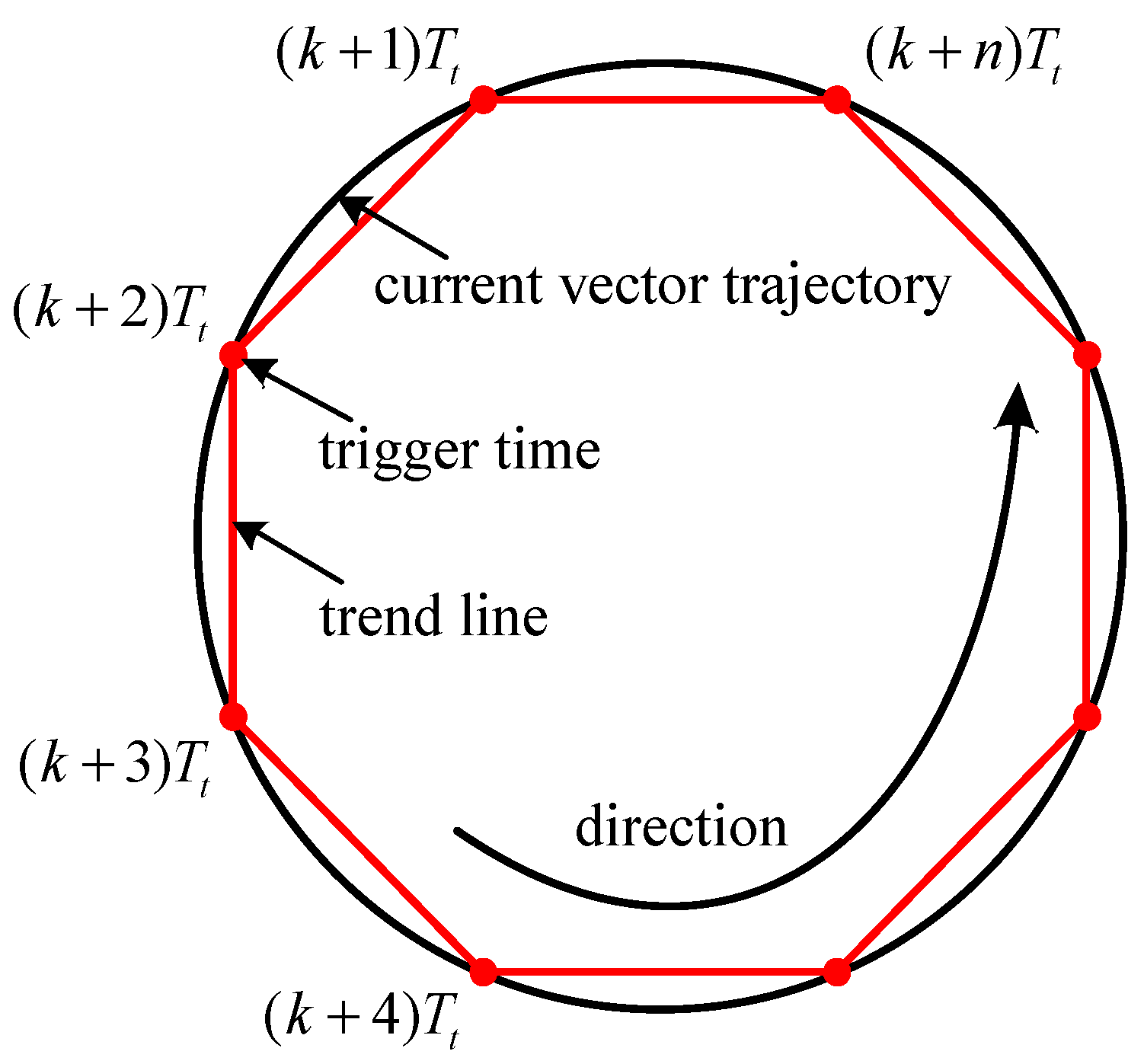
3.2. Fault Detection Combined with Current Vector Trajectory Adjacent Trend Lines
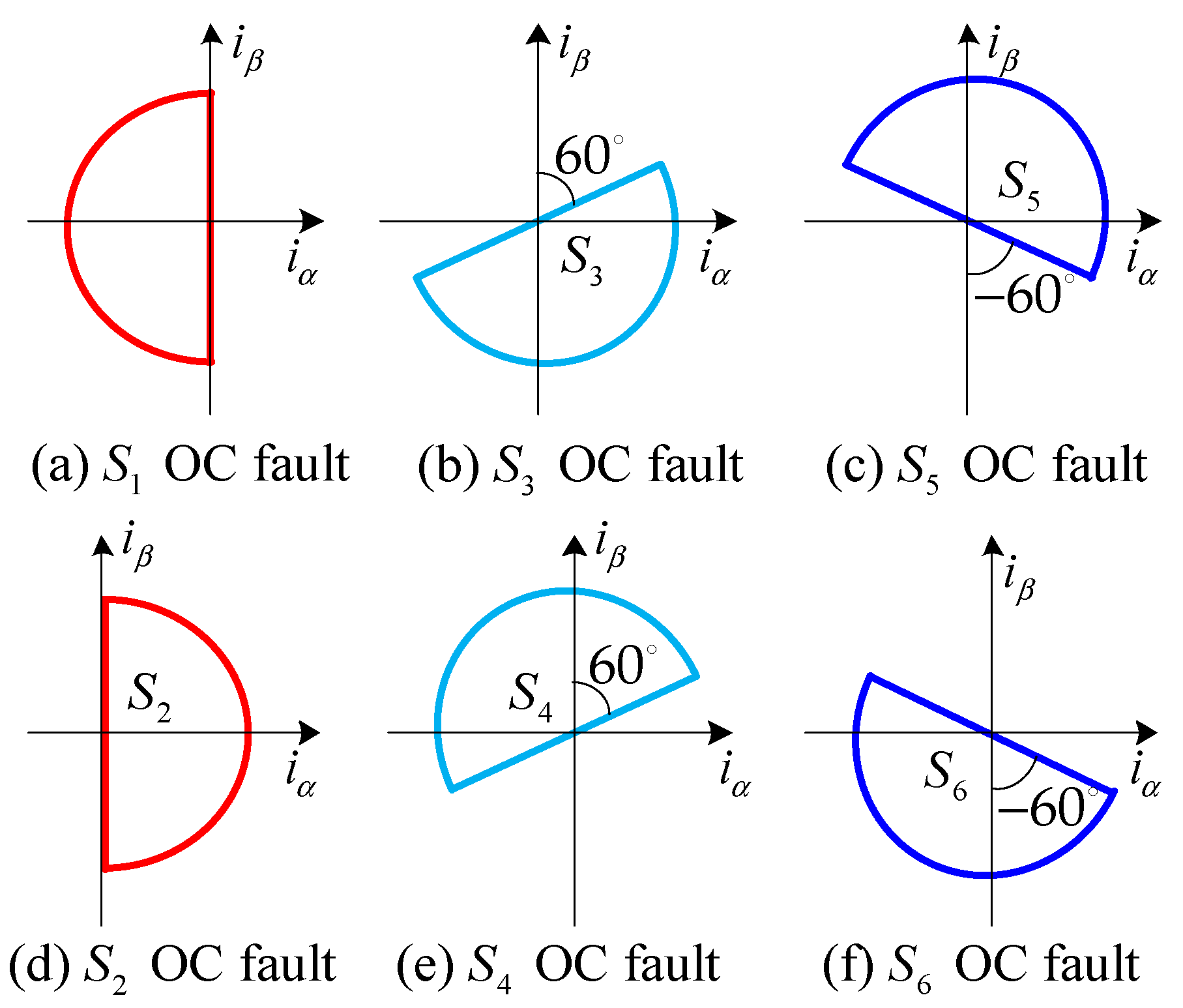
3.3. Fault Location
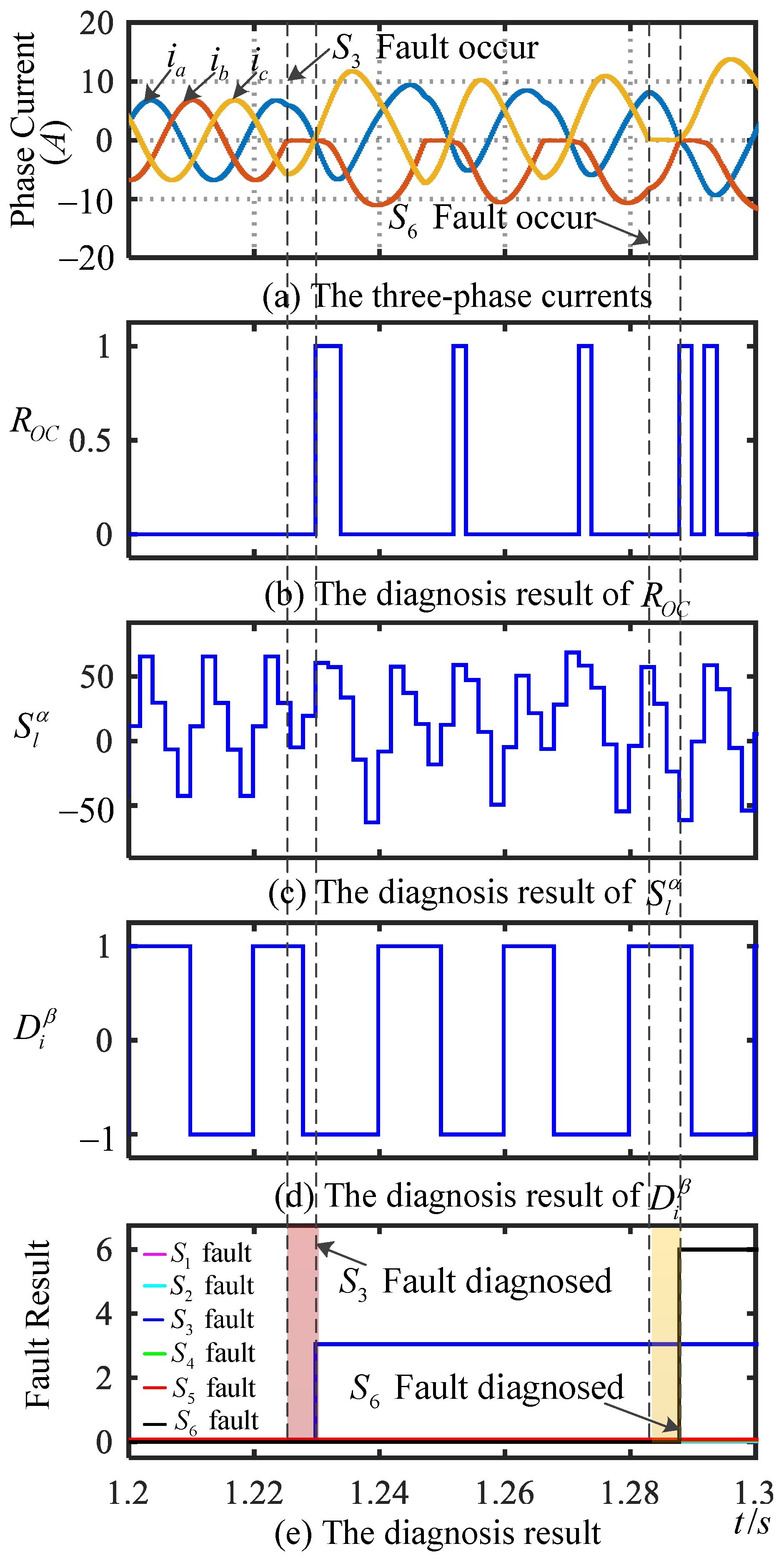
4. Simulation and Experiment Results
4.1. Simulation Results Analysis
4.1.1. Single-Switch OC Fault Diagnosis Simulation Results
4.1.2. Multiple-Switch OC Fault Diagnosis Simulation Results
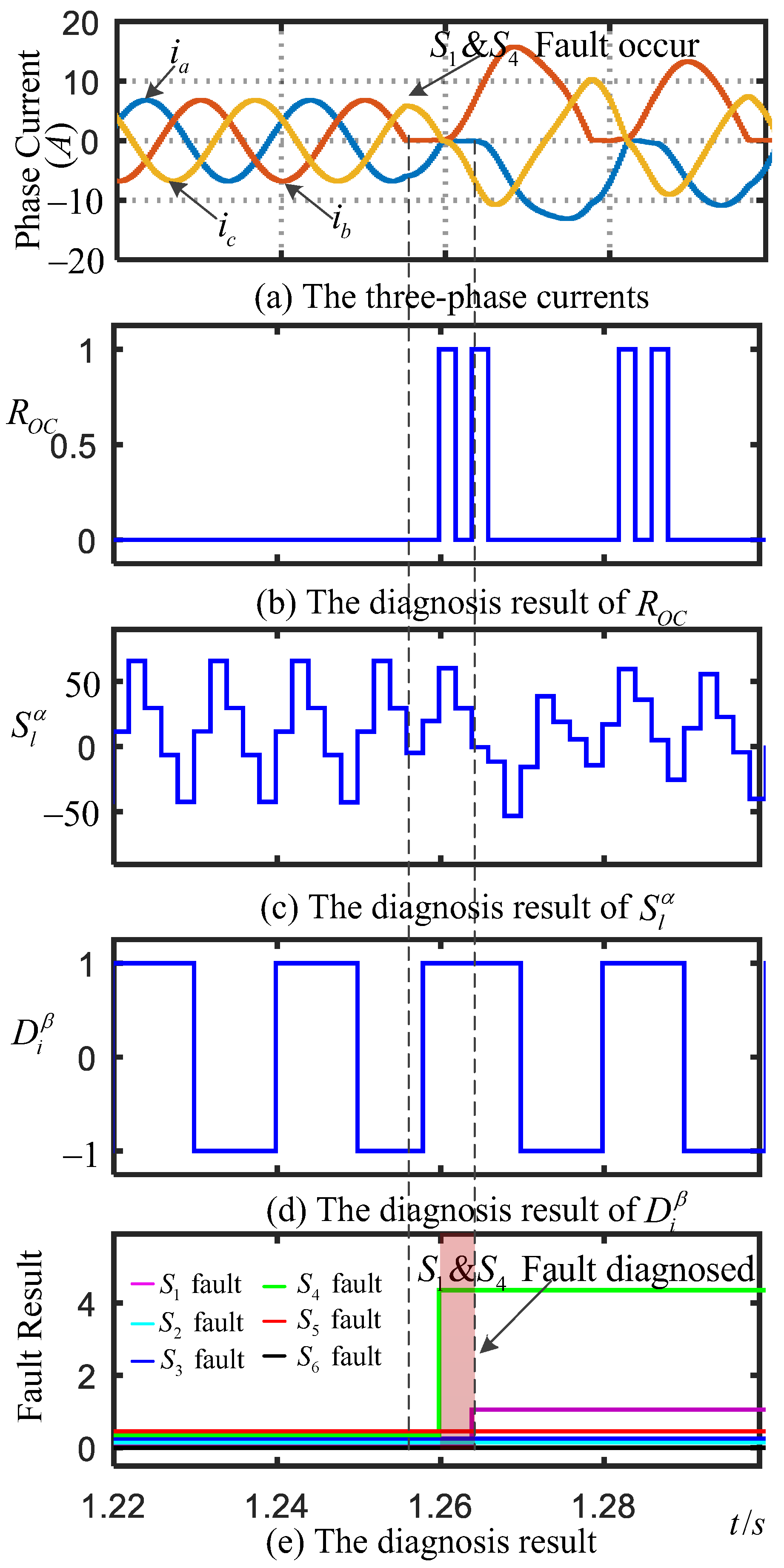
4.1.3. Simultaneous OC Faults of and Diagnosis Simulation Results
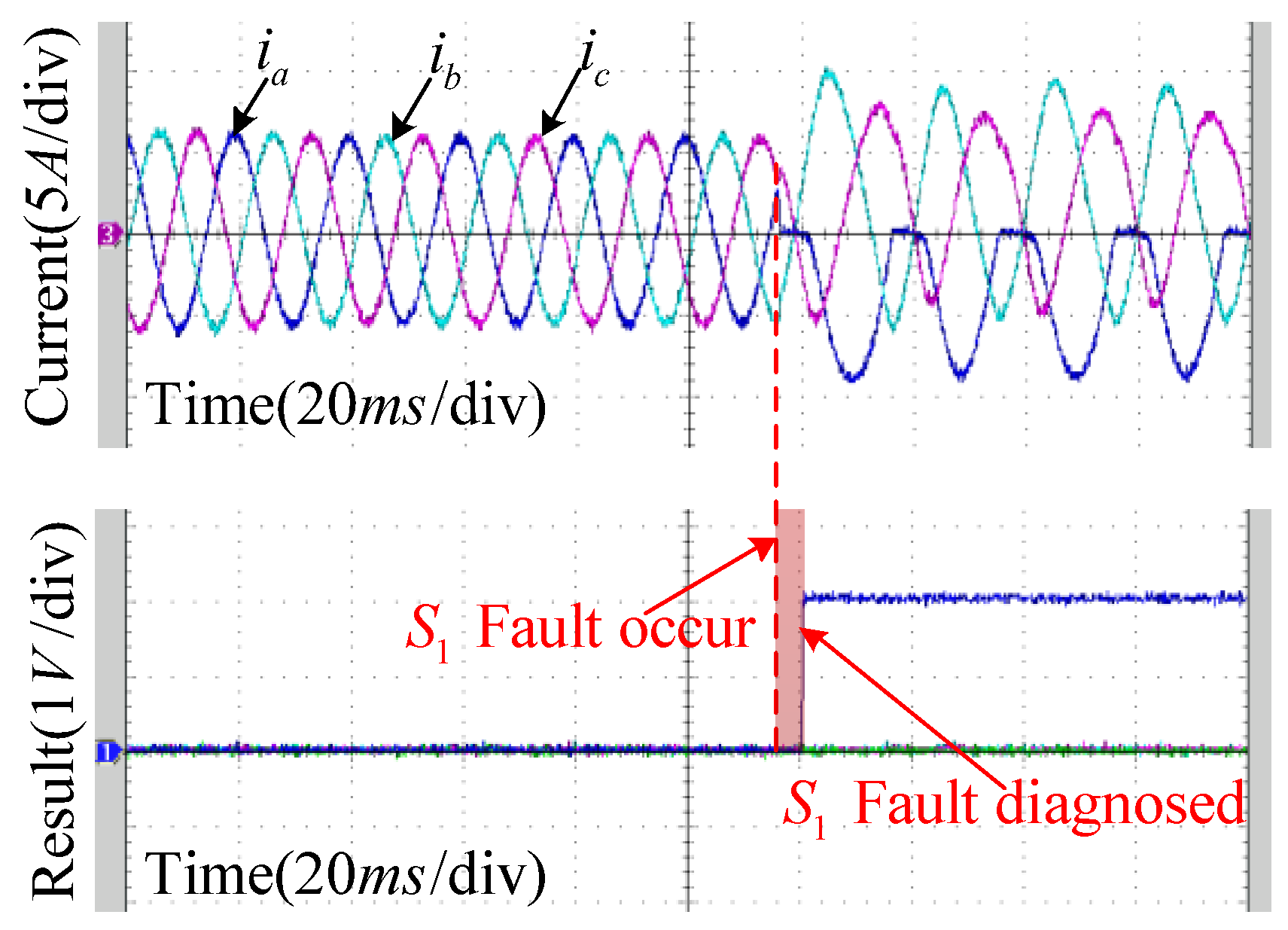
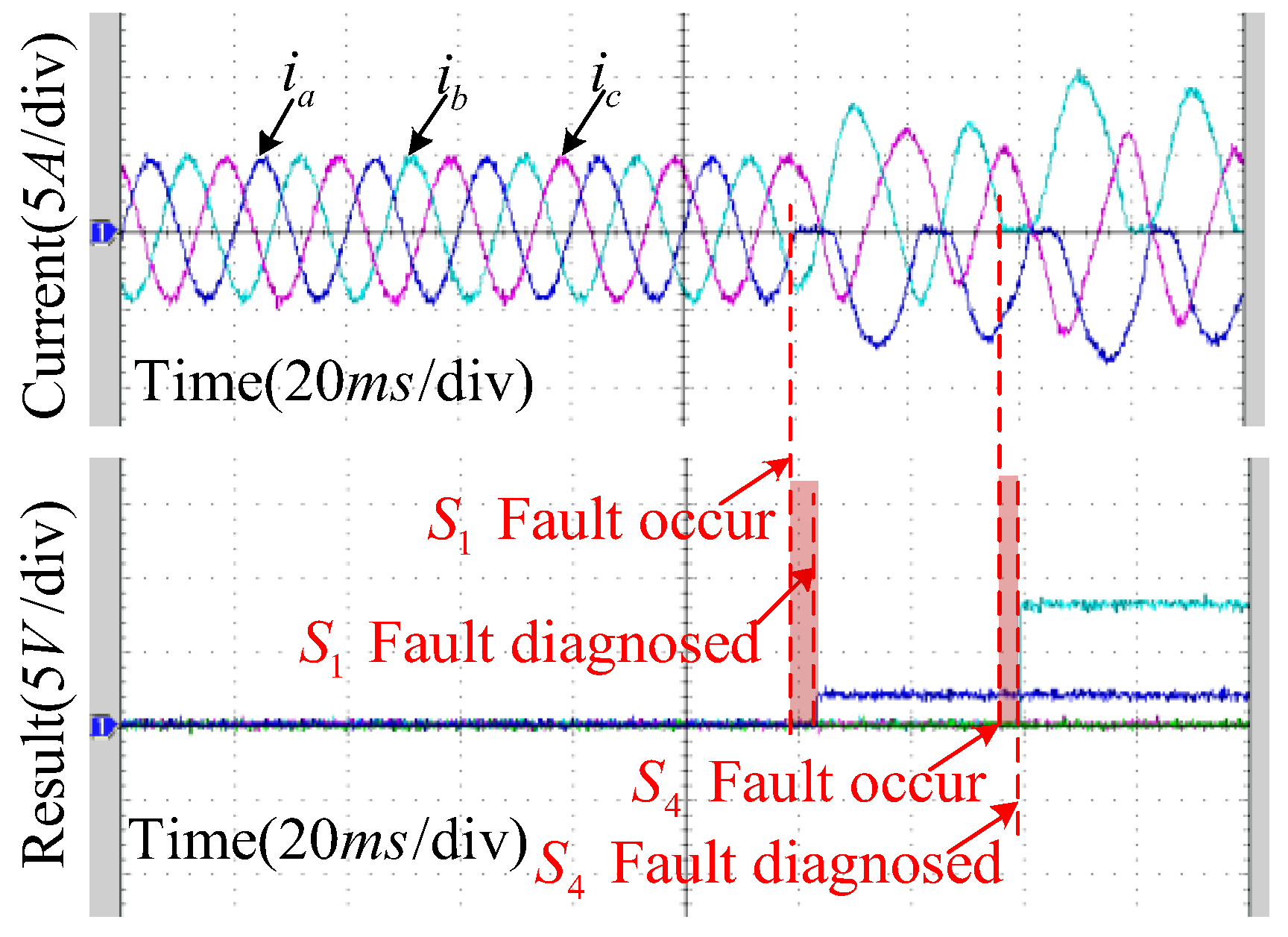
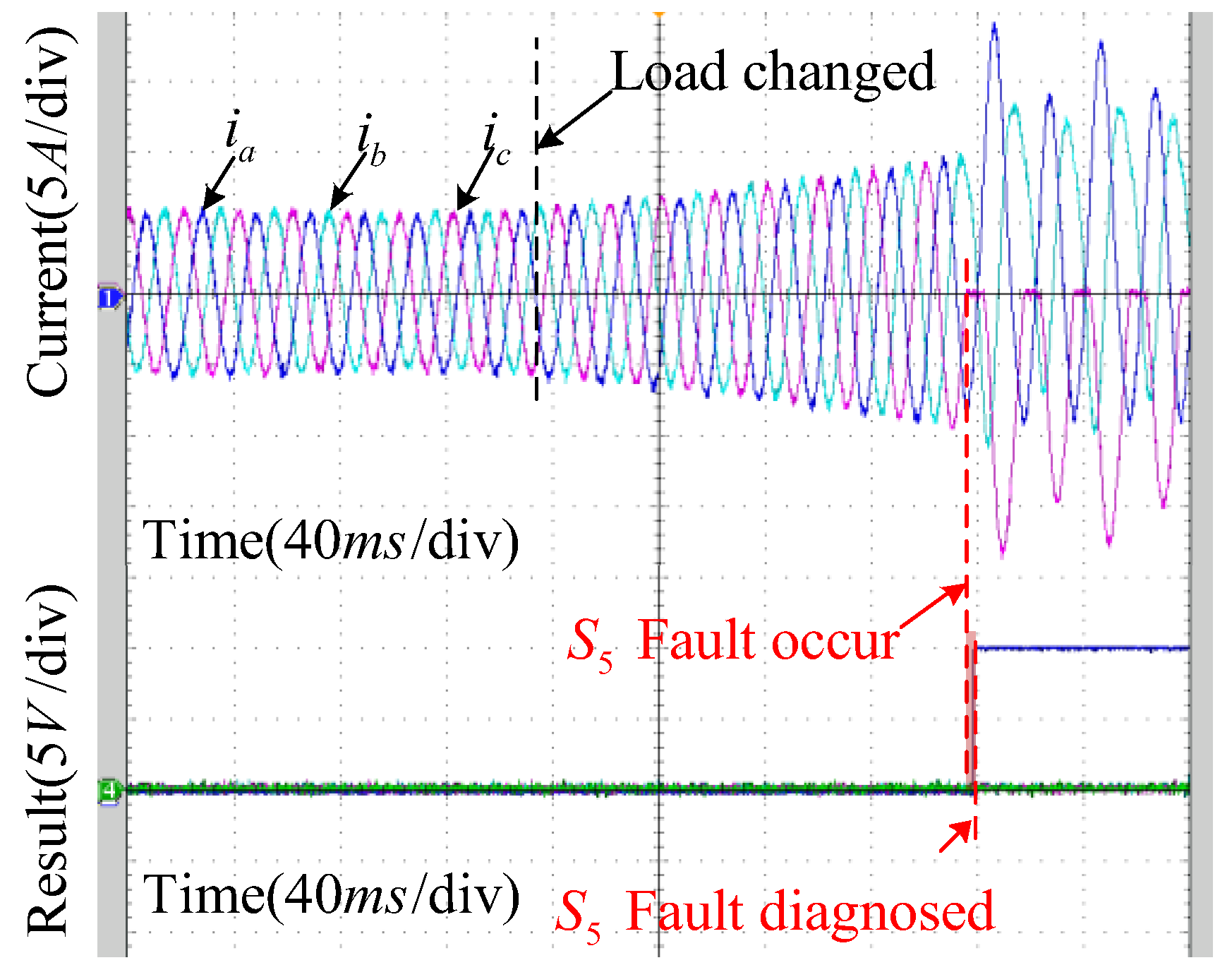
4.2. Experimental Results Analysis
4.3. Compared with Other Methods
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rajeswaran, N.; Thangaraj, R.; Mihet-Popa, L.; Krishna Vajjala, K.V.; Özer, Ö. FPGA implementation of AI-based inverter IGBT open circuit fault diagnosis of induction motor drives. Micromachines 2022, 13, 663. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, H.; Tehrani, K.; Jamshidi, M. A fault diagnosis design based on deep learning approach for electric vehicle applications. Energies 2021, 14, 6599. [Google Scholar] [CrossRef]
- Wu, B. High-Power Converters and AC Drives; Wiley-IEEE Press: Hoboken, NJ, USA, 2006; pp. 1–10. [Google Scholar]
- Yin, H.; Chen, Y.; Chen, Z. Observer-based adaptive threshold diagnosis method for open-switch faults of voltage source inverters. J. Power Electron. 2020, 20, 1573–1582. [Google Scholar] [CrossRef]
- Welchko, B.A.; Lipo, T.A.; Jahns, T.M.; Schulz, S.E. Fault tolerant three-phase AC motor drive topologies: A comparison of features, cost, and limitations. IEEE Tran. Power Electron. 2004, 19, 1108–1116. [Google Scholar] [CrossRef]
- Song, Y.T.; Wang, B.S. Survey on reliability of power electronic systems. IEEE Trans. Power Electron. 2013, 28, 591–604. [Google Scholar] [CrossRef]
- Alqarni, Z.A. Design of active fault-tolerant control system for multilevel inverters to achieve greater reliability with improved power quality. IEEE Access 2022, 10, 77791–77801. [Google Scholar] [CrossRef]
- Tehrani, K.; Weber, M.; Rasoanarivo, I. Hybrid power system optimization for microgrid. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. 1–9. [Google Scholar]
- Yang, S.; Xiang, D.; Bryant, A.; Mawby, P.; Ran, L.; Tavner, P. Condition monitoring for device reliability in power electronic converters: A review. IEEE Trans. Power Electron. 2010, 25, 2734–2752. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z.; Zhang, H. Multiple open-circuit fault diagnosis based on multistate data processing and subsection fluctuation analysis for photovoltaic inverter. IEEE Trans. Instrum. Meas. 2018, 67, 516–526. [Google Scholar] [CrossRef]
- Salehifar, M.; Arashloo, R.S.; Eguilaz, M.M.; Sala, V. FPGA based robust open transistor fault diagnosis and fault tolerant sliding mode control of five-phase pm motor drives. J. Power Electron. 2015, 15, 131–145. [Google Scholar] [CrossRef]
- Gautam, S.P.; Jalhotra, M.; Sahu, L.K.; Kumar, M.R.; Gupta, K.K. A survey on fault tolerant and diagnostic techniques of multilevel inverter. IEEE Access 2023, 11, 60866–60888. [Google Scholar] [CrossRef]
- Im, W.S.; Kim, J.S.; Kim, J.M.; Lee, D.C.; Lee, K.B. Diagnosis methods for igbt open switch fault applied to 3-phase ac/dc pwm converter. J. Power Electron. 2012, 12, 120–127. [Google Scholar] [CrossRef]
- Poon, J.; Jain, P.; Konstantakopoulos, I.C.; Spanos, C.; Panda, S.K.; Sanders, S.R. Model-based fault detection and identification for switching power converters. IEEE Trans. Power Electron. 2017, 32, 1419–1430. [Google Scholar] [CrossRef]
- Li, Z.; Wang, B.; Ren, Y.; Wang, J.; Bai, Z.; Ma, H. An Average Model-Based Transistor Open-Circuit Fault Diagnosis Method for Grid-Tied Single-Phase Inverter. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 993–998. [Google Scholar]
- An, Q.T.; Sun, L.; Sun, Z.L. Current residual vector-based open-Switch fault diagnosis of inverters in PMSM drive systems. IEEE Trans. Power Electron. 2015, 30, 2814–2827. [Google Scholar] [CrossRef]
- Huang, W.; Du, J.; Hua, W.; Lu, W.; Bi, K.; Zhu, Y.; Fan, Q. Current-based open-circuit fault diagnosis for PMSM drives with model predictive control. IEEE Trans. Power Electron. 2021, 36, 10695–10704. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Y.; Zhang, X.; Wang, B.; Ma, H. A model-data-hybrid-driven diagnosis method for open-switch faults in power converters. IEEE Trans. Power Electron. 2020, 36, 4965–4970. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Z.; Song, C.; Zhang, H. Multiscale adaptive fault diagnosis based on signal symmetry reconstitution preprocessing for microgrid inverter under changing load condition. IEEE Trans. Smart Grid. 2018, 9, 797–806. [Google Scholar] [CrossRef]
- Abdelkader, R.; Cherif, B.D.E.; Bendiabdellah, A.; Kaddour, A. An open-circuit faults diagnosis approach for three-phase inverters based on an improved variational mode decomposition, correlation coefficients, and statistical indicators. IEEE Trans. Instrum. Meas. 2022, 71, 3510109. [Google Scholar] [CrossRef]
- Hang, J.; Shu, X.; Ding, S.; Huang, Y. Robust open-circuit fault diagnosis for pmsm drives using wavelet convolutional neural network with small samples of normalized current vector trajectory graph. IEEE Trans. Ind. Electron. 2023, 70, 7653–7663. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Y.; Gou, B. A data-driven method for igbt open-circuit fault diagnosis based on hybrid ensemble learning and sliding-window classification. IEEE Trans. Ind. Inform. 2020, 16, 5223–5233. [Google Scholar] [CrossRef]
- Diao, N.; Zhang, Y.W.; Sun, X.; Song, C.; Wang, W.; Zhang, H. A real-time open-circuit fault diagnosis method based on hybrid model flux observer for voltage source inverter fed sensorless vector controlled drives. IEEE Trans. Power Electron. 2023, 38, 2539–2551. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Xu, M.; Ma, H. A comparative study of two diagnostic methods based on the switching voltage pattern for igbt open-circuit faults in voltage-source inverters. J. Power Electron. 2016, 16, 1087–1096. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Y.; Gou, B. Fault detection of open-switch damage in voltage-fed PWM motor drive systems. IEEE Trans. Power Electron. 2003, 18, 587–593. [Google Scholar]
- An, Q.T.; Sun, L.Z.; Zhao, K.; Sun, L. Switching function model-based fast-diagnostic method of open-switch faults in inverters without sensors. IEEE Trans. Power Electron. 2011, 26, 587–593. [Google Scholar] [CrossRef]
- Caseiro, L.M.A.; Mendes, A.M.S. Real-time IGBT open-circuit fault diagnosis in three-level neutral-point-clamped voltage-source rectifiers based on instant voltage error. IEEE Trans. Ind. Electron. 2014, 62, 1669–1678. [Google Scholar] [CrossRef]
- Karimi, S.; Poure, P.; Saadate, S. Fast power switch failure detection for fault tolerant voltage source inverters using FPGA. IET Power Electron. 2009, 2, 346–354. [Google Scholar] [CrossRef]
- Li, Z.; Ma, H.; Bai, Z.; Wang, Y.; Wang, B. Fast transistor open-circuit faults diagnosis in grid-tied three-phase VSIs based on average bridge arm pole-to-pole voltages and error-adaptive thresholds. IEEE Tran. Power Electron. 2017, 33, 8040–8051. [Google Scholar] [CrossRef]
- Zhao, H.; Cheng, L. Open-switch fault-diagnostic method for back-to-back converters of a doubly fed wind power generation system. IEEE Trans. Power Electron. 2017, 33, 3452–3461. [Google Scholar] [CrossRef]
- Yan, H.; Xu, Y.; Zou, J.; Fang, Y.; Cai, F. A novel open-circuit fault diagnosis method for voltage source inverters with a single current sensor. IEEE Trans. Power Electron. 2017, 33, 8775–8786. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, S.; Yoo, D.S.; Kim, K.H. A diagnostic method of simultaneous open-switch faults in inverter-fed linear induction motor drive for reliability enhancement. IEEE Trans. Ind. Electron. 2014, 62, 4065–4077. [Google Scholar] [CrossRef]
- Zidani, F.; Diallo, D.; Benbouzid, M.E.H.; Naït-Saïd, R. A fuzzy-based approach for the diagnosis of fault modes in a voltage-fed PWM inverter induction motor drive. IEEE Trans. Ind. Electron. 2008, 55, 586–593. [Google Scholar] [CrossRef]
- Freire, N.M.A.; Estima, J.O.; Cardoso, A.J.M. Open-circuit fault diagnosis in PMSG drives for wind turbine applications. IEEE Trans. Ind. Electron. 2012, 60, 3957–3967. [Google Scholar] [CrossRef]
- Estima, J.O.; Cardoso, A.J.M. A new approach for real-time multiple open-circuit fault diagnosis in voltage-source inverters. IEEE Trans. Ind. Appl. 2011, 47, 2487–2494. [Google Scholar] [CrossRef]
- Hajary, A.; Kianinezhad, R.; Seifossadat, S.G.; Mortazavi, S.S.; Saffarian, A. Detection and localization of open-phase fault in three-phase induction motor drives using second order rotational park transformation. IEEE Trans. Power Electron. 2019, 34, 11241–11252. [Google Scholar] [CrossRef]
- Zhou, D.; Li, Y.; Zhao, J.; Wu, F.; Luo, H. An embedded closed-loop fault-tolerant control scheme for nonredundant VSI-fed induction motor drives. IEEE Trans. Power Electron. 2016, 32, 3731–3740. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z.; Zhang, H. A diagnosis algorithm for multiple open-circuited faults of microgrid inverters based on main fault component analysis. IEEE Trans. Energy Convers. 2018, 33, 925–937. [Google Scholar] [CrossRef]
- Bae, C.J.; Lee, D.C.; Nguyen, T.H. Detection and identification of multiple IGBT open-circuit faults in PWM inverters for AC machine drives. IET Power Electron. 2019, 12, 923–931. [Google Scholar] [CrossRef]
- Estima, J.O.; Cardoso, A.J.M. A new algorithm for real-time multiple open-circuit fault diagnosis in voltage-fed PWM motor drives by the reference current errors. IEEE Trans. Ind. Electron. 2012, 60, 3496–3505. [Google Scholar] [CrossRef]
- Chen, T.; Pan, Y. Current vector phase-based diagnostic method for multiple open-circuit faults in voltage-source inverters. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 1005–1012. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z. A fault diagnosis algorithm for microgrid three-phase inverter based on trend relationship of adjacent fold lines. IEEE Trans. Ind. Inform. 2020, 16, 267–276. [Google Scholar] [CrossRef]
- Song, C.; Zhao, X.; Sun, X.; Diao, N.; Zhao, J. Fast in-loop single-tube open-circuit fault diagnosis for voltage source inverter based on duality of current-time pairs. IEEE Trans. Ind. Electron. 2023, 70, 9572–9581. [Google Scholar] [CrossRef]
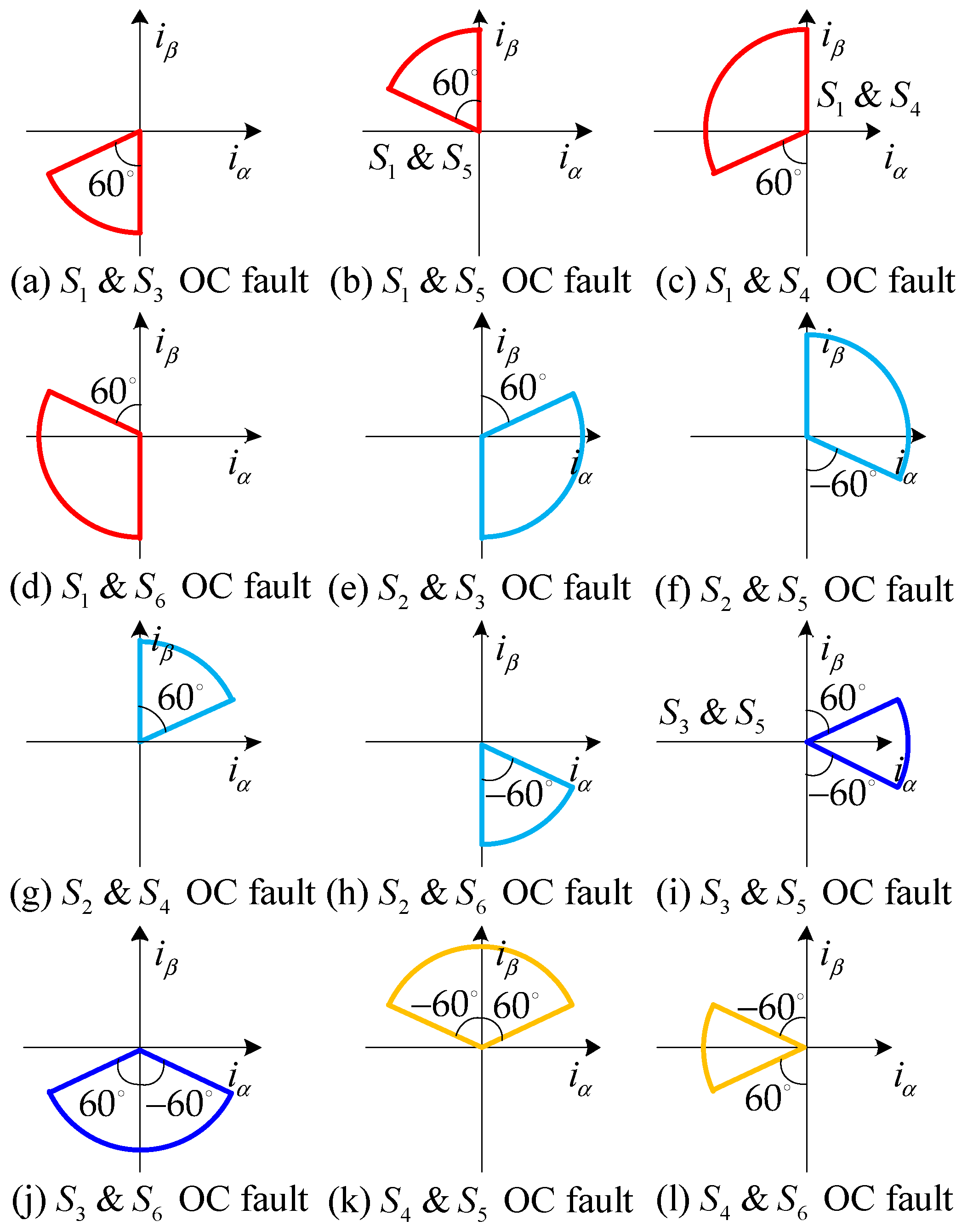


| Fault Type | Fault Location | ||||||
|---|---|---|---|---|---|---|---|
| Single- switch OC fault | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | ||
| Multiple-switch OC Faults | 1 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 1 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | 1 | 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | 1 | 0 | ||
| 0 | 1 | 0 | 0 | 0 | 1 | ||
| 0 | 0 | 1 | 0 | 1 | 0 | ||
| 0 | 0 | 1 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 | 1 | 0 | ||
| 0 | 0 | 0 | 1 | 0 | 1 |
| Parameters | Symbol | Value |
|---|---|---|
| DC bus voltage | 540 V | |
| Motor rated power | 2.2 kw | |
| Motor rated voltage | 380 V | |
| Motor rated frequency | 50 Hz | |
| Motor rated current | 5.8 A | |
| Pole logarithm | 2 |
| Research Algorithms | [23] | [24] | [21] | [43] | Proposed Method |
|---|---|---|---|---|---|
| Consider load variation | yes | no | yes | yes | yes |
| Consider multiple-switch faults | no | yes | yes | no | yes |
| Parameter sensitivity | yes | no | no | no | no |
| Computational complexity | medium | low | high | low | low |
| Extra hardware circuit | no | yes | no | no | no |
| Diagnosis time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Diao, N.; Song, C.; Qiu, Y.; Zhao, X. An Open-Circuit Fault Diagnosis Method Based on Adjacent Trend Line Relationship of Current Vector Trajectory for Motor Drive Inverter. Machines 2023, 11, 928. https://doi.org/10.3390/machines11100928
Sun X, Diao N, Song C, Qiu Y, Zhao X. An Open-Circuit Fault Diagnosis Method Based on Adjacent Trend Line Relationship of Current Vector Trajectory for Motor Drive Inverter. Machines. 2023; 11(10):928. https://doi.org/10.3390/machines11100928
Chicago/Turabian StyleSun, Xianrui, Naizhe Diao, Chonghui Song, Yunlong Qiu, and Xiaolong Zhao. 2023. "An Open-Circuit Fault Diagnosis Method Based on Adjacent Trend Line Relationship of Current Vector Trajectory for Motor Drive Inverter" Machines 11, no. 10: 928. https://doi.org/10.3390/machines11100928
APA StyleSun, X., Diao, N., Song, C., Qiu, Y., & Zhao, X. (2023). An Open-Circuit Fault Diagnosis Method Based on Adjacent Trend Line Relationship of Current Vector Trajectory for Motor Drive Inverter. Machines, 11(10), 928. https://doi.org/10.3390/machines11100928






