1. Introduction
Precise high-end machining centers play a critical role in high-performance manufacturing due to their ability to carry out complex and diverse processes [
1]. In the realm of high-performance machining and manufacturing, the tool serves as the direct executor of the machining process and is prone to chemical wear, physical wear, and various abnormal states, all of which directly impact the surface quality, machining accuracy, and overall lifespan of the workpiece [
2]. Consequently, the state of the tool significantly influences the quality of the workpiece during the machining process. According to statistics from the period between 2000 and 2010, approximately 20% of machine tool shutdowns can be attributed to tool failures, resulting in actual service lives that range from 50% to 80% of the recommended service life [
3,
4]. Although the data are relatively outdated, annual economic loss directly or indirectly caused by tool failure is still very large. Therefore, tool wear monitoring technology has garnered extensive attention from industrial engineers and scientific researchers. Monitoring the state of tool wear holds enormous significance for maintaining cutting performance and ensuring the surface quality of the workpiece, thereby mitigating adverse effects caused by worn-out tools on both the workpiece and the processing equipment [
5].
Monitoring tool wear state involves two primary steps: collecting the data generated during the tool wear process and building a model based on this data to predict tool wear state. According to the type of data collected, they can be divided into direct method and indirect method. In the direct method, an image of the worn tool is captured using a CCD camera and a lighting unit. The information within the image is then utilized to predict the tool wear state. Kerr et al. [
6] used digital image-processing technology to analyze the wear image of the tool and complete the evaluation of the tool wear state. Kassim et al. [
7] utilized tool surface texture to indicate wear status and conducted tool status monitoring using machine vision techniques including image enhancement and segmentation. The field of tool wear state monitoring has seen extensive application of computer vision technology due to advancements in information technology. Zhou et al. [
8] successfully detected tool wear state on-site by applying computer vision technology based on deep learning, significantly enhancing detection efficiency.
The direct method offers a significant advantage due to its versatility in addressing various machine tools and cutting conditions, enabling precise outcomes through the implementation of machine vision and computer vision technologies. Nonetheless, challenges emerge from issues such as the splashing of cutting fluid during machining and the spatial orientation of the tool on the workpiece, which hinder the acquisition of tool images. Moreover, avoiding the uneven distribution of light on a curved tool’s surface when capturing images poses a challenge. As a result, the demanding processing environment, the constrained and intricate spatial relationship between the tool and the workpiece, and the lighting intricacies during image capture confine direct measurement technology primarily to laboratory settings, with limited applicability in industrial contexts.
The indirect approach involves monitoring signals during the cutting process, including cutting force, acoustic emission, and current, among others, to forecast the tool’s condition. Silva et al. [
9] believed that cutting force becomes highly responsive to friction after tool wear, rendering it the most dependable technique for prognosticating the tool’s wear state through the utilization of cutting force data obtained from the dynamometer. The gradual deterioration of the tool is intricately linked to the material’s brittle fracture and plastic deformation. Wang et al. [
10] leveraged the clustering energy of the AE burst signal as a means to decide the wear state of the tool flank. Loenzo et al. [
11] comprehensively investigated cutting tool lifecycle from initial use to failure, subsequently discovering the capacity of cumulative cutting power to accurately pinpoint the tool’s fractured condition. Despite the capability of these indirect measurement technologies to monitor tool wear state, practical application is significantly curtailed by the intricate and personalized sensor installation and fixation procedures, coupled with their substantial cost.
Sensors for acoustic and vibration signals have attracted the attention of researchers due to their affordability and ease of installation. Li et al. [
12] employed Fast Fourier Transform (FFT) and a band-pass filter to eliminate acoustic signal noise during the cutting process. Subsequently, they applied the Blind Source Separation (BSS) algorithm for denoising. Following initial signal preprocessing, Short-Time Fourier Transform (STFT), Power Coherence Transform (PCT), and Wigner–Ville Distribution (WVD) were employed to individually convert the audio signal into spectrogram images. The identification of tool wear state was conducted by integrating three sub-Convolutional Neural Network (CNN) models. Zhou et al. [
13] monitored tool wear acoustics using a two-layer angular kernel Extreme Learning Machine (ELM), utilizing a subset of acoustic sensor parameters for wear condition identification. Prakash and Samraj [
14] applied Singular Value Decomposition (SVD) to analyze acoustic signals for tool wear monitoring in close-gap turning. Vibration, akin to cutting force, also exhibits strong sensitivity to tool conditions. Shi et al. [
15] achieved tool wear prediction by extracting multi-dimensional features from distinct feature domains in the original vibration signal. Twardowski et al. [
16] predicted tool wear in cast iron milling through various machine learning classification tree forms using vibration signals. Bahador et al. [
17] introduced tool wear detection in the turning process utilizing a one-dimension neural network and transfer learning. Wang et al. [
18] transformed vibration sensor data into images, serving as inputs for CNN models to monitor mechanical fault conditions in the manufacturing industry. Whether relying on acoustic or vibration signals or not, individual sensors often provide incomplete signal information due to inherent limitations and environmental interference.
The method of multi-sensor fusion monitoring harnesses the synergistic advantages of multiple sensor signals, thereby improving anti-interference capabilities and ensuring a more comprehensive monitoring signal. This establishes a robust correlation with tool wear [
19]. Rafezi et al. [
20] monitored tool wear utilizing both acoustic and vibration signals in tandem with Wavelet Packet Decomposition (WPD). Similarly, Gomes et al. [
21] employed Support Vector Machines (SVM) to analyze vibration and sound signals, subsequently leveraging Recursive Feature Elimination (RFE) to discern the most pertinent features for tool wear during micro milling. Not all features from multi-source signals are relevant to the model, underscoring the significance of feature selection strategy. Niaki et al. [
22] implemented Principal Component Analysis (PCA) to categorize monitoring features, thus eliminating superfluous and irrelevant data to bolster monitoring accuracy. Meanwhile, Niu et al. [
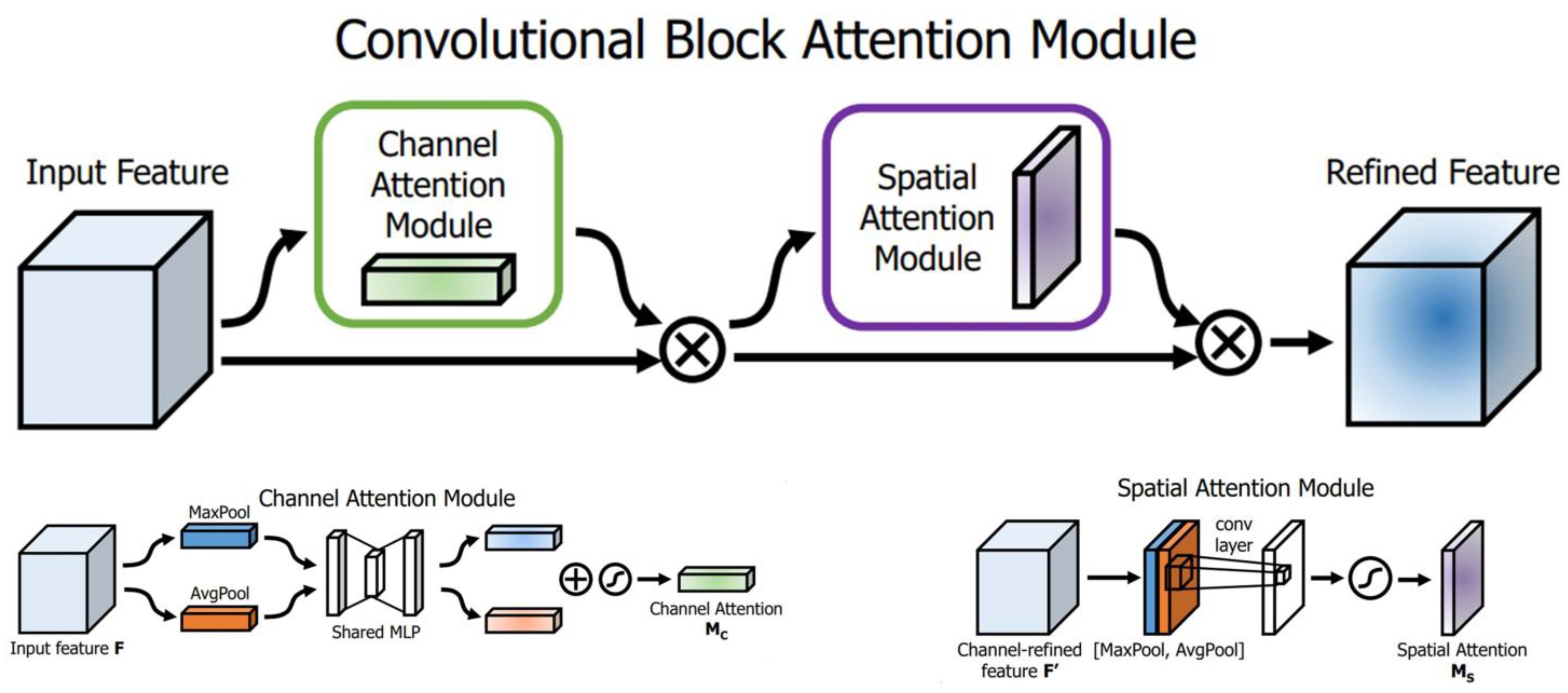
23] extracted features from time, frequency, and time-frequency domains, utilizing an information measure-based feature selection method to reduce dimensionality, selecting those features strongly correlated with tool wear. However, the above feature selection strategy does not consider the relevant information about the tool itself. In addition, the importance of features cannot be adaptively adjusted according to changes in features. However, the attention module in deep learning can selectively highlight those more discriminative features. Moreover, the pyramid convolution-pooling module can collect and fuse features at multiple scales. Therefore, this research endeavors to amalgamate multi-sensor features with intrinsic tool characteristics to craft a vibroacoustic signal fusion feature infographic for the cutting process. Employing deep learning techniques, a convolutional neural network is devised to discern the condition of a worn tool using this infographic.
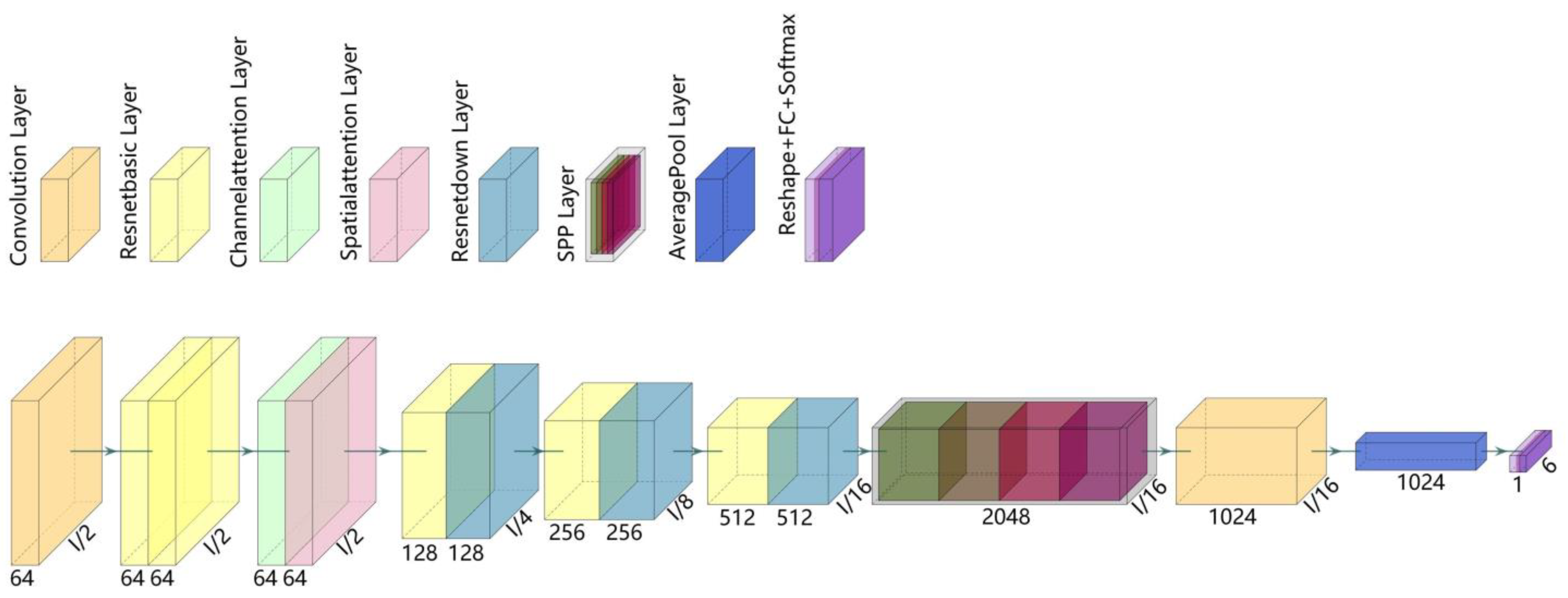
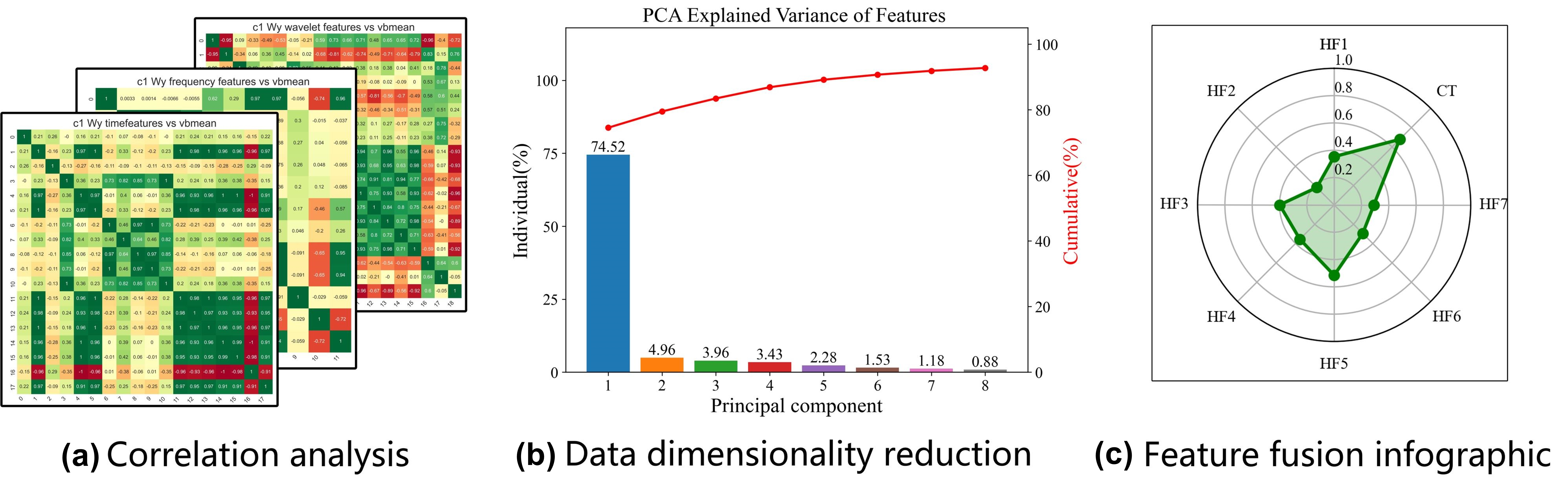
In this study, we initially process the features of multi-sensor signals across multiple domains. The selected features are those acutely sensitive to and strongly correlated with tool wear. These salient features are fused using Principal Component Analysis (PCA). An infographic based on fused features and the cut times is constructed. The fused feature map contains feature information that is highly related to tool wear and the intrinsic information of the tool. Then, we introduce a double-attention pyramid convolutional network model, devised to adaptively discern features within infographics crucial for tool wear state identification. The dual-attention module adeptly extracts spatial features and judiciously allocates them. To mitigate challenges like vanishing gradients in deep networks, our model employs residual blocks. Additionally, the spatial pyramid convolution-pooling module captures pertinent information across various scales within the network. Hence, this research leverages machine learning and computer vision methodologies to identify tool wear state. The fusion of multi-sensor signal features into an infographic, in tandem with the double-attention pyramid convolutional network model, is helpful in elevating the precision and accuracy of tool wear state identification.
The paper is structured as follows:
Section 2.1 details the creation of the vibroacoustic signal fusion feature infographic.
Section 2.2 presents the fundamental theory of the network architecture, followed by descriptions of its constituent modules.
Section 2.3 outlines the tool wear state identification methodology.
Section 3.1 describes the experimental setup and data collection process.
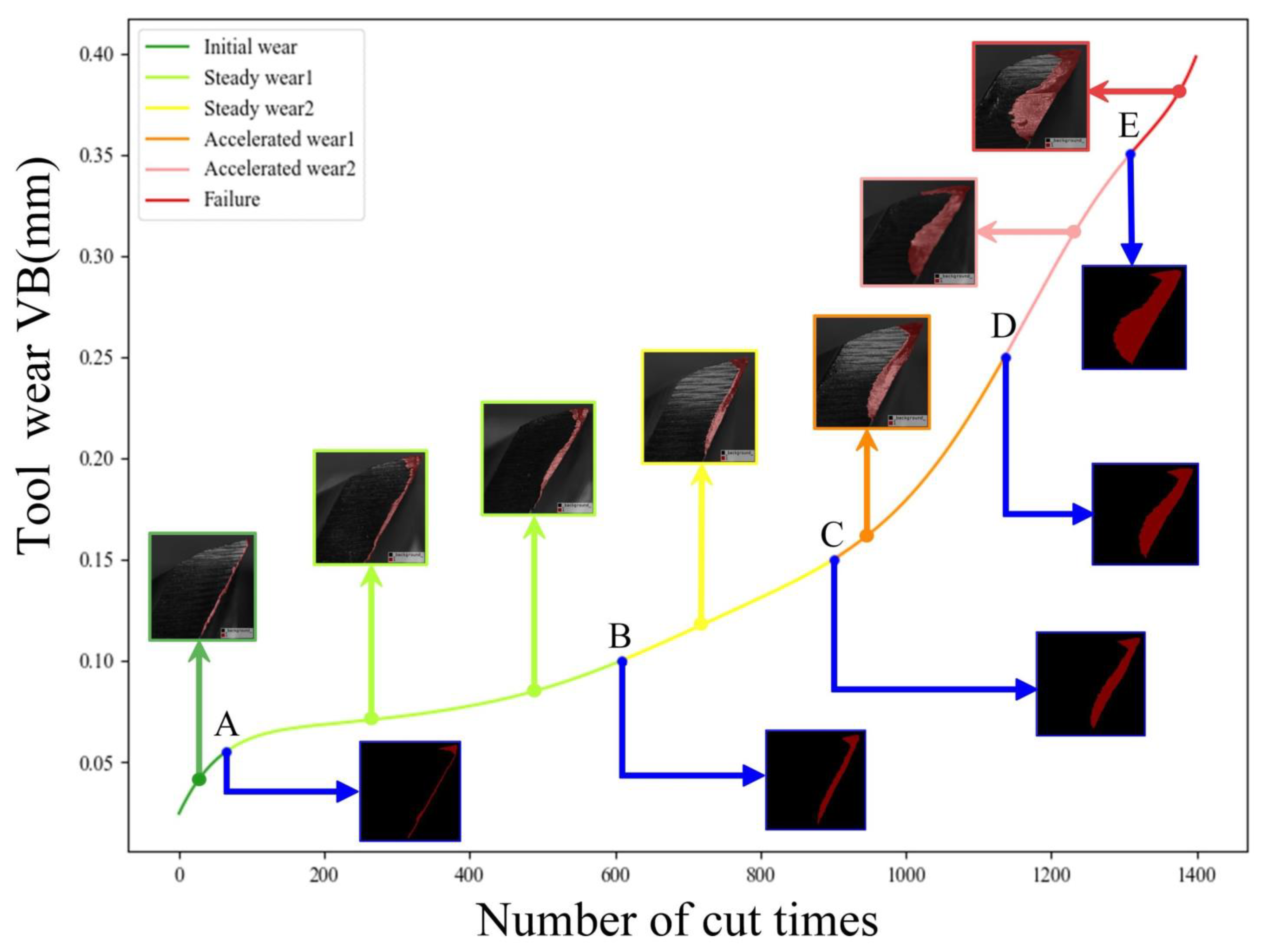
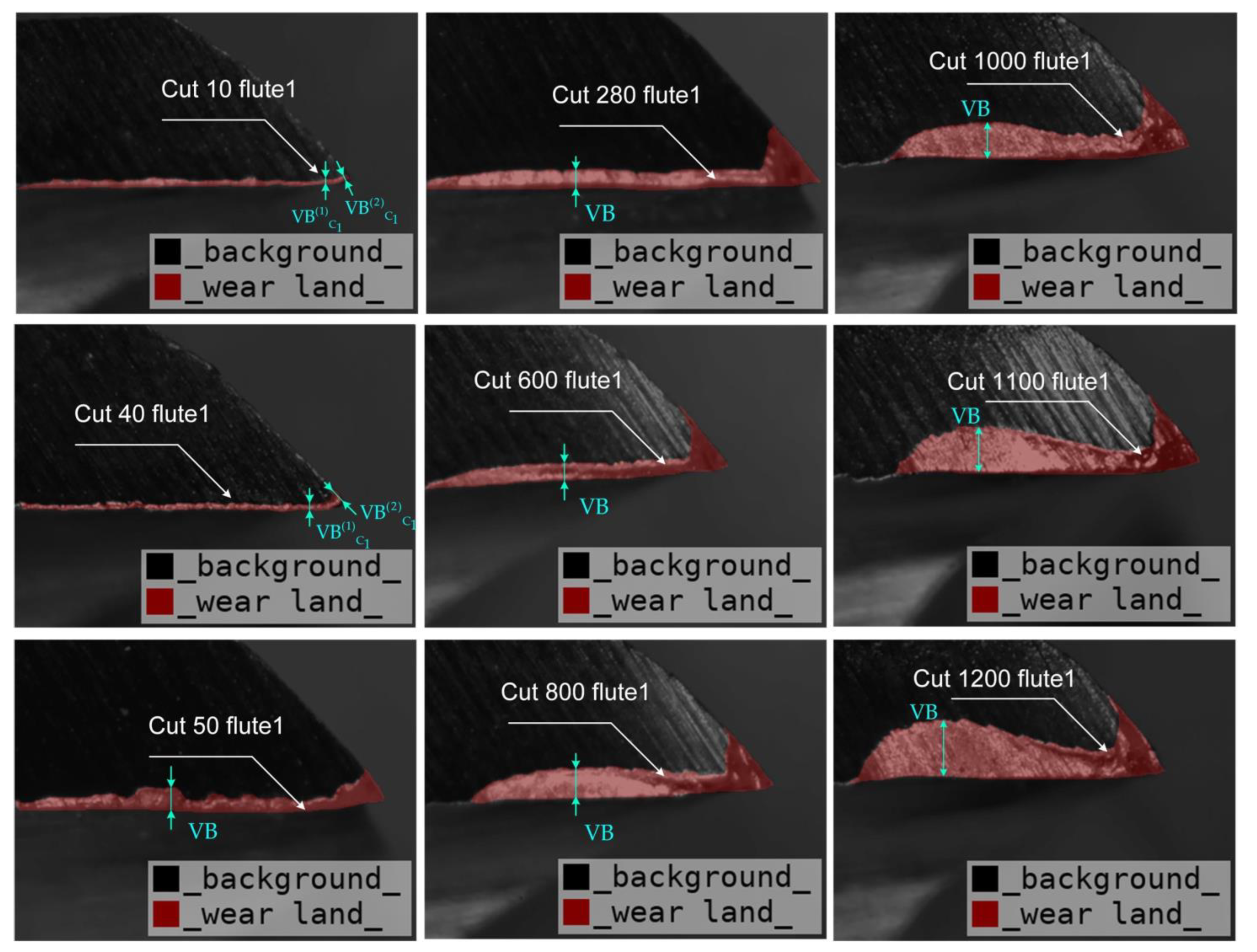
Section 3.2 focuses on the measurement of flank wear VB during experiments.
Section 3.3 discusses data preprocessing and the utilization of the dataset for model training and validation. In
Section 4.1, we compare the training and performance of various models.
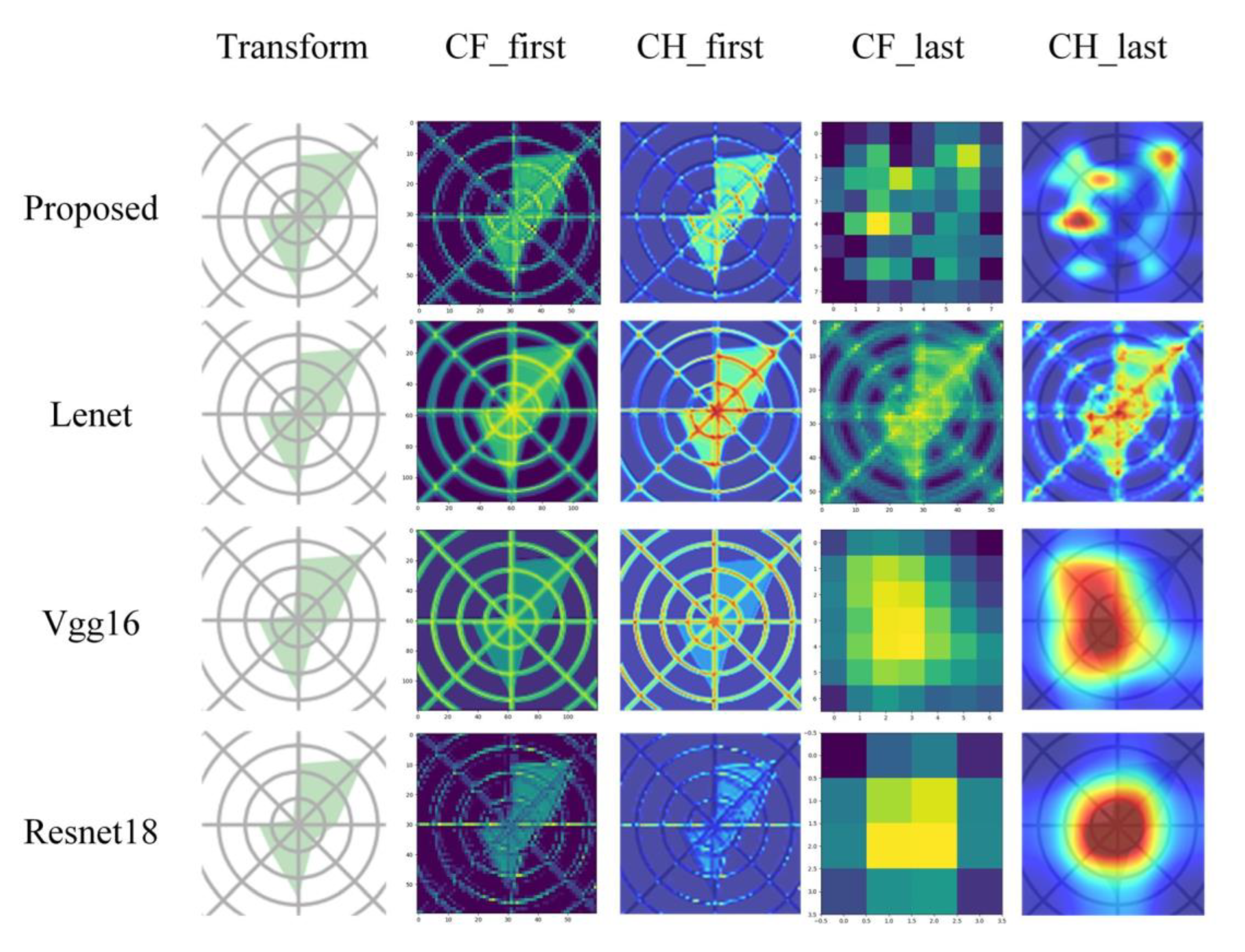
Section 4.2 delves into model interpretability. Finally, conclusions and prospects are addressed in
Section 5.
5. Conclusions and Future Work
Comprehensive experiments and model comparisons validate the efficacy of the method of identification of tool wear. There are some conclusions as follows:
1. The proposed vibroacoustic signal fusion feature infographic effectively amalgamates information directly related to tool wear. It not only minimizes noise interference from signal features but also captures the dynamic attributes of the cutting process.
2. The double-attention mechanism applied in our proposed model focusing on channels and spatial aspects adaptively perceives network weight for infographics associated with wear categories. Notably, when benchmarked against Resnet18, the double-attention model built on infographics elevates the F1 score by 13.4%, exhibiting superior accuracy, precision, and recall.
In future work, because of the inconsistent dynamic nature of machine tools, we will collect data from different machine tools under different cutting conditions to augment the dataset to enhance the robustness of the model.