Narrow Tilting Vehicle Drifting Robust Control
Abstract
1. Introduction
2. Narrow Tilting Vehicle Dynamics System for Drifting Controller Design
2.1. Narrow Tilting Vehicle Dynamics Equations
2.2. Vertical Load Transfer
2.3. Tire Models and Equations
2.3.1. UniTire
2.3.2. The Linearized Tire Equations
3. Narrow Tilting Vehicle Drifting Controller Design
3.1. Controller System State-Space Expression
3.2. Robust Controller
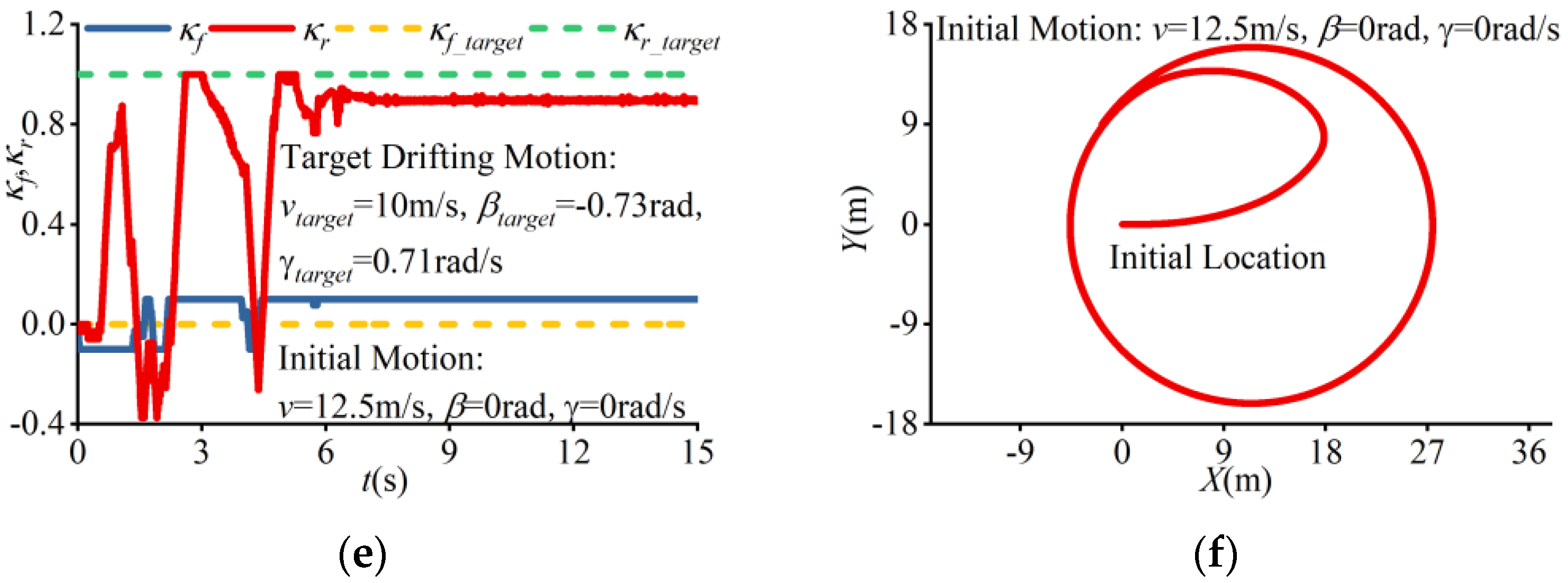
4. Narrow Tilting Vehicle Drifting Control Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- China Association of Automobile Manufacturers. Available online: http://en.caam.org.cn/Index/show/catid/57/id/1864.html (accessed on 15 November 2022).
- World Health Organization. Available online: https://www.who.int/news-room/fact-sheets/detail/the-top-10-causes-of-death (accessed on 9 December 2020).
- World Health Organization. Available online: https://www.who.int/publications/i/item/9789241565684 (accessed on 17 June 2018).
- World Health Organization. Available online: https://www.who.int/zh/news/item/30-06-2022-new-political-declaration-to-halve-road-traffic-deaths-and-injuries-by-2030-is-a-milestone-achievement (accessed on 30 June 2022).
- Wu, J.; Tian, Y.; Walker, P.; Li, Y. Attenuation Reference Model Based Adaptive Speed Control Tactic for Automatic Steering System. Mech. Syst. Signal Process. 2021, 156, 107631. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Yu, Y.; Zhang, Z.; Zheng, L. Study on Local Path Planning and Tracking Algorithm of Intelligent Vehicle in Complex Dynamics Environment. China J. Highw. Transp. 2022, 35, 372–386. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, J.; Tian, Y.; Li, L. A Novel Adaptive Steering Torque Control Approach for Human-Machine-Cooperation Autonomous Vehicles. IEEE Trans. Transp. Electrif. 2021, 7, 2516–2525. [Google Scholar] [CrossRef]
- Claveau, F.; Chevrel, P.; Mourad, L. Non-Linear Control of a Narrow Tilting Vehicle. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics, San Diego, CA, USA, 5–8 October 2014. [Google Scholar] [CrossRef]
- Mourad, F.; Claveau, F.; Chevrel, P. Design of a Two DOF Gain Scheduled Frequency Shaped LQ Controller for Narrow Tilting Vehicles. In Proceedings of the 2012 American Control Conference, Montreal, Canada, 27–29 June 2012. [Google Scholar] [CrossRef]
- Barker, M.; Drew, B.; Darling, J.; Edge, K.A.; Owen, G.W. Steady-State Steering of a Tilting Three-Wheeled Vehicle. Veh. Syst. Dyn. 2010, 48, 815–830. [Google Scholar] [CrossRef]
- Rajamani, R.; Gohl, L.; Alexander, L.; Starr, P. Dynamics of Narrow Tilting Vehicles. Math. Comput. Model. Dyn. Syst. 2003, 9, 209–231. [Google Scholar] [CrossRef]
- Zhang, J. Research on Active Tilt Control Technology for Vehicle Steering. Master’s Thesis, China Agricultural University, Beijing, China, 2022. [Google Scholar]
- Liu, P.; Ke, C.; Gao, R.; Li, H.; Wei, W.; Wang, Y. Design and Test of Active Roll Vehicle. Automot. Eng. 2020, 42, 1552–1557, 1584. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Gao, R.; Wang, Y.; Wei, W.; Wang, B. Research and Test on the Stability of Active Rollover Three-wheeled Vehicle. In Proceedings of the 2021 China SAE Congress and Exhibition (SAECCE), Shanghai, China, 19–21 October 2021. [Google Scholar]
- Gao, R.; Li, H.; Zhang, J.; Wang, Y.; Wei, W.; Wang, B. Research on Steering Comfort of Active Tilting Vehicles. In Proceedings of the 2021 China SAE Congress and Exhibition (SAECCE), Shanghai, China, 19–21 October 2021. [Google Scholar]
- Bianco, A.D.; Roberto, L.; Marco, M. Minimum Time Optimal Control Simulation of a GP2 Race Car. Inst. Mech. Eng. J. Automob. Eng. 2018, 232, 1180–2232. [Google Scholar] [CrossRef]
- Velenis, E.; Frazzoli, E.; Tsiotras, P. On Steady-State Cornering Equilibria for Wheeled Vehicles with Drift. In Proceedings of the Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, China, 16–18 December 2009. [Google Scholar]
- Zhang, F. Trajectory Planning and Motion Control for Extreme Maneuvers of Autonomous Vehicles. Ph.D. Thesis, Tsinghua University, Beijing, China, 2018. [Google Scholar]
- Li, B. Study on Rear Distributed Drive Vehicles Control under Extreme Drifting Maneuvers. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Jelavic, E.; Gonzales, J.; Borrelli, F. Autonomous Drift Parking using a Switched Control Strategy with Onboard Sensors. Sci. Direct 2017, 50, 2714–3719. [Google Scholar] [CrossRef]
- Qiao, W. Research on the Control Method of Vehicle Drifting Motion under Extreme Conditions. Master’s Thesis, Haerbin Institute of Technology, Haerbin, China, 2022. [Google Scholar]
- Wang, H.; Zuo, J.; Liu, S.; Zheng, W.; Wang, L. Model-free adaptive control of steady-state drift of unmanned vehicles. Control. Theory Appl. 2021, 38, 23–32. [Google Scholar] [CrossRef]
- Spielberg, N.A.; Brown, M.; Kapania, N.R.; Kegelman, J.C.; Gerdes, J.C. Neural network vehicle models for high-performance automated driving. Sci. Robot. 2019, 4, eaaw1975. [Google Scholar] [CrossRef] [PubMed]
- Pacejka, H.B. Tyre and Vehicle Model, 2nd ed.; Elsevier: Oxford, UK, 2006; pp. 16–60. [Google Scholar]
- Zuoqiweilai. Available online: http://www.allinride.com/ (accessed on 5 December 2022).
- Guo, K.; Lu, D.; Chen, S.; Lin, W.C.; Lu, X. The UniTire model: A nonlinear and non-steady-state tyre model for vehicle dynamics simulation. Veh. Syst. Dyn. 2005, 43, 341–358. [Google Scholar] [CrossRef]
- Guo, K. UniTire: Unified Tire Model. J. Mech. Eng. 2016, 52, 90–98. [Google Scholar] [CrossRef]
- Xu, N. Study on the Steady State Tire Model under Combined Conditions. Ph.D. Thesis, Jilin University, Changchun, China, 2012. [Google Scholar]
- Wu, J.; Kong, Q.; Yang, K.; Liu, Y.; Cao, D.; Li, Z. Research on the Steering Torque Control for Intelligent Vehicles Co-Driving with the Penalty Factor of Human–Machine Intervention. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 59–70. [Google Scholar] [CrossRef]
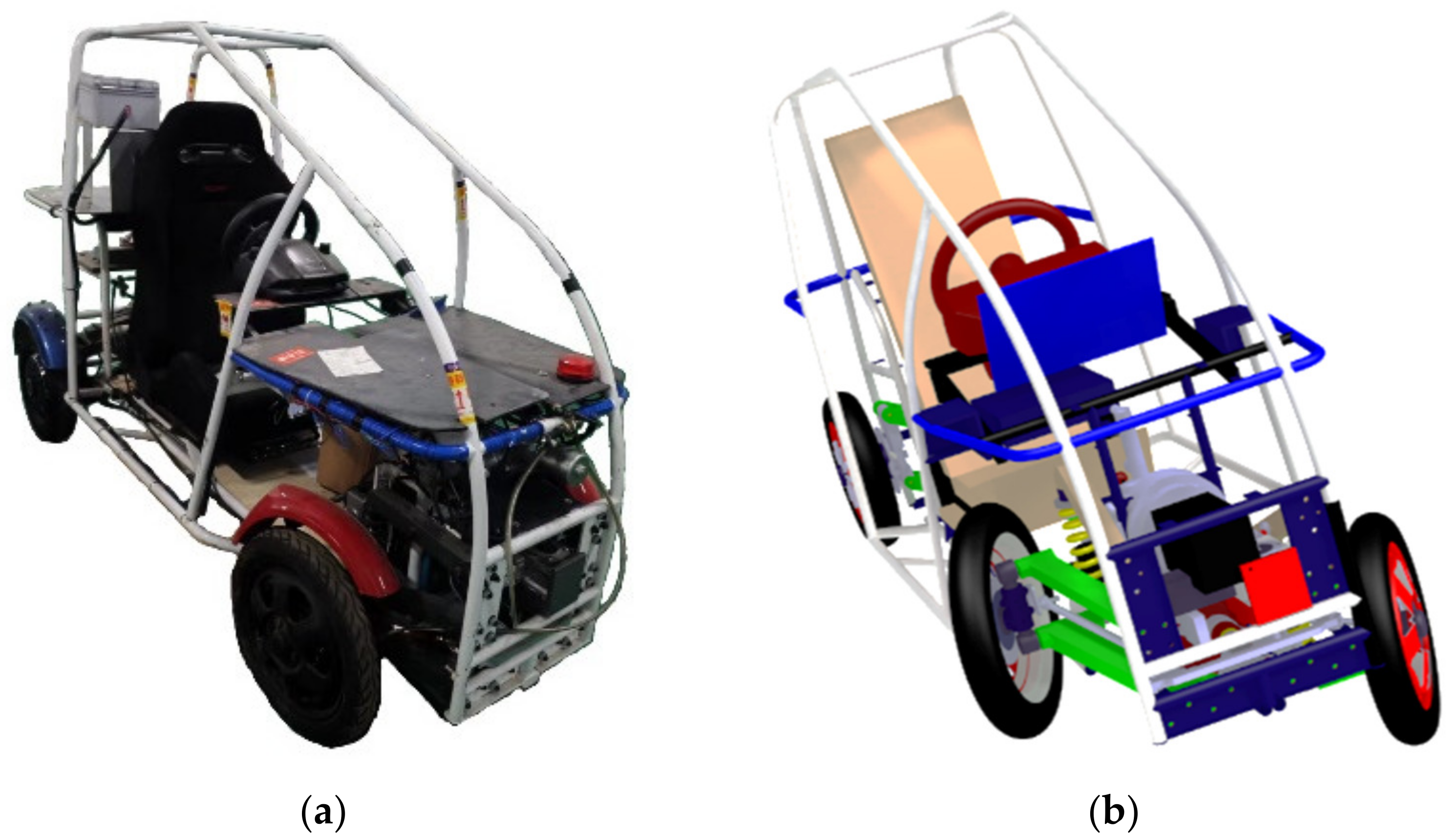














| 237.1 kg | 195.4 kg | 243.2 kg∙m2 | 0.73 m | 0.80 m | 0.68 m | 0.70 m | 0.42 m |
| Target Group | |||||||
|---|---|---|---|---|---|---|---|
| (1) | 3.49 m/s | −0.32 rad | 1.95 rad/s | 0.1 rad | 0 | 0.64 | 0.75 |
| (2) | 10 m/s | −0.73 rad | 0.71 rad/s | −0.35 rad | 0 | 1 | 0.75 |
| Initial Group | |||||||
|---|---|---|---|---|---|---|---|
| (1) | 5 m/s | 0 rad | 0 rad/s | 0 rad | 0 | 0 | 0.75 |
| (2) | 8 m/s | 0 rad | 0 rad/s | 0 rad | 0 | 0 | 0.75 |
| (3) | 10 m/s | 0 rad | 0 rad/s | 0 rad | 0 | 0 | 0.75 |
| (4) | 12.5 m/s | 0 rad | 0 rad/s | 0 rad | 0 | 0 | 0.75 |
| (5) * | 6 m/s | −0.72 rad | 1.16 rad/s | −0.34 rad | 0 | 1 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Han, Y.; Han, X.; Wang, Y.; Wang, G. Narrow Tilting Vehicle Drifting Robust Control. Machines 2023, 11, 90. https://doi.org/10.3390/machines11010090
Xu D, Han Y, Han X, Wang Y, Wang G. Narrow Tilting Vehicle Drifting Robust Control. Machines. 2023; 11(1):90. https://doi.org/10.3390/machines11010090
Chicago/Turabian StyleXu, Dongxin, Yueqiang Han, Xianghui Han, Ya Wang, and Guoye Wang. 2023. "Narrow Tilting Vehicle Drifting Robust Control" Machines 11, no. 1: 90. https://doi.org/10.3390/machines11010090
APA StyleXu, D., Han, Y., Han, X., Wang, Y., & Wang, G. (2023). Narrow Tilting Vehicle Drifting Robust Control. Machines, 11(1), 90. https://doi.org/10.3390/machines11010090






