Model Predictive Control Method for Autonomous Vehicles in Roundabouts †
Abstract
1. Introduction
1.1. Introduction
1.2. Related Works
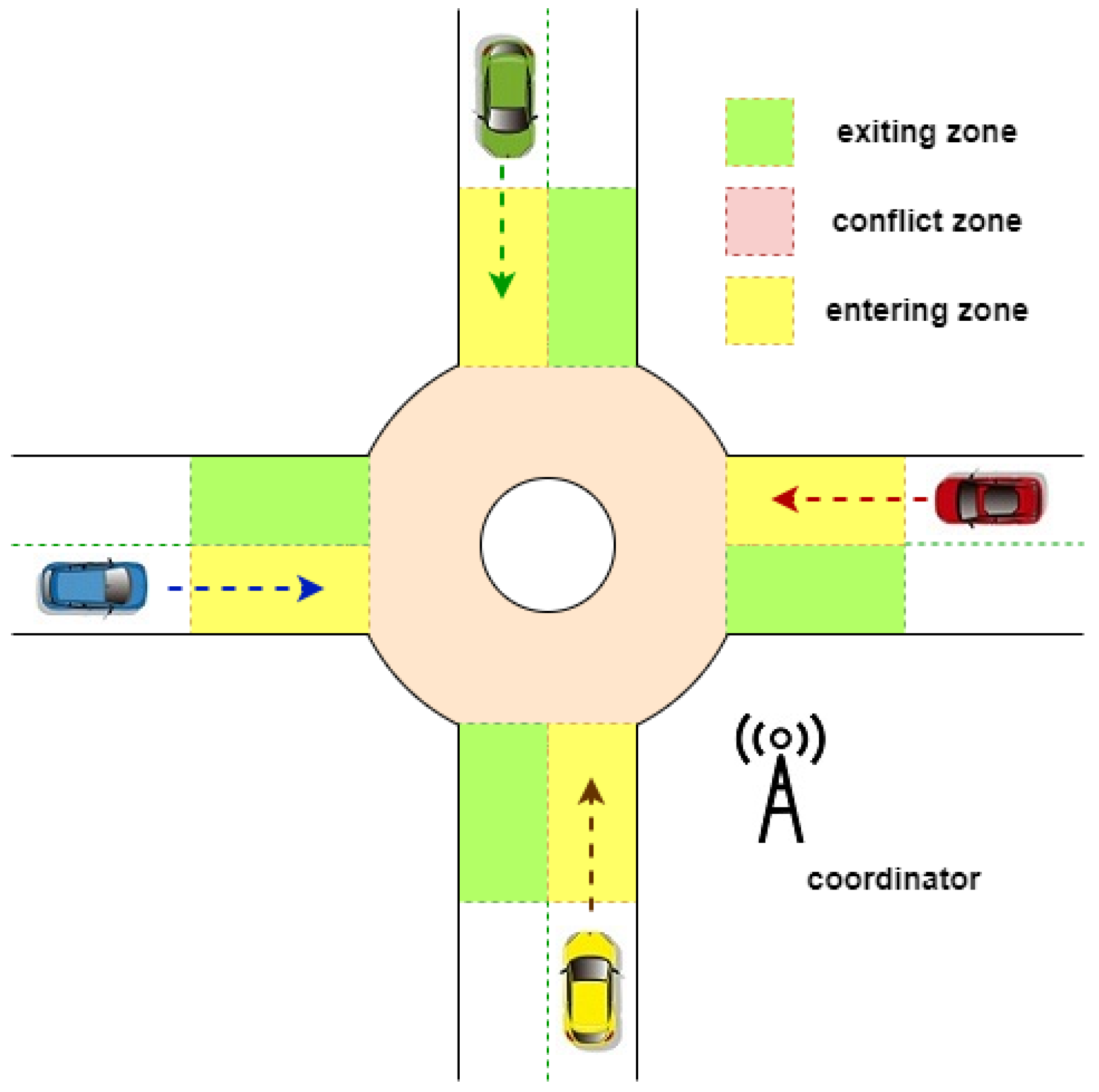
2. Problem Statement
- Safety criteria: automated vehicles may be in an accident-prone situation when approaching the roundabout. Accordingly, the purpose of the roundabout controller is to ensure that incoming AVs enter the roundabout simultaneously, so that any collision can be eliminated.
- Traveling time and efficiency criteria: depending on the geometrical parameters of the roundabout and the road surface friction, the automated vehicles try to drive into the roundabout at the required maximum speed.
- Based on the initial vehicle entry data, the centralized model predictive controller defines the entering and exiting times of AVs entering the roundabout at each time step, assuming AVs are accelerating to the required maximum speed and decelerating with a constant value.
- Based on the comparison of the entry times obtained as a result of the above calculation, the latest entry vehicle is selected, the acceleration of which thus remains unchanged on the basis of the above calculation. Acceleration of additional vehicles will be reduced until their entry time is the same as the latest entry vehicle time.
3. Roundabout Control Method for Autonomous Vehicles
3.1. Roundabout Scenario
3.2. Constraints for the Control Design
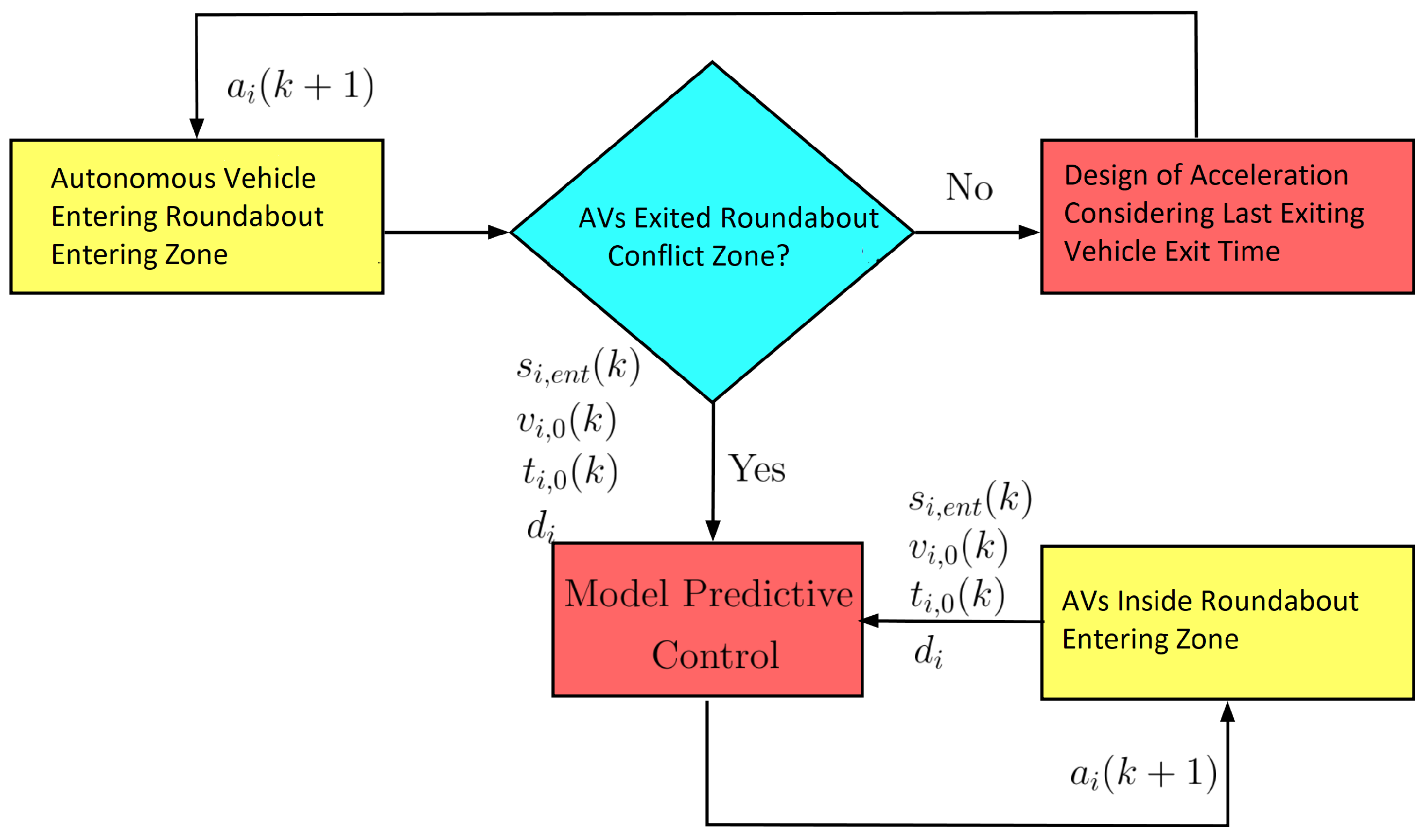
3.3. Time-Optimal Roundabout Control Design
- First, the maximum vehicle speed i∈ [] is defined for each vehicle, based on initial velocity and position, and the adhesion of the road and the roundabout geometry, along with the predefined acceleration limits. Corresponding acceleration values i∈ [] are calculated for each vehicle.
- The vehicle having the maximal entry time is selected as benchmark, while the acceleration values of other AVs are decreased iteratively; their entry time given in (6) becomes equal to the maximal entry time, i.e., ∀i∈ [].
- Lastly, in the case that additional vehicles approach the roundabout and the AVs inside the conflict zone exit, the procedure is repeated with new initial conditions for all vehicles. In the case that the conflict zone is still employed by AVs, the entry times of the new entering vehicles are set with the following constraint considered: ∀i∈ []. Hence, the newly entered AVs might decrease their velocities in order not to conflict with the last AV exiting the roundabout.
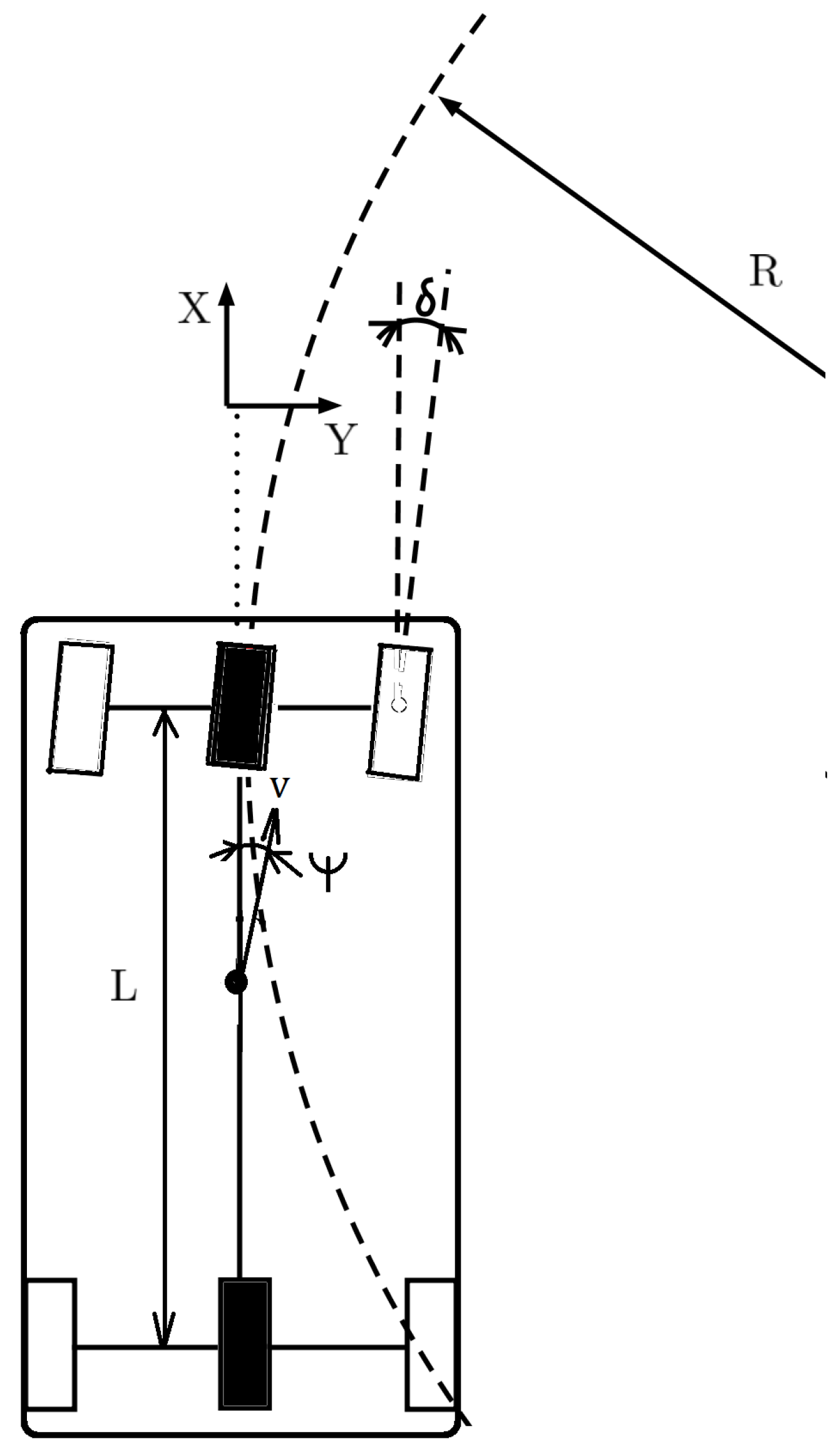
3.4. Trajectory Tracking Control
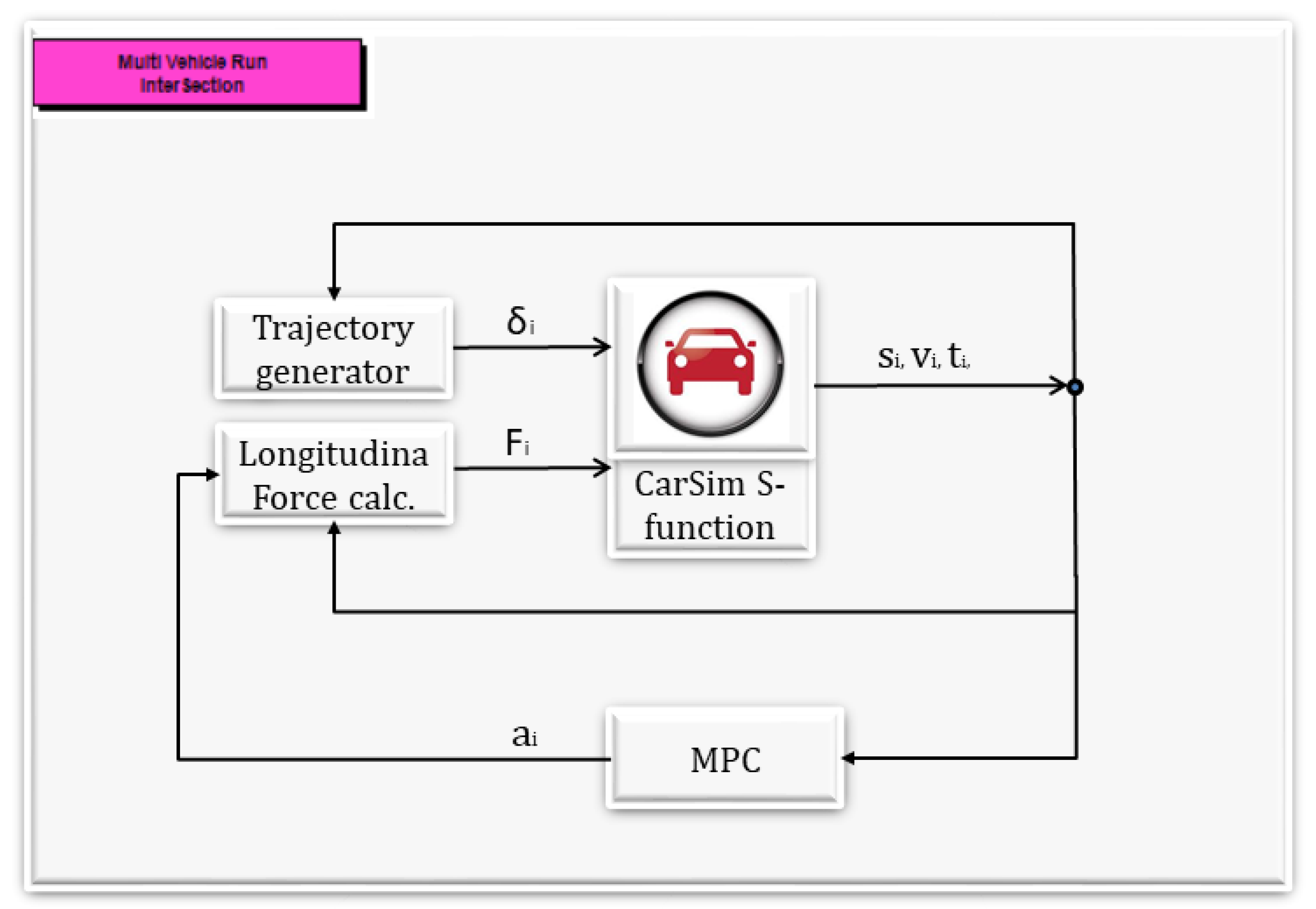
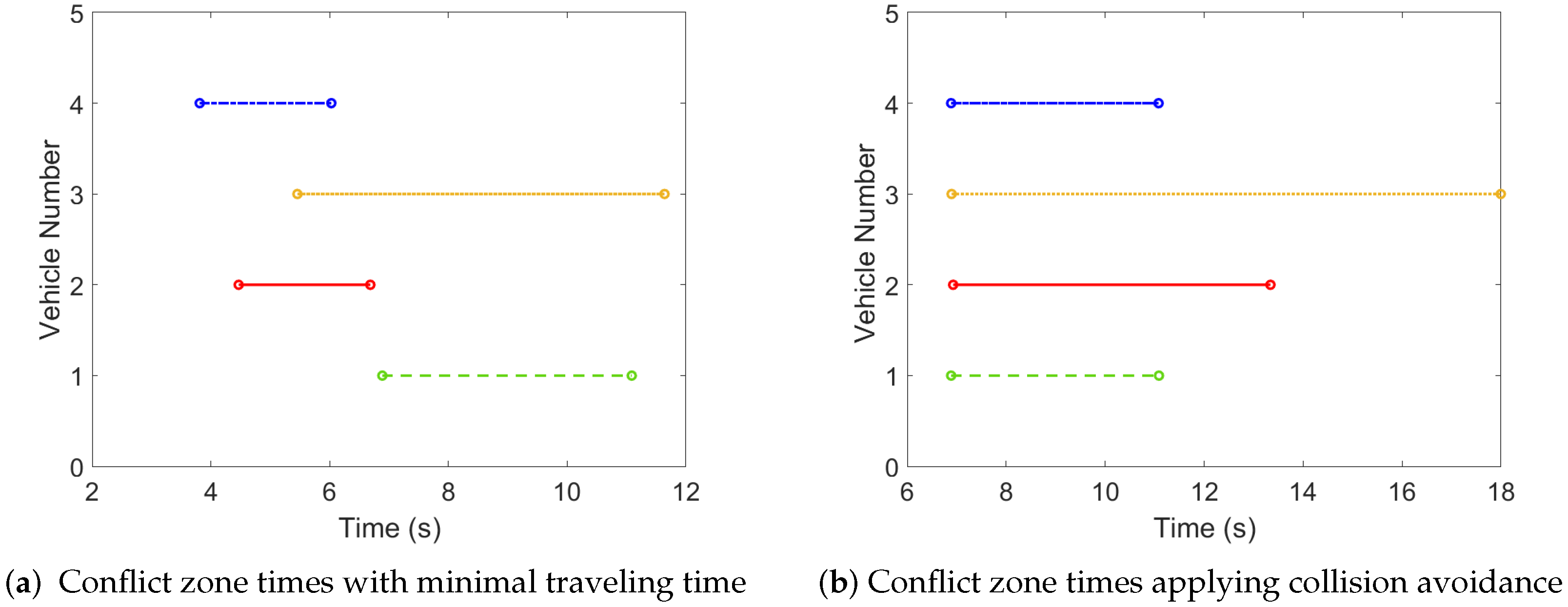
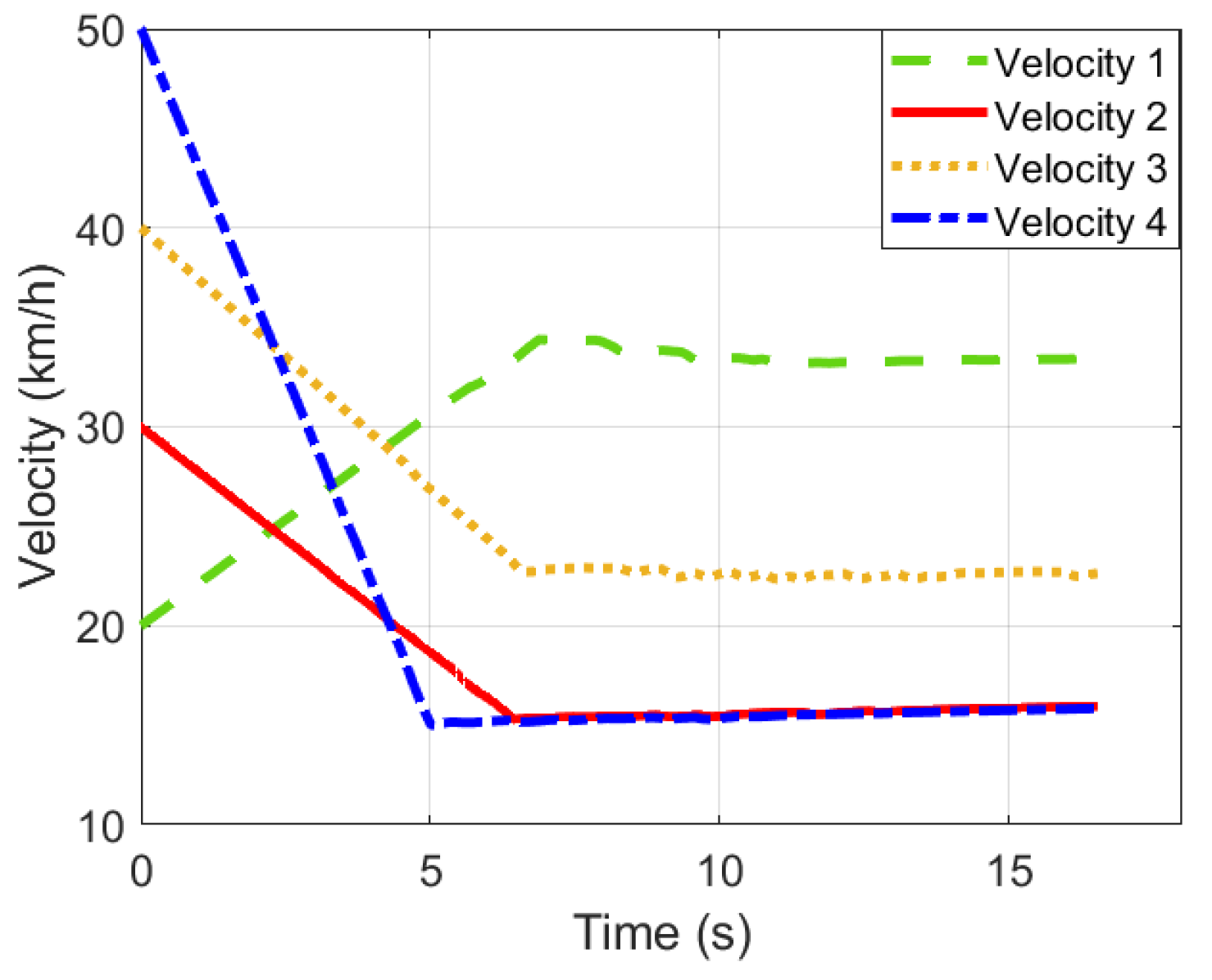
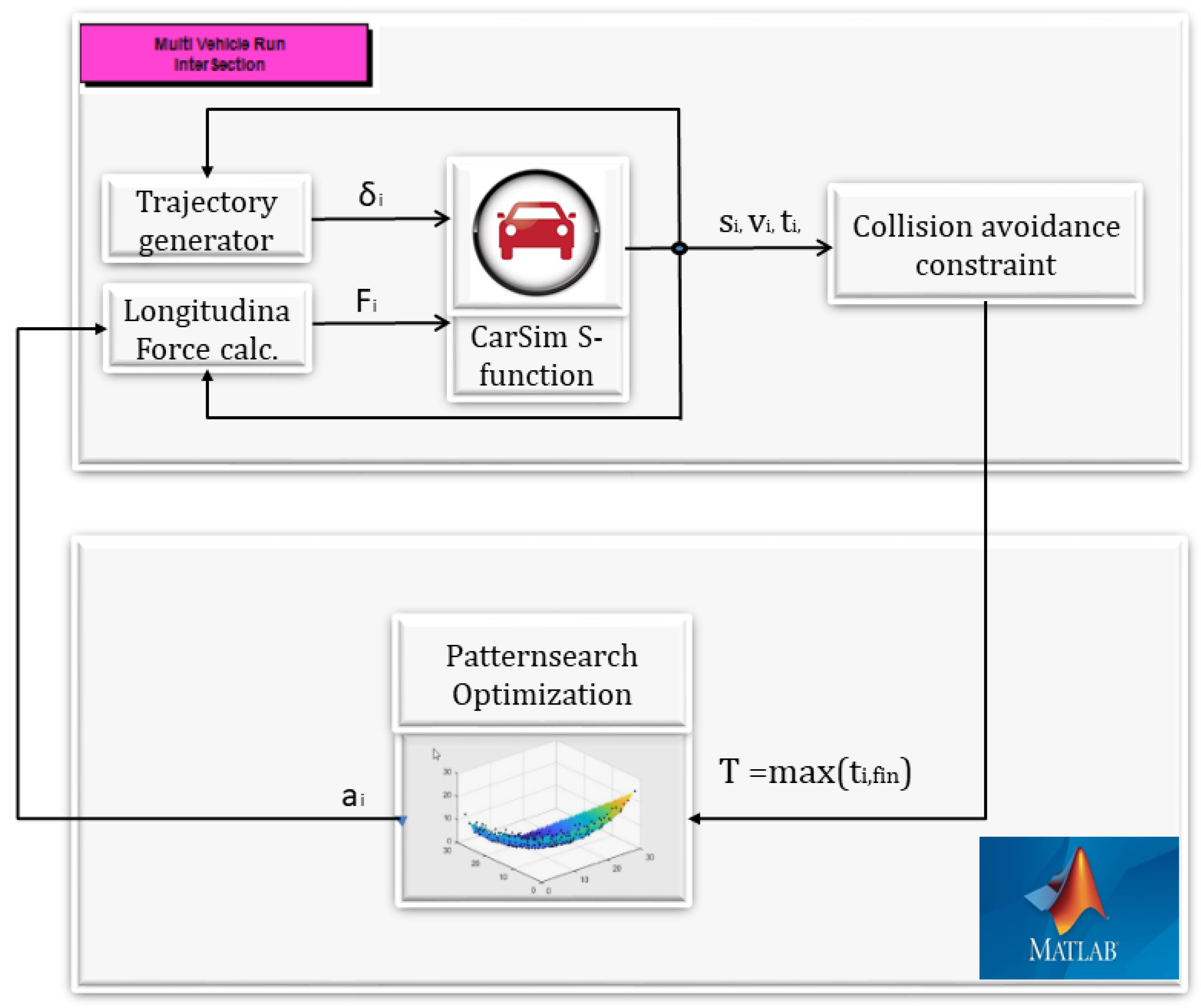
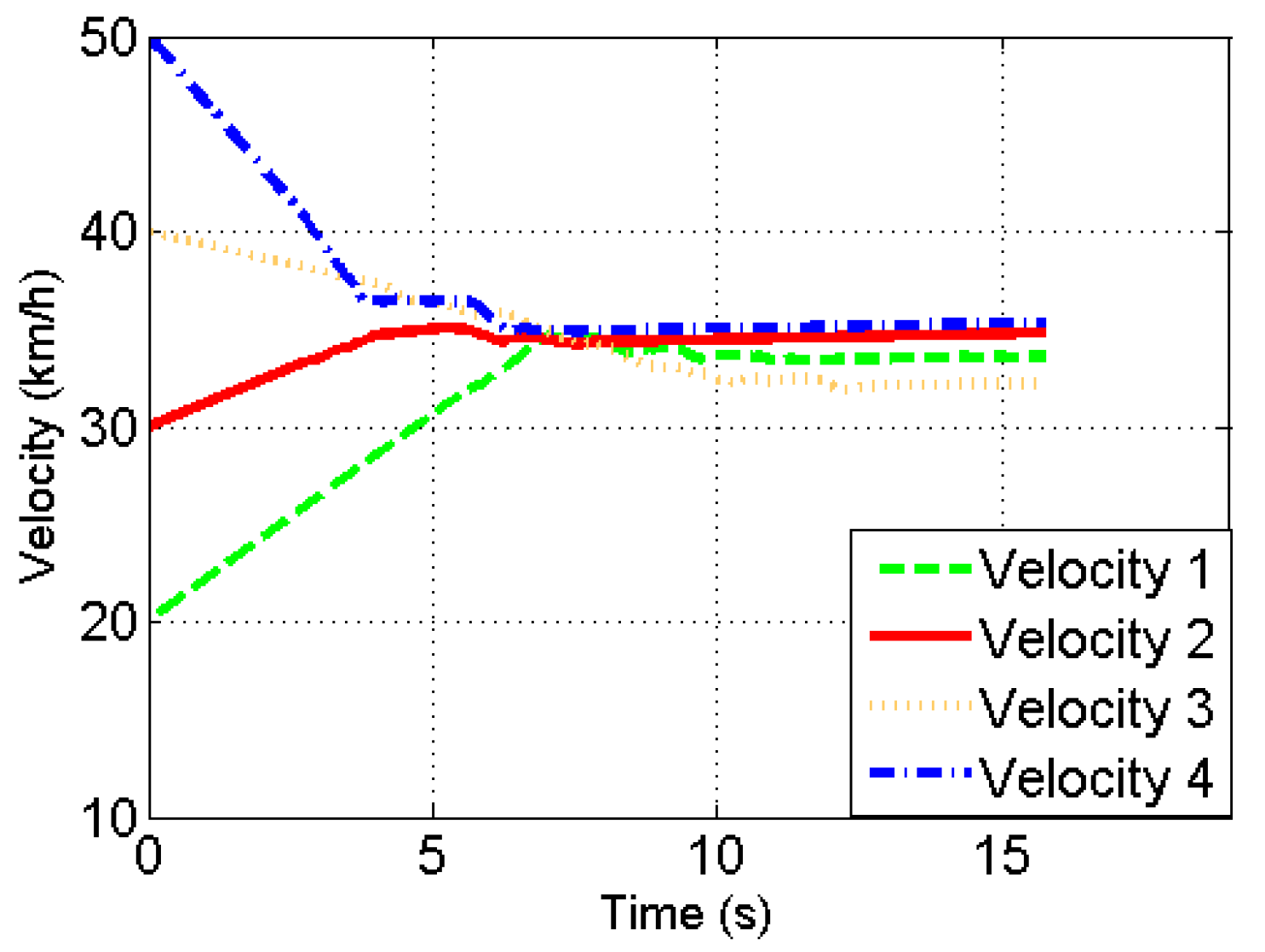
4. Simulation Example
- Upper and lower bounds for the acceleration of AVs are given based on the predefined minimal and maximal acceleration values and the geometry of the roundabout. The latter defines the maximal velocities for the AVs, by which minimal and maximal accelerations are calculated, which guarantees that safe cornering velocities are not violated.
- The multivehicle simulation in CarSim was built with the same initial conditions described earlier. Note that the acceleration values ∈ [] are used as inputs for the simulated vehicles. The iteratively running algorithm aims to find the acceleration values for AVs, by which the traveling time, defined as the last vehicle exiting time from the roundabout, can be minimized.
- In order to ensure collision avoidance, a 3 meter intervehicular distance among AVs is given as a constraint during the simulation. In practice, a large value is added to the measured simulation time in CarSim; hence, the optimization algorithm discards the result given by the actual input values.
- The constrained optimization is evaluated iteratively while it founds acceleration values for AVs, by which a local minimum for the traveling time is reached.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| Road surface | |
| g | Gravity constant |
| R | Radius of roundabout |
| m | Mass |
| v | Velocity of the vehicle |
| Maximal safe velocity | |
| Beginning velocity | |
| a | Acceleration |
| s | Distance |
| Primary distance of AVs from the roundabout center | |
| Entry time of each AV | |
| Traveling time | |
| Travel time of each AV in the entering and control zone | |
| i | ID of the vehicle |
| Maximum entry time | |
| T | Time horizon |
| Sampling time | |
| Yaw angle | |
| X and Y | Coordinates of AV |
| L | Wheelbase of AV |
| Control input | |
| Disturbances affecting the longitudinal dynamics | |
| e | Error |
| J | Const function |
| Q and r | Parameters of the control design |
| Steer input | |
| K | Feedback gain |
References
- SAE International. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles; SAE International: Warrendale, PA, USA, 2018; Available online: https://www.sae.org/standards/content/j3016_202104/ (accessed on 3 January 2023).
- Rastelli, J.P.; Peñas, M.S. Fuzzy logic steering control of autonomous vehicles inside roundabouts. Appl. Soft Comput. 2015, 35, 662–669. [Google Scholar] [CrossRef]
- Deluka Tibljaš, A.; Giuffrè, T.; Surdonja, S.; Trubia, S. Introduction of Autonomous Vehicles: Roundabouts design and safety performance evaluation. Sustainability 2018, 10, 1060. [Google Scholar] [CrossRef]
- Elvik, R. Effects on road safety of converting intersections to roundabouts: Review of evidence from non-US studies. Transp. Res. Rec. 2003, 1847, 1–10. [Google Scholar] [CrossRef]
- Ambros, J.; Novák, J.; Borsos, A.; Hóz, E.; Kieć, M.; Machciník, Š.; Ondrejka, R. Central European comparative study of traffic safety on roundabouts. Transp. Res. Procedia 2016, 14, 4200–4208. [Google Scholar] [CrossRef]
- Rodegerdts, L.; Blogg, M.; Wemple, E.; Myers, E.; Kyte, M.; Dixon, M.P.; List, G.; Flannery, A.; Troutbeck, R.; Brilon, W.; et al. Appendixes to NCHRP Report 572: Roundabouts in the United States; Technical Report; Transportation Research Board: Washington, DC, USA, 2007. [Google Scholar]
- Mohebifard, R.; Hajbabaie, A. Connected automated vehicle control in single lane roundabouts. Transp. Res. Part Emerg. Technol. 2021, 131, 103308. [Google Scholar] [CrossRef]
- Shi, Y.; Pan, Y.; Zhang, Z.; Li, Y.; Xiao, Y. A 5G-V2X Based Collaborative Motion Planning for Autonomous Industrial Vehicles at Road Intersections. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 3744–3748. [Google Scholar] [CrossRef]
- Zhao, L.; Malikopoulos, A.; Rios-Torres, J. Optimal Control of Connected and Automated Vehicles at Roundabouts: An Investigation in a Mixed-Traffic Environment. IFAC-PapersOnLine 2017, 51, 73–78. [Google Scholar] [CrossRef]
- Wang, L.; Huang, W.; Liu, X.; Tian, Y. Vehicle collision avoidance algorithm based on state estimation in the roundabout. In Proceedings of the 2012 Third International Conference on Intelligent Control and Information Processing, Dalian, China, 15–17 July 2012; pp. 407–412. [Google Scholar] [CrossRef]
- Farkas, Z.; Mihály, A.; Gáspár, P. MPC Control Strategy for Autonomous Vehicles Driving in Roundabouts. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Vouliagmeni, Greece, 28 June–1 July 2022; pp. 939–944. [Google Scholar] [CrossRef]
- Ma, F.; Yang, Y.; Wang, J.; Li, X.; Wu, G.; Zhao, Y.; Wu, L.; Aksun-Guvenc, B.; Guvenc, L. Eco-driving-based cooperative adaptive cruise control of connected vehicles platoon at signalized intersections. Transp. Res. Part Transp. Environ. 2021, 92, 102746. [Google Scholar] [CrossRef]
- Talebpour, A.; Mahmassani, H.S. Influence of connected and autonomous vehicles on traffic flow stability and throughput. Transp. Res. Part Emerg. Technol. 2016, 71, 143–163. [Google Scholar] [CrossRef]
- Li, D.; Wagner, P. Impacts of gradual automated vehicle penetration on motorway operation: A comprehensive evaluation. Eur. Transp. Res. Rev. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Min, H.; Fang, Y.; Wu, X.; Wu, G.; Zhao, X. On-ramp merging strategy for connected and automated vehicles based on complete information static game. J. Traffic Transp. Eng. (Engl. Ed.) 2021, 8, 582–595. [Google Scholar] [CrossRef]
- Zhu, J.; Easa, S.; Gao, K. Merging control strategies of connected and autonomous vehicles at freeway on-ramps: A comprehensive review. J. Intell. Connect. Veh. 2022, 5, 99–111. [Google Scholar] [CrossRef]
- Masi, S.; Xu, P.; Bonnifait, P. A Curvilinear Decision Method for Two-lane Roundabout Crossing and its Validation under Realistic Traffic Flow. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1290–1296. [Google Scholar] [CrossRef]
- Sackmann, M.; Leemann, T.; Bey, H.; Hofmann, U.; Thielecke, J. Multi-Step Training for Predicting Roundabout Traffic Situations. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 1982–1989. [Google Scholar]
- Deveaux, D.; Higuchi, T.; Uçar, S.; Wang, C.H.; Härri, J.; Altintas, O. Extraction of Risk Knowledge from Time To Collision Variation in Roundabouts. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 3665–3672. [Google Scholar]
- Xu, K.; Cassandras, C.G.; Xiao, W. Decentralized Time and Energy-Optimal Control of Connected and Automated Vehicles in a Roundabout. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 681–686. [Google Scholar]
- Masi, S.; Xu, P.; Bonnifait, P. Adapting the Virtual Platooning Concept to Roundabout Crossing. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1366–1372. [Google Scholar] [CrossRef]
- Trentin, V.; Artuñedo, A.; Godoy, J.; Villagra, J. Interaction-Aware Intention Estimation at Roundabouts. IEEE Access 2021, 9, 123088–123102. [Google Scholar] [CrossRef]
- Debada, E.; Makarem, L.; Gillet, D. A virtual vehicle based coordination framework for Autonomous Vehicles in heterogeneous scenarios. In Proceedings of the 2017 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Vienna, Austria, 27–28 June 2017; pp. 51–56. [Google Scholar] [CrossRef]
- Rodrigues, M.; McGordon, A.; Gest, G.; Marco, J. Autonomous Navigation in Interaction-Based Environments—A Case of Non-Signalized Roundabouts. IEEE Trans. Intell. Veh. 2018, 3, 425–438. [Google Scholar] [CrossRef]
- Garcia Cuenca, L.; Sanchez-Soriano, J.; Sanz, E.; Andrés, J.; Aliane, N. Machine Learning Techniques for Undertaking Roundabouts in Autonomous Driving. Sensors 2019, 19, 2386. [Google Scholar] [CrossRef]
- Chen, J.; Yuan, B.; Tomizuka, M. Model-free Deep Reinforcement Learning for Urban Autonomous Driving. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2765–2771. [Google Scholar] [CrossRef]
- Chen, J.; Yuan, B.; Tomizuka, M. Deep Imitation Learning for Autonomous Driving in Generic Urban Scenarios with Enhanced Safety. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 2884–2890. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, B.; Guo, L.; Guo, H.; Chen, H. Adaptive Decision-Making for Automated Vehicles Under Roundabout Scenarios Using Optimization Embedded Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5526–5538. [Google Scholar] [CrossRef]
- Mehran, Z.A.; Nasser, L.A. On-line Situational Awareness for Autonomous Driving at Roundabouts using Artificial Intelligence. J. Mach. Intell. Data Sci. 2021, 2, 17–24. [Google Scholar] [CrossRef]
- Chalaki, B.; Beaver, L.E.; Remer, B.; Jang, K.; Vinitsky, E.; Bayen, A.M.; Malikopoulos, A.A. Zero-Shot Autonomous Vehicle Policy Transfer: From Simulation to Real-World via Adversarial Learning. In Proceedings of the 2020 IEEE 16th International Conference on Control Automation (ICCA), Singapore, 9–11 October 2020; pp. 35–40. [Google Scholar] [CrossRef]
- Bosankic, I.; Banjanovic-Mehmedovic, L. Cooperative intelligence in roundabout intersections using hierarchical fuzzy behavior calculation of vehicle speed profile. MATEC Web Conf. 2016, 81, 01008. [Google Scholar] [CrossRef]
- Tian, R.; Li, S.; Li, N.; Kolmanovsky, I.; Girard, A.; Yildiz, Y. Adaptive Game-Theoretic Decision Making for Autonomous Vehicle Control at Roundabouts. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 321–326. [Google Scholar] [CrossRef]
- Banjanovic-Mehmedovic, L.; Halilovic, E.; Bosankić, I.; Kantardzic, M.; Kasapovic, S. Autonomous Vehicle-to-Vehicle (V2V) Decision Making in Roundabout using Game Theory. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 292–298. [Google Scholar] [CrossRef]
- Cao, H.; Zoldy, M. MPC Tracking Controller Parameters Impacts in Roundabouts. Mathematics 2021, 9, 1394. [Google Scholar] [CrossRef]
- Hidalgo, C.; Lattarulo, R.; Pérez, J.; Asua, E. Hybrid trajectory planning approach for roundabout merging scenarios. In Proceedings of the 2019 IEEE International Conference on Connected Vehicles and Expo (ICCVE), Graz, Austria, 4–8 November 2019; pp. 1–6. [Google Scholar]
- Wuthishuwong, C.; Traechtler, A. Vehicle to infrastructure based safe trajectory planning for Autonomous Intersection Management. In Proceedings of the 2013 13th International Conference on ITS Telecommunications (ITST), Tampere, Finland, 5–7 November 2013; pp. 175–180. [Google Scholar]
- Gustafsson, F. Slip-based tire-road friction estimation. Automatica 1997, 33, 1087–1099. [Google Scholar] [CrossRef]
- Li, K.; Misener, J.A.; Hedrick, K. On-board road condition monitoring system using slip-based tyre-road friction estimation and wheel speed signal analysis. Automatica 2007, 221, 129–146. [Google Scholar] [CrossRef]
- Alvarez, L.; Yi, J.; Horowitz, R.; Olmos, L. Dynamic Friction Model-Based Tire-Road Friction Estimation and Emergency Braking Control. J. Dyn. Syst. Meas. Control 2005, 127, 22–32. [Google Scholar] [CrossRef]
- Bichiou, Y.; Rakha, H.A. Real-time optimal intersection control system for automated/cooperative vehicles. Int. J. Transp. Sci. Technol. 2019, 8, 1–12. [Google Scholar] [CrossRef]
- Chohan, N. Robust Trajectory Planning of Autonomous Vehicles at Intersections with Communication Impairments. Master’s Thesis, Aalto University, Espoo, Finland, 2019. [Google Scholar]
- Khayatian, M.; Mehrabian, M.; Shrivastava, A. RIM: Robust Intersection Management for Connected Autonomous Vehicles. In Proceedings of the 2018 IEEE Real-Time Systems Symposium (RTSS), Nashville, TN, USA, 11–14 December 2018. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kiencke, U.; Majjad, R.; Kramer, S. Modeling and performance analysis of a hybrid driver model. Control. Eng. Pract. 1999, 7, 985–991. [Google Scholar] [CrossRef]
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A Review on Autonomous Vehicles: Progress, Methods and Challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Lim, H.S.M.; Taeihagh, A. Algorithmic Decision-Making in AVs: Understanding Ethical and Technical Concerns for Smart Cities. Sustainability 2019, 11, 5791. [Google Scholar] [CrossRef]
- Ryan, M. The Future of Transportation: Ethical, Legal, Social and Economic Impacts of Self-driving Vehicles in the Year 2025. Sci. Eng. Ethics 2020, 26, 1185–1208. [Google Scholar] [CrossRef] [PubMed]
- Stone, T.; Santoni de Sio, F.; Vermaas, P. Driving in the Dark: Designing Autonomous Vehicles for Reducing Light Pollution. Sci. Eng. Ethics 2020, 26, 1–17. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farkas, Z.; Mihály, A.; Gáspár, P. Model Predictive Control Method for Autonomous Vehicles in Roundabouts. Machines 2023, 11, 75. https://doi.org/10.3390/machines11010075
Farkas Z, Mihály A, Gáspár P. Model Predictive Control Method for Autonomous Vehicles in Roundabouts. Machines. 2023; 11(1):75. https://doi.org/10.3390/machines11010075
Chicago/Turabian StyleFarkas, Zsófia, András Mihály, and Péter Gáspár. 2023. "Model Predictive Control Method for Autonomous Vehicles in Roundabouts" Machines 11, no. 1: 75. https://doi.org/10.3390/machines11010075
APA StyleFarkas, Z., Mihály, A., & Gáspár, P. (2023). Model Predictive Control Method for Autonomous Vehicles in Roundabouts. Machines, 11(1), 75. https://doi.org/10.3390/machines11010075










