A Fault Tolerance Method for Multiple Current Sensor Offset Faults in Grid-Connected Inverters
Abstract
1. Introduction
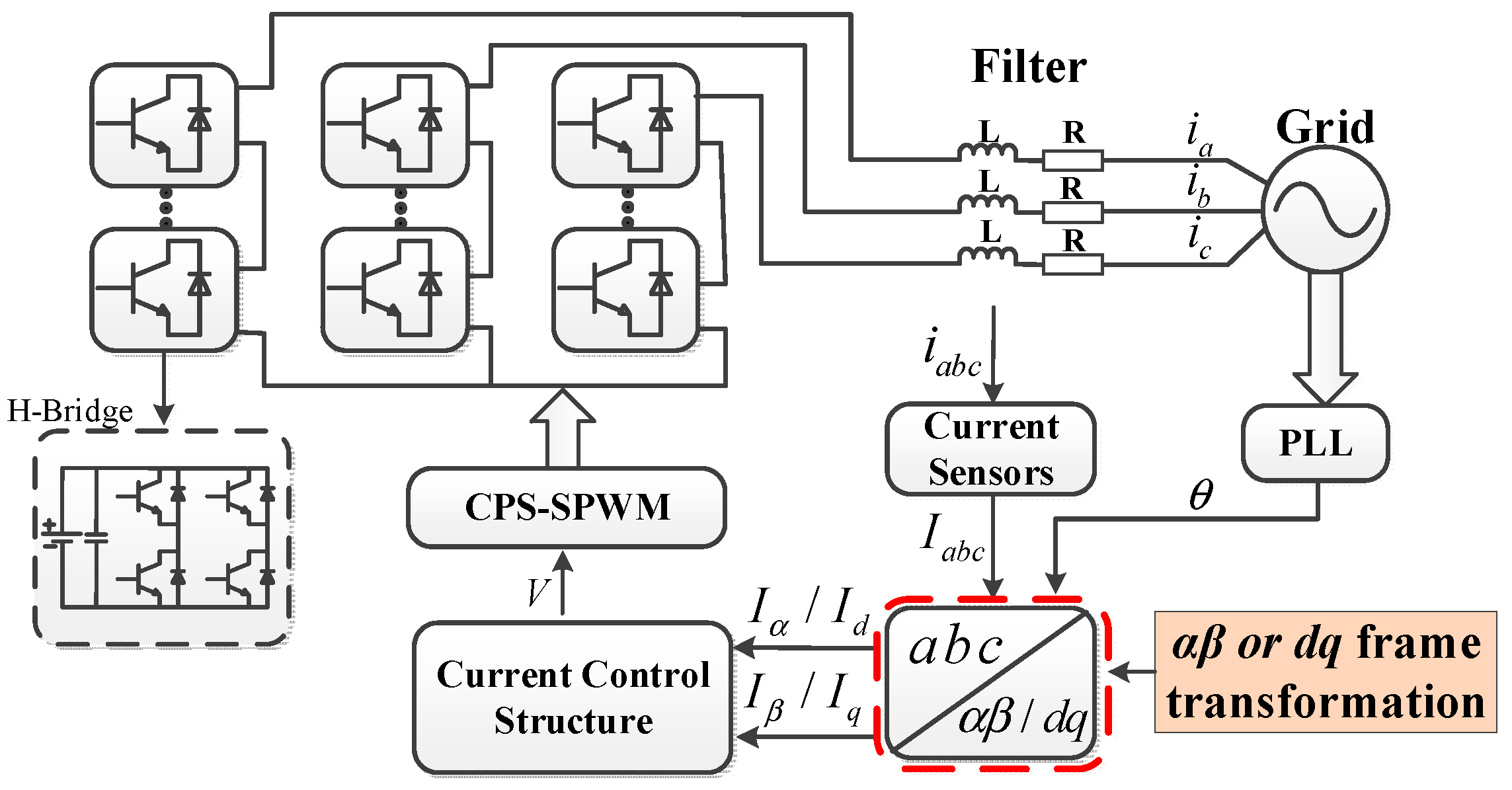
2. Problem Description
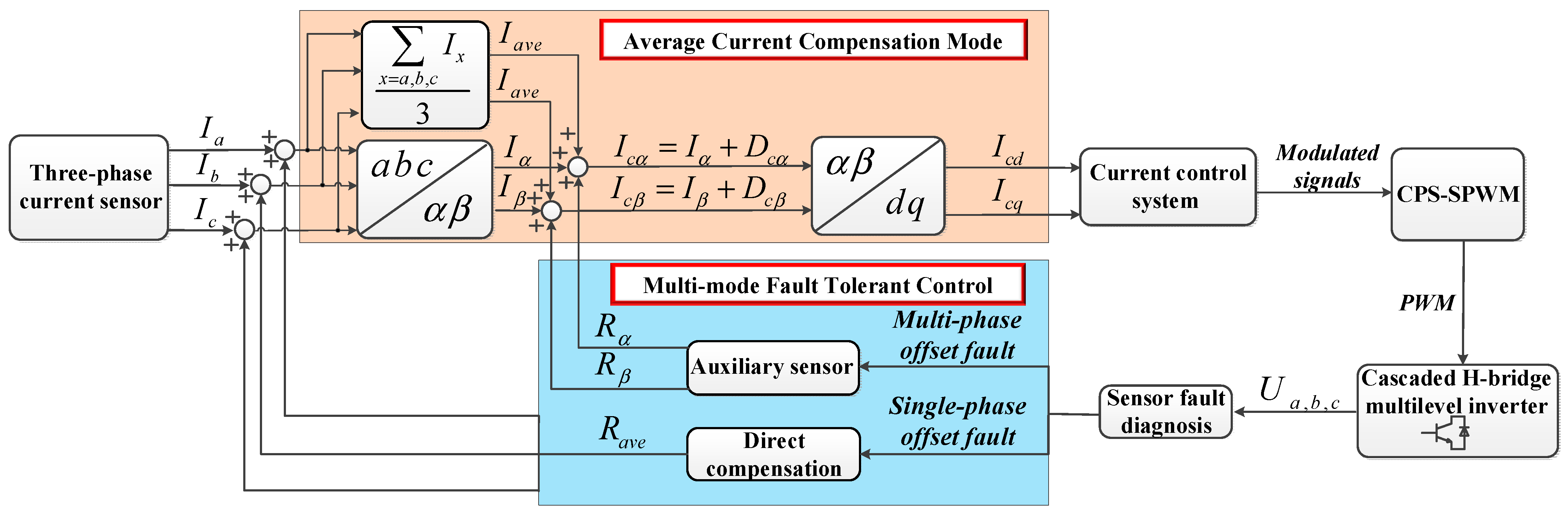
3. Multi-Mode Fault-Tolerant Control of Current Sensor Fault
3.1. Average Current Compensation Mode
3.1.1. Normal Condition
3.1.2. Offset Fault Condition
3.2. Multi-Mode Fault-Tolerant Control
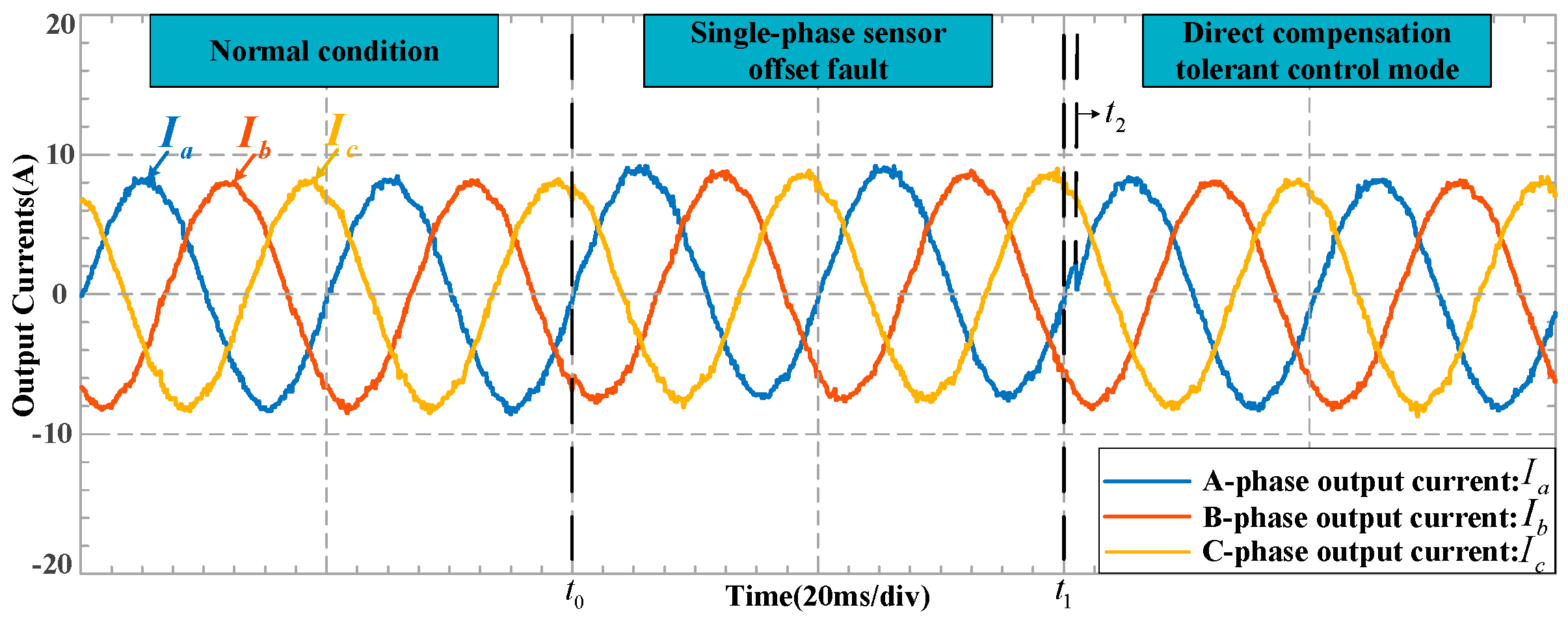
3.2.1. Direct Compensation Mode for Single-Phase Offset Fault
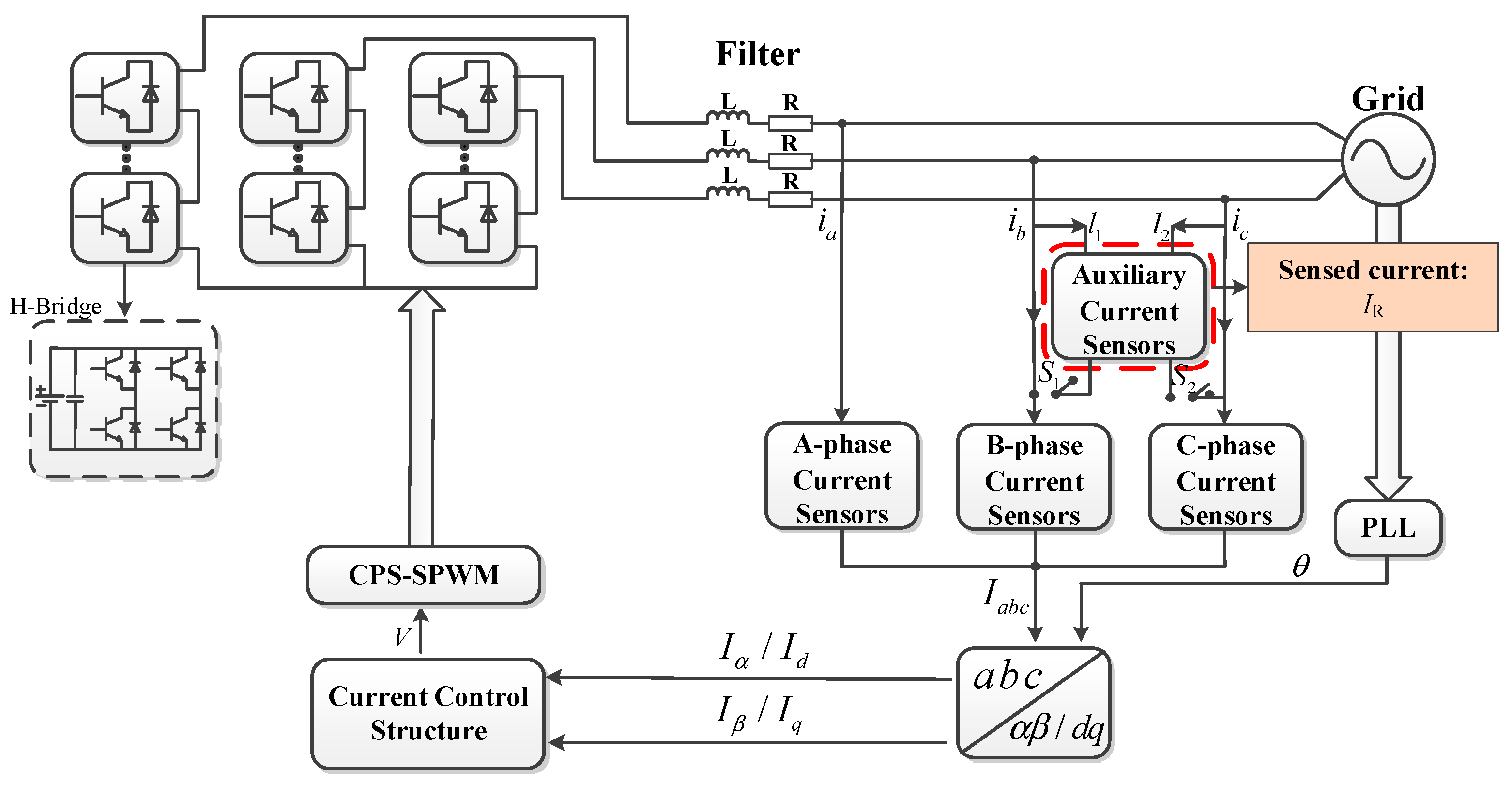
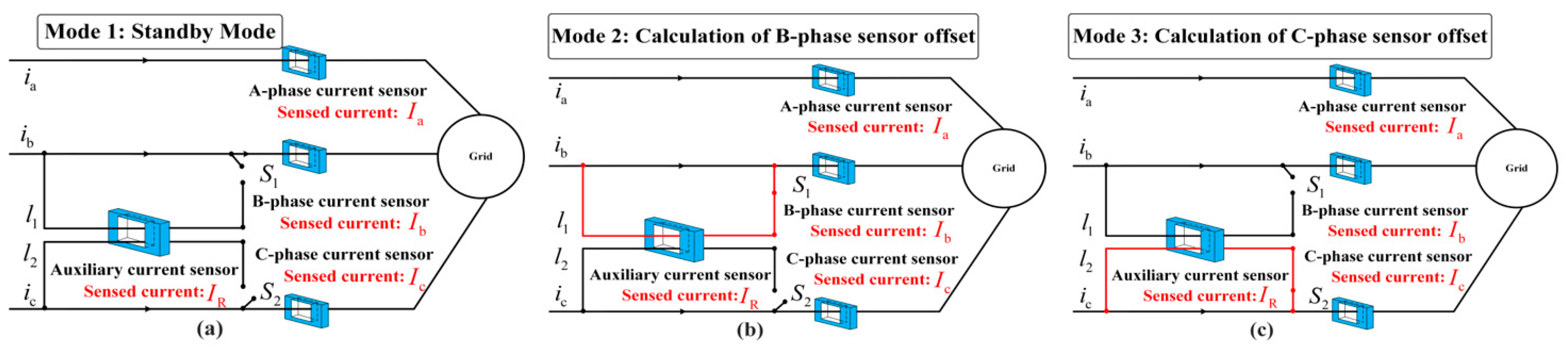
3.2.2. Indirect Compensation through An Auxiliary Current Sensor Mode for Multiphase Offset Fault
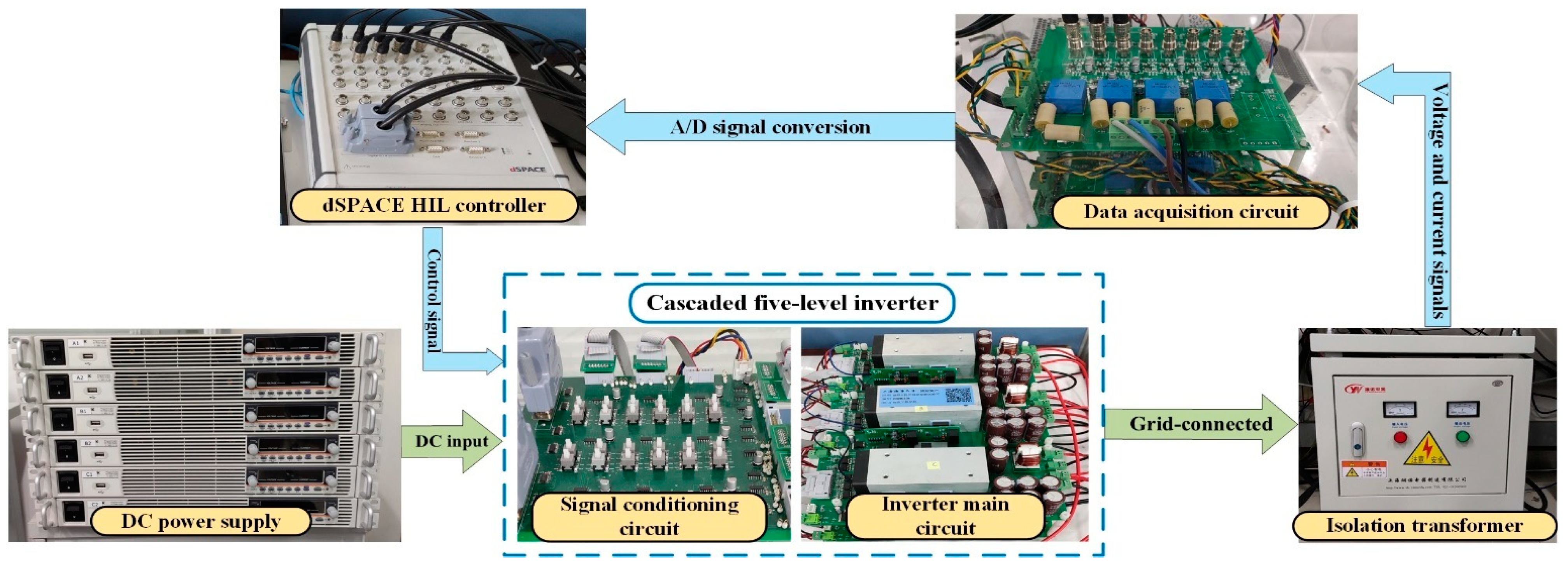
4. Experimental Result and Analysis
4.1. Data Acquisition under Various Failure Conditions
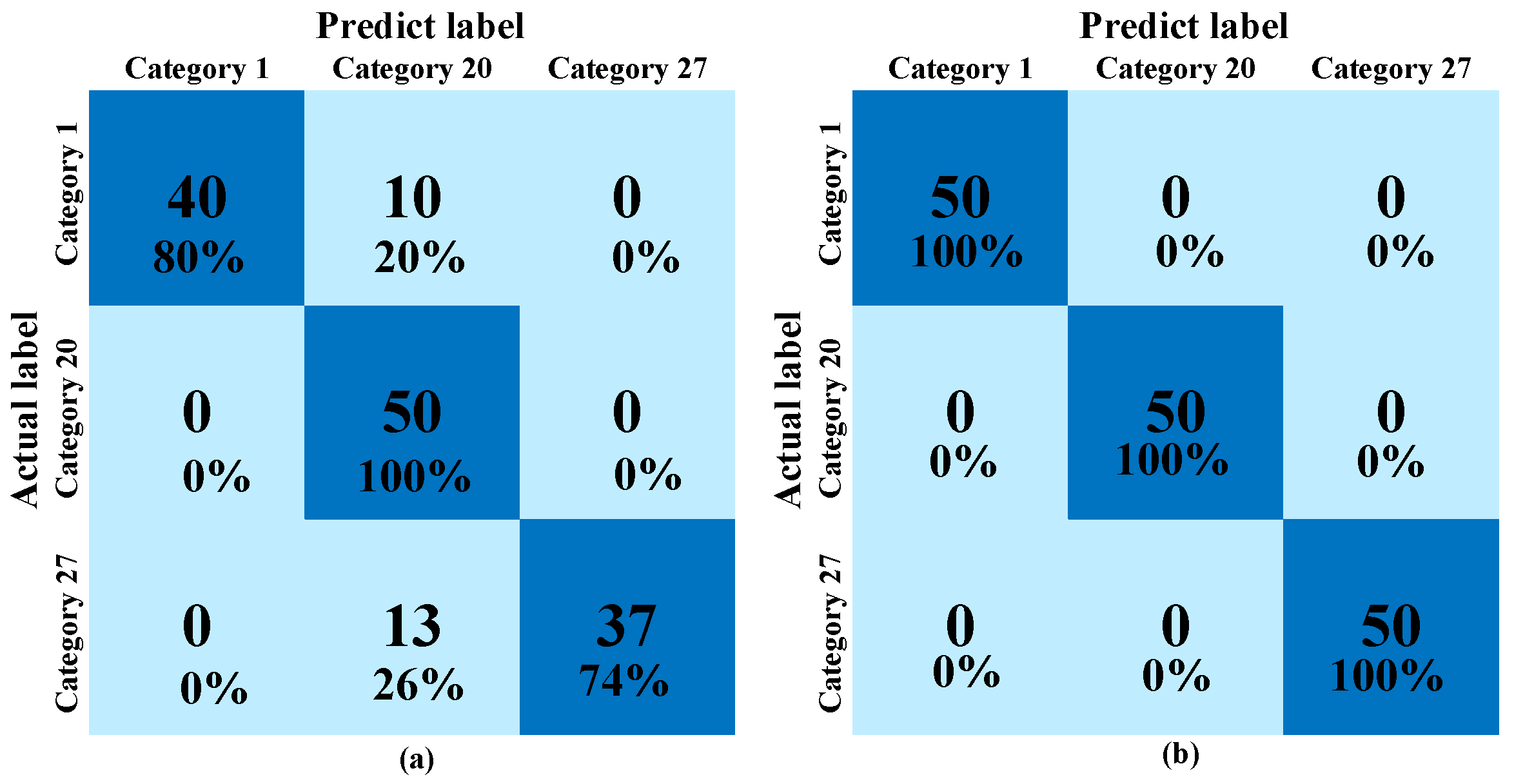
4.2. Effectiveness of Fault Diagnosis
4.2.1. Average Current Compensation Mode
4.2.2. Fault Diagnosis Results
4.3. Performance of Multi-Mode Fault-Tolerant Control
4.3.1. Direct Compensation Mode for Single-Phase Offset Fault
4.3.2. Auxiliary Sensor Mode for Multiphase Offset Fault
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. A Data-Driven Fault Diagnosis Methodology in Three-Phase Inverters for PMSM Drive Systems. IEEE Trans. Power Electron. 2017, 32, 5590–5600. [Google Scholar] [CrossRef]
- Anand, A.; Raj, N.; Jagadanand, G.; George, S. A Generalized Switch Fault Diagnosis for Cascaded H-Bridge Multilevel Inverters Using Mean Voltage Prediction. IEEE Trans. Ind. Appl. 2020, 56, 1563–1574. [Google Scholar] [CrossRef]
- Bae, C.J.; Lee, D.C.; Nguyen, T.H. Detection and identification of multiple IGBT open-circuit faults in PWM inverters for AC machine drives. IET Power Electron. 2020, 12, 923–931. [Google Scholar] [CrossRef]
- Kim, W.J.; Kim, S.H. ANN design of multiple open-switch fault diagnosis for three-phase PWM converters. IET Power Electron. 2020, 19, 4490–4497. [Google Scholar] [CrossRef]
- Mtepele, K.O.; Campos-Delgado, D.U.; Valdez-Fernández, A.A.; Pecina-Sánchez, J.A. Model-based strategy for open-circuit faults diagnosis in n-level CHB multilevel converters. IET Power Electron. 2019, 12, 648–655. [Google Scholar] [CrossRef]
- Yao, G.; Li, Y.; Li, Q.; Hu, S.; Jin, N. Model predictive power control for a fault-tolerant grid-connected converter using reconstructed currents. IET Power Electron. 2020, 13, 1181–1190. [Google Scholar] [CrossRef]
- Li, Z.; Wheeler, P.; Watson, A.; Costabeber, A.; Wang, B.; Ren, Y.; Bai, Z.; Ma, H. A Fast Diagnosis Method for Both IGBT Faults and Current Sensor Faults in Grid-Tied Three-Phase Inverters with Two Current Sensors. IEEE Trans. Power Electron. 2020, 35, 5267–5278. [Google Scholar] [CrossRef]
- Rajendran, S.; Govindarajan, U.; Senthilvadivelu, S.; Uandai, S.B. Intelligent sensor fault-tolerant control for variable speed wind electrical systems. IET Power Electron. 2013, 6, 1308–1319. [Google Scholar] [CrossRef]
- Xia, J.; Guo, Y.; Dai, B.; Zhang, X. Sensor Fault Diagnosis and System Reconfiguration Approach for an Electric Traction PWM Rectifier Based on Sliding Mode Observer. IEEE Trans. Ind. Appl. 2017, 53, 4768–4778. [Google Scholar] [CrossRef]
- Chakraborty, C.; Verma, V. Speed and Current Sensor Fault Detection and Isolation Technique for Induction Motor Drive Using Axes Transformation. IEEE Trans. Ind. Electron. 2015, 62, 1943–1954. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Xia, Y.; Deng, Q.; Ge, X. An Online Data-Driven Method for Simultaneous Diagnosis of IGBT and Current Sensor Fault of Three-Phase PWM Inverter in Induction Motor Drives. IEEE Trans. Power Electron. 2020, 35, 13281–13294. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z.; Zhang, H. A Diagnosis Algorithm for Multiple Open-Circuited Faults of Microgrid Inverters Based on Main Fault Component Analysis. IEEE Trans. Energy Convers. 2018, 33, 925–937. [Google Scholar] [CrossRef]
- Kou, L.; Liu, C.; Cai, G.; Zhou, J.; Yuan, Q.; Pang, S. Fault diagnosis for open-circuit faults in NPC inverter based on knowledge-driven and data-driven approaches. IET Power Electron. 2020, 13, 1236–1245. [Google Scholar] [CrossRef]
- Wang, T.; Xu, H.; Han, J.; Elbouchikhi, E.; Benbouzid, M.E.H. Cascaded H-Bridge Multilevel Inverter System Fault Diagnosis Using a PCA and Multiclass Relevance Vector Machine Approach. IEEE Trans. Power Electron. 2015, 30, 7006–7018. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Y.; Gou, B. A Data-Driven Method for IGBT Open-Circuit Fault Diagnosis Based on Hybrid Ensemble Learning and Sliding-Window Classification. IEEE Trans. Ind. Inform. 2020, 16, 5223–5233. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X.; Huang, B. Performance-Driven Distributed PCA Process Monitoring Based on Fault-Relevant Variable Selection and Bayesian Inference. IEEE Trans. Ind. Electron. 2016, 63, 377–386. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.; Qian, P. Wind Turbine Fault Detection and Identification Through PCA-Based Optimal Variable Selection. IEEE Trans. Sustain. Energy 2018, 9, 1627–1635. [Google Scholar] [CrossRef]
- Zhong, K.; Han, M.; Qiu, T.; Han, B.; Chen, Y.W. Distributed Dynamic Process Monitoring Based on Minimal Redundancy Maximal Relevance Variable Selection and Bayesian Inference. IEEE Trans. Control. Syst. Technol. 2020, 28, 2037–2044. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z.; Cheng, M.; Wang, W.; Hu, Y. Comprehensive Diagnosis and Tolerance Strategies for Electrical Faults and Sensor Faults in Dual Three-Phase PMSM Drives. IEEE Trans. Power Electron. 2019, 34, 6669–6684. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, Y.; Wang, B.; Huang, X.; Xu, D. Current Sensor Fault Diagnosis and Tolerant Control for VSI-Based Induction Motor Drives. IEEE Trans. Power Electron. 2018, 33, 4238–4248. [Google Scholar] [CrossRef]
- Salmasi, F.R. A Self-Healing Induction Motor Drive with Model Free Sensor Tampering and Sensor Fault Detection, Isolation, and Compensation. IEEE Trans. Ind. Electron. 2017, 64, 6105–6115. [Google Scholar] [CrossRef]
- Gou, B.; Ge, X.; Liu, Y.; Feng, X. Load-current-based current sensor fault diagnosis and tolerant control scheme for traction inverters. Electron. Lett. 2016, 52, 1717–1719. [Google Scholar] [CrossRef]
- Wang, T.; Qi, J.; Xu, H.; Wang, Y.; Liu, L.; Gao, D. Fault diagnosis method based on FFT-RPCA-SVM for Cascaded-Multilevel Inverter. ISA Trans. 2016, 60, 156–163. [Google Scholar] [CrossRef]
- 519-2014; IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. (Revision of IEEE Std 519-1992). Institute of Electrical and Electronics Engineers, Inc.: Piscataway, NJ, USA, 2014; pp. 1–29.
- Yu, Y.; Hu, X. Active Disturbance Rejection Control Strategy for Grid-Connected Photovoltaic Inverter Based on Virtual Synchronous Generator. IEEE Access 2019, 7, 17328–17336. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Sliding-Mode Control of PWM Dual Inverter-Based Grid-Connected PV System: Modeling and Performance Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 435–444. [Google Scholar] [CrossRef]
- Merabet, A.; Labib, L.; Ghias, A.M.Y.M.; Ghenai, C.; Salameh, T. Robust Feedback Linearizing Control with Sliding Mode Compensation for a Grid-Connected Photovoltaic Inverter System Under Unbalanced Grid Voltages. IEEE J. Photovolt. 2017, 7, 828–838. [Google Scholar] [CrossRef]
- Zmood, D.; Holmes, D. Stationary frame current regulation of PWM inverters with zero steady state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Timbus, A.; Liserre, M.; Teodorescu, R.; Rodriguez, P.; Blaabjerg, F. Evaluation of Current Controllers for Distributed Power Generation Systems. IEEE Trans. Power Electron. 2009, 24, 654–664. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Xia, Y.; Wilson, G.; Liu, S. An Intelligent Time-Adaptive Data-Driven Method for Sensor Fault Diagnosis in Induction Motor Drive System. IEEE Trans. Ind. Electron. 2019, 66, 9817–9827. [Google Scholar] [CrossRef]
- Balaban, E.; Saxena, A.; Bansal, P.; Goebel, K.F.; Curran, S. Modeling, Detection, and Disambiguation of Sensor Faults for Aerospace Applications. IEEE Sens. J. 2009, 9, 1907–1917. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, B. Sensor Fault Diagnosis and Fault Tolerant Control for Forklift Based on Sliding Mode Theory. IEEE Access 2020, 8, 84858–84866. [Google Scholar] [CrossRef]




| System Parameters | Values |
|---|---|
| DC voltage | 100 V |
| Filter inductance (L) | 4 mH |
| Switching frequency | 5 kHz |
| Grid voltage RMS | 110 V |
| Grid frequency | 50 Hz |
| Transformer ratio | 1:2 |
| Rated current RMS | 5.656 A |
| Fault Type | Specific Classification | Number |
|---|---|---|
| Healthy | Normal condition | 1 |
| Single-phase current sensor offset fault | positive offset 20% | 3 |
| negative offset 10% | 3 | |
| Two-phase current sensor offset fault | positive offset 20% | 6 |
| negative offset 10% | 6 | |
| Three-phase current sensor offset fault | positive offset 20% | 4 |
| negative offset 10% | 3 |
| Control Structure | FFT + PCA + BP | FFT + PCA + BP | FFT + PCA + SVM |
|---|---|---|---|
| Traditional current control system | 59.07% | 93.60% | 92.44% |
| Current control system with average current compensation mode | 94.67% | 99.06% | 100% |
| Fault-Tolerant Control Strategy | Number of Fault Sensors | Tolerance Time | Whether It Improves the Diagnosis Accuracy |
|---|---|---|---|
| Proposed strategy | Multiple | 2 ms | Yes |
| Independent observer [14] | Single or double | 8 ms | No |
| Signal reconstruction [16] | Single | 40 ms | No |
| Vector space decomposition [13] | Multiple | 10 ms | No |
| Signal compensator [15] | Single or double | 4 s | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Jin, G.; Geng, J.; Wang, T.; Han, J.; Razik, H.; Wang, Y. A Fault Tolerance Method for Multiple Current Sensor Offset Faults in Grid-Connected Inverters. Machines 2023, 11, 61. https://doi.org/10.3390/machines11010061
Zhang F, Jin G, Geng J, Wang T, Han J, Razik H, Wang Y. A Fault Tolerance Method for Multiple Current Sensor Offset Faults in Grid-Connected Inverters. Machines. 2023; 11(1):61. https://doi.org/10.3390/machines11010061
Chicago/Turabian StyleZhang, Fan, Guangfeng Jin, Junchao Geng, Tianzhen Wang, Jingang Han, Hubert Razik, and Yide Wang. 2023. "A Fault Tolerance Method for Multiple Current Sensor Offset Faults in Grid-Connected Inverters" Machines 11, no. 1: 61. https://doi.org/10.3390/machines11010061
APA StyleZhang, F., Jin, G., Geng, J., Wang, T., Han, J., Razik, H., & Wang, Y. (2023). A Fault Tolerance Method for Multiple Current Sensor Offset Faults in Grid-Connected Inverters. Machines, 11(1), 61. https://doi.org/10.3390/machines11010061









