Innovative Design and Kinematic Characteristics Analysis of Floating Mobile Chassis of Inspection Robot

Abstract

In view of the problems that exist in the working plane of the inspection robot equipped with precision instruments that cannot always maintain a stable state when moving on a complex road surface, a floating mobile chassis was designed based on the Teoriya Resheniya Izobreatatelskikh Zadatch (TRIZ) theory, and the floating suspension device was also optimized based on the substance field. The kinematic model of the floating mobile chassis was established, and the obstacle-surmounting analysis has been carried out on complex road conditions such as the boss and trench. The dynamic model and mobile performance evaluation model of the obstacle crossing wheel are established. The prototype of the non-floating mobile chassis and the prototype of the floating mobile chassis were respectively established in ADAMS, and the motion comparison simulation analysis of boss, trench crossing and complex road conditions were also carried out. The results showed that the floating mobile chassis has strong adaptive performance, and the stability of the working plane can always be maintained when crossing obstacles.

1. Introduction

An inspection robot is an intelligent inspection equipment integrating environmental awareness, autonomous navigation and positioning, behavior control and execution that is widely used in electric patrol petroleum, mining and other fields [1,2,3]. In recent years, there has been a lot of research on inspection robots in the mine field, especially. The harsh underground environment will seriously affect the health of patrol workers. Coal mine safety accidents will also affect the life safety of patrol workers [4]. Therefore, it is necessary and significant for robots to replace manual patrol. Robots can collect the downhole patrol inspection information with carried cameras and various information-sensing components such as precision instruments and sensors, but the coal mine tunnel is narrow and uneven, with many faults, broken roads and grooves. The fully mechanized mining face has many grooves, water, gravel and coal fragments, which will affect the accuracy of the data collection of underground inspection information. Therefore, the designed mobile chassis of the robot is required to have strong obstacle-surmounting ability and smooth driving ability in the unstructured environment. The mobile chassis is one of the important components of the inspection robot. The types of mobile chassis mainly include wheel type [5], crawler type [6], legged [7], wheel-track compound [8], wheel-leg compound sort [9] and other structures. Different types of mobile chassis affect the riding comfort of the inspection robot. The legged robot has high flexibility, but its motion trajectory is a set of discontinuous footprints. The legs move stably to achieve coordination and its mechanical structure and control algorithm are relatively complex [10,11]. The crawler robot has been widely used in inspection because of its excellent mobility performance, but its moving speed is slow, its volume is large and energy consumption is also large. The compound robots can adapt to complex and special environments [12,13], while their structures and control are relatively complicated. In patrol inspection practical application, therefore, the compound robot is less. The wheeled robot has been widely used in the inspection field due to its high moving speed, strong flexibility and relatively simple drive and control and so on [14]. A set of wheeled inspection robot experimental teaching platforms designed by the China University of Mining and Technology adopted a large-diameter driving wheel for the front driving wheel and small-diameter unpowered universal wheel for the rear driven wheel. The obstacle-surmounting ability of the inspection robot is improved by increasing the wheel diameter [15]. Yingjun Wei et al. [16] proposed a new type of deformable wheeled obstacle surmounting robot, which can improve the obstacle-surmounting ability of the robot in the face of an unknown environment by changing the shape and size of the deformable wheel of the robot.

The robot mentioned above has strong obstacle surmounting ability, but it does not involve its driving stability, which is an important factor affecting the accuracy of the robot’s environmental information collection. The suspension system is an important part of the ride comfort of the patrol robot. When the robot moves on uneven roads, the suspension system can well maintain the contact between the wheels and the ground. As for the six-wheeled robot Mule in the United States [17], the six-wheeled robot developed by the Robotics Research Institute of Beijing University of Aeronautics and Astronautics [18], and the six-wheeled rescue robot developed by Tianjin University of Technology [19], the adaptability of the mobile chassis to the ground by maintaining the real-time contact between the driving wheels and the ground through the swing arm suspension were enhanced. At the same time, the strong obstacle climbing capability of the robot was maintained. Jianwei Zhao et al. [20] proposed a relatively lightweight all-terrain wheel-legged robot. The design of the wheel–leg mechanism was based on the slider crank mechanism, and the robot’s obstacle-surmounting ability has been improved to realize rapid movement and adapt to complex terrain, but the robot’s motion stability has not been improved significantly. Kun Jung Kim et al. [21] proposed a wheeled mobile chassis with a body rotation mechanism to improve the maneuverability of the robot through complex terrain. Roland Siegwart et al. [22] proposed a six-wheel drive wheeled robot, which adopted a rhombus structure. Spring suspension forks are used for the front and rear wheels to ensure the best contact between the wheels and the ground in real time. Bogies are used on both sides to enhance the robot’s obstacle-surmounting ability and terrain adaptability. Compared with the wheeled robot, the crawler inspection robot has a higher ability of obstacle surmounting, but it is cumbersome and has no shock-absorbing mechanism, which generates large vibrations when moving on complex road surfaces. Songsong Chen et al. [23] proposed the design of a tracked mobile chassis with flexible suspension and verified that it has strong terrain adaptability and passing ability. Buyun Wang et al. [24] proposed a design of a double fork suspension damping mechanism to improve the damping effect and obstacle-crossing performance of the robot and improve the motion performance of the robot on complex roads.

The mobile chassis of the robot mentioned above has been significantly improved in terrain adaptation, but it did not involve whether the working surface of the mobile chassis was stable or not, and whether it can provide a stable working environment for the precision instruments carried. In addition, the structure of the suspension system designed is more complex. According to the task requirements, based on TRIZ theory, this paper innovatively designed and optimized the floating mobile chassis of the inspection robot, and the proposed floating linkage is simpler. Through simulation comparison and experimental analysis, it verifies that the working platform of the robot can create stable and good working conditions for the precision instruments carried by the robot, when it moved on the complex road surface.

2. Design of Floating Mobile Chassis Based on TRIZ Theory

TRIZ theory is a problem-solving method and theory [25,26], which has a systematic problem-solving process of analyzing problems, solving problems and proposing solutions. In addition, it can provide designers with innovative thinking modes in different dimensions and improve product design quality and efficiency.

2.1. Description of the Problem

At present, the mobile chassis of inspection robots mainly includes wheeled, tracked and legged. In a structured environment, the mobile performance and stability of such robots are better; However, when a robot patrols in a complex unstructured environments such as trenches and bosses, the ability of the mobile chassis to run smoothly is greatly reduced. Taking the wheeled mobile chassis as an example, when encountering a bulge, the plane of the mobile chassis is obviously inclined upward, and when encountering a trench, instead, it is obviously inclined downward. However, this is not conducive to the robotic arm and precision instruments mounted on the mobile chassis of the robot, and there is a physical contradiction between the two units.

2.2. Design of Floating Mobile Chassis Based on Physical Contradiction

The design of the floating mobile chassis should meet the following requirements: when the mobile chassis was faced with an unstructured environment such as bumps and potholes, its plate can always keep stable, that is, the working surface of the mobile chassis and the horizontal plane run parallel to each other. It is well known that in the unstructured environment, the plane where the mobile chassis base is located intersects the road surface. In order to improve the stability of the mobile chassis, it is required that the plane of the flat plate is parallel to the ground, and the contradictory parameters of parallelism and intersection are determined. When the mobile chassis encountered bumps and grooves, the stability of the flat plate and the intersection point between the flat plate surface and the road surface can be spatially separated. Therefore, the method of combining spatial separation and 40 inventive principles have been adopted to solve the problem. The solution flow chart was shown in Figure 1.

Finally, the 02–Principle of Extraction, 03–Principle of Local Mass and 24–Principle of Intermediary were all obtained. According to the description of the extraction principle: extract the parts and attributes that have negative effects from the object; the description of the mediator principle: use mediation to achieve the desired action. Then, the solutions were obtained. To ensure the plane of the mobile chassis base is always parallel to the ground, an up-and-down floating mechanism was added at the connection between the wheel and the plate of the mobile chassis, which can adjust the contact between the tire and the ground when the mobile chassis was on a raised or trenched road surface. The structure diagram of the floating mechanism was shown in Figure 2.

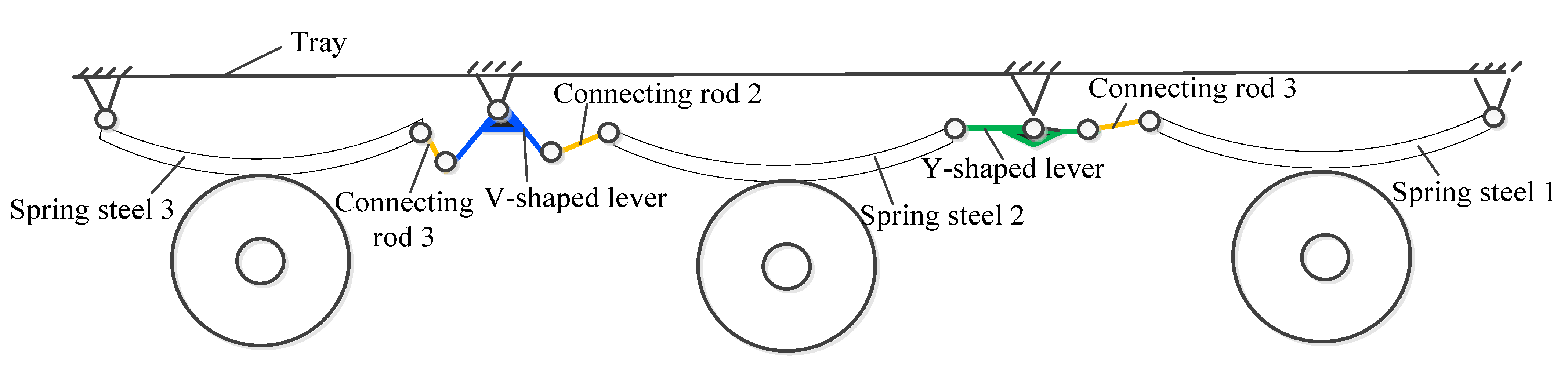
The floating mechanism was fixed on the plate through the brackets, and the tire floated up and down by the V-bar and Y-bar adjusting link. The degree of freedom of the floating mechanism was 2, that is, the mobile chassis can move up and down, as well as forward and backward.

2.3. Optimization of Floating Mobile Chassis Based on Substance–Field Analysis

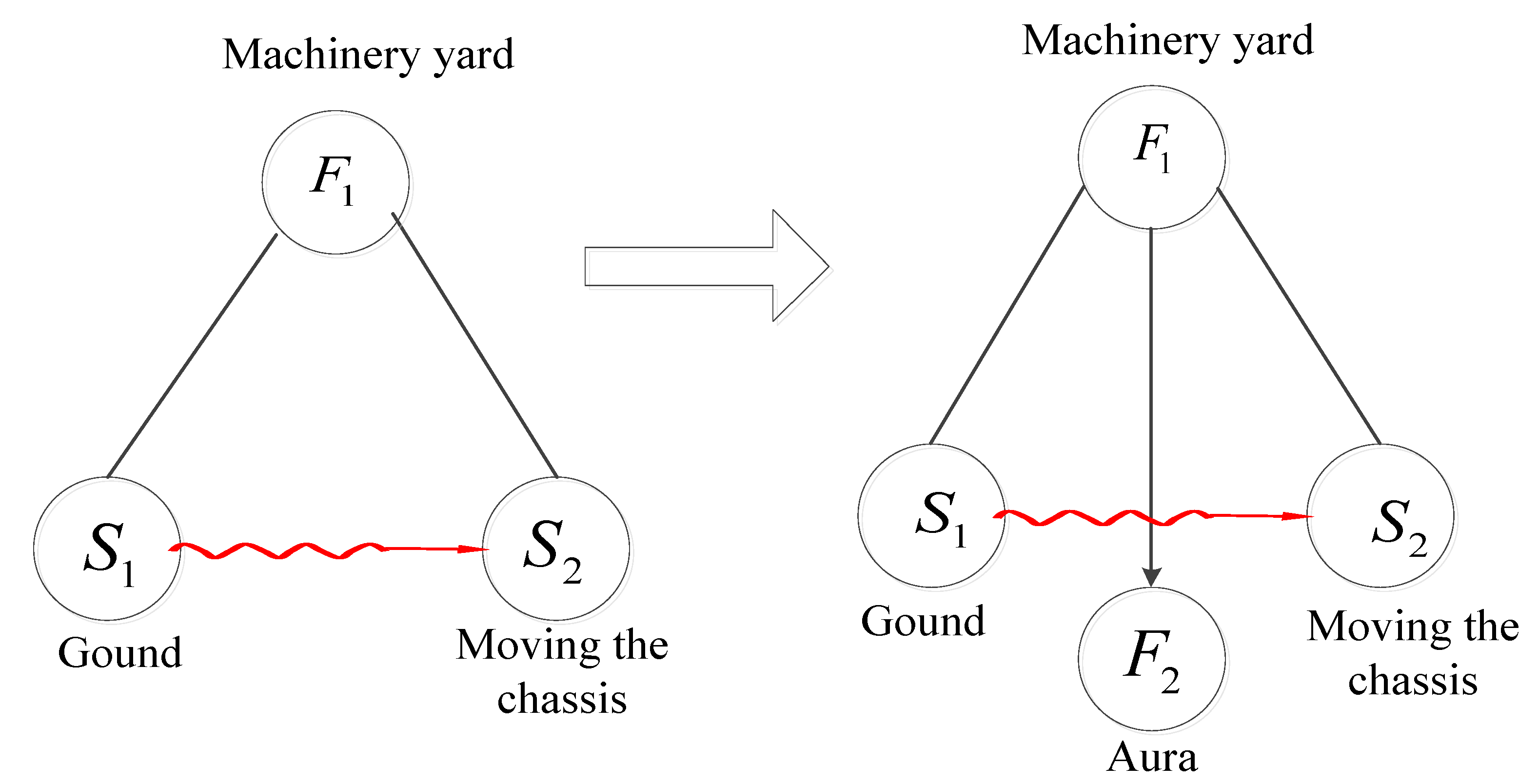
Material, function and field are three elements of the substance–field model. It has been applied to solve the problems of the existing solution from the perspective of substance and field [27]. The above floating mechanism can only meet the obstacle passing conditions on both sides of the mobile chassis. For the obstacle crossing on one side, the surface of the plate can remain horizontal in the longitudinal direction, but in the transverse direction, be still inclined. This can be regarded as a complete physical field model, but its effectiveness is insufficient. The general solution 3 was adopted, that is, another field F₂ is introduced to offset the harmful effects of the original field. In other words, in the process of unilateral obstacle crossing, the mobile chassis of the inspection robot does not tilt in the lateral direction and can run smoothly. A plan was made: introduce the gas field. Adjust the air pressure through the cylinder to keep the moving chassis in horizontally balance in the transverse direction. The improved substance–field was shown in Figure 3.

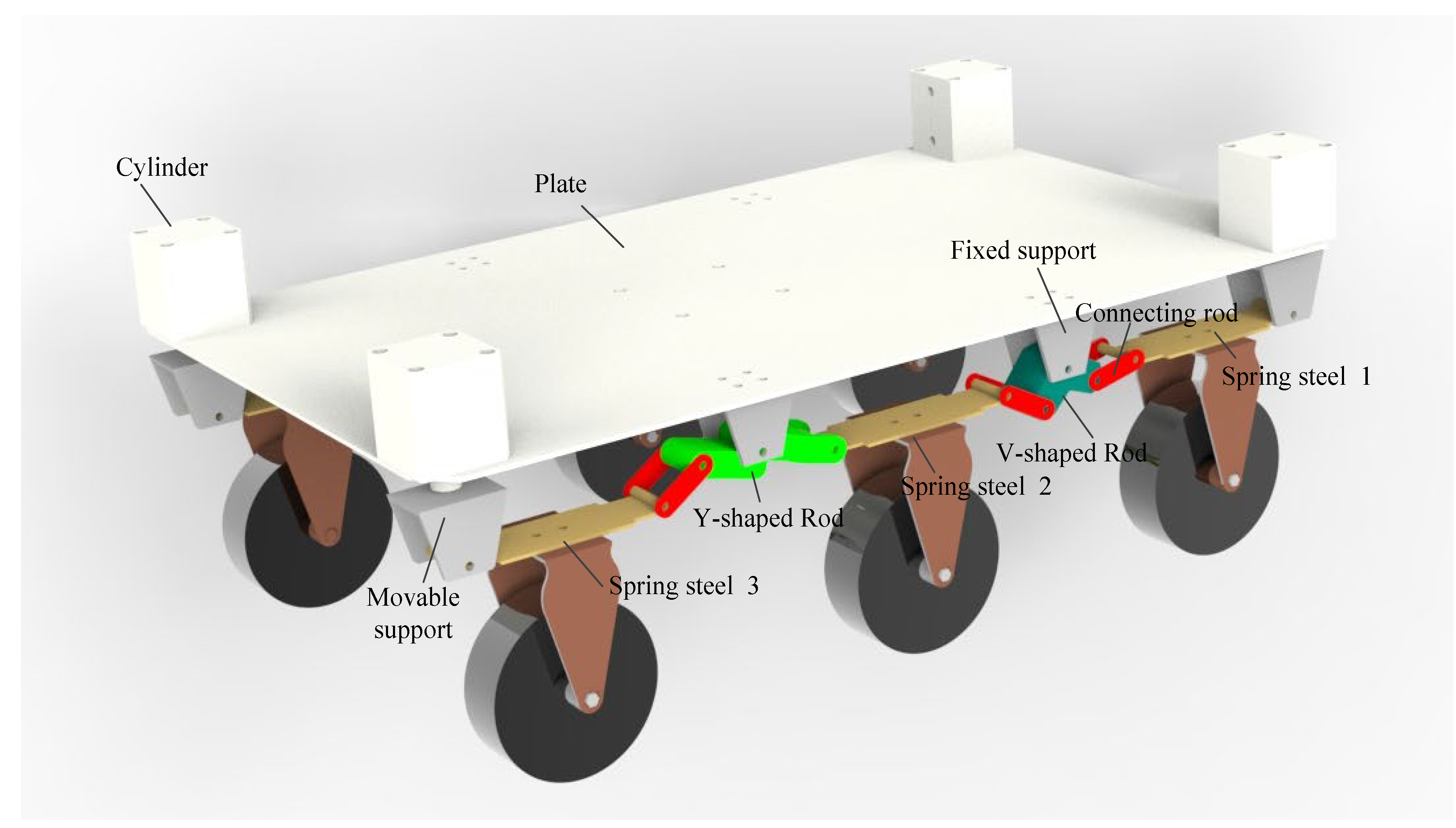
The optimized floating mobile chassis was shown in Figure 4. The floating mechanism was composed of spring steel, V-bar, Y-bar, connecting rod, movable support and fixed support. The movable support at both ends and the cylinder were fixed by screws. Both ends of the V-bar were connected to the spring steel 2 and the spring steel 3, respectively, through the connecting rod. One end of the Y-bar was directly connected to the spring steel 2, and the other end was connected to the spring steel 3 through the connecting rod. The whole floating mechanism has two degrees of freedom which can float up, down, forward and backward. The lifting distance in the vertical direction can reach 50 mm. The air cylinder was connected with the air pump through the air pipe and the valve to ensure that the surface of the plate is stable when the mobile chassis passes the obstacle on one side.

2.4. Scheme Assessment

Ideality is a concept that describes the degree of evolution of technological systems. The more reliable, simpler, and more effective any technological system evolves in the evolutionary process, the higher its ideality is.

The definition formula of ideality is:

$$I=\frac{{\displaystyle \sum _{\mathrm{i}=1}^n{B}_i}}{{\displaystyle \sum _{\mathrm{i}=1}^n{H}_i+{\displaystyle \sum _{\mathrm{i}=1}^n{C}_i}}}$$

(1)

where ${\displaystyle \sum _{i=1}^n{B}_i}$ is a collection of useful functions, ${\displaystyle \sum _{\mathrm{i}=1}^n{C}_i}$ is a collection of costs, ${\displaystyle \sum _{i=1}^n{H}_i}$ is a collection of harmful functions.

The floating mobile chassis before and after optimization was evaluated from three evaluation indexes of economy, technical feasibility and stability. The parameters in the

Table 1. Proportion of scheme parameters before and after optimization.

Name	Cost	Technical Feasibility	Stability
Before optimization	40%	80%	45%
After optimization	50%	70%	90%

were given according to the actual task requirements.

By calculation, the ideality of the mobile chassis before optimization is 3.125, and the ideality of mobile chassis after optimization is 3.2; the ideality of the mobile chassis increased significantly. The optimized floating mobile chassis is almost similar to the mobile chassis before optimization in terms of economic cost and technical feasibility. However, from the perspective of theoretical analysis, in terms of stability, when there are obstacles on one side or on both sides, the size of obstacles is different. The mobile chassis before optimization cannot meet the requirements of smooth working surface when it surmounts obstacles in the transverse direction, and the optimized scheme can solve the above problems.

3. Kinematics Analysis of Robot

3.1. Establishment of Kinematic Model of Mobile Chassis

Based on the following assumptions: (1) the mobile chassis moves on a plane; (2) the driving wheel performs pure rolling motion; and (3) the driving wheel does not slip, thus, the pure rolling equation and the non-sideslip equation of each wheel can be obtained. The kinematic model of the mobile chassis was established in Figure 5a.

Suppose $O_1,O_2,O_3,O_4,O_5,O_6$ and $v_1,v_2,v_3,v_4.v_5,v_6$ are the six-wheel center points and the moving speeds of the six wheel-center points, respectively. Thus:

$$\begin{array}{l}{v}_1=w_{1}R; v_2=w_{2}R; v_3=w_{3}R;\\ v_4=w_{4}R; v_5=w_{5}R; v_6=w_{6}R; \end{array}$$

(2)

where R is the wheel radius, ω₁, ω₂, ω₃, ω₄, ω₅ and ω₆ are angular speeds of the six wheel-center points, respectively.

Then, the traveling speed of the chassis in the $x_c$-axis direction is expressed as:

$$v_x{}_{{}_c}=\frac{v_5+v_6}{2}=\frac{w_{1}R+w_{2}R}{2}$$

(3)

The rotational angular speed of the chassis is:

$$w_c=\frac{v_2-v_1}{2B_2}=\frac{w_{1}R-w_{2}R}{2B_2}$$

(4)

where B₂ is the distance from the wheel center to the $x_c$-axis.

According to the relationship between the rotational angular velocity $v_1,v_2$ and the motion state vector of the robot center point C:

$$\left[\begin{array}{c}{w}_1\\ w_2\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\end{array}\right]\left[\begin{array}{c}{v}_x{}_{{}_c}\\ v_y{}_{{}_c}\\ w_c\end{array}\right]$$

(5)

where ${\left[\begin{array}{ccc}{v}_{xc}& v_{y\mathrm{c}}& w_c\end{array}\right]}^T$ is the motion state vector of the robot center point C.

By the same token:

$$\left[\begin{array}{c}{w}_3\\ w_4\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\end{array}\right]\left[\begin{array}{c}{v}_x{}_{{}_c}\\ v_y{}_{{}_c}\\ w_c\end{array}\right]$$

(6)

$$\left[\begin{array}{c}{w}_5\\ w_6\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\end{array}\right]\left[\begin{array}{c}{v}_x{}_{{}_c}\\ v_y{}_{{}_c}\\ w_c\end{array}\right]$$

(7)

Therefore, the kinematic equation of the mobile chassis in the $X_c{O}_c{Y}_c$ coordinate can be obtained:

$$\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\\ w_4\\ w_5\\ w_6\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\end{array}\right]\left[\begin{array}{c}{v}_x{}_{{}_c}\\ v_y{}_{{}_c}\\ w_c\end{array}\right]$$

(8)

As shown in Figure 5b, a global coordinate system XOY has been established, X_cO_cY_c is the coordinate system of the mobile chassis, and the mobile chassis is rotated $\phi$ counterclockwise with O_c as the rotation center relative to the global coordinate system, and $\gamma$ represents the position and attitude of the mobile chassis.

$$\gamma =\left[\begin{array}{l}x\\ y\\ \phi \end{array}\right]$$

(9)

The transformation matrix of the mobile chassis coordinate system $x_c{o}_c{y}_c$ relative to the global coordinate system XOY is defined as:

$$T_c=\left[\begin{array}{ccc}\cos \phi & -\sin \phi & 0\\ \sin \phi & \cos \phi & 0\\ 0& 0& 1\end{array}\right]$$

(10)

where $\cos \phi$ and $\sin \phi$ are the cosine and sine of the angle between the coordinate system of the mobile chassis and the global coordinate system, respectively.

The matrix of the angular velocity of the six wheels of the moving chassis and the center point C of the moving chassis in the global coordinate system can be obtained:

$$\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\\ w_4\\ w_5\\ w_6\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\end{array}\right]\left[\begin{array}{c}{v}_x\\ v_y\\ w_c\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\end{array}\right]T_c\gamma =\left[\begin{array}{ccc}\frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\\ \frac{1}{R}& 0& -\frac{B_2}{R}\\ \frac{1}{R}& 0& \frac{B_2}{R}\end{array}\right]\left[\begin{array}{ccc}\cos \phi & -\sin \phi & 0\\ \sin \phi & \cos \phi & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \phi \end{array}\right]$$

(11)

3.2. Analysis of Obstacle Surmounting Performance

In the process of a patrolling inspection outdoors, the robot may encounter obstacles such as steps and trenches. In order to ensure the accuracy of the precision instruments carried during operation, the mobile chassis plane is required to have a certain stability in the horizontal and longitudinal directions.

3.2.1. Boss Obstacle Surmounting

Figure 6 showed the obstacle surmounting process of the floating mobile chassis. When the mobile chassis moved forward, the front wheel touched the boss first, as shown in Figure 6a,b; the connecting rod 1 rotated clockwise by a certain angle, the spring steel 1 was compressed, the Y-bar tilts counterclockwise and the front wheel was lifted, as shown in Figure 6b,c; when the middle wheel met the boss, spring steel 2 was compressed, the Y-bar rotated clockwise relative to Figure 6a, and both the connecting rod 2 and the V-bar rotate counterclockwise and tilt upward relative to Figure 6a, as shown in Figure 6d,e. When the rear wheel passed through the obstacle, the spring steel 3 was compressed, the connecting rod 3 and the V-bar both rotated clockwise relative to Figure 6a, and both the connecting rod 1 and the Y-bar rotated clockwise downward relative to Figure 6a, as shown in Figure 6f,g.

3.2.2. Crossing the Trench

The process of the floating mobile chassis crossing the trench is shown in Figure 7. When the front wheel encountered the trench, the Y-bar drove the connecting rod 1 to incline clockwise downward relative to in Figure 7a, and the spring steel 1 was stretched, as shown in Figure 7b,c; when the middle wheel encountered the trench, spring steel 2 was stretched, the Y-bar rotated clockwise relative to Figure 7a, and both the connecting rod 2 and the V-bar inclined clockwise downward relative to Figure 7a, as shown in Figure 7d,e; when the rear wheel passed the trench, the spring steel 3 was stretched, the connecting rod 3 rotated counterclockwise with respect to Figure 7a, and the connecting rod 1 rotated counterclockwise with respect to Figure 7a, as shown in Figure 7f,g.

3.3. Dynamic Analysis of Mobile Chassis Obstacle Surmounting

The dynamic model of the floating chassis was established by D’Alembert’s principle, and the force problem of the mobile chassis in the process of obstacle crossing was solved by the static method. Taking the front wheels as an example, the mechanical analysis of the obstacle-crossing wheel was carried out. During front wheel obstacle surmounting, the middle wheel, the rear wheel and the mobile chassis body can be regarded as a whole, and the dynamic problem can be divided into the front wheel and the non-front wheel part, and the coordinate system shown in Figure 8 was established.

It is known that the speed of the front wheel center in the vertical direction is $v_1$, and the moment of inertia is $J_1$; the dynamic model of the front wheel over obstacles is established:

$$\left\{\begin{array}{l}{F}_x{}_1+\mu N_1\cos (\theta +\alpha )+\mu N_2+\mu N_3=0\\ F_y{}_1+N_2+N_3+\mu N_{1}sin(\theta +\alpha )+(M+2m)g=m{v}_1\\ M_1-\mu N_{1}sin(\theta +\alpha )R=J_1\frac{v_1}{R}\end{array}\right.$$

(12)

where M is the mass of the body, m the mass of the wheel, $N_1,N_2$ the support force of the ground to the front and middle wheels, $N_3$ the force of the boss on the front wheels, $\mu$ the frictional coefficient, $F_x{}_1,F_y{}_1$ the force of the spring steel on the front wheels, $M_1,M_2,M_3$ the driving torque received by the front, middle and rear wheels, $\theta$ the angle between the connecting line between the front wheel center and the middle wheel center and the horizontal line, $\alpha$ the angle between the connecting line between the center of the middle wheel and the contact point between the front wheel and the ground and the horizontal line.

3.4. Mathematical Evaluation Model of Mobility Performance of Mobile Chassis

3.4.1. Terrain Adaptability

During the movement of the inspection robot, the relative position of the wheels also changes with the change of the road conditions, and the contact force between the wheels and the ground also changes. The change curve is shown in Figure 9a. The adaptive evaluation coefficient of the wheel can be used to reflect the adaptability of the robot to the ground (here goes Formula (13)), and the functional relationship between the adaptive evaluation coefficient $C_s(t)$ of the wheel and the contact force $F_c(t)$ between the wheel and the ground, the adaptive evaluation curve of the mobile chassis, is obtained, as shown in Figure 9b.

$$C_s(t)=\frac{F_c(t)-F_f}{F_f}$$

(13)

where F_f refers to the contact force between the wheel and the ground in the flat environment.

3.4.2. Ride Comfort

The ride comfort of the robot is mainly reflected in the changes of the center point height, pitch angle and roll angle of the mobile chassis, while the pitch angle and roll angle depend on its structure. Therefore, the change of the center point height of the mobile chassis becomes an important index affecting the ride comfort of the robot.

The height of the center point of the moving chassis H(t) is a random process:

$$H(t)=(h\left(t_1\right),h\left(t_2\right),\dots h\left(t_n\right)),n=1,2,3\dots$$

(14)

where h(t_n) is the height of the moving chassis at t_n.

The degree of dispersion of the height ${\delta }_h{}^2(t)$ is:

$${\delta }_h{}^2(t)=E\left\{{\left[H(t)-{\mu }_H(t)\right]}^2\right\}$$

(15)

where ${\mu }_H(t)$ is the average of $H(t)$.

4. Simulation Analyses

In order to verify the plate of the floating mobile chassis is still stable when the robot moves on a complex road surface, virtual prototypes of the floating mobile chassis and the non-floating mobile chassis were established in ADAMS. The structural features of the non-floating mobile chassis were that the Y-bar and V-bar were removed, and both ends of the spring steel are connected to the support, respectively, and the wheels were fixed on the bearings and the wheel diameter is 100 mm. Here comes the motion simulation of the mobile chassis with two kinds of different structures on boss, groove and complex road conditions, respectively.

4.1. Boss Obstacle Surmounting

The height of the boss was 25 mm, and the boss obstacle surmounting was carried out for the floating mobile chassis and the non-floating mobile chassis respectively. The simulation process and simulation results of obstacle crossing are shown in Figure 10.

The barycenter curve of the non-floating mobile chassis on the flat road surface fluctuates more largely than that of the floating mobile chassis, and the obstacle crossing process of the mobile chassis with two different kinds of structures is around 1–1.4 s. The center curve of the mass of the non-floating mobile chassis fluctuates sharply up and down, while the fluctuation of the centroid curve of the floating mobile chassis is relatively gentle and approximates a straight line, as shown in Figure 10c.

4.2. Trench Obstacle Crossing

The width of the trench established was 30 mm. The floating mobile chassis and the non-floating mobile chassis were respectively subjected to crossing a ditch. The simulation process and simulation results of obstacle crossing are shown in Figure 11.

It is the obstacle surmounting process of the mobile chassis with two kinds of structures in 1–1.5 s, and the barycenter curve of the non-floating mobile chassis fluctuates more sharply than that of the floating chassis, which fluctuates relatively gently, and approximates a straight line in the process of surmounting obstacles, as shown in Figure 11c.

4.3. Complex Road Conditions

A complex pavement with a length of 3 m and a width of 800 mm was built, where bosses with a height of 25 mm and grooves a width of 30 mm were set up randomly. Motion simulation analysis of the floating mobile chassis and non-floating mobile chassis were conducted, and the center of mass of the plate of the mobile chassis was marked, respectively. Figure 12 showed the trajectories of the center of mass of the plate with two different types of structures. The trajectory of the center of mass of the floating mobile chassis is approximately a smooth straight line, while the trajectory of the center of mass of the non-floating mobile chassis has obvious fluctuations in the positions of the bosses and grooves.

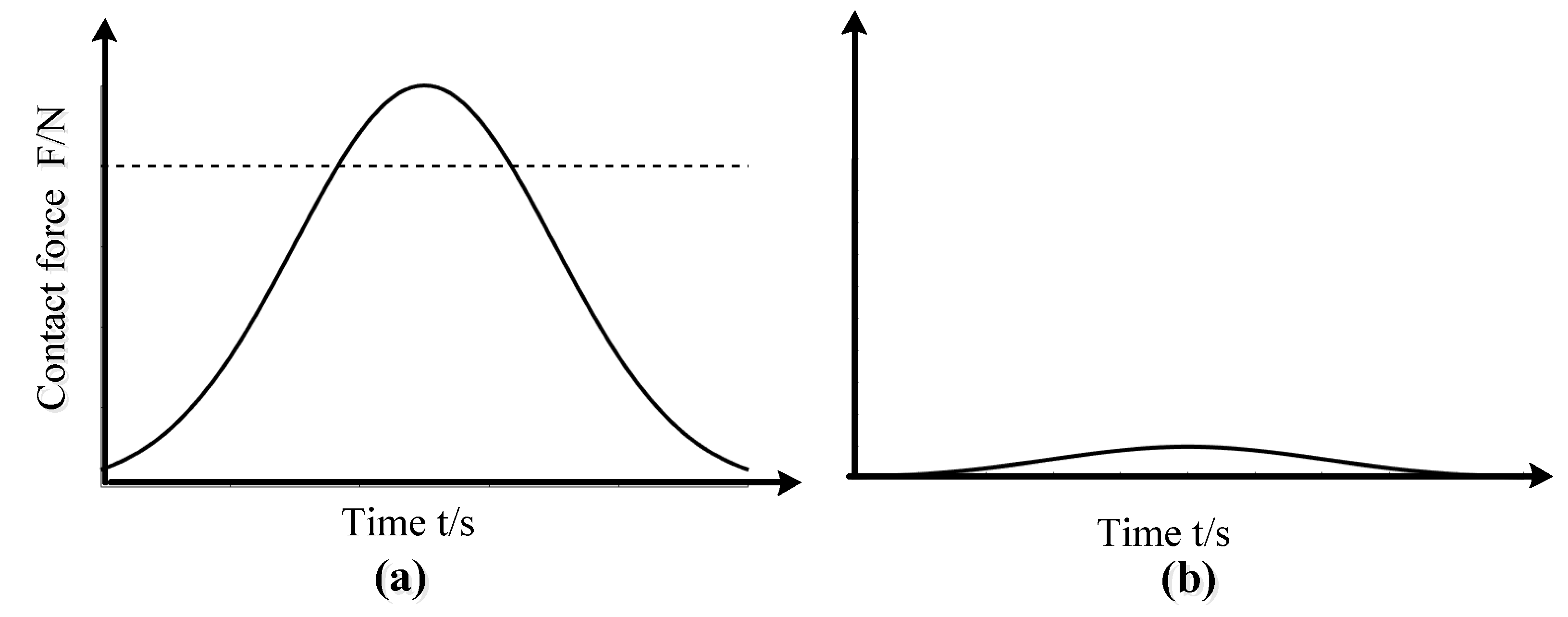
The track and contact force of the wheels of two different kinds of structures of mobile chassis on the complex road surface were obtained from the post-processing module in Adams, as shown in Figure 13. In 1.5–1.9 s, 2.6–3 s, 4.3–4.6 s, it is time for two different kinds of structures of mobile chassis to pass the bosses. It can be seen that the contact force of the front, middle and rear wheels increases sharply when surmounting obstacles, and the greater the contact force becomes, the stronger the gripping ability of the mobile chassis becomes. The contact force of the six wheels of the floating mobile chassis is obviously greater than that of the non-floating mobile chassis, which indicates that the floating mobile chassis has a stronger grip and a stronger ability to adapt to the terrain when crossing obstacles.

According to the above simulation analysis, the floating mobile chassis can complete the movement on complex roads such as bosses and grooves, and the track of the mass center of the chassis presented a straight line during the movement, that is, the floating mobile chassis can maintain the stability of its plate and provide a stable working plane for the precision instruments carried, which verified the structure design of the mobile chassis is reasonable.

5. Prototype Tests

The purposes of testing the floating mobile chassis of the inspection robot are, on the one hand, to verify the motion analysis and simulation analysis of the mobile chassis under ideal conditions; in addition, we can find out whether the structure is unreasonable by testing the floating chassis prototype. If so, it is necessary to analyze the irrationality and propose new solutions.

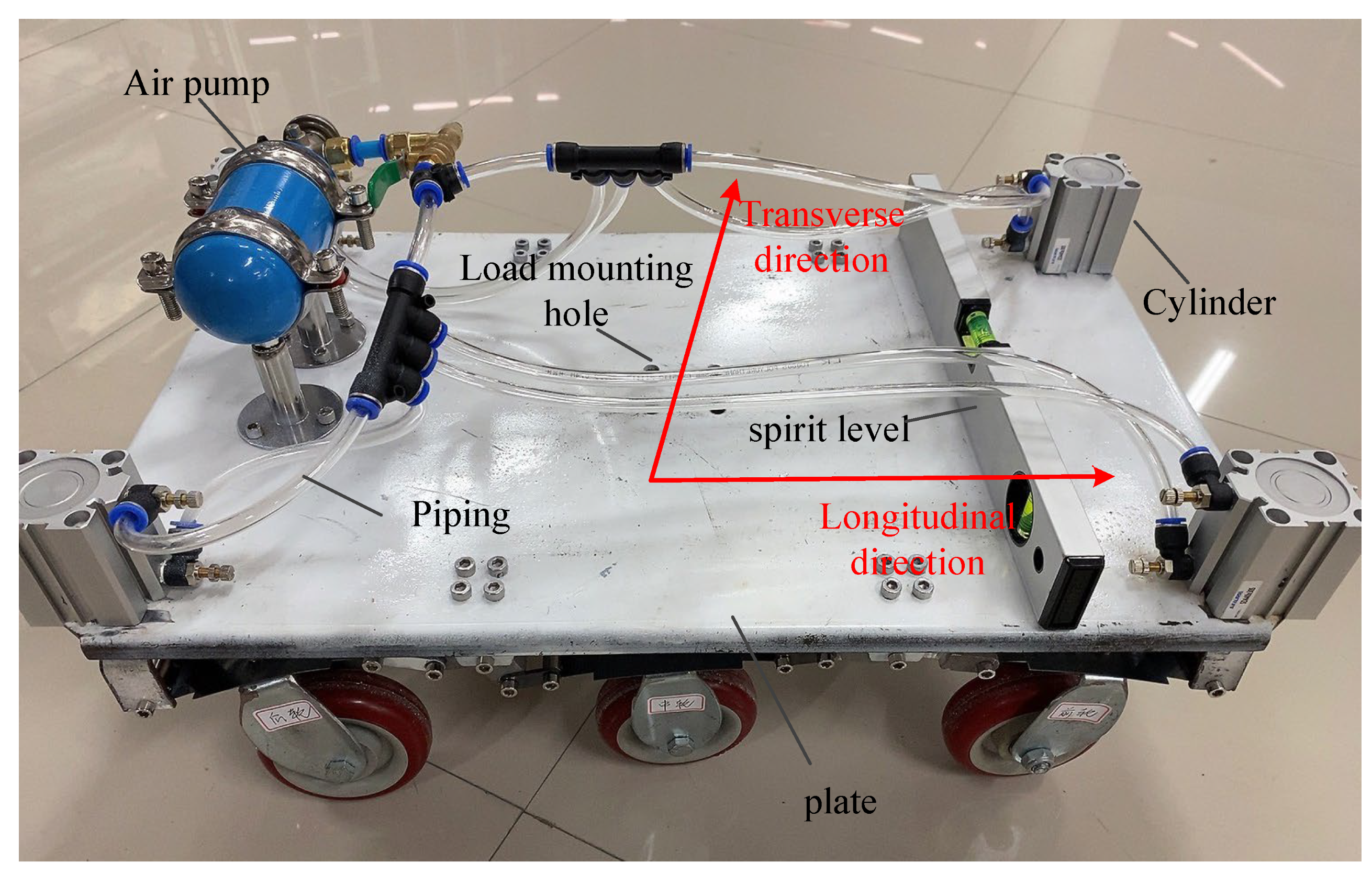
As shown in Figure 14, the floating chassis was composed of wheels, floating suspension, cylinders, air pumps, level gauges, etc. The wheel diameter is 100 mm. The cylinders were distributed at the four corners of the mobile chassis, which were connected to the air pumps through valves and pipelines. The piston rods of cylinders were connected to the movable supports of the floating suspension. Four load mounting holes were left in the middle of the plate. The adjustable stroke cylinder was selected, and the spirit level was used to measure the balance of the plate in the horizontal and vertical directions. The position of the center of mobile chassis and wheel center were marked, and were measured by a high-precision electronic digital caliper.

5.1. Obstacle Crossing Test of One Side Boss

An obstacle road with a length of 2000 mm and a width of 900 mm was built, at the center of which a boss with a height of 25 mm was set. A load of 10 kg was fixed on the plate through the mounting hole. The front and rear wheels were adjusted by air cylinder to make the floating mobile chassis in a balanced state on the horizontal plane, and a spirit level was placed in the horizontal direction and the longitudinal direction to detect the balance of the plate during the movement.

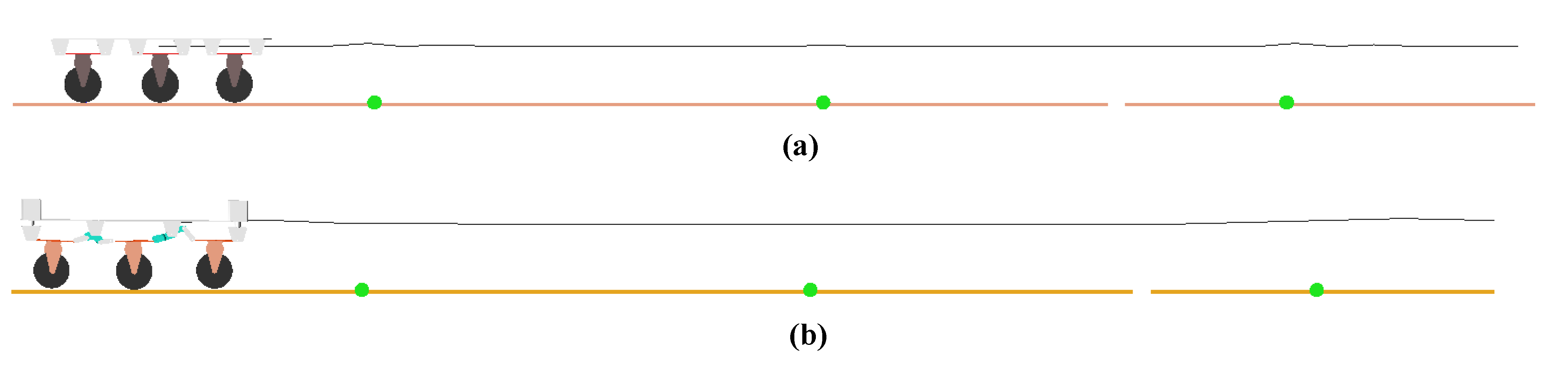
The front, middle and rear wheels on the left side of the floating mobile chassis were subject to crossing the boss in turn, while those wheels on the right side should be subject to flat motion; the obstacle crossing tests on one side are shown in Figure 15. The movement tracks of the center of the plate and each wheel center were reflected by measuring the distance between the plate and the ground, and the distance between each wheel center and the plate is shown in Figure 16.

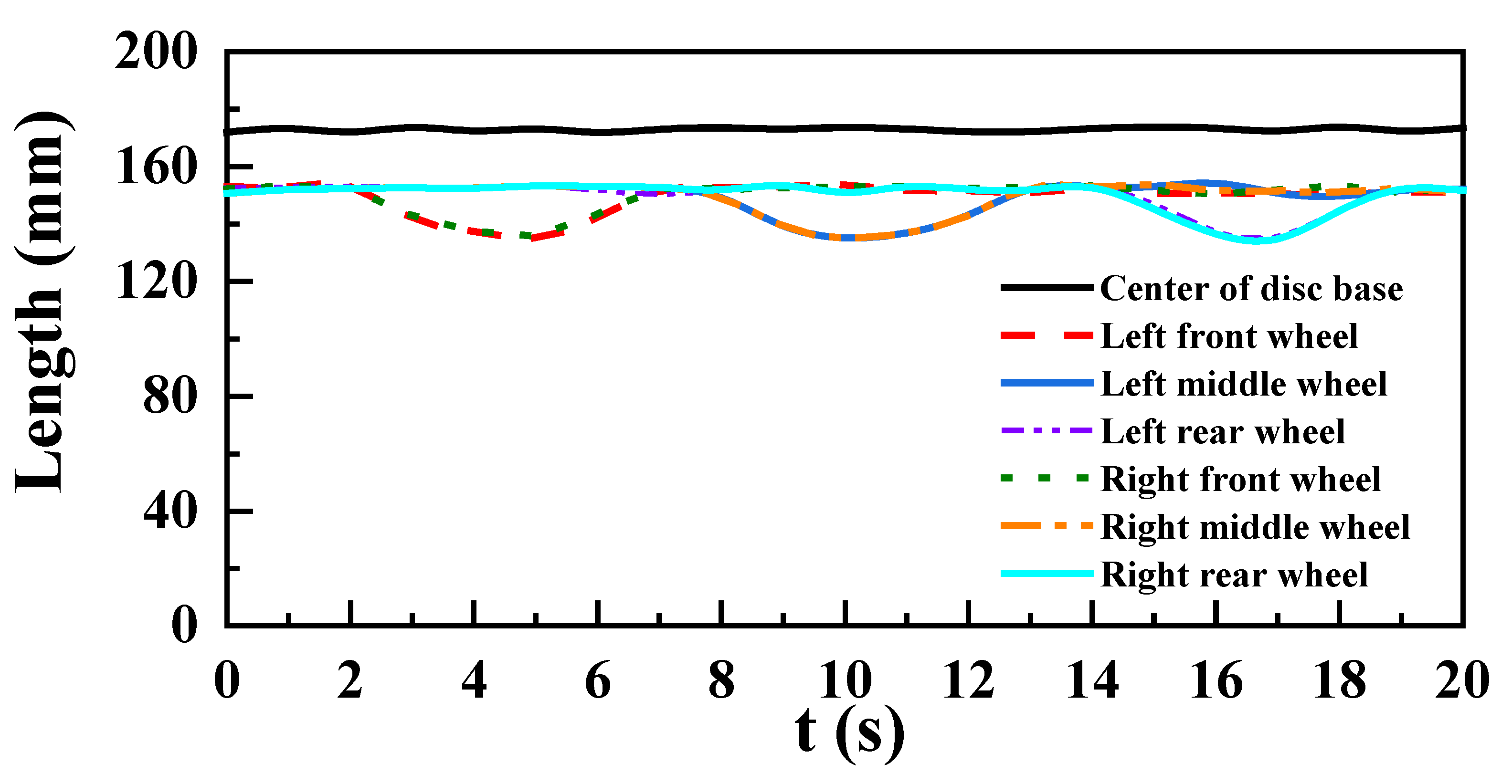
In Figure 16, it can be seen that the trajectories of the six wheel centers coincide in 0–2 s, 7–8 s, 12–14 s and 18–20 s, indicating that the chassis was moving on a horizontal road. In 2–7 s, 8–12 s and 14–18 s, the track of the front wheel center, the middle wheel center and the rear wheel center on the left side all change from small to large, corresponding to the process of the front wheel, the middle wheel and the rear wheel crossing the obstacle, respectively, as shown in Figure 15a. Meanwhile, the spirit level on the left and right sides in the longitudinal direction and the spirit level on the lateral direction were in balance. During the single side obstacle surmounting movement of the mobile chassis, the track of the mass center of the plate was approximately a straight line, and the level in the transverse and longitudinal directions was always in balance, indicating that the surface of the plate of the mobile chassis can always remain horizontal.

5.2. Obstacle Surmounting Test of Bilateral Bosses

Adjust the position of the floating moving chassis to conduct the double-sided obstacle crossing test, as shown in Figure 17. The track of the mass center of the plate and track of each wheel center are shown in Figure 18.

When crossing obstacles on both sides, the wheel center track of the obstacle crossing wheel was consistent with that of the obstacle crossing on one side; the left front wheel center track and the right front wheel center track, the left middle wheel center track and the right middle wheel center track, and the left rear wheel center track and the right rear wheel center track were close to each other. It can be seen from Figure 17 that when the front wheel, middle wheel and rear wheel cross the obstacle, respectively, the spirit level in the longitudinal and transverse directions kept horizontal balance, and the center track of the plate was approximately a straight line, indicating that the surface of the plate presents a horizontal plane when both sides of mobile chassis cross the obstacle.

5.3. Trench Crossing Test

To verify the stability of the mobile chassis of the inspection robot when crossing the trench, a trench with a width of 210 mm and a depth of 25 mm was set. Adjust the position of the floating movable chassis to conduct the cross-trench test, as shown in Figure 19. The track of the mass center of plate and the track of each wheel center are shown in Figure 20.

In the whole trench crossing process, the motion track of the mass center of the plate is approximately a straight line, and the motion tracks of the left and right front wheels, left and right middle wheels and left and right rear wheels almost coincide. The front wheels crossed the trench successfully in 4–12 s, the middle wheels made it in 9–12 s, and the rear wheels made it in 16–24 s. The spirit level always kept balance in the transverse and longitudinal directions during obstacle surmounting of mobile chassis, as shown in Figure 19, indicating that the plate can always keep horizontal in the movement of crossing the trench.

5.4. Double Wheel Obstacle Crossing Test

When two wheels on one side of the floating chassis surmounted obstacles at the same time, the stability of the moving chassis under the conditions of obstacles on one side and obstacles on both sides respectively was studied, as shown in Figure 21.

Whether the left front and middle wheels, the middle and rear wheels, or the front and rear wheels cross the obstacle, the spirit level on the plate in the transverse and longitudinal directions were in balance, as shown in Figure 21a. The same is true for double wheel crossing obstacles of both sided, as shown in Figure 21b indicating that the floating mobile chassis is suitable for complex road conditions with multiple obstacles.

5.5. Pothole Complex Pavement Test

A complex pavement with a length of 4500 mm and a width of 900 mm, where three 25 mm bosses and a 210 mm wide trench were placed randomly was set, as shown in Figure 22. The obstacle surmounting process of floating chassis was shown in Figure 23, and the movement tracks of the plate and each wheel center were displayed in Figure 24.

In Figure 24, the front wheel successfully surmounted the first boss in 2 to 7 s, and the middle wheel got it in 8 to 12 s. The rear wheel started to climb the first obstacle at 16 s, while the front wheel climbed the second boss, which is consistent with the movement process of the chassis in Figure 23a. The rear wheel successfully surmounted the first boss at 20 s, and the front wheel completed the second boss meanwhile; the front wheel crossed the trench in 23 to 27.5 s, and the middle wheel successfully crossed the second boss; the rear wheel successfully crossed the second boss in 28 to 30 s, and the trench crossing was completed by the middle wheel in 29 to 36 s; 34 to 40 s was the process of the rear wheel crossing the trench; the floating chassis moves on the flat road in 41 to 45 s, and the wheel center tracks of the six wheels coincide at this time; the front, middle and rear wheels successfully passed the third boss in turn in 47 to 52 s, in 52 to 56 s and in 56 to 59 s. During the whole process of movement, the center track of the plate is approximately a straight line, and it is known from Figure 23 that the spirit level in the horizontal and vertical directions kept balance, indicating that the floating chassis can maintain the stable state of the plate on the complex roads with potholes.

Taking the potholed and complex road as an example, the simulation analysis and prototype test of floating mobile chassis were carried out, and the results of the two were compared and analyzed, respectively, as shown in Figure 25. The data on the abscissa represent the length of the road the mobile chassis has travelled on, and the data on the ordinate are the height of the centroid of mobile chassis. Through comparison, it is found that the maximum difference between the two is 2 mm; overall, the simulation curve is basically consistent with the measured curve. The motion process is consistent with the theoretical analysis. It is verified that the design of the floating mobile chassis is reasonable and the theoretical analysis of mobile chassis is correct.

6. Discussion and Conclusions

The problem of improving the robot’s ability to surmount obstacles on the potholed and complex road has been widely studied. The underground inspection robot was taken as an example, the robot needs cameras, sensors and other precision instruments carried to complete the patrol work in the underground environment. Improving the ability to surmount obstacles is the first step for the robot to carry out patrol inspection; however, whether the robot can provide stable operating conditions for the precision instruments in the process of obstacle crossing is worth another concern. In this paper, the floating mobile chassis prototype can move on the potholed road to maintain the stability of its plate base. In this paper, a floating suspension design was proposed based on the TRIZ theory, and the design of the floating chassis was optimized through the substance-field, and the ideality of the optimized chassis significantly increased by 0.075. The kinematic model and moving performance evaluation index of the floating ground moving plate were established. The comparative study of the non-floating mobile chassis and the floating mobile chassis were also performed. The results showed that the floating mobile chassis has good stability and terrain adaptability when crossing obstacles. The floating chassis prototype was built, and the motion tests were also carried out under the conditions of one-sided boss crossing, trench crossing, two-sided boss crossing and complex road conditions. The experimental results indicate that the floating mobile chassis can maintain the stability of its working plane when surmounting the obstacles and verifies that the floating mobile chassis structure design is reasonable.

In this paper, the design of the floating suspension mobile chassis proposed is currently carried out under relatively ideal experimental conditions. For other road conditions such as turning in situ and larger obstacles, relevant parameters of the mobile chassis need to be improved in the future and compared with the existing scheme. In addition, the future will also focus on researching the motion control of the mobile chassis in the current scheme.