Simulation of Magnetorheological Plane Polishing Scratch Creation Process and Suppression Method

Highlights

What are the main findings?

• The creation process of the scratch damage during magnetorheological plane polishing.
• The suppression method of the scratch damage during magnetorheological plane polishing.

What is the implication of the main findings?

• The influence of process parameters on the distribution and morphology of scratch damage is analyzed.
• The process parameters that can inhibit the formation of scratch damage are given.

Abstract

This study was conducted to simulate the causes of, and suppress, the scratch damage on the workpiece surface during magnetorheological surface polishing. The molecular dynamics method combined with polishing contact trajectory modeling was used to simulate the scratch damage formation process, and the scratch damage morphology model was established by analyzing the scratch damage distribution characteristics in the magnetorheological plane polishing process. The effect of different process parameters on the scratch damage characteristics was predicted by simulation, and orthogonal experiments were designed to explore the preferred polishing process parameters that could suppress the scratch damage formation. Finally, it was further verified that the formation of scratch damage can be effectively suppressed by controlling the workpiece speed, polishing disc speed, and magnetic field generator speed, and adjusting the magnetic field eccentricity distance under the premise of ensuring the surface roughness and flatness of the workpiece.

1. Introduction

Magnetorheological plane finishing (MRPF) technology presents a new ultra-precision surface machining method which has the advantages of high removal precision, small surface roughness, a controllable machining process, and small sub-surface damage [1,2,3,4]. Therefore, it can be used to realize ultra-precision planarization of hard and brittle materials [5,6,7]. In this method, the rapid relative movement between the flexible “small grinding head” formed by the magnetorheological fluid in the gradient magnetic field and the workpiece ensures the material surface is subjected to a large shear force to achieve material removal [8,9]. However, with the increase in magnetic field strength, ferromagnetic particles agglomerate to form large particles, which tends to result in irregular scratch damage and surface pits on the workpiece surface (Figure 1) [10,11,12,13,14]. The workpiece with surface defects is prone to stress concentration in the subsequent processing process, resulting in huge losses due to cracks on the workpiece surface [15]. Therefore, it is necessary to investigate the surface damage process of magnetorheological polishing and try to grasp the method of controlling the surface damage formation from it.

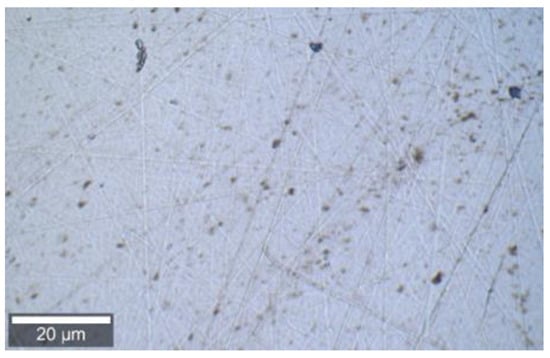
Figure 1. Surface pits and scratches caused by particle agglomeration on a wafer surface.

Many scholars have conducted studies on the simulation of workpiece surface machining processes during flat polishing. Gu et al. [16] proposed a simulation model of single abrasive particles to simulate a silicon carbide polishing process and analyzed the removal process of workpiece materials in terms of the effects of different process parameters on the surface stress distribution and the surface removal morphology. Elsewhere, Chen et al. [17] studied the relationship between mechanical action and chemical action in the process of chemical–mechanical polishing, controlling the chemical action by adjusting the mechanical parameters to reduce the surface and sub-surface damage of monocrystalline silicon. Meanwhile, Cai et al. [18] used the layer-by-layer corrosion method to remove the near-surface damage layer of a silicon wafer, comparing and analyzing the surface morphology of silicon wafers cut using a mortar wire saw and a diamond wire saw. For their part, Li et al. [19] proposed a method for improving the thickness of the damaged layer and optimizing the grinding process, observing the crystal surface morphology with different particle sizes, and analyzing the factors affecting the damaged layer in the process. Elsewhere, Zhang et al. [20] studied the surface damage of lanthanum-doped lead zirconate titanate irradiated by a high-power laser and analyzed the change in damage depth, damage diameter, and damage morphology caused by defects in the material. In a more recent study, Zhang et al. [21] conducted molecular dynamics simulation of Ni-based high-temperature alloy GH4169 in terms of different cutting speeds and cutting depths and investigated how the cutting parameters affect the nanocuttability, while in [22], the authors explored the surface damage mechanism of single-crystalline Si (100) under single-point diamond grinding and proposed that the new product of Si₃N₄ and graphite oxide was the surface damage and tool wear mechanism of silicon that occurs in ultra-precision machining processes. Meanwhile, Lin et al. [23] investigated the surface damage of 100-oriented single-crystal diamonds by comparing three different polishing methods, namely, mechanical polishing, mechanochemical polishing, and chemical–mechanical polishing. It can be seen that the current research on the removal mechanism of magnetorheological polished materials focuses on the surface roughness, flatness, and material removability, but there is less research on the mechanism and mechanism of the formation of surface scratches.

In this paper, the molecular dynamics method combined with polished contact trajectory modeling is used to simulate the scratch damage formation process. By analyzing the morphological characteristics of scratch damage distribution in the MRPF process, a scratch damage morphological model is established. The depth and width variation curves of scratch damage are obtained based on the variation of velocity and polishing force of agglomerated particles on wafer surface which are calculated from the polished contact trajectory model. The simulation of scratch formation process and the prediction of scratch characteristics are realized by means of simulation, and the optimization of process parameters to suppress the formation of scratch damage is mastered by combining with orthogonal experiments.

2. Micro Material Removal Simulation

2.1. Modeling of Scratch Process on Workpiece Surfaces

In the MRPF process, agglomerated particles scratch the workpiece surface due to the combined action of polishing disc, polishing head, magnetic field generator, and polishing fluid, resulting in scratch damage on the machined surface [24], as shown in Figure 2. To comprehensively explore the formation law of scratch damage, the scratch process pertaining to workpiece surfaces was simulated using the molecular dynamics method [25,26]. Relevant parameter settings of the molecular dynamics model are shown in Table 1.

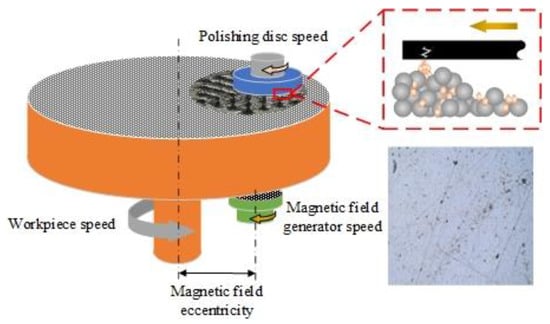
Figure 2. Scratch movement between agglomerated particles and workpiece surface.

Table 1. Parameters applied in the simulation model.

Variable Name	Variable Value
Matrix material	GaAs
Matrix size	45a × 30a × 15a (a = 0.565 nm)
Agglomerated particles material	C
Agglomerated particles size	R = 80 nm
Boundary condition	Periodic boundary conditions
Ensemble	Microcanonical ensemble
Temperature control method	Nose–Hoover method, maintain 300 K
Velocity model	Velocity-Verlet algorithm
Potential function	BOP potential function describes the interaction between GA and As atomsZBL potential function describes the interaction between agglomerated particles and GaAs
Time step	1 fs
Scratch speed	100 m/s
Scratch distance	2 nm, 4 nm, 6 nm, 8 nm, 10 nm, 12 nm

After simulating the scratching process with LAMMPS, scratch morphology can be observed by visualization software Ovito. Figure 3 shows the simulation results of the workpiece surface scratch damage caused by spherical stacking abrasive action. The atoms on a scratch-damaged surface essentially accumulate in front of the agglomerated particles, with the level of atom accumulation increasing with the increase in scratch distance, ultimately resulting in various atomic accumulation peaks.

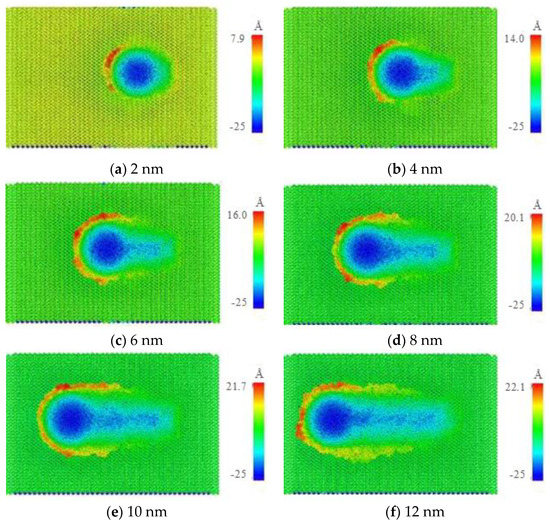
Figure 3. Scratch damage with different scratch lengths.

During the scratch process, certain atomic structures of gallium arsenide (GaAs) crystals are changed. To accurately observe the variation in GaAs atomic structure, structural analysis of the matrix material was performed. Figure 4 shows the types of atoms that undergo structural changes following the scratch process. With the increase in scratch length, the number of changing atoms continuously increases, with the atoms of the CD-1 and HD-1 types in the system also gradually increasing.

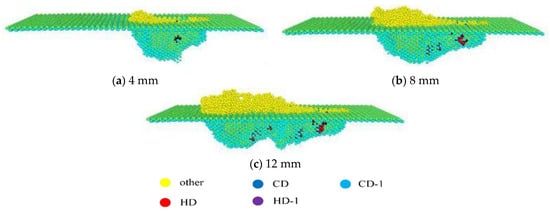
Figure 4. Atomic structure with different scratch lengths.

2.2. Influence of Polishing Medium on Scratch Damage Characteristics

2.2.1. Influence of Load

Figure 5 shows a scratch morphology with different indentation depths. With the increase in load, the actual depth of the scratch damage increased, while the atomic stacking height on the workpiece surface also gradually increased. The plastic deformation produced during the scratch process also exhibited an increasing trend, which was due to the increase in the contact area between the agglomerated particles and the matrix material.

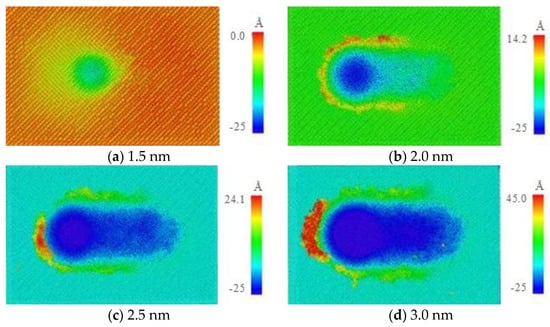
Figure 5. Scratch morphology with different indentation depths.

Meanwhile, Figure 6 shows the relationship between atomic structure and indentation depth. Here, when the pressing depth was 1.5 nm, there were no clear scratches, and the pressing effect of the agglomerated particles could be entirely offset by the elastic recovery of the GaAs material. However, the change in the internal atomic structure was not restored, meaning plastic deformation occurred under the matrix material.

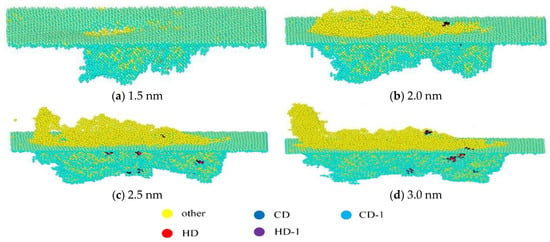
Figure 6. Atomic structure with different indentation depths.

2.2.2. Influence of Shape and Size of the Agglomerated Particles

Two different shapes and sizes of agglomerated particles were used for the scratch simulation, as shown in Figure 7a,b, with the results shown in Figure 7c,d. In terms of pyramidal agglomerated particles, the accumulation of atomic surface materials only occurred in front of the agglomerated particles, while there was no accumulation on either side of the agglomerated particles. In terms of spherical agglomerated particles, the accumulation of atomic surface materials mainly occurred in front of the agglomerated particles, while there was also some atomic accumulation on both sides of the particles. This was mainly due to the different shapes of the two forms of agglomerated particles, which led to a different contact area between the particles and the matrix material. In short, the contact area of spherical agglomerated particles is larger than that of pyramidal agglomerated particles.

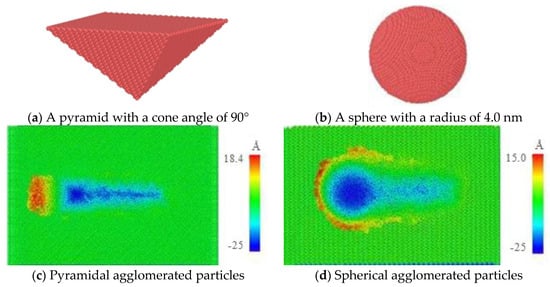
Figure 7. Scratch damage of agglomerated particles with different shapes.

To investigate the effect of agglomerated particle size on scratch damage, pyramidal agglomerated particles with cone angles of 50°, 60°, 70°, 80°, 90°, and 100°, and spherical agglomerated particles with a radius of 3, 3.5, 4, 4.5, and 5.0 nm were selected for the scratch formation simulation. The results are shown in Figure 8. Here, it was clear that following the scratch process involving agglomerated particles with different shapes and sizes, the indentation depth was always 2.0 nm, while atomic accumulation tended to occur on the substrate surface. However, with the increase in cone angle or particle radius, the stacking height of the atoms on the material surface gradually decreased.

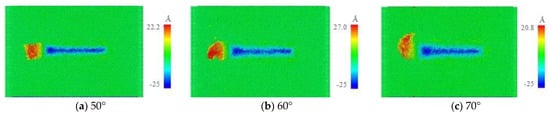
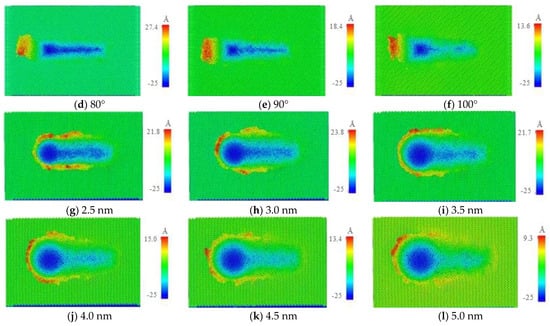
Figure 8. Scratch damage morphology with agglomerated particles of different shapes and sizes.

Scratch width was calculated based on simulation data using MATLAB Figure 9 shows the relationship between scratch width and the shape and size of the agglomerated particles. Here, when the scratch depth was constant, the contact area between the agglomerated particles and the matrix material became larger regardless of whether the cone angle of the pyramidal particles or the particle size of the spherical particles was increased, resulting in a continuous increase of the actual scratch width.

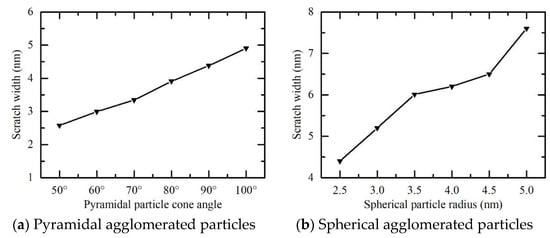
Figure 9. The actual scratch width with agglomerated particles of different shapes and sizes.

Scratch depth was calculated based on simulation data using MATLAB. Figure 10 shows the relationship between scratch depth and the shape and size of the agglomerated particles. Here, the scratch depth formed by pyramidal agglomerated particles with a cone angle of 50°–80° was approximately equal to the scratch depth formed by spherical agglomerated particles with a particle size of 2.5–3.5 nm. However, with a continuous increase in cone angle or particle size, the actual scratch depth decreased, which was mainly due to the change in contact area between the agglomerated particles and the matrix materials.

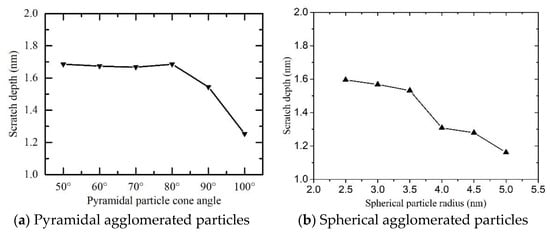
Figure 10. The actual scratch depth with different shapes and sizes of agglomerated particles.

Meanwhile, Figure 11 shows the analysis results for the internal atomic structure of the material according to the above simulation results. With the increase in cone angle or particle size, the extrusion densification degree of the matrix material was higher. This was because the increase in the size of the agglomerated particles caused some extrusion, resulting in an increasing number of atoms with broken atomic bonds. The atoms that underwent atomic structural change moved forward along the scratch direction, thus increasing the compactness of the extruded atoms.

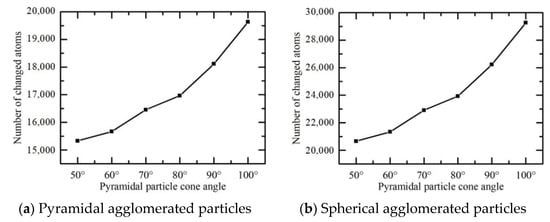
Figure 11. The number of atoms undergoing atomic structural change with agglomerated particles of different shapes and sizes.

2.2.3. Influence of Scratch Speed

Figure 12 shows the scratch morphology with different scratch speeds. Here, with the increase in scratch speed, the height of the atoms stacked in front of and on both sides of the agglomerated particles initially increased and then decreased. In addition, the atomic accumulation was more dispersed, which will likely affect the surface quality of the workpiece.

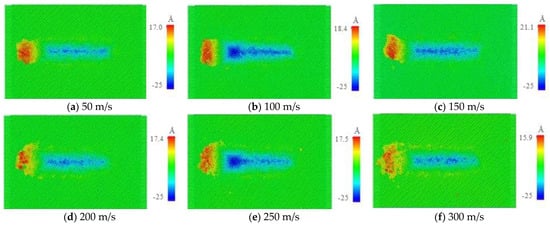
Figure 12. Scratch damage morphology with different scratch speeds.

Figure 13 shows the relationship between atomic structure and scratch speed. Here, when the agglomerated particles scratched at high speed, the atoms in front of the agglomerated particles were more easily shifted downward via extrusion and combined with the materials below them, resulting in a rougher surface with a number of scratches.

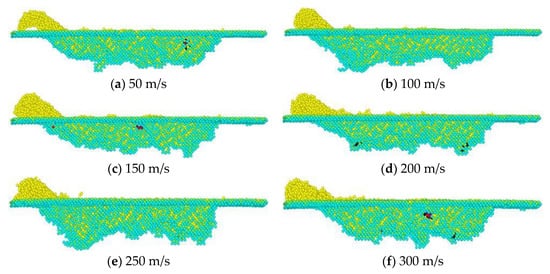
Figure 13. Internal structure with different scratch speeds.

Figure 14 shows the relationship between average scratch damage depth/width and scratch speed. Here, the increase in scratch speed had little effect on the average depth of the scratch damage, while it tended to increase the average width of the scratch damage.

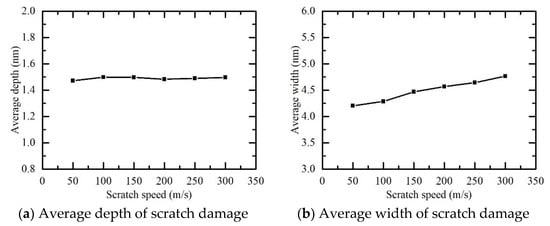
Figure 14. Variation curve for average scratch damage depth and width.

3. Scratch Damage Process Simulation

3.1. Scratch Damage Trajectory Modeling

During the MRPF process, relative motion occurs among the polishing disc, workpiece, and magnetic field generator. Under the action of shear force, agglomerated particles easily form scratches on the workpiece surface, with the scratch distribution related to the motion trajectory of the agglomerated particles. To facilitate the research work, we selected a single agglomerated particle to explore the scratch morphology of workpiece surfaces.

When analyzing the motion trajectory of agglomerated particles, the MRPF process is simplified according to the kinematics principle, and the relative motion planes of the polishing disc, workpiece, and magnetic field generator are obtained [1,27,28]. The workpiece and magnetic field generator were set at the same center position. Based on this, the kinematic MRPF model was established, as shown in Figure 15. Here,$x_1{O}_1{y}_1$ is a fixed coordinate system with the origin at the center of the polishing disc, $x_2{O}_2{y}_2$ is a dynamic coordinate system with the origin at the center of workpiece, the coordinate origin $O_3$ is the center of the magnetic field generator, ${\omega }_1$ is the rotational speed of the polishing disc, and ${\omega }_2$ is the rotational speed of the workpiece. Meanwhile, the distance $O_1{O}_2$ is defined as eccentricity $e_1$, the distance $O_2{O}_3$ is defined as eccentricity $e_2$, the distance $O_{2}P$ between any point ($P$) on the workpiece and the origin of the workpiece is defined as the radial distance of the agglomerated particles $r_p$, and the angle with the x-axis is the initial angle of the agglomerated particles ${\theta }_2$.

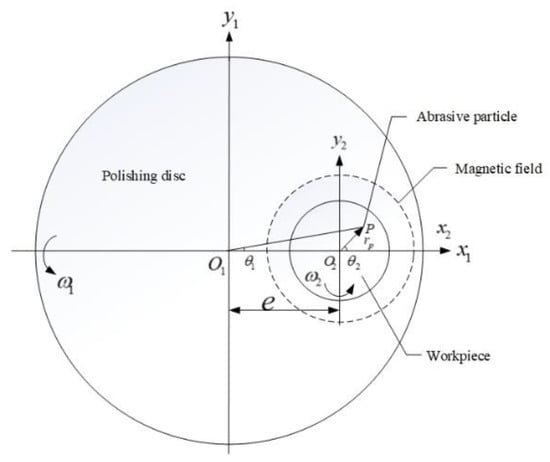
Figure 15. Kinematic MRPF model.

When eccentricity $e$ is constant, the distance between the polishing disc and the workpiece is constant, meaning the workpiece involves centering polishing. Assuming that the agglomerated particles $P$ at a distance $r_p$ from the origin of the polishing disc begin to contact the workpiece surface at a certain time, the starting angle ${\theta }_1$ could be obtained according to the following cosine theorem:

$${\theta }_1=\arccos \frac{r_p{}^2+e^2-r_w{}^2}{2e{r}_p}$$

(1)

The trajectory equation of point $P$ in coordinate system $x_1{O}_1{y}_1$ is as follows:

$$\{\begin{array}{c}{x}_p=r_p\cos ({\omega }_{1}t+{\theta }_1)\\ y_p=r_p\sin ({\omega }_{1}t+{\theta }_1)\end{array}$$

(2)

while the relative motion trajectory of the dynamic coordinate system $x_2{O}_2{y}_2$ and the fixed coordinate system $x_1{O}_1{y}_1$ is as follows:

$$\{\begin{array}{c}{x}_{O_2}=e\cos {\omega }_{2}t\\ y_{O_2}=-e\sin {\omega }_{2}t\end{array}$$

(3)

Therefore, the trajectory equation of the agglomerated particles $P$ relative to the workpiece surface is as follows:

$$\{\begin{array}{c}{x}_{p\text{'}}=r_p\cos ({\omega }_{1}t+{\theta }_1-{\omega }_{2}t)+e\cos {\omega }_{2}t\\ y_{p\text{'}}=r_p\sin ({\omega }_{1}t+{\theta }_1-{\omega }_{2}t)-e\sin {\omega }_{2}t\end{array}$$

(4)

Equation (4) could then be differentiated to obtain the instantaneous velocity of the agglomerated particles $P$, as described in the following equation:

$$\nu =\sqrt{{({\omega }_2-{\omega }_1)}_2{r}_{p^2}+{\omega }_1{}^2{e}^2+2r_p({\omega }_2-{\omega }_1)\cdot e{\omega }_1\cdot \cos {\omega }_{1}t\cdot [\sin ({\omega }_{1}t+{\theta }_1-{\omega }_{2}t)-\cos ({\omega }_{1}t+{\theta }_1-{\omega }_{2}t)]}$$

(5)

3.2. Influence of Process Parameters on Scratch Damage Characteristics

3.2.1. Influence of Workpiece Speed

Figure 16 shows the trajectory of the agglomerated particles on the workpiece surface in a single motion cycle at different workpiece speeds (200, 300, 400, 500, 600, and 700 rpm). The other process parameters were set as follows: rotational speed of the polishing disc = 30 rpm, rotational speed of the magnetic field generator = 20 rpm, and the magnetic field eccentricity = 0 mm. With the increase in workpiece speed, the motion trajectory of the agglomerated particles on the workpiece surface gradually lengthened in the single motion cycle.

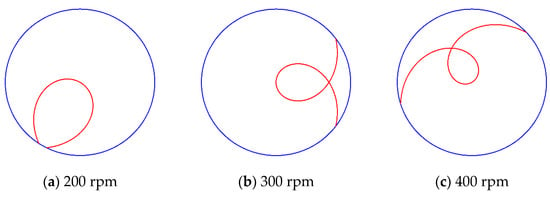
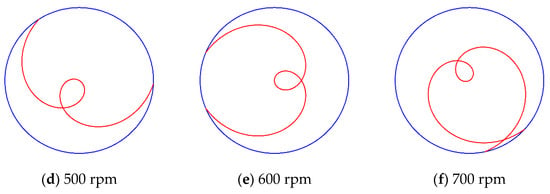
Figure 16. Motion trajectory of agglomerated particles with different workpiece speeds.

Meanwhile, the software Origin was used to analyze the data and plot the curves. Figure 17 and Figure 18 show the relationship between scratch damage depth/width and workpiece speed. While there was little variation in the trend of the scratch depth and width with different workpiece speeds, the maximum value of the scratch depth and width increased with the increase in workpiece speed. This was mainly due to the increase in the instantaneous velocity of the agglomerated particles caused by the higher speed, which affected the depth and width of the scratches.

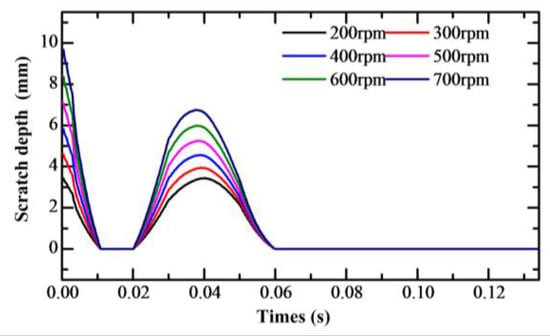
Figure 17. Scratch damage depth with different workpiece speeds.

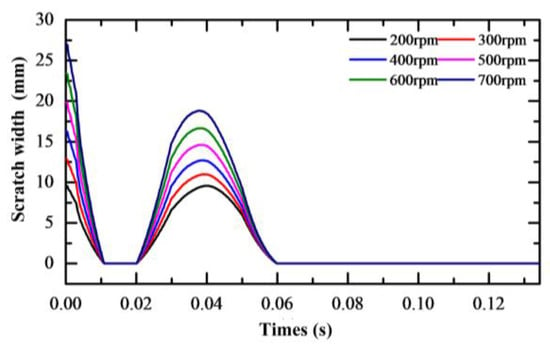
Figure 18. Scratch damage width with different workpiece speeds.

Using the scratch depth and width calculations, a three-dimensional morphology of the scratch damage on the workpiece surface was obtained with MATLAB, as shown in Figure 19. Here, the scratch damage increased with the increase in workpiece speed.

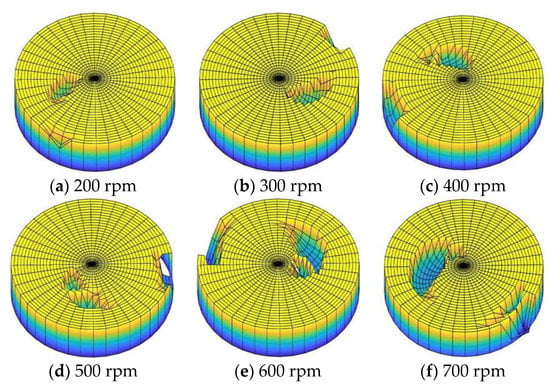
Figure 19. Scratch damage morphology on the workpiece surface with different workpiece speeds.

3.2.2. Influence of Polishing Disc Speed

Figure 20 shows the trajectory of the agglomerated particles on a workpiece surface in a single motion cycle at different polishing disc speeds (10, 20, 30, and 40 rpm). The other process parameters were set as follows: the rotational speed of the workpiece = 500 rpm, the rotational speed of the magnetic field generator = 20 rpm, and the magnetic field eccentricity = 0 mm. With the increase in polishing disc speed, the motion trajectory of the agglomerated particles on the workpiece surface gradually shortened in the single motion cycle.

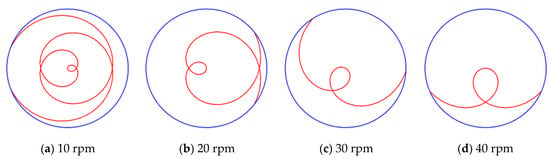
Figure 20. Motion trajectory of agglomerated particles with different polishing disc speeds.

Figure 21 shows the relationship between the scratch damage depth and the polishing disc speed. With the increase in polishing disc speed, the maximum depth of the scratch damage gradually decreased, while the number of scratches increased. In a single motion cycle, when the rotational speed of the polishing disc was 20 or 30 rpm, the scratch depth on the workpiece surface was small.

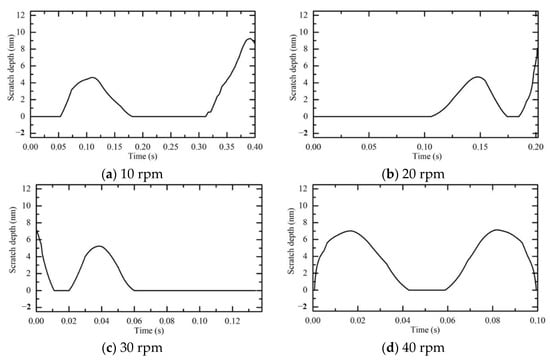
Figure 21. Scratch damage depth with different polishing disc speeds.

Figure 22 shows the relationship between the scratch damage maximum width and the polishing disc speed. With the increase in polishing disc speed, the maximum width of the scratch damage gradually decreased. In a single motion cycle, the scratch width on the workpiece surface was the largest when the rotational speed of the polishing disc was 10 rpm.

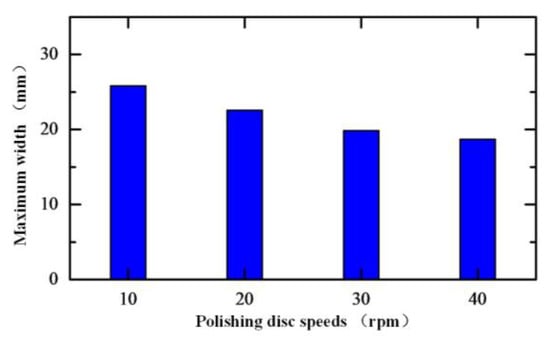
Figure 22. Scratch damage maximum width with different polishing disc speeds.

Again, using the scratch depth and width calculations, a three-dimensional morphology of the scratch damage on the workpiece surface was obtained, as shown in Figure 23. When the rotational speed of the polishing disc was 10 rpm, the scratch track on the workpiece surface was long and the scratch damage was the largest. However, when the rotational speed of the polishing disc was 20 or 30 rpm, the scratch damage on the workpiece surface was small.

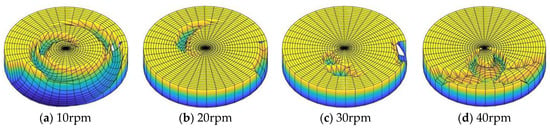
Figure 23. Scratch damage morphology on the workpiece surface with different polishing disc speeds.

3.2.3. Influence of Magnetic Field Generator Speed

Figure 24 shows the trajectory of the agglomerated particles on the workpiece surface in a single motion cycle at different magnetic field generator speeds (10, 20, 30, and 40 rpm). The other process parameters were set as follows: the rotational speed of the workpiece = 500 rpm, the rotational speed of the polishing disc = 30 rpm, and the magnetic field eccentricity = 0 mm. Overall, the trajectory of the agglomerated particles was independent of the magnetic field generator speed and was mainly related to the speed ratio (ratio of workpiece speed to polishing disc speed).

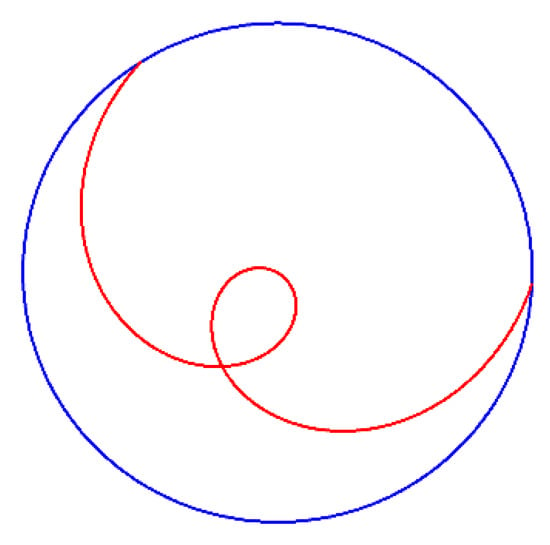
Figure 24. Motion trajectory of agglomerated particles with different magnetic field speeds.

Figure 25 shows the relationship between scratch damage depth and magnetic field generator speed. Here, there was little variation in the trend of the scratch depth with different workpiece speeds. When the rotational speed of the magnetic field generator was 40 rpm, scratches took longer to form. Therefore, the scratch depth formed when using a lower speed for the magnetic field generator was small.

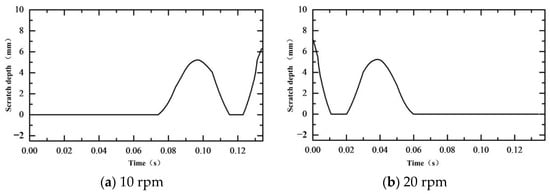
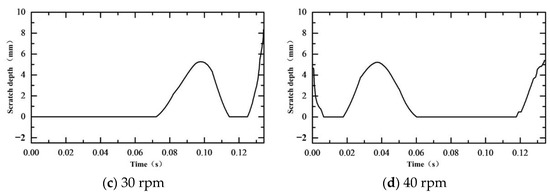
Figure 25. Scratch damage depth with different magnetic field speeds.

Figure 26 shows the relationship between the scratch damage maximum width and the magnetic field generator speed. Here, the maximum width of the scratch damage was the largest when the rotational speed of the magnetic field generator was 30 rpm, while it was the smallest when the rotational speed of the magnetic field generator was 10 rpm.

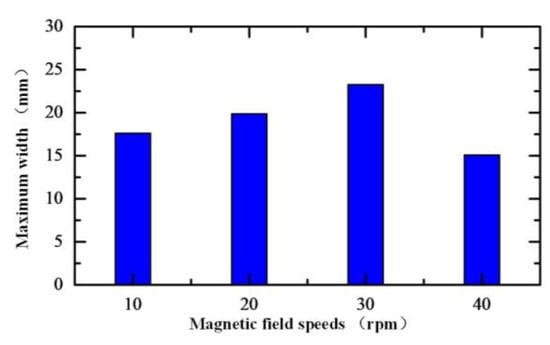
Figure 26. Scratch damage maximum width with different magnetic field speeds.

Using the scratch depth and width calculations, a three-dimensional morphology of the scratch damage on the workpiece surface was obtained, as shown in Figure 27. Here, it was clear that the scratch damage on the workpiece surface was the largest when the rotational speed of the magnetic field generator was 30 rpm, while it was the smallest when the rotational speed was 10 or 20 rpm.

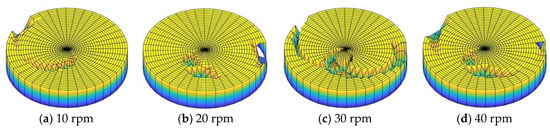
Figure 27. Scratch damage morphology on the workpiece surface with different magnetic field speeds.

3.2.4. Influence of Magnetic Field Eccentricity

Figure 28 shows the trajectory of the agglomerated particles on the workpiece surface in a single motion cycle with different magnetic field eccentricity values (−40, −20, 0, 20, and 40 mm). The other process parameters were set as follows: the rotational speed of the workpiece = 500 rpm, the rotational speed of the polishing disc = 30 rpm, and the rotational speed of the magnetic field generator = 20 rpm. With the increase in magnetic field eccentricity, the motion trajectory of the agglomerated particles on the workpiece surface gradually shortened in the single motion cycle.

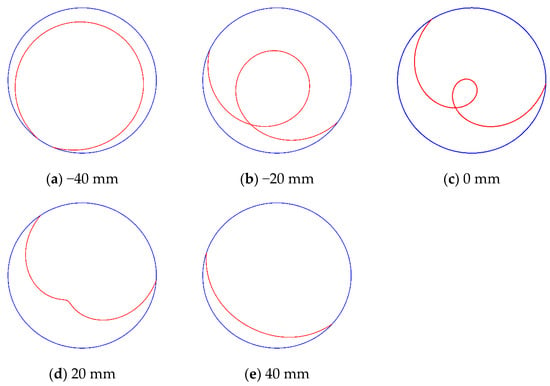
Figure 28. Motion trajectory of the agglomerated particles with different magnetic field eccentricities.

Figure 29 shows the relationship between the scratch damage depth and the magnetic field eccentricity. Here, there was little variation in the trend of the scratch depth with different magnetic field eccentricity values, with the minimum scratch depth observed when the eccentricity was 0 mm.

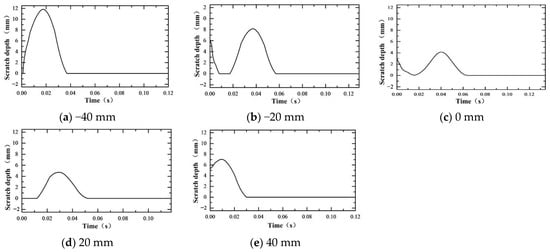
Figure 29. Scratch damage depth with different magnetic field eccentricities.

Figure 30 shows the relationship between the scratch damage maximum width and the magnetic field eccentricity. Here, the maximum width of the scratch damage was the largest when the eccentricity was −40 mm, while it was the smallest when the eccentricity was 20 mm.

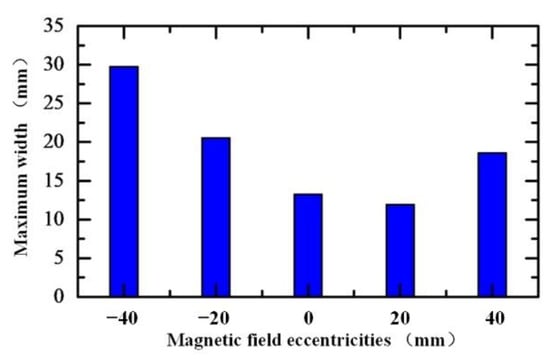
Figure 30. Scratch damage maximum width with different magnetic field eccentricities.

Using the scratch depth and width calculations, a three-dimensional morphology of the scratch damage on the workpiece surface was obtained, as shown in Figure 31. Here, it was clear that the scratch damage on the workpiece surface was the smallest when the magnetic field eccentricity was 0 or 20 mm.

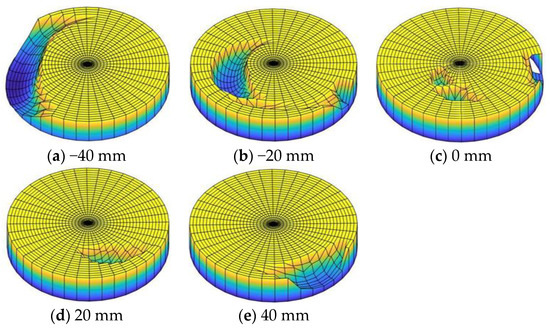
Figure 31. Scratch damage morphology on the workpiece surface with different magnetic field eccentricities.

4. Experimental Procedure and Results

The effects of different factors, including workpiece speed, polishing disc speed, magnetic field generator speed, and magnetic field eccentricity, on the characteristics of the scratch damage were investigated using an orthogonal experimental design method. Here the optimal combination of process parameters for inhibiting the formation of scratch damage was determined, with various magnetorheological polishing experiments subsequently conducted to verify the results. The experimental factors and the corresponding level parameters were determined according to the experimental conditions, as shown in Table 2.

Table 2. Orthogonal experimental factors and level parameters.

Factors	Parameters	Level 1	Level 2	Level 3
A	Workpiece speed (rpm)	400	500	600
B	Polishing disc speed (rpm)	10	20	30
C	Magnetic field generator speed (rpm)	10	20	30
D	Magnetic field eccentricity (mm)	−20	0	20

In this experiment, an L9 (3⁴) orthogonal table was selected without considering the interactions among various factors. The attendant levels and factors are shown in Table 3.

Table 3. Orthogonal experimental design table.

	Factor	A	B	C	D
Levels
1		1	1	1	1
2		1	2	2	2
3		1	3	3	3
4		2	1	2	3
5		2	2	3	1
6		2	3	1	2
7		3	1	3	2
8		3	2	1	3
9		3	3	2	1

The simulation experiments were conducted in sequence according to the orthogonal table. After obtaining the movement track of the agglomerated particles and the variation in scratch damage depth and width, the scratch damage morphology on the workpiece surface was estimated, as shown in Figure 32. Here, the scratch damage of Nos. 4, 7, and 8 was larger, while that of Nos. 2 and 3 was smaller.

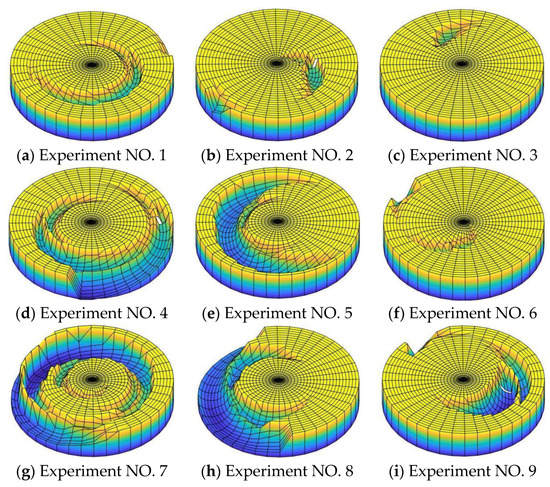
Figure 32. Scratch damage morphology on the workpiece surface with experimental parameters.

The mean value of the scratch damage depth was subsequently analyzed, with the results shown in Table 4. After comparing the calculation results for the same factor at different levels, the factors were sorted according to the degree of influence as follows: workpiece speed > polishing disc speed > magnetic field generator speed > magnetic field eccentricity. Therefore, the optimal combination of factors that can inhibit scratch damage depth was deemed to be A1B3C1D3.

Table 4. Scratch depth mean value analysis.

	Factor	A	B	C	D
Levels
1		5.263	7.644	6.582	7.077
2		7.554	7.336	7.964	7.154
3		8.334	6.171	6.605	6.920
δ		3.070	1.473	1.381	0.233
Patch		1	2	3	4

Following this, we analyzed the range of scratch damage depth, with the results shown in Table 5. After comparing the calculation results for the same factor at different levels, the factors were sorted according to the degree of influence as follows: workpiece speed > polishing disc speed > magnetic field generator speed > magnetic field eccentricity. Therefore, the optimal combination of factors that can inhibit scratch damage depth was deemed to be A1B3C2D3.

Table 5. Scratch width average analysis.

	Factor	A	B	C	D
Levels
1		14.22	21.17	18.30	19.95
2		20.96	20.45	18.01	19.20
3		23.23	16.80	22.09	18.80
δ		9.01	4.37	4.08	1.15
Patch		1	2	3	4

Finally, we assessed the range of scratch damage length, with the results shown in Table 6. After comparing the calculation results for the same factor at different levels, the factors were sorted according to the degree of influence as follows: polishing disc speed > workpiece speed > magnetic field generator speed > magnetic field eccentricity. Therefore, the optimal combination of factors that can inhibit scratch damage depth was deemed to be A1B3C1D3.

Table 6. Scratch track length average analysis.

	Factor	A	B	C	D
Levels
1		317.5	592.6	368.7	438.1
2		382.9	315.6	372.2	371.9
3		429.7	221.9	389.1	320.0
δ		112.2	370.7	20.3	118.1
Patch		1	2	3	4

Based on the above orthogonal experimental results, it was clear that the workpiece speed and the polishing disc speed have the greatest influence on the distribution characteristics of scratch damage. To verify the accuracy of the simulation results, a GaAs material was subjected to magnetorheological polishing on equipment specifically self-developed for this experiment, as shown in Figure 33a. The maximum speed of the workpiece rotating axis is 2000 rpm, the maximum speed of the polishing disc is 100 rpm, and the maximum speed of the cluster magnetic field generator is 50 rpm. The maximum radial dimension of the magnetorheological polishing fluid flow area is 300 mm.

Figure 33. Experimental equipment.

The main components of the polishing fluid used in the polishing experiments are deionized water, agglomerated particles, hydroxy iron powder and other additives. The agglomerated particles selected in this experiment were alumina with a mass fraction of 8%, hydroxy iron powder with a particle size of 5 μm and a mass fraction of 61%, other additives with a mass fraction of 9%, and the rest was deionized water. The magnetorheological polishing experiments were carried out according to the experimental parameters in Table 7.

Table 7. Experimental parameters.

	Workpiece Speed (rpm)	Polishing Disc Speed (rpm)	Magnetic Field Generator Speed (rpm)	Magnetic Field Eccentricity (mm)
(a)	600	20	20	0
(b)	600	30	20	0
(c)	500	20	20	0
(d)	500	30	20	0
(e)	400	20	20	0
(f)	400	30	20	0

Figure 34 shows six forms of workpiece surface morphology. On observing the samples in experiments (a), (c), and (e), it was clear that the higher the workpiece speed, the greater the number of surface scratches, while on observing the samples in experiments (e) and (f), it was clear that the higher the polishing disc speed, the lower the number of surface scratches.

Figure 34. Workpiece surface morphology.

The scratches on the surface of each workpiece were measured using a white light interferometer (Zegage Plus, Zygo Inc., Middlefield, CT, USA), as shown in Figure 33b. The shape and number of scratches can be clearly observed in Figure 35. In figure (a), the number of long scratches in the range of 900*900 μm is 13, and all of them are deep scratches. In figure (b), the number of scratches is 4, and all of them are deep scratches, and the surface roughness is large and there are many pits. In figure (c), the number of long scratches is 15, and the number of deep scratches is 3. In figure (d), the number of long scratches is 7, and the number of deep scratches is 1. In figure (e), there are two scratches, and one of them is deep, and in figure (f), there is one scratch, but the depth of the scratch is shallow. The results verified the accuracy of the simulation results and the feasibility of the combination of parameters that could minimize the scratch damage.

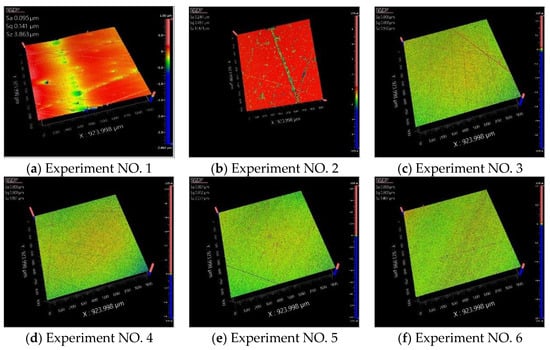
Figure 35. Scratch morphology of the workpiece surface.

5. Conclusions

The following conclusions were drawn from the study on the simulation of the causes and suppression of scratch damage on the workpiece surface during magnetorheological surface polishing.

(1) The established scratch creation simulation method can effectively analyze the scratch damage formation process by using molecular dynamics method combined with polishing contact trajectory modeling, which is useful as a guide for practical processing.

(2) The change of the workpiece speed parameter mainly affects the scratch depth and width, but not the scratch length; the adjustment of the polishing disc speed parameter not only changes the maximum value of the scratch depth and width, but also affects the number of scratches; the change of the magnetic field transposition parameter has less influence on the scratch damage; the adjustment of the eccentric distance parameter affects the scratch damage mainly in the change of the scratch length within a single motion cycle.

(3) The continuous scratches can be effectively suppressed by reducing the rotational speed of the workpiece and the magnetic field, increasing the rotational speed of the polishing disc, and reducing the eccentric distance of the magnetic field.