Abstract
The modeling of compliant bridge-type displacement amplification mechanisms has challenges due to the intrinsic coupling of kinematic and mechanical behaviors. A structure load performance integrated model method for the bridge-type displacement amplification mechanism is presented. The established modeling based on Castigliano’s second theorem considers the deformations of all members, the effect of external load and the nonlinear shear effect. Compared to the finite element model (FEM) and existing models, the established modeling precisely predicts significant nonlinearity of the displacement amplification ratio (DAR) with the driving force, strong sensitivity of DAR to the external load and corresponding relationships of structural parameters with DAR, which is the closest to the FEM result over existing models. The variance-based sensitivities of structural parameters to DAR are thoroughly analyzed, indicating that sensitive structure parameters need to be focused on. Modeling applications further prove the reliability and expandability of the proposed model method. The proposed model method can provide support for the design, optimization and control of compliant systems with bridge-type displacement amplification mechanisms.
1. Introduction
The piezoelectric actuator (PEA) is a kind of high-precision actuator that can efficiently convert electric energy into mechanical energy based on the inverse piezoelectric effect [1]. The piezoelectric actuators contain flextensional-type piezoelectric actuators, tube-type piezoelectric actuators, shear-type piezoelectric actuators and stack-type piezoelectric actuators [2,3]. The flextensional-type piezoelectric actuator can produce large output displacement through bending deformation, but its output force is small [4]. The tube-type piezoelectric actuator can realize nanoscale motion with three degrees of freedom (DOFs), but low resonance frequency limits its application in high-speed scanning fields [5]. The shear-type piezoelectric actuator has a compact structure, high resonance frequency and is suitable for high-speed application, but its output displacement is limited [6]. The stack-type piezoelectric actuator is formed by stacking a plurality of piezoelectric pieces, and the output displacement is the sum of all piezoelectric pieces [2]. With the excellent benefits of nanometer resolution, high resonance frequency, large output force and fast response, stack-type piezoelectric actuators are widely used in precision engineering. However, the output displacement of the stack-type piezoelectric actuator is approximately 0.1~0.2% of its length [7], which is difficult to meet the requirements of strokes of several hundred microns. Therefore, it is necessary to amplify the output displacement of piezoelectric actuators to meet application requirements.
Compared with rigid-body displacement amplification mechanisms, flexure-based compliant displacement amplification mechanisms transmit motion and force through the deformation of flexible components, having the benefits of an integral structure, variable rigidity, no friction, no wear and no lubrication and assembly [8,9]. Due to these advantages, the compliant amplification mechanism has been widely used, including in lithography manufacturing [10,11], multistable switches [12], micro-electro mechanical systems [13], precision positioning stages [14,15], micro/nano operations [16], automatic dispensing [17,18], microvibration suppression [19], optical alignment [20] and so on. Flexure-based compliant displacement amplification mechanisms mainly include lever-type, triangle-type and hybrid-type [14]. The lever-type displacement amplification mechanism has a simple structure and easy displacement amplification ratio (DAR) calculation, but it usually takes a lot of space to achieve large DAR. Triangle-type displacement amplification mechanisms include Bridge-type [21,22], Hybats-type [23], Moonie-type [24], cymbal-type [25] and so on; the bridge-type displacement amplification mechanism is the most widely used. The bridge-type displacement amplification mechanism has a compact structure that can realize a large DAR in limited space. However, the analytical modeling of the bridge-type displacement amplification mechanism is complicated due to the intrinsic coupling of kinematic and mechanical behaviors. The hybrid-type displacement amplification mechanism can be regarded as the superposition of lever-type and triangle-type [26,27]. Hybrid bridge–lever mechanisms can realize larger DAR. The analytical modeling of bridge–lever displacement amplification mechanisms is more complicated due to the intrinsic coupling of kinematic and mechanical behaviors of the bridge-type mechanism. Therefore, it is significant to establish an analytical model of the bridge-type displacement amplification mechanism for performance evaluation, parameter optimization and future application of a compliant mechanism with the bridge-type mechanism or the hybrid bridge–lever mechanism.
Many researchers have proposed various mathematical models to describe the performance of the bridge-type displacement amplification mechanism. Pokines et al. [28] derived the ideal DAR of the bridge-type mechanism using the geometric relationship. Lobontiu et al. [29] established a mathematical model for DAR and stiffness calculations of the bridge-type mechanism based on Castigliano’s second theorem. Kim et al. [30] proposed a matrix model of the 3D bridge-type amplifier regarding flexure hinges. Ma et al. [31] derived the ideal DAR model of the bridge-type mechanism using kinematic theory, and then the theoretical model of DAR considering the elastic deformation of flexible hinges was established using the elastic beam theory. Xu et al. [32] established the analytical model for DAR, input stiffness and resonance frequency predictions of a compound bridge-type (CBT) displacement amplifier. Qi et al. [22] developed a theoretic model for DAR of the bridge-type mechanism using the elastic beam theory; then, the relationship between DAR and geometric dimensions was deeply analyzed. Based on the energy conservation law and the elastic beam theory, Ling et al. [33] proposed an enhanced mathematical model for the bridge-type compliant mechanism considering the translational and rotational stiffness. Choi et al. [34] established a new mathematical model for DAR of the bridge-type amplification mechanism considering the deformation of all members of the amplification mechanism. The above-mentioned analytical models only paid attention to the characteristics of the bridge-type displacement amplification mechanisms as independent components. However, the bridge-type displacement amplification mechanisms were usually connected to the displacement guiding mechanisms, which can be regarded as an external load of variable stiffness. The external load had a great influence on DAR, so it is highly significant to incorporate the effect of external load into analytical models.
To improve modeling accuracy, numerous analytical models considering the effect of external load have been proposed. Liu et al. [35] used the pseudo-rigid body modeling approach to develop a novel analytical model for the bridge-type amplifier, which assumed that the elastic deformations only occur at the flexure hinges. Liu et al. [21] and Pan et al. [36] proposed nonlinear models for the bridge-type displacement amplification mechanism based on the Timoshenko Beam Constraint Model (TBCM). Li et al. [37] established an improved DAR model for the bridge-type mechanism considering the input displacement loss. Lin et al. [38] derived a new analytical model for the DAR of the bridge-type amplifier employing the energy conservation law and the elastic beam theory. The four above-mentioned analytical models assumed that only the flexible hinges and connecting bodies are elastically deformed. Zhang et al. [39] proposed a novel theoretical model for DAR of the bridge-type amplification mechanism considering the deformation of all members of the mechanism. Although these advanced models markedly improve calculation accuracy, the deformation of all members of the mechanism, the effect of external load and the nonlinear shear effect need to be considered for special bridge-type displacement amplification mechanisms, such as large DAR mechanism, large driving force mechanism and large external load mechanism.
A structure load performance integrated model approach for the bridge-type displacement amplification mechanism is presented here, taking the deformations of all members of the mechanism, the effect of external load and the nonlinear shear effect into consideration. The analytical model is established based on Castigliano’s second theorem, which can precisely calculate DAR, input displacement, output displacement, input stiffness and output stiffness. Model verification and analysis reveal the relationships of DAR with driving force, external load and structural parameters, and the sensitivity of DAR to structural parameters. The vertical micro/nano-positioning mechanism with the bridge-type displacement amplification mechanism is modeled and analyzed to validate the effectiveness of the proposed model.
2. Analytical Modeling
The bridge-type displacement amplification mechanism is an integral symmetrical structure consisting of a fixed body, input bodies, connecting bodies, an output body and flexible hinges. The bridge-type displacement amplification mechanism is shown in Figure 1. A piezoelectric actuator is installed in the bridge-type displacement amplification mechanism, and it is connected with input bodies by a certain preload. The output body is usually connected with the displacement guiding mechanism, which is equivalent to an external load for the bridge-type displacement amplification mechanism. The driving voltage is applied to the piezoelectric actuator, and the displacement and driving force generated by the piezoelectric actuator drive input bodies. The bridge-type displacement amplification mechanism elastically deforms transmitting motion and force to the output body. All parts of the bridge-type displacement amplification mechanism are compliant.
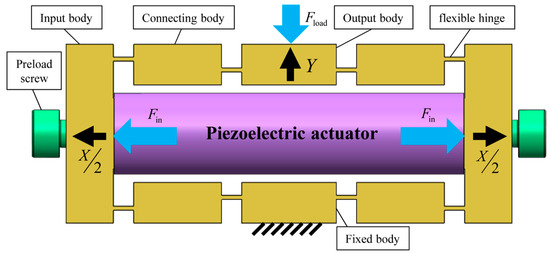
Figure 1.
Schematic diagram of the bridge-type displacement amplification mechanism.
Due to the symmetrical structure of the bridge-type displacement amplification mechanism, only the 1/4 integral mechanism is used to establish analytical modeling. The mechanical analysis of the ¼ mechanism is shown in Figure 2, where , , and represent the lengths of input body, connecting body, output body and flexible hinge, respectively; , , and represent the thicknesses of input body, connecting body, output body and flexible hinge, respectively; represents the interval of adjacent flexible hinges; and represents the width of the mechanism. To simplify the derivation, it is assumed that and represent the equivalent force applied on input and output bodies, respectively; represents the equivalent bending moment at the end of the output body; and represents the equivalent bending moment at the driving position. Based on force and moment balance, the following equations can be obtained:
where and represent the equivalent force applied on every member of the 1/4 mechanism in the X-axis direction and the Y-axis direction, respectively; represents the driving force of the piezoelectric actuator; and represents the external load applied to the output body. It can be obtained from Equations (3) and (4):
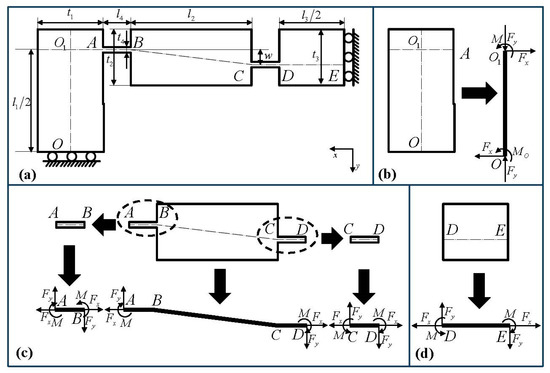
Figure 2.
Mechanical analysis diagram of the bridge-type displacement amplification mechanism. (a) The 1/4 integral mechanism. (b) Input body. (c) Connecting body and flexible hinges. (d) Output body.
According to the mechanical balance, the inner forces of any sections for the ith (i = 1, 2, 3, 4, 5) flexure member of the 1/4 mechanism can be obtained; the inner forces include the inner tensile force , shear force and bending moment .
The total strain energy of the 1/4 mechanism can be obtained as follows:
where represents the cross-sectional areas of ith member, which satisfies the following relationships: ,, , , . represents the inertia moments of ith member, which satisfies the following relationships: , , , , . represents the Young’s modulus, represents the shear modulus and represents the dimensionless factor related to shape of the cross-section, which is usually 6/5 for a rectangular cross-section. Based on Castiglioni’s second theorem [9], the input displacement and the output displacement of the 1/4 mechanism can be obtained as follows:
Substituting Equations (7)–(12) into Equation (13), the relationship between displacement and force of the 1/4 mechanism can be derived:
where is the compliance matrix of the 1/4 mechanism considering the deformation of all members, the effect of external load and the nonlinear shear effect. Every element of the compliance matrix can be expressed as follows:
According to Equation (14), the total input displacement and the total output displacement of the bridge-type displacement amplification mechanism are detailed as:
Based on Equations (16) and (17), the DAR of the bridge-type displacement amplification mechanism is expressed:
Under no external load or small external load, DAR and input stiffness of the bridge-type displacement amplification mechanism are calculated by Equations (19) and (20):
When the input force is set to zero, the output stiffness of the bridge-type displacement amplification mechanism is obtained as follows:
Once structural parameters and driving force are determined, DAR decreases as external load increases. When external load increases to a certain value, the displacement amplification ability of the mechanism decreases. The ultimate load of the mechanism is obtained with the assumption of .
Considering piezo actuator driver properties, the driving force applied to the bridge-type displacement amplification mechanism can be expressed as follows:
where is the driving voltage, is the piezoelectric constant and is the stiffness of the piezoelectric actuator. Substituting Equation (23) into Equation (16), the input displacement and output displacement of the bridge-type displacement amplification mechanism considering piezoelectric actuator driver properties are derived:
Substituting Equations (23) and (24) into Equation (17), the output displacement and output displacement of the bridge-type displacement amplification mechanism considering piezoelectric actuator driver properties are derived:
According to Equations (24) and (25), the DAR of the bridge-type displacement amplification mechanism considering piezoelectric actuator driver properties is expressed:
3. Modeling Verification and Analysis
The established model was verified and analyzed using FEM and existing models, and the sensitivities of structure parameters to DAR were examined based on the proposed model.
Based on common application requirements of the bridge-type displacement amplification mechanism [22,33,35,38,40], the initial structural parameters are assumed as listed in Table 1. The material Al7075 with excellent deformability is selected, and its specific parameters are listed in Table 2. The FEM is established with the software package ANSYS, and adaptive mesh division is adopted. The fixed constraint is applied to the fixed body, the driving forces are applied to the input bodies and the external load is applied to the output body. The input displacement and output displacement are extracted, and the DAR of the bridge-type displacement amplification mechanism is obtained. One of the deformation results of the bridge-type displacement amplification mechanisms is shown in Figure 3.

Table 1.
The given structural parameters of the bridge-type amplification mechanism.

Table 2.
The material parameters of Al7075 alloy.
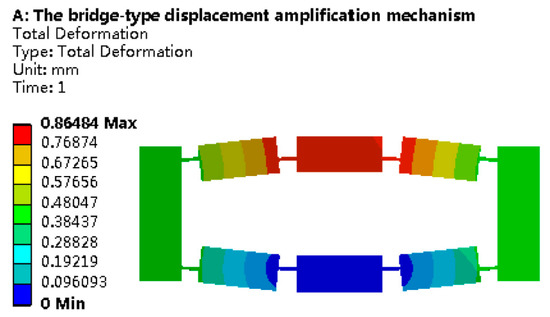
Figure 3.
The deformation results of the bridge-type displacement amplification mechanism.
3.1. Effect of Loads on DAR
The influence of driving force and external load on DAR were investigated; the structural parameters of the bridge-type displacement amplification mechanism were set as constants, as listed in Table 1.
With the external load set to 30 N, the changes in DAR with driving forces are plotted in Figure 4. There is a nonlinear relationship between DAR and driving forces. DAR increases as the driving force increases. The proposed model is in agreement with FEM, with a 1.08% difference at the maximum driving force, which is the closest to FEM. The proposed model is more accurate than the model in [35] because the deformations of input bodies, connecting bodies and output body are taken into account in the proposed model. The proposed model outperforms the model in [39] since the nonlinear shear effect is incorporated into the proposed model. As a result, the proposed model, which takes the deformations of all members, the effect of external load and the impacts of nonlinear shear effect into consideration, accurately captures the nonlinear relationship between DAR and driving force, especially in the case of large driving force mechanisms.
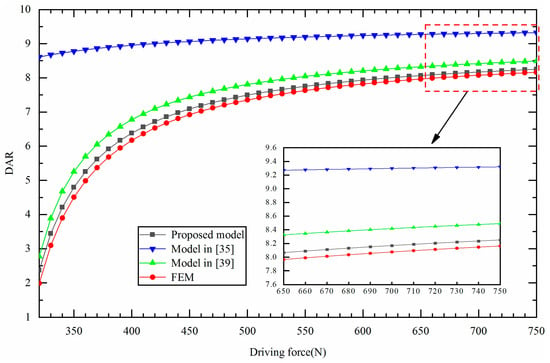
Figure 4.
The changes in DAR with varied driving forces.
With the driving force set to 500 N, the changes in DAR with external loads are plotted in Figure 5. DAR is sensitive to external loads. DAR reduces as external load rises. The proposed model and FEM have a difference of less than 9.93%, which is lower than the existing models. The difference between the proposed model and the model in [35] is that the latter ignores the deformations of the input bodies, connecting bodies and output body. The difference between the proposed model and the model in [39] is attributed to the fact that the latter does not take the nonlinear shear effect into account. Therefore, the proposed model taking the deformation of all members, the effect of external load and the nonlinear shear effect into consideration can accurately predict the sensitivity of DAR to external load, especially in the case of large external load mechanisms.
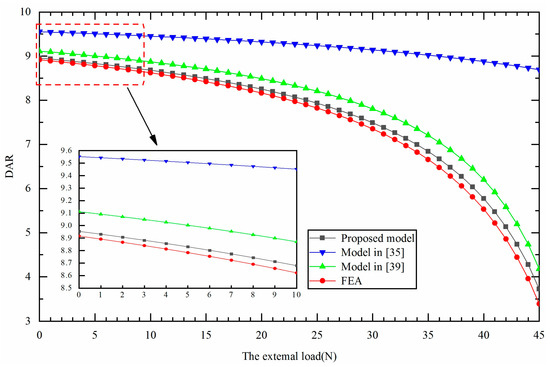
Figure 5.
The changes in DAR with varied external loads.
3.2. Effect of Structural Parameters on DAR
In this section, the relationships of structural parameters with DAR are explored. When one structural parameter varies, other structural parameters are set as constants, as listed in Table 1, and the driving force and external load are defined as 300 N and 20 N, respectively.
The variation in DAR with the input body is shown in Figure 6. In Figure 6a, the length of the input body has a negative correlation with DAR, which is attributable to the fact that the longer input body can introduce some input displacement loss. The difference between the proposed model with FEM is less than 0.89%. In Figure 6b, the thickness of the input body is positively correlated with DAR because the thicker input body can resist some input displacement loss. The proposed model well matches FEM, with a maximum difference of only 1.65%. From the preceding analysis, it can be concluded that the accuracy of the proposed model can be considerably enhanced by incorporating the input body into the analytical model.
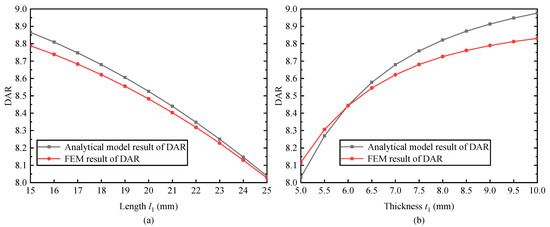
Figure 6.
The changes in DAR with the input body varied. (a) The input body length . (b) The input body thickness .
The variation in DAR with the connecting body is shown in Figure 7. In Figure 7a, DAR nearly linearly increases with the length of the connecting body because the increment of causes additional displacement in the output direction. Compared with the FEM, the difference of the proposed model is less than 0.66%. In Figure 7b, DAR hardly varies with the thickness of the connecting body. The difference between the proposed model and FEM is only 0.76%. Conclusions that the length of the connecting body has a great influence on DAR and that a large DAR can be obtained by a longer connecting body are given based on the proposed analytical model.
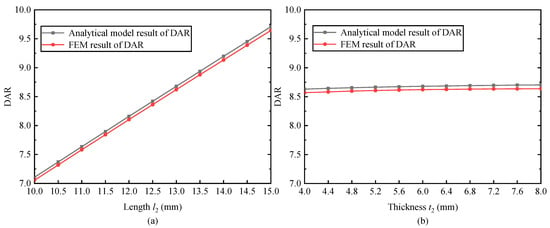
Figure 7.
The changes in DAR with the connecting body varied. (a) The connecting body length . (b) The connecting body thickness .
The variation in DAR with the output body is shown in Figure 8. In Figure 8a, DAR hardly varies with the length of output body. The proposed model is in good agreement with FEM, as the difference is less than 0.69%. In Figure 8b, DAR almost does not change with the thickness of the output body. Compared with the FEM, the maximum difference of the established model is only 0.89%. As a result, the changes in the output body have little influence on DAR, and the proposed model well represents the relationship of the output body with DAR.
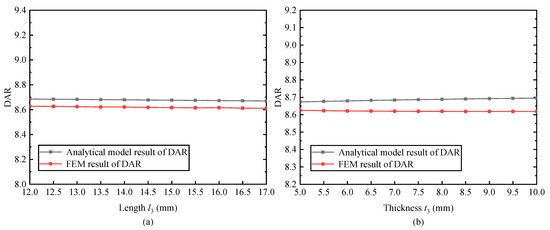
Figure 8.
The changes in DAR with the output body varied. (a) The output body length . (b) The output body thickness .
The variation in DAR with the flexure hinge is shown in Figure 9. In Figure 9a, DAR is sensitive to the length of the flexible hinge. DAR becomes larger as the flexible hinge becomes longer. The increment of causes additional displacement in the output motion direction, resulting in DAR increasing. The theoretical model is consistent with FEM, and the maximum difference is only 0.88%. In Figure 9b, DAR is also sensitive to the thickness of the flexible hinge. DAR becomes smaller as the flexible hinge becomes thicker. The increase in the thickness leads to the deterioration of the deformability. The analytical model is basically consistent with FEM, with a maximum difference of only 2.06%. Therefore, a large DAR can be obtained with longer and thinner flexible hinges, and the proposed model can accurately predict the relationships of the flexure hinge with DAR.
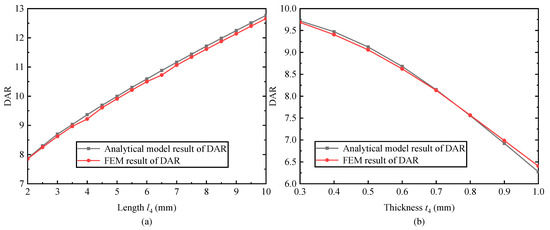
Figure 9.
The changes in DAR with the flexure hinge varied. (a) The flexure hinge length . (b) The flexure hinge thickness .
The variation in DAR with the interval of adjacent flexure hinges is plotted in Figure 10. When the interval between adjacent flexible hinges increases, DAR first increases rapidly to reach a peak value, then gradually decreases. Thus, it is important to select the appropriate interval of adjacent flexure hinges for different application requirements. The peak value of DAR is related to structural parameters, driving force and external load, and the interval of adjacent flexure hinges in the peak DAR can be obtained by the following equation: . When the interval between adjacent flexible hinges changes, the proposed model matches well with FEA. The difference of the proposed model from FEM at the peak DAR is 1.18%, which validates the effectiveness of the proposed modeling method. As a result, the proposed model can provide theoretical support for interval selection of adjacent flexure hinges.
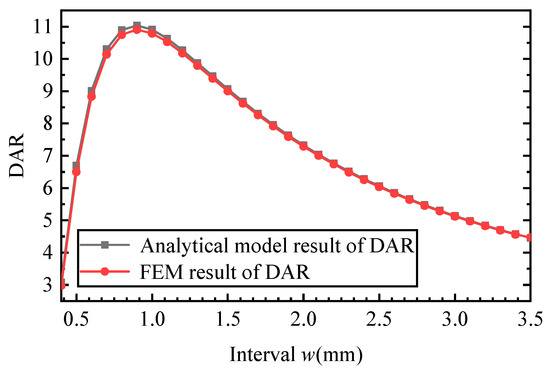
Figure 10.
The changes in DAR with the interval of adjacent flexure hinges varied.
3.3. Global Sensitivity Analysis of Structural Parameters to DAR
The variance-based global sensitivity analysis of structure parameters to DAR was carried out.
The structure parameters of the bridge-type displacement amplification mechanism are , , , , , , , and , expressed by the vector .
The structure parameter is normalized, and the normalized structure parameter is given in Equation (28):
where and denote the upper and lower limits of the structure parameter , respectively. The response function of DAR is defined in the unit hypercube . The high-dimensional model representations of the response function can be uniquely expressed as follows [41,42]:
where represents the expectation of the high-dimensional model with normalized structure parameters, which is constant. represents the function value corresponding to the ith normalized structure parameter. represents the function value corresponding to the interaction of the ith normalized structure parameter and the jth normalized structure parameter; the rest of the high-order terms of the function are obtained by analogy. The integral of sub-functions of the high-dimensional model representations concerning its variable is zero.
The sub-function of the high-dimensional model representations are given by the following:
where expresses the expectation for . According to Equation (31), the variances of the sub-function are obtained as follows:
where expresses the variance for . The sensitivities of structure parameters are evaluated by the contribution of the conditional variance to the unconditional variance. The first-order sensitivity index and the global sensitivity index are calculated as follows:
where represents the main contribution of to the output variance, but ignores the interaction of with others. reflects the effect of on the output variance considering the interaction of with others.
To simplify the calculation, the numerical estimation method based on Monte Carlo is introduced to calculate the sensitivity indices [43]. In the procedure, an (N, 2k) matrix of random numbers in the unit hypercube is generated, where k is the number of input structure parameters and N is the number of samples for input structure parameters. Then, the matrix and the matrix are defined, each containing half of the (N, 2k) matrix of random numbers. Next, the matrix is generated, which is formed by all columns of B except the ith column with the ith column of A. Finally, calculating the model output for all the input values in matrices , and , three model outputs vectors , and are obtained:
The method estimates the first-order sensitivity index and the global sensitivity index, as follows:
In the calculating process, N is set to 10,000 and the ranges of structure parameters are given as listed in Table 3. The first-order sensitivity index and the global sensitivity index of structure parameters calculated by Equations (36) and (37) are listed in Table 4. Some conclusions can be obtained from the calculation results:
- (1)
- The sum of the first-order sensitivity index is 0.788389, and the sensitivity of interaction is . Therefore, the interaction of structure parameters should be considered.
- (2)
- For the first-order sensitivity index, the following relationships are satisfied: . For the global sensitivity index, the following relationships are satisfied: . Therefore, the four most sensitive structure parameters for DAR are the interval of the adjacent flexible hinges, the thickness of the flexure hinge, the length of the flexure hinge and the length of the connecting body.
- (3)
- For the difference between the first-order sensitivity index with the global sensitivity index, the following relationships exists:. As a result, the interaction between the interval of the adjacent flexible hinges with other structure parameters and the interaction between the thickness of the flexure hinge with other structure parameters are stronger, and the rest of the interactions are weaker.

Table 3.
The ranges of structure parameters.
Table 3.
The ranges of structure parameters.
| Structure Parameters | Ranges (mm) | Structure Parameters | Ranges (mm) |
|---|---|---|---|

Table 4.
The sensitivity of structure parameters to DAR.
Table 4.
The sensitivity of structure parameters to DAR.
| Structure Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.003015 | 0.021555 | 0.000003 | 0.101713 | 0.005916 | 0.000042 | 0.000030 | 0.069836 | 0.586279 | |
| 0.007334 | 0.026691 | 0.000002 | 0.137926 | 0.016331 | 0.000055 | 0.000007 | 0.220367 | 0.785078 |
4. Model Application
The proposed model method was applied to the modeling of the vertical micro/nano-positioning mechanism with the bridge-type displacement amplification mechanism, which is the key component of phase-shifting devices. The 3D model of the phase-shifting device is shown in Figure 11a, which meets the requirements of phase-shifting scanning through the movement of vertical micro/nano-positioning mechanisms. The structural model of the vertical micro/nano-positioning mechanism is described in Figure 11b, which includes the bridge-type displacement amplification mechanism and the displacement guiding mechanism. In the actual working process, the external load on the bridge-type displacement amplification mechanism includes the force exerted by the displacement guiding mechanism and the external load applied to the vertical micro/nano-positioning mechanism.
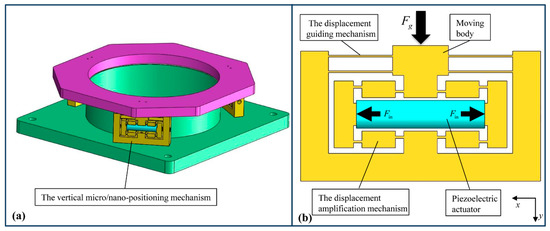
Figure 11.
(a) The phase-shifting device. (b) The vertical micro/nano-positioning mechanism.
4.1. Analytical Modeling of the Vertical Micro/Nano-Positioning Mechanism
The basic unit of the displacement guiding mechanism is the displacement guiding beam. As depicted in Figure 12a, the double parallelogram symmetrical structure is composed of four displacement guiding beams, improving the movement accuracy in the vertical motion direction. The mechanical model of the displacement guiding beam is shown in Figure 12b, where is the generalized force applied at the end of the displacement guiding beam and is the output displacement in the vertical motion direction. The relationship between the end deformation and the load of the displacement guiding beam is obtained using the elastic beam theory [44]:
where , and represent the length, the width and the thickness of the displacement guiding beam, respectively. According to Equation (38), the stiffness of the displacement guiding beam is expressed as follows:
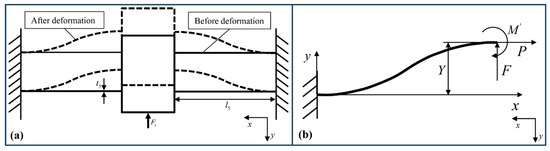
Figure 12.
(a) Deformation schematic of the displacement guiding mechanism. (b) Mechanical model of the displacement guiding beam.
Therefore, the stiffness of the displacement guiding mechanism is given in the following equation:
For the vertical micro/nano-positioning mechanism, the external load applied to the bridge-type displacement amplification mechanism is calculated by the following formula:
where is the external load applied to the vertical micro/nano-positioning mechanism and is the compliance of the displacement guiding mechanism, which satisfies . Substituting Equation (41) into Equations (16) and (17), the input displacement and output displacement of the vertical micro/nano-positioning mechanism can be obtained:
Based on Equations (42) and (43), the DAR of the vertical micro/nano-positioning mechanism can be expressed as follows:
4.2. Modeling Verification of the Vertical Micro/Nano-Positioning Mechanism
The FEM of the vertical micro/nano-positioning mechanism is established using the structural parameters listed in Table 5, and the material Al7075 is adopted. The mechanism is fixed through fixed holes. Different driving forces are applied to input bodies of the bridge-type displacement amplification mechanism and different external loads are applied to the moving body of the displacement guiding mechanism. The input and output displacements of the vertical micro/nano-positioning mechanism are extracted; then, the DAR of the vertical micro/nano-positioning mechanism is obtained. One of the deformation results of the vertical micro/nano-positioning mechanism is shown in Figure 13.

Table 5.
The structural parameters of the vertical micro/nano-positioning mechanism.
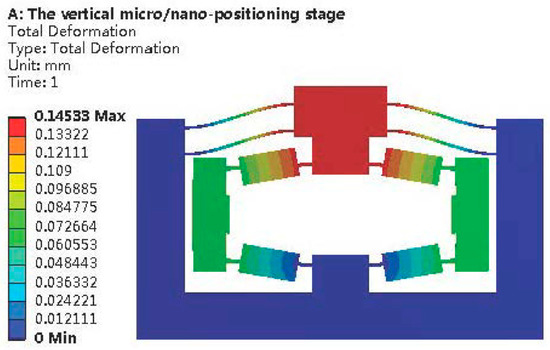
Figure 13.
The deformation results of the vertical micro/nano-positioning mechanism.
The analytical model and FEM of the vertical micro/nano-positioning mechanism are compared to verify the expandability of the proposed modeling method. The comparison results in Table 6 show that the maximum difference of the output displacement between the theoretical model and FEM is 5.97%, which verifies the accuracy of the proposed modeling method in describing the nonlinear behavior of the vertical micro/nano-positioning mechanism. The comparison results also exhibit that the difference in DAR between the theoretical model and FEM increases as the external load applied to the vertical micro/nano-positioning mechanism increases, which indicates the necessity of taking the deformations of all members, the effect of external load and the nonlinear shear effect into consideration in the proposed modeling method.

Table 6.
The analysis results of the vertical micro/nano-positioning mechanism.
5. Conclusions
In this paper, we propose a structure load performance integrated model approach for the bridge-type displacement amplification mechanism, which considers the deformations of all members, the effect of external load and the nonlinear shear effect. The mathematical modeling was established based on Castigliano’s second theorem, which can precisely calculate DAR, input displacement, output displacement, input stiffness and output stiffness. The proposed model was verified with the existing analytical models and FEM, and the comparison results indicate that the established model is closest to the FEM result over the existing models. With the driving force and the external load change, the maximum differences of DAR with the FEM are 1.26% and 9.93%, respectively, proving the accuracy of the proposed model. Moreover, when the interval of the adjacent flexible hinges changes, the difference between the proposed model and FEM at the peak DAR is 1.18%, which is much lower than the existing models. The variance-based global sensitivity of structure parameters to DAR was thoroughly analyzed. The sensitivity analysis results show significant sensitivity of DAR to the changes in the interval of adjacent flexible hinges, the thickness of flexure hinges, the length of flexure hinges and the length of connecting bodies, and weak sensitivity of other structure parameters to DAR. Finally, the proposed model was applied to the modeling and analysis of the vertical micro/nano-positioning mechanism with the bridge-type displacement amplification mechanism, validating the effectiveness and expansibility of the proposed modeling method.
Author Contributions
Conceptualization, B.H.; methodology, F.T. and S.L.; validation, F.T., P.W. and X.H.; formal analysis, F.T., P.W. and X.H.; writing—original draft preparation, F.T.; writing—review and editing, F.T., P.W. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (no. 61905275).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the data also forming part of an ongoing study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, Z.; Xu, Q. Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages. Actuators 2018, 7, 5. [Google Scholar] [CrossRef]
- Niezrecki, C.; Brei, D.; Balakrishnan, S.; Moskalik, A. Piezoelectric Actuation: State of the Art. Shock Vib. Dig. 2001, 33, 269–280. [Google Scholar] [CrossRef]
- Dogan, A.; Tressler, J.; Newnham, R.E. Solid-State Ceramic Actuator Designs. Aiaa J. 2015, 39, 1354–1362. [Google Scholar] [CrossRef]
- Liu, R.; Cross, L.E.; Knowles, G.; Bower, B.; Childers, B. A Stackable Bonding-Free Flextensional Piezoelectric Actuator. J. Electroceramics 2000, 4, 201–206. [Google Scholar] [CrossRef]
- Schitter, G.; Stemmer, A. Identification and open-loop tracking control of a piezoelectric tube scanner for high-speed scanning-probe microscopy. IEEE Trans. Control Syst. Technol. 2004, 12, 449–454. [Google Scholar] [CrossRef]
- Rost, M.J.; Crama, L.; Schakel, P.; Van Tol, E.; Van Velzen-Williams, G.B.E.M.; Overgauw, C.F.; Ter Horst, H.; Dekker, H.M.; Okhuijsen, B.; Seynen, M.; et al. Scanning probe microscopes go video rate and beyond. Rev. Sci. Instrum. 2005, 76, 999. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Zeng, M.; Li, Q. Optimal design of a piezo-actuated 2-DOF millimeter-range monolithic flexure mechanism with a pseudo-static model. Mech. Syst. Signal Process. 2019, 115, 120–131. [Google Scholar] [CrossRef]
- Trease, B.P.; Moon, Y.M.; Kota, S. Design of Large-Displacement Compliant Joints. J. Mech. Des. 2004, 127, 788–798. [Google Scholar] [CrossRef]
- Ling, M.; Howell, L.L.; Cao, J.; Chen, G. Kinetostatic and Dynamic Modeling of Flexure-Based Compliant Mechanisms: A Survey. Appl. Mech. Rev. 2020, 72, 030802. [Google Scholar] [CrossRef]
- Lee, C.; Lee, J.W.; Ryu, S.G.; Oh, J.H. Optimum design of a large area, flexure based XYθ mask alignment stage for a 12-inch wafer using grey relation analysis. Robot. Comput. Integr. Manuf. 2019, 58, 109–119. [Google Scholar] [CrossRef]
- Ryu, J.W.; Gweon, D.-G.; Moon, K.S. Optimal design of a flexure hinge based XYφ wafer stage. Precis. Eng. 1997, 21, 18–28. [Google Scholar] [CrossRef]
- Oh, Y.S.; Kota, S. Synthesis of Multistable Equilibrium Compliant Mechanisms Using Combinations of Bistable Mechanisms. J. Mech. Des. 2009, 131, 021002. [Google Scholar] [CrossRef]
- Kota, S.; Joo, J.; Li, Z.; Rodgers, S.M.; Sniegowski, J. Design of Compliant Mechanisms: Applications to MEMS. Analog Integr. Circuits Signal Process. 2001, 29, 7–15. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, X.; Wen, Z.; Ren, J.; Liu, P. A novel flexure-based vertical nanopositioning stage with large travel range. Rev. Sci. Instrum. 2015, 86, 105112. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Xu, Q. Design, fabrication, and testing of a new compact piezo-driven flexure stage for vertical micro/nanopositioning. IEEE Trans. Autom. Sci. Eng. 2018, 16, 908–918. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, X.; Li, H.; Wei, J.; Fatikow, S. Nonlinear analysis and optimal design of a novel piezoelectric-driven compliant microgripper. Mech. Mach. Theory 2017, 118, 32–52. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, J.; Liu, Y.; Zheng, H.; Liu, W. Droplet formation study of a liquid micro-dispenser driven by a piezoelectric actuator. Smart Mater. Struct. 2019, 28, 055003. [Google Scholar] [CrossRef]
- Lu, S.; Yao, Y.; Liu, Y.; Zhao, Y. Design and experiment of a needle-type piezostack-driven jetting dispenser based on lumped parameter method. J. Adhes. Sci. Technol. 2015, 29, 716–730. [Google Scholar] [CrossRef]
- Sun, X.; Yang, B. A new methodology for developing flexure-hinged displacement amplifiers with micro-vibration suppression for a giant magnetostrictive micro drive system. Sens. Actuators A Phys. 2017, 263, 30–43. [Google Scholar] [CrossRef]
- Chen, F.; Dong, W.; Yang, M.; Sun, L.; Du, Z. A PZT Actuated 6-DOF Positioning System for Space Optics Alignment. IEEE/ASME Trans. Mechatron. 2019, 24, 2827–2838. [Google Scholar] [CrossRef]
- Liu, P.; Yan, P. Kinetostatic Modeling of Bridge-Type Amplifiers Based on Timoshenko Beam Constraint Model. Int. J. Precis. Eng. Manuf. 2018, 19, 1339–1345. [Google Scholar] [CrossRef]
- Qi, K.-Q.; Xiang, Y.; Fang, C.; Zhang, Y.; Yu, C.-S. Analysis of the displacement amplification ratio of bridge-type mechanism. Mech. Mach. Theory 2015, 87, 45–56. [Google Scholar] [CrossRef]
- Tolliver, L.; Xu, T.B.; Jiang, X. Finite element analysis of the piezoelectric stacked-HYBATS transducer. Smart Mater. Struct. 2013, 22, 35015. [Google Scholar] [CrossRef]
- Lalande, F.; Chaudhry, Z.; Rogers, C.A. A simplified geometrically nonlinear approach to the analysis of the Moonie actuator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 21–27. [Google Scholar] [CrossRef]
- Dogan, A.; Uchino, K. Composite piezoelectric transducer with truncated conical endcaps “cymbal”. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 597–605. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, L.; Qiu, D. A lever-bridge combined compliant mechanism for translation amplification. Precis. Eng. 2021, 67, 383–392. [Google Scholar] [CrossRef]
- Wei, D.; Chen, F.; Gao, F.; Miao, Y.; Sun, L.; Du, Z.; Tang, J.; Zhang, D. Development and analysis of a bridge-lever-type displacement amplifier based on hybrid flexure hinges. Precis. Eng. 2018, 54, 171–181. [Google Scholar] [CrossRef]
- Pokines, B.J.; Garcia, E. A smart material microamplification mechanism fabricated using LIGA. Smart Mater. Struct. 1998, 7, 105–112. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E. Analytical model of displacement amplification and stiffness optimization for a class of flexure-based compliant mechanisms. Comput. Struct. 2003, 81, 2797–2810. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, S.H.; Kwak, Y.K. Development and optimization of 3-D bridge-type hinge mechanisms. Sens. Actuators A Phys. 2004, 116, 530–538. [Google Scholar] [CrossRef]
- Ma, H.-W.; Yao, S.-M.; Wang, L.-Q.; Zhong, Z. Analysis of the displacement amplification ratio of bridge-type flexure hinge. Sens. Actuators A Phys. 2006, 132, 730–736. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier. Mech. Mach. Theory 2011, 46, 183–200. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Zeng, M.; Lin, J.; Inman, D.J. Enhanced mathematical modeling of the displacement amplification ratio for piezoelectric compliant mechanisms. Smart Mater. Struct. 2016, 25, 075022. [Google Scholar] [CrossRef]
- Choi, K.-B.; Lee, J.J.; Kim, G.H.; Lim, H.J.; Kwon, S.G. Amplification ratio analysis of a bridge-type mechanical amplification mechanism based on a fully compliant model. Mech. Mach. Theory 2018, 121, 355–372. [Google Scholar] [CrossRef]
- Liu, P.; Yan, P. A new model analysis approach for bridge-type amplifiers supporting nano-stage design. Mech. Mach. Theory 2016, 99, 176–188. [Google Scholar] [CrossRef]
- Pan, B.; Zhao, H.; Zhao, C.; Zhang, P.; Hu, H. Nonlinear characteristics of compliant bridge-type displacement amplification mechanisms. Precis. Eng. 2019, 60, 246–256. [Google Scholar] [CrossRef]
- Li, J.; Yan, P.; Li, J. Displacement amplification ratio modeling of bridge-type nano-positioners with input displacement loss. Mech. Sci. 2019, 10, 299–307. [Google Scholar] [CrossRef]
- Lin, C.; Shen, Z.; Wu, Z.; Yu, J. Kinematic characteristic analysis of a micro-/nano positioning stage based on bridge-type amplifier. Sens. Actuators A Phys. 2018, 271, 230–242. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Peng, Y.; Pu, H.; Yang, Y. A novel amplification ratio model of a decoupled XY precision positioning stage combined with elastic beam theory and Castigliano’s second theorem considering the exact loading force. Mech. Syst. Signal Process. 2020, 136, 106473. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Lin, J. Modular kinematics and statics modeling for precision positioning stage. Mech. Mach. Theory 2017, 107, 274–282. [Google Scholar] [CrossRef]
- Abbiati, G.; Marelli, S.; Tsokanas, N.; Sudret, B.; Stojadinović, B. A global sensitivity analysis framework for hybrid simulation. Mech. Syst. Signal Process. 2021, 146, 106997. [Google Scholar] [CrossRef]
- Liu, Q.; Tong, N.; Wu, X.; Han, X.; Chen, C. A generalized sensitivity analysis method based on variance and covariance decomposition of summatory functions for multi-input multi-output systems. Comput. Methods Appl. Mech. Eng. 2021, 385, 114009. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Smith, S.T. Flexures: Elements of Elastic Mechanisms; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).