Friction Prediction and Application to Lateral or Longitudinal Slip Force Prediction
Abstract
:1. Introduction
2. Method of Dynamic Friction Prediction
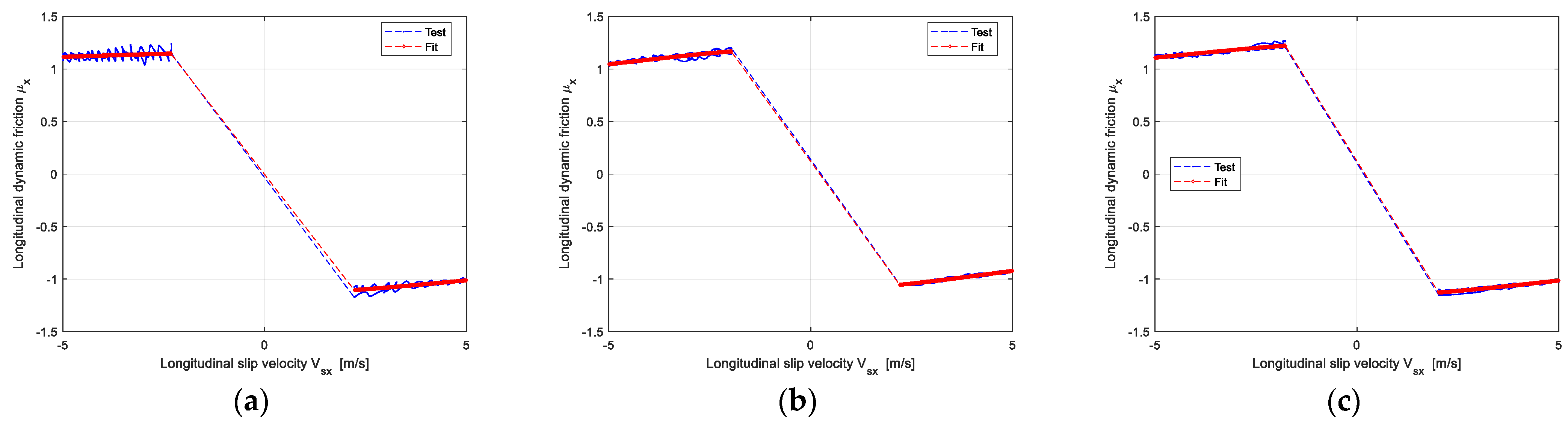
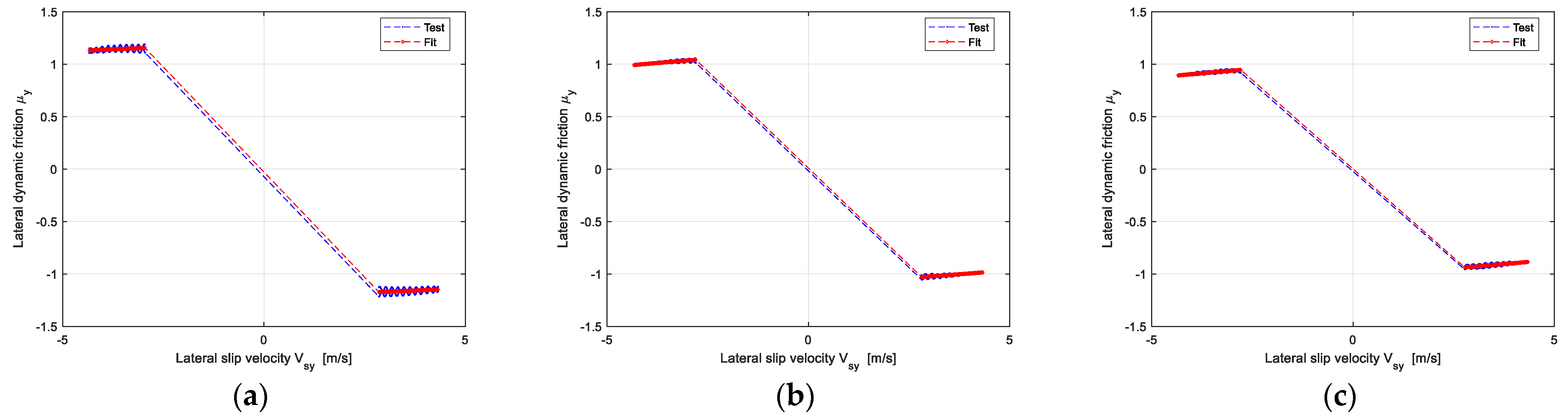
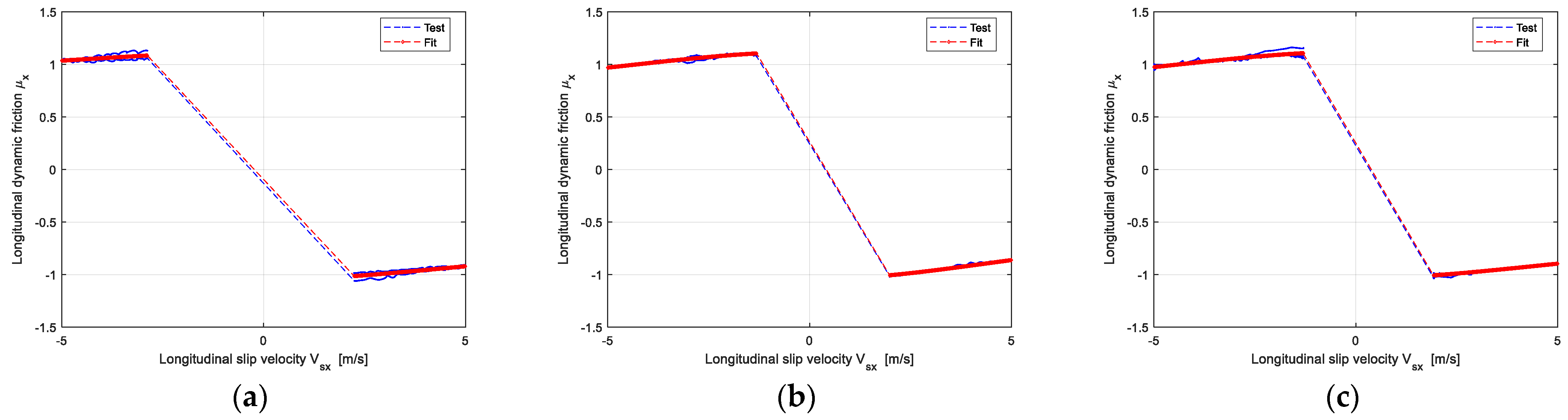
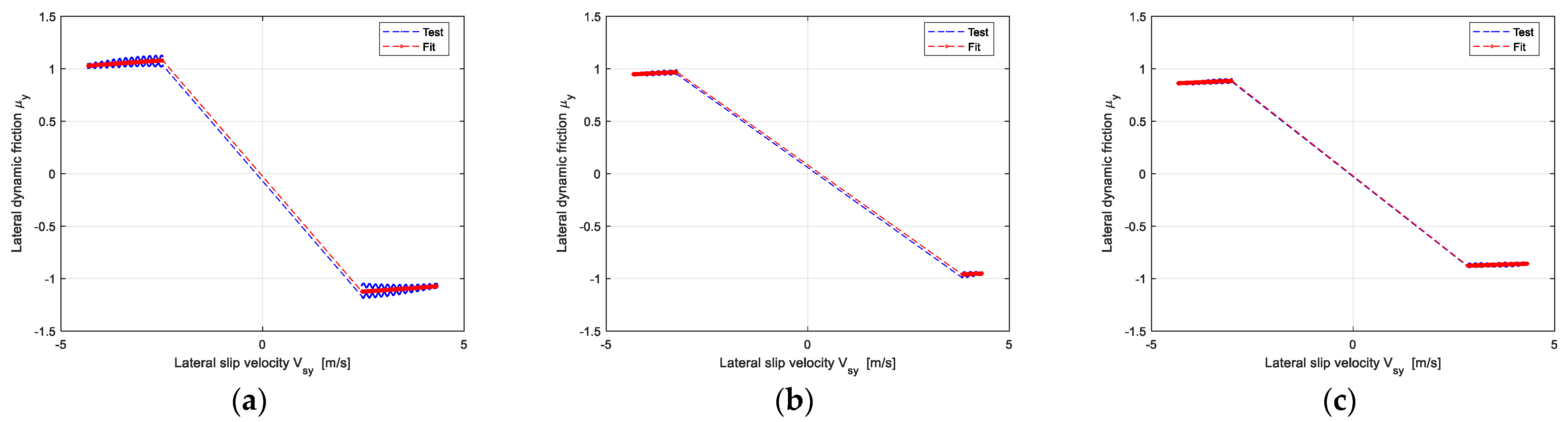
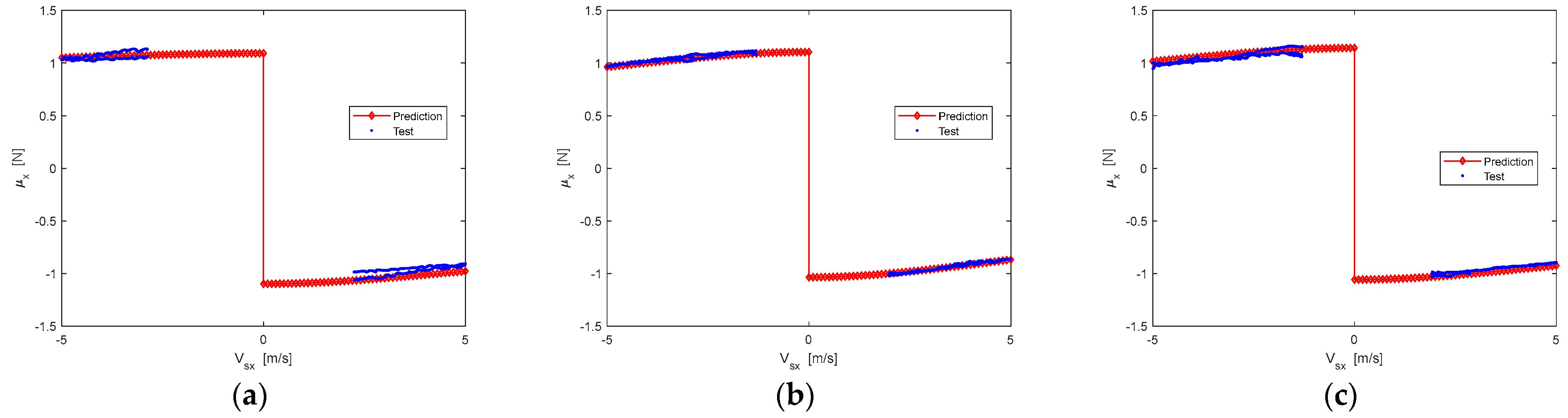
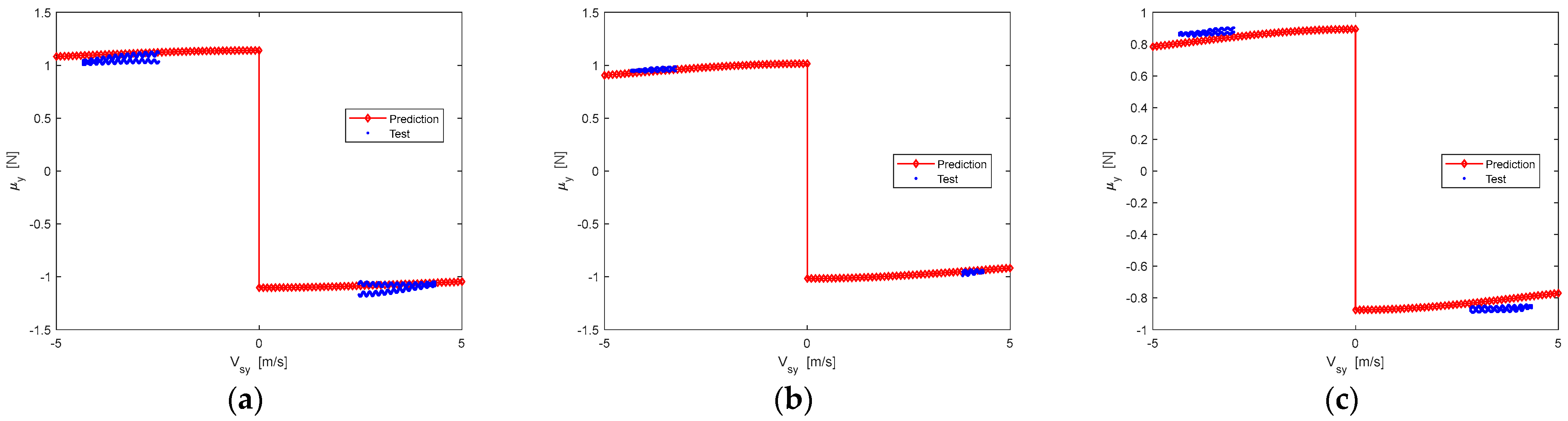
2.1. Peak Friction Coefficient Assumption and Validation
2.2. Dynamic Friction Separation Method
3. Prediction Method for Tire Forces under Pure Slip Condition
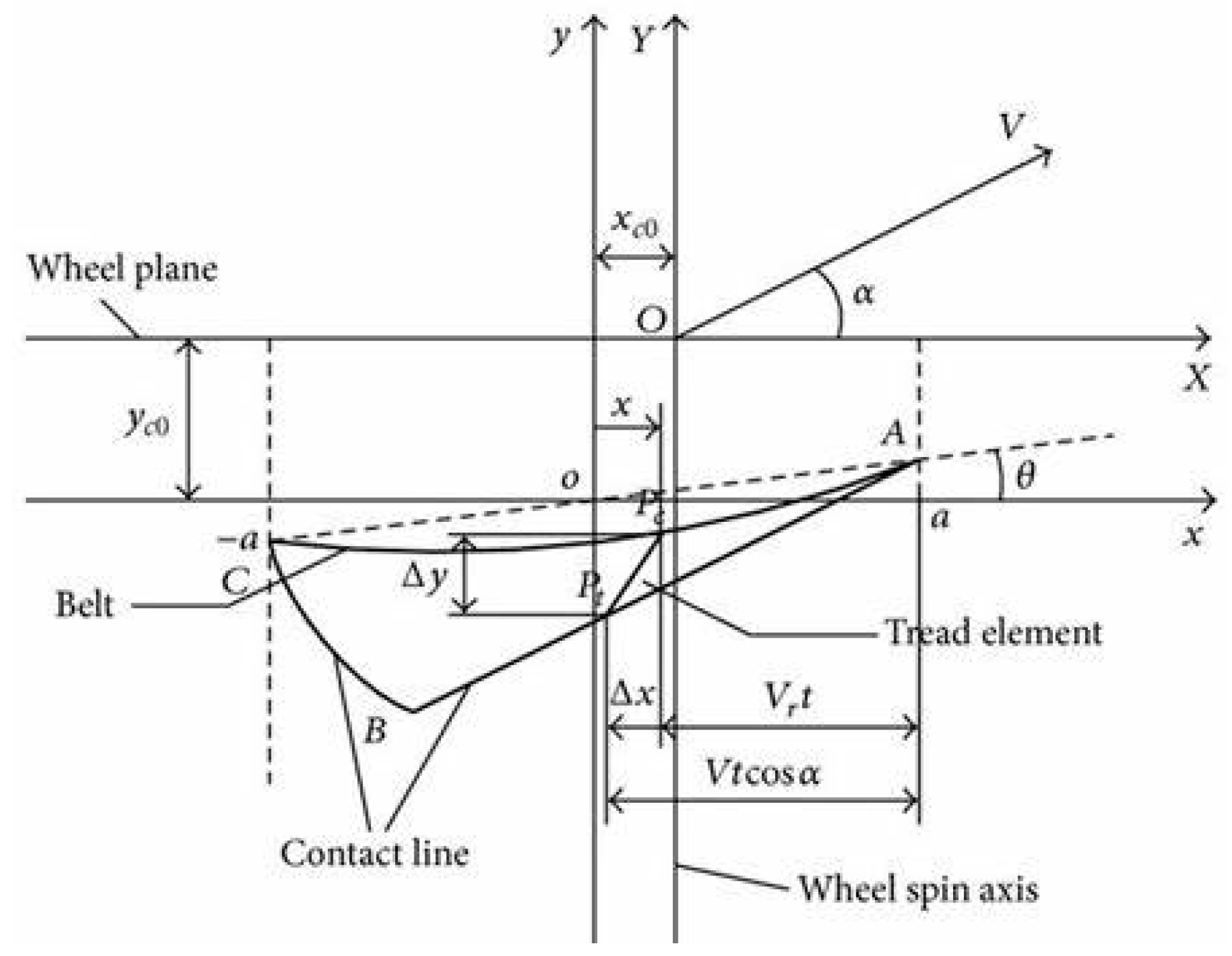
3.1. Theoretical Tire Model of Considering Belt/carcass Deformation
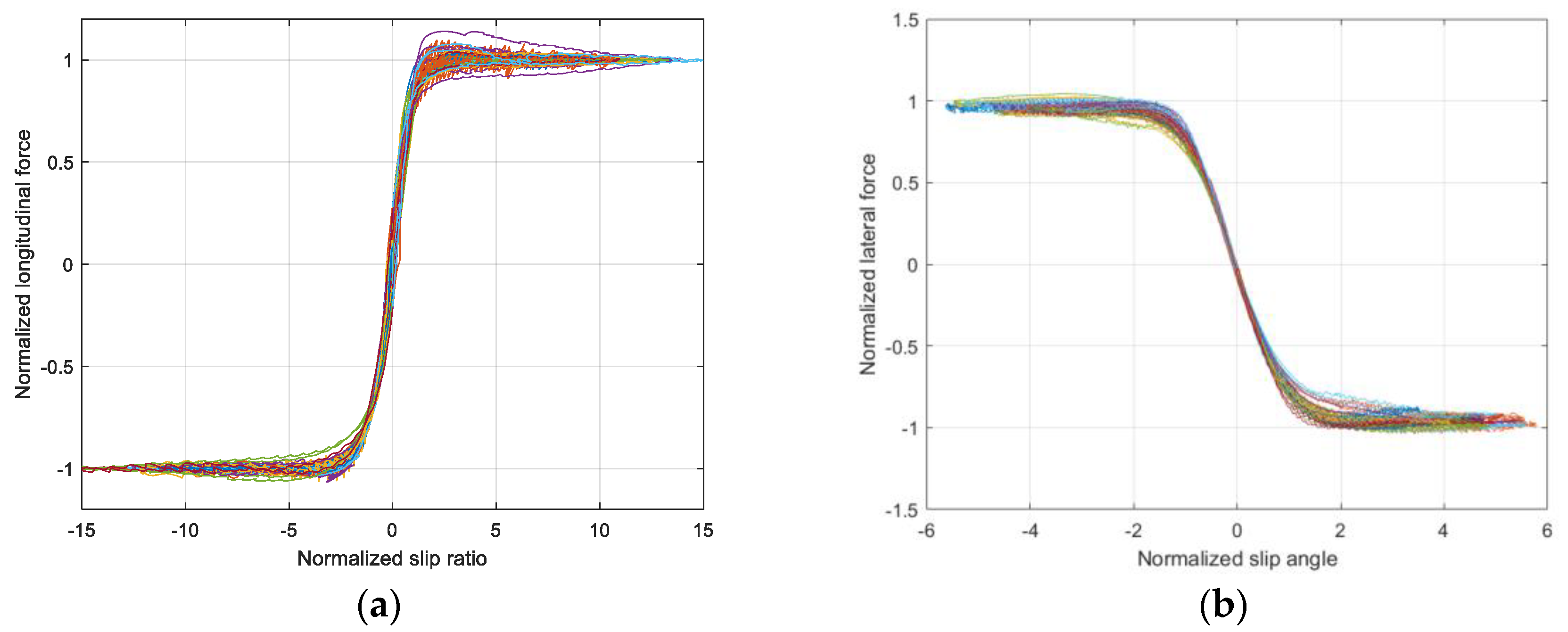
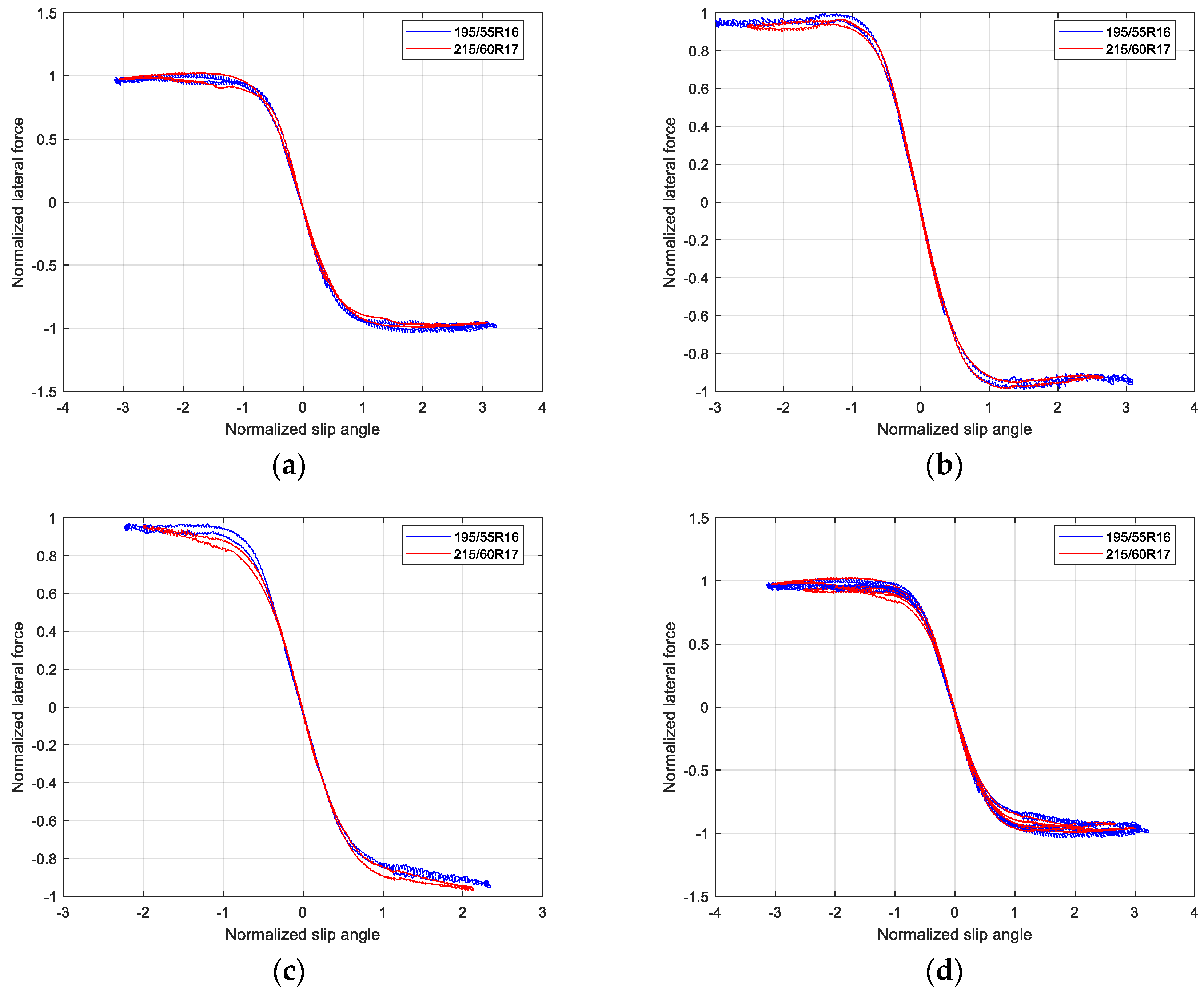
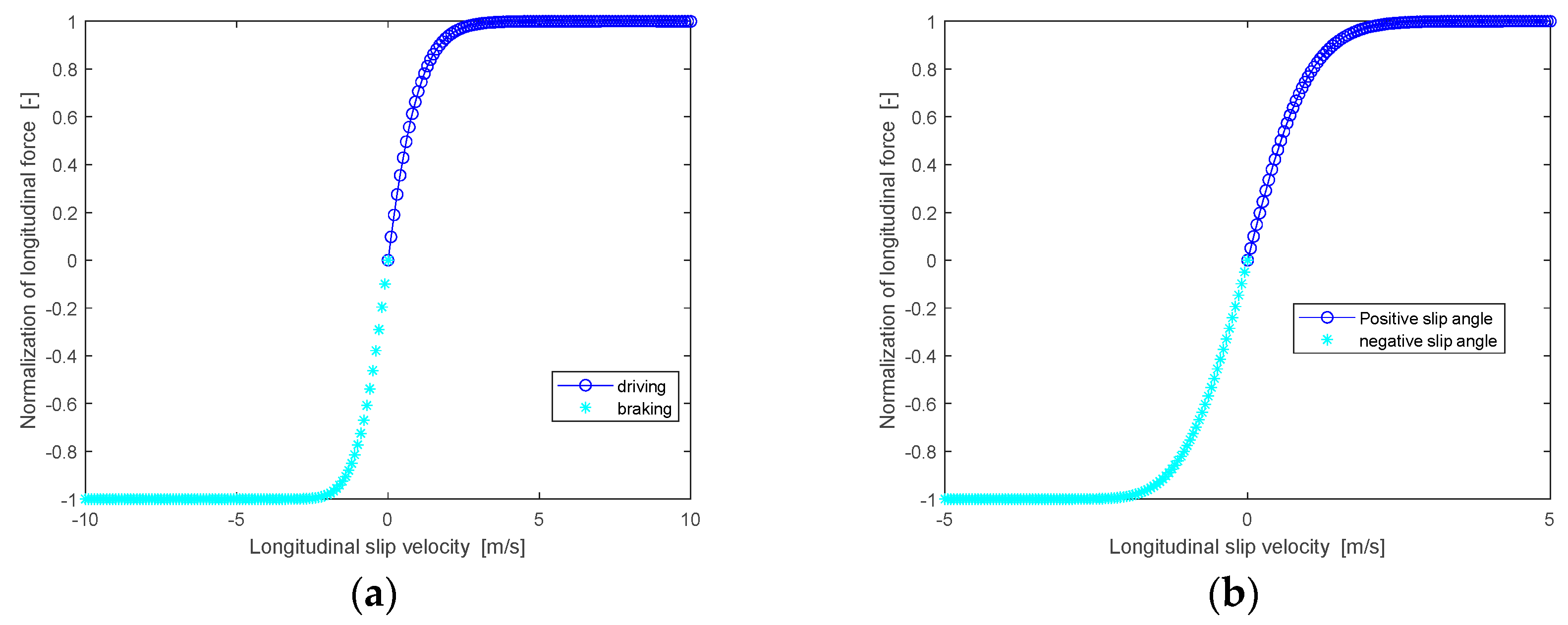
3.2. Normalization and Prediction Method for Tire Forces
4. Tire Experiments and Validation
4.1. Experiments Design
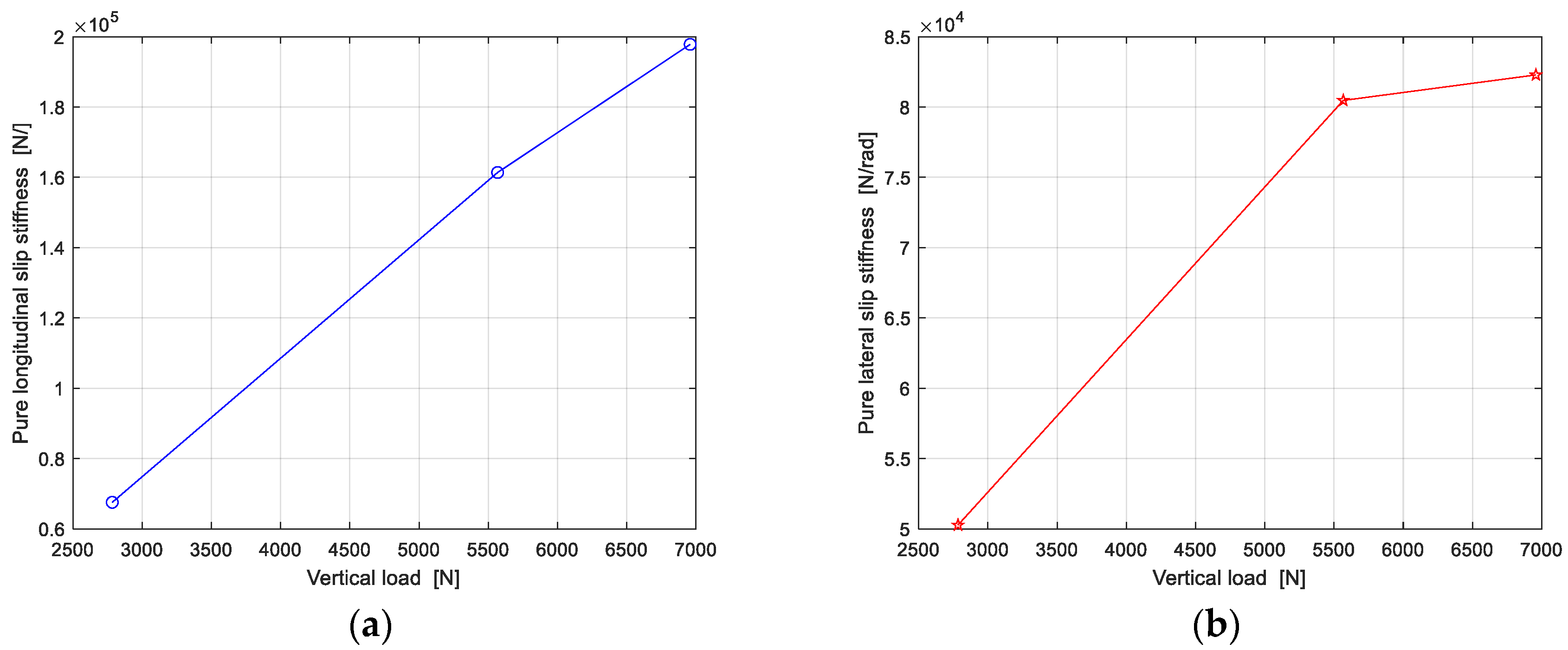
4.2. Pure slip Stiffness Calculation
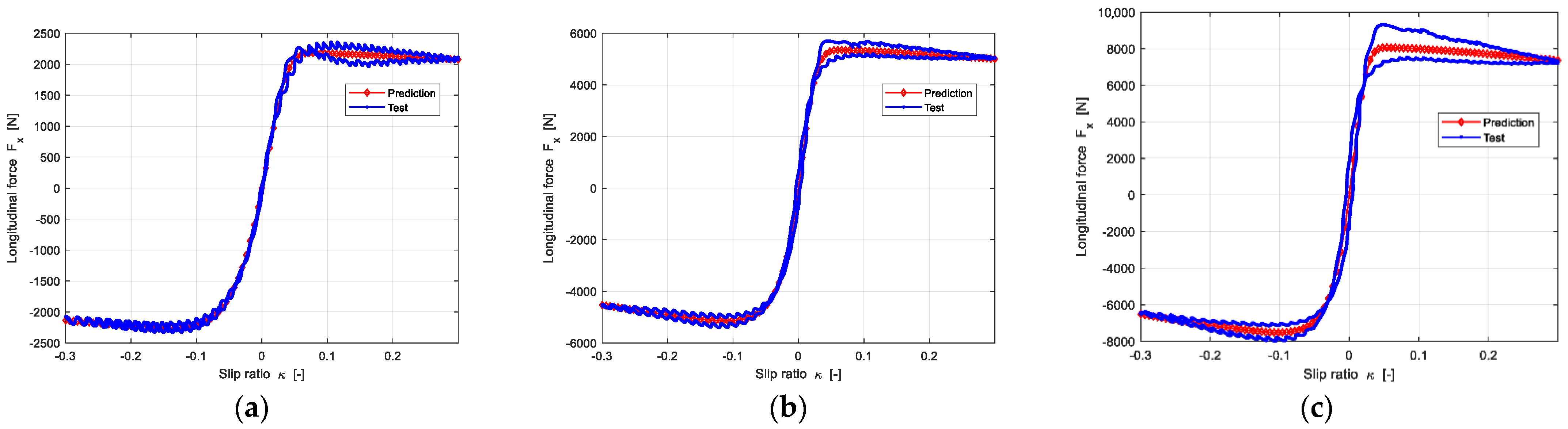
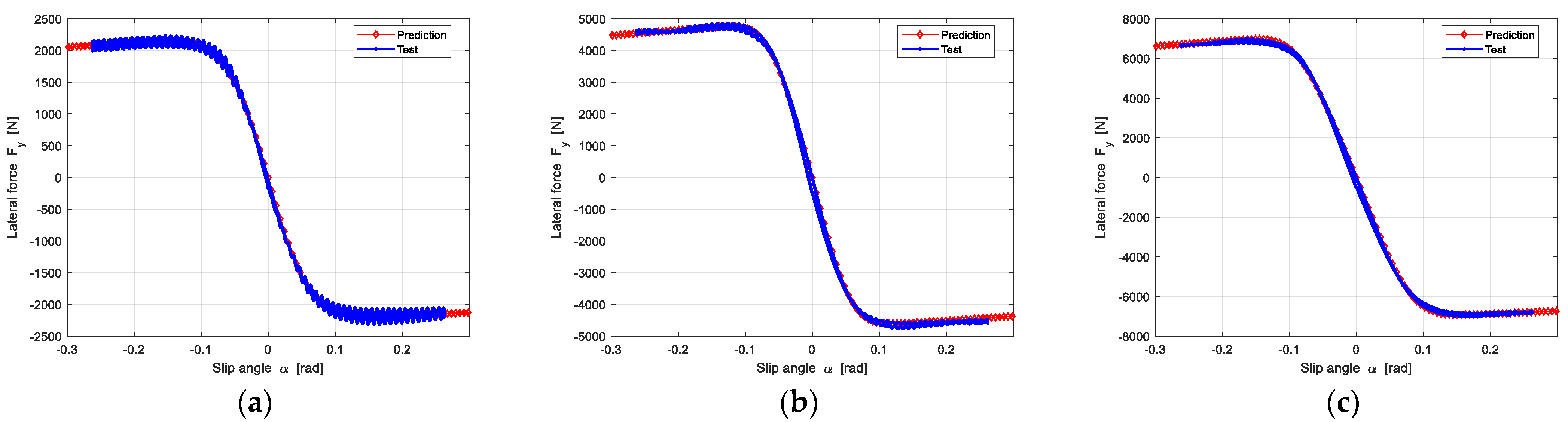
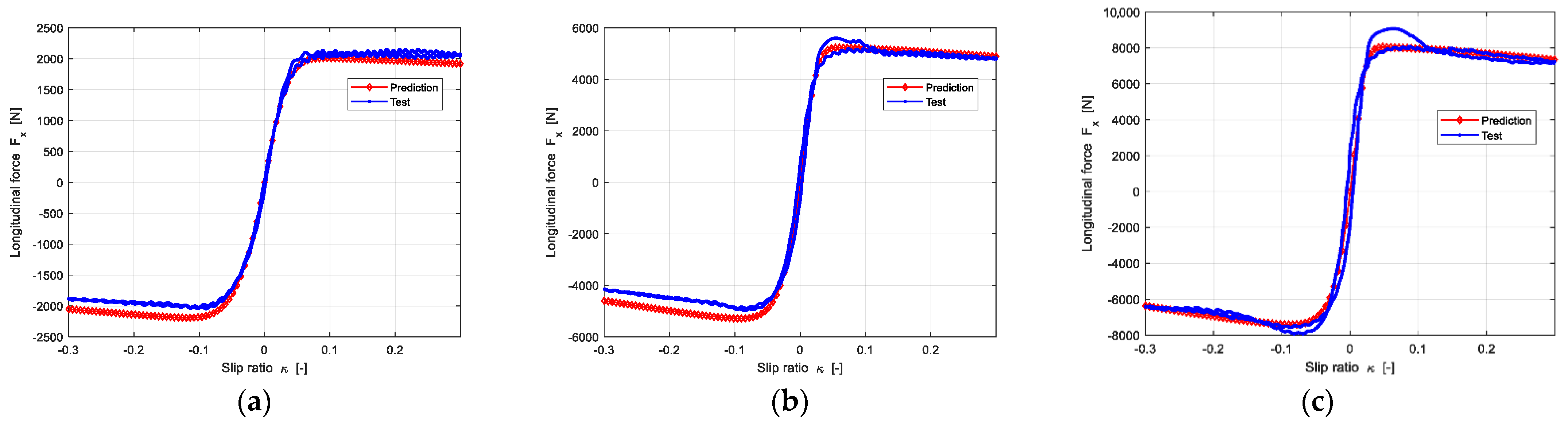
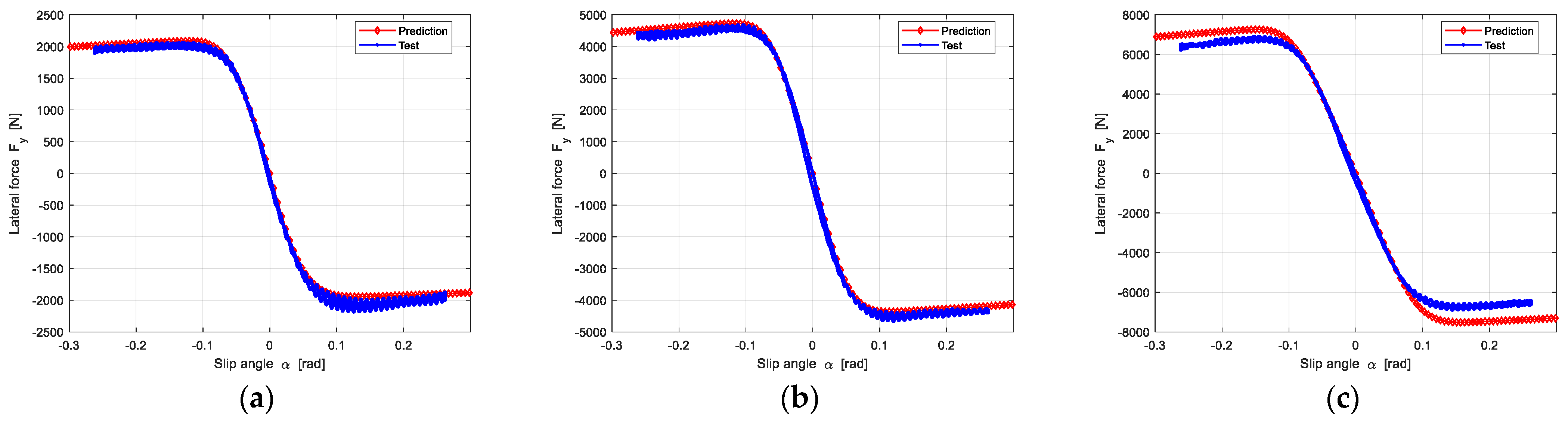
4.3. Pure Longitudinal Force and Lateral Force Prediction Results
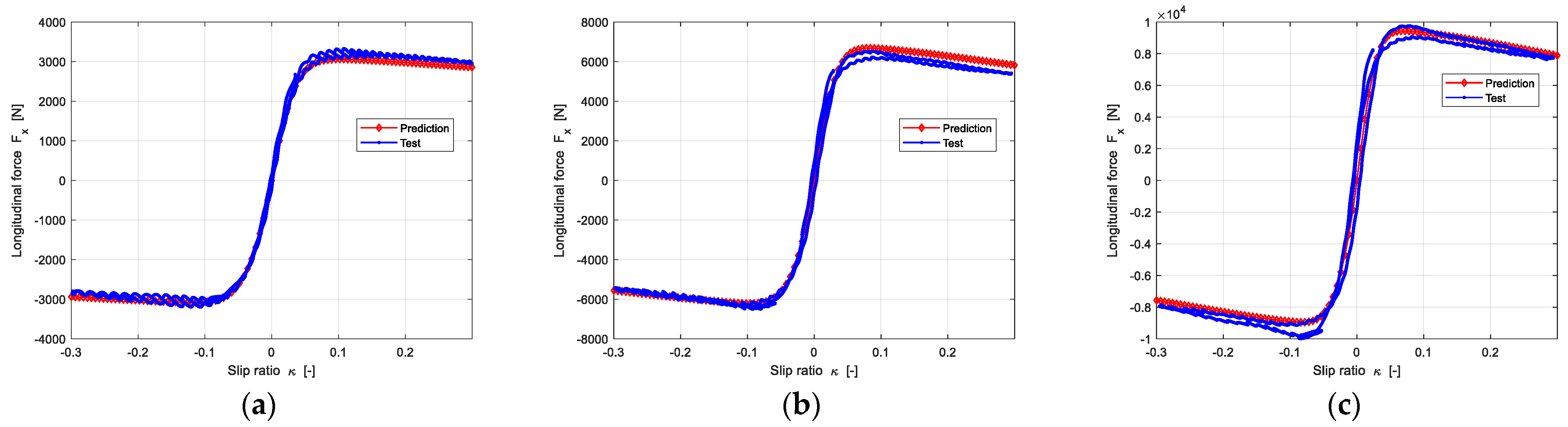
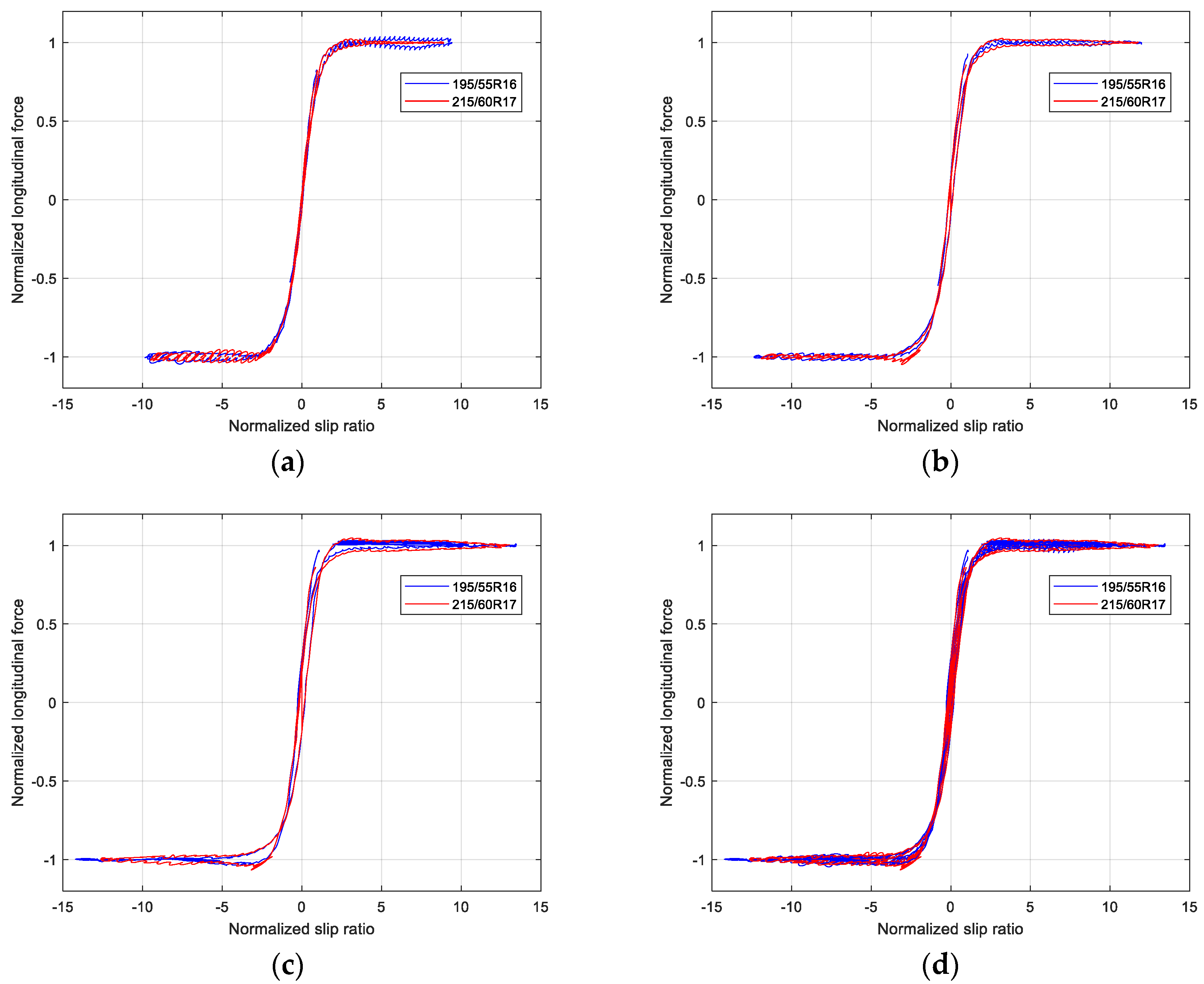
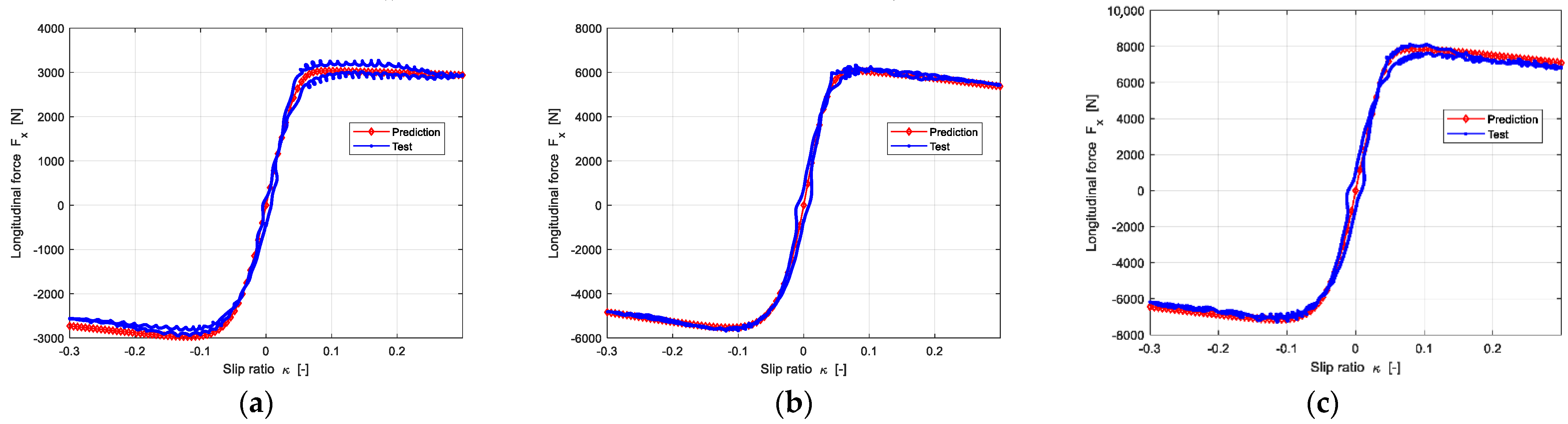
4.3.1. Pure Longitudinal Force
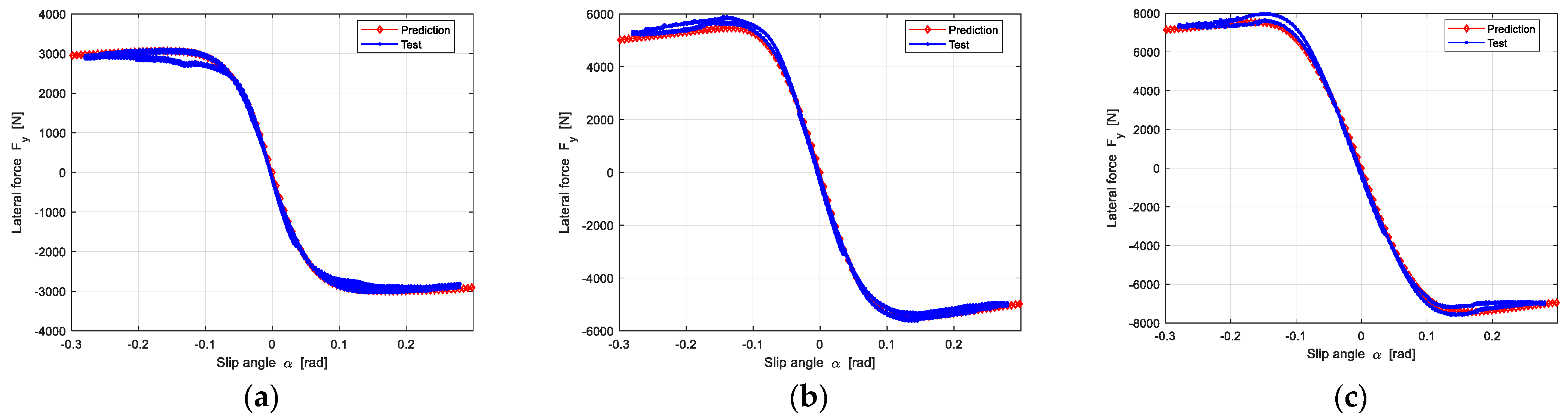
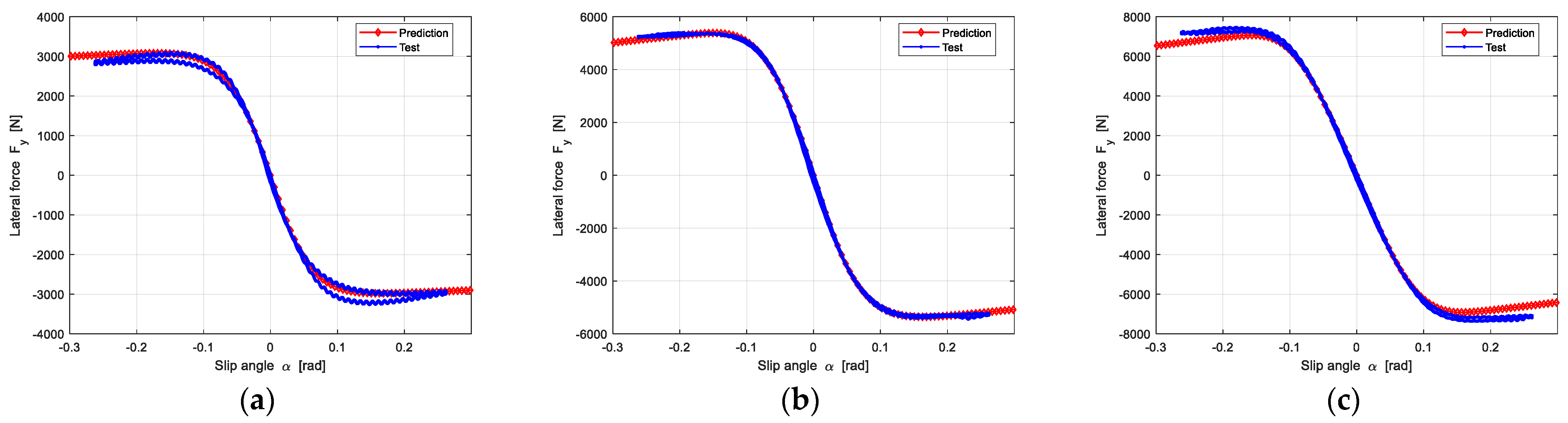
4.3.2. Pure Lateral Force
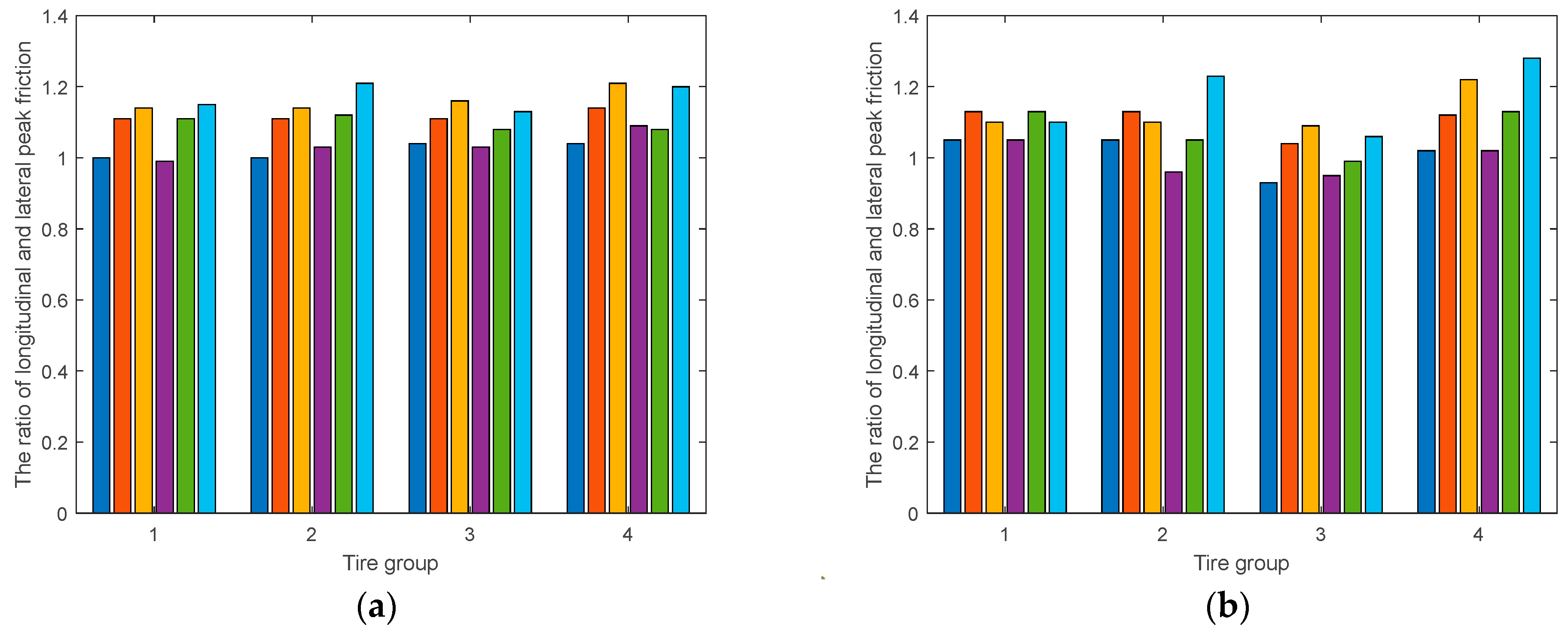
4.4. Analysis of Reference Tire Criteria
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kuiper, E.V.O.J.; Van Oosten, J.J.M. The PAC2002 advanced handling tire model. Veh. Syst. Dyn. 2007, 45 (Suppl. S1), 153–167. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tire and Vehicle Dynamics, 3rd ed.; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Pacejka, H.B.; Bakker, E. The magic formula tyre model. Veh. Syst. Dyn. 1993, 21 (Suppl. S1), 1–18. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Besselink, I.J.M. Magic formula tyre model with transient properties. Veh. Syst. Dyn. 1997, 27 (Suppl. S1), 234–249. [Google Scholar] [CrossRef]
- Hirschberg, W.; Rill, G.; Weinfurter, H. Tire model tmeasy. Veh. Syst. Dyn. 2007, 45 (Suppl. S1), 101–119. [Google Scholar] [CrossRef]
- Rill, G. TMeasy—A Handling Tire Model based on a three-dimensional slip approach. In Proceedings of the XXIII International Symposium on Dynamic of Vehicles on Roads and on Tracks (IAVSD 2013), Quingdao, China, 19–23 August 2013; pp. 19–23. [Google Scholar]
- Rill, G. Road Vehicle Dynamics: Fundamentals and Modeling, 1st ed.; Taylor & Francis: Boca Raton, FL, USA, 2011. [Google Scholar]
- Guo, K.; Lu, D.; Chen, S.K.; Lin, W.C.; Lu, X.P. The UniTire model: A nonlinear and non-steady-state tyre model for vehicle dynamics simulation. Veh. Syst. Dyn. 2005, 43 (Suppl. 1), 341–358. [Google Scholar] [CrossRef]
- Guo, K.; Lu, D. UniTire: Unified tire model for vehicle dynamic simulation. Veh. Syst. Dyn. 2007, 45 (Suppl. S1), 79–99. [Google Scholar] [CrossRef]
- Gim, G.; Choi, Y.; Kim, S. A semiphysical tyre model for vehicle dynamics analysis of handling and braking. Veh. Syst. Dyn. 2005, 43 (Suppl. S1), 267–280. [Google Scholar] [CrossRef]
- Février, P.; Fandard, G. Thermal and mechanical tyre modelling for handling simulation. ATZ Worldw. 2008, 110, 26–31. [Google Scholar] [CrossRef]
- Pearson, M.; Blanco-Hague, O.; Pawlowski, R. TameTire: Introduction to the model. Tire Sci. Technol. 2016, 44, 102–119. [Google Scholar] [CrossRef]
- Jansen, S.T.; Verhoeff, L.; Cremers, R.; Schmeitz, A.J.; Besselink, I.J. MF-Swift simulation study using benchmark data. Veh. Syst. Dyn. 2005, 43 (Suppl. S1), 92–101. [Google Scholar] [CrossRef]
- Schmeitz, A.J.C.; Besselink, I.J.M.; Jansen, S.T.H. Tno mf-swift. Veh. Syst. Dyn. 2007, 45 (Suppl. S1), 121–137. [Google Scholar] [CrossRef]
- Gipser, M. FTire—the tire simulation model for all applications related to vehicle dynamics. Veh. Syst. Dyn. 2007, 45 (Suppl. S1), 139–151. [Google Scholar] [CrossRef]
- Gipser, M. FTire and puzzling tyre physics: Teacher, not student. Veh. Syst. Dyn. 2016, 54, 448–462. [Google Scholar] [CrossRef]
- Gallrein, A.; De Cuyper, J.; Dehandschutter, W.; Bäcker, M. Parameter identification for LMS CDTire. Veh. Syst. Dyn. 2005, 43 (Suppl. S1), 444–456. [Google Scholar] [CrossRef]
- Gallrein, A.; Bäcker, M. CDTire: A tire model for comfort and durability applications. Veh. Syst. Dyn. 2007, 45 (Suppl. S1), 69–77. [Google Scholar] [CrossRef]
- Oertel, C.; Fandre, A. Ride comfort simulations and steps towards life time calculations: RMOD-K tyre model and ADAMS. In Proceedings of the International ADAMS Users’ Conference, Berlin, Germany, 17–18 November 1999. [Google Scholar]
- Oertel, C.; Fandre, A. Tire model RMOD-K 7 and misuse load cases. In SAE Technical Paper; SAE International: Warrendale, PA, USA, 2009. [Google Scholar] [CrossRef]
- Flat-Trac Tire Test Systems [EB/OL]. Available online: http://www.mts.com/cs/groups/public/documents/library/dev_002227.pdf (accessed on 14 October 2014).
- Xu, N.; Hashemi, E.; Tang, Z.; Khajepour, A. Data-Driven Tire Capacity Estimation with Experimental Verification. IEEE Trans. Intell. Transp. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Bhoopalam, A.K.; Sandu, C. Review of the state of the art in experimental studies and mathematical modeling of tire performance on ice. J. Terramech. 2014, 53, 19–35. [Google Scholar] [CrossRef]
- Braghin, F.; Cheli, F.; Sabbioni, E. Environmental effects on Pacejka’s scaling factors. Veh. Syst. Dyn. 2006, 44, 547–568. [Google Scholar] [CrossRef]
- Arosio, D.; Braghin, F.; Cheli, F.; Sabbioni, E. Identification of Pacejka’s scaling factors from full-scale experimental tests. Veh. Syst. Dyn. 2005, 43 (Suppl. S1), 457–474. [Google Scholar] [CrossRef]
- Waluś, K.J. Experimental Determination of Vehicle Lateral Drift Characteristics under Laboratory Conditions. Appl. Mech. Mater. 2012, 232, 836–840. [Google Scholar] [CrossRef]
- Persson, B.N.J. Rubber friction and tire dynamics. J. Phys. Condens. Matter 2010, 23, 015003. [Google Scholar] [CrossRef] [PubMed]
- Lugaro, C.; Schmeitz, A.; Ogawa, T.; Murakami, T.; Huisman, S. Development of a parameter identification method for MF-Tyre/MF-Swift applied to parking and low speed manoeuvres. SAE Int. J. Passeng. Cars-Mech. Syst. 2016, 9, 892–903. [Google Scholar] [CrossRef]
- Zhu, J.J.; Khajepour, A.; Spike, J.; Chen, S.K.; Moshchuk, N. An integrated vehicle velocity and tyre-road friction estimation based on a half-car model. Int. J. Veh. Auton. Syst. 2016, 13, 114–139. [Google Scholar] [CrossRef]
- Liu, X.; Cao, Q.; Wang, H.; Chen, J.; Huang, X. Evaluation of vehicle braking performance on wet pavement surface using an integrated tire-vehicle modeling approach. Transp. Res. Rec. 2019, 2673, 295–307. [Google Scholar] [CrossRef]
- Khaleghian, S.; Emami, A.; Taheri, S. A technical survey on tire-road friction estimation. Friction 2017, 5, 123–146. [Google Scholar] [CrossRef]
- Acosta, M.; Kanarachos, S.; Blundell, M. Road Friction Virtual Sensing: A Review of Estimation Techniques with Emphasis on Low Excitation Approaches. Appl. Sci. 2017, 7, 1230. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Wang, F.A.; Dong, H.; Yan, Y.; Ren, Y.; Zhou, C.; Yin, G. Tire road friction coefficient estimation: Review and research perspectives. Chin. J. Mech. Eng. 2022, 35, 6. [Google Scholar] [CrossRef]
- Kanafi, M.M.; Kuosmanen, A.; Pellinen, T.K.; Tuononen, A.J. Macro- and micro-texture evolution of road pavements and correlation with friction. Int. J. Pavement Eng. 2015, 16, 168–179. [Google Scholar] [CrossRef]
- Du, Y.; Liu, C.; Song, Y.; Li, Y.; Shen, Y. Rapid Estimation of Road Friction for Anti-Skid Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2461–2470. [Google Scholar] [CrossRef]
- Leng, B.; Jin, D.; Xiong, L.; Yang, X.; Yu, Z. Estimation of tire-road peak adhesion coefficient for intelligent electric vehicles based on camera and tire dynamics information fusion. Mech. Syst. Signal Processing 2021, 150, 107275. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Kamai, K.; Seki, R. Intelligent tires for identifying coefficient of friction of tire/road contact surfaces using three-axis accelerometer. Smart Mater. Struct. 2014, 24, 025010. [Google Scholar] [CrossRef]
- Paul, D.; Velenis, E.; Humbert, F.; Cao, D.; Dobo, T.; Hegarty, S. Tyre–road friction μ-estimation based on braking force distribution. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2030–2047. [Google Scholar] [CrossRef]
- Müller, S.; Uchanski, M.; Hedrick, K. Estimation of the Maximum Tire-Road Friction Coefficient. ASME J. Dyn. Sys. Meas. Control 2003, 125, 607–617. [Google Scholar] [CrossRef]
- Xia, X.; Xiong, L.; Sun, K.; Yu, Z.P. Estimation of maximum road friction coefficient based on Lyapunov method. Int. J. Automot. Technol. 2016, 17, 991–1002. [Google Scholar] [CrossRef]
- Nishihara, O.; Masahiko, K. Estimation of Road Friction Coefficient Based on the Brush Model. ASME J. Dyn. Sys. Meas. Control 2011, 133, 041006. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Li, T.; Yang, Y.-Y.; Ji, X.-W.; Wu, J. Estimation of tire-road friction coefficient based on combined APF-IEKF and iteration algorithm. Mech. Syst. Signal Processing 2017, 88, 25–35. [Google Scholar] [CrossRef]
- de Menezes Lourenço, M.A.; Eckert, J.J.; Silva, F.L.; Santiciolli, F.M.; Silva, L.C.A. Vehicle and twin-roller chassis dynamometer model considering slip tire interactions. Mech. Based Des. Struct. Mach. 2022, 1–18. [Google Scholar] [CrossRef]
- Radt, H.S.; Glemming, D.A. Normalization of Tire Force and Moment Data. Tire Sci. Technol. TSTCA 1993, 21, 91–119. [Google Scholar] [CrossRef]
- Radt, H.S., Jr.; Milliken, W.F., Jr. Non-dimensionalizing tyre data for vehicle simulation. In Proceedings of the Road Vehicle Handling, I Mech E Conference Publications 1983-5. Sponsored by Automobile Division of the Institution of Mechanical Engineers under Patronage of Federation Internationale des Societies d’Ingenieurs des Techniques de l’Automobile (FISITA) he (No. C133/83), Nuneaton, UK, 24–26 May 1983. [Google Scholar]
- Kasprzak, E.M.; Lewis, K.E.; Milliken, D.L. Inflation pressure effects in the nondimensional tire model. SAE Trans. 2006, 115, 1781–1792. [Google Scholar]
- Kasprzak, E.M.; Lewis, K.E. Tire asymmetries and pressure variations in the Radt/Milliken nondimensional tire model. In Proceedings of the SAE Automotive Dynamics, Stability and Controls Conference and Exhibition, Novi, MI, USA, 14–16 February 2006; pp. 1–1968. [Google Scholar]
- Sharp, R.S. Testing and improving a tyre shear force computation algorithm. Veh. Syst. Dyn. 2004, 41, 223–247. [Google Scholar] [CrossRef]
- Sharp, R.S.; Bettella, M. On the construction of a general numerical tyre shear force model from limited data. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2003, 217, 165–172. [Google Scholar] [CrossRef]
- Sharp, R.S.; Bettella, M. Shear Force and Moment Descriptions by Normalisation of Parameters and the “Magic Formula”. Veh. Syst. Dyn. 2003, 39, 27–56. [Google Scholar] [CrossRef]
- Guo, K. Automotive Tire Dynamics; Science Press: Beijing, China, 2018; p. 1. (In Chinese) [Google Scholar]
- Guo, K.H. A Unified Tire Model for Braking Driving and Steering Simulation. In Proceedings of the Fifth International Pacific Conference on Automotive Engineering, Beijing, China, 5–10 November 1989. [Google Scholar]
- Fiala, E. Seitenkrafte am rollenden luftreifen (Lateral forces on rolling pneumatic tires). Z. VDI 1954, 96, 973–979. [Google Scholar]
- Xu, N.; Guo, K.; Zhang, X.; Karimi, H.R. An Analytical Tire Model with Flexible Carcass for Combined Slips. Math. Probl. Eng. Theory Methods Appl. 2014, 2014, 397538. [Google Scholar] [CrossRef]
- Sakai, H. Theoretical and Experimental Studies on the Dynamic Properties of Tyres, Part 2: Experimental Investigation of Rubber Friction and Deformation pf a Tyre. Ins. J. Veh. Des. 1981, 2, 182–226. [Google Scholar]
- Guo, K.; Sui, J. A theoretical observation on empirical expression of tire shear forces. Veh. Syst. Dyn. 1996, 25, 263–274. [Google Scholar] [CrossRef]

| Group | Tire Size | Tire No. | Pressure [kPa] | Tread Depth [mm] |
|---|---|---|---|---|
| (1) Same tire mold and tread compound, different structural design | 205/55R16-P1-C1-T1 | 1 | 230 | 6.8 |
| 205/55R16-P1-C1-T2 | 2 | 230 | 6.8 | |
| (2) Same tire mold, different tread compound and structural design | 205/55R16-P1-C1-T1 | 3 | 230 | 6.8 |
| 205/55R16-P1-C2-T3 | 4 | 230 | 6.8 | |
| (3) Same tire pattern, different size, tread compound and structural design | 215/55R18-P2-C3-T4 | 5 | 250 | 7.6 |
| 215/60R17-P2-C4-T5 | 6 | 250 | 7.2 | |
| (4) Different size with different tire manufacturer | 195/55R16-P3-C5-T6 | 7 | 225 | 7.3 |
| 215/60R17-P4-C6-T7 | 8 | 245 | 7.2 |
| Tire No. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.19 | 1.18 | 1.11 | 1.19 | 1.06 | 0.97 | 1.00 | 1.11 | 1.14 |
| 2 | 1.18 | 1.17 | 1.11 | 1.19 | 1.06 | 0.97 | 0.99 | 1.11 | 1.15 |
| 3 | 1.19 | 1.18 | 1.11 | 1.19 | 1.06 | 0.97 | 1.00 | 1.11 | 1.14 |
| 4 | 1.15 | 1.16 | 1.16 | 1.11 | 1.04 | 0.96 | 1.03 | 1.12 | 1.21 |
| 5 | 1.24 | 1.20 | 1.16 | 1.19 | 1.08 | 1.00 | 1.04 | 1.11 | 1.16 |
| 6 | 1.27 | 1.22 | 1.14 | 1.23 | 1.13 | 1.01 | 1.03 | 1.08 | 1.13 |
| 7 | 1.20 | 1.17 | 1.15 | 1.16 | 1.02 | 0.95 | 1.04 | 1.14 | 1.21 |
| 8 | 1.17 | 1.15 | 1.13 | 1.08 | 1.07 | 0.94 | 1.09 | 1.08 | 1.20 |
| Tire No. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | −1.27 | −1.18 | −1.06 | −1.21 | −1.04 | −0.96 | 1.05 | 1.13 | 1.10 |
| 2 | −1.26 | −1.16 | −1.06 | −1.21 | −1.03 | −0.96 | 1.05 | 1.13 | 1.10 |
| 3 | −1.27 | −1.18 | −1.06 | −1.21 | −1.04 | −0.96 | 1.05 | 1.13 | 1.10 |
| 4 | −1.12 | −1.10 | −1.15 | −1.16 | −1.04 | −0.94 | 0.96 | 1.05 | 1.23 |
| 5 | −1.10 | −1.12 | −1.11 | −1.18 | −1.08 | −1.02 | 0.93 | 1.04 | 1.09 |
| 6 | −1.19 | −1.13 | −1.05 | −1.25 | −1.13 | −1.00 | 0.95 | 0.99 | 1.06 |
| 7 | −1.14 | −1.12 | −1.12 | −1.12 | −1.00 | −0.92 | 1.02 | 1.12 | 1.22 |
| 8 | −1.12 | −1.15 | −1.14 | −1.09 | −1.02 | −0.89 | 1.02 | 1.13 | 1.28 |
| Item | Pt [%Pt0] | Vr [km/h] | γ [°] | Fz [%Fz0] | α [°] | κ [%] |
|---|---|---|---|---|---|---|
| Pure driving /braking | 100 | 60 | 0 | 40, 80, 100 | 0 | Sweep, rate = 10%/s −2→30 → −30 → 2 |
| Pure cornering | 100 | 60 | 0 | 40, 80, 100 | Sweep, rate = 4°/s −2→15 → −15 → 2 | 0 |
| Groups | ||
|---|---|---|
| 1 | 8.63 | 2.79 |
| 2 | 8.10 | 5.98 |
| 3 | 10.15 | 3.18 |
| 4 | 4.68 | 3.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, D.; Liu, Q.; Lu, D. Friction Prediction and Application to Lateral or Longitudinal Slip Force Prediction. Machines 2022, 10, 791. https://doi.org/10.3390/machines10090791
Xia D, Liu Q, Lu D. Friction Prediction and Application to Lateral or Longitudinal Slip Force Prediction. Machines. 2022; 10(9):791. https://doi.org/10.3390/machines10090791
Chicago/Turabian StyleXia, Danhua, Qianjin Liu, and Dang Lu. 2022. "Friction Prediction and Application to Lateral or Longitudinal Slip Force Prediction" Machines 10, no. 9: 791. https://doi.org/10.3390/machines10090791
APA StyleXia, D., Liu, Q., & Lu, D. (2022). Friction Prediction and Application to Lateral or Longitudinal Slip Force Prediction. Machines, 10(9), 791. https://doi.org/10.3390/machines10090791





