Design, Analysis and Experimental Research of Dual-Tendon-Driven Underactuated Gripper

Abstract

To improve the adaptive clamping performance of traditional single-tendon-driven underactuated grippers for grasping multiple categories of objects, a novel dual-tendon-driven underactuated gripper is proposed in this paper. First, two independent tendons with different winding paths are designed in the gripper to realize the changeable resultant moment of the end knuckle rotating joint and the movement sequences of gripper knuckles driven by different tendons are analysed too. Then, some kinematic analysis and dynamical simulations are carried out to verify the validation of the knuckle structure and dual-tendon winding path design. At last, a prototype of the novel gripper is manufactured and some grasping experiments are carried out on multiple categories of objects, with different sizes and shapes. The experimental results show that all the objects can be clamped tightly. Compared with the traditional single-tendon-driven gripper, the novel one can achieve a more flexible grasping operation and a larger end clamping force, which are more suitable for the adaptive grasping requirements of robotic automatic sorting.

1. Introduction

In the past few decades, to meet the diverse needs of different customers, the traditional single production mode has been transformed into the intelligent manufacturing mode, which puts forward high requirements for the flexible production capacity of a production line [1]. For flexible manufacturing, it is necessary to improve the universal clamping capability for multi-category targets of industrial robot grippers [2]. With simple structure, convenient control and strong adaptive grasping ability, tendon-driven underactuated grippers have been studied for a long time and many research results have been obtained [3,4,5]. In addition, more application scenarios for tendon-driven grippers have been developed, such as industrial field defect detection [6] and agricultural fruit picking [7].

According to the literature, the underactuated grippers have been researched since the 1970s. In 1977, Hirose proposed and designed an underactuated gripper for a multi-finger tendon driver. By studying the relationship between the number of gripper knuckles and the gripping torque, the relationship between the end clamping force and the length of the driving tendon was verified at the theoretical level [8]. In 2008, Gosselin et al. [9] designed a gripper using a tandem rotatable pulley as an intermediate transmission unit. By adjusting the position of the rotatable pulley in stages, the input torque can be evenly distributed to the end of each finger, thereby minimizing the variation in the clamping force. In 2011, Odhner [10,11] designed a two-finger gripper with flexible joints and multiple drive sources, in which each knuckle is controlled by a separate drive source. Further, an algorithm is used to control the cooperative action of each driving source to realize the multi-finger cooperative grasping action, which is difficult to achieve using general grippers. Aukes et al. [12,13] increased the grasping stiffness in a gripper by adding electronic brakes at the joints of each finger, preventing the gripper from loosening or dislodging the target. In 2013, Ciocarlie et al. [14,15] added a restraining tendon and a stretching tendon to each finger and used a gradient optimization algorithm to optimize the parameters as tendon stiffness, tendon path and gripper size to enable the gripper to perform a variety of clamping actions in a larger clamping range. However, due to the single transmission path at the end clamping force, this kind of gripper cannot achieve a wide range of end clamping force adjustments. In addition, the shape memory alloy material can also be used to change the clamping stiffness of the gripper. In 2015, Firouzeh et al. [16,17] used shape memory alloy material to make the rotary joint of the gripper and adjusted the rotating joint stiffness of the gripper by changing the temperature in the shape memory alloy to achieve variable stiffness gripping. To improve the clamping accuracy of a tendon-driven gripper, Palli et al. [18] proposed a friction compensation mechanism, which can be used to eliminate the influence of position errors at the joints of the gripper on the end positioning accuracy. In addition, a variety of optimization research on the structural parameters has also been carried out to improve the clamping performance of tendon-driven grippers. In 2018, a genetic algorithm [19,20] was used to optimize the finger joint length, tendon winding path, guide wheel diameter and also the shape of the gripper fingertip, to meet the universal grasping requirements of more types of targets and improve the grasping stability. In 2020, Ma Tao et al. [21] designed and optimized a three-finger tendon-driven underactuated gripper, which can achieve both fingertip clamping and envelope clamping actions. In the same year, Bao Jialei et al. [22] designed an underactuated gripper based on metamorphic theory, which improved the gripping stability by making the end knuckle of the gripper completely passively enveloped. The metamorphic theory was also used by Li et al. [23] to design a three-knuckle gripper, which has two working modes. When grasping some tiny objects, the gripper works in linear parallel pinching mode and can be regarded as a two-joint finger with better stability; when grasping some larger objects, the gripper works in an adaptive grasping mode and can be regarded as a three-joint finger with larger clamping range. On the other hand, in order to expand the clamping range of a tendon-driven gripper, a length-adjustable linkage mechanism [24] is integrated between two rotatory joints of the gripper knuckle, which is controlled by an antagonistic tendon pair.

In summary, optimizing the structural parameters and the control algorithm can improve the clamping performance of existing single-tendon-driven underactuated grippers, but the simple and rigid clamping postures cannot meet the universal grasping requirement of multi-category targets in the automatic robotic sorting scenarios. Although installing additional drive motors at the gripper joints or integrating deformable mechanism into the gripper knuckles can increase the degrees of freedom in the gripper and, thus, realize complex grasping operation, this will increase the control complexity and production cost of the gripper, which is not conducive to the popular application of the gripper.

Therefore, a novel dual-tendon-driven underactuated gripper is proposed in this paper, which can achieve more types of clamping postures and larger range of end clamping force. Different from the traditional single-tendon-driven gripper, the novel gripper is driven by two independent tendons, which can be switched by forward or reverse rotation of the driving motor. Due to the different winding paths, for each driving tendon, the resultant moment of the end knuckle rotating joint is different, which will result in a different rotating direction for the end knuckle and, thereby, a different movement sequence of gripper knuckles.

The main accomplishments of this paper are listed as follows:

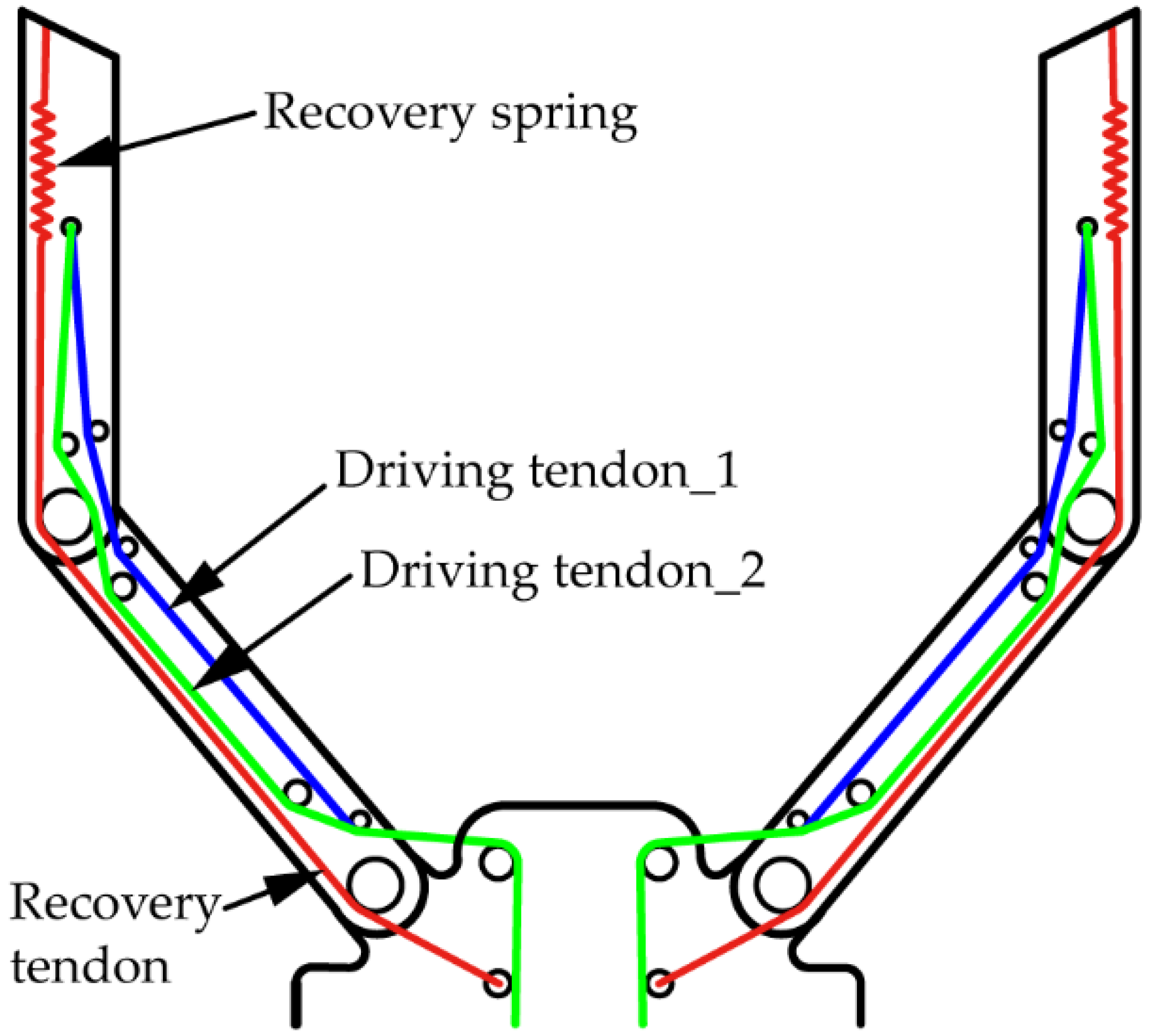
• We designed a novel dual-tendon-driven underactuated gripper, which is driven by two independent tendons with different winding paths and can achieve four kinds of clamping postures.
• We calculated and compared the resultant moments of end knuckle rotary joints driven by different tendons and analysed the conditions of knuckles moving when driven by different tendons.
• We simulated the end clamping force and movement of gripper knuckles with different clamping postures and verified the validation of the structure and tendon winding path design.
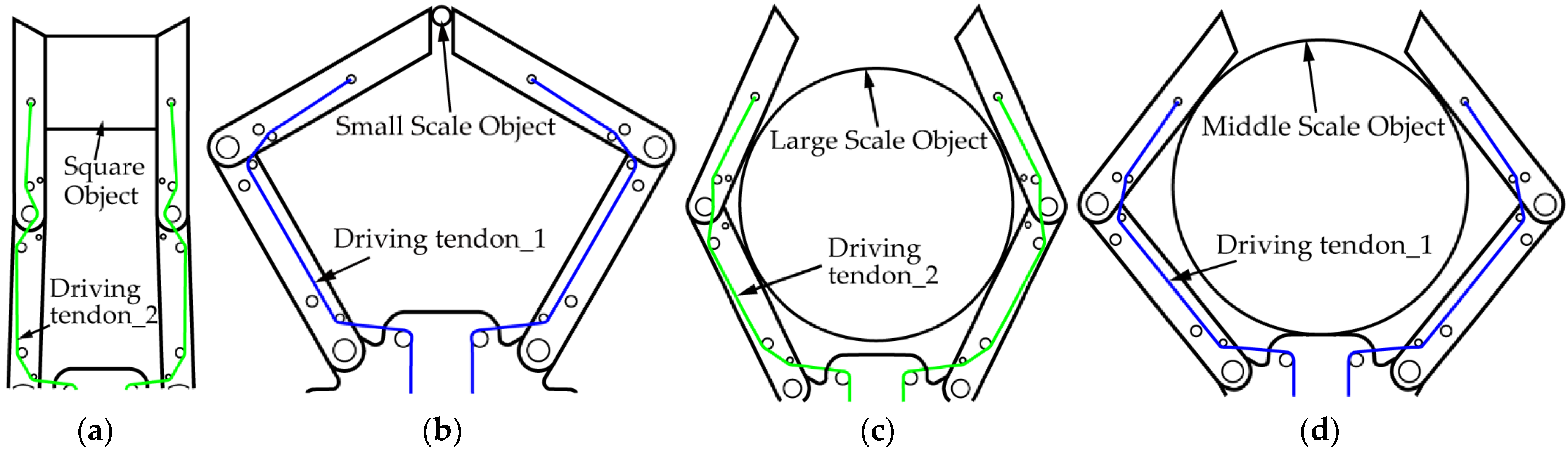
• We manufactured a prototype of the novel gripper and conducted some grasping experiments. The experimental result shows that four kinds of objects can be clamped tightly by the gripper proposed in this paper.

2. Gripper Structure Design

2.1. Calculate the Degrees of Freedom

Since the structure of the two-finger gripper is completely symmetrical from left to right, it is convenient to analyse and calculate the degrees of freedom for only the right-half part of the gripper.

As shown in Figure 1, the right-half part of the gripper consists of a frame, two mechanical knuckles and two plane rotary joints, which means that each finger of the gripper consists of one frame, two linkages and two rotating pairs, so its degrees of freedom can be calculated by the following equation:

$$Dof=3\times n-2\times P_L=2$$

(1)

where n represents the number of gripper linkages (frame is also considered as one linkage) and P_L represents the number of rotating pairs.

Since the gripper is driven by only one motor, the gripper designed in this paper is a typical underactuated mechanism.

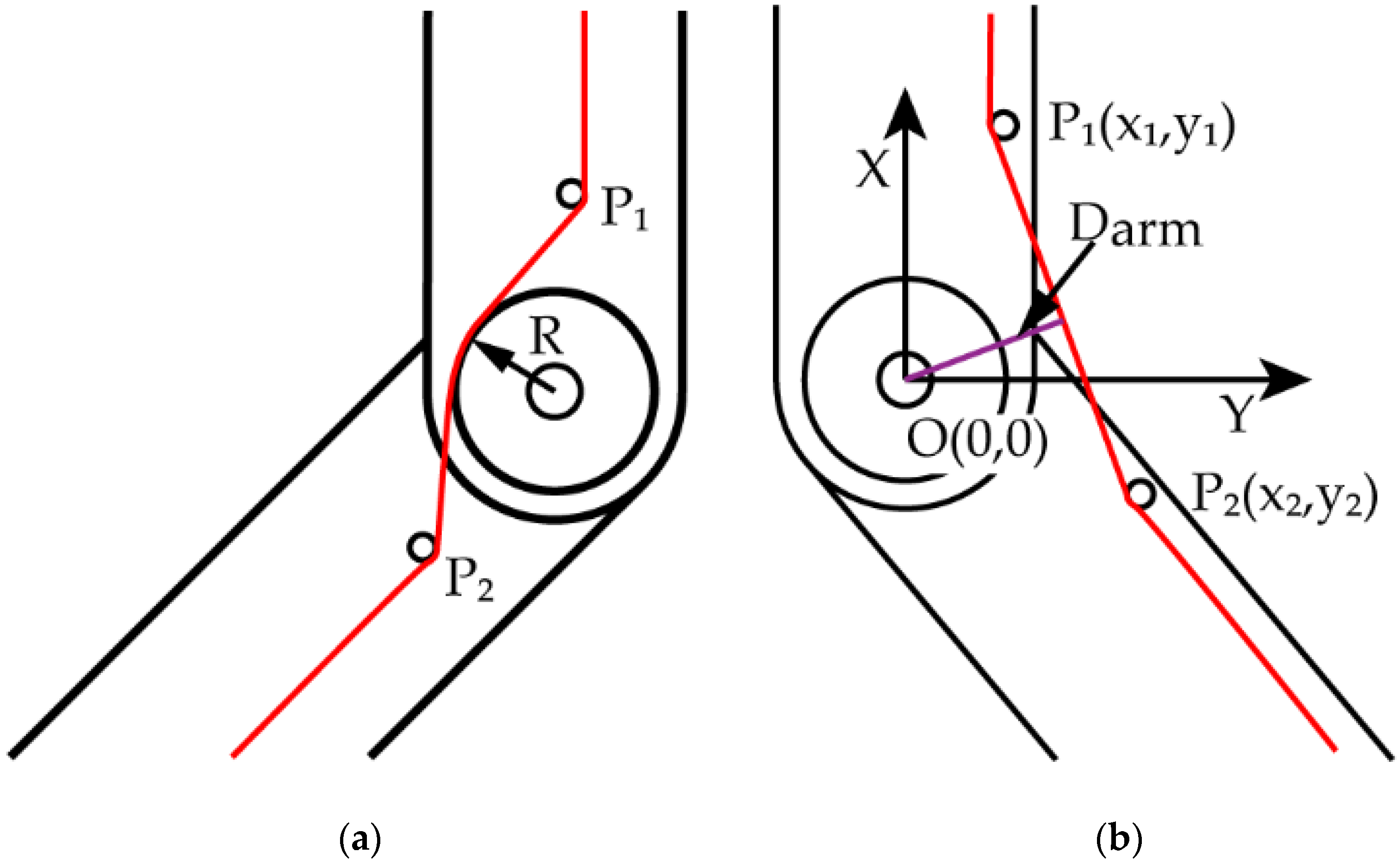
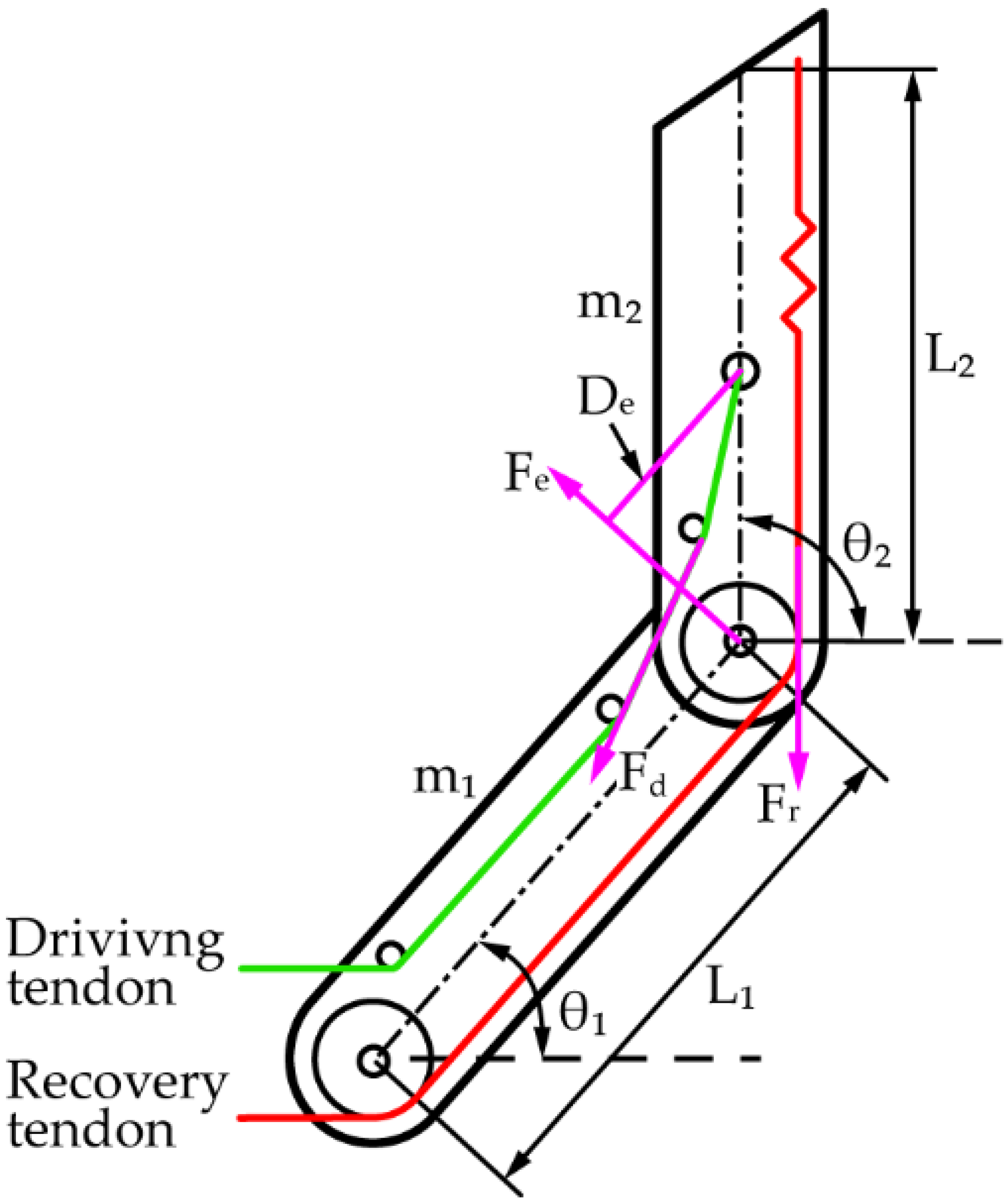
2.2. Calculation of the Moment Acted on the Joint

Each knuckle is driven by the resultant moments of the rotary joint, which is generated by the driving tendon. Therefore, to study the clamping postures of the tendon-driven gripper, it is necessary to investigate the mechanism of moment generation at the knuckle rotary joints.

Figure 2 shows a schematic diagram of the two contact types between the tight driving tendon and the rotary joint of the knuckles, where the red line represents the driving tendon, the black circle with radius R represents the guide wheel mounted at the rotary joint, P₁ and P₂ are the driving tendon winding points and D_arm is the moment arm of the driving tendon tension.

It can be seen from Figure 2 that the moment arm of a tendon tension varies with the contact situation of the driving tendon and guide wheel. When the driving tendon is in contact with the guide wheel, the moment arm of a tendon tension is R. When the driving tendon is out of contact with the guide wheel, the moment arm of the driving tendon can be calculated by the following steps:

The formula for the line between P₁ and P₂ is

$$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$

(2)

It can be transformed as

$$(y_2-y_1)x-(x_2-x_1)y+x_2{y}_1-x_1{y}_2=0$$

(3)

According to the distance formula from point to line, the moment arm of the driving tendon tension can be calculated as follows:

$$D_{arm}=\frac{x_2{y}_1-x_1{y}_2}{\sqrt{{(y_2-y_1)}^2+{(x_2-x_1)}^2}}$$

(4)

Above all, the value of the moment arm can be summarized as follows:

$$D_{arm}=\{\begin{array}{l}R\\ \frac{x_2{y}_1-x_1{y}_2}{\sqrt{{(y_2-y_1)}^2+{(x_2-x_1)}^2}}\end{array}$$

(5)

Therefore, the moment generated by the driving tendon tension on the joint is:

$$T=F\cdot D_{arm}$$

(6)

where F is the value of the driving tendon tension.

2.3. Force Analysis of End Knuckle at joint_2

As shown in Figure 3, the green line represents the driving tendon and the red line represents the recovery tendon. F_d, D_d, F_r, D_r represent the tension and moment arm of the driving and recovery tendons at joint_i, respectively. F_e is the reaction force of root knuckle acting on the end knuckle at joint_2.

When the gripper works normally, the driving and recovery tendons exert two opposite-direction tensions at the knuckle rotary joint. Therefore, the knuckle can rotate around joint_i (i = 1,2) in the corresponding direction according to the resultant moment, which can be calculated as:

$$T_{\mathrm{i}}=F_d\cdot D_d-F_r\cdot D_r (\mathrm{i}=1,2)$$

(7)

When the root knuckle and the end knuckle rotate together around joint_1, the moment of inertia of the whole finger can be calculated as:

$$J_t=\frac{1}{3}{m}_1{L}_1^2+\frac{1}{12}{m}_2{L}_2^2+m_2{\left(L_1\cos {\theta }_1+\frac{1}{2}{L}_2\cos {\theta }_2\right)}^2+m_2{\left(L_{1}sin{\theta }_1+\frac{1}{2}{L}_{2}sin{\theta }_2\right)}^2$$

(8)

where m₁ and m₂ represent the mass of the root and end knuckles, respectively, L₁ and L₂ represent the length of the root and end knuckle, respectively, and θ₁ and θ₂ represent the angle between each knuckle and the horizontal line, respectively.

When the root knuckle is rotating, the angular acceleration α_r can be calculated as

$${\alpha }_r=T_1/J_t$$

(9)

where T₁ is the combined torque of the root knuckle and the end knuckle at joint_1.

Without considering the end knuckle, if the root knuckle is rotating with an angular acceleration α_r, its own rotational inertia J_r and the required driving torque T_req can be calculated as below:

$$J_r=\frac{1}{3}{m}_1{L}_1^2$$

(10)

$$T_{req}=J_r{\alpha }_r$$

(11)

Therefore, the moment of the end knuckle acting on the root knuckle is:

$$T_{er}=T_1-T_{req}$$

(12)

Since the forces of the root knuckle and the end knuckle at joint_2 are reaction forces, the force acting on the end knuckle by the root knuckle can be calculated as:

$$F_e=T_{er}/L_1$$

(13)

The direction of F_e is perpendicular to the centreline of the root knuckle.

2.4. Movement Sequence Analysis

As shown in Figure 3, the end knuckle is enacted by three forces, such as F_d, F_r and F_e, which are enacted by the driving tendon, recovery tendon and root knuckle, respectively. Therefore, the rotating direction of the end knuckle is determined by comparing the magnitude of the torque T_d, T_r and T_e at joint_2, which are generated by F_d, F_r and F_e, respectively; the direction of T_d is anticlockwise and the directions of T_r and T_e are clockwise. The movement sequence of the end knuckle enacted by different resultant moment at joint_2 is analysed as follows:

• If $T_d>T_r+T_e$, the resultant moment acting on the end knuckle at joint_2 is counter clockwise. Under this condition, the movement sequence of two knuckles is: the end knuckle first rotates counterclockwise around joint_2, while the root knuckle remains stationary. When the end knuckle moves to the limit position, the relative position of the root knuckle and the end knuckle no longer changes. Then, the root knuckle and the end knuckle rotate counterclockwise around joint_1 synchronously to achieve the grasping of the object.
• If $T_d<T_r+T_e$, the resultant moment acting on the end knuckle at joint_2 is clockwise. Under this condition, the movement sequence of two knuckles is: the root knuckle rotates counterclockwise around joint_1, while the end knuckle rotating clockwise around joint_2 simultaneously, so that the relative posture of the end knuckle to the frame remains constant. When the root knuckle is in contact with the object, the root knuckle stops rotating and the end knuckle rotates counterclockwise around joint_2 until the object is clamped.

Based on the above analysis, under the premise of constant tendon tension, if two driving tendons are designed to realize two difference moment arms at joint_2, the magnitude and direction of the resultant moment at joint_2 can both be adjusted and, thereby, the movement sequence of each knuckle can also be changed.

2.5. Tendon Winding Path Design

To achieve two different driving torques at joint_2, two different tendon winding paths are designed in this paper.

As shown in Figure 4, three tendons are arranged in the gripper, of which the blue line in driving tendon_1, the green line is driving tendon_2, and the red line is recovery tendon. Different from the fact that driving tendon_2 is tightly attached to the guide wheel, driving tendon_1 is farther away from the centre of joint_2, which means that under the premise of constant tendon tension, the moment of driving tendon_1 acting on joint_2 is larger than that of driving tendon_2. The other ends of tendon_1 and tendon_2 are wound in opposite directions on the driving motor shaft, so when motor turns in one direction, one tendon tightens and the other loosens and, thereby, the driving tendons can be switched by the forward and reverse rotation of the drive motor.

Under the respective action of the two driving tendons, the gripper can perform four clamping postures, such as parallel clamping, fingertip clamping, envelope clamping and general clamping. As shown in Figure 5, the fingertip clamping and general clamping postures are achieved by driving tendon_1 and the parallel clamping and envelope clamping postures are achieved by driving tendon_2.

3. Dynamic Simulation of Gripper

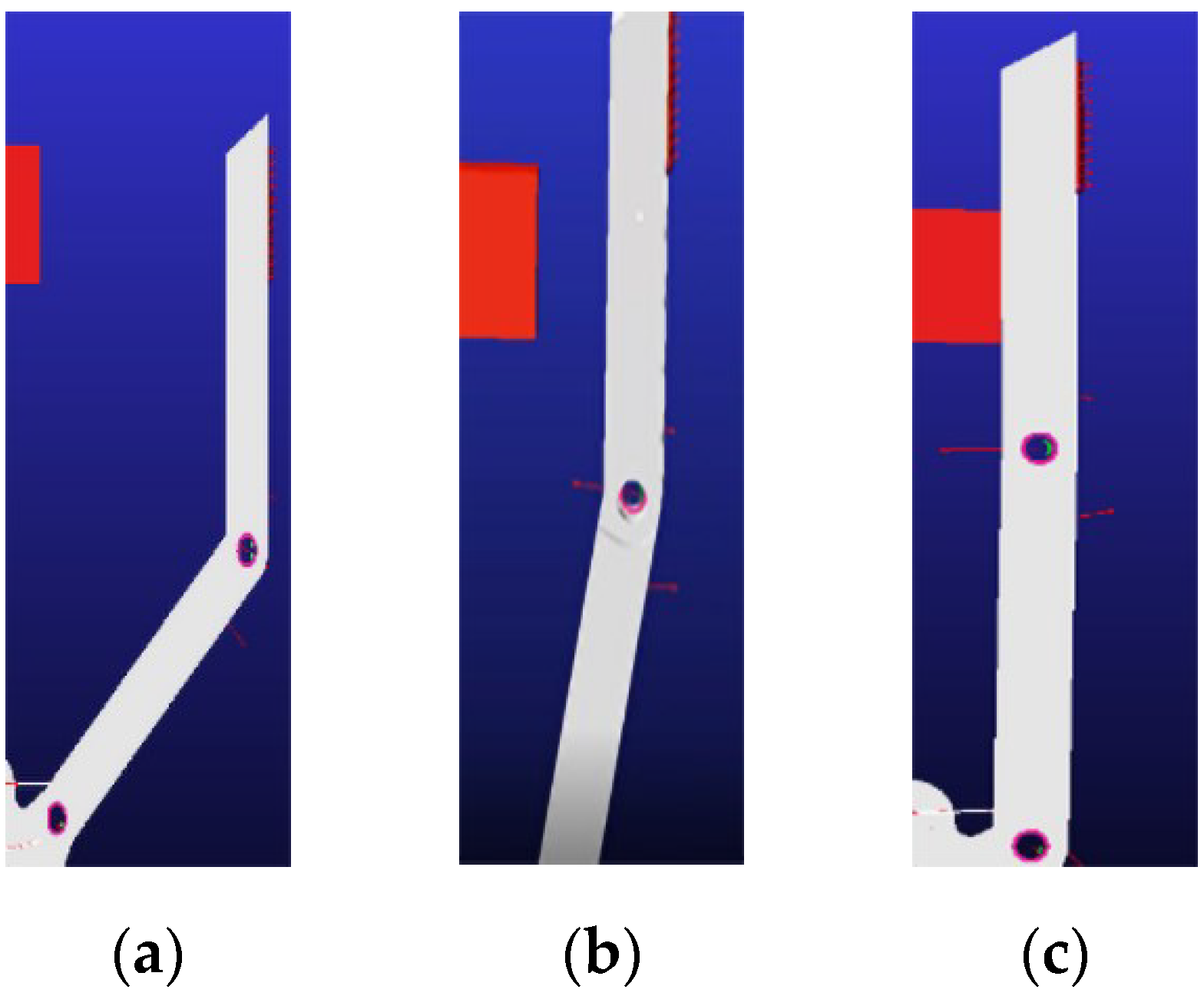
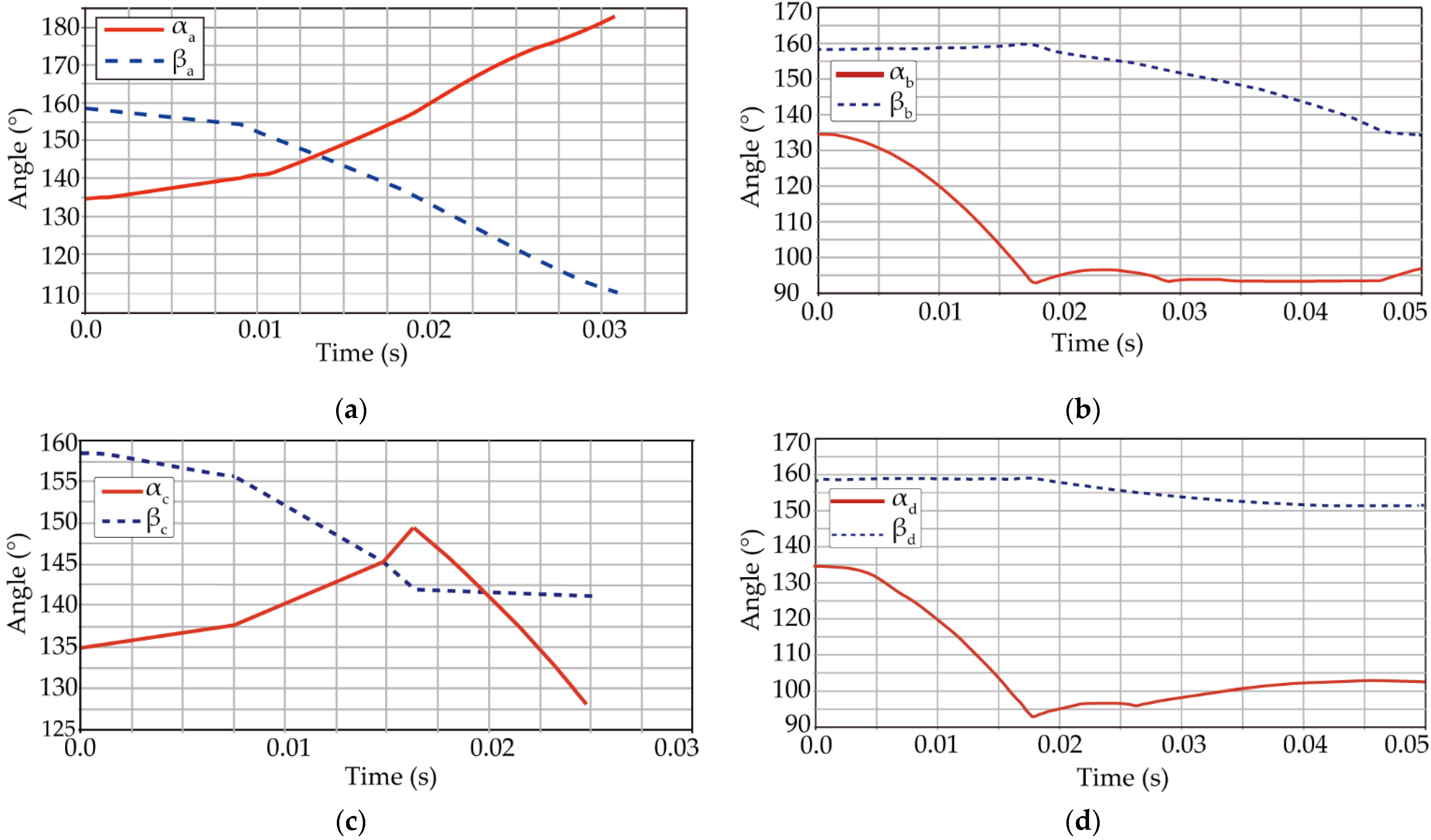
3.1. Movement Sequence Simulation

To verify the rationality of the designed driving tendon winding paths, some dynamic simulations of the knuckles’ movement sequence driven by different tendons have been carried out in this paper. As an example, the dynamic simulation of parallel clamping driven by tendon_2 is shown in Figure 6. The simulation results of four clamping postures are shown in Figure 7, where α represents the angle between the centrelines of the end knuckle and root knuckle and β represents the obtuse angle between the root knuckle and the horizontal line. According to Figure 3, α and β can be calculated as follows:

$$\alpha =\pi -{\theta }_2+{\theta }_1$$

(14)

$$\beta =\pi -{\theta }_1$$

(15)

Figure 7a shows the simulated angle curves when the gripper is driven by tendon_2 for parallel clamping. When driving tendon_2 is tightened, the end knuckle starts to rotate clockwise around joint_2, while the root knuckle rotates counterclockwise around joint_1 simultaneously, so α_a keeps increasing and β_a keeps decreasing slowly. When the end knuckle contacts the target, the root knuckle keeps rotating counterclockwise around joint_1, while the end knuckle remains stationary. Therefore, α_a keeps increasing while β_a1 keeps decreasing until the two knuckles reach their limit position, respectively, thereby, achieving tight clamping.

Figure 7b shows simulated angle curves of fingertip clamping driven by tendon_1. When tendon_1 is tightened, the end knuckle rotates counterclockwise around joint_2, while the root knuckle remains stationary, so α_b keeps decreasing and β_b remains constant. When the end knuckle reaches the limit position, the relative position between the root and end knuckles will be fixed, which means that α_b tends to be stable. As the tendon continues to be tightened, the root knuckle and the end knuckle rotate counterclockwise around joint_1 simultaneously, so β_b keeps decreasing until the target is tightly clamped.

Figure 7c shows the simulated angle curves of envelope clamping driven by tendon_2. When tendon_2 is tightened, the end knuckle starts to rotate clockwise around joint_2, while the root knuckle rotates counterclockwise around joint_1 simultaneously, so α_c keeps increasing while β_c keeps decreasing. Since the target is big, the root knuckle touches the target first, then it will stop, so β_c remain constant. As the tendon continues to be tightened, the end knuckle starts to rotate counterclockwise, which means that the angle α_c will turn to decrease, until the target is clamped tightly.

Figure 7d shows the simulated angle curves of general clamping driven by tendon_1. When tendon_1 is tightened, the end knuckle rotates counterclockwise around joint_2, while the root knuckle remains stationary, so α_d keeps decreasing while β_d keeps increasing. When the end knuckle touches the target, the clamping range formed by two knuckles will be extended due to the larger size of the target. It is specifically expressed as the counterclockwise rotation of the root knuckle and the clockwise rotation of the end knuckle. Therefore, α_d keeps increasing while β_d keeps decreasing until a stable clamping is achieved.

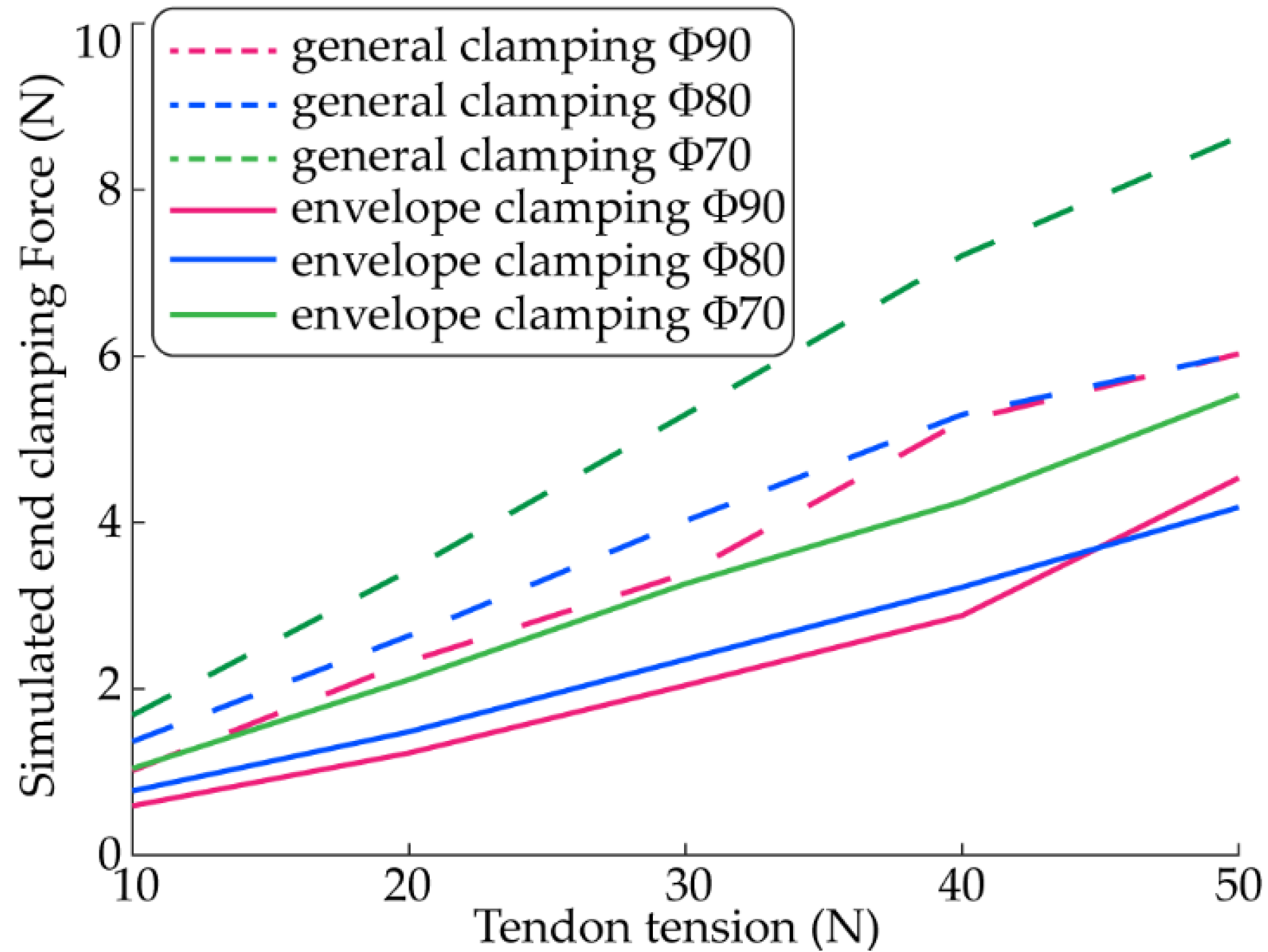
3.2. Simulation of End Clamping Force

Under the premise of constant tendon tension, the resultant moment at joint_2 can be adjusted by switching the driving tendon and, thereby, the end clamping force of the gripper can be changed too. To compare and analyse the end clamping force driven by different tendons, envelope clamping and general clamping are chosen and simulated to grasp four different sizes of objects. The simulated results are shown in Figure 8.

It can be seen from the simulation results that, for grasping a same-sized object, the end clamping forces of general clamping are generally larger than those of envelope clamping.

Therefore, it is theoretically possible to adjust the end clamping force by changing the driving tendon.

4. Prototype Experimental Testing

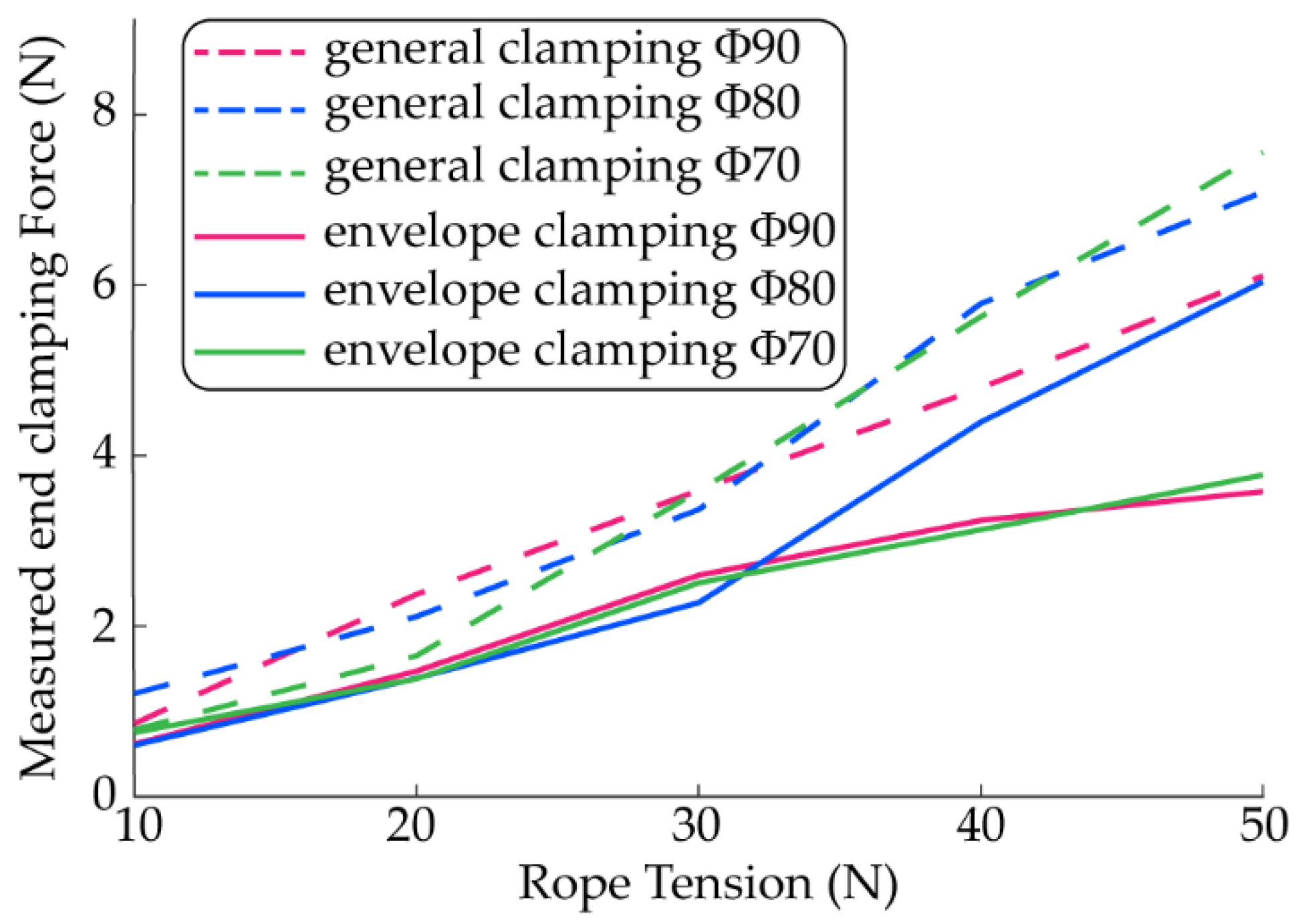
4.1. Measurement of End Clamping Force

To verify the influence of the dual-tendon winding path design on the end clamping force, an experimental platform of end clamping force measurement was built and some relevant clamping experiments were carried out.

As shown in Figure 9, the experimental platform consists of a protype of the gripper, two end pressure sensors, a digital pull force gauge, a tendon tension adjuster and several objects with different sizes. Information on the sensors and equipment used in the experimental platform is shown in

Table 1. Sensor and other equipment information on the experiment platform.

Equipment	Type
End pressure sensor	(DYHW-108, DAYSEN-SOR, China)
Digital pull force gauge	(DS2-500N, PUYAN, China)
Driving motor	(42BYG34-401A, China)

.

Similar to the simulation, when the prototype gripper grasps an object in a specific clamping posture, for each specific tendon tension, which is adjusted by the adjuster, the relevant end clamping force is repeatedly measured ten times by the end pressure sensors. The mean values and standard deviations of FoE (End Clamping Force of Envelope Clamping) and FoG (End Clamping Force of General Clamping) are listed in

Table 2. The end clamping forces measured by the sensors.

Object Size	Tendon Tension (N)	FoE (N)	FoG (N)	Increase
Φ70	10	0.76 ± 0.05	0.85 ± 0.07	11.8%
	20	1.38 ± 0.21	1.57 ± 0.13	13.8%
	30	2.51 ± 0.17	3.26 ± 0.46	29.9%
	40	3.13 ± 0.25	5.68 ± 0.74	81.5%
	50	3.77 ± 0.41	7.44 ± 0.98	97.3%
Φ80	10	0.60 ± 0.04	1.21 ± 0.13	101.7%
	20	1.38 ± 0.16	2.13 ± 0.18	54.3%
	30	2.51 ± 0.32	3.38 ± 0.27	34.7%
	40	3.14 ± 0.25	5.78 ± 0.81	84.1%
	50	3.76 ± 0.41	7.09 ± 0.89	88.6%
Φ90	10	0.61 ± 0.09	0.86 ± 0.09	41.0%
	20	1.47 ± 0.12	2.37 ± 0.21	61.2%
	30	2.59 ± 0.19	3.59 ± 0.47	38.6%
	40	3.25 ± 0.49	4.80 ± 0.43	47.7%
	50	3.58 ± 0.27	6.11 ± 0.86	70.7%

and the curves are shown in Figure 10.

It can be seen from the experimental results that, for grasping a same-sized object, the end clamping force of general clamping is larger than the envelope clamping, increasing by at least 11% and at most 101%, which is consistent with the simulation results. Therefore, it is feasible to adjust the end clamping force of the gripper by switching the tendon winding path.

4.2. Test of Grasping Objects

To test the performance of grasping objects of different sizes, a prototype dual-tendon-driven gripper (as shown in Figure 11) was fabricated by 3D printing and four kinds of objects with different shapes and sizes were selected as the grasping targets. By switching the driving tendon, all the targets are grasped tightly for at least 10 s by four different clamping postures, as shown in Figure 12. The dimension and mass of each target are shown in

Table 3. The results of clamping experiments.

Serial Number	Target	Size (mm)	Mass (g)
Figure 12a	Square box	64.42	9.13
Figure 12b	Spanners	1.47	4.31
Figure 12c	Tapes	129.90	12.49
Figure 12d	Paper rolls	57.89	155.53

.

5. Conclusions

In order to meet the adaptive clamping requirements of multi-category objects on the occasion of robotic autonomous sorting, a novel dual-tendon-driven underactuated gripper is proposed in this paper. Different from the traditional single-tendon-driven gripper, the novel gripper is driven by two tendons. Since each tendon winding path is different, the resultant moment at the rotating joint of the end knuckle enacted by each driving tendon is different, which will change the movement sequence of the two knuckles. Compared with the traditional tendon-driven gripper, the novel gripper enables more flexible grasping operations and is more suitable for the sorting of multi-category objects. In addition to that, the end clamping force of the novel gripper can also be adjusted in a larger range. When grasping some objects with similar dimensions but large weight differences, the end clamping force can be enlarged by switching the driving tendon. According to the experimental results in this paper, by switching the driving tendon, the end clamping force of the gripper prototype can be increased by at least 11% and at most 101%. The specific increase magnitude may be different due to the difference in friction and structural assembly process in another experiment platform.

Although the novel gripper proposed in this paper performs well in the laboratory environment, it still has some shortcomings and limitations. The existing problems will continue be researched in subsequent studies:

• Although the resultant moment at the rotating joint of the end knuckle can be adjusted by switching the driving tendon, this kind of method is a little discrete; a more stepless adjusting method should be studied in the future.
• The end clamping force of a tendon-driven gripper can also be enlarged by optimising the geometric parameters of the gripper, such as the length and width of the knuckle, which is another area of research and has already been studied for some time.
• The end clamping force of a tendon-driven gripper is hardly influenced by the magnitude of a tendon tension; slight fluctuations in tendon tension may cause a sudden release by the gripper. Therefore, a kind of anti-loosen mechanism should be added to the gripper.
• The grasping operation of the gripper is not smooth enough, so it is necessary to improve the rotating joint structure of each knuckle to improve the clamping efficiency.