1. Introduction
As an important element of mechanical structures, the multi-link mechanism has the advantages of a simple structure, good reliability, and strong bearing capacity. In recent years, it has been the focus of mechanism research and has attracted the attention of many scholars. In the analysis of such a mechanism’s motion, it is usually assumed that a kinematic pairing is ideal. However, in practice, the clearance of kinematic pairing is inevitable due to tolerances in the design, manufacturing defects, and wear. Clearances will increase certain additional and uncontrollable degrees of freedom, cause additional wear, and impact various elements in the kinematic pair. It will also lead to the deterioration of dynamics performance or adverse vibrations and will mean that the dynamics behavior of the actual mechanism with clearance will deviate from the dynamics behavior of an ideal mechanism. The degree of freedom brought by a clearance joint is a significant source of error [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11]. Aiming at the problems of low stability and intensified wear during the operation of a mechanism containing clearances, according to its kinematic and dynamics characteristics, we addressed this problem through the dynamics optimization of a mechanism with a clearance. The vibration and noise caused by poor clearance can be effectively reduced and the stability and reliability of the mechanism could be improved [
12,
13,
14].
How to reduce the adverse effects of clearances on dynamics performance and improve the accuracy and performance of mechanisms is a hot topic. Many scholars have carried out a series of theoretical studies examining this problem. Based on the continuous contact model, some scholars have carried out the dynamics optimization of a four-bar mechanism containing revolute clearances [
15,
16]. Sardashti et al. [
15] assumed a four-bar mechanism, considering a single clearance as an example, and proposed an algorithm based upon particle swarm optimization to solve the optimization problem. Erkaya et al. [
16] regarded kinematic clearance as a massless virtual rigid bar; they established a dynamics equation for a four-bar mechanism, considering revolute clearance using the Lagrange equation, and optimized the parameters at joint clearance with a genetic algorithm. Based on the Taguchi method, Meng et al. [
17] considered clearance, the pin radius, and the friction factor as controllable factors and used collision force as the noise factor to optimize the transmission mechanism of a high-voltage circuit breaker and found that the three controllable factors can effectively affect the dynamics performance of the mechanism. Bai et al. [
18] established the normal contact force at clearance by using a nonlinear spring-damper model. The influence of the clearance of a kinematic pair on the dynamics response of a satellite antenna mechanism is studied, and a dynamics optimization method for a satellite antenna driving mechanism with clearance was proposed. Li et al. [
19] analyzed the dynamics response and optimized design of a planar rigid–flexible-coupling crank-slider mechanism with double clearances, established a motion differential equation based on the absolute node coordinate method, and studied the effects of a single clearance joint, double clearance joints, and harmonic drive on rigid body dynamics and the rigid–flexible coupling dynamics of the mechanism. Varedi et al. [
20] proposed an optimization methodology for a crank-slider mechanism containing clearances based on the particle swarm optimization algorithm, which reduces or eliminates the collision force at the clearance joint by optimizing the mass, centroid position, the moment of inertia of the connection rod, and the mass of the end effector. Sun et al. [
21] took a crank-slider mechanism as an example to carry out kinematic analysis and a robust optimization design for a mechanical system containing clearances and proposed a prediction methodology, based on the Baumgarte method and confidence region methodology, to analyze the motion error of a mechanical system. In order to improve the pointing accuracy of a satellite antenna, Ding et al. [
22] took the deployment mechanism of a plate satellite antenna as the research object, studied the influence of revolute clearance on pointing accuracy, proposed an analytical method of block modeling using the matrix method, optimized the model based on the particle swarm optimization algorithm, and obtained an optimal solution with a specific configuration. Li et al. [
23] optimized the dynamics of the actuator of a multi-link articulated high-voltage circuit breaker with clearance, using the selected clearance size as a design variable. Daniali et al. [
24] proposed a comprehensive optimization methodology for the kinematic optimization and dynamics optimization of a four-bar mechanism while considering clearance at the same time, which can reduce the collision of a clearance pair in terms of the dynamics response of the whole mechanism by modifying the mass distribution of the rod, and solved this highly nonlinear optimization problem based upon particle swarm optimization. Ahmedalbashir et al. [
25] added a spring between the connecting rod and the swing rod to improve the dynamics responses of a planar four-bar mechanism containing clearances and improve the mechanism’s dynamics performance.
Dynamics accuracy refers to the accuracy changes of a mechanism under the influence of working conditions. The reliable performance of dynamics accuracy could better reflect the actual situation of the mechanism. However, research on the dynamics reliability of a mechanism with clearance has mainly focused on a simple mechanism containing a single clearance, while studies on the reliability of the kinematic and mechanical characteristics of a complex mechanism with multiple clearances were relatively few. Gao et al. [
26] analyzed the reliability and sensitivity of a crank-slider mechanism considering multiple clearances and optimized the design of a mechanism containing several clearances, based on an analysis of the design’s reliability and sensitivity. Zhang et al. [
27] proposed a novel time-dependent reliability methodology to forecast the probability of meeting specific motion requirements within a predetermined time. Through the analysis of many kinds of four-bar mechanisms, the effectiveness of this method was proved. Wei et al. [
28] introduced a reliability sensitivity analysis of time-varying parameters and a global reliability sensitivity analysis. An envelope function methodology and the first-order approximation of a motion error function were introduced to effectively estimate several time-dependent PRS and GRS indices. The importance and effectiveness of the proposed methodology were proved with a four-bar mechanism and automobile rack and pinion steering linkage. Zhang et al. [
29] took a multi-loop Hoberman radial linkage as their research object, its reliability having been analyzed. Based on the effective length model, the influence of universal joint clearance on dynamics response was established, and the position deviation of the mechanism was analyzed with an improved loop increment methodology. A reliability evaluation model based on the probability density function was established, and the structure of the mechanism was optimized. Chen et al. [
30] took a 2-
DOF seven-bar mechanism containing clearances as an example, for which a dynamics accuracy and reliability model was established based upon the stress strength interference theory. The influences of the different parameters on dynamics accuracy and the reliability of the mechanism were studied. Yu et al. [
31] built a comprehensive reliability analysis model of a rolling bearing. By modeling the probability distribution of an actual bearing’s working clearance and studying the life factor, the reliability of the results was analyzed. Zhao et al. [
32] analyzed the reliability of a slider’s displacement of a crank-slider mechanism containing clearance and friction and investigated the effect of different random parameters on the reliability of the slider’s displacement.
To sum up, the working of a clearance pair leads to a series of problems, such as poor stability, high noise levels, and intensified wear of the mechanism, which reduces the stability, accuracy, and service life of the mechanism. Therefore, it is urgent to optimize the dynamics of a mechanism with clearance to reduce the negative impact of clearance on the dynamics response of the mechanism. However, the published research on the optimization of a mechanism with clearance mainly focuses on a simple mechanism with a single rotating-pair clearance or on improving the performance of the mechanism by adding springs. There are relatively few studies on the dynamics optimization of a complex mechanism with multiple clearances. The center track at a clearance joint reflects the real motion track of the shaft in the bearing, including their function in free flight mode, continuous contact mode, and impact mode, which directly determines the mechanism’s dynamics performance. It is necessary to optimize and improve the dynamics performance of a multi-link mechanism with multiple clearances by reducing the difference between an actual center track and an ideal track, so as to reduce the adverse impact caused by clearance. Clearance exists in almost all motion mechanisms and has a significant impact on motion accuracy. Reliability analysis of a mechanism with clearance has important research significance and application value as a way to improve a mechanism’s reliability.
The main aim of this paper is to propose an efficient dynamics optimization method for a planar complex multi-link mechanism including multiple clearances. In this paper, a 2-DOF nine-bar mechanism that can be used as the main transmission mechanism of a hybrid drive multi-link press is taken as the research object. In order to improve the dynamics performance of the mechanism, based on the principle of mass distribution, a dynamics optimization model of a 2-DOF nine-bar mechanism, considering multiple clearances by using a genetic algorithm is proposed. Two optimization criteria are used to minimize the maximum acceleration of the slider and to minimize the difference between the actual central trajectory and the ideal trajectory. Based on the optimization results, the nonlinear characteristics before and after optimization are analyzed via a phase diagram and a Poincaré map. The effect of dynamics optimization on the dynamics accuracy and reliability of the mechanism are also analyzed.
The main structure of this paper is as follows. The clearance model is built in
Section 2. The dynamics optimization model of the mechanism, containing clearances, is built in
Section 3. The dynamics accuracy and reliability model of the mechanism, including the clearances, is established in
Section 4. In
Section 5, the effects of optimization on the dynamics responses and dynamics accuracy and reliability of a mechanism with clearances are analyzed. A test platform was built to study the dynamics of the mechanism when incorporating clearances. Our conclusions are presented in
Section 6.
In view of the adverse effect of the clearance of the kinematic pair on the dynamics response of the mechanism, based on the genetic algorithm, this paper proposes two different dynamics optimization modeling methods for a multi-link mechanism with multiple clearances. Two optimization criteria are used to reduce the influence of clearance on the mechanism, which are to minimize the maximum acceleration of the slider as the optimization objective function and to minimize the difference between the actual center trajectory and the ideal trajectory as the optimization’s objective function. According to the optimization results, it was found that when the optimization’s objective function is to minimize the difference between the actual trajectory and ideal trajectory, the optimization effect is stronger than that when the optimization objective function is to minimize the maximum acceleration of the slider. The results show that the peak and vibration frequencies of dynamics response are significantly reduced. Based on the optimization results obtained by taking the minimum difference between the actual center trajectory and the ideal trajectory as the optimization objective, the nonlinear characteristics and dynamics accuracy and reliability before and after optimization were analyzed. The results show that optimization improves the nonlinear characteristics and reliability of the mechanism and also makes the mechanism more stable.
2. Establishment of the Clearance Model
A clearance model of a revolute pair is shown in
Figure 1.
R1 and
R2 are the radii of the bearing and shaft, respectively. The eccentricity vector of dry friction clearance can be written as:
where
and
are the position vectors of the centroid of the shaft and the bearing of the dry friction revolute clearance joint in the fixed coordinate system, respectively.
The unit vector of the eccentric vector is:
The embedding depth of clearance of the rotating pair can be expressed as:
where
is the clearance value,
,
represents the magnitude of eccentricity vector of dry friction revolute clearance joint, and
.
Due to the clearance of the revolute pair, according to the geometric relationship between the bearing and shaft, motion states between the shaft and bearing are divided into the free flight state, continuous contact state, and impact state, as shown in
Figure 2.
The criteria for collision between elements in the revolute clearance are as follows:
When the embedding depth
, there is no collision between the shaft and bearing, and they are in free flight mode, with a contact force
. When the embedding depth
, the shaft and bearing collide with each other and they are in impact mode, so that the contact force
. When the embedding depth
, the shaft and bearing are in continuous contact mode, with a contact force
. The change in contact status could be further detected as:
When , and , at this moment, the motion state at the clearance joint changes from a free flight state to an impact state. When , and , at this moment, the motion state at the clearance joint changes from an impact state to a free flight state.
The position vector of the collision point can be expressed as:
When the bearing collides with the shaft, the speed at the contact point is:
where
.
The Lankarani–Nikravesh model (L–N model) is a nonlinear viscoelastic model that is suitable for general mechanical contact and collision problems, especially when the coefficient of restitution is high and the energy dissipation in the collision process is relatively small. In addition, the model considers not only energy loss but also the material properties, local elastic deformation, collision speed, and other factors. This model has the advantages of convenient calculation, a fast convergence speed, and so on. It is widely used in the study of the dynamics of mechanisms with clearances [
2,
18,
26,
33,
34]:
where
,
,
and
are the Poisson’s ratio,
and
are the elastic modulus,
is the recovery coefficient, and
is the initial impact velocity. When
,
and
, the time of collision is between
and
and the impact velocity at time
is
.
A modified Coulomb friction model is used for tangential friction [
2,
13,
27,
35,
36]:
where
is the friction coefficient and
is the dynamics correction coefficient, and
.
3. Dynamics Optimization Model of a Mechanism with Clearances
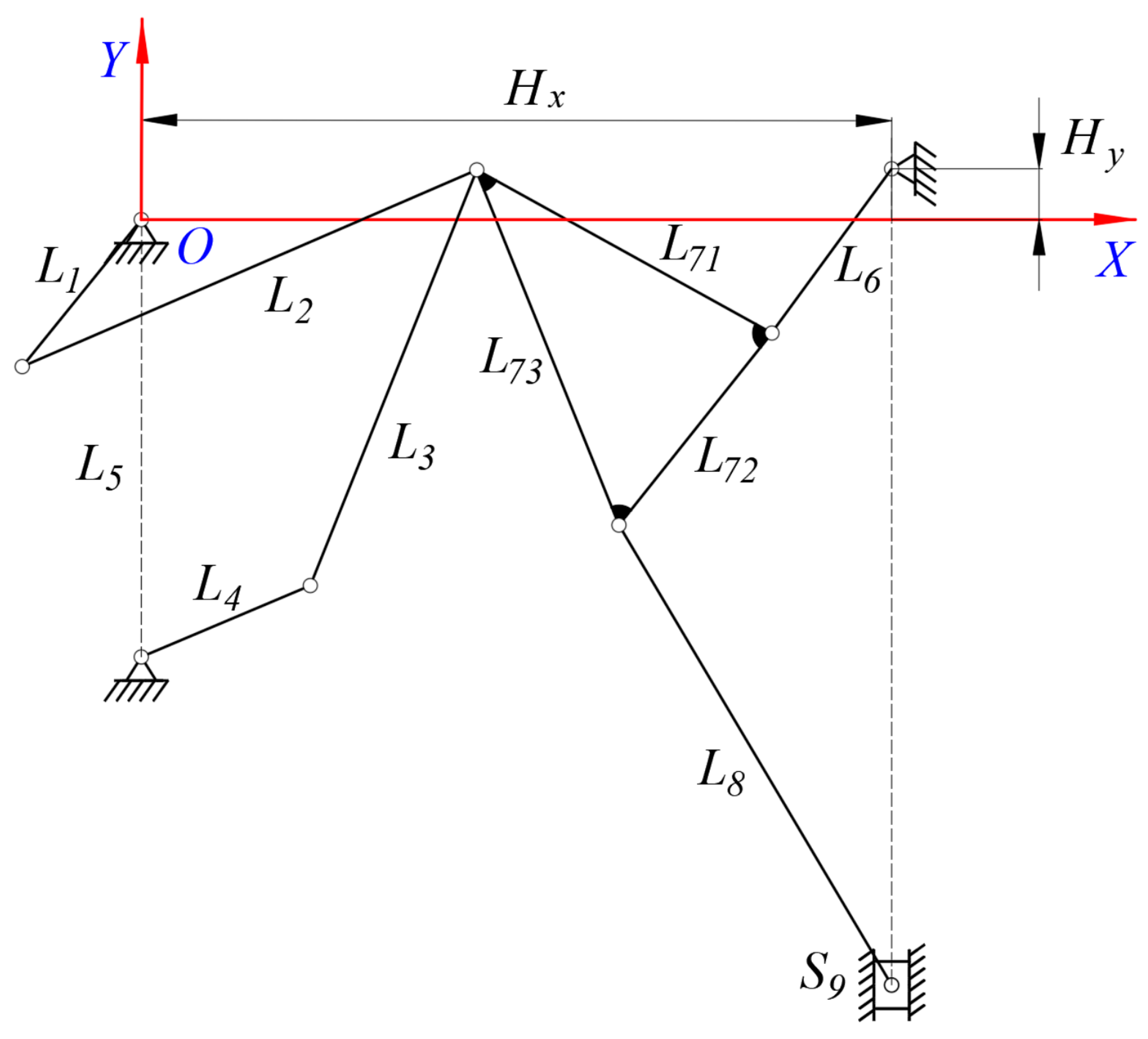
The diagram for a 2-
DOF nine–bar mechanism is shown in
Figure 3. The 2-
DOF nine–bar mechanism is composed of crank 1 (
L1), rod 2 (
L2), rod 3 (
L3), crank 4 (
L4), frame 5 (
L5), rod 6 (
L6), a triangle plate 7 (
L71,
L72,
L73), rod 8 (
L8), and a slider (S
9). It is known that the mechanism has eight movable members (crank 1, rod 2, rod 3, crank 4, rod 6, triangle plate 7, rod 8, and the slider) and one fixed member (frame 5). The revolute pair and translational pair are lower pairs; the number of lower pairs in this mechanism is 11. According to the calculation formula for the degree of freedom (
DOF), the
DOF of this mechanism is:
where
is the
DOF of the mechanism, n is the total number of moving components of the mechanism,
PL is the number of lower pairs, and
PH is the number of higher pairs.
It can be seen that the DOF of the mechanism is 2. When the mechanism has two drives, the mechanism has a unique motion; that is, the slider makes a reciprocating linear motion along the guide rail. The 2-DOF nine–bar mechanism has the following positive motion characteristics, such as the low and stable running speed of the slider at the bottom in the dead center, rapid return characteristics, good flexibility, the strong bearing capacity of the mechanism, etc. This 2-DOF nine–bar mechanism could be effective when applied to the main transmission mechanism of a hybrid drive multi–link mechanical press.
Since the clearance of the revolute pair
A is between crank 1 and rod 2, and the clearance of the revolute pair
B is between crank 4 and rod 3, the impact forces at clearances
A and
B directly affect the dynamics of the mechanism. Consequently, this paper focuses on the influence of revolute pair clearances
A and
B on the mechanism. A structural diagram of the 2-
DOF nine-bar mechanism with revolute clearances is shown in
Figure 4.
3.1. Design Variable
Since clearances
A and
B are located on two separate driving components, the end effector directly affects the motion characteristics of the whole mechanism, and the parameters of rod 2, rod 3, and the slider are selected for optimization. Mass, the centroid position, and the moment of inertia are important factors determining the mass distribution of components. Because rods 2 and 3 are long bars, the mass, the center of mass position, and the moment of inertia of the rods will affect the dynamics of the mechanism. Therefore, it is necessary to optimize mass, centroid position, and the moment of inertia of rods 2 and 3. As an end effector, the slider directly affects the motion characteristics of the whole mechanism, so it needs to be optimized. Because the slider moves in translation within the guide rail, its moment of inertia has little effect on the dynamics response of the mechanism. Compared with rods 2 and 3, the length of the slider is relatively short, resulting in the relatively small influence of its center of mass position on the dynamics of the mechanism. Therefore, the quality of the slider is selected as the optimization design variable. To sum up, taking the mass, centroid position, and moment of inertia of rod 2 and rod 3 and the slider’s mass as the optimization design variables:
3.2. Constraint Conditions
The constraints of the dynamics optimization model are:
where
XcU and
XcL are the upper and lower limits of the optimized design variables. The value ranges of
XcU and
XcL are shown in
Table 1. Among them, the lower limit of component quality is half the size of the original quality, and the upper limit of component quality is twice the size of the original quality. The upper limit and lower limit of the centroid position of the member are taken as the limit positions of the member, respectively. The lower limit of the moment of inertia assumes that the rotating shaft passes through the center of mass of the rod, and the upper limit of the moment of inertia assumes that the rotating shaft passes through the end point of the rod [
20,
33].
3.3. Objective Functions
3.3.1. Optimize the Maximum Acceleration of the Slider
As the end effector of the 2-
DOF nine–bar mechanism, the kinematic characteristics of the slider have important research significance. Acceleration is a bridge connecting kinematics and the dynamics of the mechanism, which is closely related to the force of the system. At the same time, the peak value of the slider’s acceleration intensifies the vibration due to the surge of its clearance value. Therefore, it is of great practical significance to optimize the maximum acceleration of the slider. The objective function of the optimization design is to minimize the maximum value of the slider’s acceleration; the specific expression can be expressed as:
where
is the slider’s acceleration. Here,
, which is the maximum of all the absolute values of slider acceleration.
3.3.2. Optimize the Central Trajectory at the Clearance Joint
Due to the existence of clearance, the movement of the clearance shaft in the bearing may be random and arbitrary. Therefore, by optimizing the central trajectory at the clearance point, increasing the continuous contact state between the shaft and bearing, and reducing the generation of the collision state, the undesirable influence of clearance on the mechanism can be reduced effectively.
Taking the minimum difference between the actual center trajectory and the ideal trajectory as the optimization objective, the specific expression of the objective function can be expressed as:
where
and
are the weighing factors, and expressions of
and
can be written as:
where
and
are the components of eccentricity between the shaft and bearing in revolute joint
A in the
X and
Y directions, respectively.
and
are the components of eccentricity between the shaft and bearing in the revolute joint
B in the
X and
Y directions, respectively.
and
are the clearance sizes of joints
A and
B, respectively.
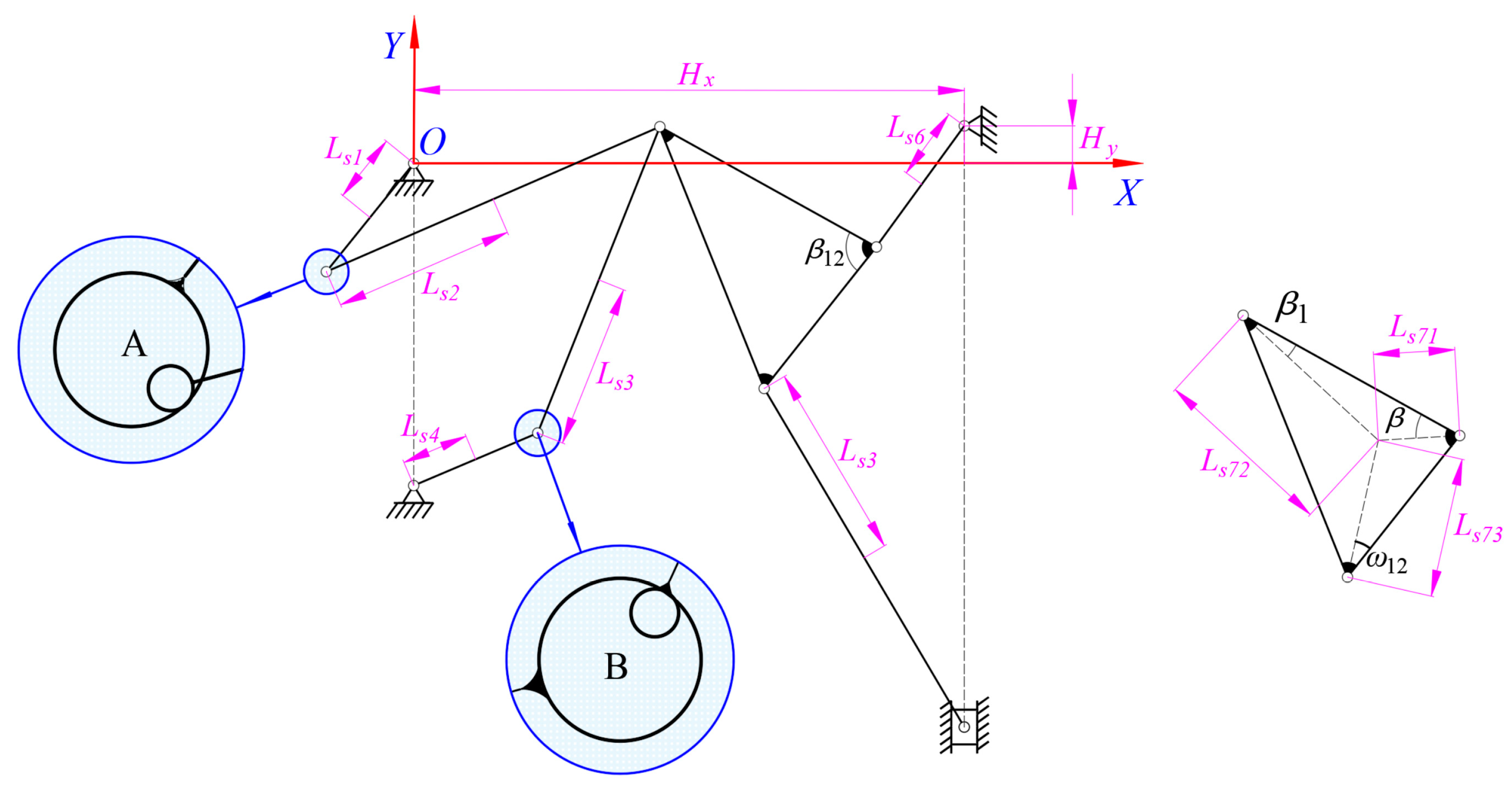
Based on the structural diagram of the mechanism with clearances shown in
Figure 1, the expressions of
and
can be expressed as:
3.3.3. Optimization Method
The genetic algorithm is a multi-objective optimization algorithm that can find an optimal solution by simulating the process of natural evolution. Firstly, the initial population is randomly generated as the candidate solution. Then, according to the fitness value, individuals are selected, crossed, and mutated. The cycle is repeated to obtain a group satisfying the conditions. Finally, the optimal solution of the optimal design variables is obtained.
The steps of the optimization are as follows
- (1)
Set the initial parameters: chromosome length, population size, maximum genetic algebra, coding type, mutation probability, crossover probability, etc;
- (2)
Randomly generate an initial population with size N, ;
- (3)
Calculate the fitness value of each individual in the population ;
- (4)
By comparing the fitness value of each individual, select individuals according to the selection operator, and keep the selected individuals with a larger fitness value until the number of the population is N;
- (5)
Optimize the combination of some genes of the surviving parent individuals, exchanging the genes at some corresponding positions of the two parent individuals according to the crossover probability, so as to produce two new individuals; the individuals that have not been crossed directly replicate into the new species group;
- (6)
The genes at some coding positions are mutated according to the mutation probability. The mutated individual replaces the original individual in the new species group. Individuals without compilation directly enter the new population. This completes an evolutionary process and selects the next generation of the population ;
- (7)
If the fitness has reached saturation or the number of iterations has reached the upper limit, it will stop. Otherwise, go to step 3.
3.4. Establishment of a Dynamics Optimization Model of a 2-DOF Nine-Bar Mechanism with Multiple Clearances
The generalized coordinates of each component are set as:
where
and
are the position components of component
i in the
X and
Y directions in the system coordinate system, and
is the rotation angle of member
i.
The 2-
DOF nine-bar mechanism has 24 generalized coordinates; the generalized coordinates of the mechanism can be expressed as:
The dynamics optimization model of the mechanism with clearances is the set of the dynamics model and the optimization design variables. A displacement constraint equation with multiple clearances, including optimization design variables, could be written as:
where the values of
β,
β1,
β12, and
ω12 are 34.11°, 22.22°, 83.24°, and 36.19°, respectively.
Hx and
Hy are 0.08 m and 0.645 m, respectively.
,
,
,
.
Velocity is a constraint equation that can be expressed as [
37]:
where
is the Jacobian matrix,
,
represents the generalized velocity vector,
, and
can be written as
The Jacobian matrix of the mechanism can be expressed as:
where
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
The acceleration constraint equations could be expressed as [
37]:
where
represents the generalized acceleration vector,
is the partial derivative of the Jacobian matrix with respect to time,
,
is the partial derivative of
with respect to time,
, and
is the vector of quadratic velocity terms.
can be written as:
where:
,
,
,
,
,
,
,
.
The system dynamics equation considering optimal design variables can be expressed as follows [
38]:
where
is the mass matrix of the system,
is the Lagrange multiplier, and
is the generalized force of the system, including gravity, external force, and external torque.
A quality matrix considering the optimal design variables of a 2-
DOF nine–bar mechanism with clearances can be expressed as:
The generalized force of a system with optimal design variables can be expressed as:
where
(
i = A,
B;
j = X,
Y) are the components of contact force in the
j directions at clearance joint
i, respectively.
and
are the collision points of the bearing and shaft in rotating pair
A, respectively.
and
are the collision points of the bearing and shaft in rotating pair
B, respectively:
where
and
are unit normal vectors of clearances
A and
B, respectively.
and
are the center points of the bearing and shaft in revolute
A, respectively.
and
are the center points of the bearing and shaft in revolute
A, respectively:
The dynamics equation of the mechanism can be obtained by solving Equations (23) and (25), and the equation expression is as follows:
In order to overcome the default of the dynamics equation, based on the Baumgarte default stability algorithm, a strong nonlinear equation with optimal design variables is solved [
39,
40,
41]:
where
α and
β are the correction parameters, and
.
Because the dynamics equation of the mechanism containing the clearances is a very nonlinear equation, it is difficult to solve the equation stably. Variable-order numerical differentiation algorithms (NDFs) are used to solve the dynamics equations, while the high-order equations are transformed into low-order equations. Therefore, the ode15s function in MATLAB is used to solve Equation (32) and convert the second-order differential equation into a first-order differential equation:
where
represents the generalized coordinates and
is the number of generalized coordinates.
6. Conclusions
The dynamics optimization research and dynamics accuracy and reliability analysis of a complex multi-link mechanism containing clearances are researched in this paper.
(1) The dynamics optimization model and dynamics accuracy and reliability model of a mechanism are built, considering the clearances.
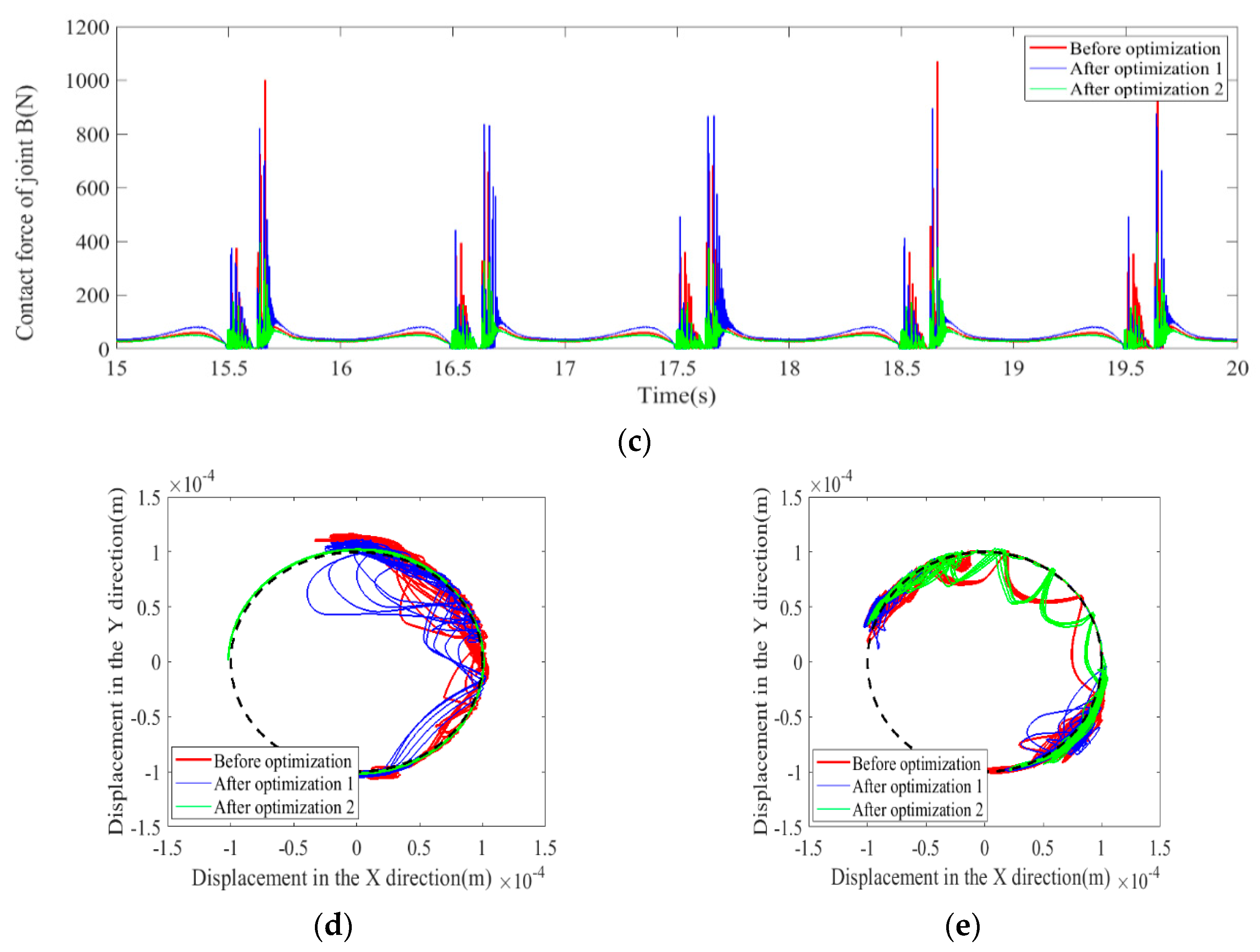
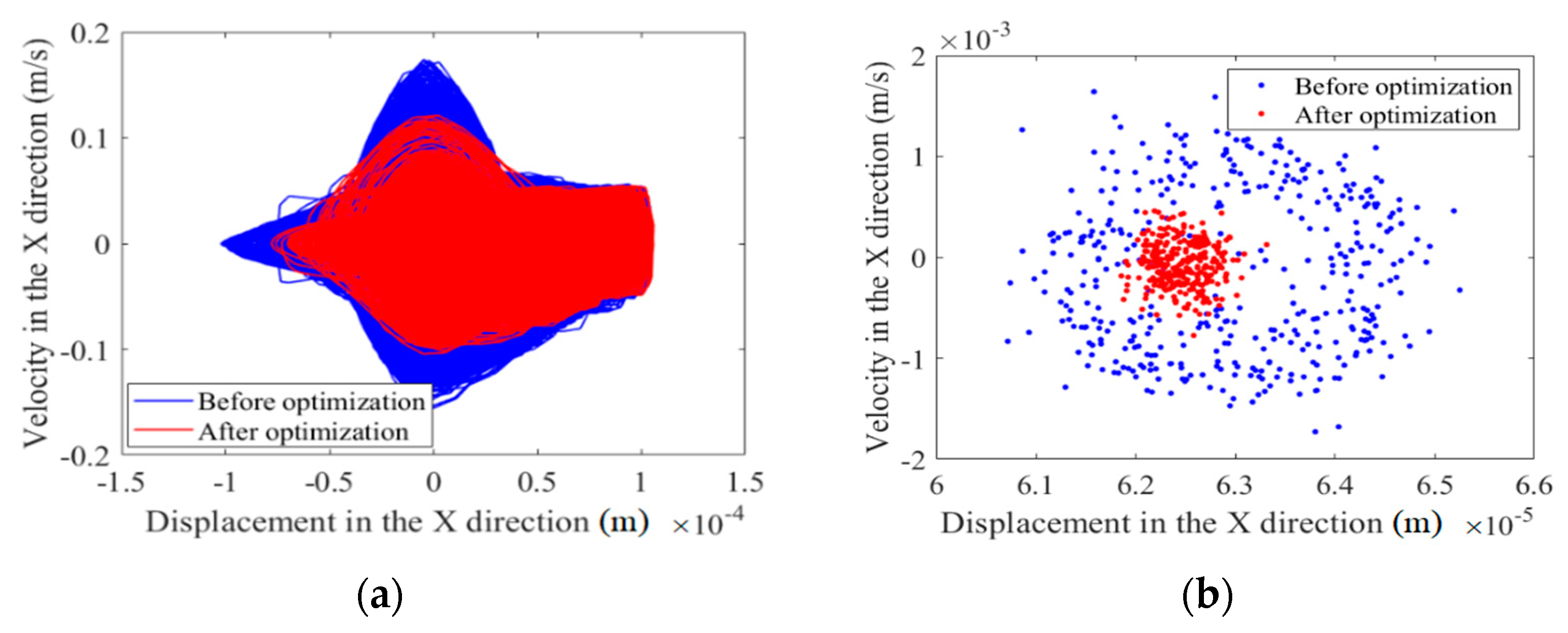
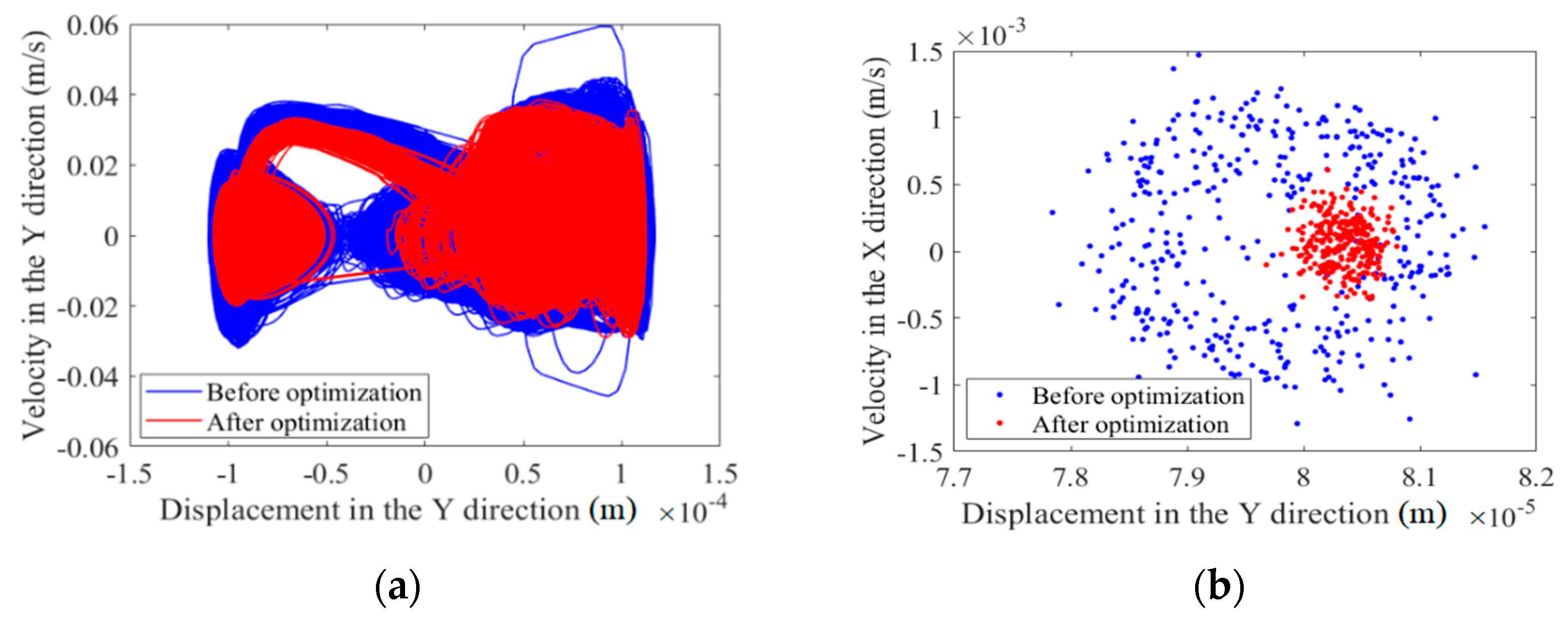
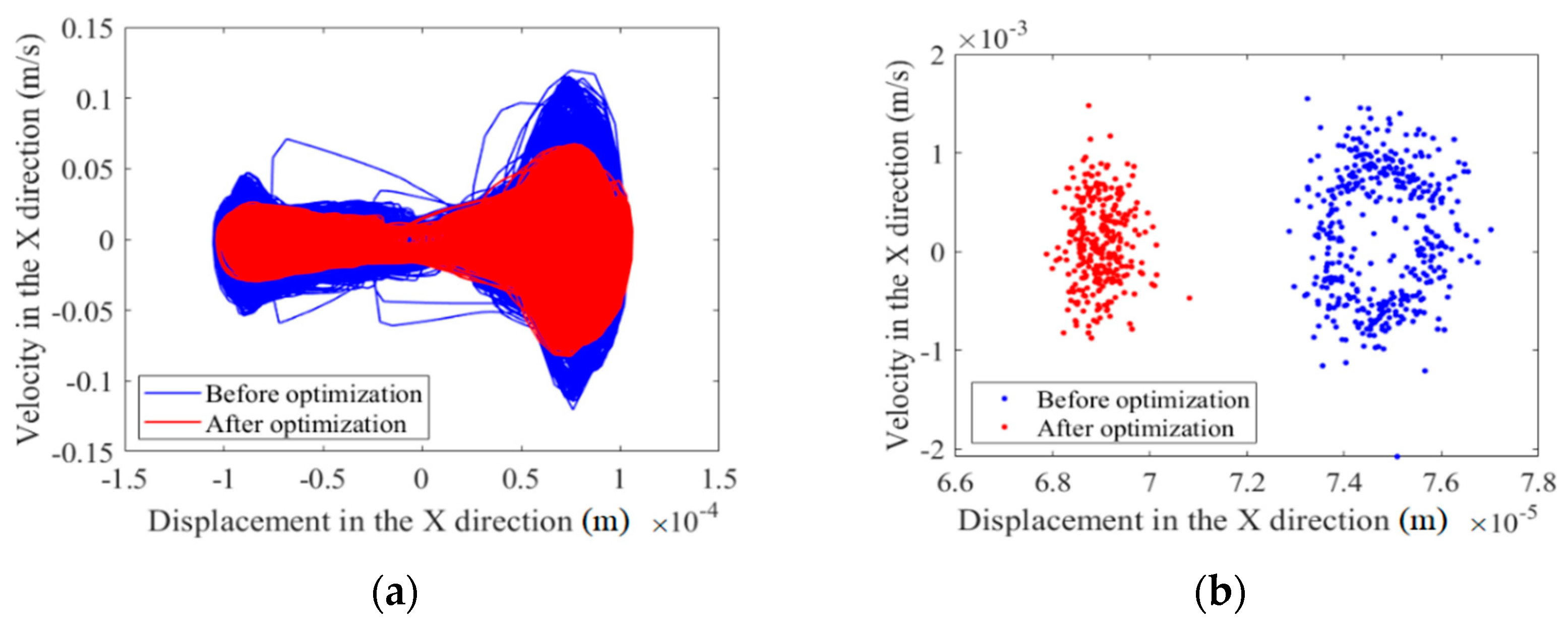
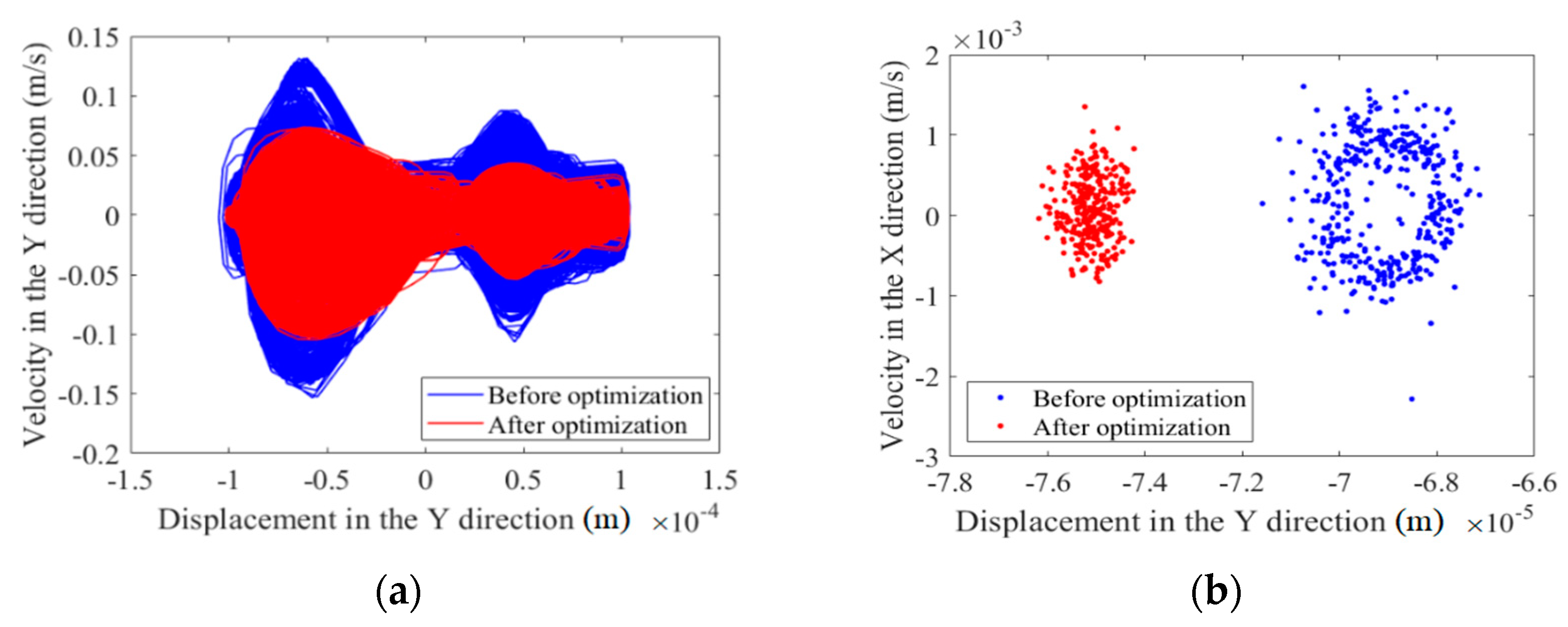
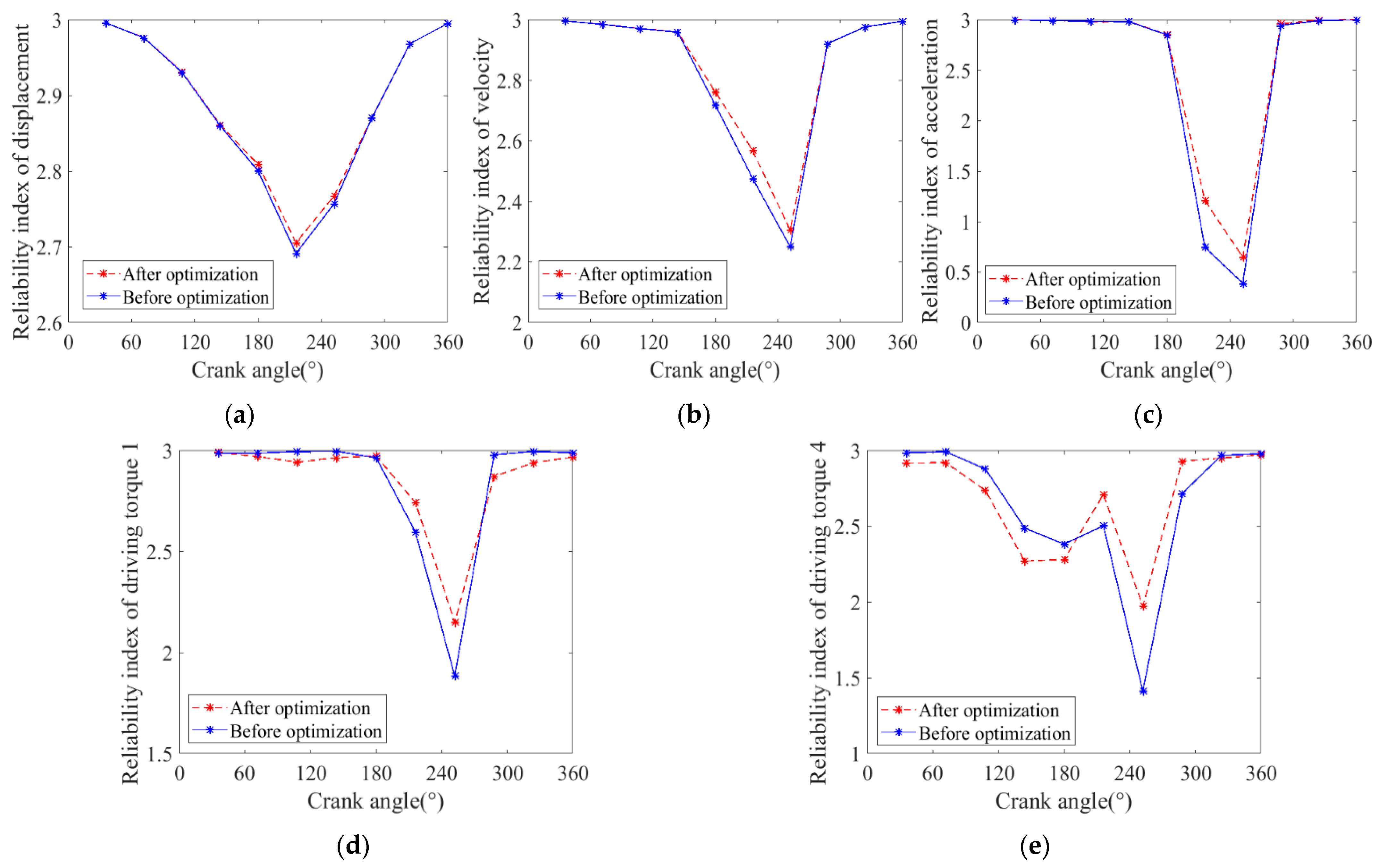
(2) The effects of two different optimization objective functions on the dynamics optimization of a mechanism with clearances are compared and analyzed, and the effects on dynamics responses and the nonlinear characteristics of the mechanism before and after optimization are analyzed. It is found that optimization effectively improves the dynamics performance of the mechanism considering clearances; it weakens the mechanism’s chaos phenomena and improves the mechanism’s stability.
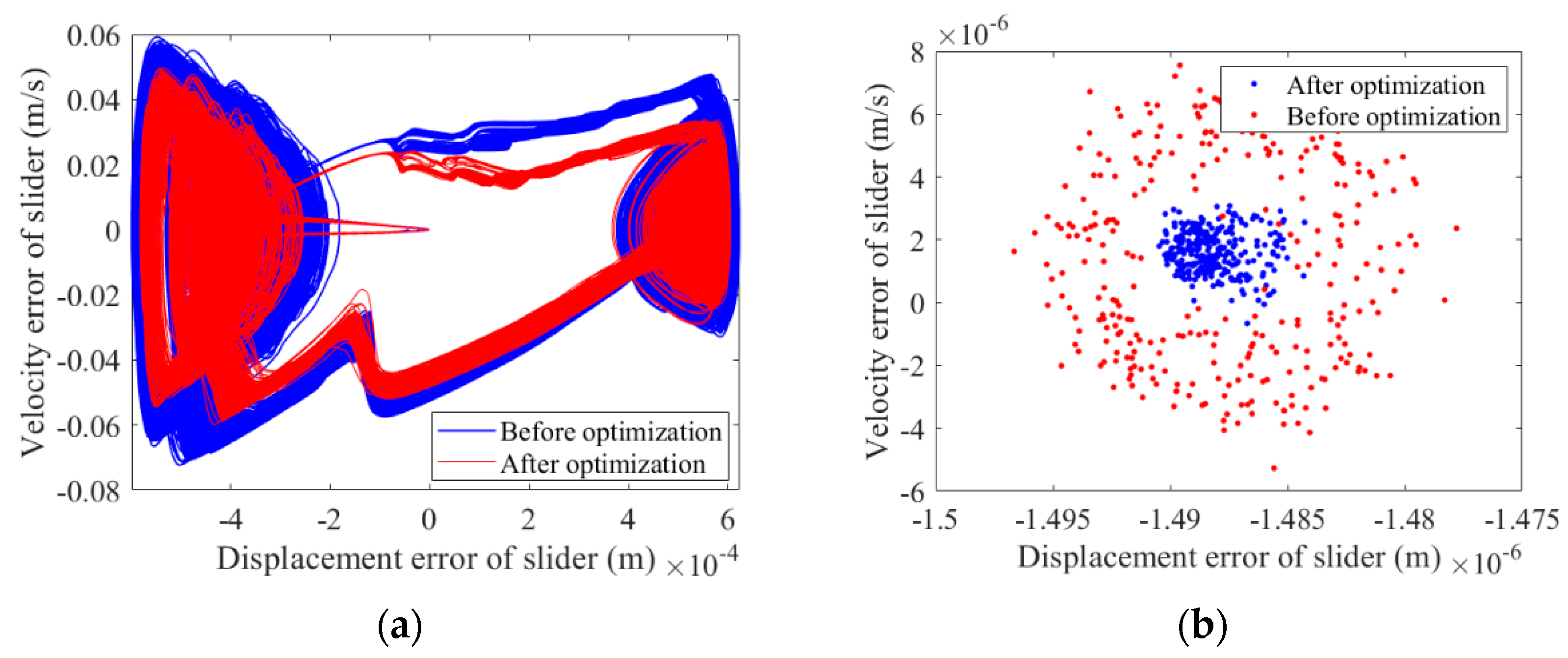
(3) The dynamics accuracy and reliability of the mechanism containing clearances before and after optimization is studied. It is found that the optimization effectively improves the reliability of the mechanism containing clearances.
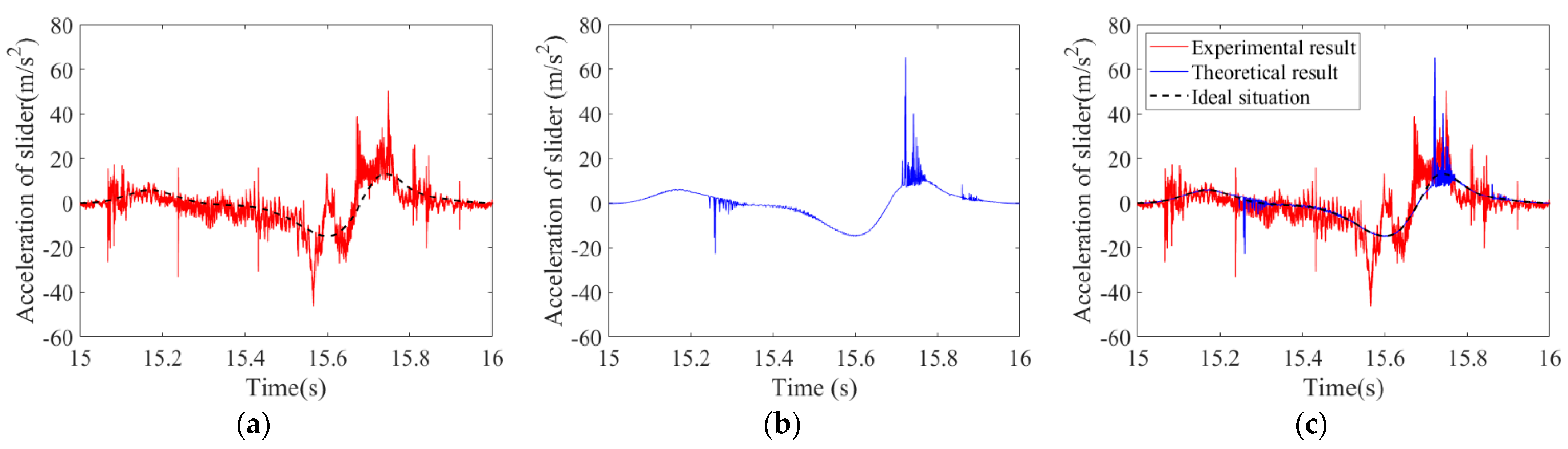
(4) A test platform was built to study the dynamics of the mechanism with clearances. The theoretical result and the experimental result are basically consistent in terms of trends, but there is a certain difference in value. The error rate between the theoretical result and the experimental result is 23.03%, which basically verifies the correctness of the theoretical results.