Study on Electromagnetic–Dynamic Coupled Modeling Method—Detection by Stator Current of the Induction Motors with Bearing Faults

Abstract

Detecting motor bearing faults by stator currents is of great importance as it improves the adaptability of measurement means to different environments and reduces the number of sensors. Therefore, many studies have been conducted to investigate bearing faults by constructing motor models, most of which have used signal models to simulate the dynamics of the bearings. However, the signal model may be exposed to the issue that the nonlinearities in the bearing operation are neglected, thus oversimplifying the coupling effects between the electromagnetic and dynamics models. Hence, a coupled electromagnetic–dynamic modeling method for induction motors based on multiple coupled circuit theory and the rotor-bearing dynamics model is proposed in this study to implement the coupled simulation of electromagnetic and dynamic models. The air gap length and rotor velocity are used as coupled parameters for the calculation of stator–rotor mutual inductance and ball contact deformation, respectively. The simulation results show that the proposed model can effectively implement the electromagnetic–dynamic coupled and reflect the bearing fault characteristics in the current signal. Experiments were conducted on induction motors with typical winding configurations under laboratory conditions. The comparison results verify the effectiveness of the proposed modeling method.

1. Introduction

Induction motor is most widely used in the field of industry with significant advantages in reliability and cost. The typical structure is shown in Figure 1. Despite induction motor itself being low cost, it is often used to drive various moving parts in industrial production activity, some of which are vital to local and even entire task chains. In the event of induction motor failure, the consequent loss can be catastrophic. According to statistics, around 44% of induction motor failure cases are related to bearings [1,2,3]. Therefore, early effective condition monitoring and fault diagnosis against induction motor bearing failures are of practical significance to ensure the stable operation of industrial production activity.

Since the 1960s, plentiful literature has been published on fault diagnosis of induction motors, covering all aspects of the process. Research results can be labeled at each stage by the basic process of “signal acquisition—signal processing—fault diagnosis”. In the phase of signal acquisition, the main types of developed signals are vibration, current, sound, temperature, magnetic flux, etc. Among them, vibration signals, as the most classic and straightforward means of transmitting fault characteristics, have received the most attention from researchers. In the phase of signal processing, the main concern is how to highlight fault characteristics and distinguish compound faults, which are generally processed in the time domain, frequency domain, and time–frequency domain. The methods adopted in the phase of fault diagnosis are generally divided into the data-driven method and model-driven method. In early days, model-driven approaches were mostly used for fault diagnosis in order to analyze fault mechanisms and characterization forms, while the situation has changed with the advent of artificial intelligence algorithms such as neural networks. In the past fifteen years, numerous research results of fault diagnosis combined with artificial intelligence algorithms have emerged with the increase in computer computing ability and the popularity of deep learning methods, forming a data-driven type of diagnostic method. Currently, data-driven methods represented by artificial intelligence algorithms have performed well in terms of fault feature fitting and diagnostic accuracy [4]. However, the lack of physical interpretability in structure as well as the insatiable data volume requirements is still the biggest obstacle to the wider application of data-driven methods, though some studies have recently explored this issue [5,6]. In contrast to data-driven methods, Randall [7] summarizes the advantages of a model-driven method represented modeling techniques. Sufficient representative signals can be generated by simulating machine faults through the model to meet the data volume requirements of the data-driven method, avoiding the economic considerations of a large number of fault tests. Furthermore, the capability of the fault model to simulate multiple fault conditions facilitates testing and comparison of diagnostic algorithms, as well as an understanding of the physical relationships that exist in the machine. Accordingly, the model-driven method based on failure mechanisms is still receiving much attention in the current field of fault diagnosis research.

Most of the current modeling methods for diagnosing motor bearing faults concentrate on the construction of a bearing dynamic model, consequently analyzing the time and frequency domain information in vibration signals in the hope of discovering the type and extent of faults of signal characteristics. For instance, Niu et al. [8] proposed a bearing dynamic model with six degrees of freedom considering the ball bearing based on the dynamic model established by Gupta [9] and discussed the influence of ball three-dimensional motion on the vibration response of bearings with ball bearing defects in the time domain and frequency domain. Considering that most bearing models can only describe single defects such as surface ripples and local defects, Liu et al. [10] proposed a ball bearing dynamic model with combined defects, including surface waviness and localized defects on the raceway. Zhao et al. [11] established a bearing dynamic model based on Hertz theory to study the influence of raceway defects on the nonlinear dynamic behavior of bearings. Yang et al. [12] used the impulse sequence model and nonlinear multi-body dynamic bearing model to explain the causes and influencing factors of bearing fault characteristics in the rotor-bearing housing system. Considering the double pulse behavior in bearing spalling faults, Wu et al. [13] analyzed the vibration characteristics of the rolling element in and out of spalling position by establishing a nonlinear dynamic model of rolling bearing, obtaining a positive correlation between the double pulse phenomenon and spalling dimension. Considering the edge characteristics of spalling defects, Liu et al. [14] proposed a new defect expansion and shape modeling, and analyzed the influence of defect edge characteristics evolution of the defect edge characteristics on the vibration of cylindrical roller bearings.

Compared with the dynamics modeling and the analysis of vibration signal, fewer studies establish the electromagnetism model against bearing fault motor and analysis of the current signal. Schoen et al. [15] analyzed the influence of vibration of faulty bearings on air gap length fluctuations, and simply defined the formula of characteristic frequency reflected by bearing faults to stator current. Boldt et al. [16] later carried out a detailed theoretical derivation of this characteristic formula and obtained an extended formula with more abundant frequency components. In the same paper, Boldt et al. also analyzed the performance of bearing faults in stator current from the perspective of torque fluctuations. Based on Schoen et al. and Boldt et al., two viewpoints of air gap fluctuation and torque fluctuation have been gradually formed in the research of motor bearing fault detection. For example, based on Schoen’s air gap fluctuation theory, Bouchikhi et al. [17] used the motor multiple coupled circuit (MCC) model under mixed eccentricity to simulate the stator current signal under bearing fault and proposed a diagnostic index based on subtraction residual energy. Ojaghi et al. [18] calculated the stator mutual inductance based on Blodt’s air gap frequency formula by winding function approach (WFA) and constructed the MCC model by using the non-uniform air gap function with bearing faults, as well as determining the characteristic frequency of bearing faults in current signals. Han et al. [19] obtained a non-uniform time-varying air gap from the rotor system dynamics model and input magnetic equivalent circuits (MEC) model to solve stator current, validated by finite element analysis and dynamic tests. Similar to Boldt, Jafarian et al. obtained the accurate representation of bearing faults in the stator current spectrum by introducing the Dirac function into the finite element (FE) model of the motor to simulate bearing faults. Based on the d-q model, Zhang et al. [20] proposed a method to estimate bearing faults by reconstructing the radial air gap displacement profile. Trajin et al. [21] paid more attention to the torque disturbance model in the case of bearing fault and proposed a bearing fault detection method based on current spectrum energy estimation. Fourati et al. [22] chose to establish an electro-mechanical model in the angular domain rather than the time domain and verified the detectability of bearing defects by simulating the torque disturbance generated by bearing local defects.

Modeling methods used in the above studies are d-q, MCC, MEC, and FE, in increasing order of complexity. Less complex models, such as the d-q model, face difficulties in accurately simulating multiple types of motor faults, whereas complex models often mean higher computational accuracy and time cost, which are detrimental to the implementation of online fault diagnosis based on a model-driven method. As Randall [7] mentioned, one of the main purposes of fault modeling and simulation is to provide a large amount of data for diagnostic algorithms, which cannot be achieved by overly complex models and too long a simulation time. A typical example is that, as commonly used methods of inductance calculation in the MCC model [23,24,25], WFA and FE methods differ significantly in the time cost of inductance calculation. In the work of Lubin et al. [26], on the same computer, it took 8 h to calculate the inductance using FEM, and only 1 min using WFA to calculate the inductance with 10× resolution. Sapena-Bano et al. [27] used the WFA and FE methods to calculate the inductance of the given parameter times 7.571 s and 3 h 9 min, respectively, and the calculation results of the two were similar. As a result, the model’s ability to balance complexity and types of faults is essential to develop online model-driven fault diagnosis problems. The MCC model, MEC model, and FE model are all capable of simulating most types of motor faults to varying degrees. The MCC model, as a lumped parameter model, has lower calculation accuracy than MEC and FE models, but its consideration of the geometry and winding layout of the motor still makes it suitable for analyzing induction motors with arbitrary winding distribution and asymmetries. Therefore, for several mechanical and electrical faults that may occur, the MCC model has a significant advantage in the ratio of the types of faults that can be simulated to the computational cost. At present, the MCC model has been widely used in the modeling of induction motor stator winding faults, rotor bar breakage, and other faults. In addition, a small number of studies focusing on bearing faults have adopted the MCC method. However, from the point of view of air gap fluctuations, the modeling studies selected for the MCC theory for bearing failures have been limited to modeling bearing failure characteristics utilizing non-uniform air gap distribution signal models [18,28]. The signal model ignores a variety of nonlinear factors in the bearing system and simplifies the dynamic response of the rotor-bearing system into a specific function, which is not conducive to reflecting the actual physical condition of motor model output. By coupled the electromagnetic model and the dynamic model, the motor system model which is more consistent with the actual electric magnetic force interaction condition can be constructed, and the simplified error of the signal model can be avoided. According to the survey, there are relatively few studies on the coupled modeling between the electromagnetic and the dynamic model, and there is no study on the application of the MCC model to the coupled model.

Consequently, based on MCC theory and the bearing dynamics modeling method, we proposed and constructed an electromagnetic–dynamic coupled model combining the motor model and the rotor-bearing system dynamics model. The electromagnetic–dynamic coupled model based on MCC is capable of simulating the dynamic response characteristics of motors under most electrical and mechanical faults with low computational cost, facilitating rapid data support for fault mechanism studies and online intelligent diagnosis methods. Firstly, the induction motor is decomposed into a generic MCC structure and described by a series of electromagnetic equations. The non-uniform time-varying air gap is introduced into the MCC when calculating the inductance parameters through the WFA. Secondly, a rotor-bearing system dynamics model was established in the radial direction of the rotor, in which the Hertzian contact and radial clearance in the bearing were considered. The non-uniform time-varying air gap is calculated from the displacement response of the rotor-bearing system, being used as the coupled parameter between the sub-models together with the rotor velocity. Finally, concurrent with the above electromagnetic and vibration differential equations, the dynamic response of the coupled model is solved by a numerical iterative algorithm. The contribution of this work is to propose a modeling approach that couples MCC with a rotor-bearing dynamic model, which has the potential to serve for mechanism analysis and data expansion in fault diagnosis. Many previous studies have validated the ability of the MCC model to simulate electrical faults such as turn-to-turn shorts, broken rotor strips, and missing phases. Therefore, this work focuses on the ability of this coupled model to reflect the mechanical fault characteristics from the kinetic model into the electromagnetic model, which is of interest to investigate the fault transmission mechanism and the detection of bearing faults by stator current. The model’s availability is measured by whether the fault characteristics of the simulated signals match the theoretical analysis and the experimental signals.

The structure of this paper is as follows. In Section 2, dynamic fault characteristics of ball bearings and the reflection of the fault in stator current are reviewed. Section 3 briefly introduces the construction of MCC motor models and the calculation of inductance parameters. Section 4 presents the bearing fault dynamics modeling method considering the Hertzian contact and radial clearance. Section 5 analyses and proposes the coupling path of the electromagnetic–dynamic model. Section 6 reports and analyses the simulation and experimental results under two types of faults. The conclusion of this study is given in Section 7.

2. Bearing Fault Characteristics in Stator Current

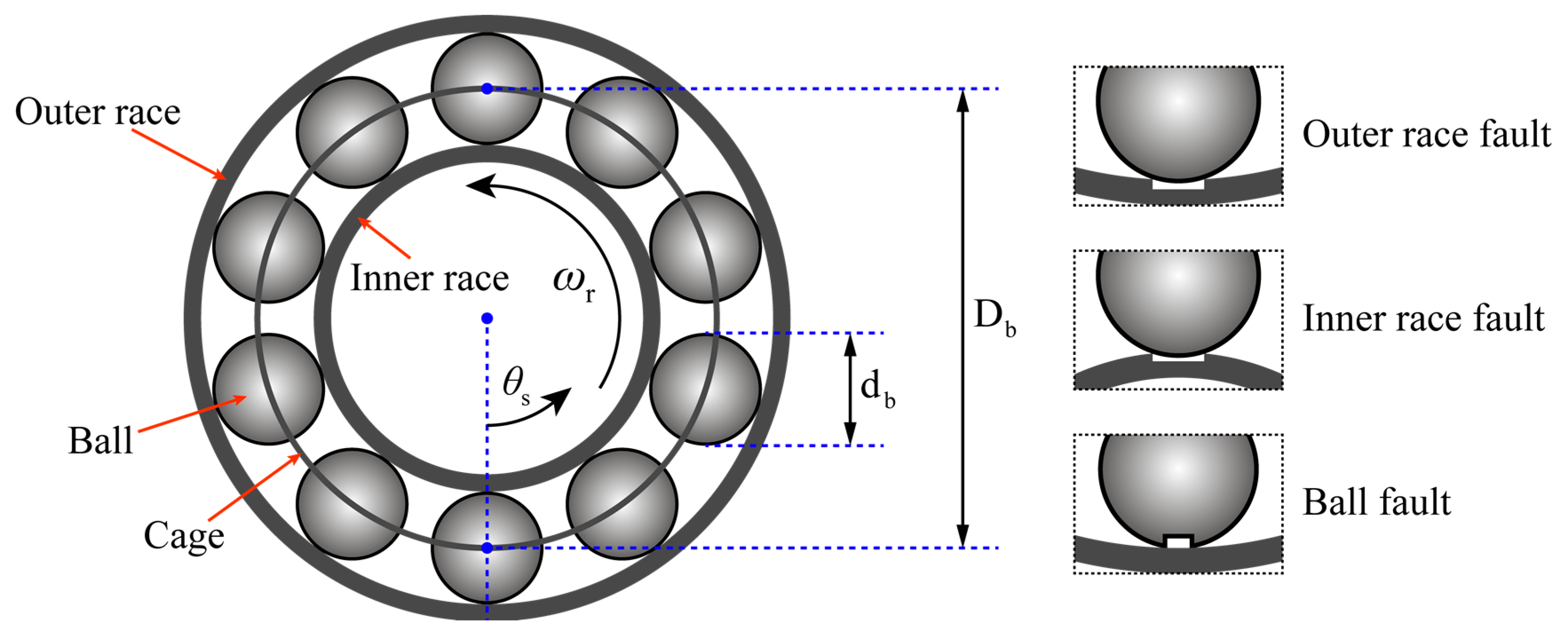
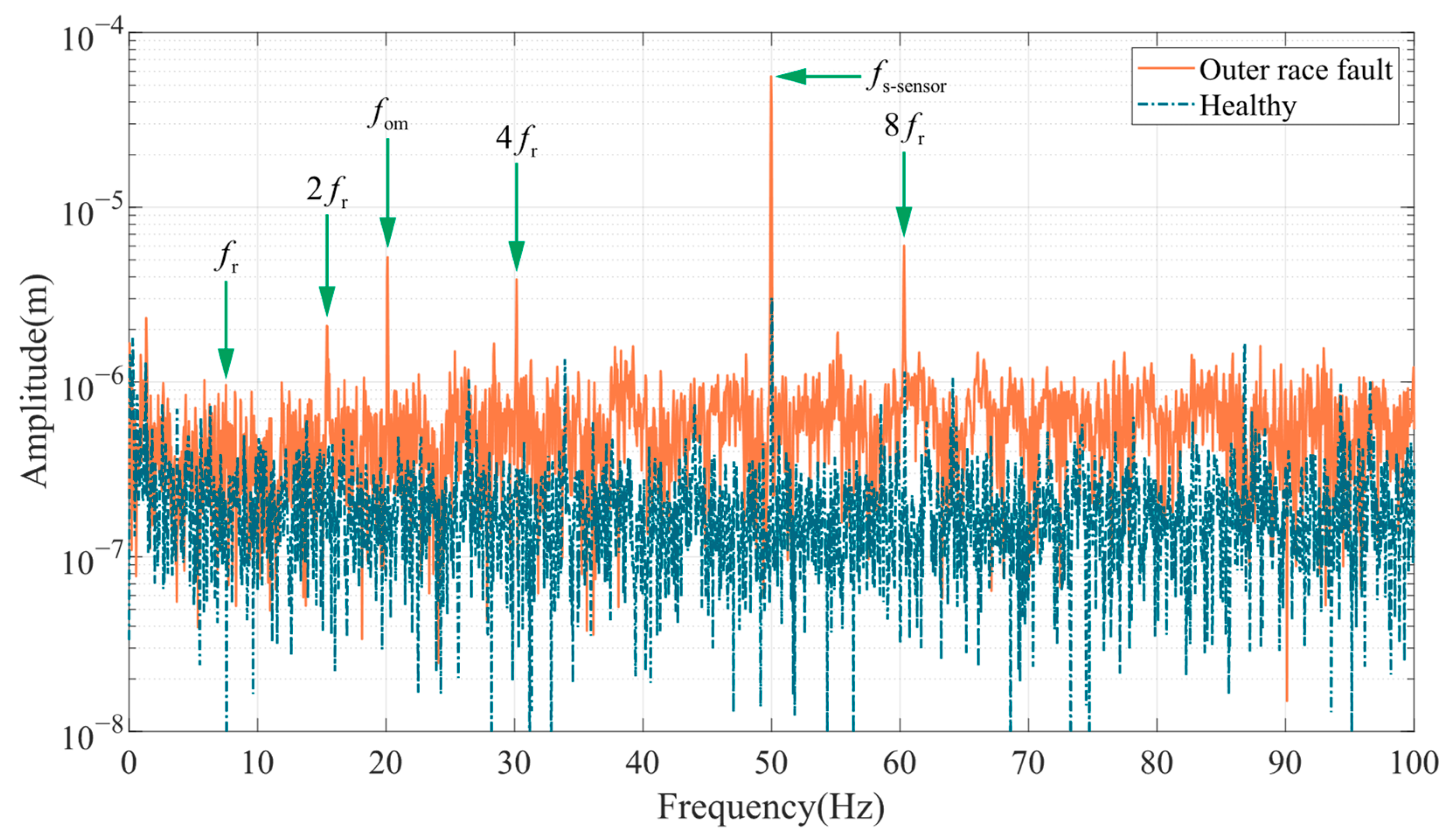
The defects causing bearing failures can be classified as distributed or localized. Distributed defects usually exist at various locations on the bearing components that are difficult to be characterized by definite frequency features. Therefore, single point defects and other localized faults with specific frequency characteristics are generally considered for the study of bearing failures. For the ball bearing in Figure 2, ${\mathrm{n}}_{\mathrm{b}}$ is the number of balls, ${\mathrm{d}}_{\mathrm{b}}$ is the ball diameter, ${\mathrm{D}}_{\mathrm{b}}$ is the bearing pitch diameter, ${\omega }_{\mathrm{r}}$ is the inner ring angular velocity, and $f_{\mathrm{r}}$ is the rotation frequency. The classification of single point defects and their characteristic frequencies are listed below:

• Outer race fault:

$$f_{\mathrm{om}}=\frac{{\mathrm{n}}_{\mathrm{b}}}{2}{f}_{\mathrm{r}}\left(1-\frac{{\mathrm{d}}_{\mathrm{b}}}{{\mathrm{D}}_{\mathrm{b}}}\cos \beta \right).$$

(1)

• Inner race fault:

$$f_{\mathrm{im}}=\frac{{\mathrm{n}}_{\mathrm{b}}}{2}{f}_{\mathrm{r}}\left(1+\frac{{\mathrm{d}}_{\mathrm{b}}}{{\mathrm{D}}_{\mathrm{b}}}\cos \beta \right).$$

(2)

• Ball fault:

$$f_{\mathrm{bm}}=\frac{{\mathrm{D}}_{\mathrm{b}}}{{\mathrm{d}}_{\mathrm{b}}}{f}_{\mathrm{r}}\left(1-\frac{{\mathrm{d}}_{\mathrm{b}}^2}{{\mathrm{D}}_{\mathrm{b}}^2}{\cos }^2\beta \right).$$

(3)

Schoen et al. [15] pointed out that the bearing failure causes the change in air gap length, which in turn affects the stator–rotor inductance and thus the stator current, and gave the corresponding calculation formula. For a motor with a power supply frequency $f_{\mathrm{s}}$ and a bearing fault characteristic frequency $f_{\mathrm{fm}}$, the fault characteristic frequency of the stator current is

$$f_{\mathrm{fe}}=|k{f}_{\mathrm{fm}}\pm f_{\mathrm{s}}|.$$

(4)

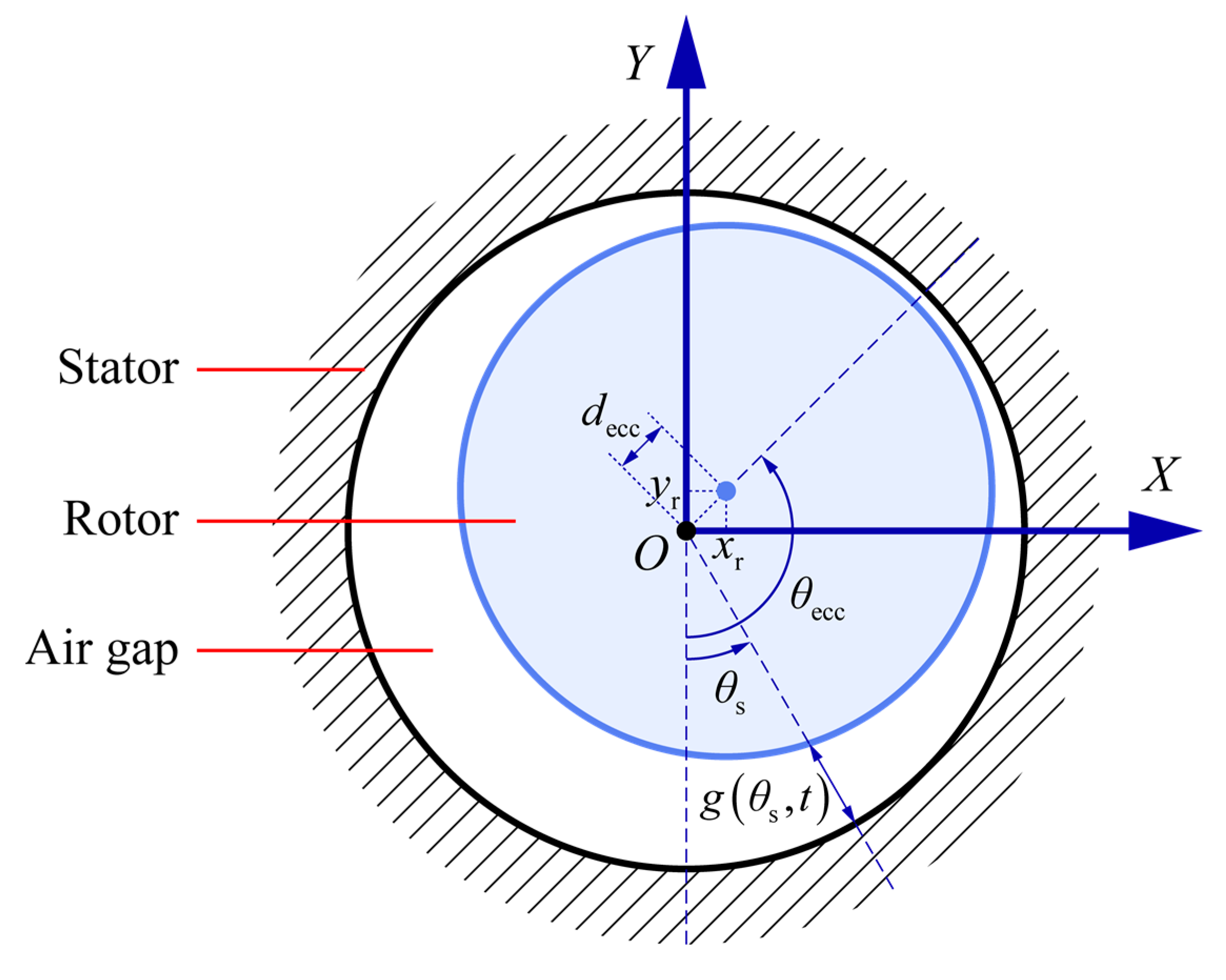
Blodt et al. [16] introduced the Dirac generalized function to derive formulas on the principle of reflecting bearing faults to stator currents, thus theoretically proving that air gap variations can be reflected in the frequency components of stator currents. Firstly, in the presence of a bearing fault, the generalized expression for the air gap length $g$ can be defined as

$$\begin{array}{cc}\hfill g\left({\theta }_{\mathrm{s}},t\right)& =g_0\left[1-e\cos \left({\theta }_{\mathrm{s}}+\psi \left(t\right)\right){\displaystyle {\displaystyle \sum }_{k=-\infty }^{+\infty }}\delta \left(t-\frac{k}{f_{\mathrm{mf}}}\right)\right],\hfill \\ \hfill \psi \left(t\right)& =\{\begin{array}{ll}0,\hfill & \mathrm{outer} \mathrm{race} \mathrm{fault}\hfill \\ {\omega }_{\mathrm{r}}t,\hfill & \mathrm{inner} \mathrm{race} \mathrm{fault}\hfill \\ {\omega }_{\mathrm{cage}}t,\hfill & \mathrm{ball} \mathrm{fault},\hfill \end{array}\hfill \end{array}$$

(5)

where ${\theta }_{\mathrm{s}}$ is the stator mechanical angle, $g_0$ is the uniform air gap length without eccentricity, $e$ is the eccentricity introduced by bearing faults, and $\psi \left(t\right)$ is an introduced angular position function that considers the change of defect position with the rotation of the inner race.

According to the air gap permeance formula $\mathcal{P}=\mu A_{\mathrm{g}}/g$, the air gap permeance formula in case of bearing failure is obtained:

$$\begin{array}{cc}\hfill \mathcal{P}\left({\theta }_{\mathrm{s}},t\right)& ={\mathcal{P}}_0\frac{1}{\left[1-e\cos \left({\theta }_{\mathrm{s}}+\psi \left(t\right)\right){\displaystyle {\displaystyle \sum }_{k=-\infty }^{+\infty }}\delta \left(t-\frac{k}{f_{\mathrm{mf}}}\right)\right]}’\hfill \\ \hfill {\mathcal{P}}_0& =\frac{{\mu }_{\mathrm{r}}{\mu }_0{A}_{\mathrm{g}}}{g_0}\hfill \end{array}$$

(6)

where ${\mu }_{\mathrm{r}}$ is the relative permeability, ${\mu }_0$ is the permeability of free space, and $A_{\mathrm{g}}$ is equivalent air gap cross-sectional area.

According to the first-order approximation of the Taylor expansion of $\frac{1}{1-x}$, the Fourier series expansion of the Dirac generalized function is:

$$\begin{array}{cc}\hfill \frac{1}{1-x}& =1+x+x^2+\cdots \approx 1+x,\hfill \\ \hfill {\displaystyle {\displaystyle \sum }_{k=-\infty }^{+\infty }}\delta \left(t-\frac{k}{f_{\mathrm{mf}}}\right)& ={\displaystyle {\displaystyle \sum }_{k=-\infty }^{+\infty }}{a}_k{e}^{-j2\pi f_{\mathrm{mf}}tk}=a_0+2{\displaystyle {\displaystyle \sum }_{k=1}^{+\infty }}{a}_k\cos \left({\omega }_{\mathrm{mf}}tk\right),\hfill \end{array}$$

(7)

where $\left|x\right|<1$ and the Fourier coefficient $a_k=f_{\mathrm{mf}}$.

Equation (6) can be reduced to

$$\mathcal{P}\left({\theta }_{\mathrm{s}},t\right)\approx {\mathcal{P}}_0\left\{1+e{a}_0\cos \left({\theta }_{\mathrm{s}}+\psi \left(t\right)\right)+e{\displaystyle \sum }_{k=1}^{+\infty }{a}_k\cos \left({\theta }_{\mathrm{s}}+\psi \left(t\right)+l{\omega }_{\mathrm{mf}}t\right)+e{\displaystyle \sum }_{k=1}^{+\infty }{a}_k\cos \left({\theta }_{\mathrm{s}}+\psi \left(t\right)-l{\omega }_{\mathrm{mf}}t\right)\right\}.$$

(8)

Suppose the magnitude of the magnetomotive force is ${ℱ}_0$, the number of motor poles is $p$, the supply angular frequency is ${\omega }_{\mathrm{s}}$, and the initial phase angle is $\phi$, then the magnetomotive force function is

$$ℱ\left({\theta }_{\mathrm{s}},t\right)={ℱ}_0\cos \left(\frac{p}{2}{\theta }_{\mathrm{s}}-{\omega }_{\mathrm{s}}t+\phi \right).$$

(9)

We can then derive the motor flux density distribution:

$$\begin{array}{ll}\Phi \left({\theta }_{\mathrm{s}},t\right)& =\mathcal{F}\left({\theta }_{\mathrm{s}},t\right)·\mathcal{P}\left({\theta }_{\mathrm{s}},t\right)\\ & ={\mathcal{F}}_0{\mathcal{P}}_0\cos \left(\frac{p}{2}{\theta }_{\mathrm{s}}-{\omega }_{\mathrm{s}}t+\phi \right)+{\displaystyle \sum _{k=0}^{+\infty }{B}_k\left[\cos \left(\left(\frac{p}{2}\pm 1\right){\theta }_{\mathrm{s}}\pm \psi \left(t\right)\pm k{\omega }_{\mathrm{mf}}-{\omega }_{\mathrm{s}}t+\phi \right)\right]},\end{array}$$

(10)

where $B_k$ is the magnitude of the flux density wave associated with bearing faults.

Voltage equations for stator phases $m\left(m=a,b,c\right)$:

$$V_m\left(t\right)=R_s{I}_m\left(t\right)+\frac{\mathrm{d}{\Phi }_m\left(t\right)}{\mathrm{d}t}.$$

(11)

For a motor powered by a balanced three-phase voltage source, the stator current contains the frequency component of the flux derivative and can be written as follows:

$$I_m\left(t\right)={\displaystyle \sum _{k=0}^{+\infty }{I}_k\cos \left[\pm \psi \left(t\right)\pm k{\omega }_{\mathrm{mf}}t-{\omega }_{\mathrm{s}}t+{\phi }_m\right]},$$

(12)

where $I_k$ is the amplitude of each frequency component.

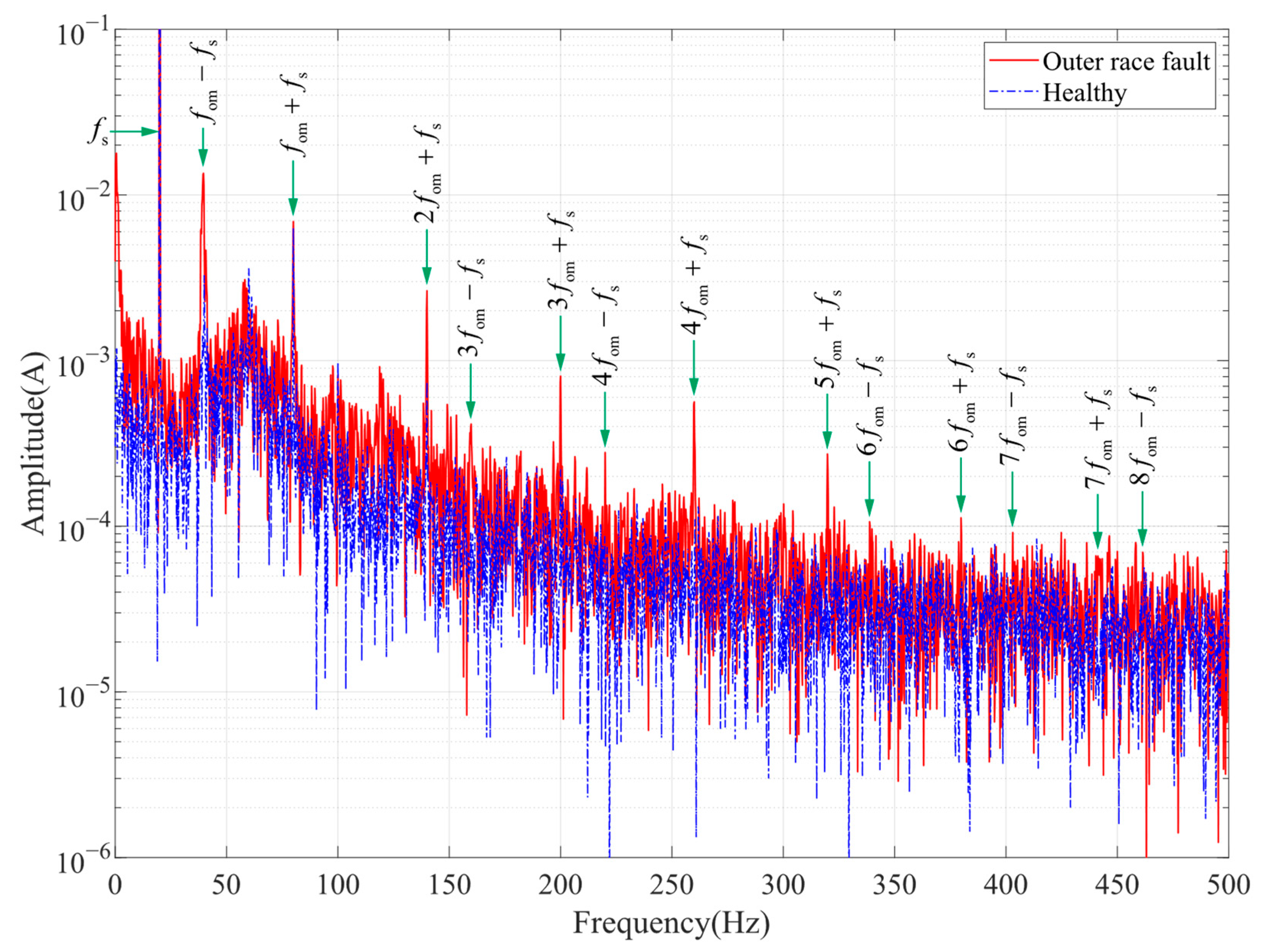
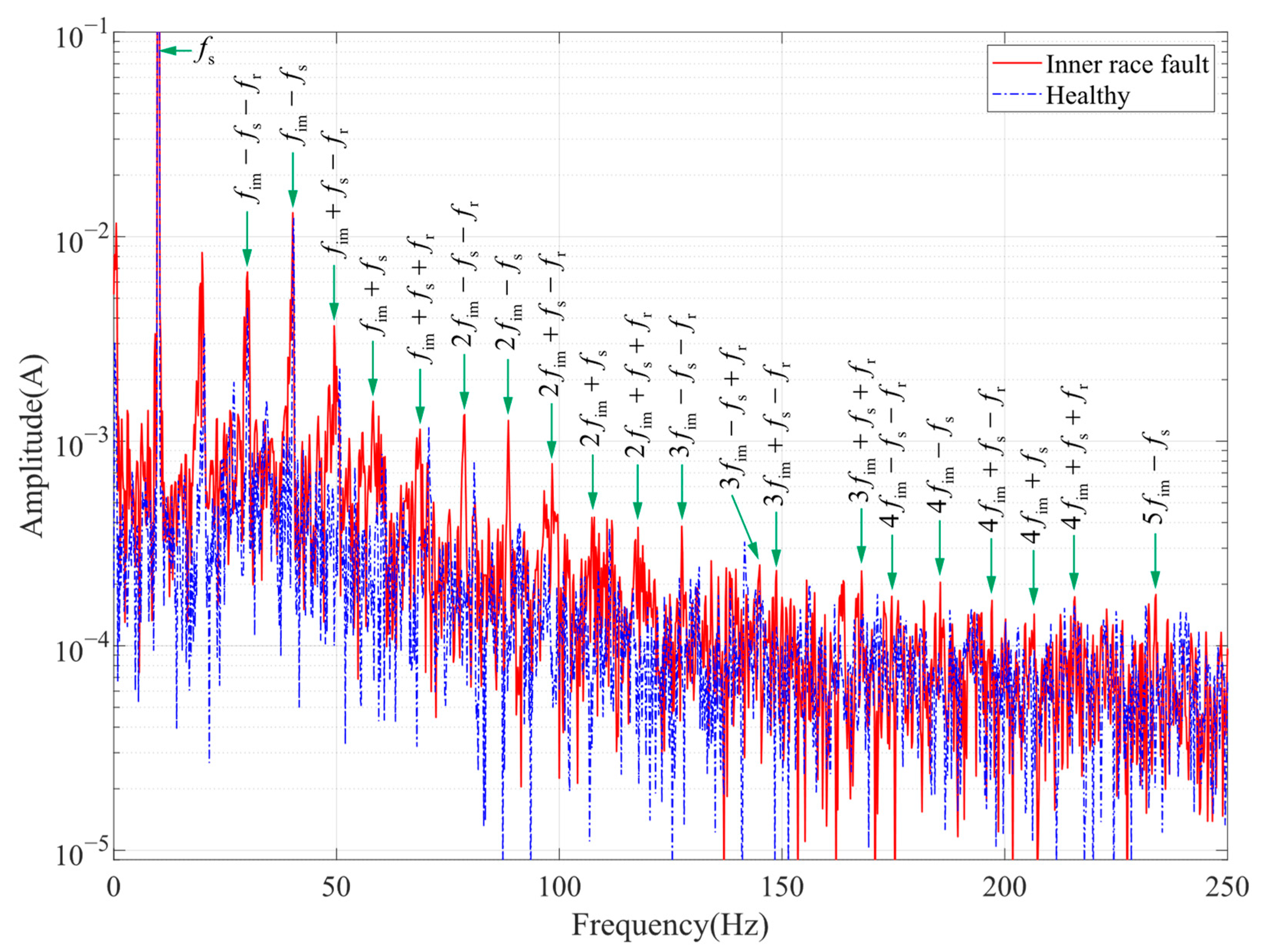
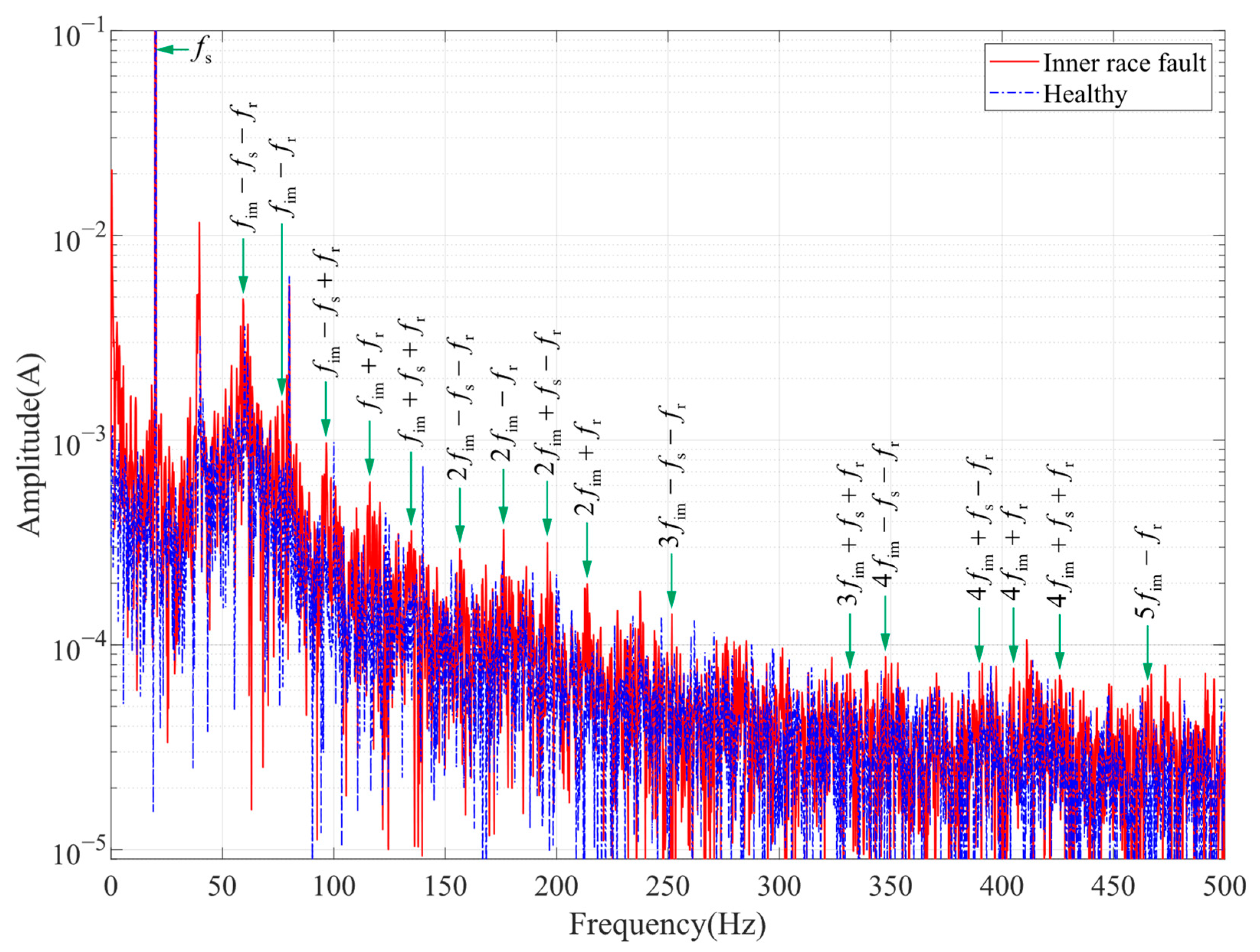
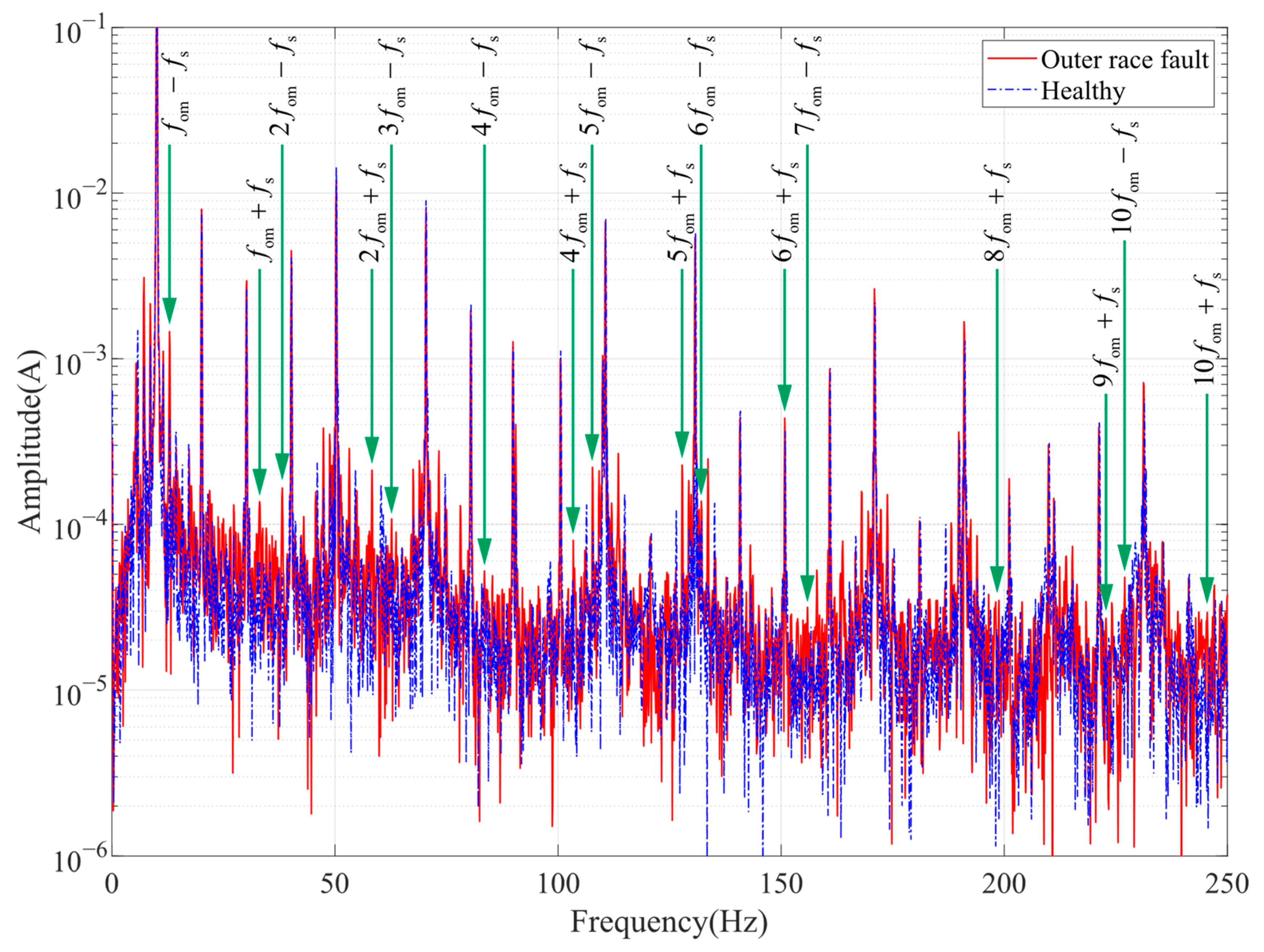
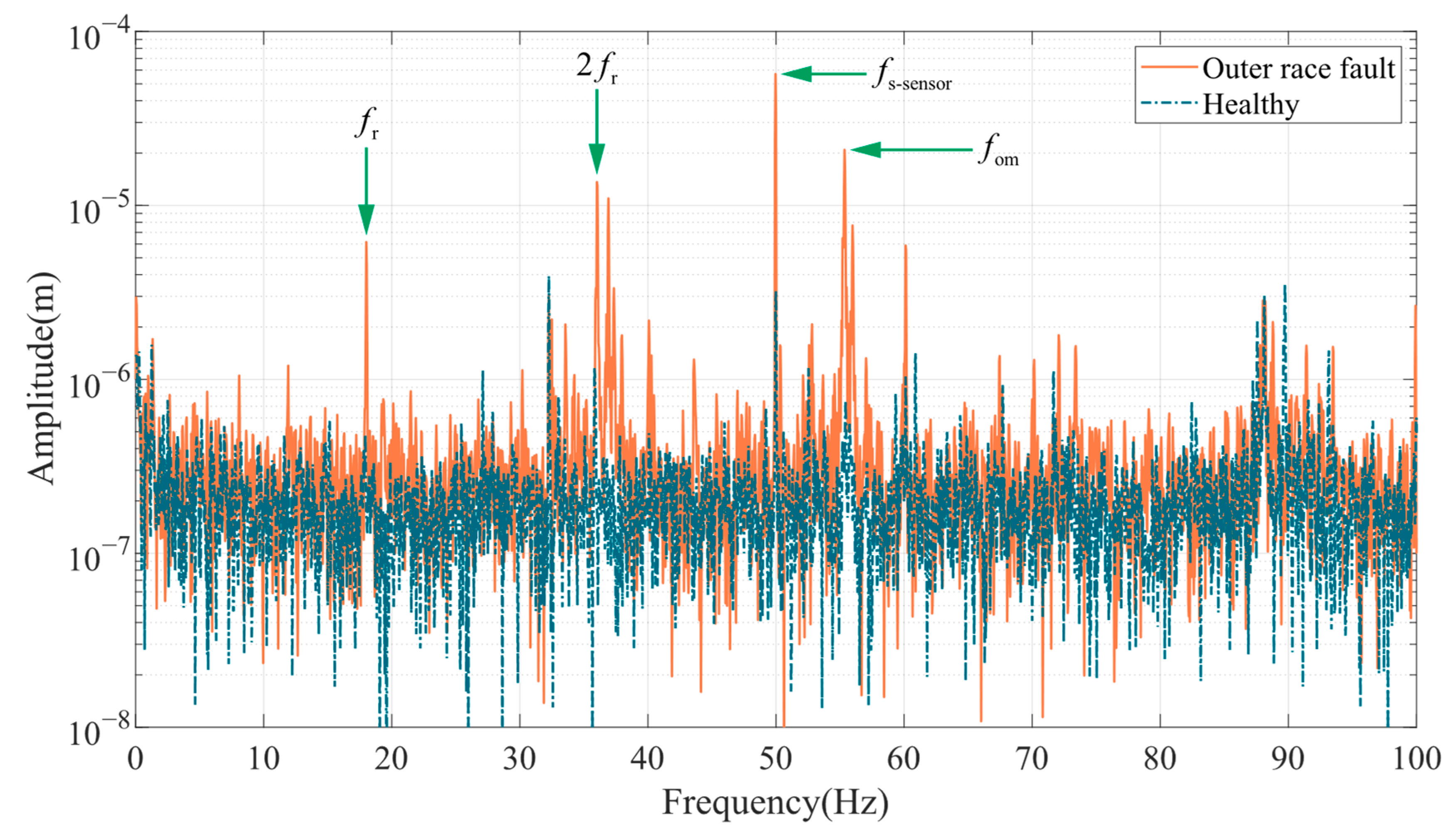
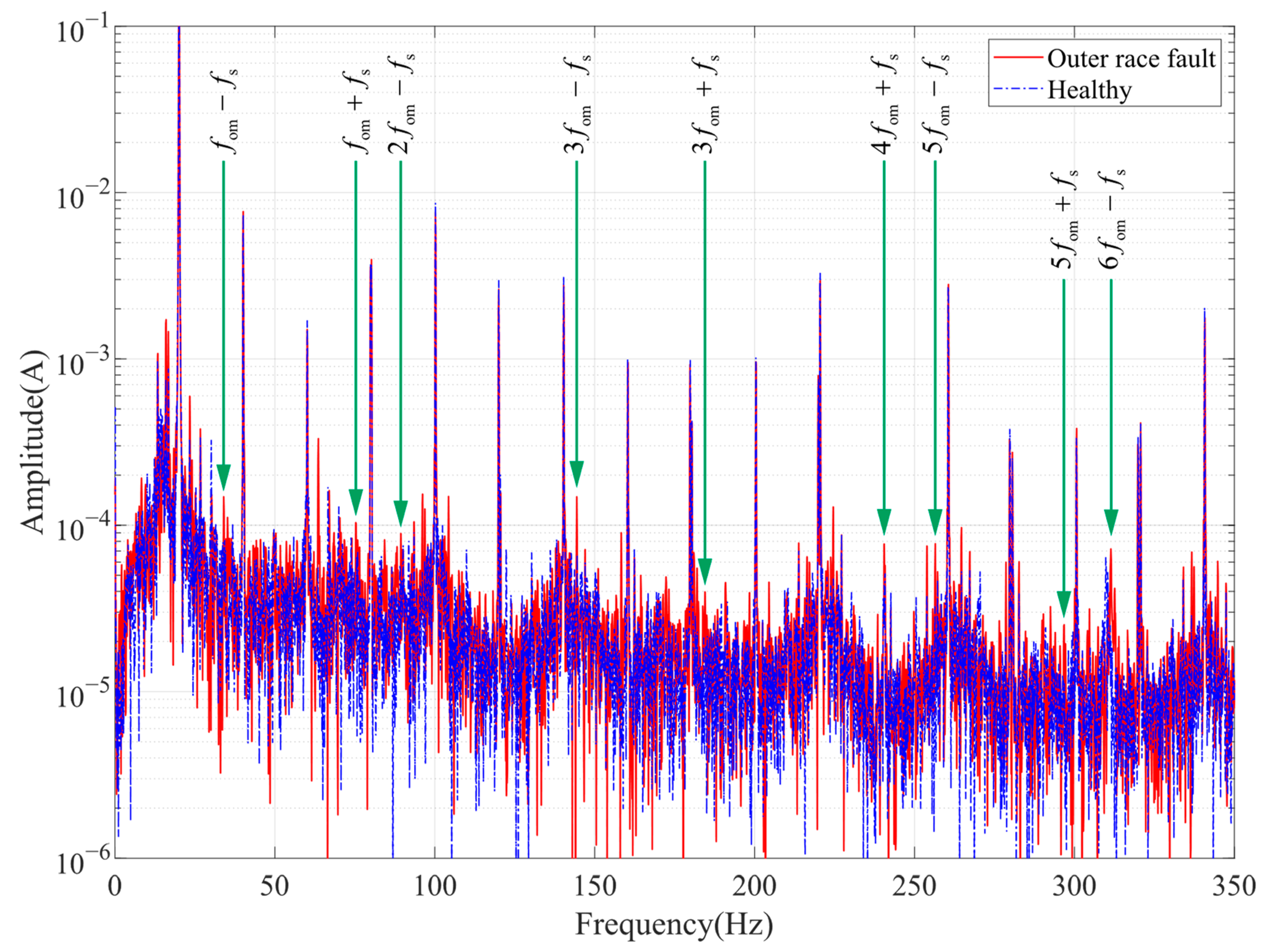
From Equation (12), it can be seen that air gap fluctuations generated by bearing faults will introduce a specific frequency component in the stator current. For different fault types, the theoretical fault characteristic frequencies are as follows.

• Outer race fault:

$$f_{\mathrm{oe}}=k{f}_{\mathrm{om}}\pm f_{\mathrm{s}}.$$

(13)

• Inner race fault:

$$f_{\mathrm{ie}}=k{f}_{\mathrm{im}}\pm f_{\mathrm{s}}\pm f_{\mathrm{r}}.$$

(14)

• Ball fault:

$$f_{\mathrm{be}}=k{f}_{\mathrm{bm}}\pm f_{\mathrm{s}}\pm f_{\mathrm{cage}}.$$

(15)

Since the rotation of the ball in the raceway is often not frictionless strict rolling, and accompanied by the possibility of spin in all directions, ball spalling failure characteristics in the bearing with the ball as the rolling element does not appear in a definite and uniform impact. Therefore, we will not discuss the ball spalling failure in ball bearings for the time being.

3. Multiple Coupled Circuit Modeling for Induction Motors

3.1. Multiple Coupled Circuit Theory

Industrial motors inevitably operate with asymmetric power supplies, accompanied by saturation effects, eddy current losses, and friction losses. The MCC theory achieves a compromise between complexity and accuracy of motor electromagnetic models by some reasonable simplifying assumptions. We aimed to explore the effective coupling path between the electromagnetic and dynamics models, and therefore, the MCC modeling relies on the popular assumptions used in most studies. In this study, the development of the MCC model relies on the following assumptions:

• The motor is a linear system powered by a balanced three-phase voltage source;
• Saturation, eddy current loss, and friction loss are not considered; and
• Rotor bars are insulated from each other.

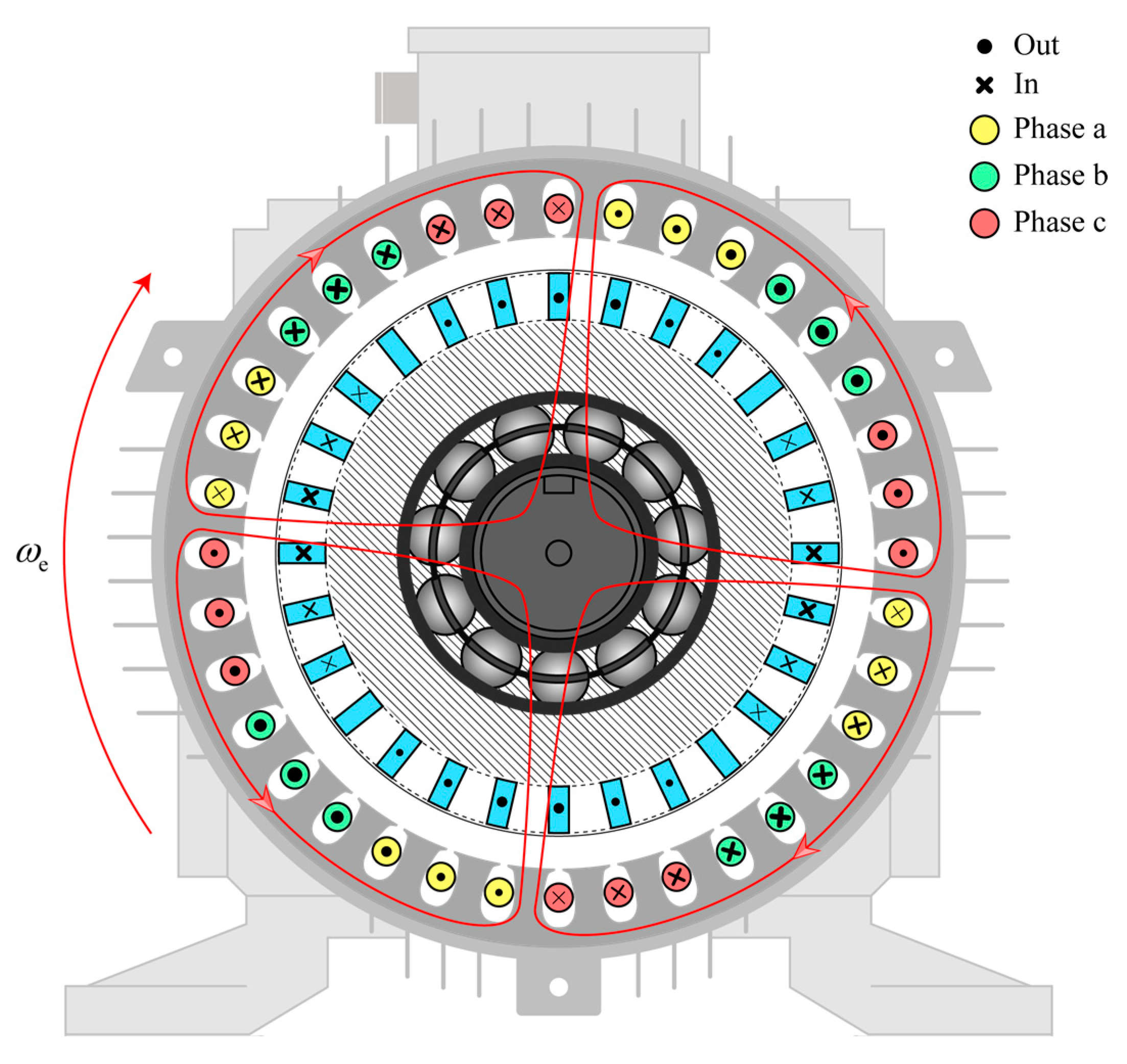
Based on these assumptions, as shown in Figure 3 and Figure 4, by equating each phase stator winding as a series circuit of resistance and leakage inductance, as well as considering the cage rotor as a circuit uniformly distributed in space, the voltage equation of a three-phase squirrel-cage induction motor with a star connection can be expressed as

$${\mathit{U}}_{\mathrm{s}}={\mathit{I}}_{\mathrm{s}}{\mathit{R}}_{\mathrm{s}}+\frac{\mathrm{d}}{\mathrm{d}t}{\lambda }_{\mathrm{s}},$$

(16)

$$\mathbf{0}={\mathit{I}}_{\mathrm{r}}{\mathit{R}}_{\mathrm{r}}+\frac{\mathrm{d}}{\mathrm{d}t}{\lambda }_{\mathrm{r}},$$

(17)

where $U_{\mathrm{s}}$ is the stator voltage vector; $I_{\mathrm{s},\mathrm{r}}$, $R_{\mathrm{s},\mathrm{r}}$, and ${\lambda }_{\mathrm{s},\mathrm{r}}$ are the current vector, resistance matrix, and magnetic chain vector of the stator and rotor, respectively;

$${\mathit{U}}_{\mathrm{s}}=\left[\begin{array}{c}{U}_{\mathrm{sa}}\\ U_{\mathrm{sb}}\\ U_{\mathrm{sc}}\end{array}\right],{\mathit{I}}_{\mathrm{s}}=\left[\begin{array}{c}{i}_{\mathrm{sa}}\\ i_{\mathrm{sb}}\\ i_{\mathrm{sc}}\end{array}\right],{\mathit{R}}_{\mathrm{s}}=\left[\begin{array}{ccc}{R}_{\mathrm{s}}& 0& 0\\ 0& R_{\mathrm{s}}& 0\\ 0& 0& R_{\mathrm{s}}\end{array}\right],{\lambda }_{\mathrm{s}}=\left[\begin{array}{c}{\lambda }_{\mathrm{sa}}\\ {\lambda }_{\mathrm{sb}}\\ {\lambda }_{\mathrm{sc}}\end{array}\right],$$

$$R_{\mathrm{r}}=\left[\begin{array}{cccccc}2\left(R_{\mathrm{b}}+R_{\mathrm{e}}\right)& -R_{\mathrm{b}}& 0& \cdots & -R_{\mathrm{b}}& -R_{\mathrm{e}}\\ -R_{\mathrm{b}}& 2\left(R_{\mathrm{b}}+R_{\mathrm{e}}\right)& -R_{\mathrm{b}}& \cdots & 0& -R_{\mathrm{e}}\\ 0& -R_{\mathrm{b}}& 2\left(R_{\mathrm{b}}+R_{\mathrm{e}}\right)& \cdots & 0& -R_{\mathrm{e}}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ -R_{\mathrm{b}}& 0& 0& \cdots & 2\left(R_{\mathrm{b}}+R_{\mathrm{e}}\right)& -R_{\mathrm{e}}\\ -R_{\mathrm{e}}& -R_{\mathrm{e}}& -R_{\mathrm{e}}& \cdots & -R_{\mathrm{e}}& {\mathrm{n}}_{\mathrm{b}}{R}_{\mathrm{e}}\end{array}\right],{\mathit{i}}_{\mathrm{r}}=\left[\begin{array}{c}{i}_{\mathrm{r}1}\\ i_{\mathrm{r}2}\\ i_{\mathrm{r}3}\\ ⋮\\ i_{{\mathrm{rn}}_{\mathrm{b}}}\\ i_{\mathrm{e}}\end{array}\right],{\lambda }_{\mathrm{r}}=\left[\begin{array}{c}{\lambda }_{\mathrm{r}1}\\ {\lambda }_{\mathrm{r}2}\\ {\lambda }_{\mathrm{r}3}\\ ⋮\\ {\lambda }_{{\mathrm{rn}}_{\mathrm{b}}}\\ {\lambda }_{\mathrm{e}}\end{array}\right],$$

$U_{\mathrm{sa},\mathrm{sb},\mathrm{sc}}$ is the three-phase voltage of the stator; $i_{\mathrm{sa},\mathrm{sb},\mathrm{sc}}$ is the current of the three-phase stator winding; $R_{\mathrm{s}}$ is the single-phase stator winding resistance under the assumption of stator symmetry; ${\lambda }_{\mathrm{sa},\mathrm{sb},\mathrm{sc}}$ is the flux linkage of the three-phase stator winding; ${\mathrm{n}}_{\mathrm{b}}$ is the number of rotor bars; $R_{\mathrm{b}}$ is the rotor bar resistance; $R_{\mathrm{e}}$ is the rotor end ring resistance; $i_{\mathrm{r}i}\left(i=1,2,\dots ,{\mathrm{n}}_{\mathrm{b}}\right)$ and $i_{\mathrm{r}i}\left(i=1,2,\dots ,{\mathrm{n}}_{\mathrm{b}}\right)$ are the current and flux linkage in the $i\text{-}\mathrm{th}$ rotor loop, respectively; and $i_{\mathrm{e}}$ and ${\lambda }_{\mathrm{e}}$ are the current and flux linkage in the end ring, respectively.

The equation of the flux linkage of the stator and rotor is expressed as

$${\lambda }_{\mathrm{s}}=L_{\mathrm{ss}}{I}_{\mathrm{s}}+L_{\mathrm{sr}}{I}_{\mathrm{r}},$$

(18)

$${\lambda }_{\mathrm{r}}=L_{\mathrm{rs}}{I}_{\mathrm{s}}+L_{\mathrm{rr}}{I}_{\mathrm{r}}=L_{\mathrm{sr}}^{\mathrm{T}}{I}_{\mathrm{s}}+L_{\mathrm{rr}}{I}_{\mathrm{r}},$$

(19)

where $L_{\mathrm{ss}}$ and $L_{\mathrm{rr}}$ are the stator self-inductance matrix and rotor self-inductance matrix, respectively; $L_{\mathrm{sr}}$ and $L_{\mathrm{rs}}$ are stator–rotor mutual inductance matrix and rotor-stator mutual inductance matrix respectively, here $L_{\mathrm{rs}}=L_{\mathrm{sr}}^{\mathrm{T}}$;

$$L_{\mathrm{ss}}=\left[\begin{array}{ccc}{L}_{\mathrm{sasa}}& L_{\mathrm{sasb}}& L_{\mathrm{sasc}}\\ L_{\mathrm{sbsa}}& L_{\mathrm{sbsb}}& L_{\mathrm{sbsc}}\\ L_{\mathrm{scsa}}& L_{\mathrm{scsb}}& L_{\mathrm{scsc}}\end{array}\right],L_{\mathrm{sr}}=\left[\begin{array}{cccccc}{L}_{\mathrm{sar}1}& L_{\mathrm{sar}2}& L_{\mathrm{sar}3}& \cdots & L_{{\mathrm{sarn}}_{\mathrm{b}}}& 0\\ L_{\mathrm{sbr}1}& L_{\mathrm{sbr}2}& L_{\mathrm{sbr}3}& \cdots & L_{{\mathrm{sbrn}}_{\mathrm{b}}}& 0\\ L_{\mathrm{scr}1}& L_{\mathrm{scr}2}& L_{\mathrm{scr}3}& \cdots & L_{{\mathrm{scrn}}_{\mathrm{b}}}& 0\end{array}\right],$$

$$L_{\mathrm{r}}=\left[\begin{array}{cccccc}{L}_{\mathrm{r}1\mathrm{r}1}+2\left(L_{\mathrm{b}}+L_{\mathrm{e}}\right)& L_{\mathrm{r}1\mathrm{r}2}-L_{\mathrm{b}}& L_{\mathrm{r}1\mathrm{r}3}& \cdots & L_{{\mathrm{r}1\mathrm{rn}}_{\mathrm{b}}}-L_{\mathrm{b}}& -L_{\mathrm{e}}\\ L_{\mathrm{r}2\mathrm{r}1}-L_{\mathrm{b}}& L_{\mathrm{r}2\mathrm{r}2}+2\left(L_{\mathrm{b}}+L_{\mathrm{e}}\right)& L_{\mathrm{r}2\mathrm{r}3}-L_{\mathrm{b}}& \cdots & L_{{\mathrm{r}2\mathrm{rn}}_{\mathrm{b}}}& -L_{\mathrm{e}}\\ L_{\mathrm{r}3\mathrm{r}1}& L_{\mathrm{r}3\mathrm{r}2}-L_{\mathrm{b}}& L_{\mathrm{r}3\mathrm{r}3}+2\left(L_{\mathrm{b}}+L_{\mathrm{e}}\right)& \cdots & L_{{\mathrm{r}3\mathrm{rn}}_{\mathrm{b}}}& -L_{\mathrm{e}}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ L_{{\mathrm{rn}}_{\mathrm{b}}\mathrm{r}1}-L_{\mathrm{b}}& L_{{\mathrm{rn}}_{\mathrm{b}}\mathrm{r}2}& L_{{\mathrm{rn}}_{\mathrm{b}}\mathrm{r}3}& \cdots & L_{{\mathrm{rn}}_{\mathrm{b}}{\mathrm{rn}}_{\mathrm{b}}}+2\left(L_{\mathrm{b}}+L_{\mathrm{e}}\right)& -L_{\mathrm{e}}\\ -L_{\mathrm{e}}& -L_{\mathrm{e}}& -L_{\mathrm{e}}& \cdots & -L_{\mathrm{e}}& {\mathrm{n}}_{\mathrm{b}}{L}_{\mathrm{e}}\end{array}\right],$$

$L_{\mathrm{s}i\mathrm{s}j}\left(i=1,2,3;j=1,2,3\right)$ is the mutual inductance between stator phase $i$ and stator phase $j$, $L_{\mathrm{s}i\mathrm{r}j}\left(i=a,b,c;j=1,2,\dots ,{\mathrm{n}}_{\mathrm{b}}\right)$ is the mutual inductance between the stator phase $i$ and the $j\text{-}\mathrm{th}$ rotor loop, $L_{\mathrm{r}i\mathrm{r}j}\left(i=1,2,\dots ,{\mathrm{n}}_{\mathrm{b}},j=1,2,\dots ,{\mathrm{n}}_{\mathrm{b}}\right)$ is the mutual inductance between the $i\text{-}\mathrm{th}$ and $j\text{-}\mathrm{th}$ rotor circuits, and $L_{\mathrm{b}}$ and $L_{\mathrm{e}}$ are the leakage inductance of rotor bar and end ring, respectively.

From the magnetic co-energy equation for linear motor systems, the matrix form of the electromagnetic torque equation can be derived as:

$$\begin{array}{ll}{T}_{\mathrm{e}}& =\frac{1}{2}\frac{\mathrm{p}}{2}{\left[\begin{array}{c}{I}_{\mathrm{s}}\\ I_{\mathrm{r}}\end{array}\right]}^{\mathrm{T}}\frac{\mathrm{d}}{\mathrm{d}{\theta }_{\mathrm{e}}}\left[\begin{array}{cc}{L}_{\mathrm{ss}}& L_{\mathrm{sr}}\\ L_{\mathrm{rs}}& L_{\mathrm{rr}}\end{array}\right]\left[\begin{array}{c}{I}_{\mathrm{s}}\\ I_{\mathrm{r}}\end{array}\right]\\ & =\frac{1}{2}\frac{\mathrm{p}}{2}\left(I_{\mathrm{s}}^{\mathrm{T}}\frac{\mathrm{d}{L}_{\mathrm{ss}}}{\mathrm{d}{\theta }_{\mathrm{e}}}{I}_{\mathrm{s}}+I_{\mathrm{s}}^{\mathrm{T}}\frac{\mathrm{d}{L}_{\mathrm{sr}}}{\mathrm{d}{\theta }_{\mathrm{e}}}{I}_{\mathrm{r}}+I_{\mathrm{r}}^{\mathrm{T}}\frac{\mathrm{d}{L}_{\mathrm{rs}}}{\mathrm{d}{\theta }_{\mathrm{e}}}{I}_{\mathrm{s}}+I_{\mathrm{r}}^{\mathrm{T}}\frac{\mathrm{d}{L}_{\mathrm{rr}}}{\mathrm{d}{\theta }_{\mathrm{e}}}{I}_{\mathrm{r}}\right),\end{array}$$

(20)

where $\mathrm{p}$ is the number of motor poles and ${\theta }_{\mathrm{e}}$ is the electrical angle.

The motor dynamic equation is

$$T_{\mathrm{e}}=\mathrm{J}\frac{\mathrm{d}{\omega }_{\mathrm{r}}}{\mathrm{d}t}+T_{\mathrm{l}},$$

(21)

where $\mathrm{J}$ is the rotor inertia, ${\omega }_{\mathrm{m}}$ is the mechanical angular velocity, and $T_{\mathrm{l}}$ is the load torque.

3.2. Inductance Calculation

Accurate inductance calculations are the basis for proper multi-loop modeling. Leakage inductance in the stator, rotor bars, and end loops can be calculated from motor geometry parameters, but the time-varying self and mutual inductance in the stator and rotor are usually difficult to measure or accurately estimate. Considering that the winding structure determines the motor magnetomotive force as well as most of the air gap permeability, WFA provides an effective way to calculate inductance using the motor winding and air gap length distribution. Similarly, based on the assumptions of the multi-loop model, WFA extends some necessary assumptions:

• The flux passes radially through the air gap, i.e., the axial flux is negligible;
• Infinite magnetic permeability of magnetic materials; and
• Negligible slot effect.

Through the derivation based on Gauss’s law and Ampere’s law, the formula for calculating the mutual inductance between any coil $\mathrm{x}$ and coil $\mathrm{y}$ by WFA can be expressed as

$$L_{\mathrm{xy}}={\mu }_{0}rl{\displaystyle {\int }_0^{2\pi }{n}_{\mathrm{x}}\left({\theta }_{\mathrm{s}}\right)}·N_{\mathrm{y}}\left({\theta }_{\mathrm{s}}\right)·g^{-1}\left({\theta }_{\mathrm{s}}\right)\mathrm{d}{\theta }_{\mathrm{s}},$$

(22)

where ${\mu }_0$ is the air gap permeability, $r$ is the radius of the center of the air gap, $l$ is the stack length, $n_{\mathrm{x}}\left({\theta }_{\mathrm{s}}\right)$ is the turn function (TF) of coil $\mathrm{x}$, $N_{\mathrm{y}}\left({\theta }_{\mathrm{s}}\right)$ is the winding function (WF) of coil $y$, and $g^{-1}\left({\theta }_{\mathrm{s}}\right)$ is the air gap inverse function.

In the motor, considering the relative motion between the stator and rotor, and introducing the rotor mechanical angular position ${\theta }_{\mathrm{r}}$, Equation (22) can be rewritten as

$$L_{\mathrm{xy}}\left({\theta }_{\mathrm{r}}\right)={\mu }_{0}rl{\displaystyle {\int }_0^{2\pi }{n}_{\mathrm{x}}\left({\theta }_{\mathrm{s}},{\theta }_{\mathrm{r}}\right)}·N_{\mathrm{y}}\left({\theta }_{\mathrm{s}},{\theta }_{\mathrm{r}}\right)·g^{-1}\left({\theta }_{\mathrm{s}},{\theta }_{\mathrm{r}}\right)\mathrm{d}{\theta }_{\mathrm{s}}.$$

(23)

Alternatively, it can be rewritten as a function of time $t$:

$$L_{\mathrm{xy}}\left(t\right)={\mu }_{0}rl{\displaystyle {\int }_0^{2\pi }{n}_{\mathrm{x}}\left({\theta }_{\mathrm{s}},t\right)}·N_{\mathrm{y}}\left({\theta }_{\mathrm{s}},t\right)·g^{-1}\left({\theta }_{\mathrm{s}},t\right)\mathrm{d}{\theta }_{\mathrm{s}}.$$

(24)

In the calculation of the WFA, the winding distribution of the motor stator and rotor is expressed by TFs. The TF represents the turn spatial distribution of a stator winding or rotor loop at one side of motor, while the WF represents the magnetic potential spatial distribution of a stator winding or rotor loop due to current passage. Obviously, the WF is a function of the TF and the air gap length:

$$N_{\mathrm{y}}\left({\theta }_{\mathrm{s}}\right)=n_{\mathrm{y}}\left({\theta }_{\mathrm{s}}\right)-\frac{1}{2\pi \langle g^{-1}\left({\theta }_{\mathrm{s}}\right)\rangle }{\displaystyle {\int }_0^{2\pi }{n}_{\mathrm{y}}\left({\theta }_{\mathrm{s}}\right)·g^{-1}\left({\theta }_{\mathrm{s}}\right)\mathrm{d}{\theta }_{\mathrm{s}}},$$

(25)

where $\langle g^{-1}\left({\theta }_{\mathrm{s}}\right)\rangle$ is the average value of air gap inverse function.

For a stator with a one-layer winding distribution, the TF of each winding phase can be defined as

$$\begin{array}{cc}\hfill i& =1:1:p/2,\hfill \\ \hfill n_{\mathrm{start}}& =2Q_{\mathrm{s}}\left(i-1\right)/p,\hfill \\ \hfill n_{\mathrm{s}}\left({\theta }_{\mathrm{s}}\right)& =\{\begin{array}{ll}{Z}_{\mathrm{s}}·j,\hfill & j=n_{\mathrm{start}}+\left(1:1:Q_{\mathrm{pp}}\right)\hfill \\ Z_{\mathrm{s}}·Q_{\mathrm{pp}},\hfill & j=n_{\mathrm{start}}+\left(\left(Q_{\mathrm{pp}}+1\right):1:3Q_{\mathrm{pp}}\right)\hfill \\ Z_{\mathrm{s}}\left(Q_{\mathrm{pp}}-i\right),\hfill & j=n_{\mathrm{start}}+\left(\left(3Q_{\mathrm{pp}}+1\right):1:4Q_{\mathrm{pp}}\right)\hfill \\ 0,\hfill & j=n_{\mathrm{start}}+\left(\left(4Q_{\mathrm{pp}}+1\right):1:2Q_{\mathrm{s}}/p\right)\hfill \end{array},\hfill \end{array}$$

(26)

where $Z_{\mathrm{s}}$ is the number of turns per winding, $Q_{\mathrm{pp}}$ is the number of slots per pole and phase, and $Q_{\mathrm{s}}$ is the total number of stator slots.

The TF of a single rotor bar can be defined as:

$$n_{\mathrm{r}}\left({\theta }_{\mathrm{s}}\right)=\{\begin{array}{cc}1,& {\theta }_{\mathrm{bar}}\le {\theta }_{\mathrm{s}}\le {\theta }_{\mathrm{bar}}+{\alpha }_{\mathrm{r}}\\ 0,& \mathrm{else}\end{array},$$

(27)

where ${\theta }_{\mathrm{bar}}$ is the mechanical angle position of the rotor bar, and ${\alpha }_{\mathrm{r}}$ is the angular displacement between two consecutive bars.

Taking the three-phase and four-pole induction motor shown in Figure 1 as an example, the motor design parameters are shown in

Table 1. Motor parameters.

Parameters	Values
Number of phases	3
Number of poles	4
Number of stator turns in series	61
Stack length	1.25 × 10−1 m
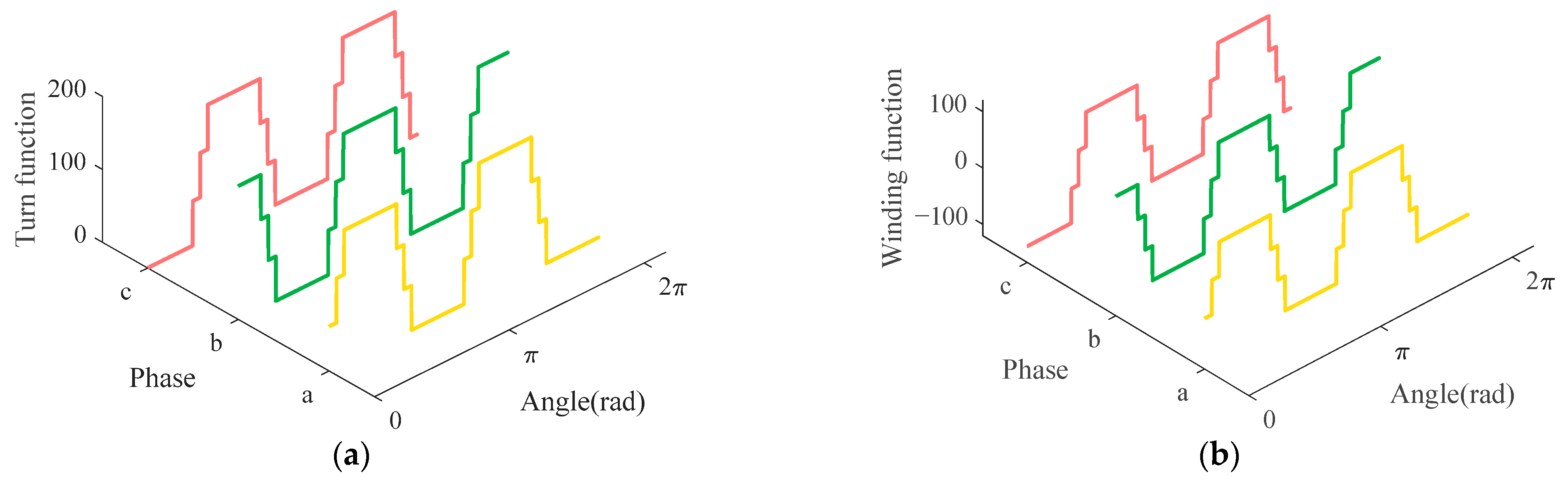
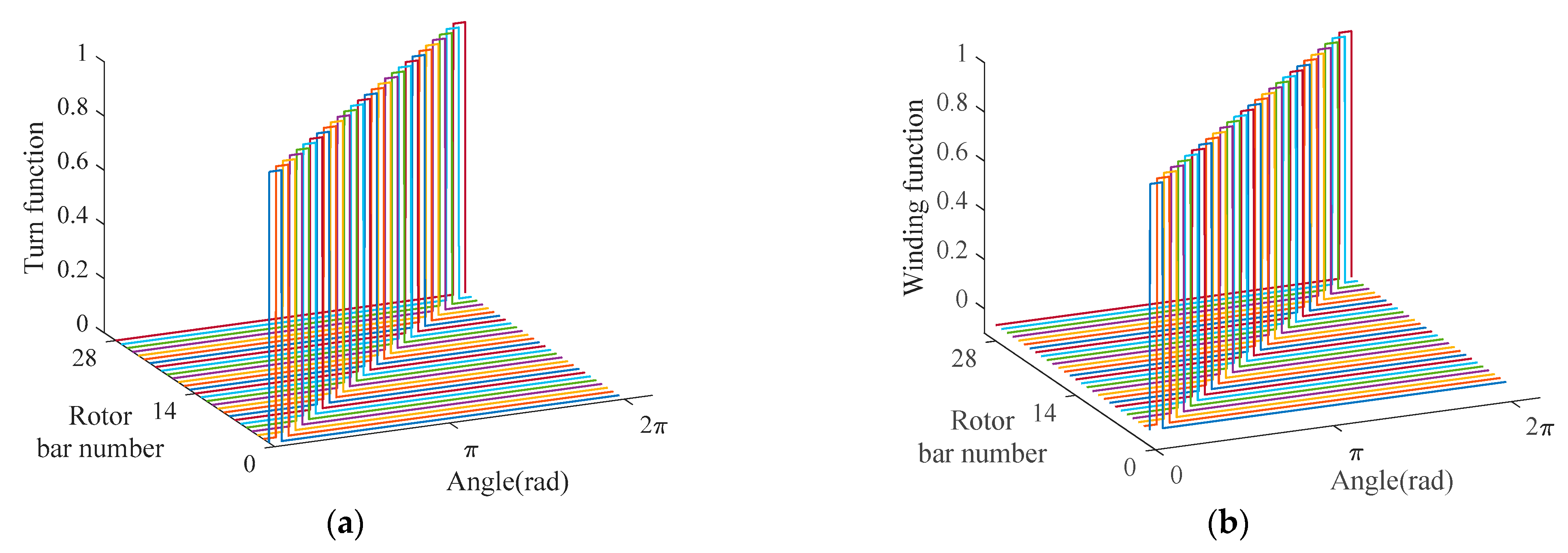
Air gap center radius	4.55 × 10−2 m

. According to the motor winding structure, the TF spatial distribution curve of the stator and rotor can be obtained, and the corresponding WF can be calculated by Equation (23). Figure 5 and Figure 6 show the stator and rotor TFs and the calculated WFs under the assumption of a uniform air gap, respectively.

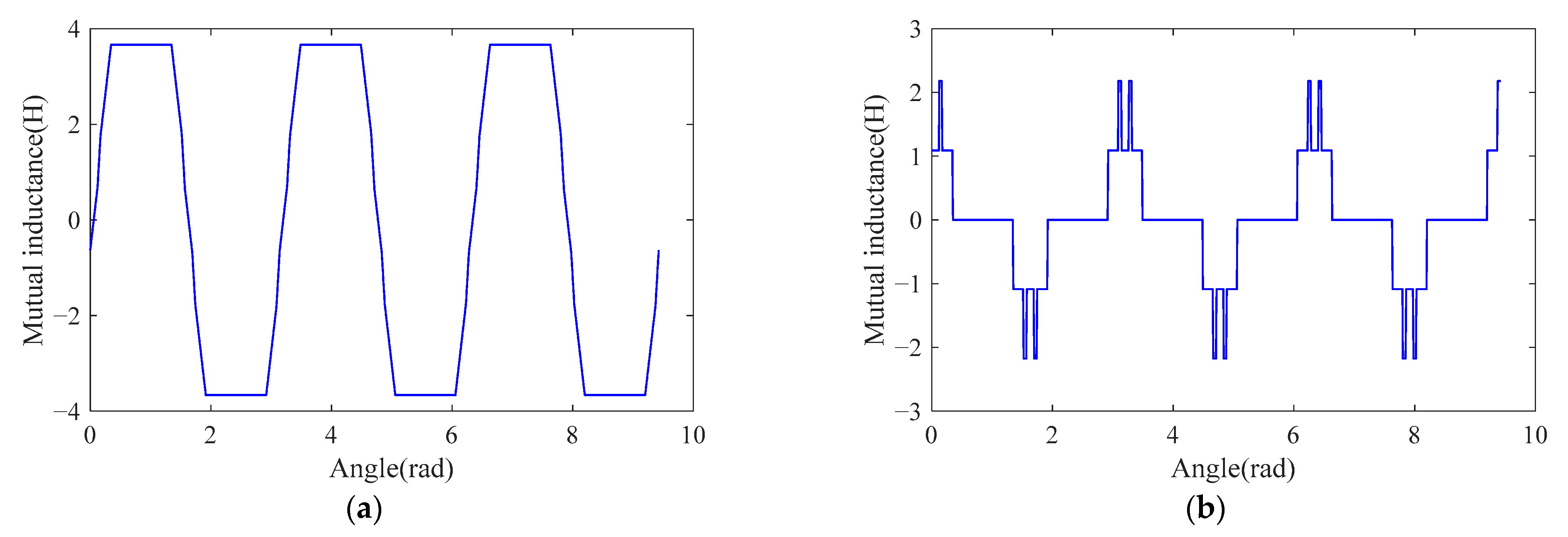
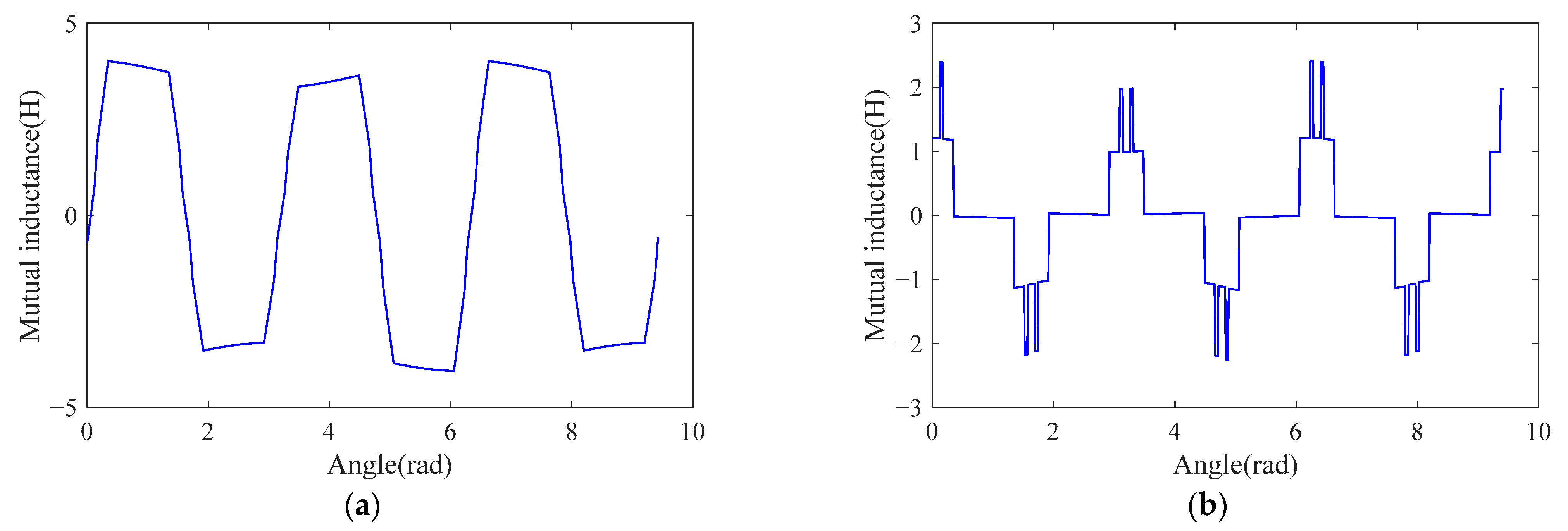
The self and mutual inductance of the stator and rotor can be calculated from Equation (8). Figure 7 shows the mutual inductance curves of stator phase a and rotor bar 1 in the rotor angular range $\left[0,3\pi \right]$ and their differentials, which allow us to determine the time-varying characteristics of the inductor during the motor operation. As shown in Figure 8, when the air gap is inhomogeneous due to static or dynamic eccentricity, etc., the mutual inductance curve will be distorted with respect to the eccentricity. This phenomenon of air gap length distribution affecting inductance variation can be explained by the air gap inverse function included in Equation (8).

In the MCC model, the inductance is coupled with the current through the flux linkage. While affecting the stator–rotor inductance matrix, the air gap length distribution can be derived by solving the rotor-bearing dynamics model. Therefore, the air gap length can be considered a common parameter of the MCC and dynamic models. Thus, the numerical calculation of the coupled model integrating these two models can be realized by parameter transfer.

4. Rotor-Bearing System Dynamic Modeling

The rotor-bearing system is shown in Figure 9. Differential equation of vibration of rotor-bearing system:

$$m_{\mathrm{r}}{\ddot{x}}_{\mathrm{r}}+c{\dot{x}}_{\mathrm{r}}+F_{\mathrm{bx}1}+F_{\mathrm{bx}2}=0,$$

(28)

$$m_{\mathrm{r}}{\ddot{y}}_{\mathrm{r}}+c{\dot{y}}_{\mathrm{r}}-F_{\mathrm{by}1}-F_{\mathrm{by}2}=-m_{\mathrm{r}}g,$$

(29)

where $m_{\mathrm{r}}$ is rotor mass, $c$ is rotor damping, $F_{\mathrm{bx}i}\left(i=1,2\right)$ is the restoring force of the $i\text{-}\mathrm{th}$ bearing in the x-direction, $F_{\mathrm{by}i}\left(i=1,2\right)$ is the restoring force of the $i\text{-}\mathrm{th}$ bearing in the Y-direction, and $g$ is the gravitational acceleration.

According to Hertzian contact theory, the total restoring force in both directions for a bearing with ball number ${\mathrm{n}}_{\mathrm{b}}$ is

$$F_{\mathrm{bx}}={\displaystyle \sum _{j=1}^{{\mathrm{n}}_{\mathrm{b}}}{\lambda }_j{K}_{\mathrm{c}}{\delta }_j^{3/2}\sin {\theta }_j}$$

(30)

$$F_{\mathrm{by}}={\displaystyle \sum _{j=1}^{{\mathrm{n}}_{\mathrm{b}}}{\lambda }_j{K}_{\mathrm{c}}{\delta }_j^{3/2}\cos {\theta }_j}$$

(31)

where ${\delta }_j$ is the contact deformation of the $j\text{-}\mathrm{th}$ ball; ${\lambda }_j$ is the contact coefficient of the $j\text{-}\mathrm{th}$ ball and ${\lambda }_j=1$ when ${\delta }_j>0$, otherwise, ${\lambda }_j=0$; $K_{\mathrm{c}}$ is the contact stiffness; and ${\theta }_j$ is the angular position of the $j\text{-}\mathrm{th}$ ball.

In the pure rolling case, where $d_{\mathrm{b}}$ is the ball diameter, $D_{\mathrm{b}}$ is the bearing pitch diameter, ${\omega }_{\mathrm{b}}$ is the orbital angular velocity of ball, $\alpha$ is the contact angle, and ${\omega }_{\mathrm{r}}$ is the rotor angular velocity, the ${\theta }_j$ at moment $t$ can be determined by the following equation:

$${\theta }_j\left(t\right)={\omega }_{\mathrm{b}}t+\frac{2\pi \left(j-1\right)}{{\mathrm{n}}_{\mathrm{b}}},$$

(32)

$${\omega }_{\mathrm{b}}=\frac{1}{2}{\omega }_{\mathrm{r}}\left(1-\frac{d_{\mathrm{b}}}{{\mathrm{D}}_{\mathrm{b}}}\cos \alpha \right).$$

(33)

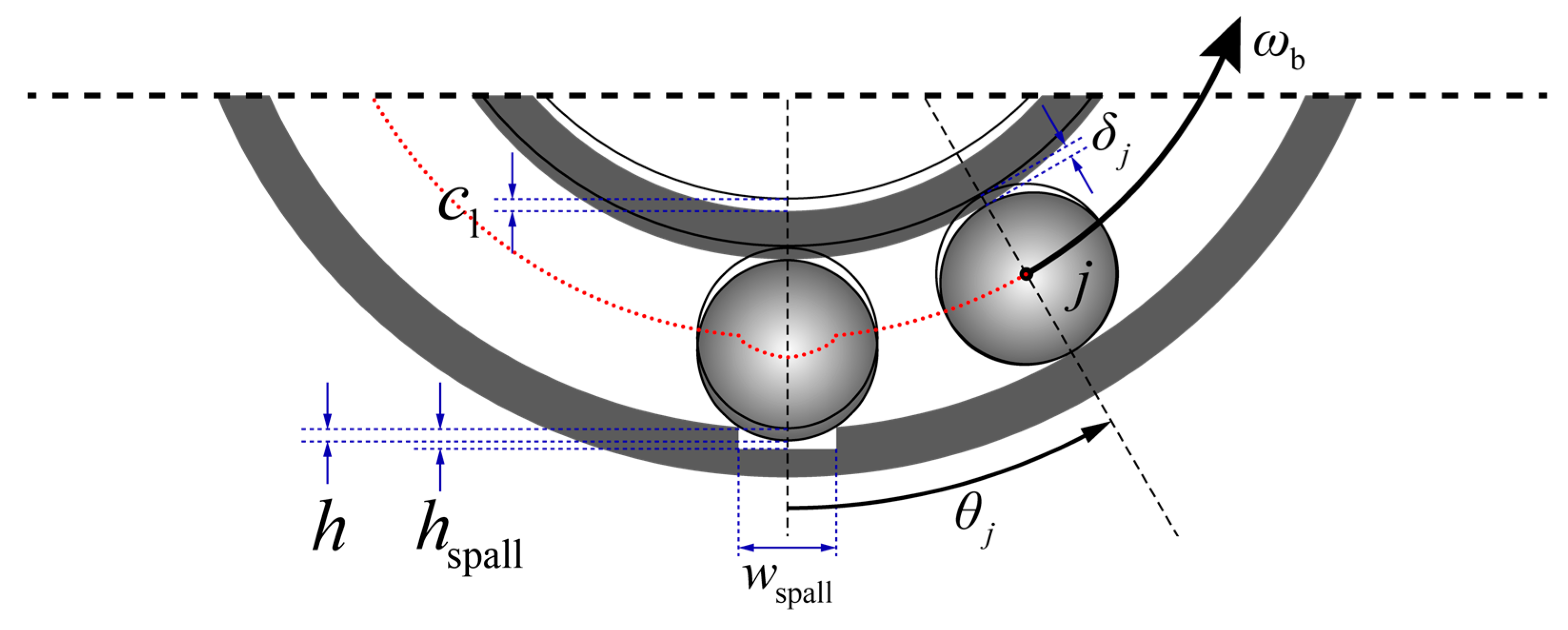
For the bearing’s outer and inner race spalling defect, the contact deformation of the $j\text{-}\mathrm{th}$ ball is

$${\delta }_j=x\sin {\theta }_j+y\cos {\theta }_j-c_{\mathrm{l}}-c_{\mathrm{l}j},$$

(34)

where $c_{\mathrm{l}}$ is the radial clearance of the bearing, and $c_{\mathrm{l}j}$ is the additional radial clearance when the ball passes through the spalling position.

As shown in Figure 10, Han et al. [19] simulated this additional radial clearance by the half-wave sine function, and its formula is expressed as

$$c_{\mathrm{l}j}=\{\begin{array}{ll}h\sin \left(\frac{\pi }{\Delta {\theta }_{\mathrm{spall}}}\left({\theta }_j-{\theta }_{\mathrm{spall}}\right)\right),\hfill & \mathrm{mod}\left({\theta }_j-{\theta }_{\mathrm{spall}},2\pi \right)<\Delta {\theta }_{\mathrm{spall}},\hfill \\ 0,\hfill & \mathrm{else},\hfill \end{array}$$

(35)

$$h=\{\begin{array}{cc}\left(\frac{d_{\mathrm{b}}}{2}-\sqrt{{\left(\frac{d_{\mathrm{b}}}{2}\right)}^2-{\left(\frac{w_{\mathrm{spall}}}{2}\right)}^2}\right)-\left(R_{\mathrm{o}}-\sqrt{R_{\mathrm{o}}^2-{\left(\frac{w_{\mathrm{spall}}}{2}\right)}^2}\right),& \mathrm{Outer} \mathrm{race} \mathrm{fault},\\ \left(\frac{d_{\mathrm{b}}}{2}-\sqrt{{\left(\frac{d_{\mathrm{b}}}{2}\right)}^2-{\left(\frac{w_{\mathrm{spall}}}{2}\right)}^2}\right)+\left(R_{\mathrm{i}}-\sqrt{R_{\mathrm{i}}^2-{\left(\frac{w_{\mathrm{spall}}}{2}\right)}^2}\right),& \mathrm{Inner} \mathrm{race} \mathrm{fault},\end{array}$$

(36)

$$\Delta {\theta }_{\mathrm{spall}}=\begin{array}{c}2\arcsin \left(\frac{w_{\mathrm{spall}}}{2R_{\mathrm{o}}}\right)\end{array},$$

(37)

where $h$ is the equivalent spalling depth considering the ball does not touch the bottom of the spalling, $w_{\mathrm{spall}}$ is the spalling width, $R_{\mathrm{o}}$ is the bearing outer race radius, ${\theta }_{\mathrm{spall}}$ is the angular position of the starting edge of the spalling, and $\Delta {\theta }_{\mathrm{spall}}$ is the spalling angle.

5. Electromagnetic–Dynamic Model Coupling Path

The rotor radial displacement in the rotor-bearing system dynamics model is decomposed into two directions that determine the air gap distribution between the stator and the rotor, as shown in Figure 11. In general terms, due to manufacturing errors and other reasons, the air gap of the motor in actual operation is usually uneven, and the additional radial displacement of the rotor caused by bearing failure exacerbates the situation. With the motor running, the dynamic eccentricity of the rotor is caused by the pulsation of the restoring force due to bearing failure, which in turn generates a time-varying air gap. The distribution of the air gap can be calculated in each numerical iteration. From the rotor displacement in both directions at moment $t$, the rotor eccentricity and eccentricity angle introduced due to bearing failure are

$$\begin{array}{c}{d}_{\mathrm{ecc}}=\sqrt{x_{\mathrm{r}}^2+y_{\mathrm{r}}^2}\hfill \\ {\theta }_{\mathrm{ecc}}=\{\begin{array}{ll}\arccos \left(-\frac{y_{\mathrm{r}}}{d_{\mathrm{ecc}}}\right),\hfill & x_{\mathrm{r}}\ge 0\hfill \\ 2\pi -\arccos \left(-\frac{y_{\mathrm{r}}}{d_{\mathrm{ecc}}}\right),\hfill & x_{\mathrm{r}}<0\hfill \end{array}\end{array}$$

(38)

Therefore, the distribution of the air gap length at moment $t$ is

$$g\left({\theta }_{\mathrm{s}},t\right)=g_0-d_{\mathrm{ecc}}\cos \left({\theta }_{\mathrm{ecc}}-{\theta }_{\mathrm{s}}\right)$$

(39)

The air gap length distribution is associated with the inductance through Equations (23) and (24), which in turn affects the stator current in the MCC, which is a clear path from the rotor-bearing system dynamics model coupled to the induction motor MCC model. Accordingly, the feedback of the dynamic behavior of the MCC model to the rotor-bearing dynamics model is achieved through the transfer of rotor angular velocity parameters by Equations (30) and (31). Therefore, by coupling the induction motor MCC model with the rotor-bearing dynamics model through the air gap length distribution and rotational velocity, we obtained the coupled electromagnetic–dynamic model of the induction motor, and its program is shown in Figure 12.

6. Simulation Results and Experimental Verification

6.1. Model Parameters

In order to verify the effectiveness of the coupled model, the bearing fault simulation of the three-phase, two-pole induction motor (Marathon D391) used in the experiment was conducted. The induction motor stator winding structure is single-layer, and the parameters of the MCC model as well as the rotor-bearing system model are given in

Table 2. MCC model parameters of the induction motor.

Parameters	Values
Number of phases	3
Number of poles	2
Power	1/3 Hp
Number of stator slots	24
Number of stator turns in series	61
Stator resistance	2.2 Ω
Number of rotor bars	34
Stack length	6 × 10−2 m
Rotor inertia	1.41882 × 10−3 kg∙m2
Rotor bar resistance	8 × 10−5 Ω
Rotor end ring resistance	2.375 × 10−5 Ω
Initial air gap	3 × 10−4 m
Air gap center radius	4.025 × 10−2 m

and

Table 3. Parameters of the rotor-bearing dynamic model.

Parameters	Values
Rotor mass	2.2299 kg
Rotor damping	600 N∙s/m
Bearing outside diameter	4 × 10−2 m
Bearing bore diameter	1.7 × 10−2 m
Bearing pitch diameter	2.9001 × 10−2 m
Bearing ball diameter	6.7564 × 10−3 m
Number of bearing balls	8
Bearing radial clearance	5 × 10−6 m
Contact stiffness	1.188 × 109 N/m3/2

, respectively.

6.2. Simulation Results

For the SKF 6203 bearing parameters given in Table 3, the fault characteristic frequency can be calculated by Equations (1)–(3). The frequency of outer race fault in the bearing is $f_{\mathrm{om}}=3.0681f_{\mathrm{r}}$, the frequency of inner race fault is $f_{\mathrm{im}}=4.9319f_{\mathrm{r}}$, and the frequency of ball fault is $f_{\mathrm{bm}}=4.0594f_{\mathrm{r}}$. Two types of failures, outer ring failure and inner ring failure, are simulated in the coupling model, where the spalling position of the outer ring failure is set to ${\theta }_{\mathrm{spall}}=0^{°}$ to ensure effective contact between the ball and the spalling. Since the spalling on the inner race rotates with the rotor, the inner race fault is not affected by the initial position of the spalling.

Firstly, simulation and analysis of the outer race fault were performed. Figure 13 shows the vibration spectrum in the Y-direction of the rotor (equivalent to the Y-direction of the inner race of the bearing) when powered by a 10 Hz supply frequency, where the two cases of normal and outer race failure are compared. From the comparison, it is clear that the overall vibration amplitude of the bearing dynamics model with outer race fault is higher than normal, while it has prominent amplitude at the outer race fault frequency and its harmonic frequency. This phenomenon is consistent with the vibration characteristics of real bearing outer race faults. It is worth noting that the vibration spectrum under normal conditions also has a prominent amplitude at the outer race fault characteristic frequency, which is determined by the bearing’s own characteristics. In the process of circumferential motion of rolling elements with bearing operation, the arrangement of rolling elements in the bearing repeats when the latter rolling element $j$ moves to the position of the former rolling element $j+1$, which means the bearing compliance (or stiffness) has a certain periodicity. Therefore, it is called variable flexibility (VC) vibration in the related literature [29,30]. In single-row bearings, the VC frequency is exactly equal to the rolling element passage frequency and also equal to the bearing outer race fault frequency.

The frequency domain plots of the stator currents with two power supply frequencies obtained by the electromagnetic–dynamic coupled model simulation are given in Figure 14 and Figure 15, where the two cases of normal and outer ring faults are compared. From the comparison, it can be seen that the bearing fault frequency is reflected in the stator current spectrum through the coupling path. Besides the power supply frequency and its harmonic components, the current spectrum under the outer race fault condition is still obviously higher than the normal condition at some of the characteristic frequencies, although the outer race fault characteristic frequency is close to some of the power supply harmonic frequencies due to the bearing parameters. Some of the characteristic frequencies, such as $f_{\mathrm{om}}-f_{\mathrm{s}},2f_{\mathrm{om}}+f_{\mathrm{s}},3f_{\mathrm{om}}+f_{\mathrm{s}}$, etc., have better performance in reflecting outer race fault at both supply frequencies.

Then, the inner race fault was simulated and analyzed. The vibration spectrum of the rotor in the Y-direction in the case of inner race fault is shown in Figure 16, where the characteristic frequency of the inner race fault and its multiplier amplitude are obvious. Since the inner race spalling rotates at rotor velocity during bearing operation, it results in a large modulation sideband around the inner race fault characteristic frequency and its multiplication. The interval between these modulation sidebands is exactly the rotor rotation frequency. In addition, the inner race fault did not cause a significant amplitude gain at the VC frequency, which laterally reflects the overlap between the outer race fault frequency and the VC frequency.

The stator current spectrum shown in Figure 17 and Figure 18 for the inner race fault case has a more complex frequency component than that of the outer race fault, associated with the presence of rotational velocity modulation in the inner race fault. Several fault characteristic frequencies including Equations (4) and (14) can be found on the spectrum, such as $f_{\mathrm{im}}-f_{\mathrm{s}}-f_{\mathrm{r}},f_{\mathrm{im}}+f_{\mathrm{s}}$, etc., which verifies the validity of these formulas to a certain extent. Furthermore, due to the velocity modulation, the limited energy originally concentrated at the inner race fault characteristic frequency is dispersed into other frequency components. The amplitude at the inner race fault characteristic frequency and its harmonic frequency is lower than that of the outer race fault. An intuitive explanation of this phenomenon is provided by Stack et al. [31]. A spalling defect located on the inner race rotates in and out of the load zone formed by the gravity of the rotor with the rotation of the shaft. In this case, the strong fault features generated when the defect is in the load zone are averaged with the weaker features obtained when the defect is outside the load zone, which has the effect of attenuating the magnitude of the inner race feature fault frequency. Simulation results in the work of Patel et al. [32] verified that the effect of inner race defects on vibration is weaker than that of outer race defects with the same spall size. The lower the vibration amplitude, the lower the amplitude of the characteristic frequency component reflected to the stator current through the air gap fluctuation, which means that the detection of bearing inner race fault by characteristic frequency amplitude is more difficult than the detection of outer race fault.

6.3. Experimental Platform and Measurement Condition

The experiments in this study were conducted on a machinery fault simulator. As shown in Figure 19, the experimental bench mainly consists of an induction motor, inverter, brake, and photoelectric sensor. The photoelectric sensor is used to obtain the rotor rotation velocity of the motor. The FLUKE i200 s AC current clamp is used to measure the current signal in the stator three-phase windings. The motor end cap vibration signal is measured by the IMI 608A11 acceleration sensor.

The bearing outer race spalling fault is simulated by cutting grooves on the inner surface of the outer race with a spalling width of about 3 mm, as shown in Figure 20. Due to the limitation of the type of bearing fault motor provided by the experimental platform, only outer ring spalling fault experiments were conducted in this study.

6.4. Experimental Results

Figure 21 and Figure 22 show the vibration spectrum and the stator current spectrum of the motor drive end cap at 10 Hz supply frequency, respectively. In the vibration spectrum, beyond the rotational frequency and its multiples, significant bearing outer race fault characteristic components can be observed, i.e., the outer race spalling exhibits significant dynamic characteristics. The presence of a 50 Hz sensor supply frequency may be due to the measurement system not being fully grounded. In the stator current spectrum, the amplitude of the multiplication of the fundamental frequency of the power supply is significantly higher than the simulated spectrum due to the non-ideal sinusoidal waveform of the supply voltage output from the inverter. The modulation sidebands that exist around the power-related frequency may be due to torque fluctuations. Excluding the interference components mentioned above, the amplitude gain at the bearing outer race fault characteristic frequency is still visible. Although the gain of the characteristic frequency in the experimental signal is lower than that in the simulated signal because of reasons that are difficult to take into account in the simulation model, such as noise, the characteristic frequency of the experimental signal matches well with that of the simulated signal. The characteristic frequencies $f_{\mathrm{om}}-f_{\mathrm{s}},2f_{\mathrm{om}}+f_{\mathrm{s}},4f_{\mathrm{om}}+f_{\mathrm{s}}$, etc., all have obvious amplitude gain generated by the outer race fault. In the same experimental conditions using a power supply frequency of 20 Hz, the vibration spectrum and stator current spectrum are shown in Figure 23 and Figure 24, respectively. The outer race fault characteristics are still significantly represented in its vibration spectrum. In the stator current spectrum, there are significant amplitude gains at the characteristic frequencies $f_{\mathrm{om}}-f_{\mathrm{s}},3f_{\mathrm{om}}-f_{\mathrm{s}},4f_{\mathrm{om}}+f_{\mathrm{s}}$. The above experimental results initially verify the derivation of the motor bearing fault characteristic frequency equation and the validity of the electromagnetic–dynamic coupled model.

7. Conclusions

We propose a modeling method for constructing a coupled electromagnetic–dynamic model of an induction motor based on the MCC model and rotor-bearing system dynamics model. The time-varying air gap length distribution was obtained from the rotor-bearing system dynamics model. The stator–rotor time-varying mutual inductance was calculated by WFA. The MCC model was applied to simulate the electromagnetic behavior and dynamics of the motor; its velocity was fed back into the rotor-bearing system dynamics model to implement iterative calculations. The characteristic frequency corresponding with bearing faults in the stator currents are obtained by derivation and examined in the frequency domain of the simulation and experimental results, which validates the effectiveness of this electromagnetic–dynamic coupled modeling method.

The coupled modeling method integrating a multi-loop model and a rotor-bearing system dynamics model advanced in this paper is capable of simulating a wide range of mechanical and electrical faults in motors, providing a new way to construct models that can reflect the electromagnetic and dynamic states of motors centrally. This method takes into account the model complexity and computational cost as much as possible, and facilitates the rapid updating of motor model parameters and the online application of advanced fault diagnosis algorithms. For experimental constraints, we only experimentally verified the bearing outer ring spalling fault. In future studies, we will perfect the experimental conditions to further investigate the reflection of motor bearing fault characteristics in stator current, including inner ring and ball spalling faults. Moreover, we will investigate how to further improve the calculation efficiency of inductance parameters and optimize the model structure in our upcoming work.