Mechanism Design and Performance Analysis of a Sitting/Lying Lower Limb Rehabilitation Robot
Abstract
:1. Introduction
2. Range of Motion Analysis of Lower Limbs in Humans’ Sitting/Lying Position
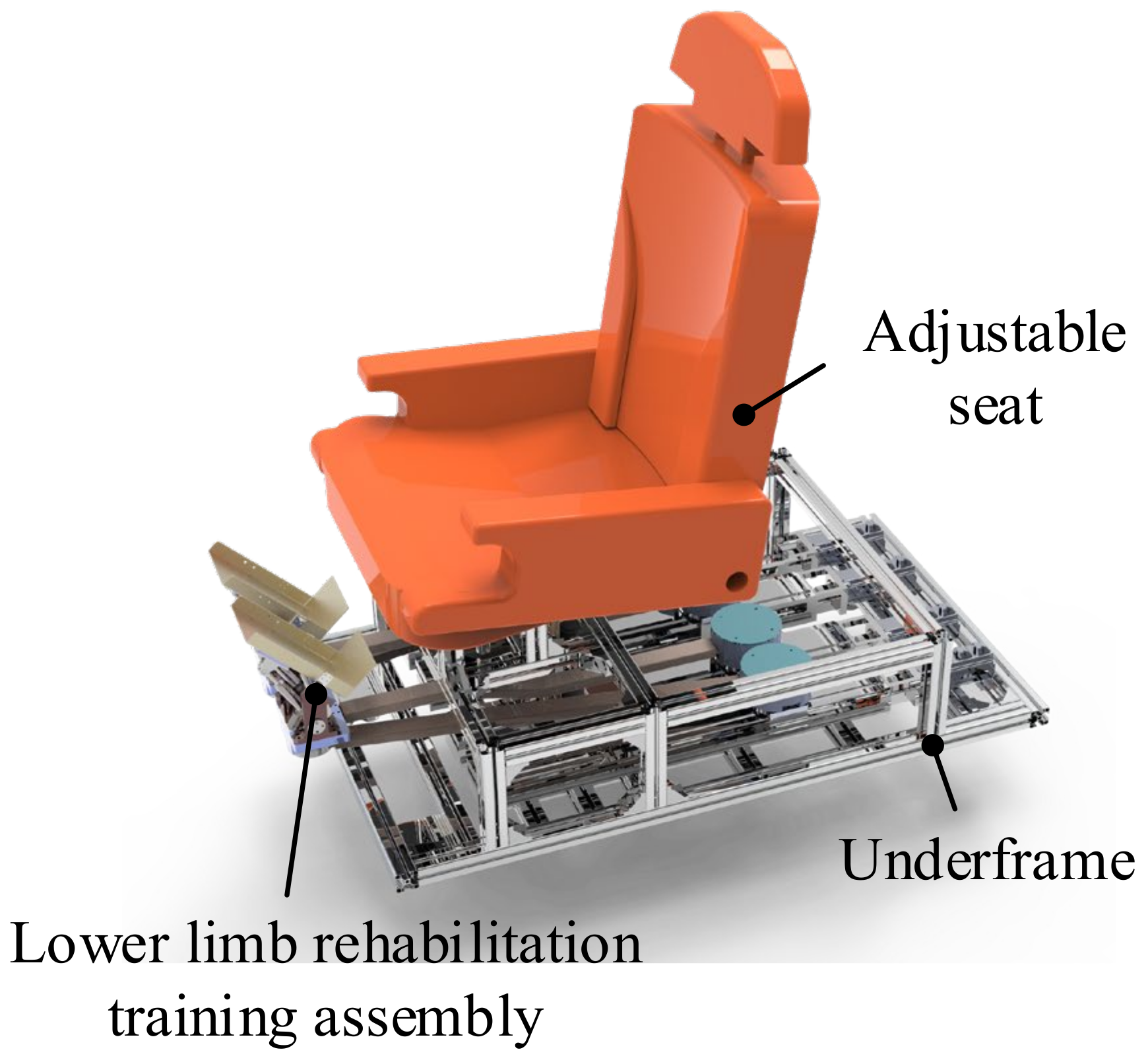
3. Mechanical Structure Design
3.1. Mechanical Structure Description
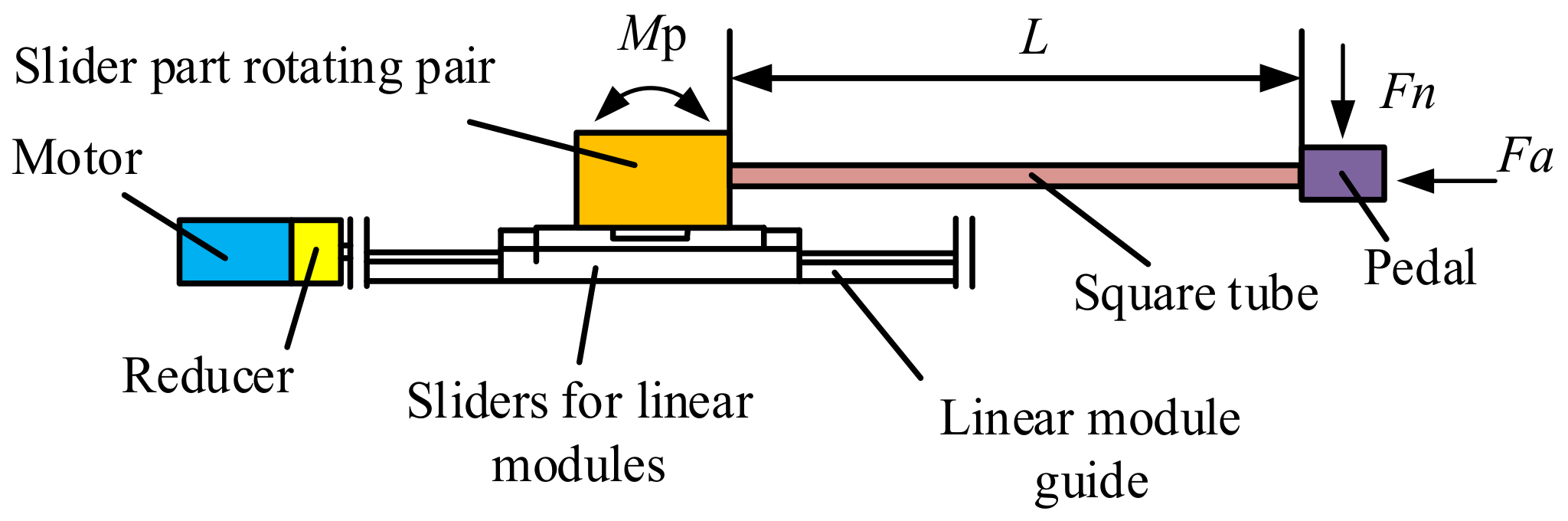
3.2. Selection of Motor Drive
3.2.1. Precision Linear Module Selection
3.2.2. Selection of Drive Motor and Reducer
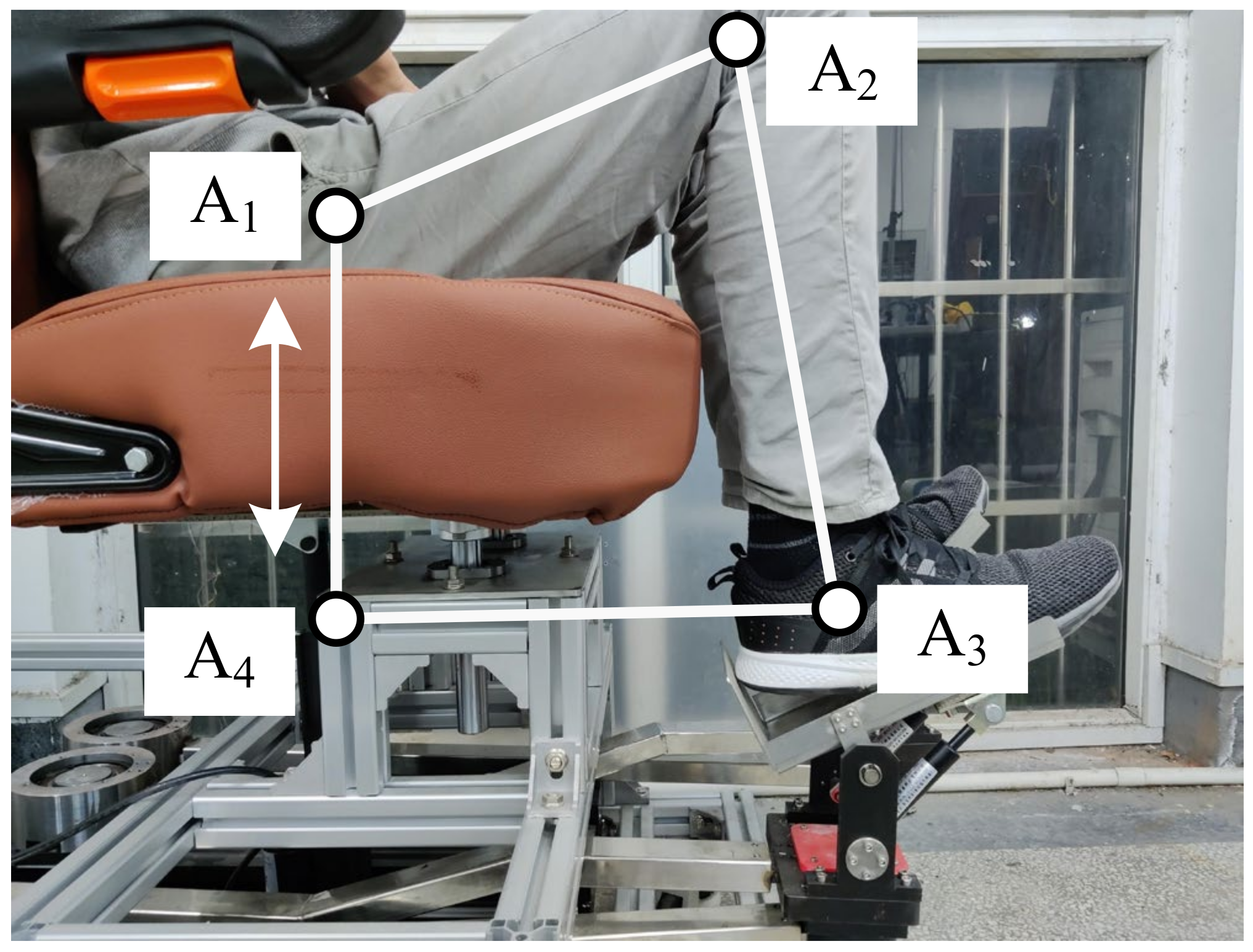
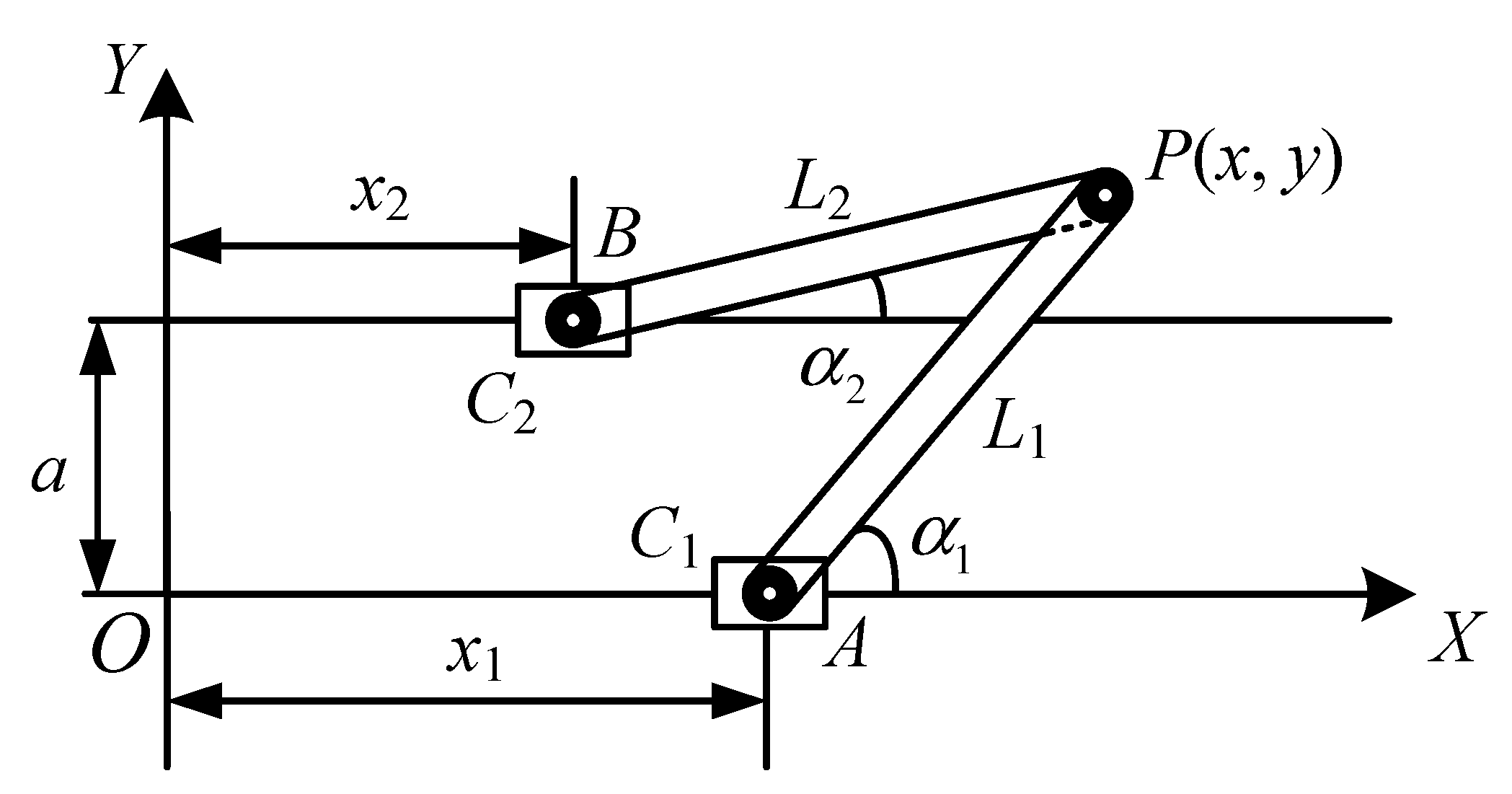
4. Kinematics Analysis of Mechanism
4.1. Forward and Inverse Kinematics
4.2. Jacobian Matrices and Singularity Analysis
4.2.1. Jacobian Matrix
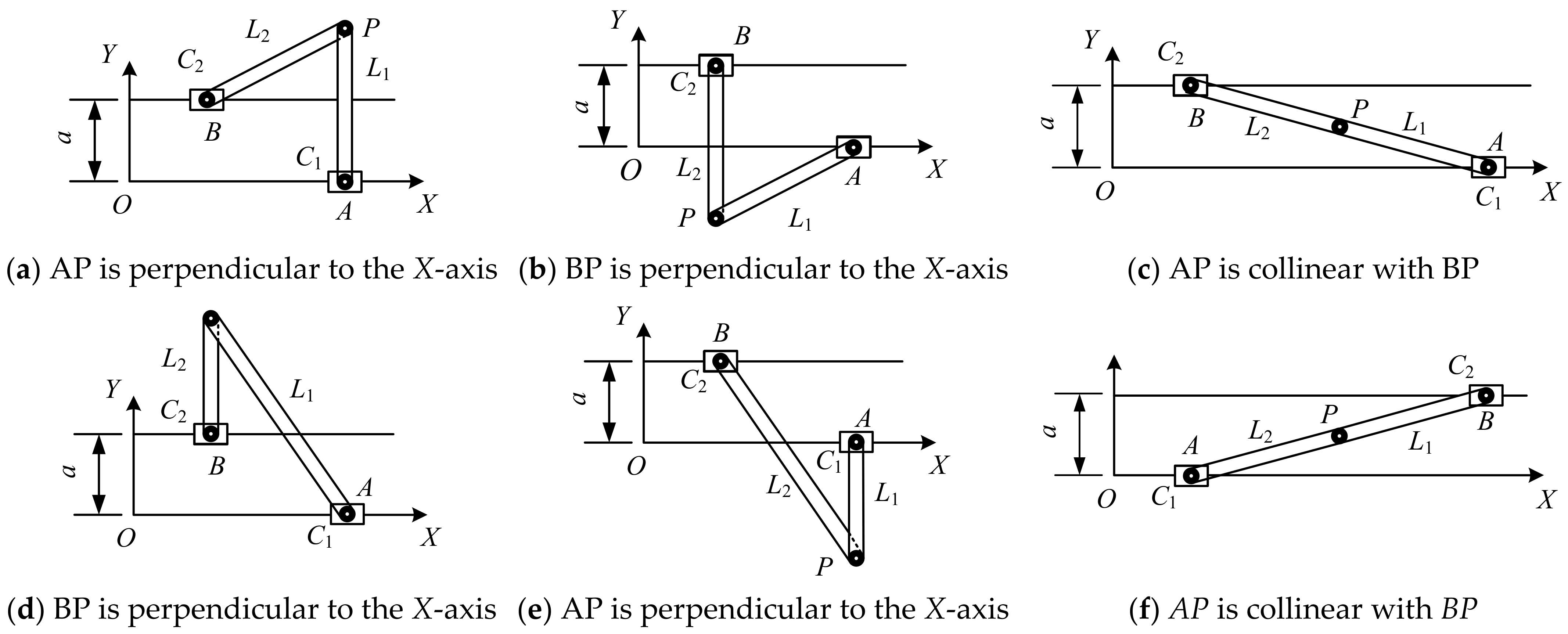
4.2.2. Singularity Analysis
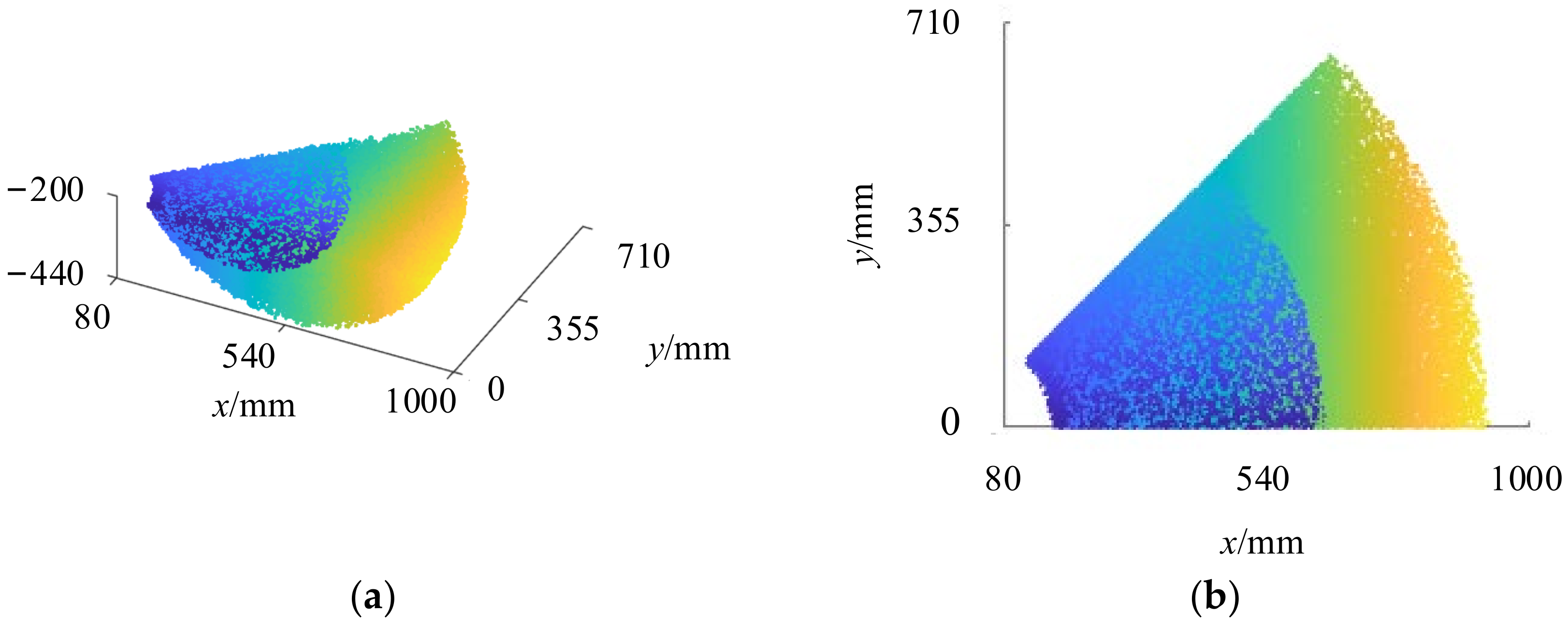
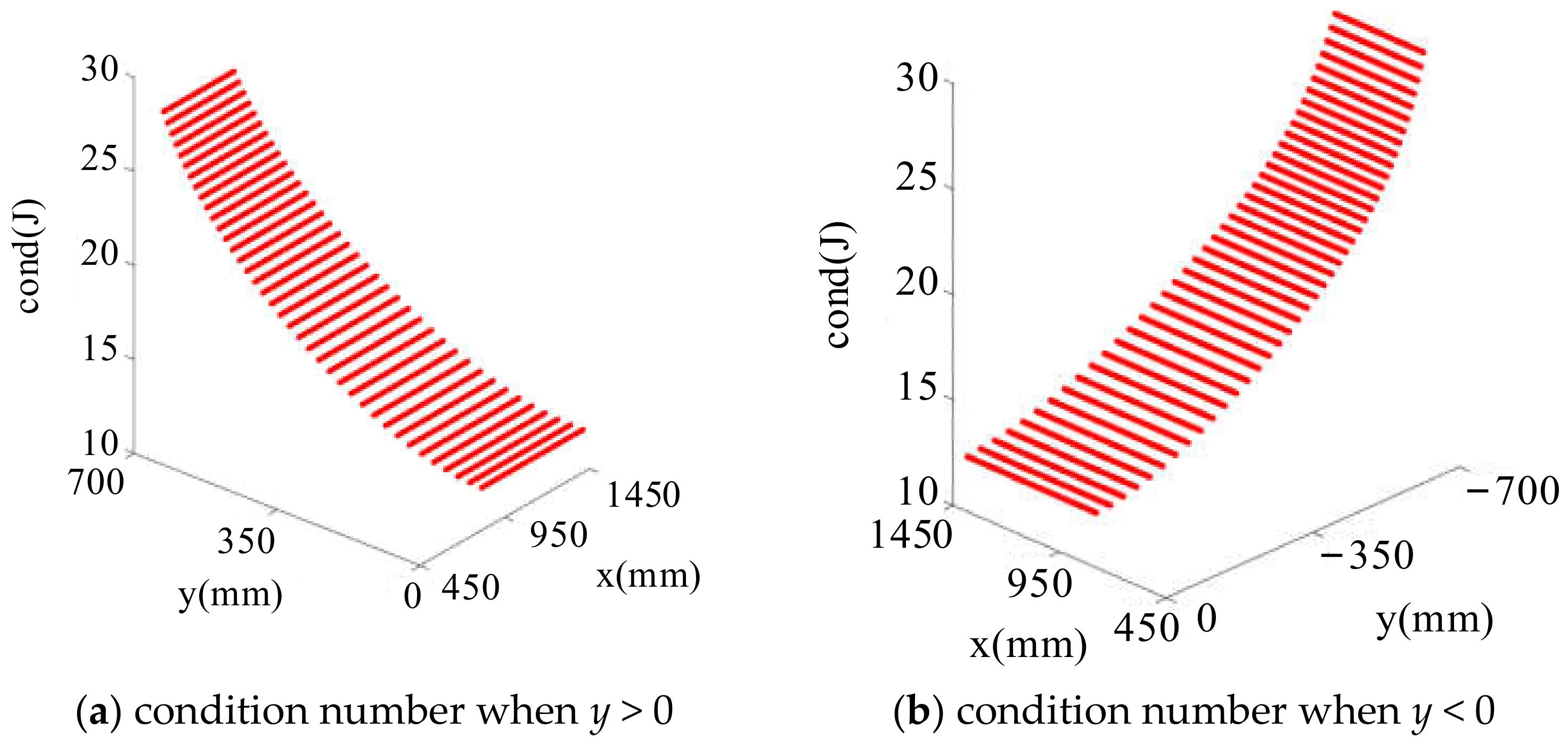
4.3. Condition Number
5. Trajectory Planning
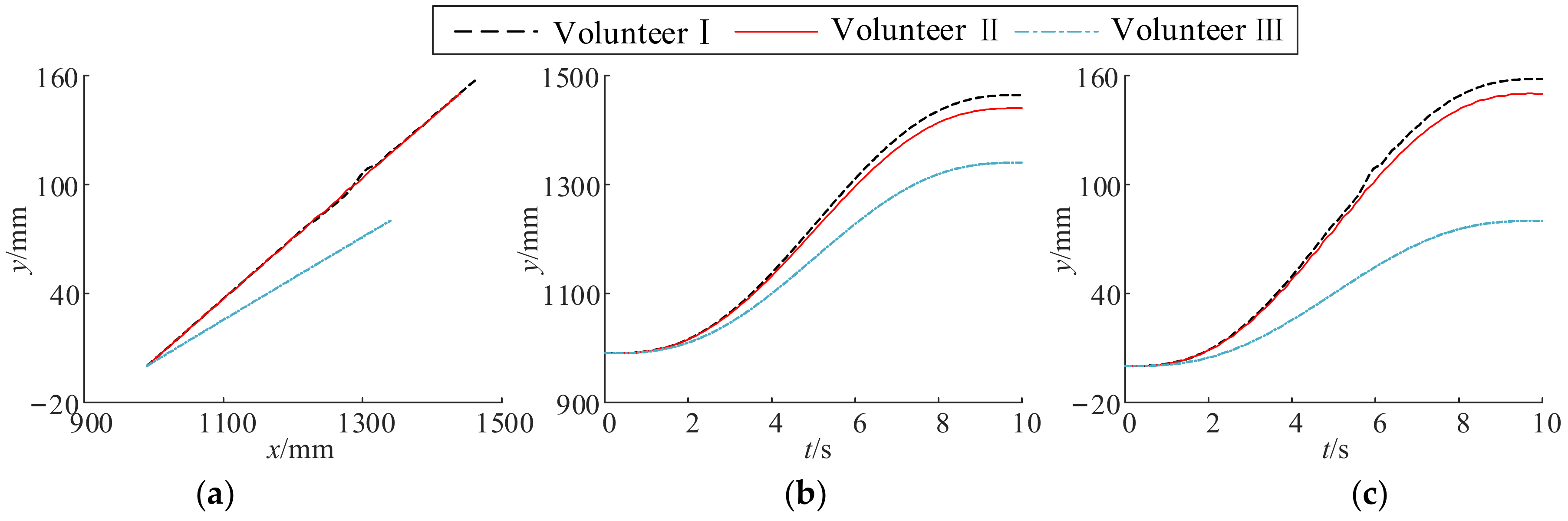
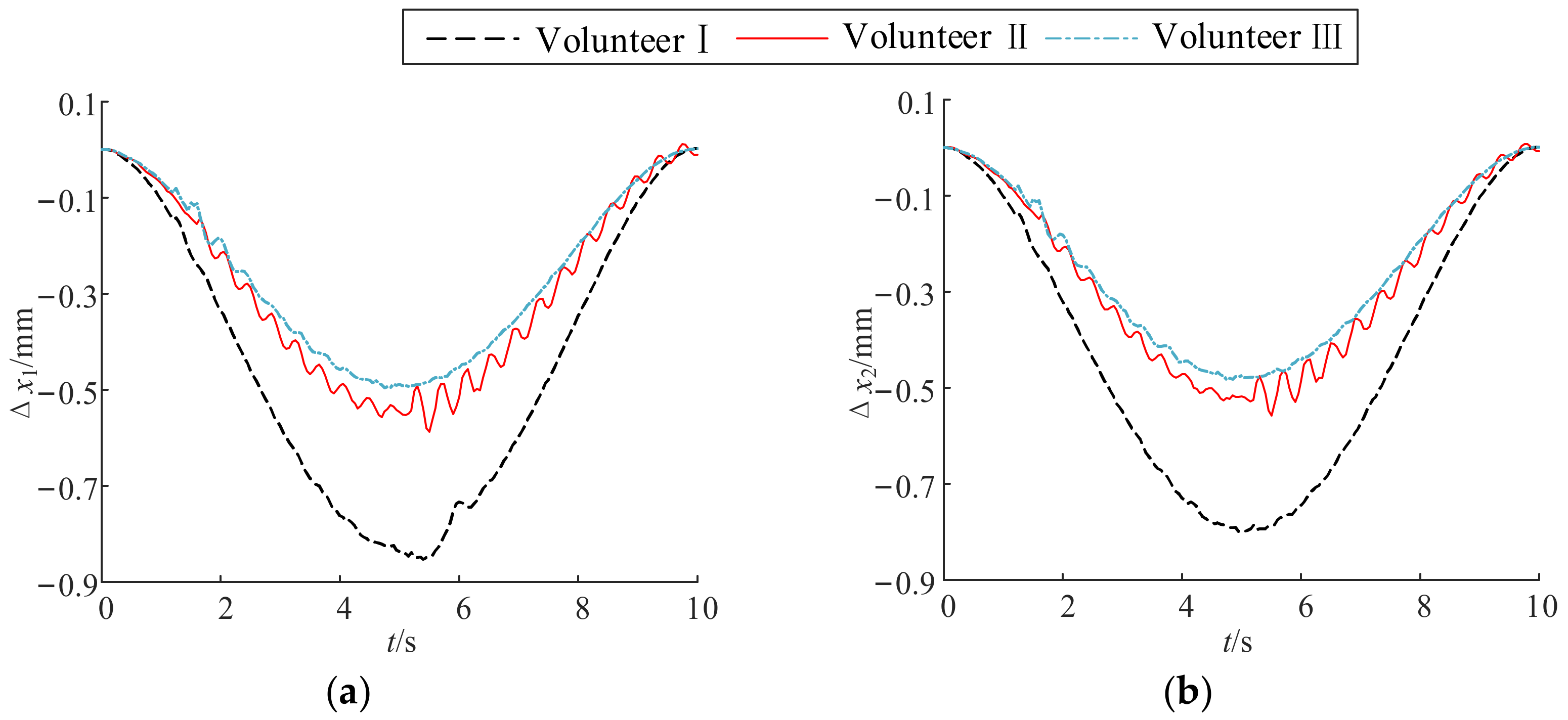
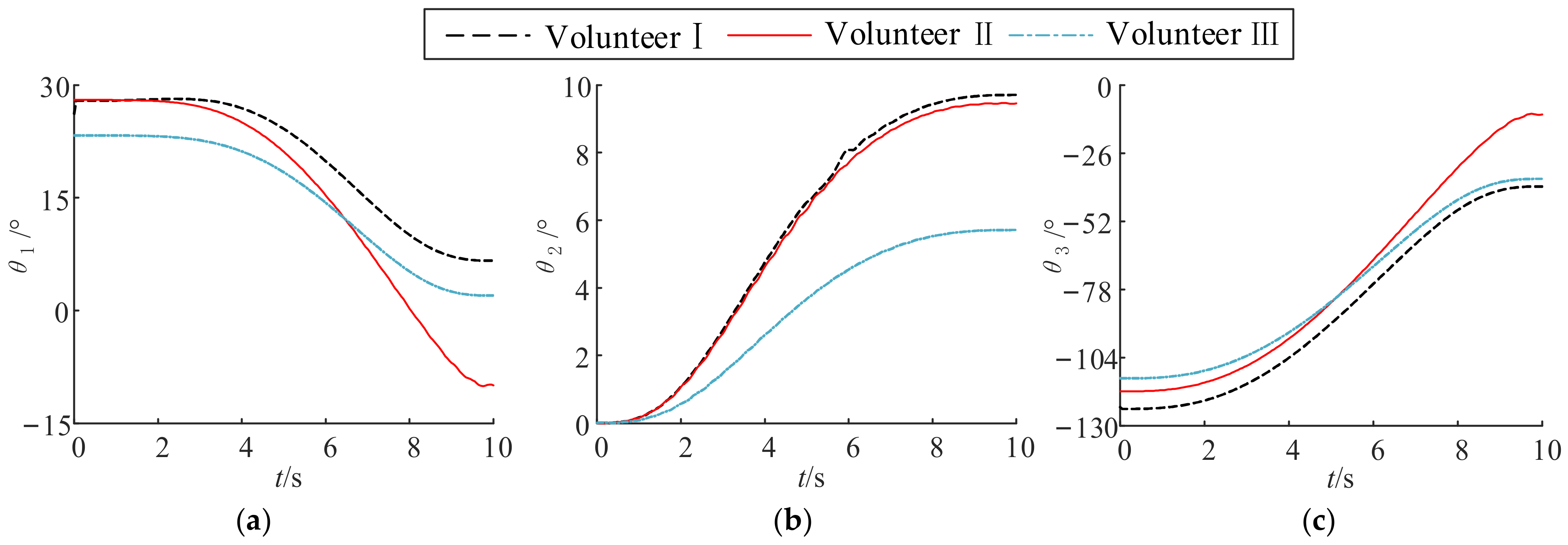
6. Experiment and Evaluation
6.1. Experimental Setup
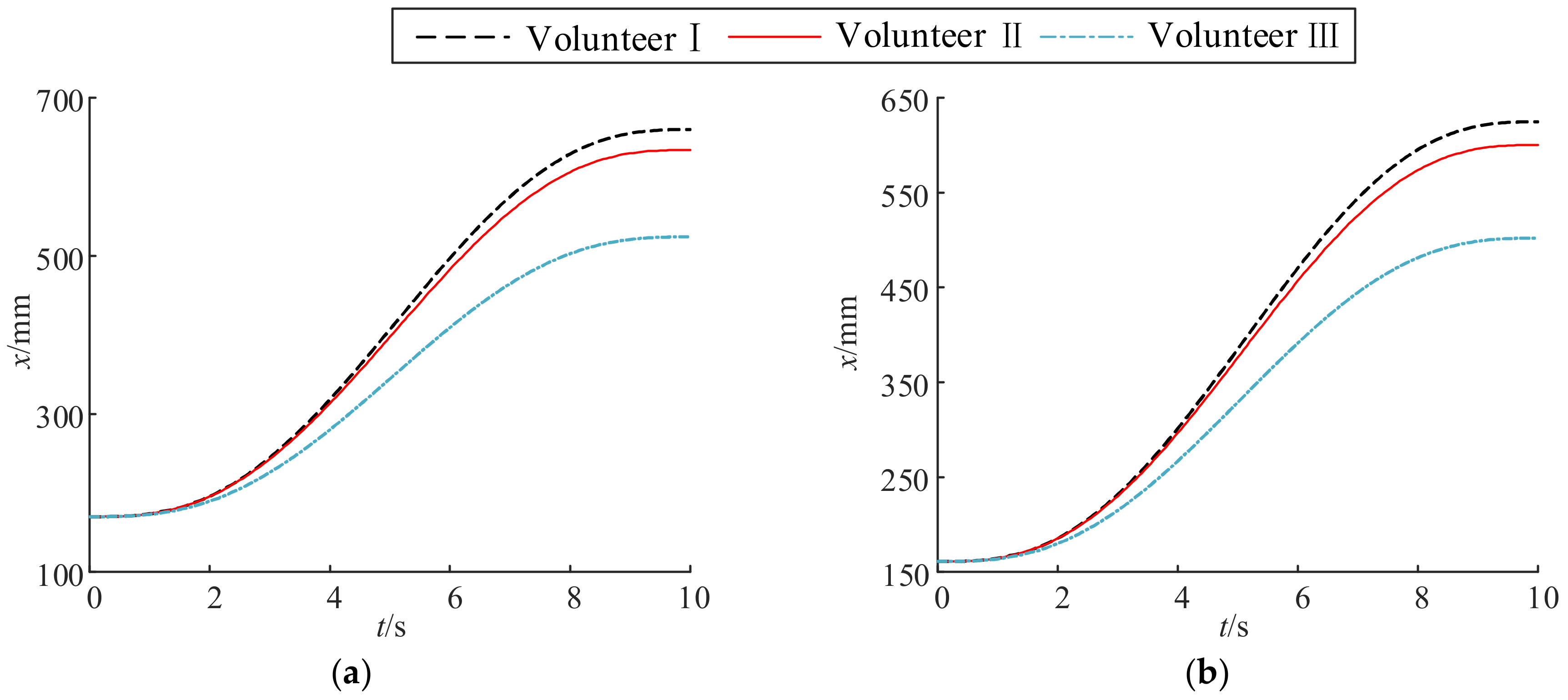
6.2. Experimental Result and Evaluation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, J.P.; Gao, J.W.; Song, R.; Li, R.H.; Li, Y.N.; Jiang, L.L. The design and control of a 3DOF lower limb rehabilitation robot. Mechatronics 2016, 33, 13–22. [Google Scholar] [CrossRef]
- De Rooij, I.J.; Van De Port, I.G.; Meijer, J.G. Effect of virtual reality training on balance and gait ability in patients with stroke: Systematic review and metaanalysis. Phys. Ther. 2016, 96, 1905–1918. [Google Scholar] [CrossRef] [PubMed]
- Dharma, K.K.; Damhudi, D.; Yardes, N.; Haeriyanto, S. Increase in the functional capacity and quality of life among stroke patients by family care-giver empowerment program based on adaptation model. Int. J. Nurs. Sci. 2018, 5, 357–364. [Google Scholar]
- Almaghout, K.; Tarvirdizadeh, B.; Alipour, K.; Hadi, A. Design and control of a lower limb rehabilitation robot considering undesirable torques of the patient’s limb. Proc. Inst. Mech. Eng. Part H: J. Eng. Med. 2020, 234, 1457–1471. [Google Scholar] [CrossRef]
- Miao, M.D.; Gao, X.S.; Zhu, W. A construction method of lower limb rehabilitation robot with remote control system. Appl. Sci. 2021, 11, 867. [Google Scholar] [CrossRef]
- Wu, S.M.; Wu, B.; Liu, M.; Chen, Z.M.; Wang, W.Z.; Anderson, C.S.; Sandercock, P.; Wang, Y.J.; Huang, Y.N.; Cui, L.Y.; et al. Stroke in China: Advances and challenges in epidemiology, prevention, and management. Lancet Neurol. 2019, 18, 394–405. [Google Scholar] [CrossRef]
- Costandi, M. Rehabilitation: Machine recovery. Nature 2014, 510, S8–S9. [Google Scholar] [CrossRef]
- Wang, F.; Qian, Z.Q.; Lin, Y.Z.; Zhang, W.J. Design and rapid construction of a cost-effective virtual haptic device. IEEE/ASME Trans. Mechatron. 2020, 26, 66–77. [Google Scholar] [CrossRef]
- Deaconescu, T.; Deaconescu, A. Pneumatic muscle actuated isokinetic equipment for the rehabilitation of patients with disabilities of the bearing joints. In Proceedings of the International Multi-Conference of Engineers and Computer Scientists, Hongkong, China, 18–20 March 2009; pp. 1823–1827. [Google Scholar]
- Feng, Y.F.; Wang, H.B.; Lu, T.T.; Vladareanuv, V.; Li, Q.; Zhao, C.S. Teaching training method of a lower limb rehabilitation robot. Int. J. Adv. Robot. Syst. 2016, 13, 57. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Ma, H.; Qin, L.Y.; Gao, F.; Chan, K.M.; Law, S.W.; Qin, L.; Liao, W.H. Recent developments and challenges of lower extremity exoskeletons. J. Orthop. Transl. 2016, 5, 26–37. [Google Scholar] [CrossRef] [Green Version]
- Hwang, S.H.; Sun, D.I.; Han, J.; Kim, W.S. Gait pattern generation algorithm for lower-extremity rehabilitation–exoskeleton robot considering wearer’s condition. Intell. Serv. Robot. 2021, 14, 345–355. [Google Scholar] [CrossRef]
- Long, Y.; Du, Z.J.; Wang, W.D.; Dong, W. Human motion intent learning based motion assistance control for a wearable exoskeleton. Robot. Comput.–Integr. Manuf. 2018, 49, 317–327. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, A.; Lobo-Prat, J.; Font-Llagunes, J.M. Systematic review on wearable lower-limb exoskeletons for gait training in neuromuscular impairments. J. Neuroeng. Rehabil. 2021, 18, 1–21. [Google Scholar] [CrossRef]
- Chen, B.; Zhong, C.H.; Zhao, X.; Ma, H.; Guan, X. A wearable exoskeleton suit for motion assistance to paralysed patients. J. Orthop. Transl. 2017, 11, 7–18. [Google Scholar] [CrossRef]
- Vaughan-Graham, J.; Brooks, D.; Rose, L.; Nejat, G.; Pons, J.; Patterson, K. Exoskeleton use in post-stroke gait rehabilitation: A qualitative study of the perspectives of persons post-stroke and physiotherapists. J. Neuroeng. Rehabil. 2020, 17, 1–15. [Google Scholar] [CrossRef]
- Esquenazi, A.; Talaty, M.; Jayaraman, A. Powered exoskeletons for walking assistance in persons with central nervous system injuries: A narrative review. PMR 2017, 9, 46–62. [Google Scholar] [CrossRef]
- Yang, X.; She, H.T.; Lu, H.J.; Fukuda, T.; Shen, Y.J. State of the Art: Bipedal Robots for Lower Limb Rehabilitation. Appl. Sci. 2017, 7, 1182. [Google Scholar] [CrossRef] [Green Version]
- Morone, G.; Paolucci, S.; Cherubini, A.; De Angelis, D.; Venturiero, V.; Coiro, P.; Iosa, M. Robot-assisted gait training for stroke patients: Current state of the art and perspectives of robotics. Neuropsychiatr. Dis. Treat. 2017, 13, 1303–1311. [Google Scholar] [CrossRef] [Green Version]
- Calabrò, R.S.; Cacciola, A.; Bertè, F.; Manuli, A.; Leo, A. Robotic gait rehabilitation and substitution devices in neurological disorders: Where are we now? Neurol. Sci. 2016, 37, 503–514. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Y.P.; Guo, X.B.; Zhou, S.T.; Jia, L.F. Parameter identification and adaptive compliant control of rehabilitation exoskeleton based on multiple sensors. Measurement 2020, 159, 107765. [Google Scholar] [CrossRef]
- Chrif, F.; Nef, T.; Lungarella, M.; Dravid, R.; Hunt, K.J. Control design for a lower-limb paediatric therapy device using linear motor technology. Biomed. Signal Processing Control 2017, 38, 119–127. [Google Scholar] [CrossRef]
- Eiammanussakul, T.; Sangveraphunsiri, V. A lower limb rehabilitation robot in sitting position with a review of training activities. J. Healthc. Eng. 2018, 2018, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohanta, J.K.; Mohan, S.; Deepasundar, P.; Kiruba-Shankar, R. Development and control of a new sitting-type lower limb rehabilitation robot. Comput. Electr. Eng. 2017, 67, 330–347. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, T.M.; Wang, L.P.; Chen, F.F. Improving tracking accuracy of a novel 3-DOF redundant planar parallel kinematic machine. Mech. Mach. Theory 2018, 119, 198–218. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, L.; Zheng, H.Y.; Zhou, Y.; Peng, Y.; Lyu, S.N. Kinematic stability of a 2-DOF deployable translational parallel manipulator. Mech. Mach. Theory 2021, 160, 104261. [Google Scholar] [CrossRef]
- Yu, Y.; Tao, H.B. A parallel mechanism and a control strategy based on interactive force using on hip joint power assist. Int. J. Mechatron. Autom. 2014, 4, 39–51. [Google Scholar] [CrossRef]
- Girone, M.; Burdea, G.; Bouzit, M.; Popescu, V.; Deutsch, J.E. A Stewart platform-based system for ankle telerehabilitation. Auton. Robot. 2001, 10, 203–212. [Google Scholar] [CrossRef]
- Erdogan, A.; Celebi, B.; Satici, A.C.; Patoglu, V. ASSIST ON-ANKLE: A reconfigurable ankle exoskeleton with series-elastic actuation. Auton. Robot. 2017, 41, 743–758. [Google Scholar] [CrossRef]
- Giberti, H.; Cinquemani, S.; Legnani, G. A practical approach to the selection of the motor-reducer unit in electric drive systems. Mech. Based Des. Struct. Mach. 2011, 39, 303–319. [Google Scholar] [CrossRef]






| Joint | Datum Plane | Movement | Angle Range (°) |
|---|---|---|---|
| Hip | Sagittal plane | Flexion (lying pos.) | 0~125 |
| Flexion (sitting pos.) | 0~45 | ||
| Coronal plane | Abduction (lying pos.) | 0~45 | |
| Adduction (sitting pos.) | 0~45 | ||
| Knee | Sagittal plane | Flexion | −150~0 |
| Ankle | Sagittal plane | Dorsiflexion | 0~20 |
| Flexion | 0~45 |
| Control Component | Model | Basic Parameters | Number |
|---|---|---|---|
| Upper computer | HP 15-bc011TX | i5-6300HQ CPU @ 2.30 GHz | 1 |
| Motor | SDGA-02C12BD | 0.2 KW, 36 V, 0.64 N.m | 4 |
| Linear module | NDC86-1510-740-1-P-F0-S2 | 610 mm | 4 |
| Speed reducer | 60ZDF5-400T1 | 5:1 | 4 |
| Actuators | TSDA-C11A | RS-232 | 4 |
| Relay board | WF-16i-16o | RS-485 | 1 |
| Encoder | / | 2500 p/r | 4 |
| Software | QT 5.9.7 | / | 1 |
| Volunteer | Gender | Thigh Length | Calf Length |
|---|---|---|---|
| Ⅰ | Male | 560 mm | 450 mm |
| Ⅱ | Male | 500 mm | 435 mm |
| Ⅲ | Male | 480 mm | 390 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, F.; Li, H.; Feng, Y. Mechanism Design and Performance Analysis of a Sitting/Lying Lower Limb Rehabilitation Robot. Machines 2022, 10, 674. https://doi.org/10.3390/machines10080674
Dong F, Li H, Feng Y. Mechanism Design and Performance Analysis of a Sitting/Lying Lower Limb Rehabilitation Robot. Machines. 2022; 10(8):674. https://doi.org/10.3390/machines10080674
Chicago/Turabian StyleDong, Fangyan, Haoyu Li, and Yongfei Feng. 2022. "Mechanism Design and Performance Analysis of a Sitting/Lying Lower Limb Rehabilitation Robot" Machines 10, no. 8: 674. https://doi.org/10.3390/machines10080674
APA StyleDong, F., Li, H., & Feng, Y. (2022). Mechanism Design and Performance Analysis of a Sitting/Lying Lower Limb Rehabilitation Robot. Machines, 10(8), 674. https://doi.org/10.3390/machines10080674






