Intelligent Diagnosis Method for Mechanical Faults of High-Voltage Shunt Reactors Based on Vibration Measurements
Abstract
1. Introduction
- (1)
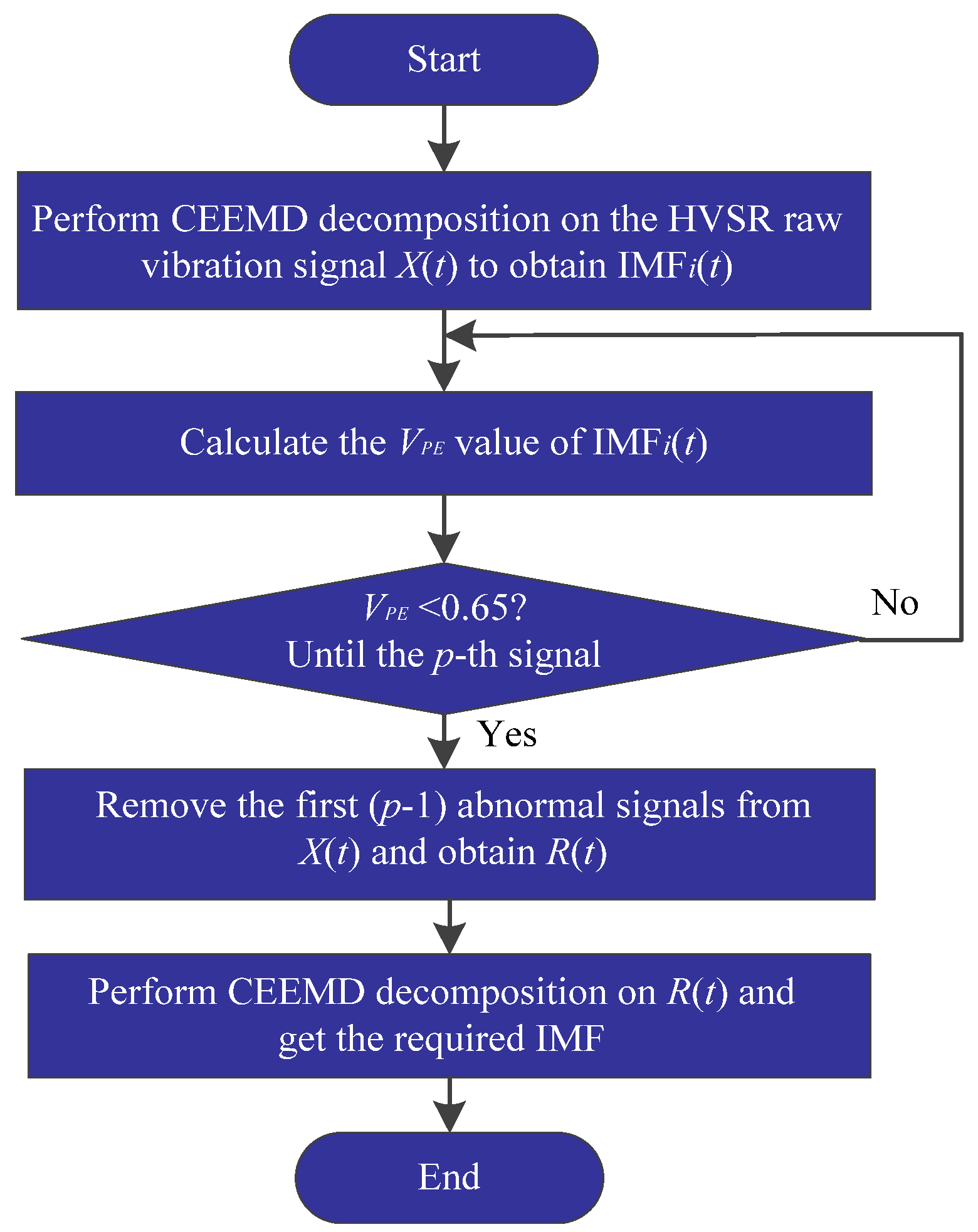
- Aiming at the problem of modal aliasing, we introduce permutation entropy (PE) into CEEMD to remove noise and abnormal components that cause mode confusion so as to obtain more effective feature quantities.
- (2)
- To reduce the redundancy of features and improve the effectiveness of features, this paper uses MI to calculate the correlation between the IMF components and the original vibration signal, and takes the IMF component with the highest correlation as the feature quantity. Furthermore, MFE is used to quantify features to quantitatively reflect different fault types and fault degrees of HVSR.
- (3)
- To improve the accuracy of fault feature recognition, an IGOA-PNN fault recognition model is proposed in this study. The smoothing factor of the PNN is optimized with the optimized IGOA to achieve the best classification.
2. Research Methodology
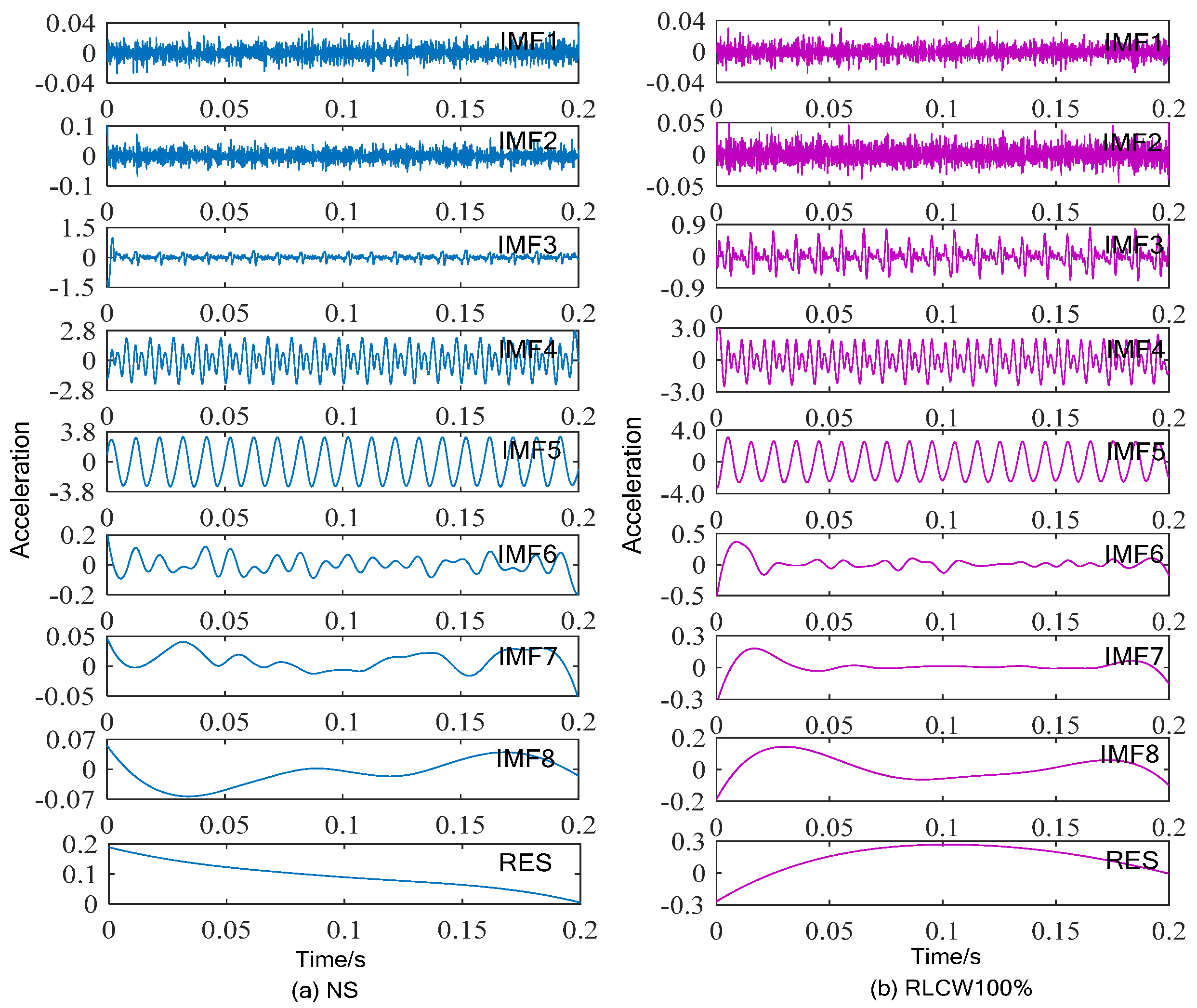
2.1. MCPCEEMD Method
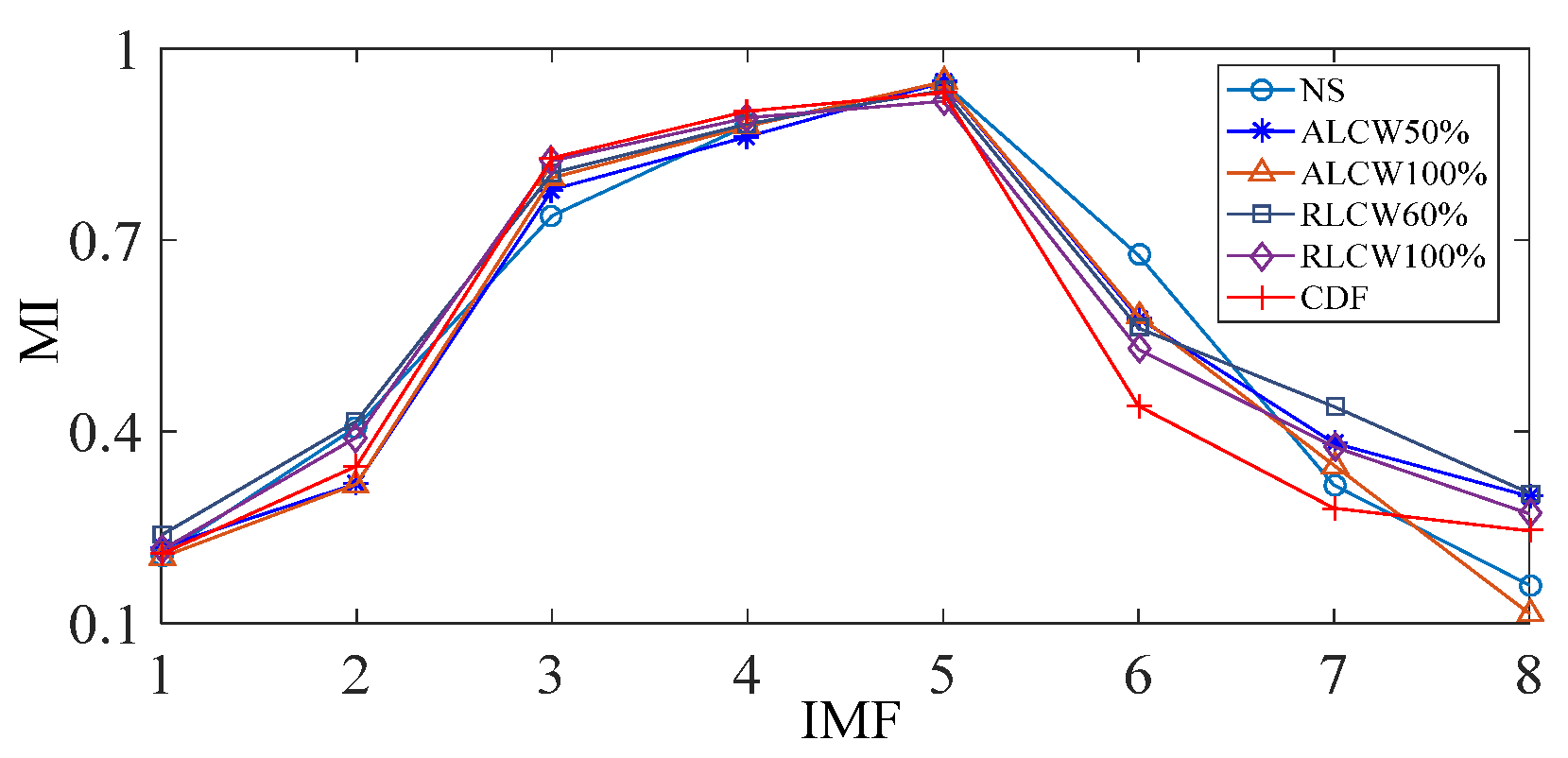
2.2. Mutual Information Introduction
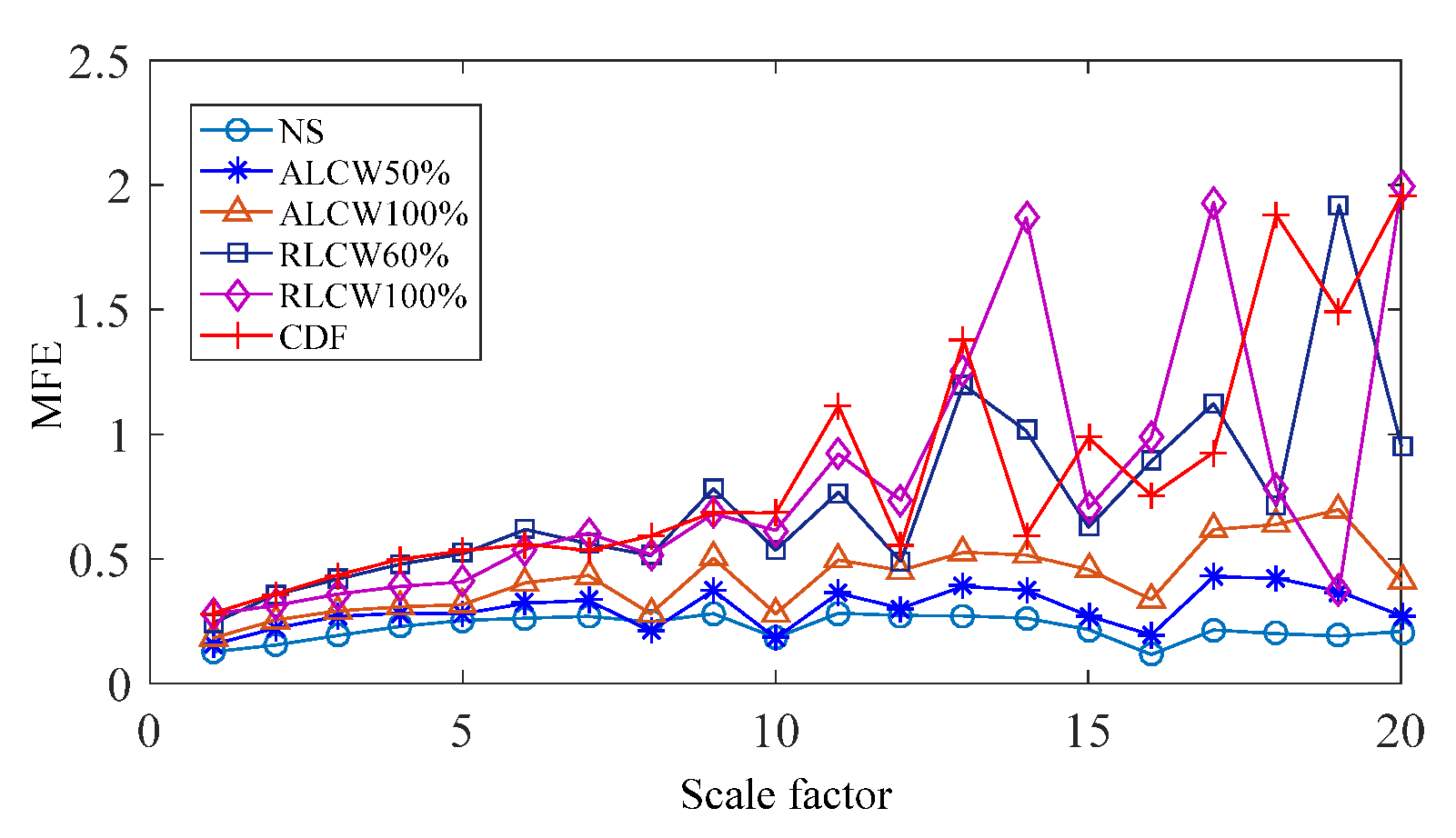
2.3. Multiscale Fuzzy Entropy
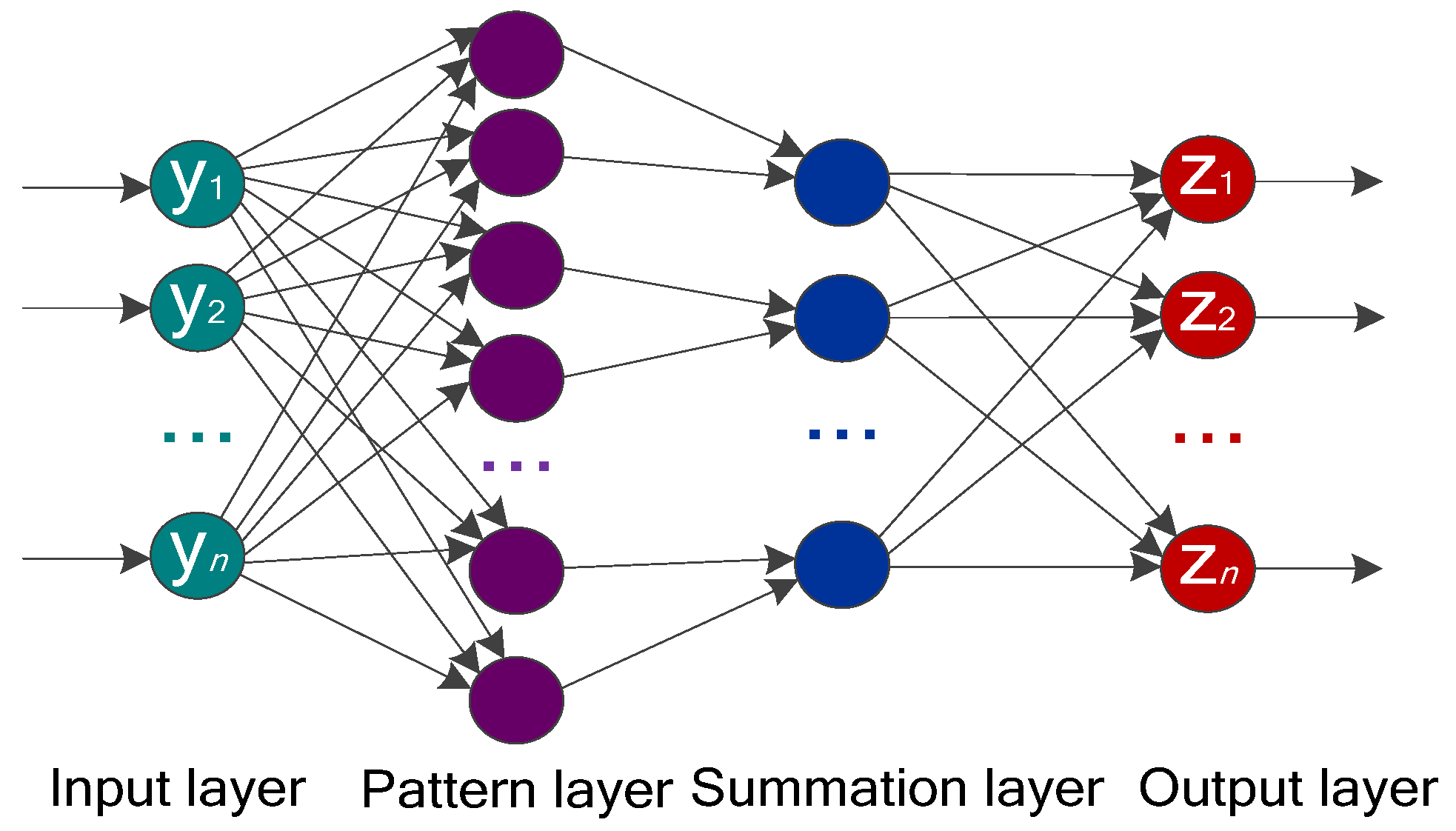
2.4. Proposed IGOA-PNN Model
2.4.1. Probabilistic Neural Network
2.4.2. Proposed IGOA Algorithm
- (1)
- When is less than , is 0.9.
- (2)
- When is greater than and less than , belongs to .
- (3)
- When is greater than , is 0.2.
2.4.3. IGOA-PNN
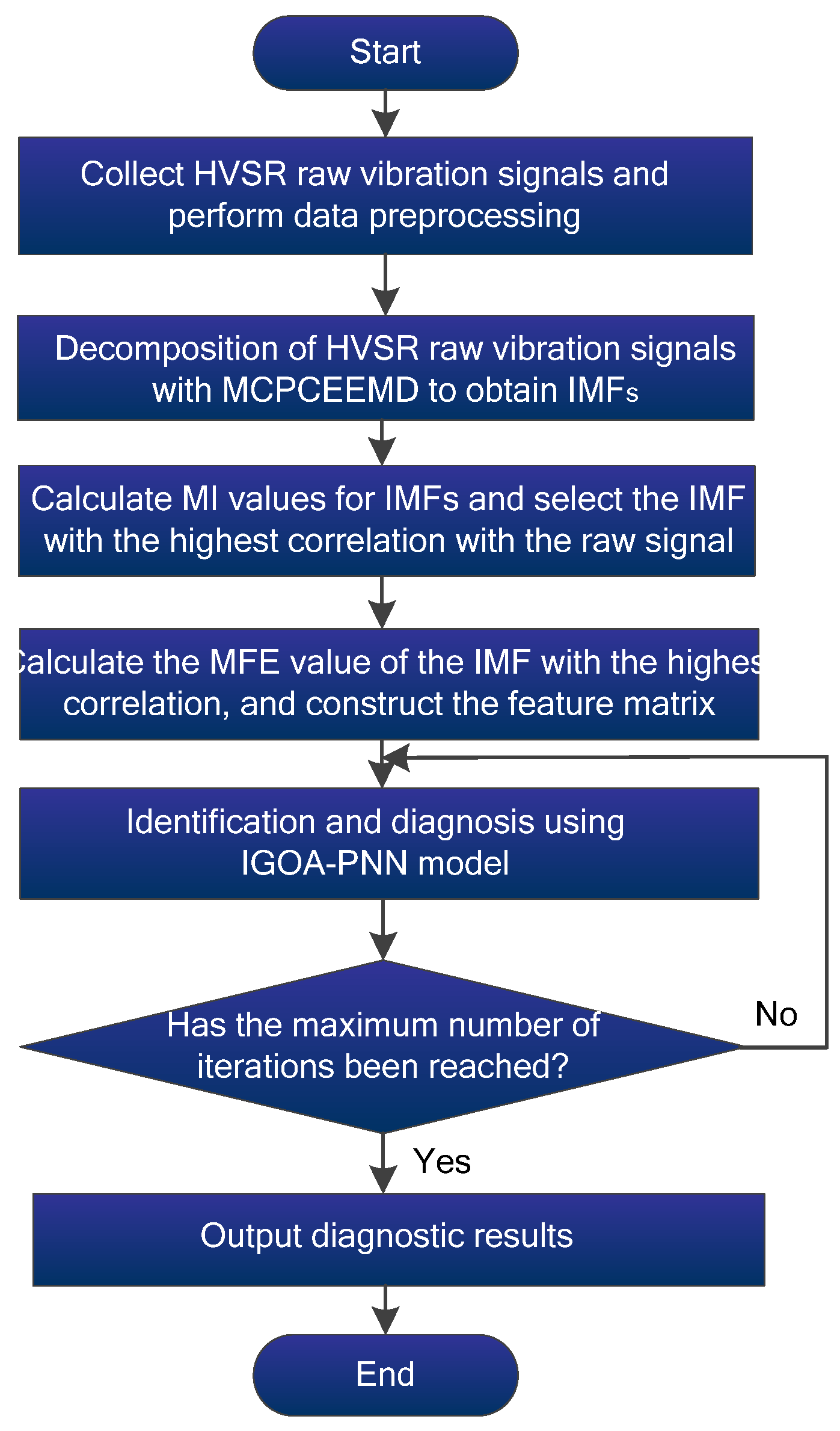
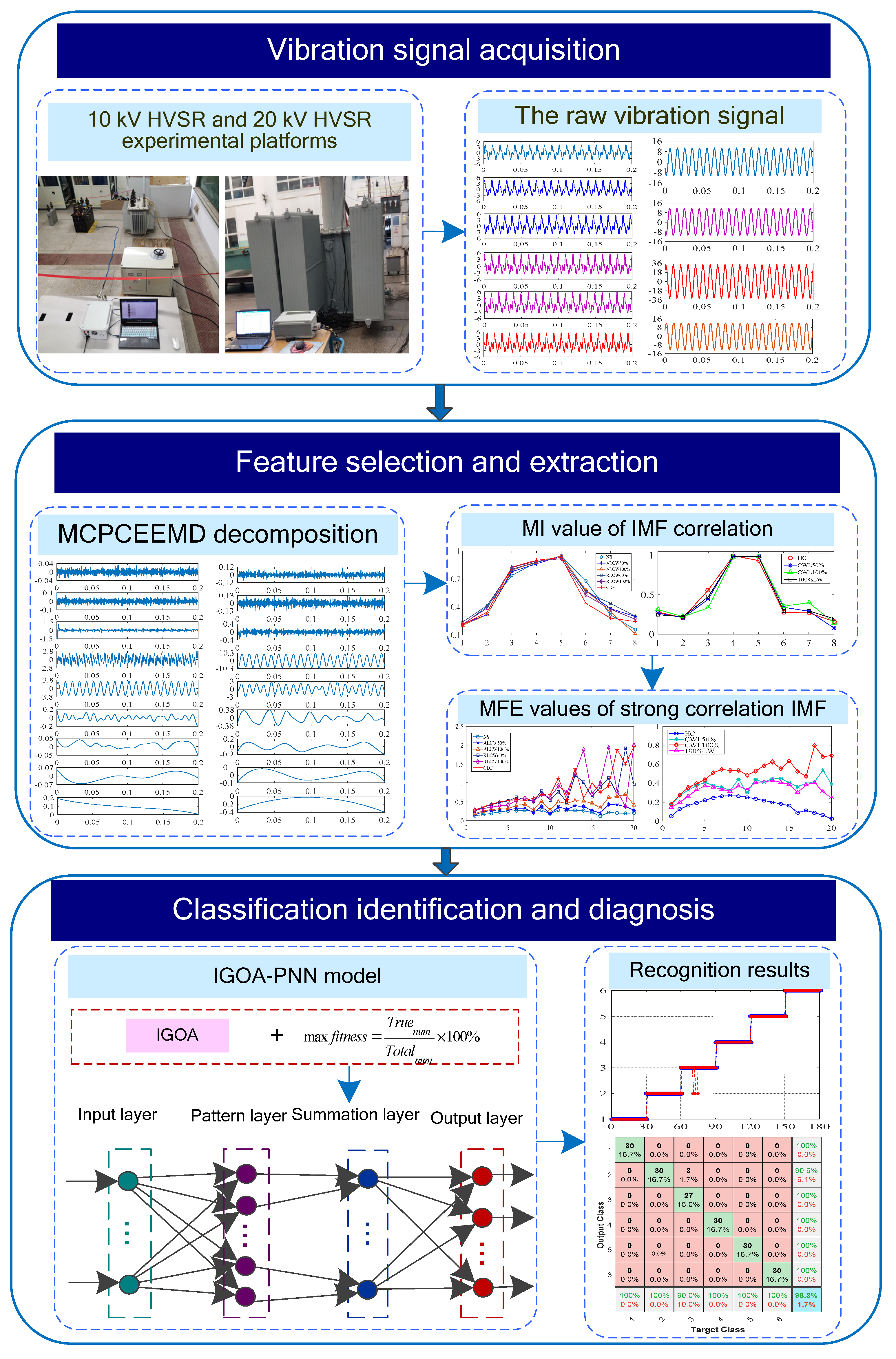
3. Proposed Framework
4. Experiment Verification and Discussion
4.1. Case 1: 10 kV HVSR Experimental Verification and Discussion
4.1.1. Experimental Platform and Data Collection
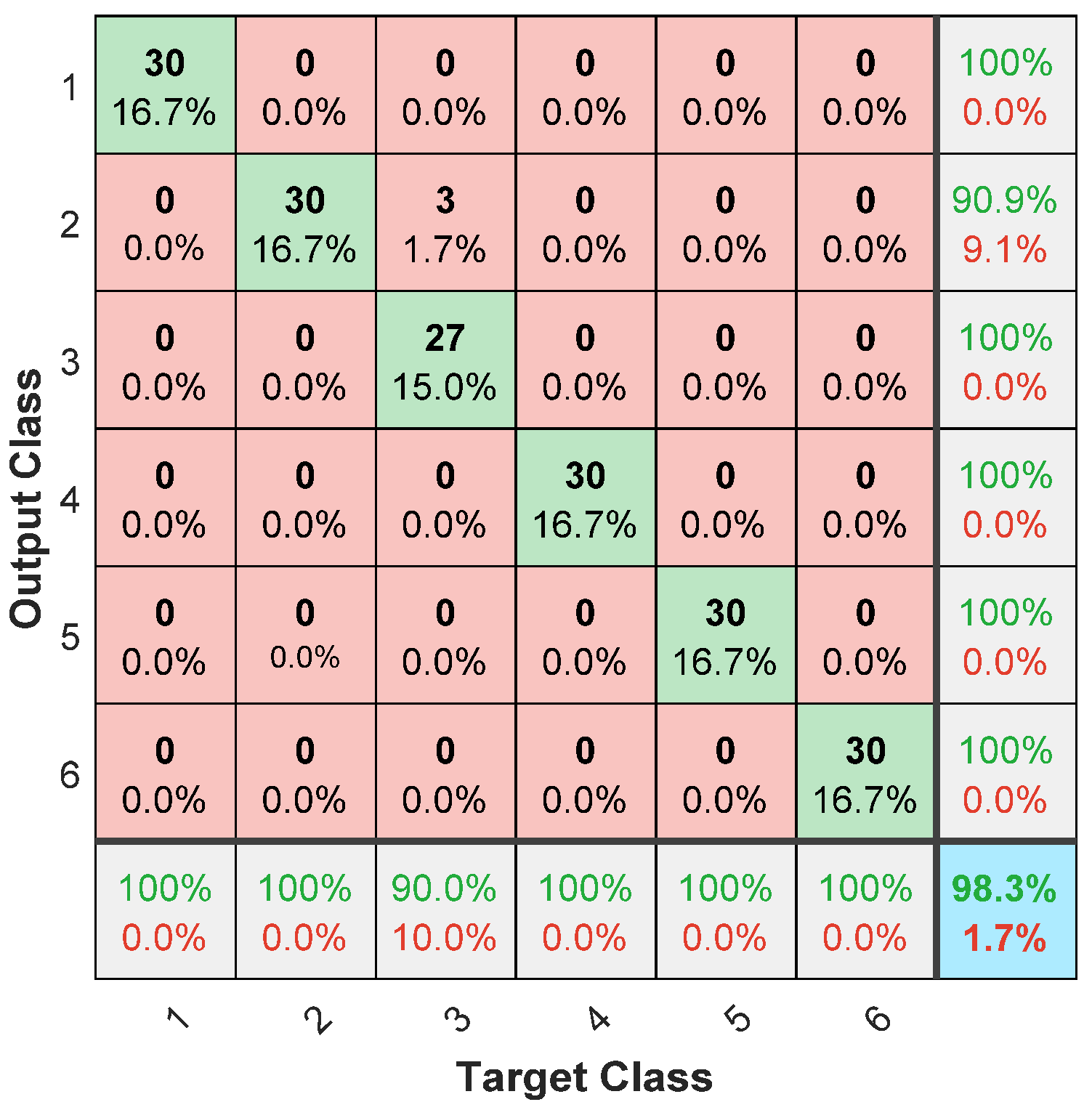
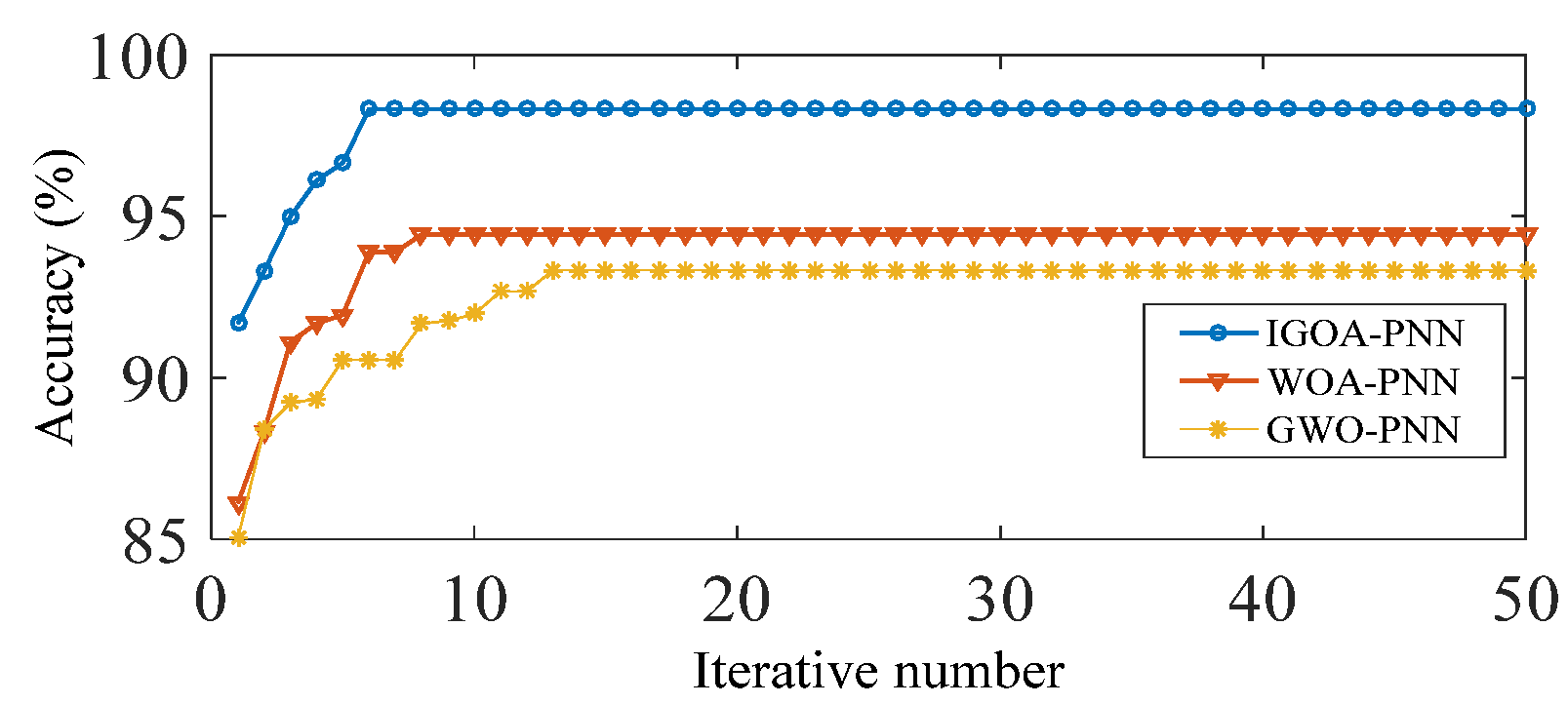
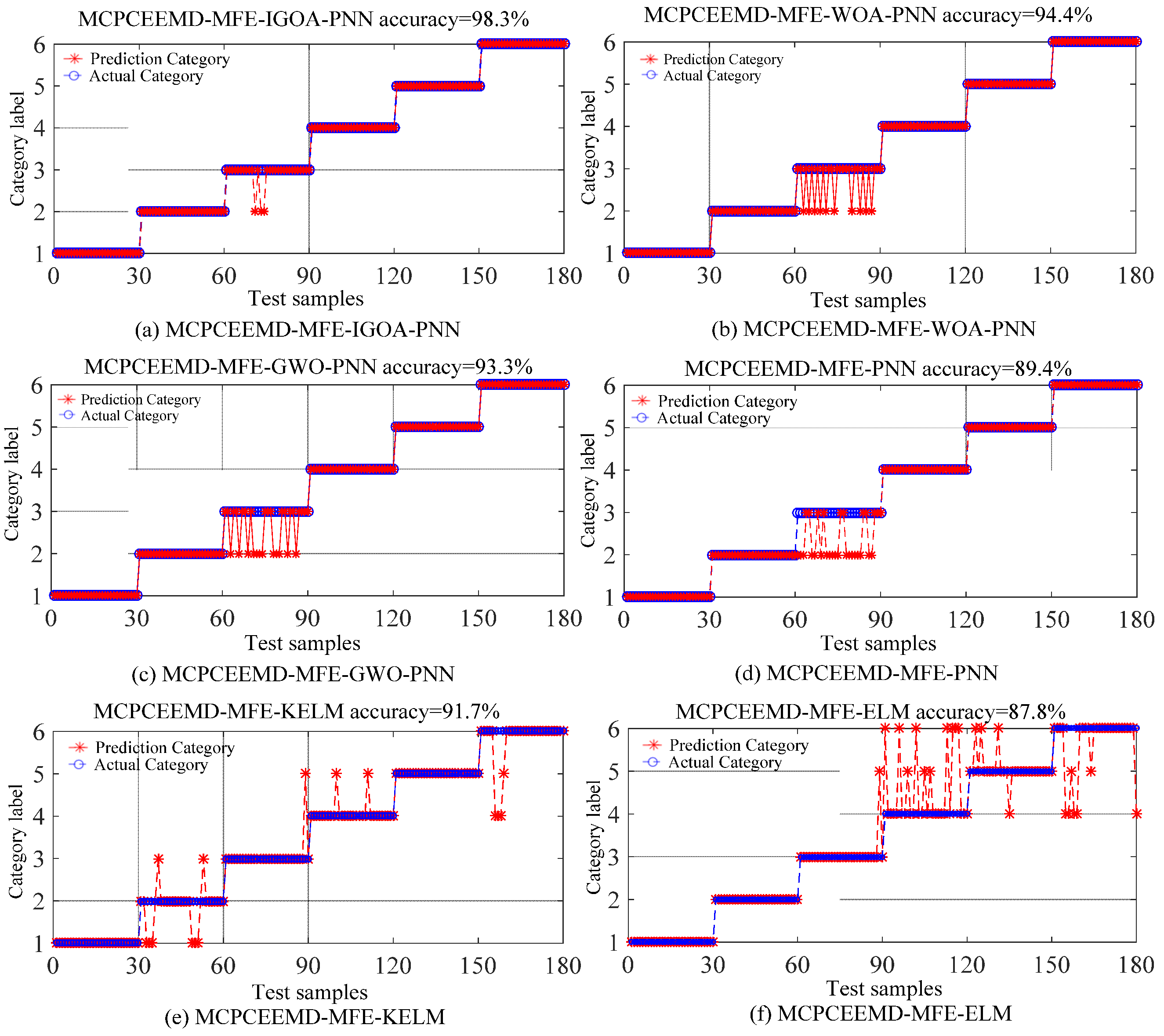
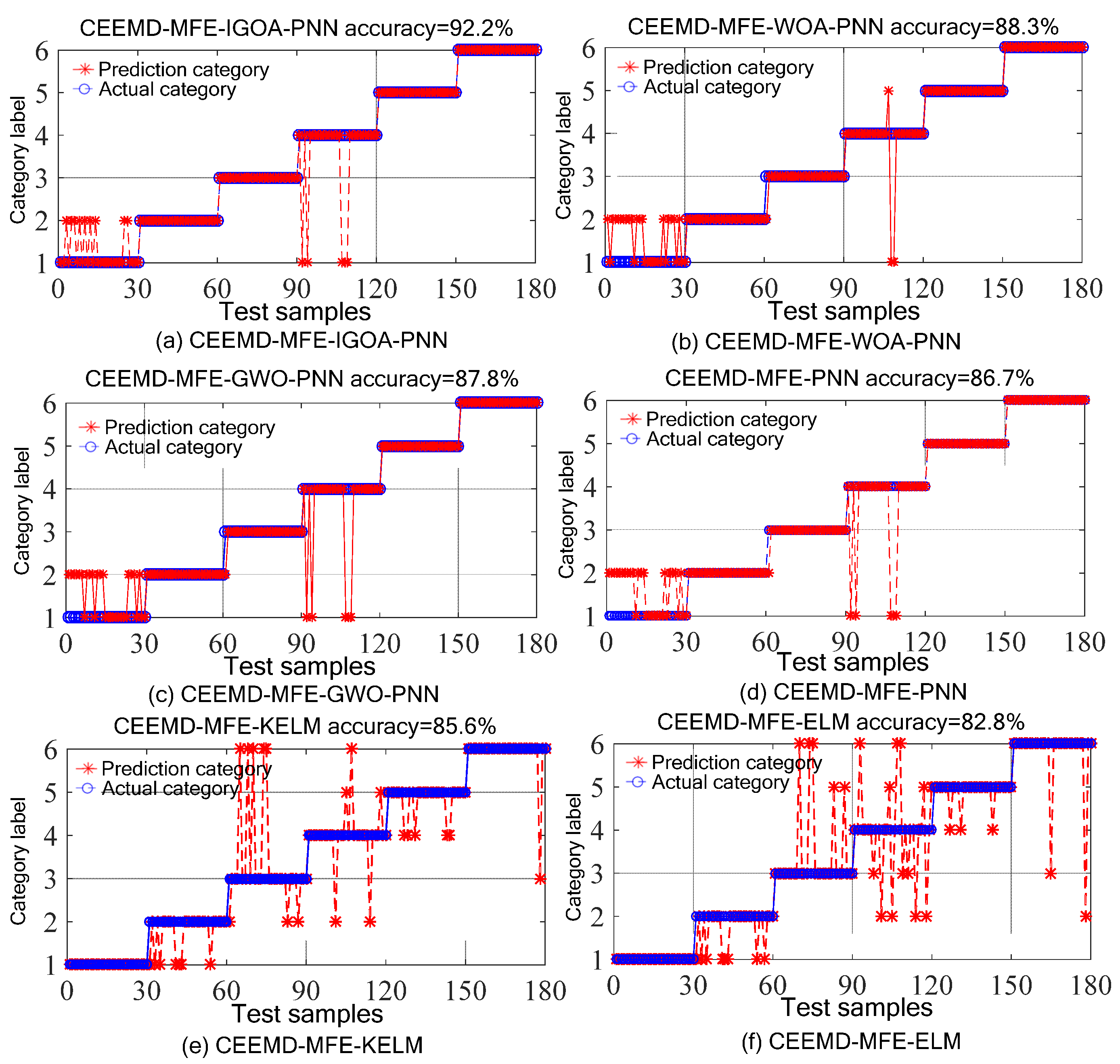
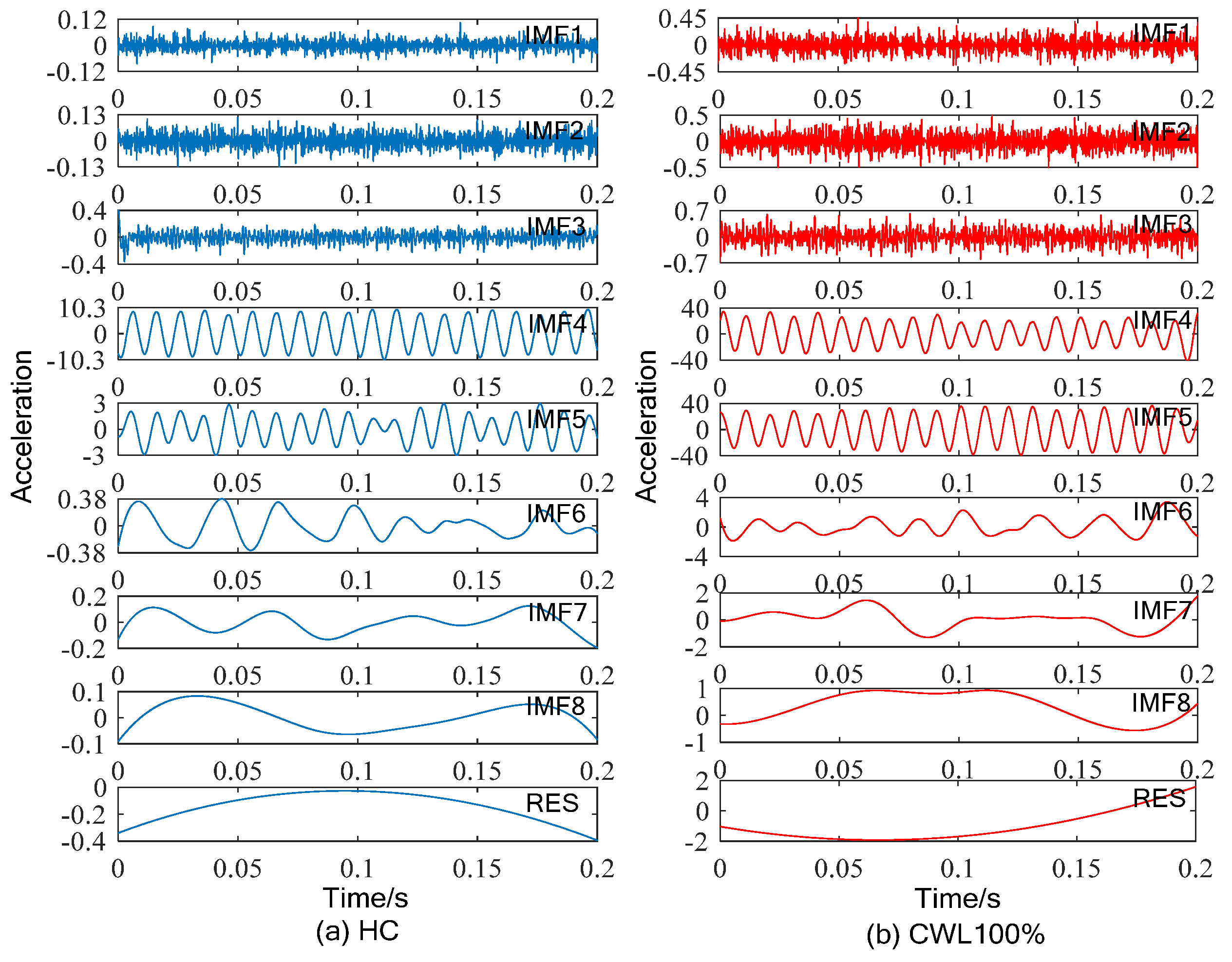
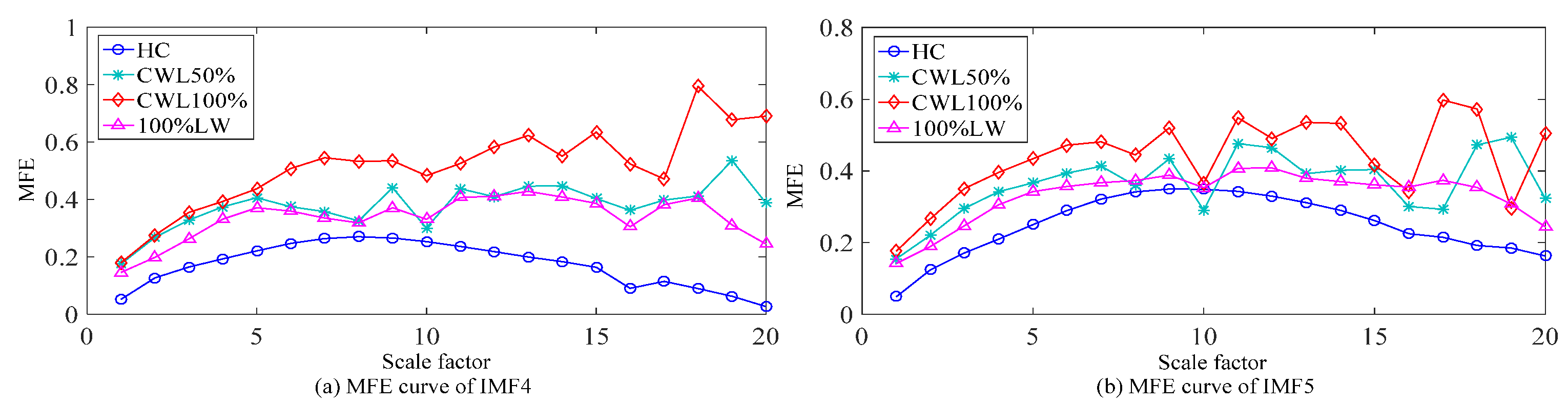
4.1.2. Analysis of Results
4.1.3. Discussion
4.2. Case 2: 20 kV HVSR Experimental Verification
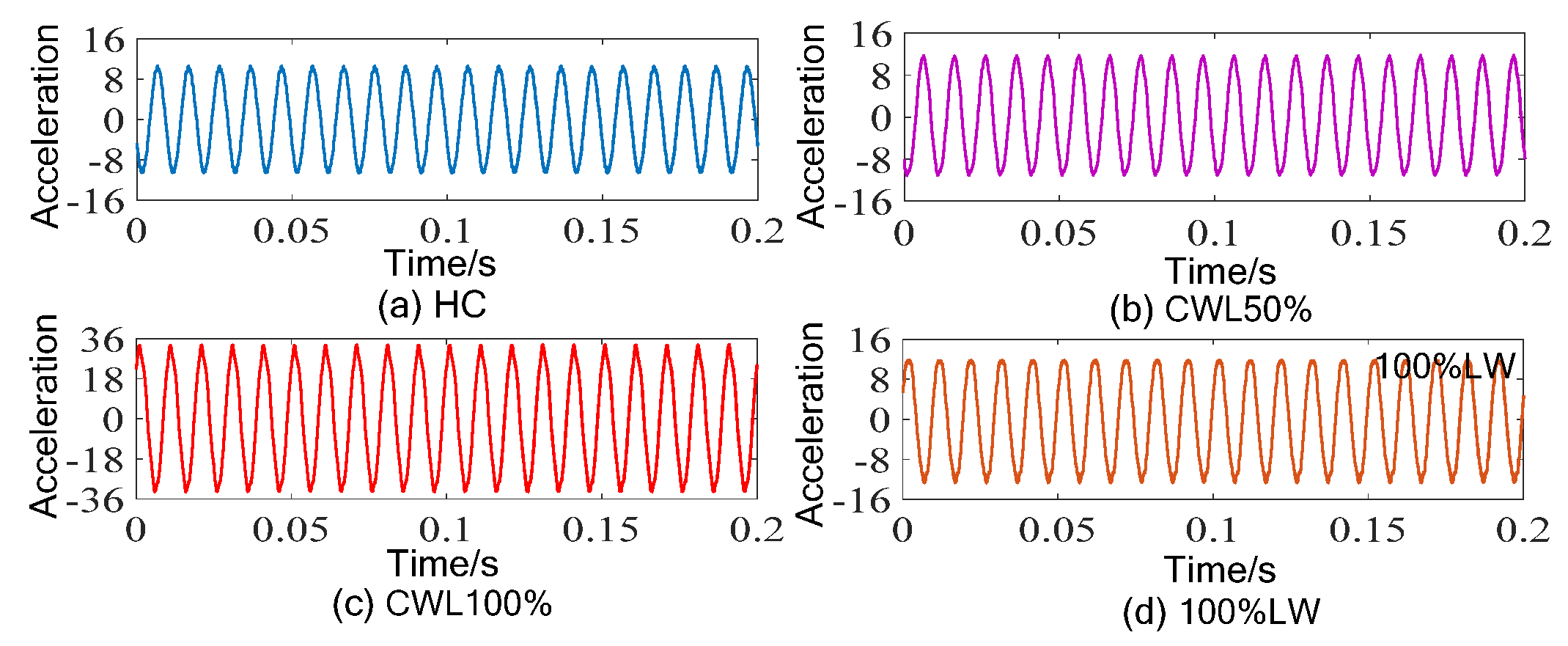
4.2.1. Experimental Platform and Data Collection
4.2.2. Analysis of Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, C.; Li, F.; Wang, B.; Fan, Y.; Jing, L.; Chen, W.; Wang, C. Anti-interference adaptive single-phase auto-reclosing schemes based on reactive power characteristics for transmission lines with shunt reactors. Electr. Power Syst. Res. 2019, 170, 176–183. [Google Scholar] [CrossRef]
- Xie, C.; Li, F. Adaptive comprehensive auto-reclosing scheme for shunt reactor-compensated transmission lines. IEEE Trans. Power Del. 2020, 35, 2149–2158. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, S.; Zeng, X.; Wei, G.; Liu, H.; Chen, T. Suppression measures for overvoltage caused by vacuum circuit breaker switching off 10-kV shunt reactor. IEEE Trans. Power Del. 2020, 35, 540–548. [Google Scholar] [CrossRef]
- Velasquez, R.M.A.; Lara, J.V.M. Root cause analysis for shunt reactor failure in 500 kV power system. Eng. Fail. Anal. 2019, 104, 1157–1173. [Google Scholar] [CrossRef]
- Das, S.; Sidhu, T.S.; Zadeh, M.R.D.; Zhang, Z.Y. A novel hybrid differential algorithm for turn to turn fault detection in shunt reactors. IEEE Trans. Power Del. 2017, 32, 2537–2545. [Google Scholar] [CrossRef]
- Velasquez, R.M.A.; Lara, J.V.M. Methodology for failure analysis in shunt reactor by electromagnetic influence caused by high vibration in overload condition. Eng. Fail. Anal. 2019, 104, 589–608. [Google Scholar] [CrossRef]
- Yao, C.; Zhao, Z.; Li, C.; Chen, X.; Zhao, Y.; Zhao, X. Noninvasive method for online detection of internal winding faults of 750 kV EHV shunt reactors. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2833–2840. [Google Scholar] [CrossRef]
- Zhang, P.; Li, L.; Cheng, Z.; Tian, C.; Han, Y. Study on vibration of iron core of transformer and reactor based on maxwell stress and anisotropic magnetostriction. IEEE Trans. Mag. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Xiao, R.; Zhang, Z.; Wu, Y.; Jiang, P.; Deng, J. Multi-scale information fusion model for feature extraction of converter transformer vibration signal. Measurement 2021, 180, 109555. [Google Scholar] [CrossRef]
- Zollanvari, A.; Kunanbayev, K.; Bitaghsir, S.A.; Bagheri, M. Transformer fault prognosis using deep recurrent neural network over vibration signals. IEEE. Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Hou, P.; Ma, H.; Ju, P.; Chen, X.; Zhu, C. A new vibration analysis approach for monitoring the working condition of a high-voltage shunt reactor. IEEE Access 2021, 9, 46487–46504. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M. Fractal dimension and data mining for detection of short-circuited turns in transformers from vibration signals. Meas. Sci. Technol. 2019, 31, 025902. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, Z.; Tang, C.; Qian, G.; Islam, S. Diagnostic of transformer winding deformation fault types using continuous wavelet transform of pulse response. Measurement 2019, 140, 197–206. [Google Scholar] [CrossRef]
- Zhen, S.; Liu, C.; Liu, X. Research on vibration saltation of the transformer core caused by DC bias of based on empirical mode decomposition. J. Electr. Eng. Technol. 2021, 16, 1185–1192. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Cao, C.; Xu, B.; Li, X. Monitoring method on loosened state and deformational fault of transformer winding based on vibration and reactance information. IEEE Access 2020, 8, 215479–215492. [Google Scholar] [CrossRef]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The pearson correlation coefficient is superior to the mander’s overlap coefficient. Cytometry A 2010, 77, 733–742. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, G.; Yao, W.; Yang, Z. Morphological correlation coefficient and its application in geochemical data analysis. J. Geol. 2019, 43, 103–110. [Google Scholar]
- Walczak, Z. Total correlations and mutual information. Phys. Lett. A 2009, 373, 1818–1822. [Google Scholar] [CrossRef][Green Version]
- Ma, Y.; Cheng, J.; Wang, P.; Wang, J.; Yu, Y. Rotating machinery fault diagnosis based on multivariate multiscale fuzzy distribution entropy and fisher score. Measurement 2021, 179, 109495. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, J.; Yang, Y. Roller bearing fault diagnosis based on local mean decomposition and morphological fractal dimension. J. Vib. Shock 2013, 32, 90–94. [Google Scholar]
- Noman, K.; Li, Y.; Peng, Z.; Wang, S. Continuous health monitoring of bearing by oscillatory sparsity indices under non stationary time varying speed condition. IEEE Sens. J. 2022, 22, 4452–4462. [Google Scholar] [CrossRef]
- Li, C.; Zhou, N.; Liao, J.; Wang, Q. Multiscale multivariate fuzzy entropy-based technique to distinguish transformer magnetizing from fault currents. IET Gener. Transm. Distrib. 2019, 13, 2319–2327. [Google Scholar] [CrossRef]
- Yang, X.; Chen, W.; Li, A.; Yang, C.; Xie, Z.; Dong, H. BA-PNN-based methods for power transformer fault diagnosis. Adv. Eng. Inform. 2019, 39, 178–185. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Zhao, X.; Cheng, J.; Wang, P.; Yang, Y. A rotating machinery fault diagnosis method using composite multiscale fuzzy distribution entropy and minimal error of convex hull approximation. Meas. Sci. Technol. 2020, 32, 025010. [Google Scholar] [CrossRef]
- Zheng, D.; Han, B.; Liu, G.; Li, Y.; Yu, H. Cross-Domain intelligent fault diagnosis method of rotating machinery using multi-scale transfer fuzzy entropy. IEEE Access 2021, 9, 95481–95492. [Google Scholar]
- Chen, H.; Xiong, Y.; Li, S.; Song, Z.; Hu, Z.; Liu, F. Multi-Sensor Data Driven with PARAFAC-IPSO-PNN for Identification of Mechanical Nonstationary Multi-Fault Mode. Machines 2022, 10, 155. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Zhang, J.; Zhong, M.; Zhang, J. Detection for weak fault in planetary gear trains based on an improved maximum correlation kurtosis deconvolution. Meas. Sci. Technol. 2019, 31, 025101. [Google Scholar] [CrossRef]
- Ye, X.; Hu, Y.; Shen, J.; Feng, R.; Zhai, G. An improved empirical mode decomposition based on adaptive weighted rational quartic spline for rolling bearing fault diagnosis. IEEE Access 2020, 8, 123813–123827. [Google Scholar] [CrossRef]
- Yun, K.; Chong, Y.; Song, E.; Yang, L.; Quan, D. A weak fault diagnosis scheme for common rail injector based on MGOA-MOMEDA and improved hierarchical dispersion entropy. Meas. Sci. Technol. 2020, 32, 025012. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, L.; Hu, Z.; Yang, S. A Grasshopper Optimization-based fault-tolerant control algorithm for a human occupied submarine with the multi-thruster system. Ocean Eng. 2021, 242, 110101. [Google Scholar] [CrossRef]
- Ding, J.; Xiao, D.; Li, X. Gear fault diagnosis based on genetic mutation particle swarm optimization VMD and probabilistic neural network algorithm. IEEE Access 2020, 8, 18456–18474. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Chen, Q.; Wei, H.; Rashid, M.; Cai, Z. Kernel extreme learning machine based hierarchical machine learning for multi-type and concurrent fault diagnosis. Measurement 2021, 184, 109923. [Google Scholar] [CrossRef]
- Ding, S.; Zhao, H.; Zhang, Y.; Xu, X.; Nie, R. Extreme learning machine: Algorithm, theory and applications. Artif. Intell. Rev. 2015, 44, 103–115. [Google Scholar] [CrossRef]







| Category Labels | Different States |
|---|---|
| 1 | Normal status (NS) |
| 2 | 50% axial looseness of core winding (ALCW50%) |
| 3 | 100% axial looseness of core winding (ALCW100%) |
| 4 | 60% radial looseness of core winding (RLCW60%) |
| 5 | 100% radial looseness of core winding (RLCW100%) |
| 6 | Component drop failure (CDF) |
| Methods | Parameter Values |
|---|---|
| IGOA-PNN | Number of species R = 10 |
| Learning factor cmin = 0.0004, cmax = 1 | |
| Number of iterations T = 50 | |
| WOA-PNN | Number of species R = 10 |
| Weight factor wmin = 0.4, wmax = 0.95 | |
| Number of iterations T = 50 | |
| GWO-PNN | Number of species R = 10 |
| Number of iterations T = 50 |
| Category Labels | Different States |
|---|---|
| C1 | Healthy condition (HC) |
| C2 | Core and winding loose 50% (CWL50%) |
| C3 | Core and winding loose 100% (CWL100%) |
| C4 | 100% loose winding (100%LW) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, P.; Ma, H.; Ju, P. Intelligent Diagnosis Method for Mechanical Faults of High-Voltage Shunt Reactors Based on Vibration Measurements. Machines 2022, 10, 627. https://doi.org/10.3390/machines10080627
Hou P, Ma H, Ju P. Intelligent Diagnosis Method for Mechanical Faults of High-Voltage Shunt Reactors Based on Vibration Measurements. Machines. 2022; 10(8):627. https://doi.org/10.3390/machines10080627
Chicago/Turabian StyleHou, Pengfei, Hongzhong Ma, and Ping Ju. 2022. "Intelligent Diagnosis Method for Mechanical Faults of High-Voltage Shunt Reactors Based on Vibration Measurements" Machines 10, no. 8: 627. https://doi.org/10.3390/machines10080627
APA StyleHou, P., Ma, H., & Ju, P. (2022). Intelligent Diagnosis Method for Mechanical Faults of High-Voltage Shunt Reactors Based on Vibration Measurements. Machines, 10(8), 627. https://doi.org/10.3390/machines10080627







