Neural Network Based Adaptive Event-Triggered Control for Quadrotor Unmanned Aircraft Robotics
Abstract
:1. Introduction
- (1)
- To our best knowledge, for the first time we present an adaptive DSC scheme with a modified high-gain observer that has been designed for quadrotor UARs under the condition that only the position data of the quadrotor system are available, along with the testing of the quadrotor UAR controller in the hardware-in-loop simulation platform. Thus, the underactuation problem in quadrotor UARs is perfectly solved, and precise tracking performance is obtained.
- (2)
- By designing an event triggering mechanism for quadrotor UARs, the control signal can be updated immediately when threshold conditions are triggered. Therefore, compared with the time-triggered control mechanism, the energy consumption can be greatly reduced, and the communication pressure between the system and the control terminal is lowered using the event triggering mechanism.
- (3)
- By setting the original conditions of the high-gain state observer, adaptive control laws, and the appropriate controller parameters, a tracking performance of for underactuated quadrotor UARs is achieved.
2. Problem Statement
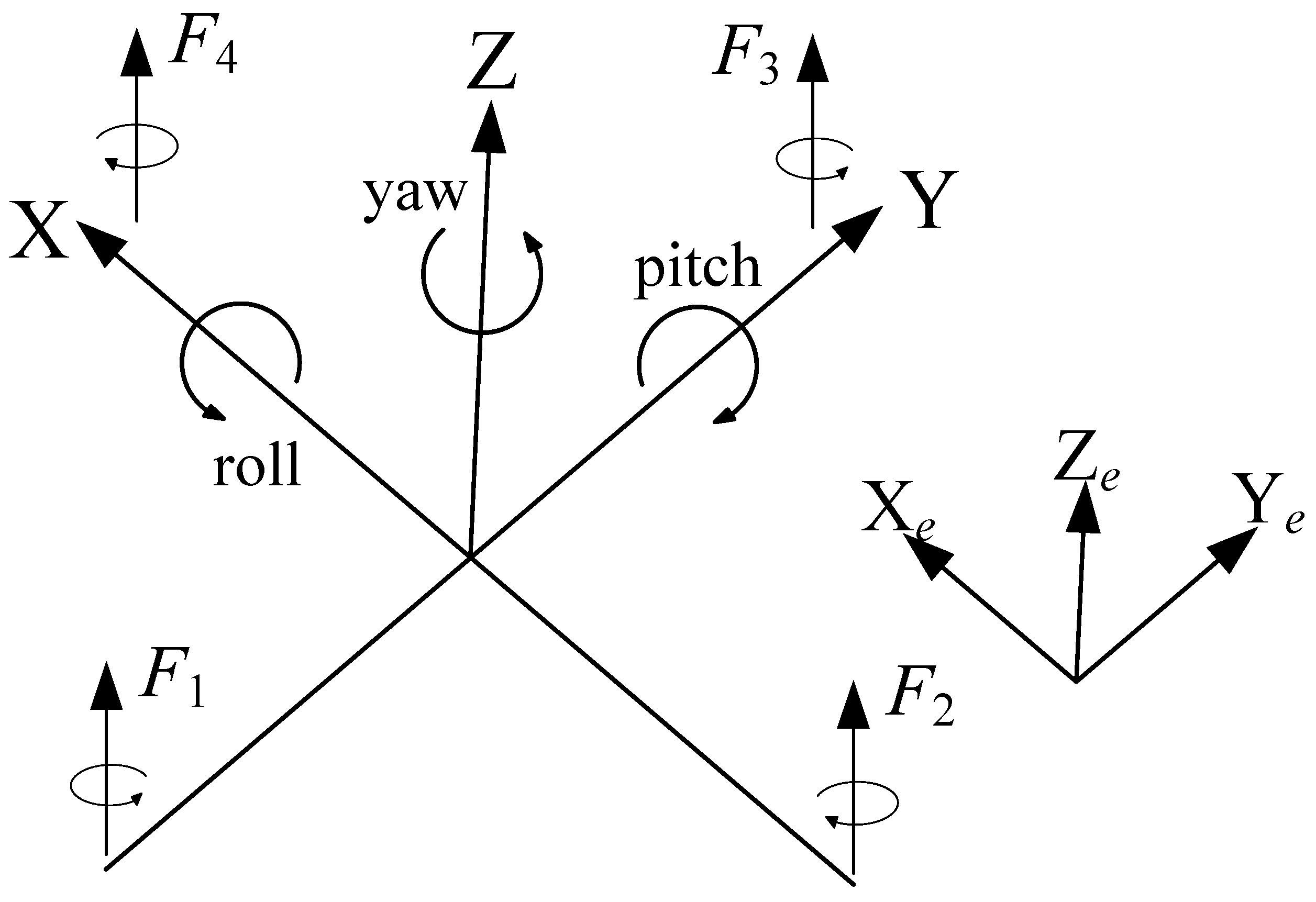
2.1. Model Construction
2.2. Radial Basis Function Neural Networks (RBFNNs)
- A1:
- The reference trajectories are , and are the smooth and bounded functions, , which are part of a set of known compact, when .
- A2:
- The external disturbances can be represented as , wherein are positive constants,
- A3:
- The angles of roll and pitch are limited to in accordance with the physical meaning. In particular, the yaw angle range of was selected for the purposes of this study.
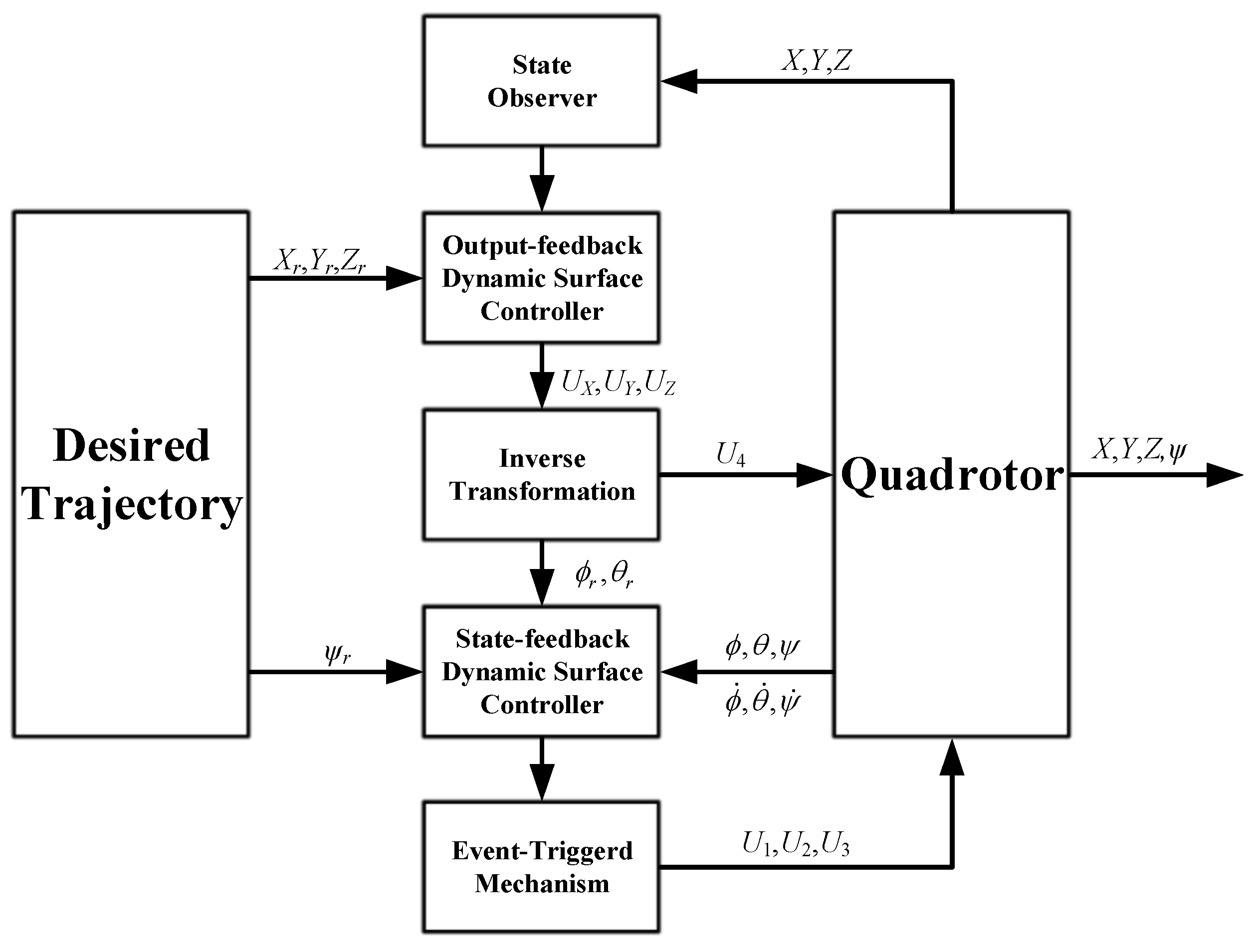
3. Proposed Methodology
3.1. Controller Design for Positioning Trajectory Tracking
Design of Controller with Dynamic Surface Control Method
3.2. Controller Design of Attitude Trajectory Tracking
3.3. Performance and the Stability of the Control Scheme
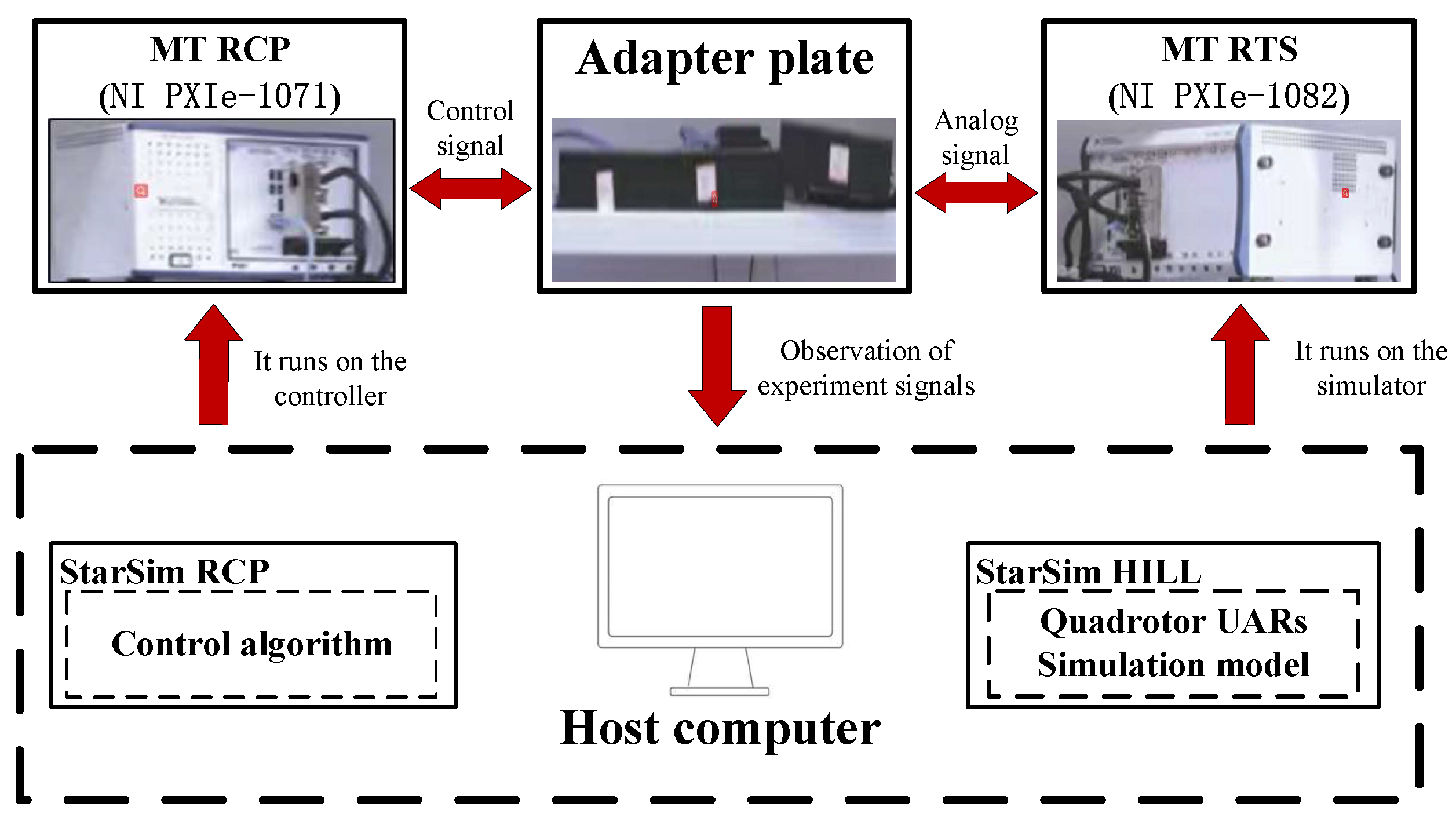
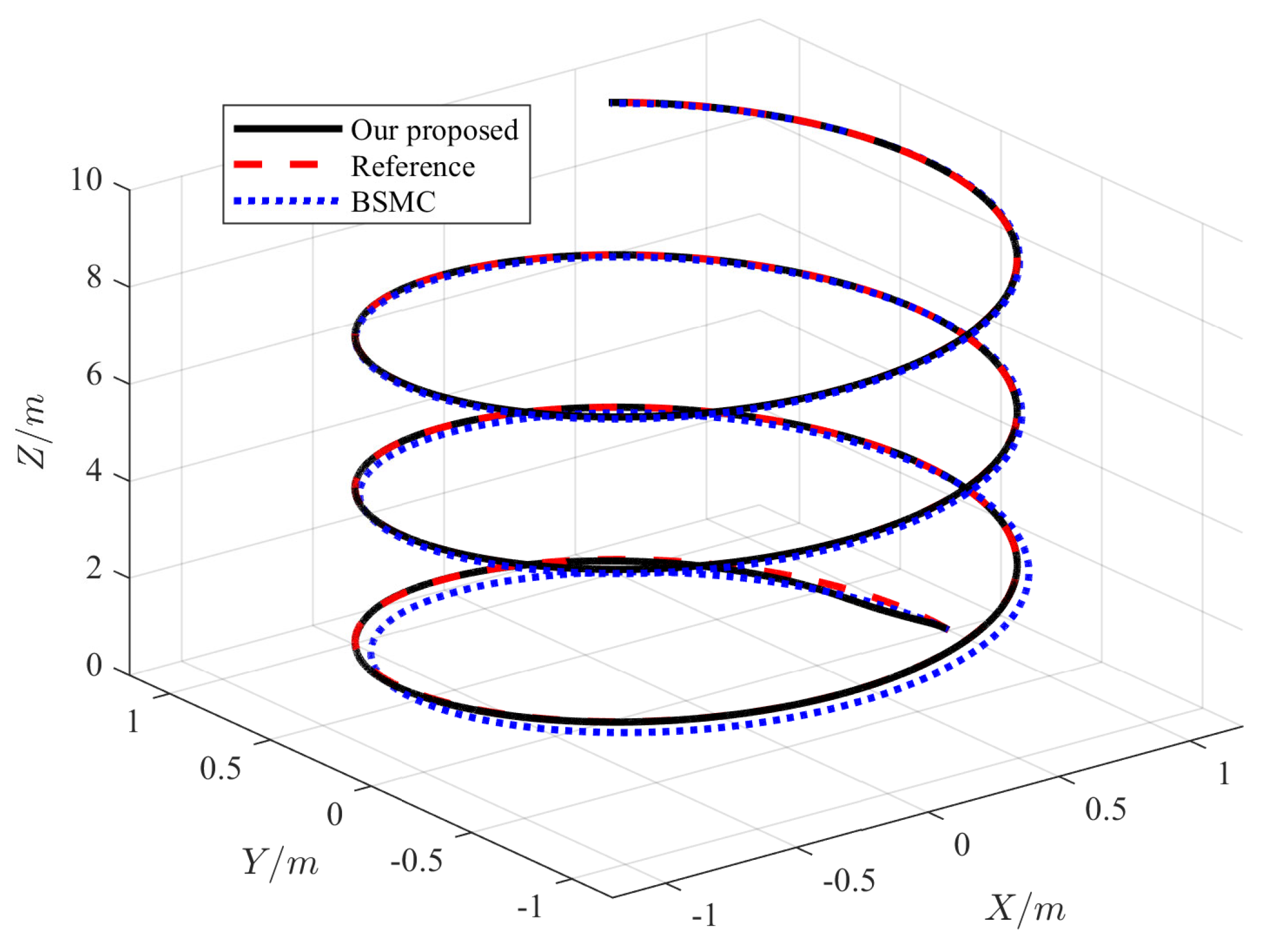
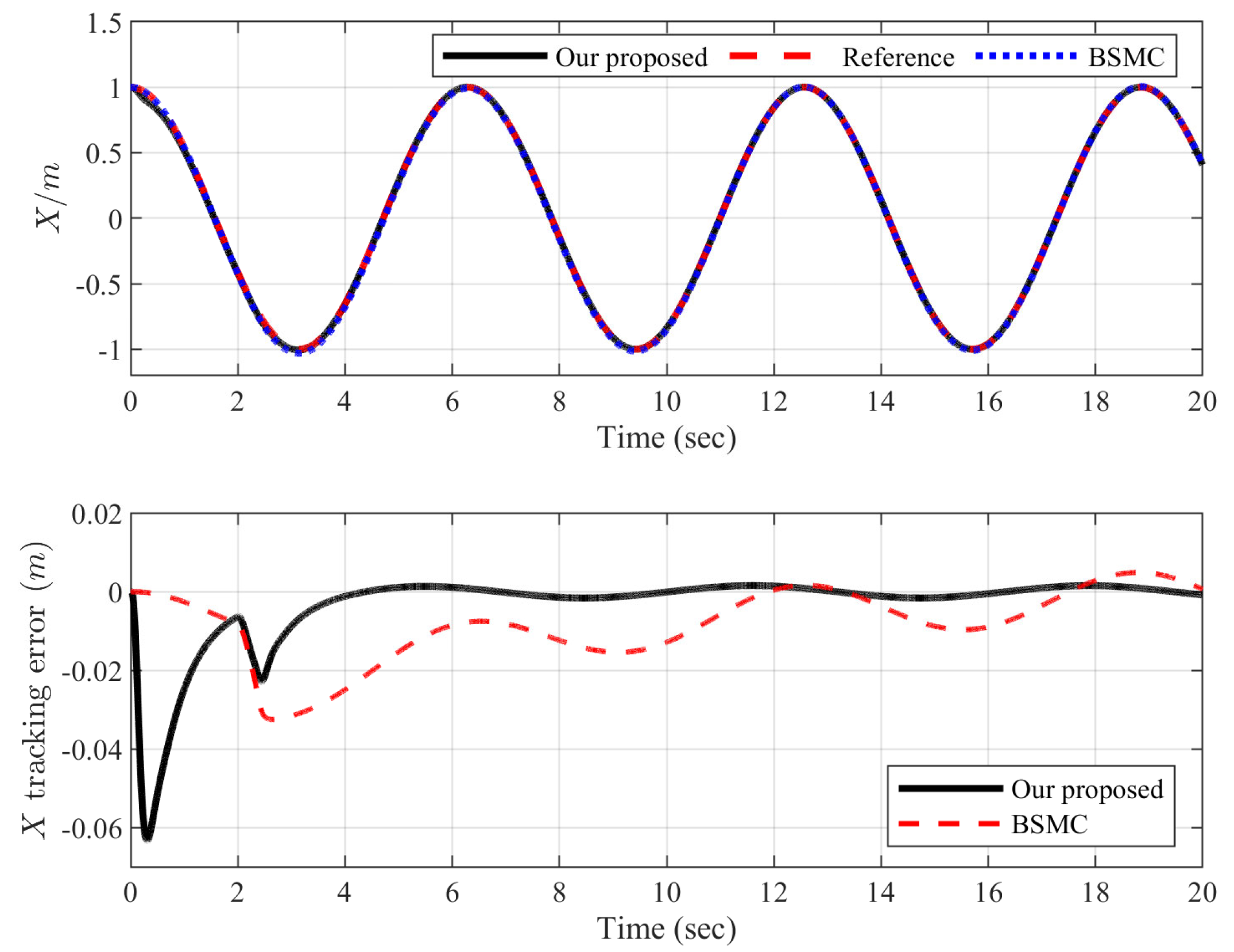
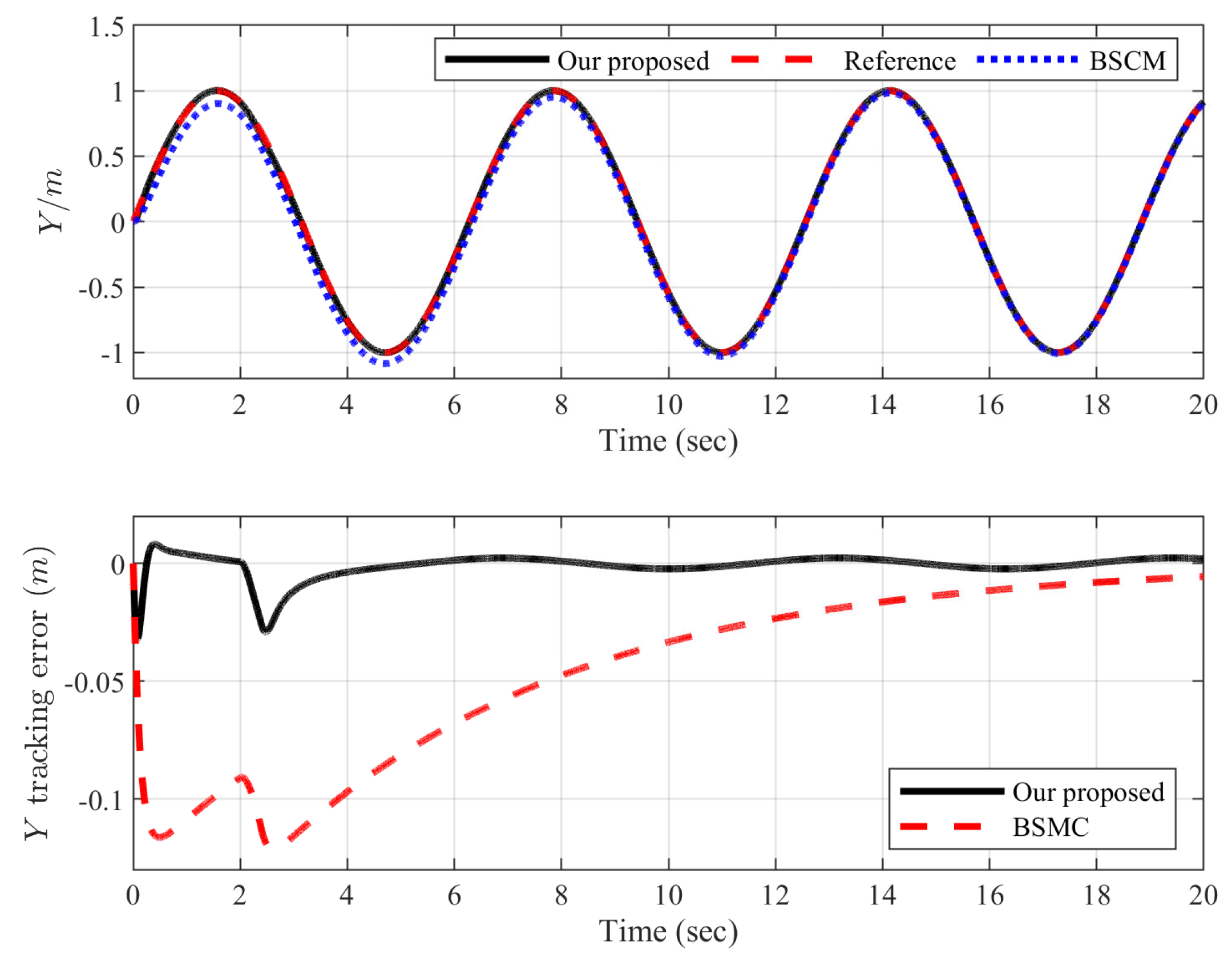
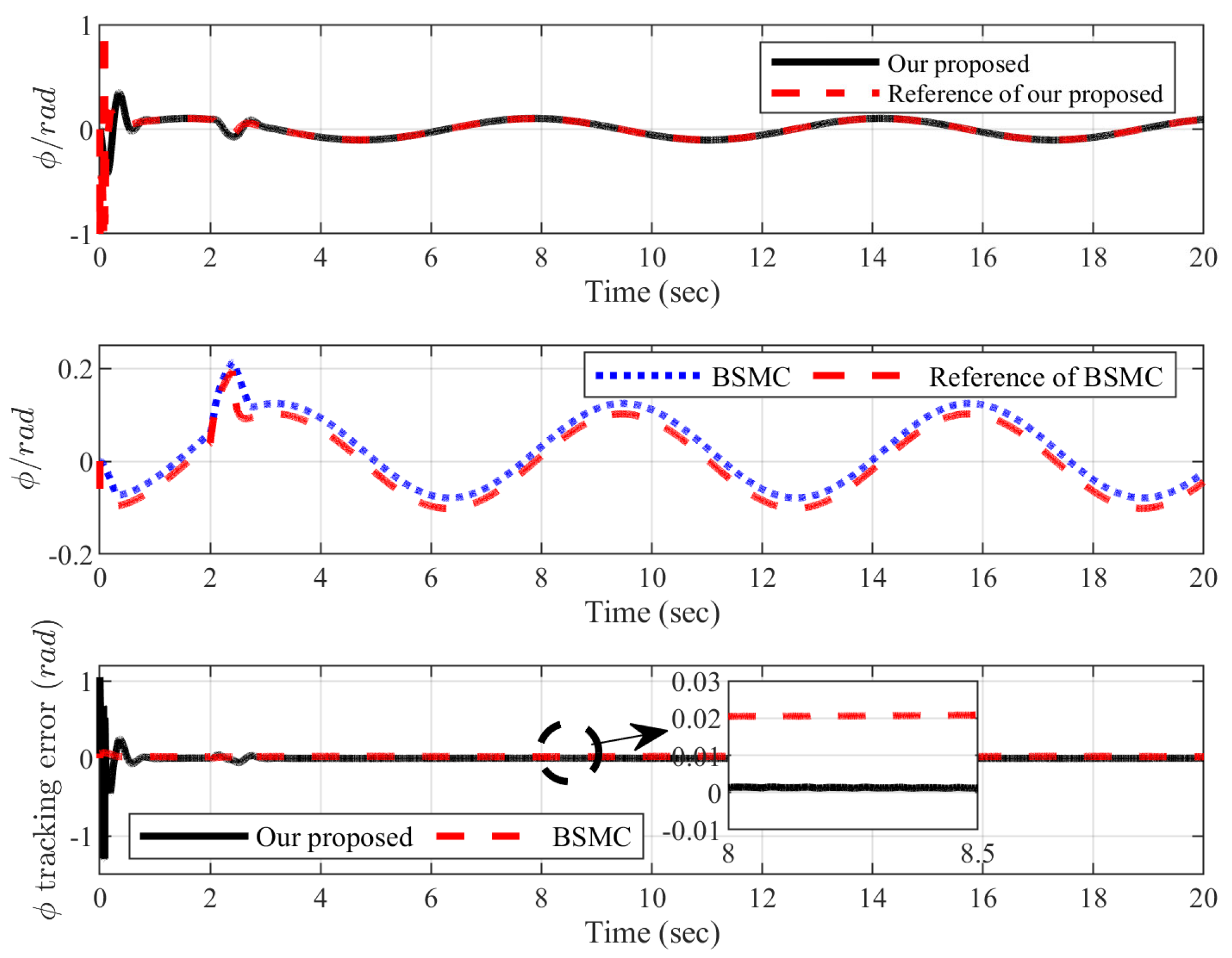
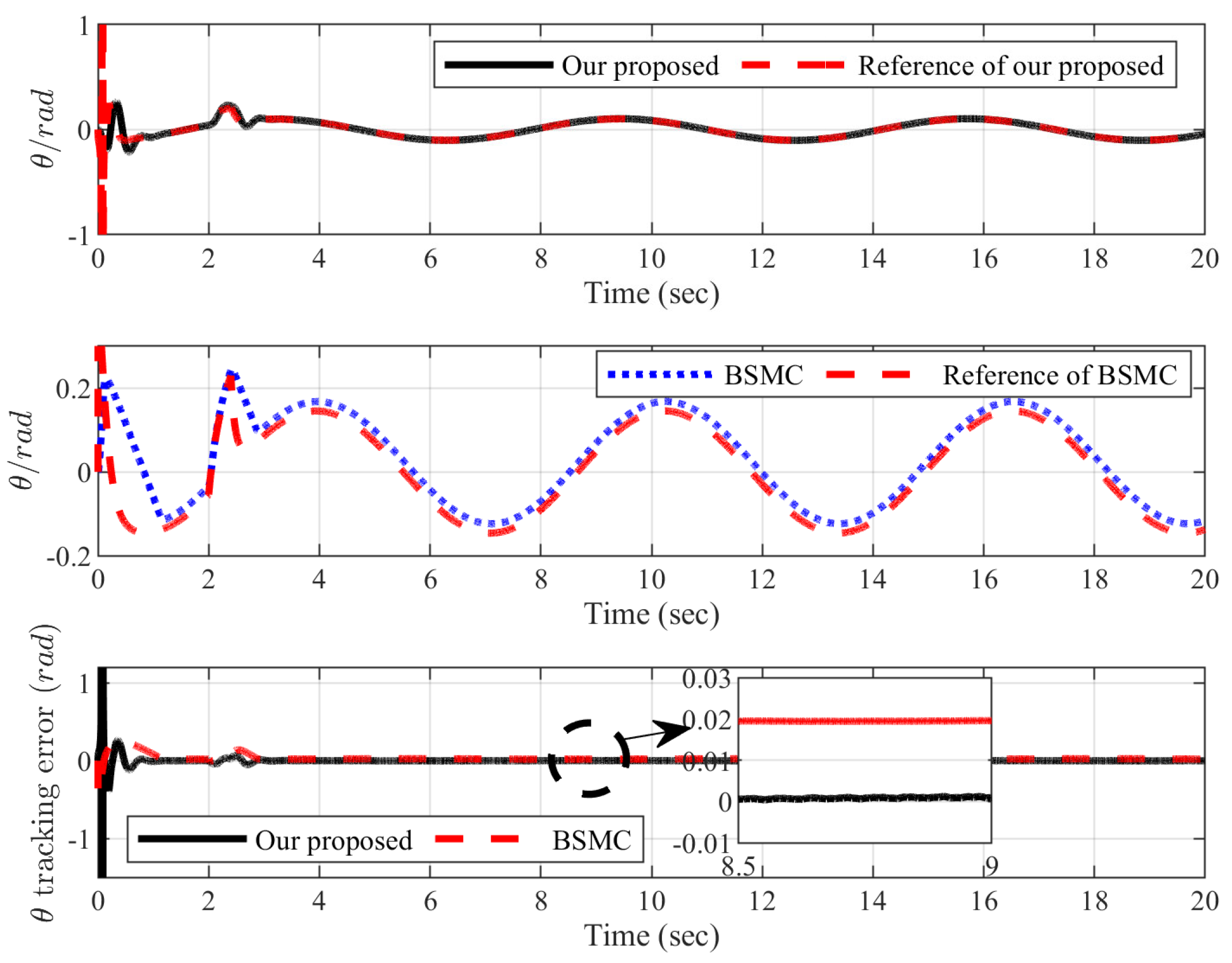
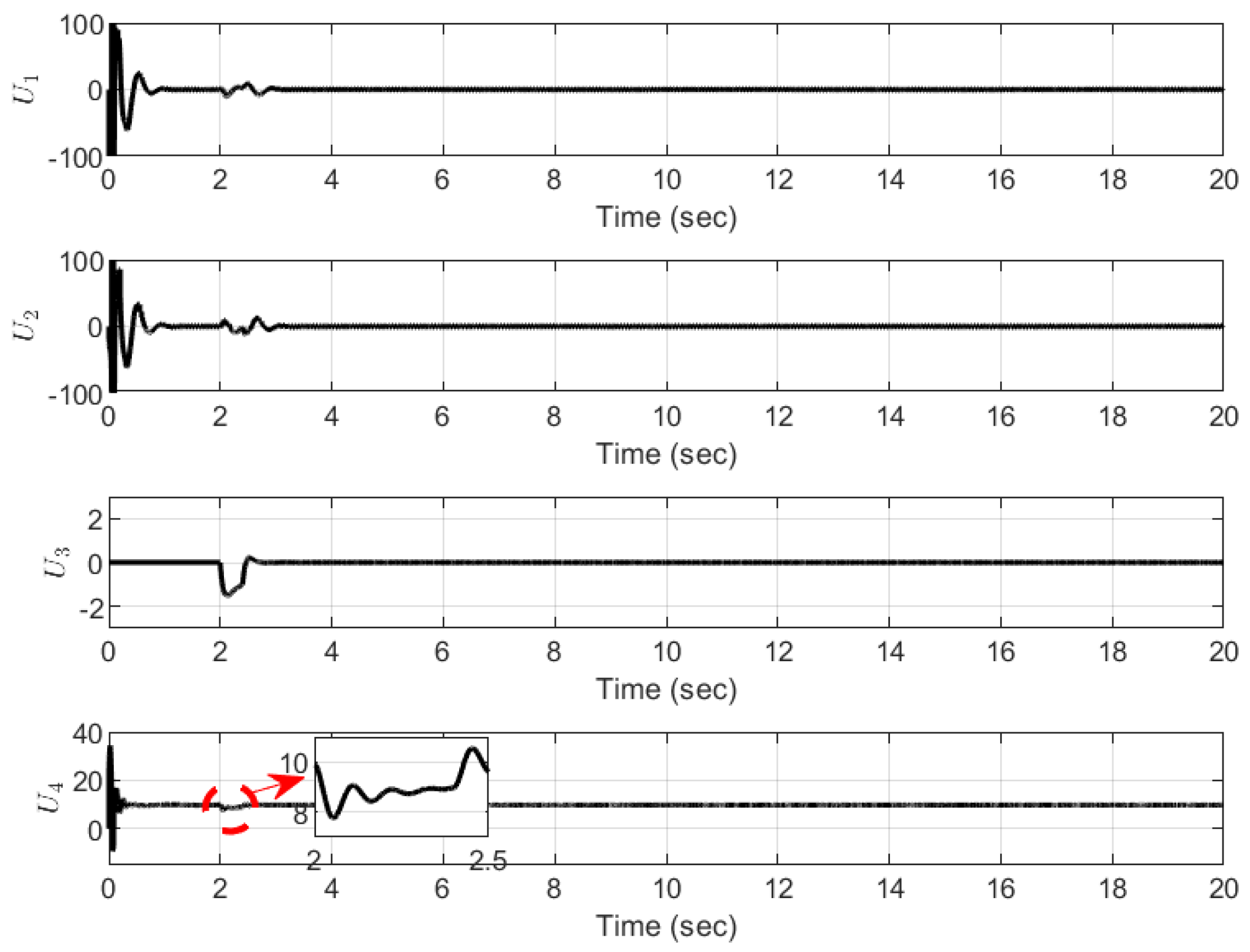
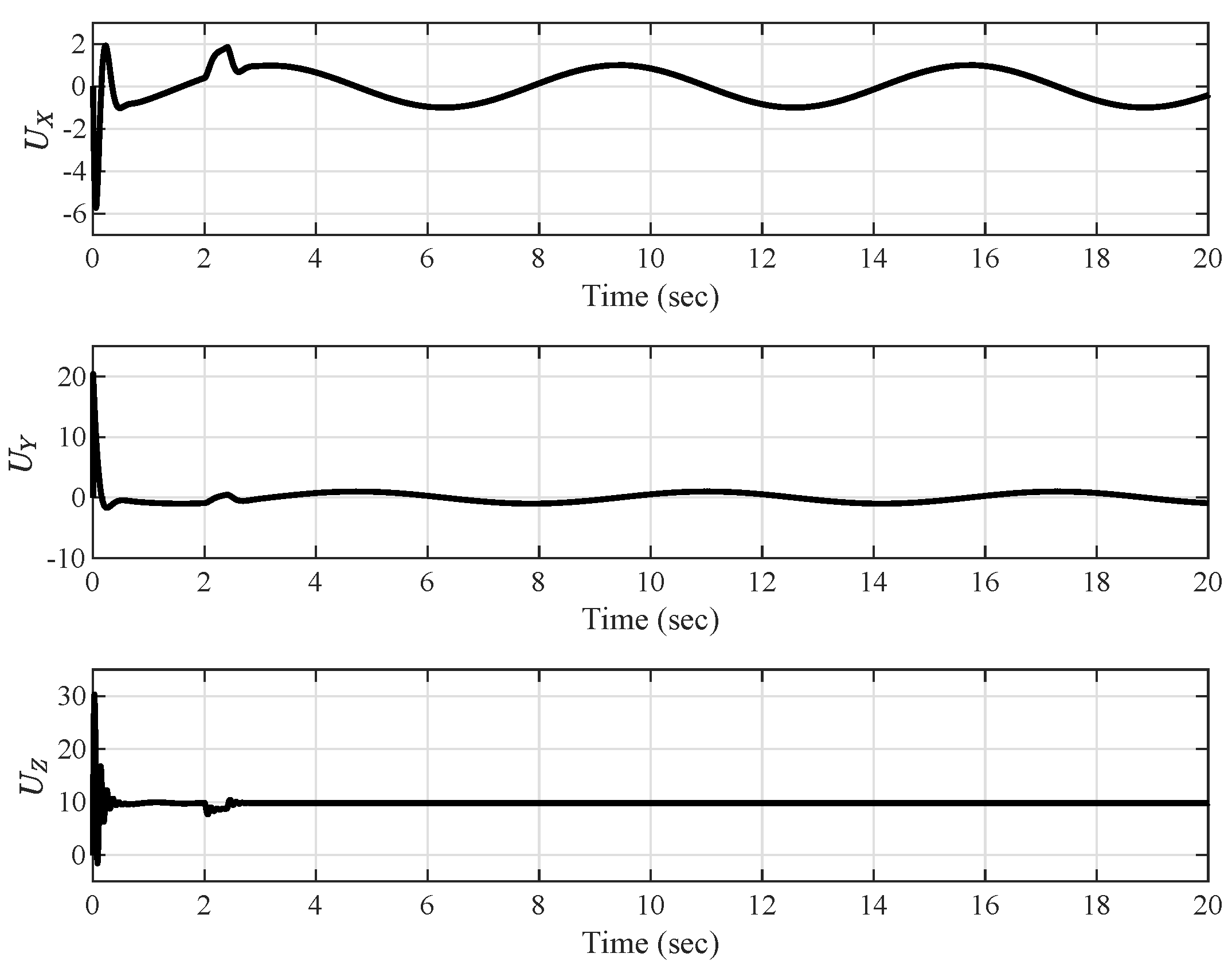
4. Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Lemma 2
Appendix A.2. Proof of Theorem 1
Appendix A.3. Proof of Theorem 2
References
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned aerial vehicles (UAVs): A survey on civil applications and key research challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Cai, C.; Cai, G. A survey of hybrid unmanned aerial vehicles. Prog. Aerosp. Sci. 2018, 98, 91–105. [Google Scholar] [CrossRef]
- Lu, Y.; Macias, D.; Dean, Z.S.; Kreger, N.R.; Wong, P.K. A UAV-mounted whole cell biosensor system for environmental monitoring applications. IEEE Trans. Nanobiosci. 2015, 14, 811–817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Lin, Y.; Wang, J. High-gain observer based decentralised output feedback control for interconnected nonlinear systems with unknown hysteresis input. Int. J. Control. 2013, 86, 1046–1059. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, W.; Zuo, Z.; Zhong, Y. Robust control for quadrotors with multiple time-varying uncertainties and delays. IEEE Trans. Ind. Electron. 2016, 64, 1303–1312. [Google Scholar] [CrossRef]
- Wu, D.; Chen, X.; Yang, L.; Fu, G.; Shi, X. Compact and low-profile omnidirectional circularly polarized antenna with four coupling arcs for UAV applications. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2919–2922. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Zhang, D.W.; Liu, G.P. Output feedback predictive control for discrete quasilinear systems with application to spacecraft flying-around. Asian J. Control. 2021, 24, 1846–1861. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, L.; Xia, Y.; Yuan, Y. Active disturbance rejection attitude control for a dual closed-loop quadrotor under gust wind. IEEE Trans. Control. Syst. Technol. 2017, 26, 1400–1405. [Google Scholar] [CrossRef]
- Ma, Z.; Jiao, S.M. Research on the attitude control of quad-rotor UAV based on active disturbance rejection control. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; pp. 45–49. [Google Scholar]
- Li, S.; Wang, Y.; Tan, J.; Zheng, Y. Adaptive RBFNNs/integral sliding mode control for a quadrotor aircraft. Neurocomputing 2016, 216, 126–134. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, R.; Zhang, K.; Jiang, B.; Tao, G. Robust backstepping sliding-mode control and observer-based fault estimation for a quadrotor UAV. IEEE Trans. Ind. Electron. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Xu, L.X.; Ma, H.J.; Guo, D.; Xie, A.H.; Song, D.L. Backstepping sliding-mode and cascade active disturbance rejection control for a quadrotor UAV. IEEE/ASME Trans. Mechatron. 2020, 25, 2743–2753. [Google Scholar] [CrossRef]
- Almakhles, D.J. Robust backstepping sliding mode control for a quadrotor trajectory tracking application. IEEE Access 2019, 8, 5515–5525. [Google Scholar] [CrossRef]
- Shi, X.; Hu, B.; Yin, C.; Cheng, Y.; Huang, X. Design of trajectory tracking controller with fractional-order backstepping sliding mode method for quadrotor UAV. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 5960–5965. [Google Scholar]
- Shao, X.; Liu, J.; Cao, H.; Shen, C.; Wang, H. Robust dynamic surface trajectory tracking control for a quadrotor UAV via extended state observer. Int. J. Robust Nonlinear Control 2018, 28, 2700–2719. [Google Scholar] [CrossRef]
- Shen, Z.; Li, F.; Cao, X.; Guo, C. Prescribed performance dynamic surface control for trajectory tracking of quadrotor UAV with uncertainties and input constraints. Int. J. Control 2020, 94, 1–21. [Google Scholar] [CrossRef]
- Muñoz, F.; González-Hernández, I.; Salazar, S.; Espinoza, E.S.; Lozano, R. Second order sliding mode controllers for altitude control of a quadrotor UAS: Real-time implementation in outdoor environments. Neurocomputing 2017, 233, 61–71. [Google Scholar] [CrossRef]
- Nowzari, C.; Cortés, J. Distributed event-triggered coordination for average consensus on weight-balanced digraphs. Automatica 2016, 68, 237–244. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Yang, Y.; Zhang, Y. Sampling-based event-triggered consensus for multi-agent systems. Neurocomputing 2016, 191, 141–147. [Google Scholar] [CrossRef]
- You, X.; Hua, C.; Guan, X. Event-triggered leader-following consensus for nonlinear multiagent systems subject to actuator saturation using dynamic output feedback method. IEEE Trans. Autom. Control. 2018, 63, 4391–4396. [Google Scholar] [CrossRef]
- Zeng, W.; Fan, H.; Wang, W. Event-triggered Adaptive Attitude Tracking Control of a Quadrotor UAV. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 2855–2860. [Google Scholar]
- Wang, C.; Guo, L.; Wen, C.; Hu, Q.; Qiao, J. Event-triggered adaptive attitude tracking control for spacecraft with unknown actuator faults. IEEE Trans. Ind. Electron. 2019, 67, 2241–2250. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Chen, T.; Hao, F. Event-triggered bipartite consensus for multiagent systems: A Zeno-free analysis. IEEE Trans. Autom. Control 2019, 65, 4866–4873. [Google Scholar] [CrossRef]
- Yu, H.; Chen, T. On Zeno behavior in event-triggered finite-time consensus of multiagent systems. IEEE Trans. Autom. Control 2020, 66, 4700–4714. [Google Scholar] [CrossRef]
- Borgers, D.P.; Heemels, W.M.H. Event-separation properties of event-triggered control systems. IEEE Trans. Autom. Control 2014, 59, 2644–2656. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Event-triggered adaptive control for a class of uncertain nonlinear systems. IEEE Trans. Autom. Control 2016, 62, 2071–2076. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Q.G. Event-triggered adaptive control of a class of nonlinear systems. ISA Trans. 2019, 94, 10–16. [Google Scholar] [CrossRef]
- Wang, C.; Wen, C.; Hu, Q. Event-triggered adaptive control for a class of nonlinear systems with unknown control direction and sensor faults. IEEE Trans. Autom. Control 2020, 65, 763–770. [Google Scholar] [CrossRef]
- Liang, H.; Liu, G.; Zhang, H.; Huang, T. Neural-network-based event-triggered adaptive control of nonaffine nonlinear multiagent systems with dynamic uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2239–2250. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, S.; Sun, L.; Ge, W.; Zhang, X. Output feedback adaptive dynamic surface sliding-mode control for quadrotor UAVs with tracking error constraints. Complexity 2020, 2020, 8537198. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Model predictive quadrotor control: Attitude, altitude and position experimental studies. IET Control Theory Appl. 2012, 6, 1812–1827. [Google Scholar] [CrossRef] [Green Version]
- Sanner, R.M.; Slotine, J. Gaussian networks for direct adaptive control. IEEE Trans. Neural Netw. 1992, 3, 837–863. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Zhu, G.; Chen, X.; Li, Z.; Wang, C.; Su, C.Y. Compound adaptive fuzzy quantized control for quadrotor and its experimental verification. IEEE Trans. Cybern. 2020, 51, 1121–1133. [Google Scholar] [CrossRef] [PubMed]
- KrstiC, M.; Kanellakopoulos, I.; KokotoviC, P.V. Nonlinear design of adaptive controllers for linear systems. IEEE Trans. Autom. Control 1994, 39, 738–752. [Google Scholar] [CrossRef] [Green Version]
- Esfandiari, F.; Khalil, H.K. Output feedback stabilization of fully linearizable systems. Int. J. Control 1992, 56, 1007–1037. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Wang, C.; Su, C.Y.; Li, Z.; Chen, X. Adaptive estimated inverse output-feedback quantized control for piezoelectric positioning stage. IEEE Trans. Cybern. 2018, 49, 2106–2118. [Google Scholar] [CrossRef] [PubMed]




| Symbol | Nomenclature |
|---|---|
| Lift force | |
| , | Unknown coefficients of air resistance |
| m | Mass of quadrotor |
| g | Acceleration of gravity |
| Relative speed of the cross-coupled rotor | |
| , , | Rotary inertia for all axis |
| Moment of inertia for all motors | |
| , | Coefficient of unknown aerodynamic drag |
| l | Distance from the center to the rotor |
| Torque | |
| Bounded external disturbances |
| Symbol | Value | Units |
|---|---|---|
| m | 1.4 | kg |
| k | 2.98 | |
| l | 0.2 | m |
| 1.14 | ||
| 1.2 | ||
| 1.8 | ||
| 1.8 | ||
| 2.4 |
| Scheme | MAE | RMSE | ||||
|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | |
| BSMC | 0.427% | 1.247% | 0.779% | 0.520% | 1.344% | 0.845% |
| Our proposed method | 0.092% | 0.156% | 0.322% | 0.104% | 0.171% | 0.352% |
| Scheme | MAE | RMSE | ||||
|---|---|---|---|---|---|---|
| BSMC | 2.258% | 2.288% | 1.137 | 2.264% | 2.299 % | 1.306 |
| Our proposed method | 0.082% | 0.098% | 1.148 | 0.093% | 0.108% | 1.282 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, P.; Liu, M.; Zhang, X.; Zhu, G.; Li, Z.; Su, C.-Y. Neural Network Based Adaptive Event-Triggered Control for Quadrotor Unmanned Aircraft Robotics. Machines 2022, 10, 617. https://doi.org/10.3390/machines10080617
Lu P, Liu M, Zhang X, Zhu G, Li Z, Su C-Y. Neural Network Based Adaptive Event-Triggered Control for Quadrotor Unmanned Aircraft Robotics. Machines. 2022; 10(8):617. https://doi.org/10.3390/machines10080617
Chicago/Turabian StyleLu, Pukun, Meng Liu, Xiuyu Zhang, Guoqiang Zhu, Zhi Li, and Chun-Yi Su. 2022. "Neural Network Based Adaptive Event-Triggered Control for Quadrotor Unmanned Aircraft Robotics" Machines 10, no. 8: 617. https://doi.org/10.3390/machines10080617
APA StyleLu, P., Liu, M., Zhang, X., Zhu, G., Li, Z., & Su, C.-Y. (2022). Neural Network Based Adaptive Event-Triggered Control for Quadrotor Unmanned Aircraft Robotics. Machines, 10(8), 617. https://doi.org/10.3390/machines10080617







