Research on Tire/Road Peak Friction Coefficient Estimation Considering Effective Contact Characteristics between Tire and Three-Dimensional Road Surface
Abstract
:1. Introduction
2. Overall Estimation Strategy
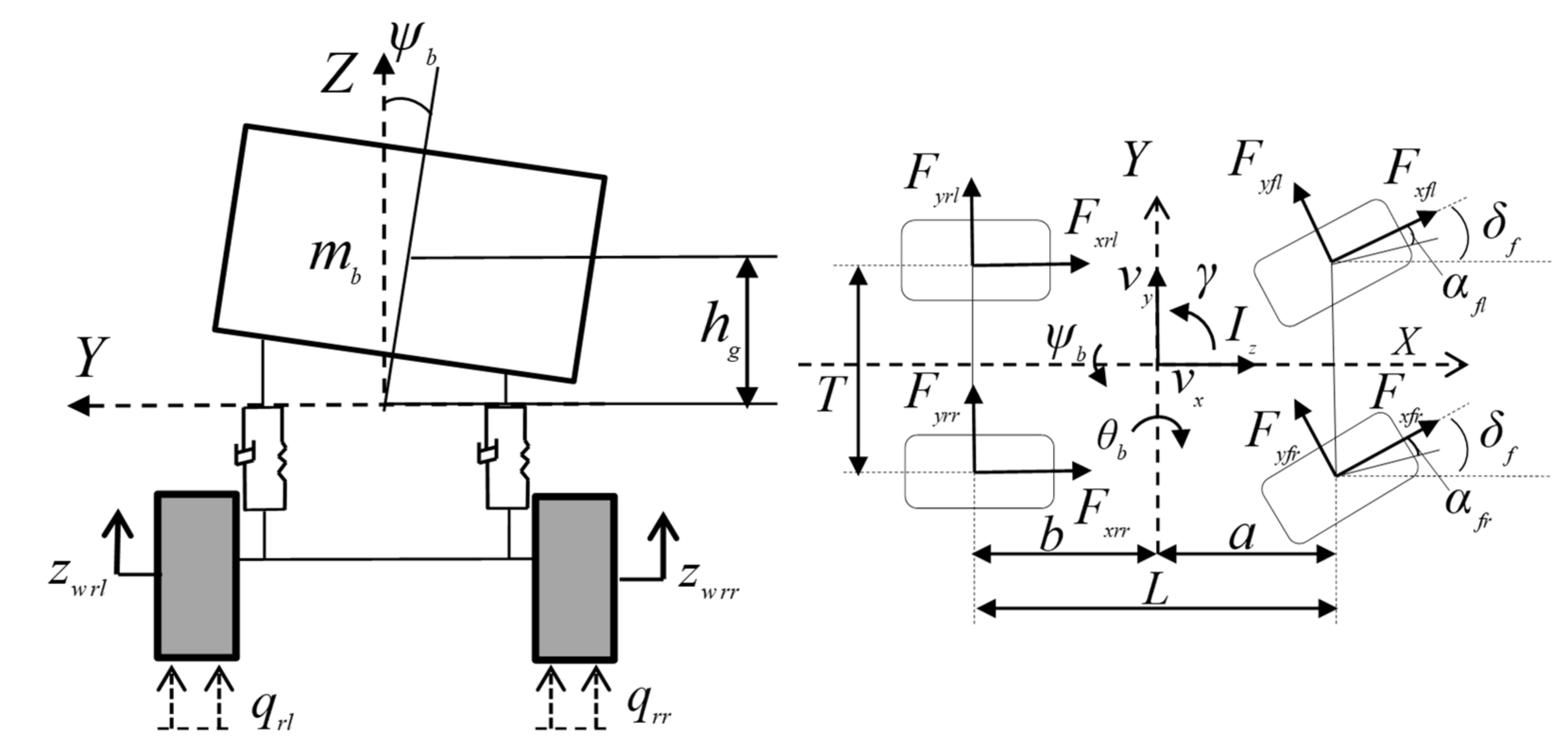
3. Establishment of Vehicle Dynamics Model
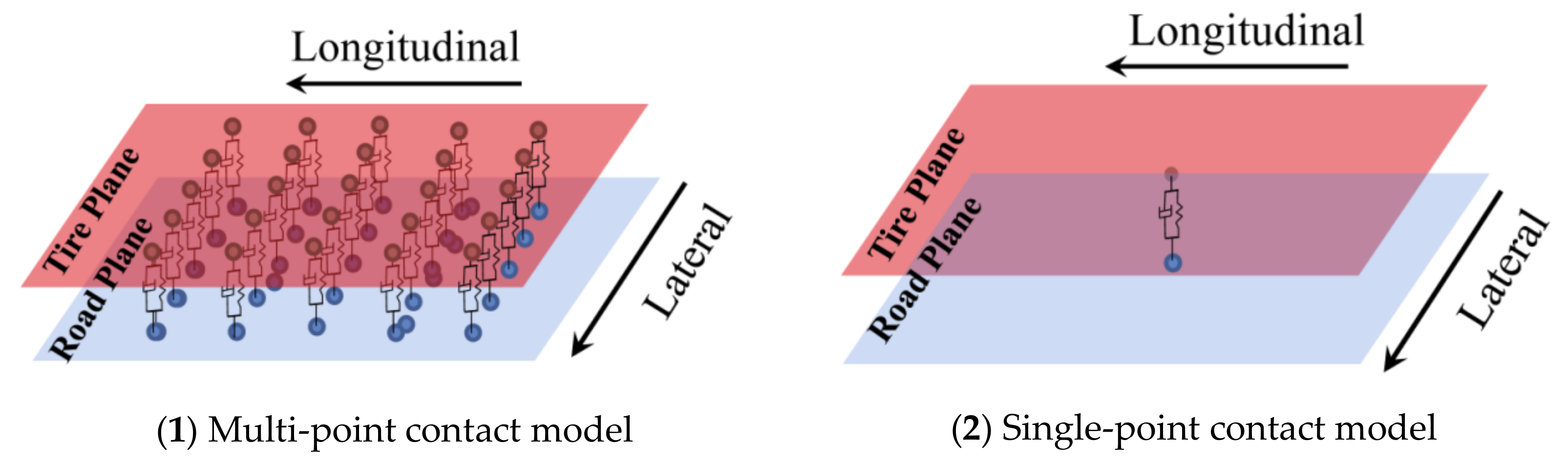
4. Modified Tire/Road Contact Model
4.1. Vertical Dynamics Model
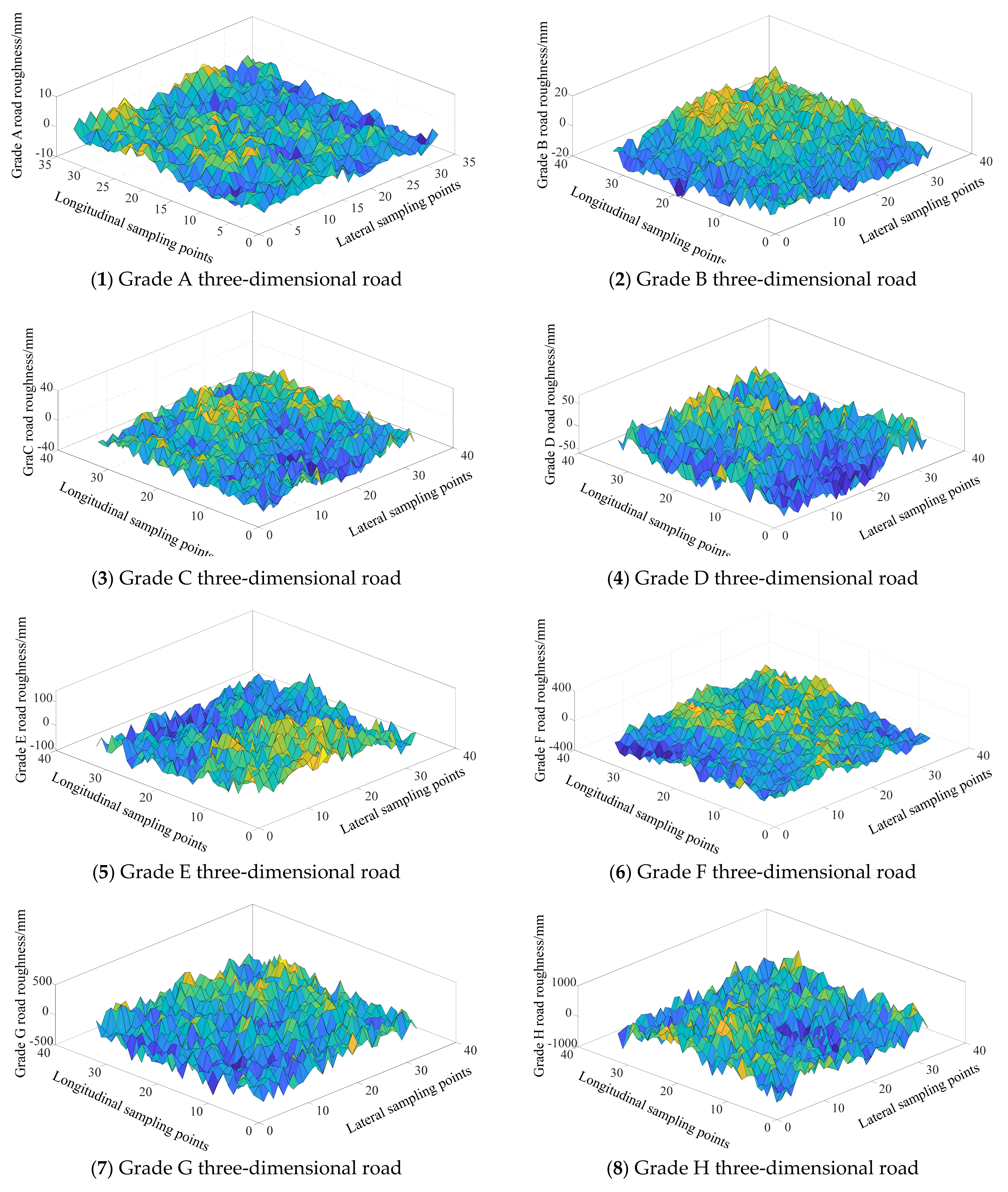
4.2. Construction of 3D Road
4.3. Modified LuGre Tire Model
4.4. Tire Model Normalization
4.5. Establishment of System Equations
5. Unscented Kalman Filter
6. Simulation Verification Analysis
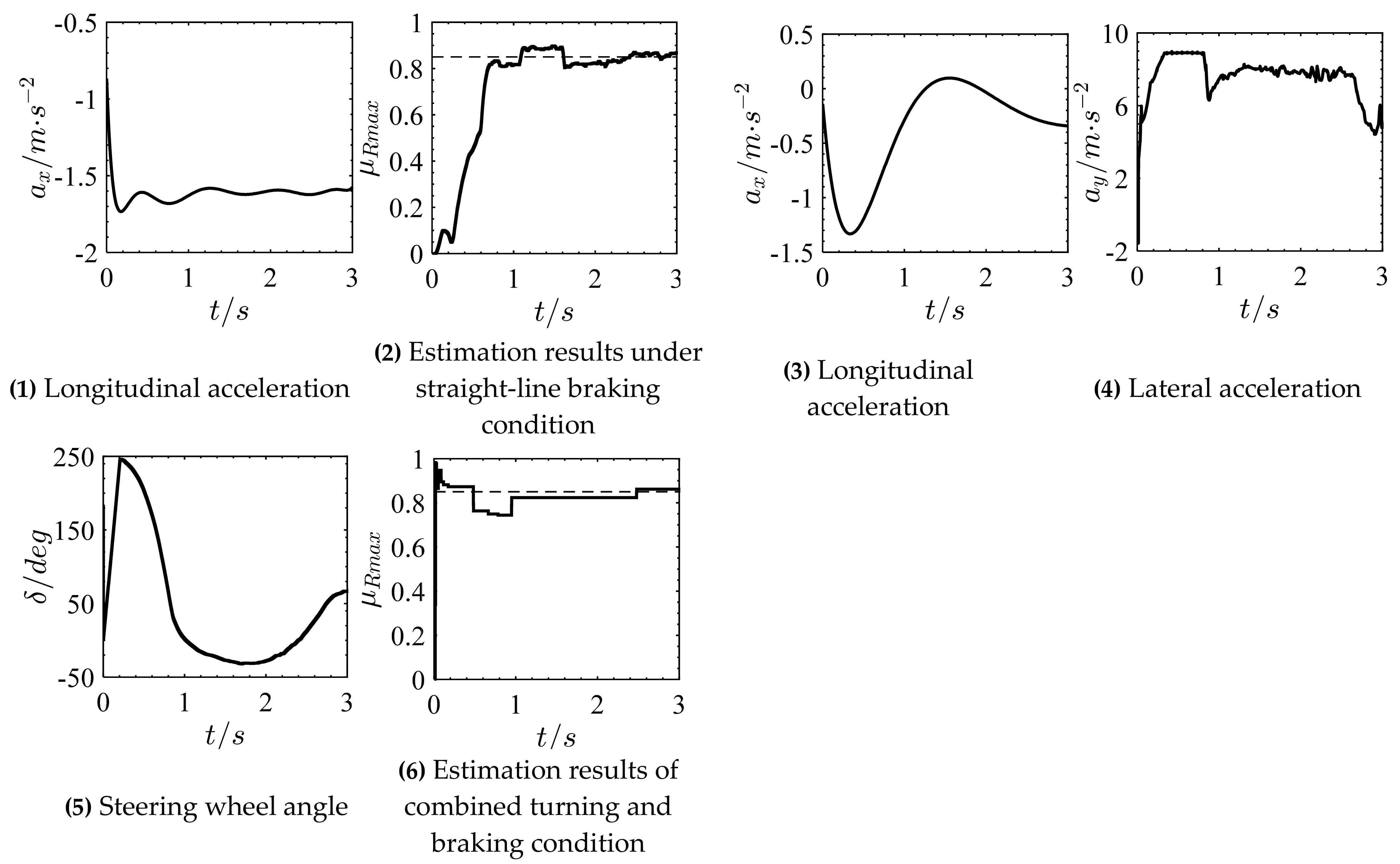
6.1. Straight-Line Braking Condition
6.2. Combined Turning and Braking Condition
7. Real Vehicle Test
7.1. Real Vehicle Test Platform
7.2. Straight-Line Test
7.3. Curved Test
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Data Traffic Accident Statistics. China National Bureau of Statistics. 2021. Available online: https://data.stats.gov.cn/easyquery.htm?cn=C01&zb=A0S0D01&sj=2021 (accessed on 25 February 2022).
- World Health Organization. Global Status Report on Road Safety 2015; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- Chen, B.; Zhang, X.; Yu, J.; Wang, Y. Impact of contact stress distribution on skid resistance of asphalt roads. Constr. Build. Mater. 2017, 133, 330–339. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, X.; Cao, Q.; Huang, X. Numerical Study of Tire Hydroplaning Based on Power Spectrum of Asphalt Road and Kinetic Friction Coefficient. Adv. Mater. Sci. Eng. 2017, 2017, 1–11. [Google Scholar]
- Wang, Y.; Hu, J.; Wang, F.; Dong, H.; Yan, Y.; Ren, Y.; Zhou, C.; Yin, G. Tire Road Friction Coefficient Estimation: Review and Research Perspectives. Chin. J. Mech. Eng. 2022, 35, 1–11. [Google Scholar] [CrossRef]
- Guo, F.; Pei, J.; Zhang, J.; Li, R.; Zhou, B.; Chen, Z. Study on the skid resistance of asphalt pavement: A state-of-the-art review and future prospective. Constr. Build. Mater. 2021, 303, 124411. [Google Scholar] [CrossRef]
- Mendoza-Petit, M.F.; Garcia-Pozuelo, D.; Diaz, V.; Garrosa, M. Characterization of the loss of grip condition in the Strain-Based Intelligent Tire at severe maneuvers. Mech. Syst. Signal Processing 2021, 168, 108586. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Kamai, K.; Seki, R. Intelligent tires for identifying coefficient of friction of tire/road contact surfaces using three-axis accelerometer. Smart Mater. Struct. 2015, 24, 025010. [Google Scholar] [CrossRef]
- Kim, M.-H.; Park, J.; Choi, S. Road Type Identification Ahead of the Tire Using D-CNN and Reflected Ultrasonic Signals. Int. J. Automot. Technol. 2021, 22, 47–54. [Google Scholar] [CrossRef]
- Yoon, J.-H.; Li, S.E.; Ahn, C. Estimation of vehicle sideslip angle and tire-road friction coefficient based on magnetometer with GPS. Int. J. Automot. Technol. 2016, 17, 427–435. [Google Scholar] [CrossRef]
- Khaleghian, S.; Emami, A.; Taheri, S. A technical survey on tire-road friction estimation. Friction 2017, 5, 123–146. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zheng, L.; Wu, H.; Zhang, Z.; Li, Y.; Liang, Y. An estimation scheme of road friction coefficient based on novel tyre model and improved SCKF. Veh. Syst. Dyn. 2021, 60, 2775–2804. [Google Scholar] [CrossRef]
- Gustafsson, F. Slip-based tire-road friction estimation. Automatica 1997, 33, 1087–1099. [Google Scholar] [CrossRef]
- Gustafsson, F. Monitoring tire-road friction using the wheel slip. IEEE Control Syst. 1998, 18, 42–49. [Google Scholar]
- Wang, J.; Alexander, L.; Rajamani, R. Friction Estimation on Highway Vehicles Using Longitudinal Measurements. J. Dyn. Syst. Meas. Control 2004, 126, 265–275. [Google Scholar] [CrossRef]
- Germann, S.; Wurtenberger, M.; Daiss, A. Monitoring of the friction coefficient between tire and road surface. In Proceedings of the IEEE Conference on Control Applications, Scotland, UK, 24–26 August 1994; IEEE: Piscataway, NJ, USA, 1994; pp. 613–618. [Google Scholar]
- de Castro, R.; Araujo, R.E.; Cardoso, J.S.; Freitas, D. A new linear parametrization for peak friction coefficient estimation in real time. In Proceedings of the Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Wang, B.; Guan, H.; Lu, P.; Zhang, A. Road surface condition identification approach based on road characteristic value. J. Terramechanics 2014, 56, 103–117. [Google Scholar] [CrossRef]
- Xin, W.; Liang, G.; Mingming, D.; Xiaolei, L. State estimation of tire-road friction and suspension system coupling dynamic in braking process and change detection of road adhesive ability. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 236, 1170–1187. [Google Scholar] [CrossRef]
- Li, G.; Fan, D.S.; Wang, Y.; Xie, R.C. Study on vehicle driving state and parameters estimation based on triple cubature Kalman filter. Int. J. Heavy Veh. Syst. 2020, 27, 126–144. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Senatore, A.; Farnam, A.; Akbari, A.; Timpone, F. A real-time approach to robust identification of tire–road friction characteristics on mixed-μ roads. Veh. Syst. Dyn. 2018, 57, 1338–1362. [Google Scholar] [CrossRef]
- Gao, L.; Xiong, L.; Lin, X.; Xia, X.; Liu, W.; Lu, Y.; Yu, Z. Multi-sensor Fusion Road Friction Coefficient Estimation During Steering with Lyapunov Method. Sensors 2019, 19, 3816. [Google Scholar] [CrossRef] [Green Version]
- Chu, L.; Cui, X.; Zhang, K.; Fwa, T.F.; Han, S. Directional Skid Resistance Characteristics of Road Pavement: Implications for Friction Measurements by British Pendulum Tester and Dynamic Friction Tester. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 793–803. [Google Scholar] [CrossRef]
- Uz, V.E.; Gökalp, I. Comparative laboratory evaluation of macro texture depth of surface coatings with standard volumetric test methods. Constr. Build. Mater. 2017, 139, 267–276. [Google Scholar] [CrossRef]
- Bitelli, G.; Simone, A.; Girardi, F.; Lantieri, C. Laser Scanning on Road Pavements: A New Approach for Characterizing Surface Texture. Sensors 2012, 12, 9110–9128. [Google Scholar] [CrossRef] [PubMed]
- Vollor, T.W.; Hanson, D.I. Development of Laboratory Procedure for Measuring Friction of HMA Mixtures—Phase I. Final Report of NCAT 06–06 (2006); National Center for Asphalt Technology, Auburn, Alabama, 2006.
- Xu, H.; Prozzi, J.A. Correlation of aggregate form properties with fourier frequencies. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 405–419. [Google Scholar] [CrossRef]
- Wang, D.; Liu, P.; Xu, H.; Kollmann, J.; Oeser, M. Evaluation of the polishing resistance characteristics of fine and coarse aggregate for asphalt road using wehner/schulze test. Constr. Build. Mater. 2018, 163, 742–750. [Google Scholar] [CrossRef]
- Hu, L.; Yun, D.; Gao, J.; Tang, C. Monitoring and optimizing the surface roughness of high friction exposed aggregate cement concrete in exposure process. Constr. Build. Mater. 2020, 230, 117005. [Google Scholar] [CrossRef]
- Hao, X.; Sha, A.; Sun, Z.; Li, W.; Zhao, H. Evaluation and comparison of real-time laser and electric sand-patch road texture-depth measurement methods. J. Transp. Eng. 2016, 142, 04016022. [Google Scholar] [CrossRef]
- Gökalp, I.; Uz, V.E.; Saltan, M. Comparative laboratory evaluation of macro texture depth of chip seal samples using sand patch and outflow meter test methods. In Bearing Capacity of Roads, Railways and Airfields; CRC Press: Boca Raton, FL, USA, 2017; pp. 915–920. [Google Scholar] [CrossRef]
- Zhu, H.; Liao, Y. Present situations of research on anti-skid property of asphalt road. Highway 2018, 63, 35–46. [Google Scholar]
- Grosch, K.A. Visco-Elastic Properties and the Friction of Solids: Relation between the Friction and Visco-elastic Properties of Rubber. Nature 1963, 197, 858–859. [Google Scholar] [CrossRef]
- Adam, C.S.; Piotrowski, M. Use of the unified theory of rubber friction for slip-resistance analysis in the testing of footwear outsoles and outsole compounds. Footwear Sci. 2012, 4, 23–35. [Google Scholar] [CrossRef]
- Mazzola, L.; Galderisi, A.; Fortunato, G.; Ciaravola, V.; Giustiniano, M. Influence of Surface Free Energy and Wettability on Friction Coefficient between Tire and Road Surface in Wet Conditions. Adv. Contact Angle Wettability Adhes. 2013, 1, 389–410. [Google Scholar] [CrossRef]
- Persson, B.N. Rubber friction: Role of the flash temperature. J. Phys. Condens. Matter 2006, 18, 7789–7823. [Google Scholar] [CrossRef]
- Ueckermann, D.; Wang, M.; Oeser, B. Steinauer, Calculation of skid resistance from texture measurements. J. Traffic Trans. Eng. 2015, 2, 3–16. [Google Scholar]
- Hertz, H. On the contact of elastic solids. J. Die Reine Angew. Math. 1882, 92, 156–171. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J. Contact of nominally flat surfaces. Proc. R. Soc. Lond. 1966, 295, 300–319. [Google Scholar]
- Carbone, G. A slightly corrected Greenwood and Williamson model predicts asymptotic linearity between contact area and load. J. Mech. Phys. Solids 2009, 57, 1093–1102. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Zhang, J.; Yang, S.; Li, Z. Study on improvement of LuGre dynamical model and its application in vehicle handling dynamics. J. Mech. Sci. Technol. 2019, 33, 545–558. [Google Scholar] [CrossRef]
- Yongjie, L.; Junning, Z.; Haoyu, L.; Zhizhe, M. Research on tire-road system coupling dynamics based on non-uniform contact. J. Mech. Eng. 2021, 57, 87–98. (In Chinese) [Google Scholar]
- Yongjie, L.; Wenqing, H.; Junning, Z. Construction of Three-Dimensional Road Surface and Application on Interaction between Vehicle and Road. Shock Vib. 2018, 2018, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Lu, Y.; Chen, N.; Wang, H. Research on the Identification of Tire Road Peak Friction Coefficient under Full Slip Rate Range Based on Normalized Tire Model. Actuators 2022, 11, 59. [Google Scholar] [CrossRef]
- Kiencke, U.; Nielsen, L. Automotive Control Systems: For Engine, Driveline, and Vehicle; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control, 2nd ed.; Springer Science: London, UK, 2012. [Google Scholar]
- Mechanical Vibration-Road Surface Profiles-Reporting of Measured Data; Standardization Administration: Beijing, China, 2006.
- Standard’s ISO 21994-2007; Standard’s Passenger Cars-Stopping Distance at Straight-Line Braking with ABS-Openloop Test Method. ISO: Geneva, Switzerland, 2007.
- Standard’s ISO 4138:2004; Standard’s Circular Driving Behaviour—Open-Loop Test Methods. ISO. ISO: Geneva, Switzerland, 2012.





| Symbol | Value and Unit | Parameter Name |
|---|---|---|
| mz | 880 kg | Total vehicle mass |
| mb | 788 kg | Sprung mass |
| L | 2.040 m | Wheel base |
| a | 1.145 m | Distance from centroid to front axle |
| b | 0.895 m | Distance from centroid to rear axle |
| hg | 0.54 m | Centroid height |
| T | 1.3 m | Wheel track width |
| Iz | 832.3 kg · m2 | Moment of inertia about the z-axis |
| Kψ | 25,041 N/rad | Tire cornering stiffness |
| Stiffness coefficient of suspension system | ||
| Damping Constant of Suspension Buffer | ||
| Tire stiffness coefficient | ||
| Tire damping coefficient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Lu, Y.; Liu, J.; Zhang, J. Research on Tire/Road Peak Friction Coefficient Estimation Considering Effective Contact Characteristics between Tire and Three-Dimensional Road Surface. Machines 2022, 10, 614. https://doi.org/10.3390/machines10080614
Han Y, Lu Y, Liu J, Zhang J. Research on Tire/Road Peak Friction Coefficient Estimation Considering Effective Contact Characteristics between Tire and Three-Dimensional Road Surface. Machines. 2022; 10(8):614. https://doi.org/10.3390/machines10080614
Chicago/Turabian StyleHan, Yinfeng, Yongjie Lu, Jingxv Liu, and Junning Zhang. 2022. "Research on Tire/Road Peak Friction Coefficient Estimation Considering Effective Contact Characteristics between Tire and Three-Dimensional Road Surface" Machines 10, no. 8: 614. https://doi.org/10.3390/machines10080614
APA StyleHan, Y., Lu, Y., Liu, J., & Zhang, J. (2022). Research on Tire/Road Peak Friction Coefficient Estimation Considering Effective Contact Characteristics between Tire and Three-Dimensional Road Surface. Machines, 10(8), 614. https://doi.org/10.3390/machines10080614






