Sequential Reliability Analysis for the Adjusting Mechanism of Tail Nozzle Considering Wear Degradation
Abstract
:1. Introduction
2. Dynamic Analysis for the Adjusting Mechanism
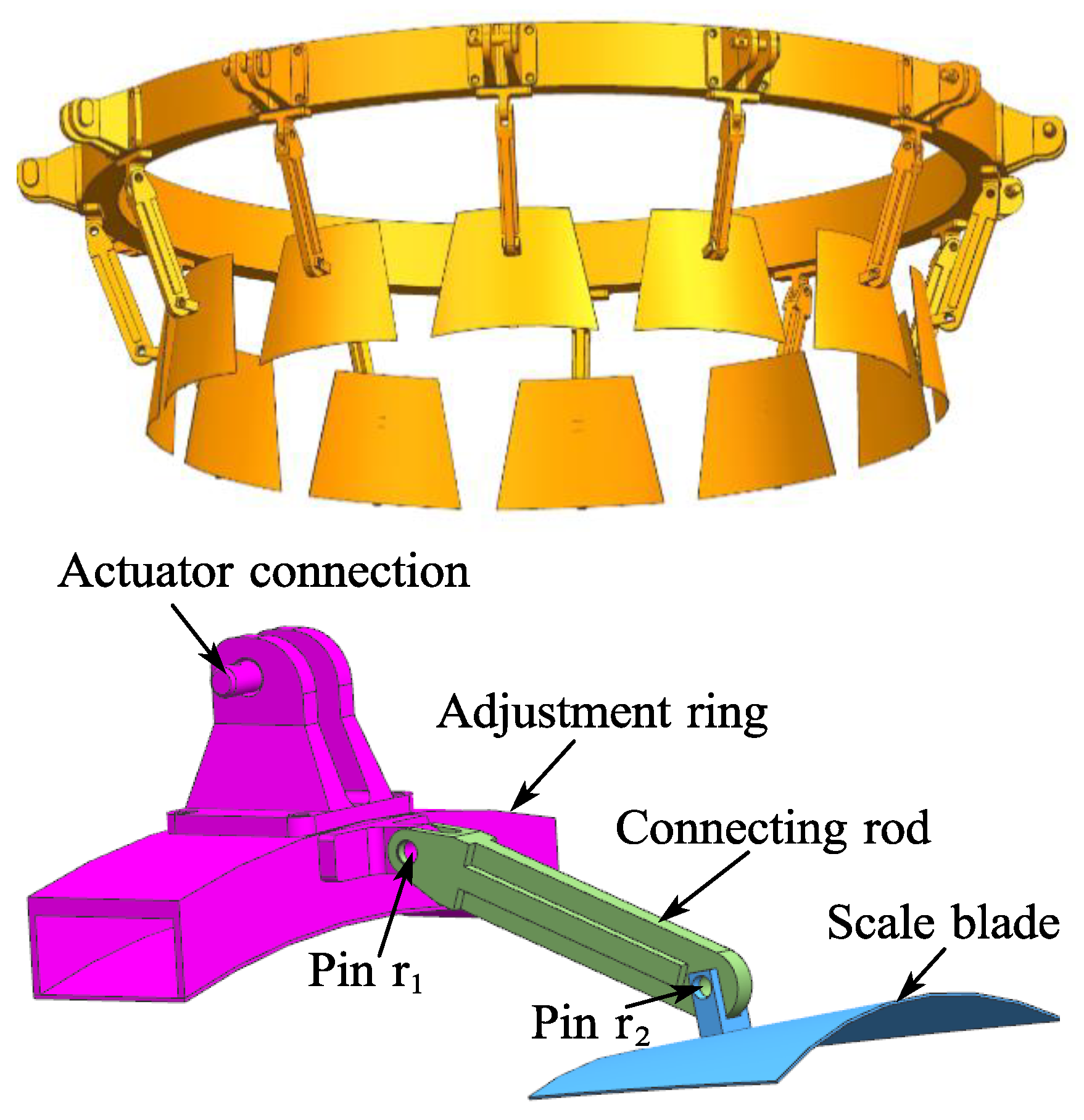
2.1. Introduction of Adjusting Mechanism Model
2.2. Clearance Degradation of Adjusting Mechanism
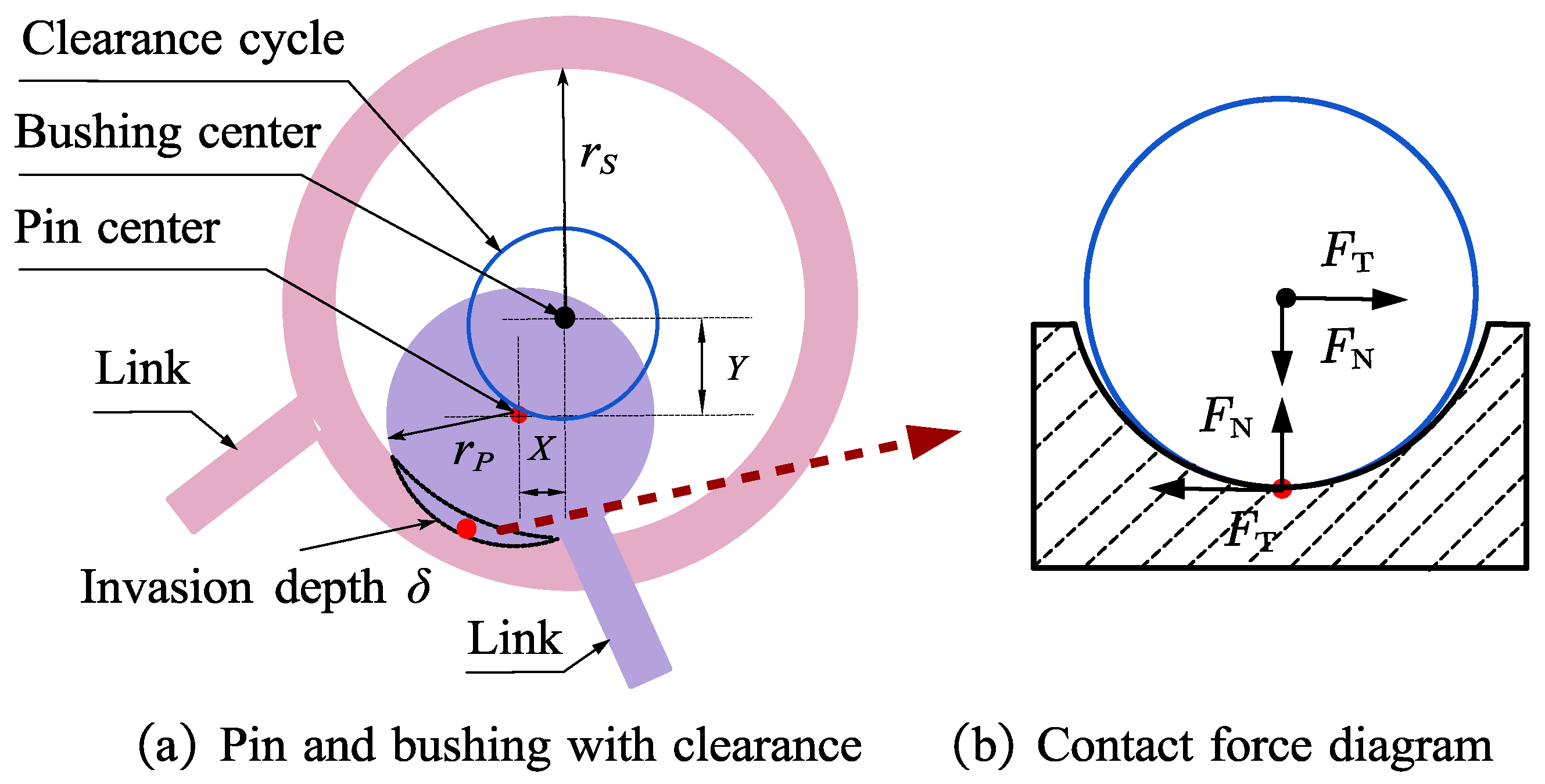
2.2.1. Theoretical Model of Contact Force in Clearance
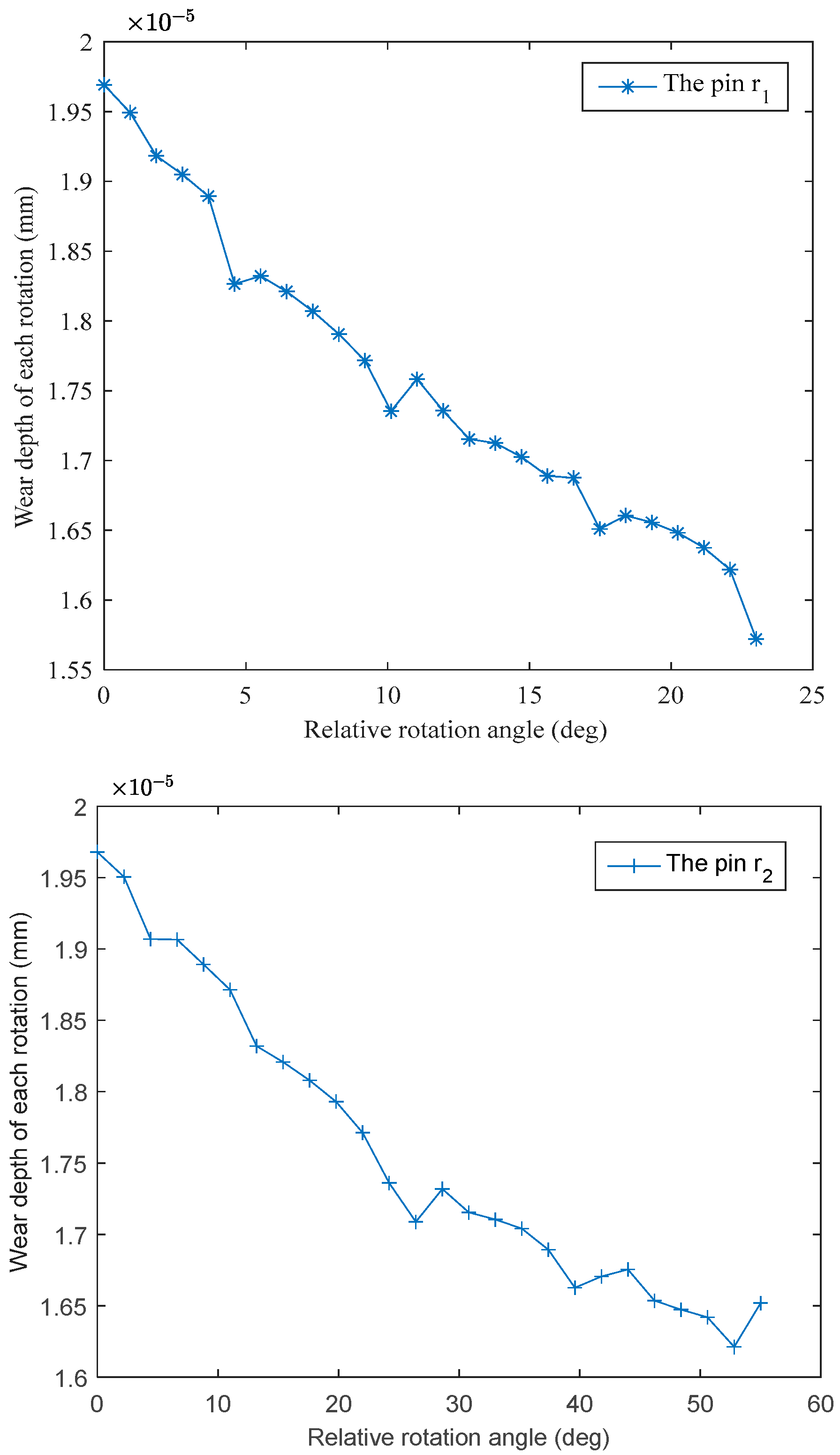
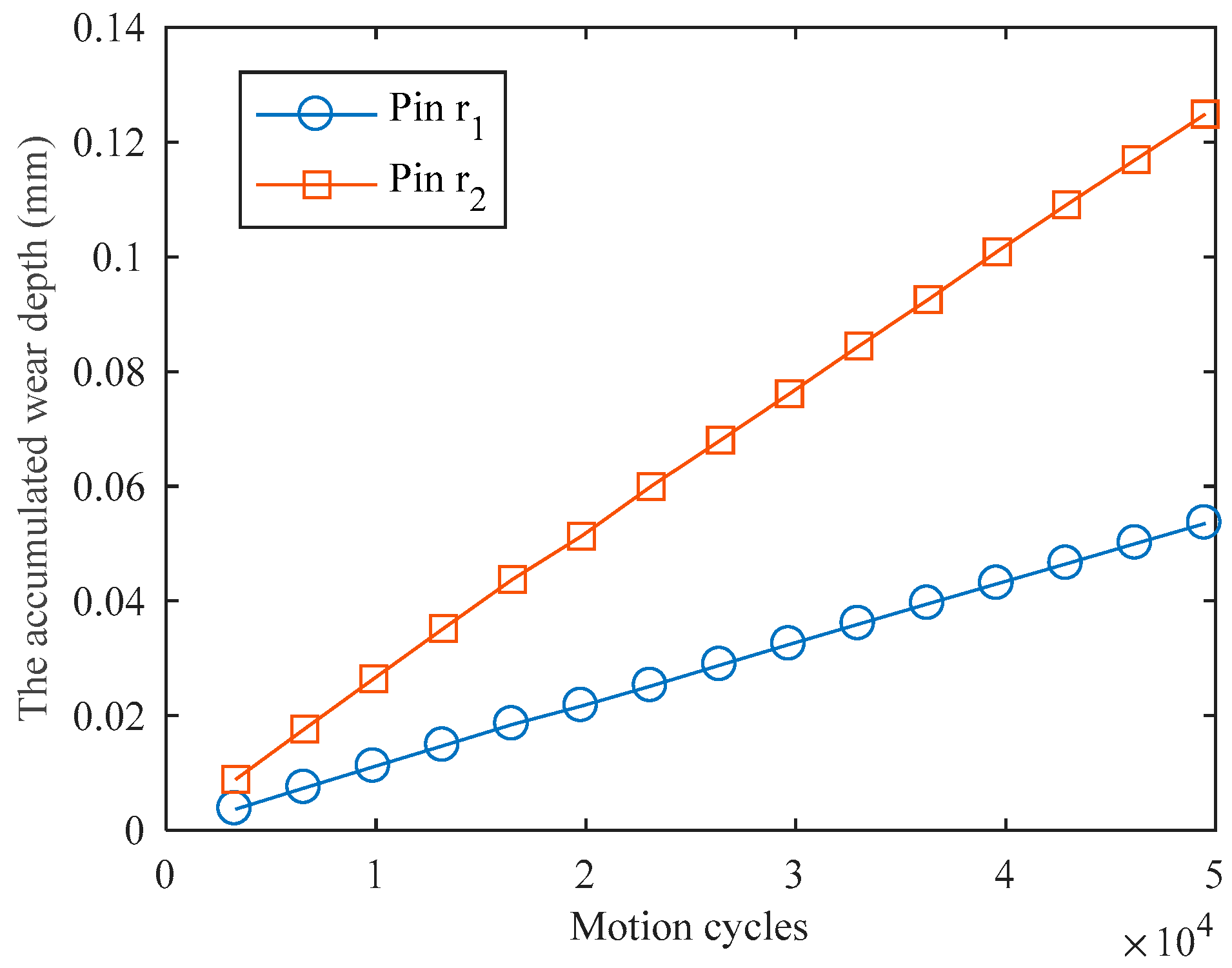
2.2.2. Wear Degradation of Pins
3. Sequential Reliability Analysis Considering Clearance Degradation
3.1. Reliability Analysis with Surrogate Model
3.2. Reliability Model Considering Clearance Degradation
3.3. Sequential Reliability Analysis Based on AK-ARBIS
3.3.1. AK-ARBIS Method
3.3.2. Advanced AK-ARBIS for Sequential Reliability
4. Validation Numerical Examples
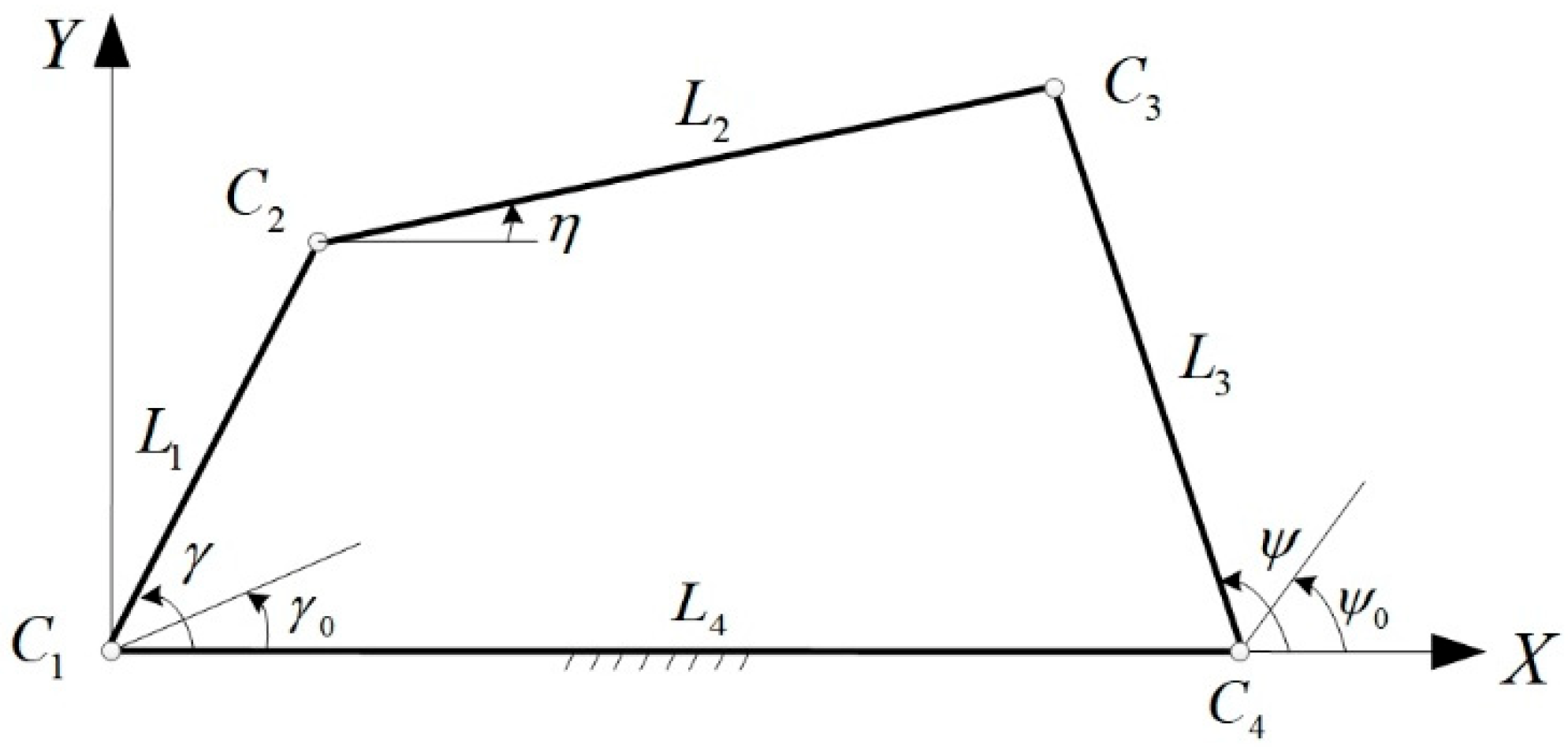
4.1. A Four-Bar Linkage Mechanism
4.2. A Steering Mechanism
5. Application of Adjusting Mechanism
5.1. Random Variables
5.2. Failure Mode
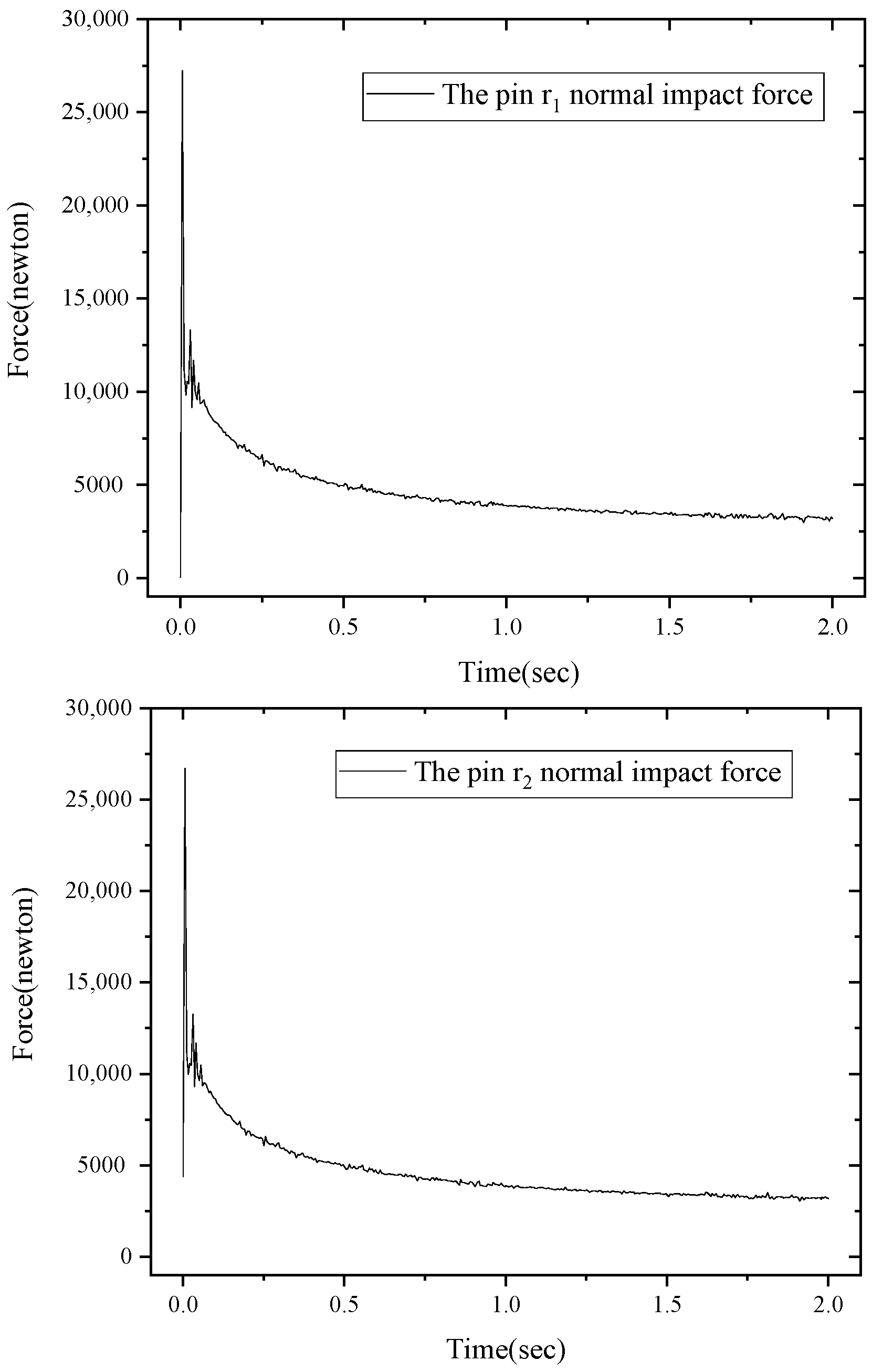
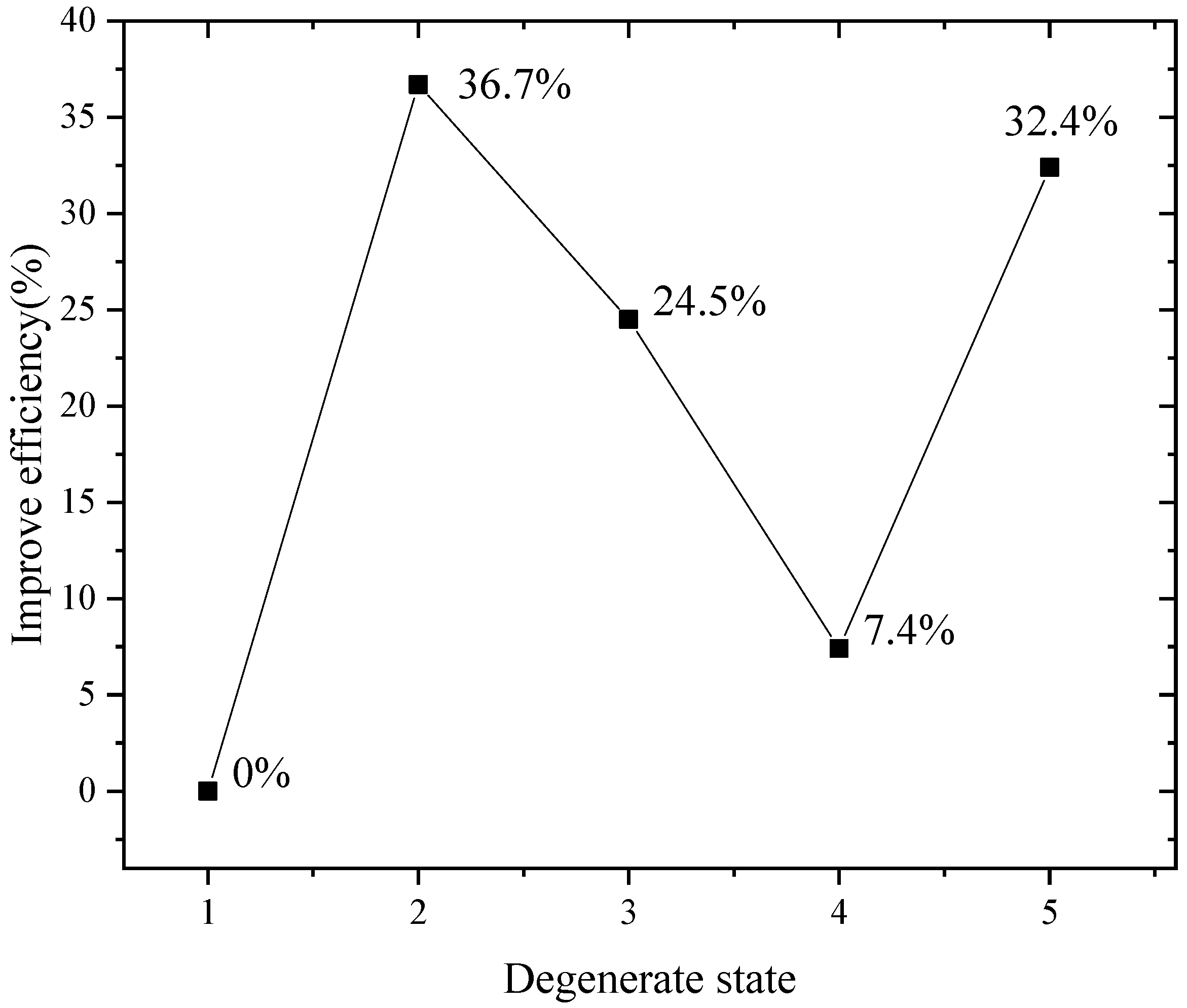
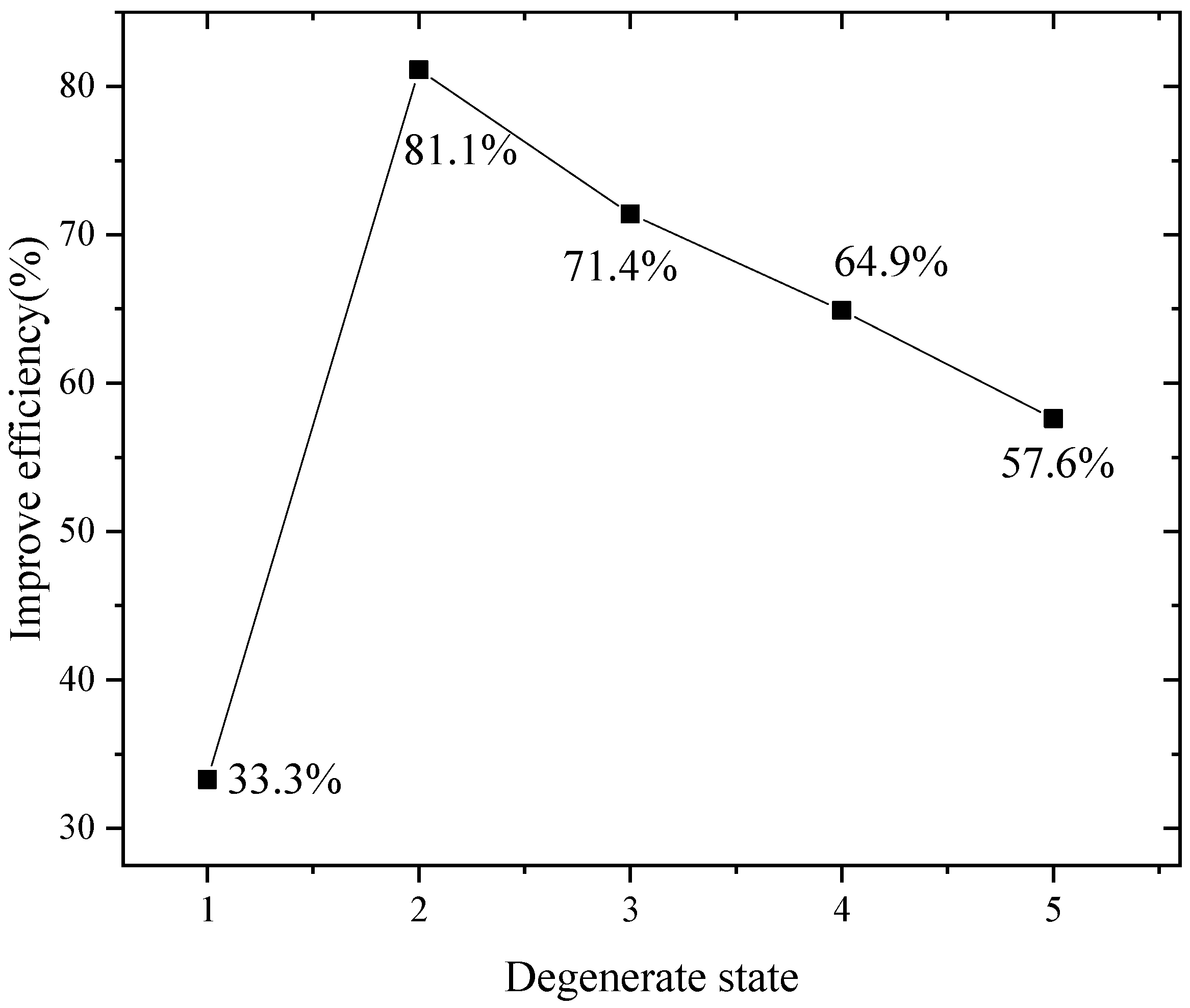
5.3. Result of Sequential Reliability Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arif, I.; Masud, J.; Shah, S. Computational Analysis of Integrated Engine Exhaust Nozzle on a Supersonic Fighter Aircraft. J. Appl. Fluid Mech. 2018, 11, 1511–1520. [Google Scholar] [CrossRef]
- Sloan, B.; Wang, J.; Spence, S.; Raghunathan, S.; Riordan, D. Aerodynamic performance of a bypass engine with fan nozzle exit area change by warped chevrons. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 224, 731–743. [Google Scholar] [CrossRef]
- Flores, P. A parametric study on the dynamic response of planar multibody systems with multiple clearance joints. Nonlinear Dyn. 2010, 61, 633–653. [Google Scholar] [CrossRef]
- Zhu, A.B.; He, S.L.; Zou, C.; Chen, W. The effect analysis of contact stiffness on wear of clearance joint. J. Tribol. 2017, 139, 031403. [Google Scholar] [CrossRef]
- Lai, X.M.; Lai, Q.F.; Huang, H.; Wang, C.; Yang, J.H.; Zhang, Y. New approach to assess and rank the impact of revolute joint wear on the kinematic accuracy in the low-velocity planar mechanism. Adv. Eng. Softw. 2016, 102, 71–82. [Google Scholar] [CrossRef]
- Sun, Z.C.; Yu, T.X.; Pang, H.; Song, B.F. Failure mechanism and reliability analysis of the rear cargo door lock of transport aircraft. Eng. Fail. Anal. 2021, 122, 105182. [Google Scholar] [CrossRef]
- Lai, X.M.; He, H.; Lai, Q.F.; Wang, C.; Yang, J.H.; Zhang, Y.; Fang, H.Y.; Liao, S.R. Computational prediction and experimental validation of revolute joint clearance wear in the low-velocity planar mechanism. Mech. Syst. Signal Process. 2017, 85, 963–976. [Google Scholar] [CrossRef]
- Zhang, J.F.; Du, X.P. Time-dependent reliability analysis for function generation mechanisms with random joint clearances. Mech. Mach. Theory 2015, 92, 184–199. [Google Scholar] [CrossRef]
- Bai, Z.F.; Zhao, Y.; Chen, J. Dynamics analysis of planar mechanical system considering revolute clearance joint wear. Tribol. Int. 2013, 64, 85–95. [Google Scholar] [CrossRef]
- Geng, X.Y.; Li, M.; Liu, Y.F.; Zheng, W.; Zhao, Z.J. Non-probabilistic kinematic reliability analysis of planar mechanisms with non-uniform revolute clearance joints. Mech. Mach. Theory 2019, 140, 413–433. [Google Scholar] [CrossRef]
- Li, J.L.; Huang, H.Z.; Yan, S.Z.; Yang, Y.Q. Kinematic accuracy and dynamic performance of a simple planar space deployable mechanism with joint clearance considering parameter uncertainty. Acta Astronaut. 2017, 136, 34–45. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Wu, J.N.; Yan, S.Z.; Li, J.N.; Gu, Y.X. Mechanism reliability of bistable compliant mechanisms considering degradation and uncertainties: Modeling and evaluation method. Appl. Math. Model. 2016, 40, 10377–10388. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.-S.; Xie, M. Stochastic modelling and analysis of degradation for highly reliable products. Appl. Stoch. Models Bus. Ind. 2015, 31, 16–32. [Google Scholar] [CrossRef]
- Wu, J.N.; Yan, S.Z.; Zuo, M.J. Evaluating the reliability of multi-body mechanisms: A method considering the uncertainties of dynamic performance. Reliab. Eng. Syst. Saf. 2016, 149, 96–106. [Google Scholar] [CrossRef]
- Li, X.Y.; Chen, W.B.; Kang, R. Performance margin-based reliability analysis for aircraft lock mechanism considering multi-source uncertainties and wear. Reliab. Eng. Syst. Saf. 2021, 205, 107234. [Google Scholar] [CrossRef]
- Zhuang, X.C.; Yu, T.X.; Shen, L.J.; Sun, Z.C.; Guo, B.Z. Time-varying dependence research on wear of revolute joints and reliability evaluation of a lock mechanism. Eng. Fail. Anal. 2019, 96, 543–561. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Lu, Z.Z.; Wang, P. A new learning function for Kriging and its applications to solve reliability problems in engineering. Comput. Math. Appl. 2015, 70, 1182–1197. [Google Scholar] [CrossRef]
- Zhang, L.G.; Lu, Z.Z.; Wang, P. Efficient structural reliability analysis method based on advanced Kriging model. Appl. Math. Model. 2015, 39, 781–793. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Zheng, P.J.; Wang, C.M.; Zong, Z.H.; Wang, L.Q. A new active learning method based on the learning function U of the AK-MCS reliability analysis method. Eng. Struct. 2017, 148, 185–194. [Google Scholar] [CrossRef]
- Hu, Z.; Mahadevan, S. A Single-Loop Kriging Surrogate Modeling for Time-Dependent Reliability Analysis. J. Mech. Des. 2016, 138, 061406. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M.; Relun, N. A combined Importance Sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models. Reliab. Eng. Syst. Saf. 2013, 111, 232–240. [Google Scholar] [CrossRef]
- Yun, W.Y.; Lu, Z.Z.; Jiang, X. An efficient reliability analysis method combining adaptive Kriging and modified importance sampling for small failure probability. Struct. Multidiscip. Optim. 2018, 58, 1383–1393. [Google Scholar] [CrossRef]
- Huang, X.X.; Chen, J.Q.; Zhu, H.P. Assessing small failure probabilities by AK–SS: An active learning method combining Kriging and Subset Simulation. Struct. Saf. 2016, 59, 86–95. [Google Scholar] [CrossRef]
- Ling, C.Y.; Lu, Z.Z.; Feng, K.X.; Zhang, X.B. A coupled subset simulation and active learning kriging reliability analysis method for rare failure events. Struct. Multidiscip. Optim. 2019, 60, 2325–2341. [Google Scholar] [CrossRef]
- Liu, H.; He, X.D.; Wang, P.; Lu, Z.Z.; Yue, Z.F. Time-dependent reliability analysis method based on ARBIS and Kriging surrogate model. Eng. Comput. 2022, 1–14. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, H.Y.; Hu, H.H.; Zhang, Z.; Li, H.H. A novel method for reliability analysis with interval parameters based on active learning Kriging and adaptive radial-based importance sampling. Int. J. Numer. Methods Eng. 2022, 123, 3264–3284. [Google Scholar] [CrossRef]
- Yun, W.Y.; Lu, Z.Z.; Jiang, X.; Zhang, L.G.; He, P.F. AK-ARBIS: An improved AK-MCS based on the adaptive radial-based importance sampling for small failure probability. Struct. Saf. 2020, 82, 101891. [Google Scholar] [CrossRef]
- Depina, I.; Le, T.M.H.; Fenton, G.; Eiksund, G. Reliability analysis with Metamodel Line Sampling. Struct. Saf. 2016, 60, 1–15. [Google Scholar] [CrossRef]
- Dumas, A.; Echard, B.; Gayton, N.; Rochat, O.; Dantan, J.Y.; Van der Veen, S. AK-ILS: An Active learning method based on Kriging for the Inspection of Large Surfaces. Precis. Eng. 2013, 37, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Su, M.J.; Xue, G.F.; Wang, D.Y.; Zhang, Y.S.; Zhu, Y. A novel active learning reliability method combining adaptive Kriging and spherical decomposition-MCS (AK-SDMCS) for small failure probabilities. Struct. Multidiscip. Optim. 2020, 62, 3165–3187. [Google Scholar] [CrossRef]
- Bichon, B.J.; Eldred, M.S.; Swiler, L.P.; Mahadevan, S.; McFarland, J.M. Efficient Global Reliability Analysis for Nonlinear Implicit Performance Functions. Aiaa J. 2008, 46, 2459–2468. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Wang, P.F. A Maximum Confidence Enhancement Based Sequential Sampling Scheme for Simulation-Based Design. J. Mech. Des. 2014, 136, 021006. [Google Scholar] [CrossRef]
- Sun, Z.L.; Wang, J.; Li, R.; Tong, C. LIF: A new Kriging based learning function and its application to structural reliability analysis. Reliab. Eng. Syst. Saf. 2017, 157, 152–165. [Google Scholar] [CrossRef]
- Jiang, C.; Qiu, H.B.; Yang, Z.; Chen, L.M.; Gao, L.; Li, P.G. A general failure-pursuing sampling framework for surrogate-based reliability analysis. Reliab. Eng. Syst. Saf. 2019, 183, 47–59. [Google Scholar] [CrossRef]
- Murray, R. Remarks on a Multivariate Transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]







| Variable | Distribution | |||||
|---|---|---|---|---|---|---|
| 2D-uniform with a circle | 0.018 | 0.019 | 0.020 | 0.021 | 0.022 | |
| Methods | States | C.O.V (%) | ||
|---|---|---|---|---|
| MCS ) | State 1 | 3.7946 | ||
| State 2 | 0.0015 | 2.5801 | ||
| State 3 | 0.0027 | 1.9219 | ||
| State 4 | 0.0044 | 1.5042 | ||
| State 5 | 0.0067 | 1.2176 | ||
| AK-MCS ) | State 1 | 50 + 115 | 4.0149 | |
| State 2 | 50 + 180 | 0.0015 | 2.5801 | |
| State 3 | 50 + 245 | 0.0027 | 1.9219 | |
| State 4 | 50 + 296 | 0.0043 | 1.5217 | |
| State 5 | 50 + 444 | 0.0065 | 1.2363 | |
| AK-ARBIS ) | State 1 | 50 + 122 | 3.9271 | |
| State 2 | 50 + 114 | 0.0015 | 2.5801 | |
| State 3 | 50 + 185 | 0.0026 | 1.9586 | |
| State 4 | 50 + 274 | 0.0043 | 1.5217 | |
| State 5 | 50 + 300 | 0.0065 | 1.2363 |
| Variable | Distribution | Mean (mm) | Standard Deviation (mm) |
|---|---|---|---|
| Normal | 111 | 0.1 | |
| Normal | 283.5 | 0.1 | |
| Normal | 650.24 | 0.1 | |
| Normal | 83.5 | 0.1 |
| Variable | Distribution | |||||
|---|---|---|---|---|---|---|
| 2D-uniform with a circle | 0.0046 | 0.0047 | 0.0048 | 0.0049 | 0.0050 | |
| Methods | States | C.O.V (%) | ||
|---|---|---|---|---|
| MCS ) | State 1 | 0.0178 | 2.3490 | |
| State 2 | 0.0198 | 2.2249 | ||
| State 3 | 0.0218 | 2.1183 | ||
| State 4 | 0.0242 | 2.0080 | ||
| State 5 | 0.0266 | 1.9129 | ||
| AK-MCS ) | State 1 | 50 + 189 | 0.0177 | 2.3558 |
| State 2 | 50 + 190 | 0.0194 | 2.2483 | |
| State 3 | 50 + 196 | 0.0218 | 2.1183 | |
| State 4 | 50 + 208 | 0.0244 | 1.9996 | |
| State 5 | 50 + 236 | 0.0269 | 1.9020 | |
| AK-ARBIS ) | State 1 | 50 + 126 | 0.0178 | 2.3490 |
| State 2 | 50 + 36 | 0.0191 | 2.2662 | |
| State 3 | 50 + 56 | 0.0215 | 2.1333 | |
| State 4 | 50 + 73 | 0.0240 | 2.0166 | |
| State 5 | 50 + 100 | 0.0270 | 1.8983 |
| Variable | Distribution Type | Distribution Parameter 1 | Distribution Parameter 2 |
|---|---|---|---|
| (mm) | Truncated normal | 2.85 | 0.05 |
| (mm) | Truncated normal | 2.85 | 0.05 |
| Uniform | 0.01 | 0.15 | |
| Uniform | 0.01 | 0.15 | |
| (N·m) | Uniform | 55.92 | 60.92 |
| Wear Cycles (Different States) | Wear Depth (mm) | Radii (Truncated Normal Distribution) | ||
|---|---|---|---|---|
| Standard Deviation (0.05) | ||||
| State 1 (initial clearance) | 0 | 0 | 2.85 | 2.85 |
| State 2 (3300 cycles) | 0.0074 | 0.0177 | 2.85–0.0074 | 2.85–0.0177 |
| State 3 (6600 cycles) | 0.0148 | 0.0355 | 2.85–0.0148 | 2.85–0.0355 |
| State 4 (9900 cycles) | 0.0221 | 0.0529 | 2.85–0.0221 | 2.85–0.0529 |
| State 5 (13,200 cycles) | 0.0294 | 0.0703 | 2.85–0.0294 | 2.85–0.0703 |
| Methods | States | C.O.V (%) | ||
|---|---|---|---|---|
| AK-MCS ) | State 1 | 25 + 5 | 0.0003 | 4.9999 |
| State 2 | 25 + 10 | 0.0011 | 3.0135 | |
| State 3 | 25 + 21 | 0.0035 | 1.6873 | |
| State 4 | 25 + 42 | 0.0091 | 1.0435 | |
| State 5 | 25 + 92 | 0.0217 | 0.6714 | |
| AK-ARBIS ) | State 1 | 25 + 2 | 0.0005 | 4.4710 |
| State 2 | 25 + 0 | 0.0013 | 2.7717 | |
| State 3 | 25 + 6 | 0.0040 | 1.5780 | |
| State 4 | 25 + 17 | 0.0088 | 1.0613 | |
| State 5 | 25 + 47 | 0.0220 | 0.6667 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Wang, P.; Zhou, H. Sequential Reliability Analysis for the Adjusting Mechanism of Tail Nozzle Considering Wear Degradation. Machines 2022, 10, 613. https://doi.org/10.3390/machines10080613
Hu H, Wang P, Zhou H. Sequential Reliability Analysis for the Adjusting Mechanism of Tail Nozzle Considering Wear Degradation. Machines. 2022; 10(8):613. https://doi.org/10.3390/machines10080613
Chicago/Turabian StyleHu, Huanhuan, Pan Wang, and Hanyuan Zhou. 2022. "Sequential Reliability Analysis for the Adjusting Mechanism of Tail Nozzle Considering Wear Degradation" Machines 10, no. 8: 613. https://doi.org/10.3390/machines10080613
APA StyleHu, H., Wang, P., & Zhou, H. (2022). Sequential Reliability Analysis for the Adjusting Mechanism of Tail Nozzle Considering Wear Degradation. Machines, 10(8), 613. https://doi.org/10.3390/machines10080613







