A Novel Ensemble of Arithmetic Optimization Algorithm and Harris Hawks Optimization for Solving Industrial Engineering Optimization Problems
Abstract
:1. Introduction
- Inspired by the algorithm architecture of the AOA and HHO, we propose a novel hybrid algorithm based on these two algorithms, named EAOAHHO.
- PIOBL helps the proposed algorithm to increase the original population diversity and the capability to escape from local optima.
- CMS can enhance the proposed algorithm exploitation and exploration to obtain better convergence accuracy.
- The performance of EAOAHHO is verified on 23 benchmark functions, the IEEE CEC2017 test suite, and four industrial engineering design problems. The experimental results demonstrate the superiority of EAOAHHO over the basic AOA, HHO, and other advanced meta-heuristic algorithms in handling the above problem.
2. Background
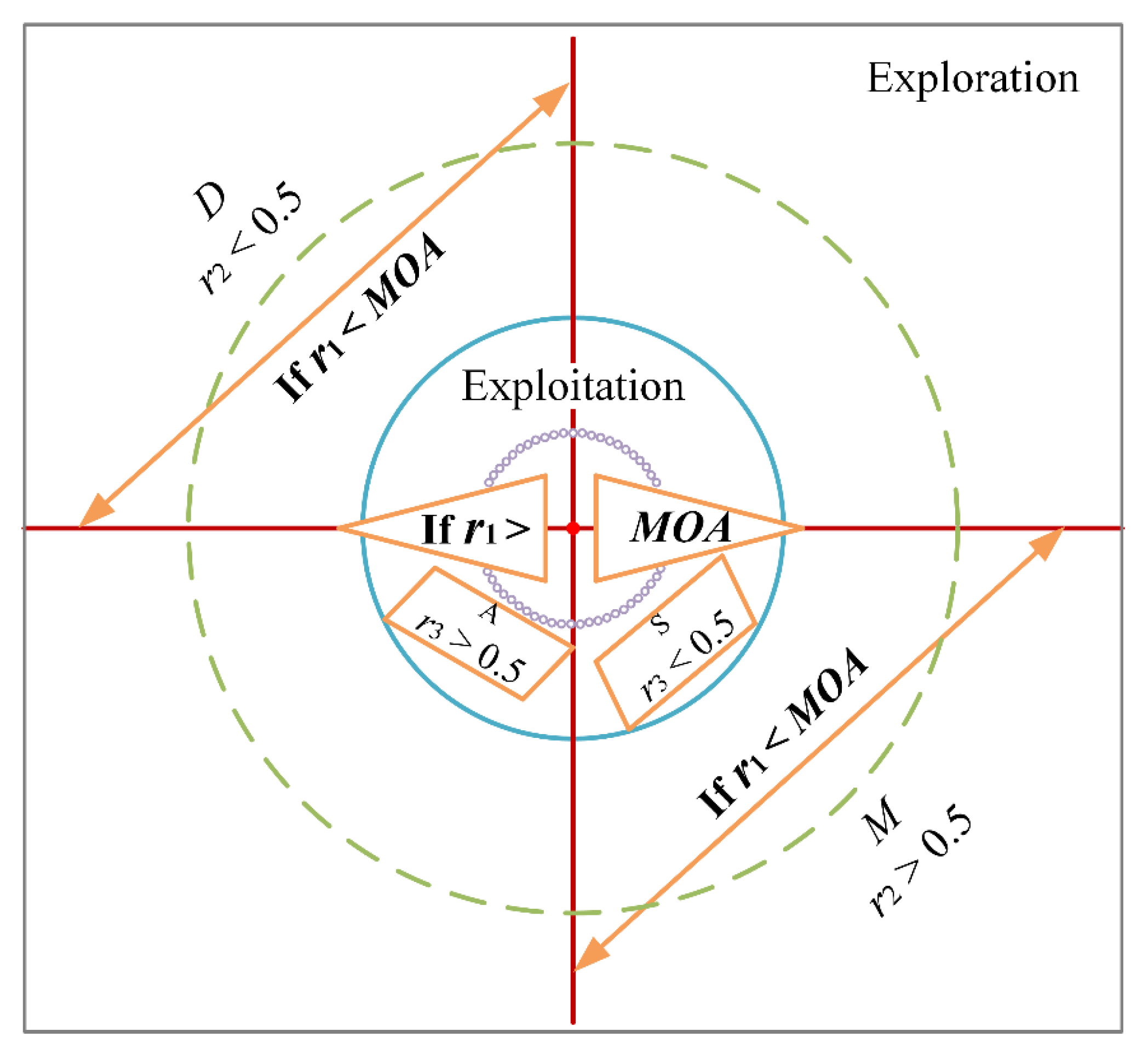
2.1. Arithmetic Optimization Algorithm (AOA)
2.1.1. Initialization Phase
2.1.2. Exploration Phase
2.1.3. Exploitation Phase
| Algorithm 1 Pseudo-code of the basic AOA |
| 1. Initialize the population size and the maximum iterations 2. Initialize the positions of each search agent 3. While 4. Check if the position goes beyond the search space boundary and then adjust it 5. Evaluate the fitness values of all search agents 6. Set as the position of current best solution 7. Calculate the value using Equation (2) 8. Calculate the value using Equation (4) 9. For to 10. If then //Exploration phase 11. Update the search agent’s position using Equation (3) 12. Else //Exploitation phase 13. Update the search agent’s position using Equation (5) 14. End If 15. End For 16. 17. End While 18. Return |
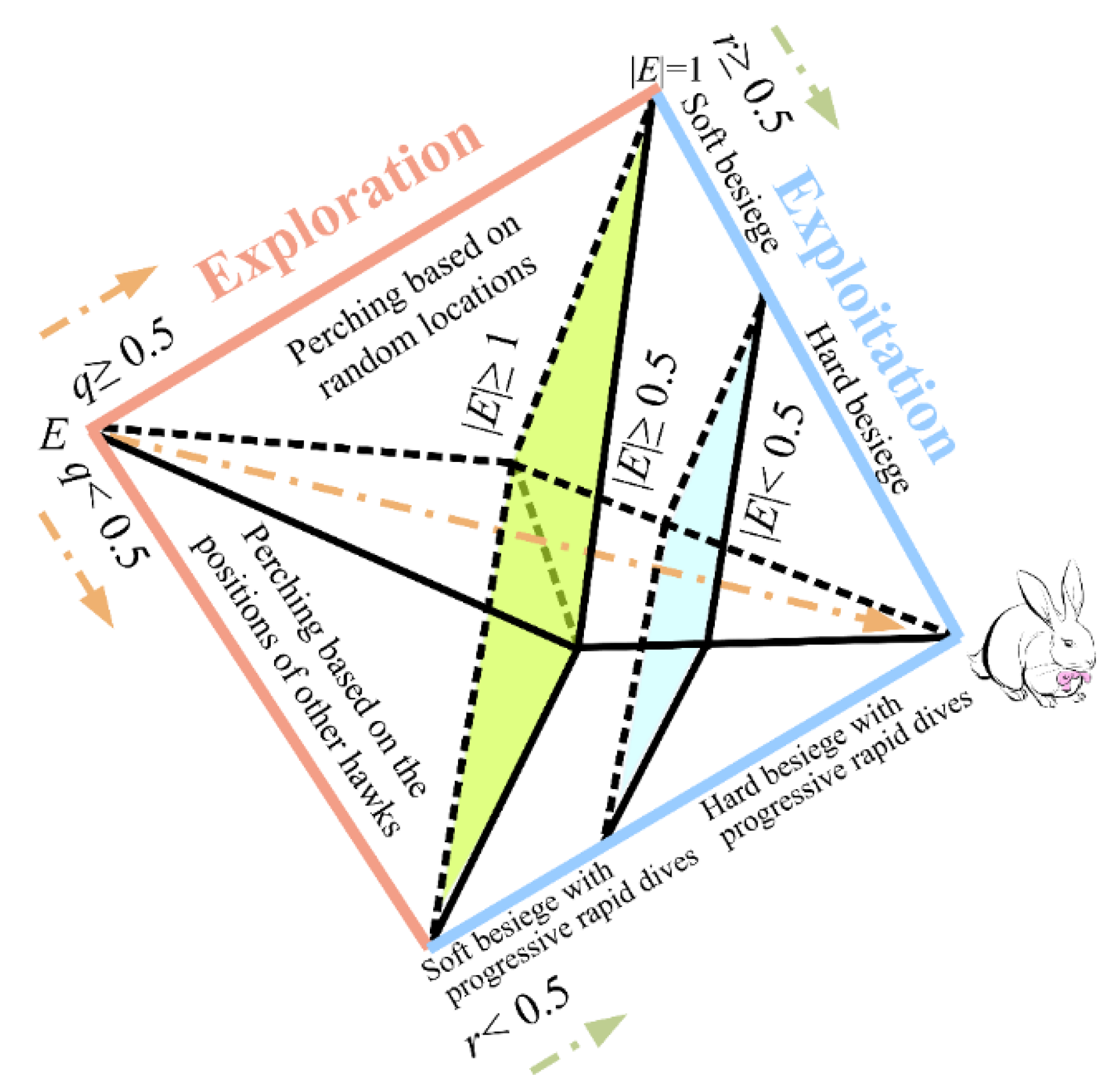
2.2. Harris Hawks Optimization (HHO)
2.2.1. Exploration Phase
2.2.2. Transition from Exploration to Exploitation
2.2.3. Exploitation Phase
- Soft besiege
- Hard besiege
- Soft besiege with progressive rapid dives
- Hard besiege with progressive rapid dives
| Algorithm 2 Pseudo-code of the basic HHO |
| 1. Initialize the population size and the maximum iterations 2. Generate the random position of each hawk 3. While 4. Check if any hawk position goes beyond the search space boundary and then adjust it 5. Evaluate the fitness values of all hawks 6. Set as the position of current best solution 7. For to 8. Calculate the prey energy using Equation (8) 9. If then //Exploration phase 10. Update the hawk’s position using Equation (6) 11. End If 12. If then //Exploitation phase 13. If and then 14. Update the hawk’s position using Equation (9) 15. Else if and then 16. Update the hawk’s position using Equation (12) 17. Else if and then 18. Update the hawk’s position using Equation (16) 19. Else if and then 20. Update the hawk’s position using Equation (19) 21. End If 22. End For 23. 24. End While 25. Return |
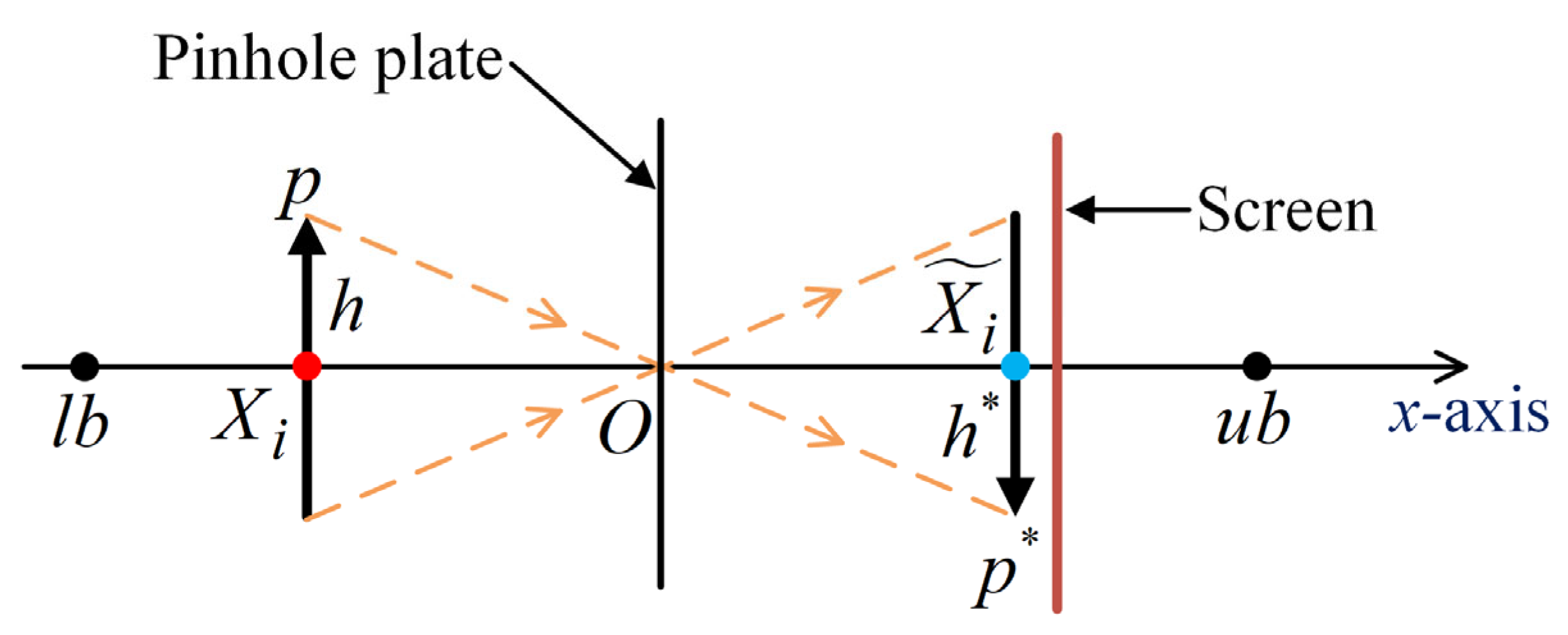
2.3. Pinhole Imaging Opposition-Based Learning
2.4. Ensemble/Composite Mutation Strategy (CMS)
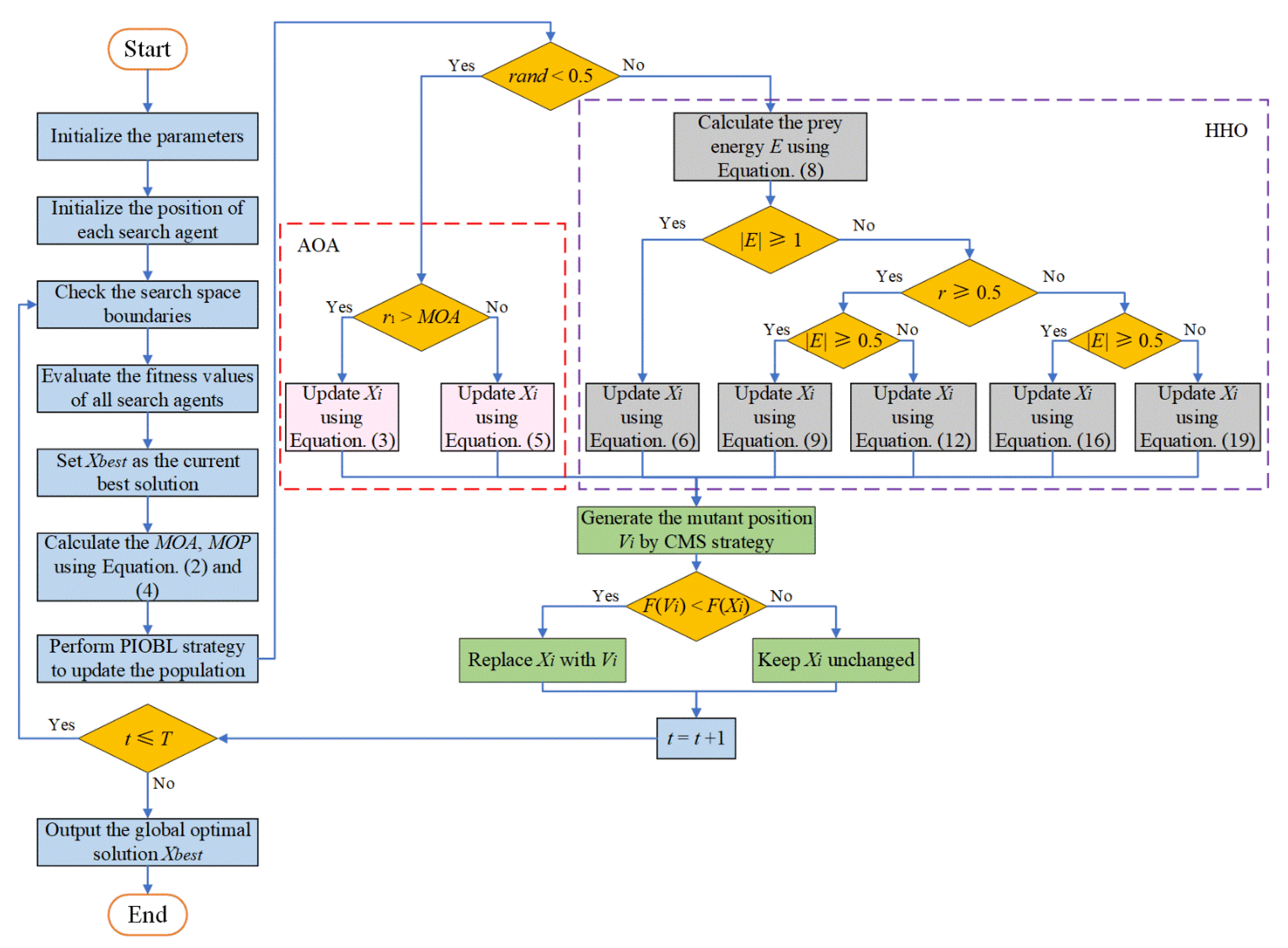
3. The Proposed EAOAHHO Algorithm
3.1. The Detailed Design of EAOAHHO
| Algorithm 3 Pseudo-code of the proposed EAOAHHO |
| 1. Initialize the population size and the maximum iterations 2. Initialize the positions of each search agent 3. While 4. Check if the position goes beyond the search space boundary and then adjust it 5. Evaluate the fitness values of all search agents 6. Set as the position of current best solution 7. Calculate the value using Equation (2) 8. Calculate the value using Equation (4) 9. Generate the opposite positions of all search agents using Equation (21) and save the ones with better fitness//PIOBL 10. For to 11. If then //AOA is a random number between 0 and 1 12. If then 13. Update the position using Equation (3) 14. Else 15. Update the position using Equation (5) 16. End If 17. Else //HHO 18. Calculate the prey energy using Equation (8) 19. If then 20. Update the position using Equation (6) 21. End If 22. If then 23. If and then 24. Update the position using Equation (9) 25. Else if and then 26. Update the position using Equation (12) 27. Else if and then 28. Update the position using Equation (16) 29. Else if and then 30. Update the position using Equation (19) 31. End If 32. Generate the new mutant positions by using Equations (24)–(26) //CMS 33. Set as the best trial vector with the lowest fitness from 34. If then 35. 36. End If 37. End If 38. End For 39. 40. End While 41. Return |
3.2. Computational Complexity Analysis
4. Experimental Results and Discussions
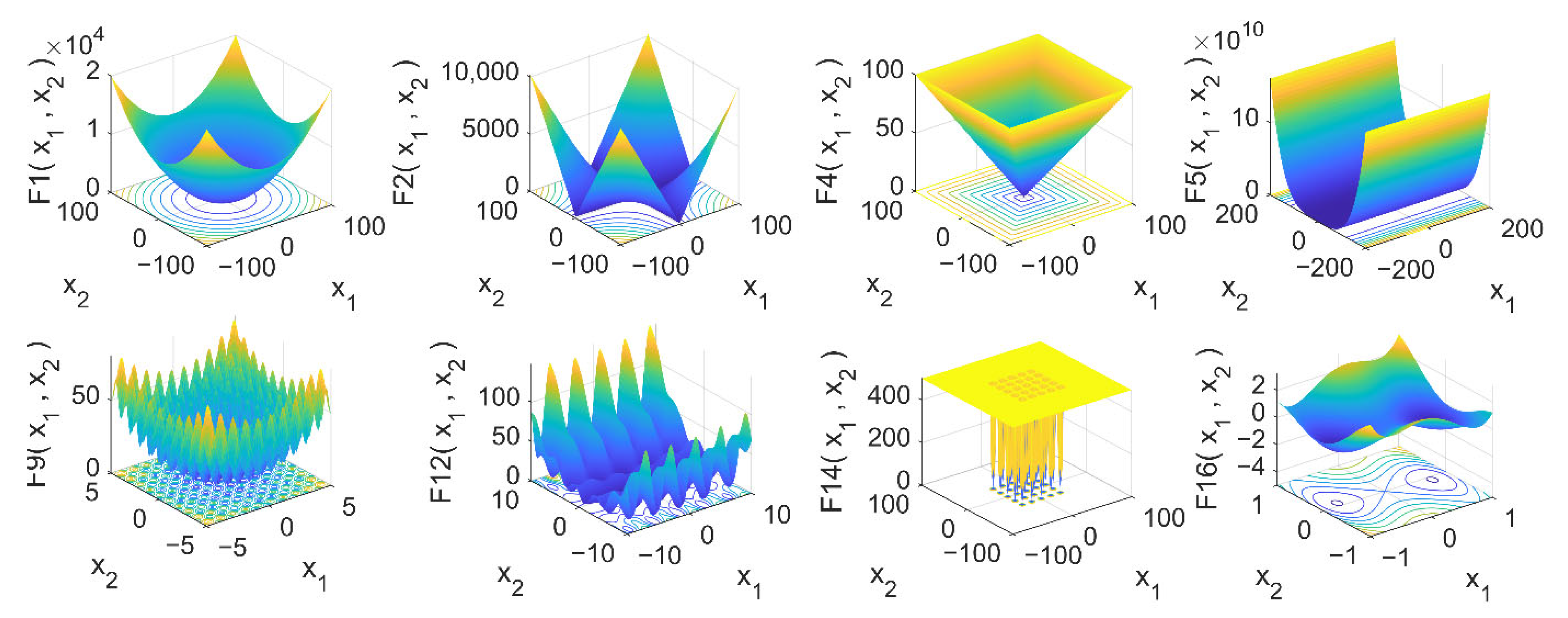
4.1. Experiment 1: Classical Benchmark Functions
4.1.1. Impacts of Components
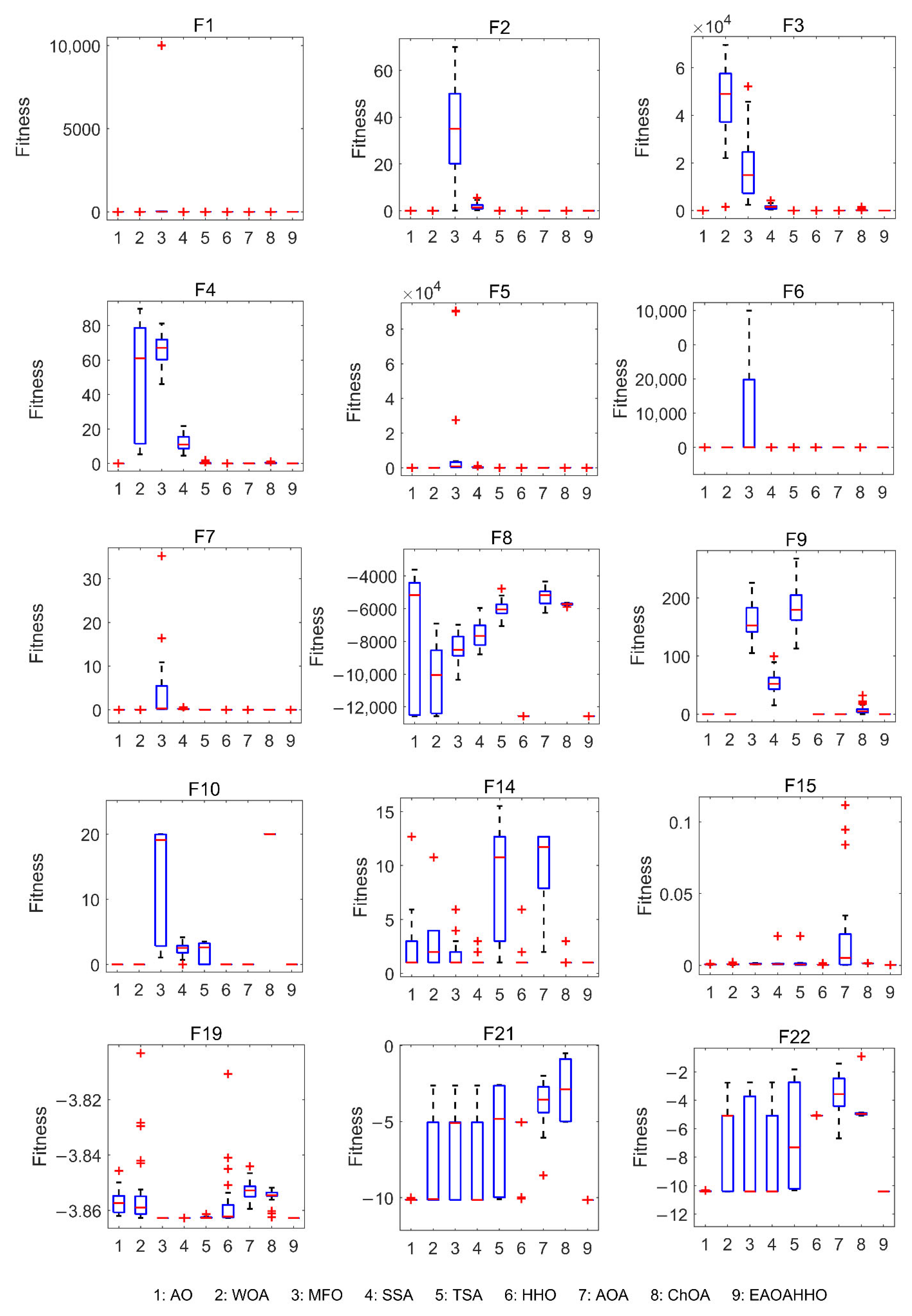
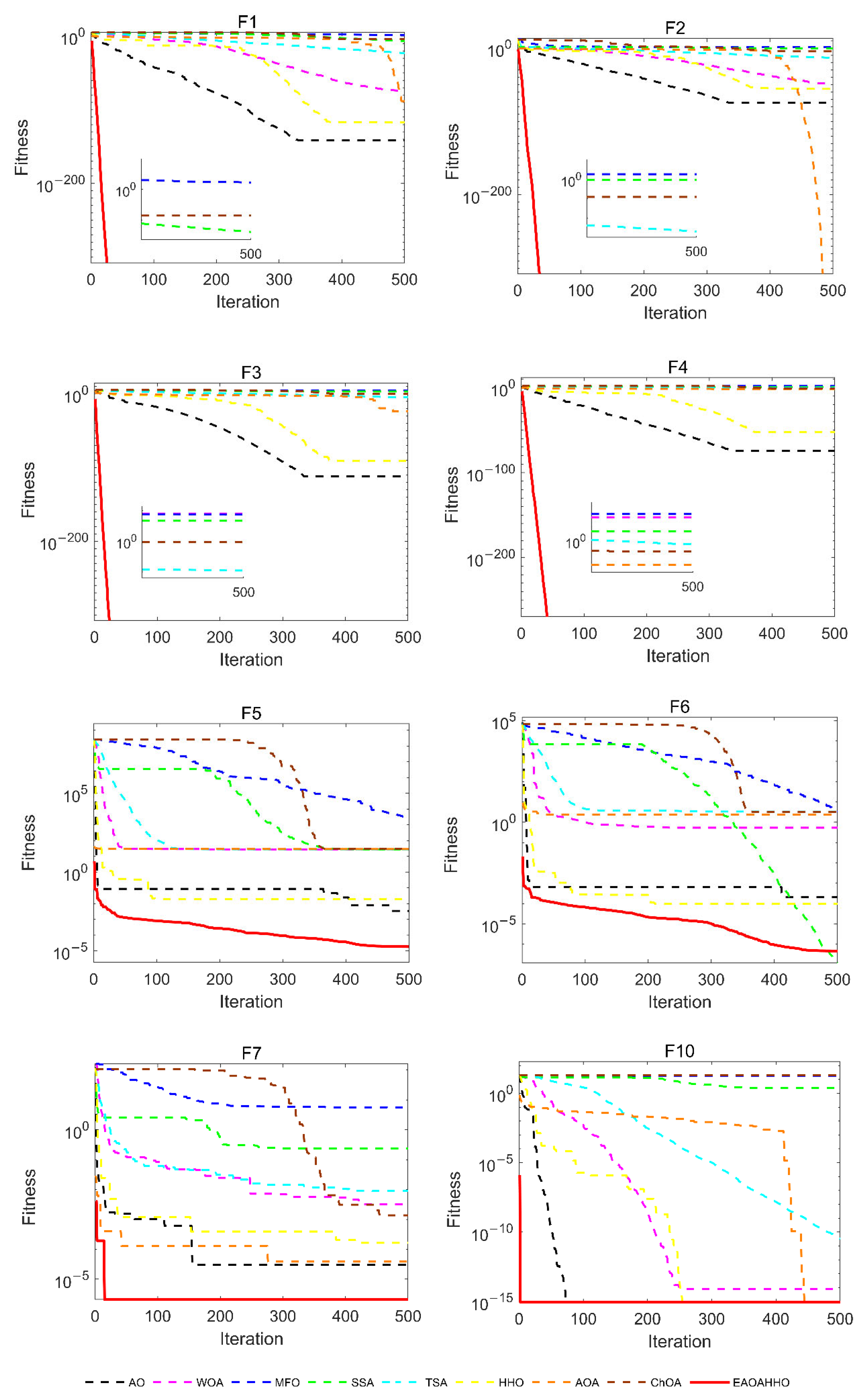
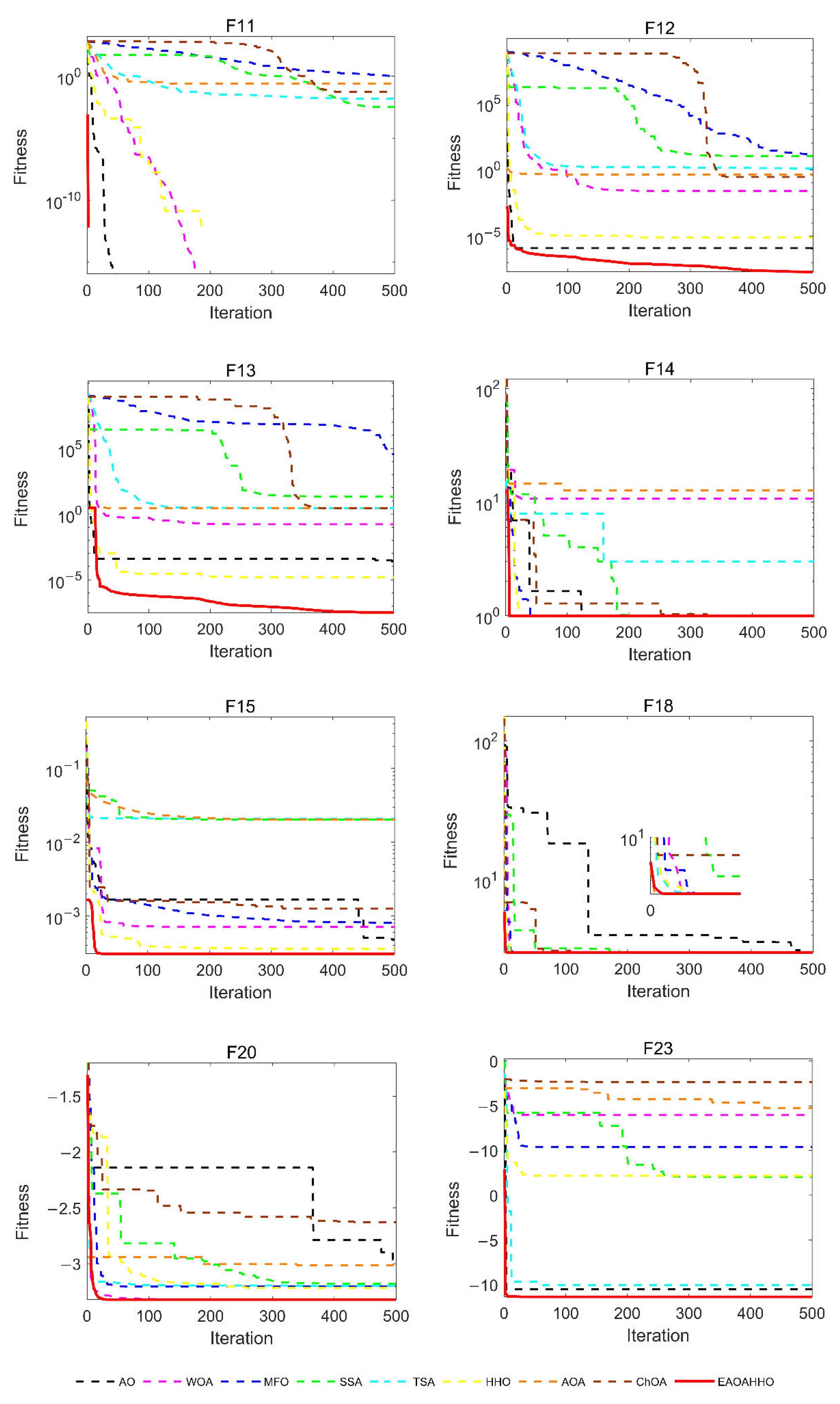
4.1.2. Comparison of EAOAHHO with Other Meta-Heuristic Algorithms
4.1.3. Scalability Test
4.1.4. Computational Time Analysis
4.1.5. Statistical Test
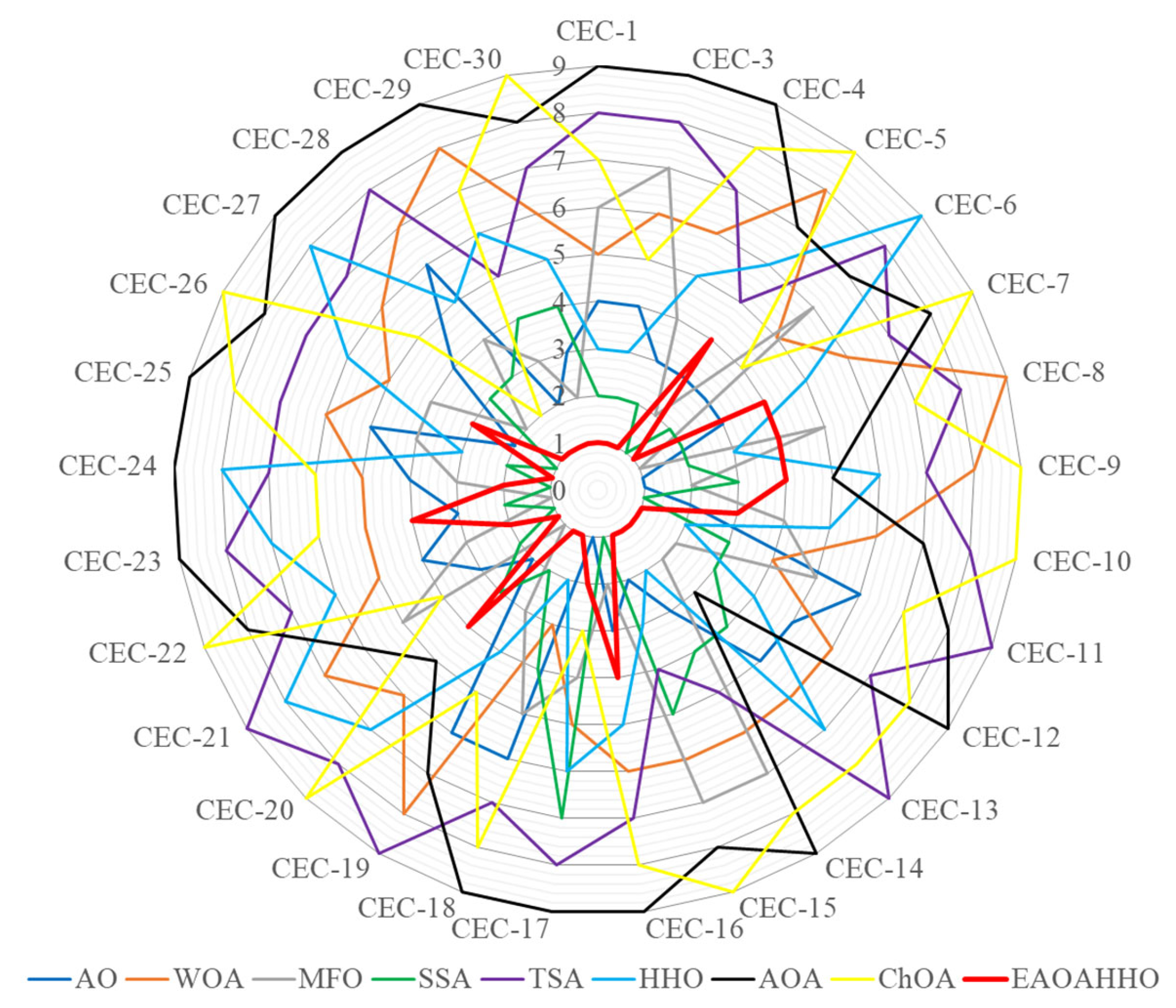
4.2. Experiment 2: IEEE CEC2017 Test Suite
5. EAOAHHO for Solving Industrial Engineering Design Problems
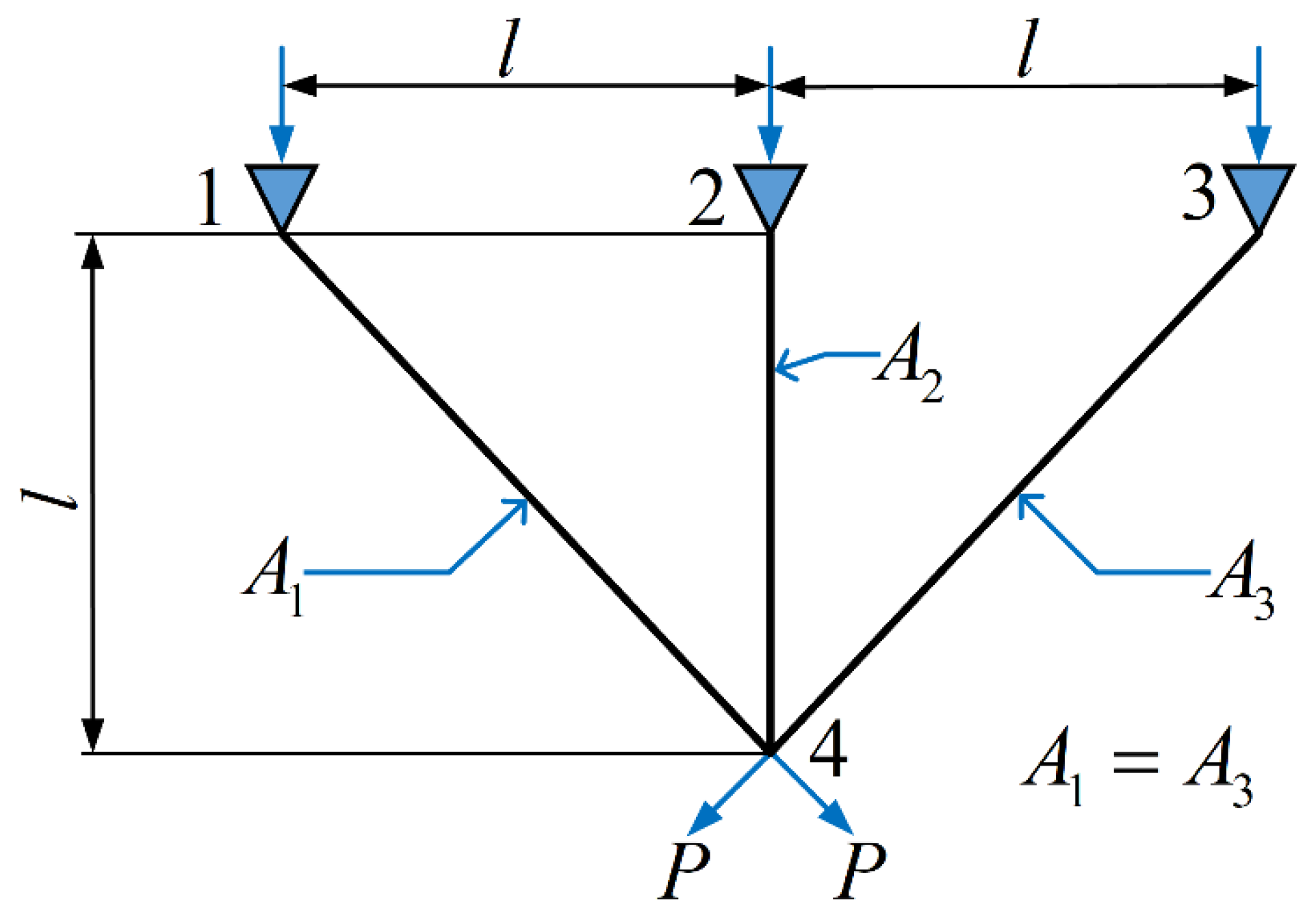
5.1. Three-Bar Truss Design Problem
5.2. Tension/Compression Spring Design Problem
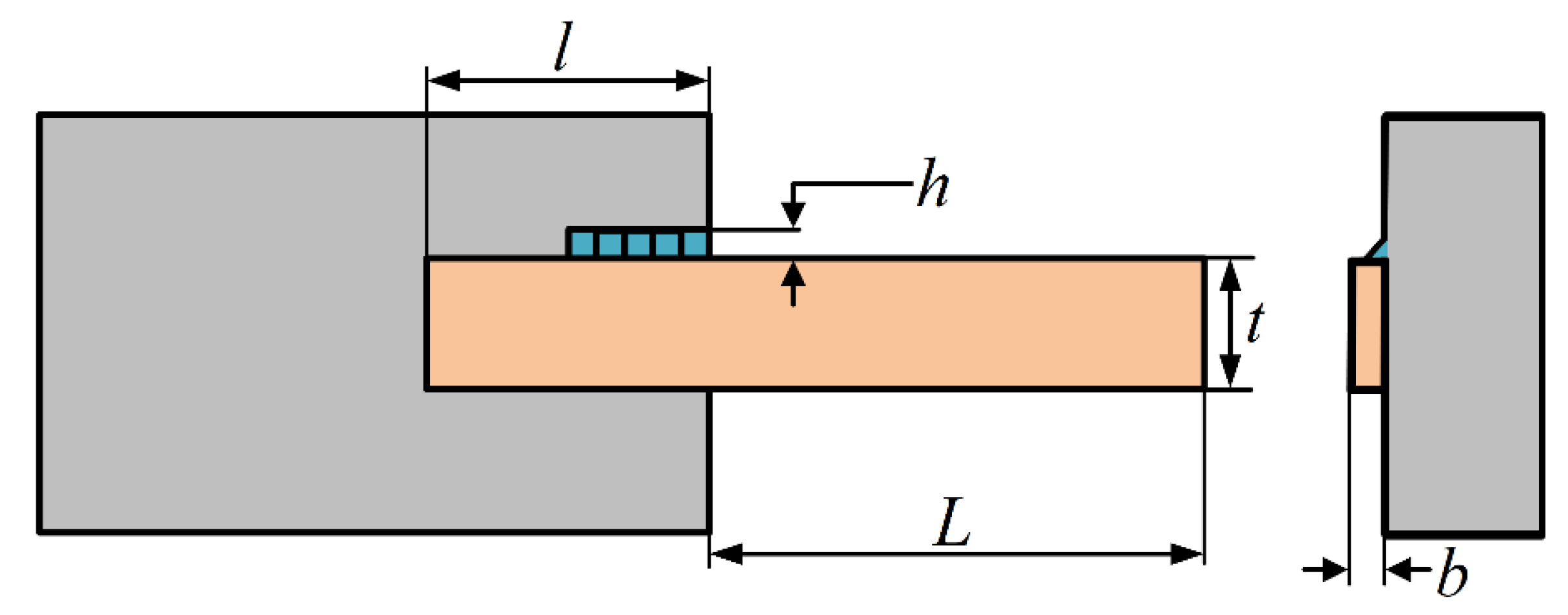
5.3. Welded Beam Design Problem
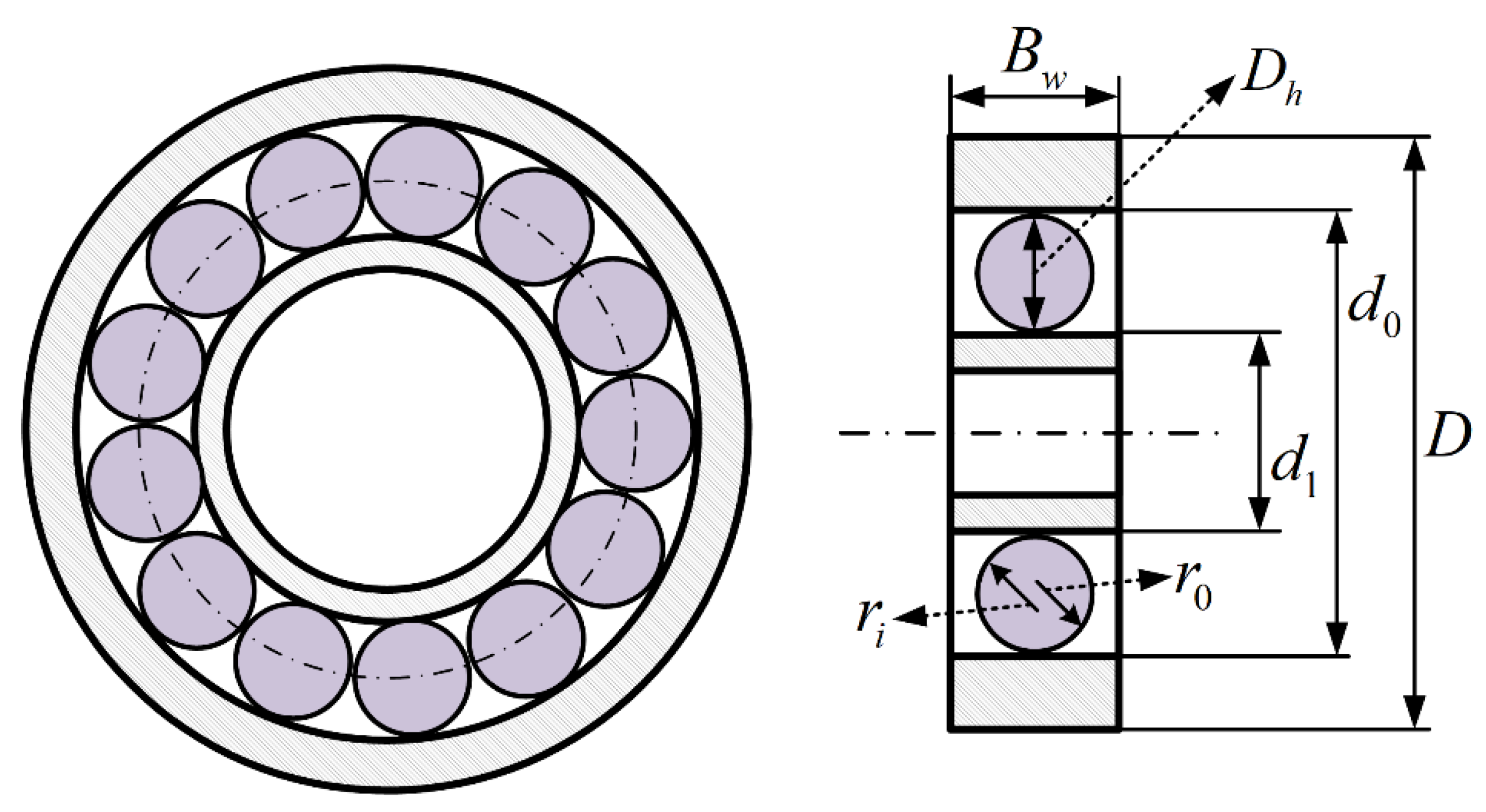
5.4. Rolling Element Bearing Design Problem
| Algorithm | EAOAHHO | HHO [27] | TLBO [62] | RUN [63] | RSA [64] | COOT [65] |
|---|---|---|---|---|---|---|
| 125.7227 | 125 | 125.7191 | 125.2142 | 125.1722 | 125 | |
| 21.42330 | 21.00000 | 21.42559 | 21.59796 | 21.29734 | 21.87500 | |
| 11.00116 | 11.09207 | 11.00000 | 11.40240 | 10.88521 | 10.77700 | |
| 0.51500 | 0.51500 | 0.51500 | 0.51500 | 0.515253 | 0.51500 | |
| 0.51500 | 0.51500 | 0.51500 | 0.51500 | 0.517764 | 0.51500 | |
| 0.50000 | 0.40000 | 0.424266 | 0.40059 | 0.41245 | 0.43190 | |
| 0.70000 | 0.60000 | 0.633948 | 0.61467 | 0.632338 | 0.65290 | |
| 0.30000 | 0.30000 | 0.30000 | 0.30530 | 0.301911 | 0.30000 | |
| 0.02000 | 0.05047 | 0.068858 | 0.02000 | 0.024395 | 0.02000 | |
| 0.600240 | 0.60000 | 0.799498 | 0.63665 | 0.6024 | 0.60000 | |
| Maximum cost | 85,539.193 | 83,011.883 | 81,859.74 | 83,680.47 | 83,486.64 | 83,918.492 |
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.C.; Zhao, K.; Niu, Y. Improved harris hawks optimization based on adaptive cooperative foraging and dispersed foraging strategies. IEEE Access 2020, 8, 160297–160314. [Google Scholar] [CrossRef]
- Xiao, Y.N.; Sun, X.; Guo, Y.L.; Li, S.P.; Zhang, Y.P.; Wang, Y.W. An Improved Gorilla Troops Optimizer Based on Lens Opposition-Based Learning and Adaptive β-Hill Climbing for Global Optimization. Cmes-Comput. Model. Eng. Sci. 2022, 131, 815–850. [Google Scholar] [CrossRef]
- Ewees, A.A.; Abd Elaziz, M.; Houssein, E.H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst. Appl. 2018, 112, 156–172. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Xiao, Y.; Sun, X.; Guo, Y.; Cui, H.; Wang, Y.; Li, J.; Li, S. An enhanced honey badger algorithm based on Lévy flight and refraction opposition-based learning for engineering design problems. J. Intell. Fuzzy Syst. 2022, 1–24. [Google Scholar] [CrossRef]
- Dewangan, R.K.; Shukla, A.; Godfrey, W.W. Three dimensional path planning using grey wolf optimizer for UAVs. Appl. Intell. 2019, 49, 2201–2217. [Google Scholar] [CrossRef]
- Yao, J.; Sha, Y.; Chen, Y.; Zhang, G.; Hu, X.; Bai, G.; Liu, J. IHSSAO: An Improved Hybrid Salp Swarm Algorithm and Aquila Optimizer for UAV Path Planning in Complex Terrain. Appl. Sci. 2022, 12, 5634. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, W.; Zheng, R.; Wang, S.; Leng, X.; Cao, N. Ensemble mutation slime mould algorithm with restart mechanism for feature selection. Int. J. Intell. Syst. 2022, 37, 2335–2370. [Google Scholar] [CrossRef]
- Tongbram, S.; Shimray, B.A.; Singh, L.S.; Dhanachandra, N. A novel image segmentation approach using fcm and whale optimization algorithm. J. Ambient. Intell. Humaniz. Comput. 2021, 1–15. [Google Scholar] [CrossRef]
- Yin, S.H.; Luo, Q.F.; Du, Y.L.; Zhou, Y.Q. p DTSMA: Dominant swarm with adaptive T-distribution mutation-based slime mould algorithm. Math. Biosci. Eng. 2022, 19, 2240–2285. [Google Scholar] [CrossRef]
- Tang, C.M.; Zhou, Y.Q.; Tang, Z.H.; Luo, Q.F. Teaching-learning-based pathfinder algorithm for function and engineering optimization problems. Appl. Intell. 2021, 51, 5040–5066. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Jain, L.C. Designing classifier fusion systems by genetic algorithms. IEEE Trans. Evol. Comput. 2000, 4, 327–336. [Google Scholar]
- Qian, W.W.; Chai, J.R.; Xu, Z.G.; Zhang, Z.Y. Differential evolution algorithm with multiple mutation strategies based on roulette wheel selection. Appl. Intell. 2018, 48, 3612–3629. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, S.; Gokasan, M. Optimal trajectory planning by big bang-big crunch algorithm. In Proceedings of the 2nd International Conference on Control, Decision and Information Technologies (CoDIT), Ecole Natl Ingenieurs Metz, Metz, France, 3–5 November 2014; pp. 557–561. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Alatas, B. ACROA: Artificial chemical reaction optimization algorithm for global optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Recioui, A. Application of a galaxy-based search algorithm to mimo system capacity optimization. Arab. J. Sci. Eng. 2016, 41, 3407–3414. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Hekimoglu, B. Optimal tuning of fractional order PID controller for DC motor speed control via chaotic atom search optimization algorithm. IEEE Access 2019, 7, 38100–38114. [Google Scholar] [CrossRef]
- Krishna, A.B.; Saxena, S.; Kamboj, V.K. hSMA-PS: A novel memetic approach for numerical and engineering design challenges. Eng. Comput. 2021, 1–35. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Jiang, J.J.; Wei, W.X.; Shao, W.L.; Liang, Y.F.; Qu, Y.Y. Research on Large-scale bi-level particle swarm optimization algorithm. IEEE Access 2021, 9, 56364–56375. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comp. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Selvi, M.; Ramakrishnan, B. Lion optimization algorithm (LOA)-based reliable emergency message broadcasting system in VANET. Soft Comput. 2020, 24, 10415–10432. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Fan, Q.; Chen, Z.J.; Li, Z.; Xia, Z.H.; Lin, Y.Q. An efficient refracted salp swarm algorithm and its application in structural parameter identification. Eng. Comput. 2022, 38, 175–189. [Google Scholar] [CrossRef]
- Kamboj, V.K.; Nandi, A.; Bhadoria, A.; Sehgal, S. An intensify harris hawks optimizer for numerical and engineering optimization problems. Appl. Soft Comput. 2020, 89, 106018. [Google Scholar] [CrossRef]
- Belge, E.; Altan, A.; Hacioglu, R. Metaheuristic Optimization-Based Path Planning and Tracking of Quadcopter for Payload Hold-Release Mission. Electronics 2022, 11, 1208. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Heidari, A.A.; Fujita, H.; Moayedi, H. A competitive chain-based Harris Hawks Optimizer for global optimization and multi-level image thresholding problems. Appl. Soft Comput. 2020, 95, 106347. [Google Scholar] [CrossRef]
- Shao, K.X.; Fu, W.L.; Tan, J.W.; Wang, K. Coordinated approach fusing time-shift multiscale dispersion entropy and vibrational Harris hawks optimization-based SVM for fault diagnosis of rolling bearing. Measurement 2021, 173, 108580. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Meth. Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Devan, P.A.M.; Hussin, F.A.; Ibrahim, R.B.; Bingi, K.; Nagarajapandian, M.; Assaad, M. An Arithmetic-Trigonometric Optimization Algorithm with Application for Control of Real-Time Pressure Process Plant. Sensors 2022, 22, 617. [Google Scholar] [CrossRef]
- Panga, N.; Sivaramakrishnan, U.; Abishek, R.; Bingi, K.; Chaudhary, J. An Improved Arithmetic Optimization Algorithm. In Proceedings of the 2021 IEEE Madras Section Conference (MASCON), Chennai, India, 27–28 August 2021; pp. 1–6. [Google Scholar]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Xiao, Y.; Sun, X.; Zhang, Y.; Guo, Y.; Wang, Y.; Li, J. An improved slime mould algorithm based on tent chaotic mapping and nonlinear inertia weight. Int. J. Innov. Comp. Inf. Control 2021, 17, 2151–2176. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Wu, T.; Xu, M.; Cai, S. Pinhole-imaging-based learning butterfly optimization algorithm for global optimization and feature selection. Appl. Soft Comput. 2021, 103, 107146. [Google Scholar] [CrossRef]
- Li, M.; Xu, G.; Fu, B.; Zhao, X. Whale optimization algorithm based on dynamic pinhole imaging and adaptive strategy. J. Supercomput. 2021, 78, 6090–6120. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. Improved multi-core arithmetic optimization algorithm-based ensemble mutation for multidisciplinary applications. J. Intell. Manuf. 2022, 1–42. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Chen, W.; Heidari, A.A.; Wang, M.; Zhao, X.; Liang, G.; Chen, H.; Zhang, X. Ensemble mutation-driven salp swarm algorithm with restart mechanism: Framework and fundamental analysis. Expert Syst. Appl. 2021, 165, 113897. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 372–379. [Google Scholar]
- Tang, A.; Zhou, H.; Han, T.; Xie, L. A modified manta ray foraging optimization for global optimization problems. IEEE Access 2021, 9, 128702–128721. [Google Scholar] [CrossRef]
- Coello Coello, C.A. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Meth. Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Mohammadi-Balani, A.; Dehghan Nayeri, M.; Azar, A.; Taghizadeh-Yazdi, M. Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Ind. Eng. 2021, 152, 107050. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Meth. Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Heidari, A.A.; Gandomi, A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, X.; Liu, J. An improved moth-flame optimization algorithm for engineering problems. Symmetry 2020, 12, 1234. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile search algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. A new optimization method based on COOT bird natural life model. Expert Syst. Appl. 2021, 183, 115352. [Google Scholar] [CrossRef]

| Algorithm | Parameter Setting |
|---|---|
| AO [28] | |
| WOA [31] | |
| MFO [48] | |
| SSA [25] | |
| TSA [49] | |
| HHO [27] | |
| AOA [38] | |
| ChOA [50] | |
| EAOAHHO |
| Function | Dim | Range | Fmin |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 |
| Function | Dim | Range | Fmin |
|---|---|---|---|
| 30 | [−500, 500] | −418.9829 × D | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−50, 50] | 0 | |
| 30 | [−50, 50] | 0 |
| Function | Dim | Range | Fmin |
|---|---|---|---|
| 2 | [−65, 65] | 0.998 | |
| 4 | [−5, 5] | 0.00030 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | 3 | |
| 3 | [−1, 2] | −3.8628 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10.1532 | |
| 4 | [0, 10] | −10.4028 | |
| 4 | [0, 10] | −10.5363 |
| Fn | Criteria | EAOAHHO-1 | EAOAHHO-2 | EAOAHHO-3 | EAOAHHO |
|---|---|---|---|---|---|
| F1 | Avg | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F2 | Avg | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F3 | Avg | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F4 | Avg | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F5 | Avg | 1.92 × 10−3 | 1.04 × 10−3 | 1.38 × 10−4 | 7.13 × 10−5 |
| Std | 6.74 × 10−3 | 1.84 × 10−3 | 6.88 × 10−4 | 1.00 × 10−4 | |
| F6 | Avg | 1.83 × 10−3 | 3.39 × 10−4 | 1.41 × 10−5 | 2.09 × 10−6 |
| Std | 3.18 × 10−3 | 5.99 × 10−4 | 3.89 × 10−5 | 2.62 × 10−6 | |
| F7 | Avg | 3.58 × 10−5 | 2.78 × 10−5 | 3.29 × 10−5 | 1.98 × 10−5 |
| Std | 4.29 × 10−5 | 2.22 × 10−5 | 2.65 × 10−5 | 2.20 × 10−5 | |
| F8 | Avg | −12,561.135 | −12,564.854 | −12,569.327 | −12,569.451 |
| Std | 2.02 × 101 | 1.34 × 101 | 6.02 × 10−1 | 1.16 × 10−1 | |
| F9 | Avg | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F10 | Avg | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 |
| Std | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F11 | Avg | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F12 | Avg | 2.94 × 10−5 | 3.01 × 10−6 | 1.35 × 10−6 | 2.21 × 10−8 |
| Std | 8.65 × 10−5 | 4.30 × 10−6 | 2.98 × 10−6 | 3.77 × 10−8 | |
| F13 | Avg | 3.01 × 10−4 | 1.57 × 10−5 | 5.67 × 10−6 | 1.86 × 10−7 |
| Std | 6.55 × 10−4 | 2.95 × 10−5 | 8.39 × 10−6 | 4.48 × 10−7 | |
| F14 | Avg | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 |
| Std | 1.67 × 10−10 | 1.12 × 10−10 | 0.00 × 100 | 0.00 × 100 | |
| F15 | Avg | 3.73 × 10−4 | 3.50 × 10−4 | 3.39 × 10−4 | 3.07 × 10−4 |
| Std | 9.91 × 10−5 | 4.34 × 10−5 | 1.67 × 10−4 | 1.34 × 10−19 | |
| F16 | Avg | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| Std | 8.23 × 10−16 | 8.63 × 10−16 | 6.92 × 10−16 | 6.78 × 10−16 | |
| F17 | Avg | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| Std | 1.34 × 10−5 | 7.07 × 10−6 | 0.00 × 100 | 0.00 × 100 | |
| F18 | Avg | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 |
| Std | 4.01 × 10−13 | 1.17 × 10−14 | 8.08 × 10−16 | 5.34 × 10−16 | |
| F19 | Avg | −3.8628 | −3.8628 | −3.8628 | −3.8628 |
| Std | 1.55 × 10−5 | 1.04 × 10−5 | 5.82 × 10−15 | 2.71 × 10−15 | |
| F20 | Avg | −3.2363 | −3.2416 | −3.2586 | −3.2863 |
| Std | 8.46 × 10−2 | 8.04 × 10−2 | 6.03 × 10−2 | 5.54 × 10−2 | |
| F21 | Avg | −9.7978 | −10.1531 | −10.1532 | −10.1532 |
| Std | 1.29 × 100 | 3.17 × 10−4 | 6.90 × 10−15 | 6.79 × 10−15 | |
| F22 | Avg | −9.6291 | −10.4028 | −10.4029 | −10.4029 |
| Std | 2.33 × 100 | 2.32 × 10−4 | 8.73 × 10−16 | 7.38 × 10−16 | |
| F23 | Avg | −9.1795 | −10.5354 | −10.3130 | −10.5364 |
| Std | 2.53 × 100 | 2.43 × 10−3 | 1.22 × 100 | 2.29 × 10−15 |
| Fn | Criteria | AO | WOA | MFO | SSA | TSA | HHO | AOA | ChOA | EAOAHHO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg | 2.49 × 10−112 | 3.58 × 10−74 | 2.01 × 103 | 1.83 × 10−7 | 1.42 × 10−21 | 4.69 × 10−92 | 5.76 × 10−35 | 9.89 × 10−6 | 0.00 × 100 |
| Std | 1.19 × 10−111 | 1.25 × 10−73 | 4.07 × 103 | 3.60 × 10−7 | 2.78 × 10−21 | 2.57 × 10−91 | 3.16 × 10−34 | 2.89 × 10−5 | 0.00 × 100 | |
| F2 | Avg | 1.89 × 10−56 | 6.84 × 10−51 | 3.38 × 101 | 1.75 × 100 | 1.00 × 10−13 | 1.00 × 10−50 | 0.00 × 100 | 4.69 × 10−5 | 0.00 × 100 |
| Std | 1.03 × 10−55 | 3.35 × 10−50 | 2.05 × 101 | 1.30 × 100 | 1.43 × 10−13 | 4.20 × 10−50 | 0.00 × 100 | 6.61 × 10−5 | 0.00 × 100 | |
| F3 | Avg | 2.35 × 10−101 | 4.69 × 104 | 1.83 × 104 | 1.50 × 103 | 7.58 × 10−4 | 4.66 × 10−75 | 2.81 × 10−3 | 1.99 × 102 | 0.00 × 100 |
| Std | 1.29 × 10−100 | 1.56 × 104 | 1.29 × 104 | 8.73 × 102 | 3.53 × 10−3 | 2.43 × 10−74 | 7.15 × 10−3 | 4.14 × 102 | 0.00 × 100 | |
| F4 | Avg | 1.92 × 10−52 | 4.85 × 101 | 6.64 × 101 | 1.20 × 101 | 3.01 × 10−1 | 8.85 × 10−48 | 2.68 × 10−2 | 3.32 × 10−1 | 0.00 × 100 |
| Std | 1.05 × 10−51 | 3.19 × 101 | 7.66 × 100 | 4.32 × 100 | 4.17 × 10−1 | 4.78 × 10−47 | 2.04 × 10−2 | 3.37 × 10−1 | 0.00 × 100 | |
| F5 | Avg | 3.88 × 10−3 | 2.81 × 101 | 1.39 × 104 | 2.26 × 102 | 2.83 × 101 | 1.41 × 10−2 | 2.84 × 101 | 2.89 × 101 | 1.64 × 10−4 |
| Std | 5.10 × 10−3 | 4.39 × 10−1 | 3.09 × 104 | 2.98 × 102 | 8.48 × 10−1 | 1.46 × 10−2 | 2.68 × 10−1 | 1.68 × 10−1 | 3.02 × 10−4 | |
| F6 | Avg | 9.27 × 10−5 | 4.43 × 10−1 | 3.01 × 103 | 5.83 × 10−7 | 3.76 × 100 | 1.58 × 10−4 | 3.14 × 100 | 3.66 × 100 | 2.26 × 10−7 |
| Std | 1.49 × 10−4 | 2.24 × 10−1 | 5.35 × 103 | 6.27 × 10−7 | 6.28 × 10−1 | 2.13 × 10−4 | 3.10 × 10−1 | 3.60 × 10−1 | 2.34 × 10−7 | |
| F7 | Avg | 1.04 × 10−4 | 4.01 × 10−3 | 3.89 × 100 | 1.82 × 10−1 | 1.02 × 10−2 | 1.39 × 10−4 | 5.25 × 10−5 | 2.44 × 10−3 | 2.61 × 10−5 |
| Std | 1.18 × 10−4 | 5.17 × 10−3 | 7.50 × 100 | 9.10 × 10−2 | 4.09 × 10−3 | 1.34 × 10−4 | 4.60 × 10−5 | 2.39 × 10−3 | 2.58 × 10−5 | |
| F8 | Avg | −7849.674 | −10,295.569 | −8411.505 | −7585.108 | −6021.436 | −12,568.997 | −5275.950 | −5725.692 | −12,569.445 |
| Std | 3.91 × 103 | 1.99 × 103 | 8.90 × 102 | 7.78 × 102 | 5.06 × 102 | 7.71 × 10−1 | 4.70 × 102 | 6.32 × 101 | 1.58 × 10−1 | |
| F9 | Avg | 0.00 × 100 | 0.00 × 100 | 1.60 × 102 | 5.37 × 101 | 1.83 × 102 | 0.00 × 100 | 0.00 × 100 | 7.50 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 3.18 × 101 | 2.06 × 101 | 3.63 × 101 | 0.00 × 100 | 0.00 × 100 | 7.60 × 100 | 0.00 × 100 | |
| F10 | Avg | 8.88 × 10−16 | 3.73 × 10−15 | 1.40 × 101 | 2.42 × 100 | 1.73 × 100 | 8.88 × 10−16 | 8.88 × 10−16 | 2.00 × 101 | 8.88 × 10−16 |
| Std | 0.00 × 100 | 2.36 × 10−15 | 7.87 × 100 | 1.01 × 100 | 1.56 × 100 | 0.00 × 100 | 0.00 × 100 | 9.97 × 10−4 | 0.00 × 100 | |
| F11 | Avg | 0.00 × 100 | 0.00 × 100 | 2.46 × 101 | 1.61 × 10−2 | 1.25 × 10−2 | 0.00 × 100 | 1.68 × 10−1 | 1.94 × 10−2 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 4.63 × 101 | 1.20 × 10−2 | 1.75 × 10−2 | 0.00 × 100 | 1.55 × 10−1 | 3.16 × 10−2 | 0.00 × 100 | |
| F12 | Avg | 1.02 × 10−6 | 2.62 × 10−2 | 2.42 × 101 | 7.02 × 100 | 7.44 × 100 | 8.34 × 10−6 | 5.01 × 10−1 | 4.75 × 10−1 | 4.37 × 10−8 |
| Std | 1.34 × 10−6 | 2.92 × 10−2 | 8.38 × 101 | 3.59 × 100 | 4.58 × 100 | 7.05 × 10−6 | 4.96 × 10−2 | 1.98 × 10−1 | 9.03 × 10−8 | |
| F13 | Avg | 3.36 × 10−5 | 5.70 × 10−1 | 1.37 × 107 | 1.46 × 101 | 2.95 × 100 | 9.44 × 10−5 | 2.83 × 100 | 2.76 × 100 | 1.73 × 10−7 |
| Std | 4.72 × 10−5 | 2.99 × 10−1 | 7.49 × 107 | 1.45 × 101 | 6.26 × 10−1 | 2.29 × 10−4 | 1.20 × 10−1 | 1.09 × 10−1 | 2.56 × 10−7 | |
| F14 | Avg | 2.89 × 100 | 3.84 × 100 | 1.89 × 100 | 1.10 × 100 | 8.56 × 100 | 1.33 × 100 | 1.02 × 101 | 1.13 × 100 | 9.98 × 10−1 |
| Std | 3.50 × 100 | 3.97 × 100 | 1.31 × 100 | 4.00 × 10−1 | 5.08 × 100 | 9.47 × 10−1 | 3.51 × 100 | 5.03 × 10−1 | 0.00 × 100 | |
| F15 | Avg | 5.21 × 10−4 | 8.37 × 10−4 | 1.01 × 10−3 | 1.59 × 10−3 | 3.94 × 10−3 | 3.91 × 10−4 | 1.73 × 10−2 | 1.31 × 10−3 | 3.07 × 10−4 |
| Std | 1.34 × 10−4 | 5.31 × 10−4 | 3.66 × 10−4 | 3.55 × 10−3 | 7.48 × 10−3 | 2.22 × 10−4 | 2.88 × 10−2 | 4.50 × 10−5 | 1.27 × 10−19 | |
| F16 | Avg | −1.0312 | −1.0316 | −1.0316 | −1.0316 | −1.0284 | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| Std | 3.77 × 10−4 | 7.51 × 10−10 | 6.78 × 10−16 | 2.42 × 10−14 | 9.65 × 10−3 | 6.71 × 10−10 | 1.05 × 10−7 | 1.25 × 10−5 | 6.78 × 10−16 | |
| F17 | Avg | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 4.11 × 10−1 | 3.99 × 10−1 | 3.98 × 10−1 |
| Std | 3.22 × 10−4 | 4.54 × 10−6 | 0.00 × 100 | 3.65 × 10−14 | 4.34 × 10−5 | 1.60 × 10−5 | 1.43 × 10−2 | 9.51 × 10−4 | 0.00 × 100 | |
| F18 | Avg | 3.03 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 1.77 × 101 | 3.00 × 100 | 8.40 × 100 | 3.00 × 100 | 3.00 × 100 |
| Std | 3.90 × 10−2 | 1.85 × 10−4 | 1.53 × 10−15 | 2.05 × 10−13 | 2.88 × 101 | 1.06 × 10−6 | 1.10 × 101 | 2.37 × 10−4 | 1.42 × 10−15 | |
| F19 | Avg | −3.8571 | −3.8541 | −3.8628 | −3.8628 | −3.8626 | −3.8578 | −3.8529 | −3.8548 | −3.8628 |
| Std | 4.19 × 10−3 | 1.31 × 10−2 | 1.65 × 10−10 | 4.56 × 10−9 | 3.41 × 10−4 | 1.04 × 10−2 | 3.52 × 10−3 | 2.40 × 10−3 | 2.71 × 10−15 | |
| F20 | Avg | −3.1913 | −3.1980 | −3.2479 | −3.2310 | −3.2729 | −3.0784 | −3.0334 | −2.5754 | −3.2863 |
| Std | 6.99 × 10−2 | 1.68 × 10−1 | 6.27 × 10−2 | 6.11 × 10−2 | 8.50 × 10−2 | 1.12 × 10−1 | 1.06 × 10−1 | 4.67 × 10−1 | 5.54 × 10−2 | |
| F21 | Avg | −10.1395 | −7.8528 | −6.7116 | −7.8105 | −6.1621 | −5.3826 | −3.7548 | −2.8730 | −10.1532 |
| Std | 3.27 × 10−2 | 2.69 × 100 | 3.19 × 100 | 3.22 × 100 | 3.44 × 100 | 1.26 × 100 | 1.37 × 100 | 2.13 × 100 | 7.01 × 10−15 | |
| F22 | Avg | −10.3873 | −6.9247 | −7.1985 | −8.1209 | −6.6915 | −5.0843 | −3.6058 | −4.1673 | −10.4029 |
| Std | 2.14 × 10−2 | 2.95 × 100 | 3.54 × 100 | 3.34 × 100 | 3.60 × 100 | 4.52 × 10−3 | 1.49 × 100 | 1.66 × 100 | 1.23 × 10−15 | |
| F23 | Avg | −10.5298 | −7.1441 | −7.3743 | −8.5583 | −6.0191 | −5.2153 | −3.5062 | −4.3408 | −10.5364 |
| Std | 7.63 × 10−3 | 3.40 × 100 | 3.72 × 100 | 3.14 × 100 | 3.80 × 100 | 1.07 × 100 | 1.77 × 100 | 1.54 × 100 | 2.06 × 10−15 |
| Fn | Criteria | AO | WOA | MFO | SSA | TSA | HHO | AOA | ChOA | EAOAHHO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg | 1.91 × 10−106 | 4.91 × 10−70 | 6.26 × 104 | 1.42 × 103 | 5.30 × 10−10 | 1.90 × 10−92 | 2.42 × 10−2 | 7.46 × 10−1 | 0.00 × 100 |
| Std | 1.05 × 10−105 | 2.68 × 10−69 | 1.61 × 104 | 4.17 × 102 | 9.45 × 10−10 | 7.70 × 10−92 | 9.72 × 10−3 | 8.66 × 10−1 | 0.00 × 100 | |
| F2 | Avg | 3.74 × 10−69 | 5.79 × 10−51 | 2.36 × 102 | 4.79 × 101 | 3.29 × 10−7 | 2.82 × 10−50 | 3.62 × 10−42 | 9.12 × 10−2 | 0.00 × 100 |
| Std | 2.03 × 10−68 | 1.43 × 10−50 | 3.77 × 101 | 5.63 × 100 | 3.62 × 10−7 | 8.96 × 10−50 | 1.98 × 10−41 | 5.87 × 10−2 | 0.00 × 100 | |
| F3 | Avg | 5.70 × 10−106 | 1.04 × 106 | 2.19 × 105 | 5.32 × 104 | 1.18 × 104 | 2.22 × 10−58 | 1.02 × 100 | 6.81 × 104 | 0.00 × 100 |
| Std | 3.12 × 10−105 | 2.40 × 105 | 4.89 × 104 | 2.81 × 104 | 6.78 × 103 | 1.22 × 10−57 | 9.30 × 10−1 | 3.11 × 104 | 0.00 × 100 | |
| F4 | Avg | 4.32 × 10−53 | 7.98 × 101 | 9.31 × 101 | 2.79 × 101 | 5.54 × 101 | 6.78 × 10−50 | 9.59 × 10−2 | 7.40 × 101 | 0.00 × 100 |
| Std | 1.65 × 10−52 | 1.96 × 101 | 2.02 × 100 | 3.01 × 100 | 1.55 × 101 | 2.27 × 10−49 | 9.35 × 10−3 | 1.65 × 101 | 0.00 × 100 | |
| F5 | Avg | 2.37 × 10−2 | 9.81 × 101 | 1.58 × 108 | 1.58 × 105 | 9.85 × 101 | 5.04 × 10−2 | 9.88 × 101 | 3.33 × 102 | 2.07 × 10−3 |
| Std | 4.26 × 10−2 | 2.36 × 10−1 | 6.63 × 107 | 8.01 × 104 | 2.41 × 10−1 | 6.49 × 10−2 | 1.75 × 10−1 | 5.47 × 102 | 4.26 × 10−3 | |
| F6 | Avg | 6.93 × 10−4 | 4.25 × 100 | 5.96 × 104 | 1.35 × 103 | 1.44 × 101 | 5.07 × 10−4 | 1.82 × 101 | 2.27 × 101 | 4.87 × 10−4 |
| Std | 1.51 × 10−3 | 1.18 × 100 | 1.58 × 104 | 5.09 × 102 | 1.22 × 100 | 6.79 × 10−4 | 7.37 × 10−1 | 2.76 × 100 | 4.83 × 10−4 | |
| F7 | Avg | 9.14 × 10−5 | 4.04 × 10−3 | 3.00 × 102 | 2.57 × 100 | 5.51 × 10−2 | 1.39 × 10−4 | 6.79 × 10−5 | 2.32 × 10−2 | 2.59 × 10−5 |
| Std | 8.92 × 10−5 | 4.57 × 10−3 | 1.25 × 102 | 5.17 × 10−1 | 2.01 × 10−2 | 1.78 × 10−4 | 5.69 × 10−5 | 1.59 × 10−2 | 1.82 × 10−5 | |
| F8 | Avg | −1.07 × 104 | −3.48 × 104 | −2.27 × 104 | −2.15 × 104 | −1.34 × 104 | −4.19 × 104 | −9.88 × 103 | −1.81 × 104 | −4.19 × 104 |
| Std | 2.12 × 103 | 5.78 × 103 | 1.97 × 103 | 2.07 × 103 | 1.19 × 103 | 1.83 × 100 | 7.35 × 102 | 1.11 × 102 | 6.87 × 100 | |
| F9 | Avg | 0.00 × 100 | 7.58 × 10−15 | 8.58 × 102 | 2.47 × 102 | 9.64 × 102 | 0.00 × 100 | 0.00 × 100 | 3.66 × 101 | 0.00 × 100 |
| Std | 0.00 × 100 | 4.15 × 10−14 | 7.98 × 101 | 4.76 × 101 | 1.48 × 102 | 0.00 × 100 | 0.00 × 100 | 1.91 × 101 | 0.00 × 100 | |
| F10 | Avg | 4.44 × 10−16 | 3.76 × 10−15 | 1.98 × 101 | 1.03 × 101 | 1.83 × 10−1 | 4.44 × 10−16 | 3.58 × 10−4 | 2.00 × 101 | 4.44 × 10−16 |
| Std | 0.00 × 100 | 2.46 × 10−15 | 1.90 × 10−1 | 1.56 × 100 | 6.97 × 10−1 | 0.00 × 100 | 9.32 × 10−4 | 4.29 × 10−3 | 0.00 × 100 | |
| F11 | Avg | 0.00 × 100 | 2.11 × 10−2 | 5.49 × 102 | 1.50 × 101 | 1.24 × 10−2 | 0.00 × 100 | 5.62 × 102 | 3.89 × 10−1 | 0.00 × 100 |
| Std | 0.00 × 100 | 8.12 × 10−2 | 1.50 × 102 | 3.47 × 100 | 1.58 × 10−2 | 0.00 × 100 | 1.62 × 102 | 2.45 × 10−1 | 0.00 × 100 | |
| F12 | Avg | 1.12 × 10−6 | 4.49 × 10−2 | 2.74 × 108 | 3.34 × 101 | 1.22 × 101 | 1.60 × 10−6 | 9.03 × 10−1 | 1.20 × 100 | 6.28 × 10−7 |
| Std | 2.38 × 10−6 | 2.01 × 10−2 | 1.54 × 108 | 1.08 × 101 | 5.04 × 100 | 2.10 × 10−6 | 2.28 × 10−2 | 3.14 × 10−1 | 9.68 × 10−7 | |
| F13 | Avg | 5.30 × 10−5 | 2.87 × 100 | 6.03 × 108 | 4.37 × 103 | 1.81 × 101 | 1.26 × 10−4 | 9.96 × 100 | 1.05 × 101 | 6.87 × 10−6 |
| Std | 1.17 × 10−4 | 9.34 × 10−1 | 3.54 × 108 | 6.77 × 103 | 2.71 × 101 | 1.68 × 10−4 | 7.28 × 10−2 | 1.61 × 100 | 1.03 × 10−5 |
| Fn | Criteria | AO | WOA | MFO | SSA | TSA | HHO | AOA | ChOA | EAOAHHO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg | 3.97 × 10−98 | 1.32 × 10−69 | 5.59 × 105 | 4.17 × 104 | 2.61 × 10−4 | 5.17 × 10−94 | 2.81 × 10−1 | 1.31 × 102 | 0.00 × 100 |
| Std | 1.80 × 10−97 | 6.55 × 10−69 | 2.29 × 104 | 4.07 × 103 | 1.72 × 10−4 | 2.81 × 10−93 | 2.50 × 10−2 | 6.40 × 101 | 0.00 × 100 | |
| F2 | Avg | 1.95 × 10−57 | 5.17 × 10−48 | 3.86 × 1024 | 2.81 × 102 | 6.11 × 10−4 | 1.89 × 10−48 | 2.27 × 10−9 | 3.85 × 100 | 0.00 × 100 |
| Std | 1.07 × 10−56 | 2.34 × 10−47 | 2.12 × 1025 | 1.34 × 101 | 3.54 × 10−4 | 7.02 × 10−48 | 1.23 × 10−8 | 1.44 × 100 | 0.00 × 100 | |
| F3 | Avg | 6.27 × 10−101 | 1.09 × 107 | 1.93 × 106 | 5.06 × 105 | 4.54 × 105 | 1.14 × 10−49 | 1.31 × 101 | 1.02 × 106 | 0.00 × 100 |
| Std | 3.43 × 10−100 | 3.49 × 106 | 2.99 × 105 | 2.05 × 105 | 8.49 × 104 | 4.93 × 10−49 | 8.36 × 100 | 2.50 × 105 | 0.00 × 100 | |
| F4 | Avg | 1.47 × 10−51 | 7.74 × 101 | 9.82 × 101 | 3.70 × 101 | 9.82 × 101 | 2.57 × 10−48 | 1.50 × 10−1 | 9.61 × 101 | 0.00 × 100 |
| Std | 7.97 × 10−51 | 2.25 × 101 | 5.68 × 10−1 | 3.46 × 100 | 1.31 × 100 | 1.11 × 10−47 | 1.59 × 10−2 | 1.72 × 100 | 0.00 × 100 | |
| F5 | Avg | 7.66 × 10−2 | 2.97 × 102 | 2.24 × 109 | 1.22 × 107 | 3.47 × 102 | 1.11 × 10−1 | 2.99 × 102 | 4.10 × 104 | 2.24 × 10−2 |
| Std | 1.58 × 10−1 | 2.37 × 10−1 | 1.94 × 108 | 2.72 × 106 | 5.92 × 101 | 1.37 × 10−1 | 5.36 × 10−2 | 4.67 × 104 | 4.04 × 10−2 | |
| F6 | Avg | 1.22 × 10−3 | 1.72 × 101 | 5.65 × 105 | 4.03 × 104 | 5.54 × 101 | 1.11 × 10−3 | 6.62 × 101 | 2.27 × 102 | 2.98 × 10−3 |
| Std | 1.98 × 10−3 | 4.99 × 100 | 2.97 × 104 | 3.85 × 103 | 1.88 × 100 | 1.37 × 10−3 | 9.33 × 10−1 | 7.57 × 101 | 3.80 × 10−3 | |
| F7 | Avg | 6.49 × 10−5 | 3.13 × 10−3 | 1.04 × 104 | 6.16 × 101 | 4.30 × 10−1 | 1.75 × 10−4 | 8.75 × 10−5 | 5.39 × 10−1 | 3.77 × 10−5 |
| Std | 5.08 × 10−5 | 4.07 × 10−3 | 1.09 × 103 | 9.95 × 100 | 1.81 × 10−1 | 3.44 × 10−4 | 9.67 × 10−5 | 4.00 × 10−1 | 4.04 × 10−5 | |
| F8 | Avg | −2.38 × 104 | −1.06 × 105 | −4.77 × 104 | −4.52 × 104 | −2.40 × 104 | −1.26 × 105 | −1.77 × 104 | −5.19 × 104 | −1.25 × 105 |
| Std | 6.18 × 103 | 1.88 × 104 | 3.90 × 103 | 3.45 × 103 | 1.75 × 103 | 8.02 × 100 | 1.10 × 103 | 4.17 × 102 | 3.36 × 103 | |
| F9 | Avg | 0.00 × 100 | 0.00 × 100 | 3.77 × 103 | 1.57 × 103 | 3.47 × 103 | 0.00 × 100 | 1.34 × 10−7 | 1.39 × 102 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 1.09 × 102 | 9.60 × 101 | 3.47 × 102 | 0.00 × 100 | 7.34 × 10−7 | 4.18 × 101 | 0.00 × 100 | |
| F10 | Avg | 4.44 × 10−16 | 4.12 × 10−15 | 2.01 × 101 | 1.37 × 101 | 1.96 × 10−3 | 4.44 × 10−16 | 6.56 × 10−3 | 2.00 × 101 | 4.44 × 10−16 |
| Std | 0.00 × 100 | 2.55 × 10−15 | 1.11 × 10−1 | 3.95 × 10−1 | 1.23 × 10−3 | 0.00 × 100 | 4.81 × 10−4 | 1.58 × 10−2 | 0.00 × 100 | |
| F11 | Avg | 0.00 × 100 | 0.00 × 100 | 5.05 × 103 | 3.64 × 102 | 2.68 × 10−2 | 0.00 × 100 | 4.19 × 103 | 2.18 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 2.27 × 102 | 3.33 × 101 | 4.53 × 10−2 | 0.00 × 100 | 6.26 × 102 | 6.03 × 10−1 | 0.00 × 100 | |
| F12 | Avg | 1.45 × 10−6 | 8.63 × 10−2 | 5.11 × 109 | 1.05 × 105 | 2.87 × 104 | 2.86 × 10−6 | 1.05 × 100 | 2.73 × 103 | 1.32 × 10−6 |
| Std | 4.39 × 10−6 | 3.07 × 10−2 | 5.14 × 108 | 1.08 × 105 | 7.43 × 104 | 3.17 × 10−6 | 1.73 × 10−2 | 1.39 × 104 | 2.21 × 10−6 | |
| F13 | Avg | 1.26 × 10−4 | 1.01 × 101 | 1.03 × 1010 | 9.04 × 106 | 5.57 × 103 | 4.87 × 10−4 | 3.01 × 101 | 2.96 × 104 | 2.99 × 10−5 |
| Std | 1.78 × 10−4 | 2.78 × 100 | 7.97 × 108 | 3.41 × 106 | 6.81 × 103 | 7.16 × 10−4 | 1.92 × 10−2 | 1.42 × 105 | 4.18 × 10−5 |
| Fn | Criteria | AO | WOA | MFO | SSA | TSA | HHO | AOA | ChOA | EAOAHHO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg | 1.70 × 10−99 | 8.31 × 10−71 | 1.14 × 106 | 9.27 × 104 | 2.42 × 10−2 | 7.09 × 10−95 | 6.49 × 10−1 | 7.28 × 102 | 0.00 × 100 |
| Std | 9.28 × 10−99 | 2.87 × 10−70 | 4.05 × 104 | 4.96 × 103 | 1.62 × 10−2 | 2.72 × 10−94 | 3.72 × 10−2 | 3.21 × 102 | 0.00 × 100 | |
| F2 | Avg | 1.29 × 10−58 | 4.90 × 10−47 | 5.80 × 10114 | 5.36 × 102 | 7.69 × 10−3 | 8.35 × 10−49 | 8.38 × 10−4 | 1.23 × 101 | 0.00 × 100 |
| Std | 6.61 × 10−58 | 2.21 × 10−46 | 3.08 × 10115 | 1.42 × 101 | 3.63 × 10−3 | 3.42 × 10−48 | 1.12 × 10−3 | 2.71 × 100 | 0.00 × 100 | |
| F3 | Avg | 3.05 × 10−94 | 3.14 × 107 | 4.74 × 106 | 1.31 × 106 | 1.32 × 106 | 1.16 × 10−25 | 3.57 × 101 | 4.00 × 106 | 0.00 × 100 |
| Std | 1.67 × 10−93 | 9.95 × 106 | 8.05 × 105 | 5.78 × 105 | 2.39 × 105 | 6.35 × 10−25 | 1.56 × 101 | 1.43 × 106 | 0.00 × 100 | |
| F4 | Avg | 3.90 × 10−52 | 7.55 × 101 | 9.89 × 101 | 3.99 × 101 | 9.92 × 101 | 1.09 × 10−47 | 1.83 × 10−1 | 9.70 × 101 | 0.00 × 100 |
| Std | 2.11 × 10−51 | 2.89 × 101 | 4.34 × 10−1 | 3.52 × 100 | 2.49 × 10−1 | 5.94 × 10−47 | 1.96 × 10−2 | 1.28 × 100 | 0.00 × 100 | |
| F5 | Avg | 8.41 × 10−2 | 4.96 × 102 | 5.01 × 109 | 3.63 × 107 | 1.08 × 105 | 2.00 × 10−1 | 4.99 × 102 | 4.61 × 105 | 4.66 × 10−2 |
| Std | 1.19 × 10−1 | 4.67 × 10−1 | 2.44 × 108 | 4.50 × 106 | 9.22 × 104 | 2.87 × 10−1 | 6.49 × 10−2 | 4.69 × 105 | 1.20 × 10−1 | |
| F6 | Avg | 8.53 × 10−4 | 3.07 × 101 | 1.16 × 106 | 9.36 × 104 | 1.03 × 102 | 2.48 × 10−3 | 1.16 × 102 | 8.75 × 102 | 6.58 × 10−3 |
| Std | 1.28 × 10−3 | 7.50 × 100 | 2.77 × 104 | 6.33 × 103 | 1.70 × 100 | 3.68 × 10−3 | 1.29 × 100 | 3.74 × 102 | 5.05 × 10−3 | |
| F7 | Avg | 1.01 × 10−4 | 4.32 × 10−3 | 3.89 × 104 | 2.81 × 102 | 2.83 × 100 | 2.01 × 10−4 | 8.69 × 10−5 | 4.52 × 100 | 2.52 × 10−5 |
| Std | 1.04 × 10−4 | 4.28 × 10−3 | 1.96 × 103 | 3.47 × 101 | 1.24 × 100 | 2.34 × 10−4 | 7.01 × 10−5 | 3.93 × 100 | 3.02 × 10−5 | |
| F8 | Avg | −4.25 × 104 | −1.78 × 105 | −6.13 × 104 | −6.09 × 104 | −3.16 × 104 | −2.09 × 105 | −2.27 × 104 | −8.51 × 104 | −2.09 × 105 |
| Std | 1.23 × 104 | 3.38 × 104 | 4.89 × 103 | 5.37 × 103 | 2.48 × 103 | 3.10 × 101 | 1.56 × 103 | 5.54 × 102 | 2.28 × 102 | |
| F9 | Avg | 3.03 × 10−14 | 0.00 × 100 | 6.97 × 103 | 3.11 × 103 | 5.68 × 103 | 0.00 × 100 | 7.28 × 10−6 | 3.23 × 102 | 0.00 × 100 |
| Std | 1.66 × 10−13 | 0.00 × 100 | 1.47 × 102 | 1.48 × 102 | 7.77 × 102 | 0.00 × 100 | 7.47 × 10−6 | 5.27 × 101 | 0.00 × 100 | |
| F10 | Avg | 4.44 × 10−16 | 4.47 × 10−15 | 2.03 × 101 | 1.43 × 101 | 1.07 × 10−2 | 4.44 × 10−16 | 7.98 × 10−3 | 2.01 × 101 | 4.44 × 10−16 |
| Std | 0.00 × 100 | 2.76 × 10−15 | 1.52 × 10−1 | 2.19 × 10−1 | 5.07 × 10−3 | 0.00 × 100 | 3.85 × 10−4 | 7.95 × 10−3 | 0.00 × 100 | |
| F11 | Avg | 0.00 × 100 | 0.00 × 100 | 1.04 × 104 | 8.42 × 102 | 4.55 × 10−2 | 0.00 × 100 | 9.50 × 103 | 7.85 × 100 | 0.00 × 100 |
| Std | 0.00 × 100 | 0.00 × 100 | 3.03 × 102 | 5.57 × 101 | 8.45 × 10−2 | 0.00 × 100 | 2.90 × 103 | 2.87 × 100 | 0.00 × 100 | |
| F12 | Avg | 1.46 × 10−6 | 9.02 × 10−2 | 1.21 × 1010 | 1.50 × 106 | 3.71 × 106 | 2.34 × 10−6 | 1.08 × 100 | 1.29 × 105 | 1.23 × 10−6 |
| Std | 2.89 × 10−6 | 3.98 × 10−2 | 5.87 × 108 | 7.13 × 105 | 3.58 × 106 | 2.99 × 10−6 | 1.07 × 10−2 | 3.52 × 105 | 1.75 × 10−6 | |
| F13 | Avg | 5.14 × 10−4 | 1.66 × 101 | 2.25 × 1010 | 3.33 × 107 | 1.87 × 106 | 5.90 × 10−4 | 5.02 × 101 | 2.18 × 105 | 6.32 × 10−5 |
| Std | 9.17 × 10−4 | 5.31 × 100 | 1.20 × 109 | 7.38 × 106 | 1.90 × 106 | 6.37 × 10−4 | 2.92 × 10−2 | 4.57 × 105 | 1.08 × 10−4 |
| Fn | AO | WOA | MFO | SSA | TSA | HHO | AOA | ChOA | EAOAHHO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.91 × 10−1 | 6.27 × 10−2 | 1.22 × 10−1 | 1.20 × 10−1 | 1.58 × 10−1 | 1.13 × 10−1 | 1.03 × 10−1 | 1.53 × 100 | 4.22 × 10−1 |
| F2 | 1.65 × 10−1 | 6.90 × 10−2 | 1.08 × 10−1 | 1.06 × 10−1 | 1.39 × 10−1 | 8.98 × 10−2 | 9.28 × 10−2 | 1.48 × 100 | 4.18 × 10−1 |
| F3 | 3.83 × 10−1 | 1.70 × 10−1 | 2.09 × 10−1 | 2.17 × 10−1 | 2.63 × 10−1 | 3.56 × 10−1 | 2.04 × 10−1 | 1.53 × 100 | 1.44 × 100 |
| F4 | 1.72 × 10−1 | 6.07 × 10−2 | 1.07 × 10−1 | 1.11 × 10−1 | 1.51 × 10−1 | 1.08 × 10−1 | 9.71 × 10−2 | 1.54 × 100 | 3.90 × 10−1 |
| F5 | 2.03 × 10−1 | 7.75 × 10−2 | 1.17 × 10−1 | 1.19 × 10−1 | 1.64 × 10−1 | 1.80 × 10−1 | 1.17 × 10−1 | 1.49 × 100 | 5.48 × 10−1 |
| F6 | 1.58 × 10−1 | 6.00 × 10−2 | 9.90 × 10−2 | 1.15 × 10−1 | 1.48 × 10−1 | 1.33 × 10−1 | 9.13 × 10−2 | 1.52 × 100 | 4.31 × 10−1 |
| F7 | 2.87 × 10−1 | 1.32 × 10−1 | 1.58 × 10−1 | 1.78 × 10−1 | 2.02 × 10−1 | 2.47 × 10−1 | 1.52 × 10−1 | 1.48 × 100 | 1.11 × 100 |
| F8 | 2.07 × 10−1 | 7.37 × 10−2 | 1.06 × 10−1 | 1.41 × 10−1 | 1.63 × 10−1 | 2.06 × 10−1 | 1.24 × 10−1 | 1.49 × 100 | 5.70 × 10−1 |
| F9 | 1.77 × 10−1 | 7.91 × 10−2 | 1.23 × 10−1 | 1.08 × 10−1 | 1.73 × 10−1 | 1.64 × 10−1 | 9.99 × 10−2 | 1.53 × 100 | 3.90 × 10−1 |
| F10 | 1.86 × 10−1 | 7.26 × 10−2 | 1.15 × 10−1 | 1.23 × 10−1 | 1.71 × 10−1 | 1.57 × 10−1 | 1.05 × 10−1 | 1.52 × 100 | 4.24 × 10−1 |
| F11 | 1.97 × 10−1 | 7.68 × 10−2 | 1.54 × 10−1 | 1.35 × 10−1 | 1.75 × 10−1 | 1.75 × 10−1 | 1.13 × 10−1 | 1.53 × 100 | 7.94 × 10−1 |
| F12 | 5.00 × 10−1 | 2.10 × 10−1 | 2.52 × 10−1 | 2.71 × 10−1 | 2.99 × 10−1 | 5.27 × 10−1 | 2.46 × 10−1 | 1.59 × 100 | 1.39 × 100 |
| F13 | 5.10 × 10−1 | 2.15 × 10−1 | 2.65 × 10−1 | 2.94 × 10−1 | 3.03 × 10−1 | 5.16 × 10−1 | 2.64 × 10−1 | 1.58 × 100 | 1.45 × 100 |
| F14 | 7.77 × 10−1 | 3.74 × 10−1 | 3.45 × 10−1 | 3.98 × 10−1 | 3.46 × 10−1 | 8.94 × 10−1 | 3.77 × 10−1 | 4.50 × 10−1 | 2.63 × 100 |
| F15 | 1.23 × 10−1 | 4.17 × 10−2 | 5.01 × 10−2 | 7.04 × 10−2 | 4.55 × 10−2 | 1.19 × 10−1 | 4.64 × 10−2 | 2.84 × 10−1 | 4.18 × 10−1 |
| F16 | 1.19 × 10−1 | 4.16 × 10−2 | 4.11 × 10−2 | 6.78 × 10−2 | 4.03 × 10−2 | 1.11 × 10−1 | 3.76 × 10−2 | 1.55 × 10−1 | 3.93 × 10−1 |
| F17 | 1.18 × 10−1 | 3.29 × 10−2 | 3.94 × 10−2 | 3.30 × 10−2 | 3.15 × 10−2 | 1.11 × 10−1 | 4.16 × 10−2 | 1.56 × 10−1 | 3.80 × 10−1 |
| F18 | 1.06 × 10−1 | 3.22 × 10−2 | 4.30 × 10−2 | 6.91 × 10−2 | 3.16 × 10−2 | 9.89 × 10−2 | 3.70 × 10−2 | 1.43 × 10−1 | 3.51 × 10−1 |
| F19 | 1.40 × 10−1 | 4.08 × 10−2 | 5.88 × 10−2 | 7.07 × 10−2 | 4.52 × 10−2 | 1.38 × 10−1 | 4.82 × 10−2 | 2.06 × 10−1 | 4.33 × 10−1 |
| F20 | 1.52 × 10−1 | 5.13 × 10−2 | 5.83 × 10−2 | 8.53 × 10−2 | 6.71 × 10−2 | 1.48 × 10−1 | 5.89 × 10−2 | 3.86 × 10−1 | 4.49 × 10−1 |
| F21 | 1.67 × 10−1 | 4.73 × 10−2 | 5.97 × 10−2 | 9.26 × 10−2 | 6.01 × 10−2 | 1.61 × 10−1 | 6.11 × 10−2 | 2.91 × 10−1 | 5.04 × 10−1 |
| F22 | 1.90 × 10−1 | 6.34 × 10−2 | 6.14 × 10−2 | 9.65 × 10−2 | 6.88 × 10−2 | 1.91 × 10−1 | 5.81 × 10−2 | 2.84 × 10−1 | 5.63 × 10−1 |
| F23 | 2.21 × 10−1 | 7.60 × 10−2 | 8.47 × 10−2 | 1.05 × 10−1 | 8.09 × 10−2 | 1.93 × 10−1 | 8.66 × 10−2 | 3.08 × 10−1 | 6.70 × 10−1 |
| Algorithms | MAE | Rank |
|---|---|---|
| AO | 205.300427 | 3 |
| WOA | 2141.9002 | 8 |
| MFO | 597,465.9 | 9 |
| SSA | 296.0374779 | 4 |
| TSA | 296.09092 | 5 |
| HHO | 0.7170996 | 2 |
| AOA | 320.163464 | 7 |
| CHOA | 309.871379 | 6 |
| EAOAHHO | 0.003309 | 1 |
| Fn | EAOAHHO vs. AO | EAOAHHO vs. WOA | EAOAHHO vs. MFO | EAOAHHO vs. SSA | EAOAHHO vs. TSA | EAOAHHO vs. HHO | EAOAHHO vs. AOA | EAOAHHO vs. ChOA |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 |
| F2 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | 1.21 × 10−12 |
| F3 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 |
| F4 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 |
| F5 | 5.46 × 10−6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.43 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 |
| F6 | 1.69 × 10−9 | 3.02 × 10−11 | 3.02 × 10−11 | 3.82 × 10−10 | 3.02 × 10−11 | 4.94 × 10−5 | 3.02 × 10−11 | 3.02 × 10−11 |
| F7 | 5.56 × 10−4 | 4.50 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.68 × 10−6 | 1.44 × 10−2 | 4.50 × 10−11 |
| F8 | 3.00 × 10−11 | 3.00 × 10−11 | 3.00 × 10−11 | 3.00 × 10−11 | 3.00 × 10−11 | 3.07 × 10−6 | 3.00 × 10−11 | 3.00 × 10−11 |
| F9 | NaN | NaN | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | NaN | 1.21 × 10−12 |
| F10 | NaN | 8.73 × 10−8 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | NaN | 1.21 × 10−12 |
| F11 | NaN | NaN | 1.21 × 10−12 | 1.21 × 10−12 | 8.87 × 10−7 | NaN | 1.21 × 10−12 | 1.21 × 10−12 |
| F12 | 1.10 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.98 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F13 | 6.70 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.18 × 10−9 | 3.02 × 10−11 | 3.02 × 10−11 |
| F14 | 1.21 × 10−12 | 1.21 × 10−12 | 6.58 × 10−5 | 7.56 × 10−13 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 |
| F15 | 2.82 × 10−11 | 2.82 × 10−11 | 2.81 × 10−11 | 2.82 × 10−11 | 2.82 × 10−11 | 2.82 × 10−11 | 2.82 × 10−11 | 2.82 × 10−11 |
| F16 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | 1.21 × 10−12 | 1.21 × 10−12 | 4.57 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 |
| F17 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | 1.93 × 10−10 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 |
| F18 | 1.26 × 10−11 | 1.26 × 10−11 | 4.90 × 10−5 | 1.26 × 10−11 | 1.26 × 10−11 | 1.26 × 10−11 | 1.26 × 10−11 | 1.26 × 10−11 |
| F19 | 1.21 × 10−12 | 1.21 × 10−12 | NaN | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 |
| F20 | 1.93 × 10−6 | 9.73 × 10−7 | 1.06 × 10−2 | 2.43 × 10−8 | 1.41 × 10−4 | 1.60 × 10−10 | 1.01 × 10−11 | 2.59 × 10−11 |
| F21 | 4.08 × 10−12 | 4.08 × 10−12 | 6.56 × 10−7 | 4.08 × 10−12 | 4.08 × 10−12 | 4.08 × 10−12 | 4.08 × 10−12 | 4.08 × 10−12 |
| F22 | 1.45 × 10−11 | 1.45 × 10−11 | 1.55 × 10−6 | 1.45 × 10−11 | 1.45 × 10−11 | 1.45 × 10−11 | 1.45 × 10−11 | 1.45 × 10−11 |
| F23 | 3.15 × 10−12 | 3.15 × 10−12 | 2.12 × 10−10 | 3.15 × 10−12 | 3.15 × 10−12 | 3.15 × 10−12 | 3.15 × 10−12 | 3.15 × 10−12 |
| + | 20 | 21 | 20 | 23 | 23 | 20 | 20 | 23 |
| = | 3 | 2 | 3 | 0 | 0 | 3 | 3 | 0 |
| − | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Function | Name | Dim | Range | Fmin |
|---|---|---|---|---|
| Unimodal functions | ||||
| CEC-01 | Shifted and Rotated Bent Cigar Function | 10 | [−100, 100] | 100 |
| CEC-03 | Shifted and Rotated Zakharov Function | 10 | [−100, 100] | 300 |
| Simple Multimodal Functions | ||||
| CEC-04 | Shifted and Rotated Rosenbrock’s Function | 10 | [−100, 100] | 400 |
| CEC-05 | Shifted and Rotated Rastrigin’s Function | 10 | [−100, 100] | 500 |
| CEC-06 | Shifted and Rotated Expanded Scaffer’s F6 Function | 10 | [−100, 100] | 600 |
| CEC-07 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 10 | [−100, 100] | 700 |
| CEC-08 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 10 | [−100, 100] | 800 |
| CEC-09 | Shifted and Rotated Levy Function | 10 | [−100, 100] | 900 |
| CEC-10 | Shifted and Rotated Schwefel’s Function | 10 | [−100, 100] | 1000 |
| Hybrid Functions | ||||
| CEC-11 | Hybrid Function 1 (N = 3) | 10 | [−100, 100] | 1100 |
| CEC-12 | Hybrid Function 2 (N = 3) | 10 | [−100, 100] | 1200 |
| CEC-13 | Hybrid Function 3 (N = 3) | 10 | [−100, 100] | 1300 |
| CEC-14 | Hybrid Function 4 (N = 4) | 10 | [−100, 100] | 1400 |
| CEC-15 | Hybrid Function 5 (N = 4) | 10 | [−100, 100] | 1500 |
| CEC-16 | Hybrid Function 6 (N = 4) | 10 | [−100, 100] | 1600 |
| CEC-17 | Hybrid Function 6 (N = 5) | 10 | [−100, 100] | 1700 |
| CEC-18 | Hybrid Function 6 (N = 5) | 10 | [−100, 100] | 1800 |
| CEC-19 | Hybrid Function 6 (N = 5) | 10 | [−100, 100] | 1900 |
| CEC-20 | Hybrid Function 6 (N = 6) | 10 | [−100, 100] | 2000 |
| Composition Functions | ||||
| CEC-21 | Composition Function 1 (N = 3) | 10 | [−100, 100] | 2100 |
| CEC-22 | Composition Function 2 (N = 3) | 10 | [−100, 100] | 2200 |
| CEC-23 | Composition Function 3 (N = 4) | 10 | [−100, 100] | 2300 |
| CEC-24 | Composition Function 4 (N = 4) | 10 | [−100, 100] | 2400 |
| CEC-25 | Composition Function 5 (N = 5) | 10 | [−100, 100] | 2500 |
| CEC-26 | Composition Function 6 (N = 5) | 10 | [−100, 100] | 2600 |
| CEC-27 | Composition Function 7 (N = 6) | 10 | [−100, 100] | 2700 |
| CEC-28 | Composition Function 8 (N = 6) | 10 | [−100, 100] | 2800 |
| CEC-29 | Composition Function 9 (N = 3) | 10 | [−100, 100] | 2900 |
| CEC-30 | Composition Function 10 (N = 3) | 10 | [−100, 100] | 3000 |
| Fn | Metric | AO | WOA | MFO | SSA | TSA | HHO | AOA | ChOA | EAOAHHO |
|---|---|---|---|---|---|---|---|---|---|---|
| CEC-1 | Avg | 3.78 × 107 | 5.79 × 107 | 1.41 × 108 | 4.01 × 103 | 3.19 × 109 | 9.59 × 106 | 1.07 × 1010 | 2.32 × 109 | 3.30 × 103 |
| Std | 9.04 × 107 | 6.42 × 107 | 4.37 × 108 | 3.49 × 103 | 3.75 × 109 | 4.71 × 107 | 4.38 × 109 | 1.70 × 109 | 3.18 × 103 | |
| CEC-3 | Avg | 2.31 × 103 | 7.56 × 103 | 8.82 × 103 | 3.25 × 102 | 9.41 × 103 | 6.46 × 102 | 1.29 × 104 | 5.01 × 103 | 3.00 × 102 |
| Std | 7.94 × 102 | 5.10 × 103 | 7.52 × 103 | 1.77 × 100 | 5.44 × 103 | 2.71 × 102 | 3.42 × 103 | 2.33 × 103 | 4.29 × 10−2 | |
| CEC-4 | Avg | 4.23 × 102 | 4.88 × 102 | 4.28 × 102 | 4.10 × 102 | 6.31 × 102 | 4.34 × 102 | 1.20 × 103 | 6.52 × 102 | 4.06 × 102 |
| Std | 2.30 × 101 | 6.83 × 101 | 3.91 × 101 | 1.77 × 101 | 3.02 × 102 | 3.48 × 101 | 5.45 × 102 | 1.88 × 102 | 1.20 × 101 | |
| CEC-5 | Avg | 5.34 × 102 | 5.64 × 102 | 5.30 × 102 | 5.24 × 102 | 5.55 × 102 | 5.57 × 102 | 5.60 × 102 | 5.65 × 102 | 5.36 × 102 |
| Std | 1.58 × 101 | 2.12 × 101 | 1.13 × 101 | 9.97 × 100 | 1.81 × 101 | 1.94 × 101 | 1.65 × 101 | 1.61 × 101 | 1.63 × 101 | |
| CEC-6 | Avg | 6.20 × 102 | 6.36 × 102 | 6.37 × 102 | 6.13 × 102 | 6.38 × 102 | 6.40 × 102 | 6.38 × 102 | 6.34 × 102 | 6.04 × 102 |
| Std | 5.79 × 100 | 1.31 × 101 | 1.29 × 101 | 8.53 × 100 | 1.32 × 101 | 1.38 × 101 | 5.93 × 100 | 1.26 × 101 | 4.57 × 100 | |
| CEC-7 | Avg | 7.58 × 102 | 7.97 × 102 | 7.39 × 102 | 7.47 × 102 | 8.00 × 102 | 7.97 × 102 | 8.04 × 102 | 8.06 × 102 | 7.78 × 102 |
| Std | 1.48 × 101 | 2.52 × 101 | 1.10 × 101 | 1.47 × 101 | 2.85 × 101 | 2.05 × 101 | 1.82 × 101 | 1.48 × 101 | 1.40 × 101 | |
| CEC-8 | Avg | 8.28 × 102 | 8.47 × 102 | 8.34 × 102 | 8.30 × 102 | 8.47 × 102 | 8.32 × 102 | 8.36 × 102 | 8.45 × 102 | 8.34 × 102 |
| Std | 8.67 × 100 | 2.14 × 101 | 1.28 × 101 | 1.38 × 101 | 1.34 × 101 | 1.04 × 101 | 9.46 × 100 | 8.12 × 100 | 9.29 × 100 | |
| CEC-9 | Avg | 1.04 × 103 | 1.61 × 103 | 1.07 × 103 | 1.10 × 103 | 1.56 × 103 | 1.53 × 103 | 1.41 × 103 | 1.63 × 103 | 1.38 × 103 |
| Std | 6.65 × 101 | 3.90 × 102 | 2.25 × 102 | 3.35 × 102 | 5.70 × 102 | 2.71 × 102 | 1.97 × 102 | 2.59 × 102 | 1.92 × 102 | |
| CEC-10 | Avg | 1.97 × 103 | 2.25 × 103 | 2.03 × 103 | 1.93 × 103 | 2.29 × 103 | 2.07 × 103 | 2.28 × 103 | 2.94 × 103 | 2.01 × 103 |
| Std | 2.24 × 102 | 3.91 × 102 | 4.25 × 102 | 1.41 × 102 | 2.44 × 102 | 2.90 × 102 | 2.94 × 102 | 3.33 × 102 | 2.76 × 102 | |
| CEC-11 | Avg | 1.28 × 103 | 1.24 × 103 | 1.26 × 103 | 1.20 × 103 | 4.41 × 103 | 1.19 × 103 | 2.91 × 103 | 1.40 × 103 | 1.15 × 103 |
| Std | 1.60 × 102 | 8.00 × 101 | 3.57 × 102 | 7.48 × 101 | 3.44 × 103 | 7.67 × 101 | 1.91 × 103 | 1.19 × 102 | 6.10 × 101 | |
| CEC-12 | Avg | 4.49 × 106 | 6.43 × 106 | 1.81 × 106 | 3.85 × 106 | 2.11 × 107 | 4.03 × 106 | 3.17 × 108 | 4.12 × 107 | 2.10 × 103 |
| Std | 5.36 × 106 | 6.73 × 106 | 4.49 × 106 | 3.97 × 106 | 1.05 × 108 | 4.25 × 106 | 3.96 × 108 | 1.03 × 108 | 1.38 × 103 | |
| CEC-13 | Avg | 1.74 × 104 | 1.80 × 104 | 1.15 × 104 | 1.53 × 104 | 5.23 × 106 | 1.89 × 104 | 1.20 × 104 | 4.61 × 104 | 1.33 × 103 |
| Std | 1.25 × 104 | 1.17 × 104 | 1.10 × 104 | 1.45 × 104 | 2.26 × 107 | 1.19 × 104 | 8.05 × 103 | 2.28 × 104 | 9.55 × 101 | |
| CEC-14 | Avg | 2.63 × 103 | 4.08 × 103 | 5.11 × 103 | 2.87 × 103 | 3.61 × 103 | 2.40 × 103 | 8.14 × 103 | 6.62 × 103 | 1.45 × 103 |
| Std | 1.05 × 103 | 2.15 × 103 | 5.97 × 103 | 3.01 × 103 | 2.15 × 103 | 1.27 × 103 | 7.87 × 103 | 1.42 × 103 | 2.90 × 101 | |
| CEC-15 | Avg | 6.50 × 103 | 1.05 × 104 | 1.22 × 104 | 8.09 × 103 | 7.19 × 103 | 6.75 × 103 | 1.90 × 104 | 1.95 × 104 | 1.53 × 103 |
| Std | 3.22 × 103 | 7.49 × 103 | 1.94 × 104 | 7.25 × 103 | 5.46 × 103 | 3.70 × 103 | 7.59 × 103 | 8.50 × 103 | 3.56 × 101 | |
| CEC-16 | Avg | 1.88 × 103 | 1.92 × 103 | 1.81 × 103 | 1.79 × 103 | 1.93 × 103 | 1.91 × 103 | 2.08 × 103 | 1.94 × 103 | 1.89 × 103 |
| Std | 1.28 × 102 | 1.55 × 102 | 1.60 × 102 | 1.56 × 102 | 1.62 × 102 | 1.65 × 102 | 1.25 × 102 | 1.03 × 102 | 1.44 × 102 | |
| CEC-17 | Avg | 1.78 × 103 | 1.82 × 103 | 1.81 × 103 | 1.85 × 103 | 1.88 × 103 | 1.84 × 103 | 1.91 × 103 | 1.80 × 103 | 1.79 × 103 |
| Std | 2.29 × 101 | 6.76 × 101 | 6.67 × 101 | 4.95 × 101 | 1.08 × 102 | 1.01 × 102 | 1.17 × 102 | 2.68 × 101 | 3.43 × 101 | |
| CEC-18 | Avg | 2.54 × 104 | 1.95 × 104 | 2.06 × 104 | 1.99 × 104 | 2.91 × 104 | 1.67 × 104 | 2.70 × 106 | 1.02 × 105 | 1.83 × 103 |
| Std | 1.46 × 104 | 1.32 × 104 | 1.35 × 104 | 9.38 × 103 | 1.61 × 104 | 1.25 × 104 | 1.22 × 107 | 6.72 × 104 | 2.25 × 101 | |
| CEC-19 | Avg | 2.80 × 104 | 1.09 × 105 | 1.68 × 104 | 6.91 × 103 | 1.15 × 105 | 2.17 × 104 | 8.40 × 104 | 2.48 × 104 | 1.90 × 103 |
| Std | 4.44 × 104 | 1.50 × 105 | 2.34 × 104 | 4.92 × 103 | 3.71 × 105 | 2.72 × 104 | 8.60 × 104 | 9.90 × 103 | 8.92 × 100 | |
| CEC-20 | Avg | 2.13 × 103 | 2.18 × 103 | 2.10 × 103 | 2.14 × 103 | 2.19 × 103 | 2.19 × 103 | 2.15 × 103 | 2.26 × 103 | 2.15 × 103 |
| Std | 4.91 × 101 | 7.99 × 101 | 6.35 × 101 | 5.70 × 101 | 8.55 × 101 | 7.53 × 101 | 7.32 × 101 | 7.61 × 101 | 6.13 × 101 | |
| CEC-21 | Avg | 2.31 × 103 | 2.34 × 103 | 2.32 × 103 | 2.30 × 103 | 2.34 × 103 | 2.34 × 103 | 2.34 × 103 | 2.31 × 103 | 2.29 × 103 |
| Std | 4.76 × 101 | 3.99 × 101 | 4.62 × 101 | 5.18 × 101 | 5.20 × 101 | 4.59 × 101 | 7.82 × 101 | 6.20 × 101 | 3.48 × 101 | |
| CEC-22 | Avg | 2.31 × 103 | 2.42 × 103 | 2.31 × 103 | 2.30 × 103 | 2.60 × 103 | 2.42 × 103 | 3.03 × 103 | 3.63 × 103 | 2.31 × 103 |
| Std | 5.11 × 100 | 4.15 × 102 | 4.35 × 101 | 2.09 × 101 | 3.28 × 102 | 4.53 × 102 | 2.58 × 102 | 7.99 × 102 | 2.21 × 101 | |
| CEC-23 | Avg | 2.64 × 103 | 2.65 × 103 | 2.62 × 103 | 2.63 × 103 | 2.71 × 103 | 2.69 × 103 | 2.75 × 103 | 2.66 × 103 | 2.65 × 103 |
| Std | 1.51 × 101 | 2.35 × 101 | 1.00 × 101 | 1.08 × 101 | 4.42 × 101 | 3.89 × 101 | 4.02 × 101 | 9.06 × 100 | 1.38 × 101 | |
| CEC-24 | Avg | 2.76 × 103 | 2.77 × 103 | 2.75 × 103 | 2.74 × 103 | 2.81 × 103 | 2.82 × 103 | 2.84 × 103 | 2.80 × 103 | 2.75 × 103 |
| Std | 4.90 × 101 | 6.68 × 101 | 4.92 × 101 | 5.34 × 101 | 7.58 × 101 | 4.15 × 101 | 8.22 × 101 | 1.63 × 101 | 4.69 × 101 | |
| CEC-25 | Avg | 2.95 × 103 | 2.96 × 103 | 2.94 × 103 | 2.93 × 103 | 3.03 × 103 | 2.93 × 103 | 3.36 × 103 | 3.05 × 103 | 2.93 × 103 |
| Std | 3.20 × 101 | 5.60 × 101 | 2.49 × 101 | 2.89 × 101 | 9.88 × 101 | 2.90 × 101 | 2.31 × 102 | 8.86 × 101 | 2.48 × 101 | |
| CEC-26 | Avg | 3.07 × 103 | 3.45 × 103 | 3.09 × 103 | 2.92 × 103 | 3.92 × 103 | 3.79 × 103 | 3.97 × 103 | 4.01 × 103 | 3.07 × 103 |
| Std | 1.79 × 102 | 5.34 × 102 | 2.88 × 102 | 2.06 × 102 | 4.47 × 102 | 6.09 × 102 | 3.09 × 102 | 3.33 × 102 | 3.02 × 102 | |
| CEC-27 | Avg | 3.11 × 103 | 3.15 × 103 | 3.09 × 103 | 3.10 × 103 | 3.17 × 103 | 3.17 × 103 | 3.26 × 103 | 3.14 × 103 | 3.09 × 103 |
| Std | 8.58 × 100 | 4.84 × 101 | 1.99 × 101 | 1.72 × 101 | 3.96 × 101 | 5.41 × 101 | 5.93 × 101 | 3.34 × 101 | 3.74 × 100 | |
| CEC-28 | Avg | 3.46 × 103 | 3.47 × 103 | 3.38 × 103 | 3.32 × 103 | 3.52 × 103 | 3.42 × 103 | 3.79 × 103 | 3.25 × 103 | 3.30 × 103 |
| Std | 7.54 × 101 | 1.33 × 102 | 9.19 × 101 | 1.15 × 102 | 1.84 × 102 | 1.68 × 102 | 1.73 × 102 | 2.95 × 101 | 1.18 × 102 | |
| CEC-29 | Avg | 3.25 × 103 | 3.40 × 103 | 3.25 × 103 | 3.31 × 103 | 3.34 × 103 | 3.38 × 103 | 3.44 × 103 | 3.39 × 103 | 3.21 × 103 |
| Std | 4.39 × 101 | 1.35 × 102 | 9.96 × 101 | 5.83 × 101 | 1.06 × 102 | 1.02 × 102 | 1.40 × 102 | 1.04 × 102 | 6.58 × 101 | |
| CEC-30 | Avg | 1.00 × 106 | 1.73 × 106 | 6.35 × 105 | 1.02 × 106 | 2.31 × 106 | 1.25 × 106 | 3.09 × 107 | 5.74 × 106 | 4.70 × 105 |
| Std | 1.22 × 106 | 1.61 × 106 | 5.46 × 105 | 7.18 × 105 | 6.59 × 106 | 1.87 × 106 | 2.82 × 107 | 4.21 × 106 | 1.15 × 106 |
| Algorithm | Optimal Values for Variables | Minimum Weight | |
|---|---|---|---|
| MFO [48] | 0.78824477 | 0.40946691 | 263.89598 |
| SSA [25] | 0.78866541 | 0.40827578 | 263.89584 |
| HHO [27] | 0.78866280 | 0.40828313 | 263.89584 |
| AOA [38] | 0.79369000 | 0.39426000 | 263.91540 |
| MVO [19] | 0.78860276 | 0.40845307 | 263.89585 |
| GEO [54] | 0.78867110 | 0.40825970 | 263.89584 |
| GOA [55] | 0.78889756 | 0.40761957 | 263.89588 |
| AHA [56] | 0.78868300 | 0.40822460 | 263.89584 |
| EAOAHHO | 0.78859304 | 0.40825052 | 263.87285 |
| Algorithm | Optimal Values for Variables | Minimum Weight | ||
|---|---|---|---|---|
| WOA [31] | 0.051207 | 0.345215 | 12.004032 | 0.0126763 |
| MFO [48] | 0.051994 | 0.364109 | 10.868422 | 0.0126669 |
| SSA [25] | 0.051207 | 0.345215 | 12.004032 | 0.0126763 |
| HHO [27] | 0.051796 | 0.359305 | 11.138859 | 0.0126654 |
| AOA [38] | 0.050000 | 0.349809 | 11.863700 | 0.0121240 |
| AHA [56] | 0.051897 | 0.361748 | 10.689283 | 0.0126660 |
| GWO [26] | 0.051690 | 0.356737 | 11.288850 | 0.0126660 |
| INFO [57] | 0.051555 | 0.353499 | 11.480340 | 0.0126660 |
| EAOAHHO | 0.052291 | 0.360263 | 10.179344 | 0.01199749 |
| Algorithm | Optimal Values for Variables | Minimum Cost | |||
|---|---|---|---|---|---|
| WOA [31] | 0.205396 | 3.484293 | 9.037426 | 0.206276 | 1.730499 |
| AOA [38] | 0.194475 | 2.570920 | 10.00000 | 0.201827 | 1.716400 |
| MVO [19] | 0.205463 | 3.473193 | 9.044502 | 0.205695 | 1.726450 |
| GWO [26] | 0.205676 | 3.478377 | 9.036810 | 0.205778 | 1.726240 |
| ROA [58] | 0.200077 | 3.365754 | 9.011182 | 0.206893 | 1.706447 |
| HGS [59] | 0.207739 | 3.230642 | 8.988778 | 0.207926 | 1.703355 |
| AVOA [60] | 0.205730 | 3.470474 | 9.036621 | 0.205730 | 1.724852 |
| IMFO [61] | 0.205730 | 3.470200 | 9.037500 | 0.205730 | 1.724900 |
| EAOAHHO | 0.195539 | 3.354588 | 9.036630 | 0.205729 | 1.693914 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Sha, Y.; Chen, Y.; Zhao, X. A Novel Ensemble of Arithmetic Optimization Algorithm and Harris Hawks Optimization for Solving Industrial Engineering Optimization Problems. Machines 2022, 10, 602. https://doi.org/10.3390/machines10080602
Yao J, Sha Y, Chen Y, Zhao X. A Novel Ensemble of Arithmetic Optimization Algorithm and Harris Hawks Optimization for Solving Industrial Engineering Optimization Problems. Machines. 2022; 10(8):602. https://doi.org/10.3390/machines10080602
Chicago/Turabian StyleYao, Jinyan, Yongbai Sha, Yanli Chen, and Xiaoying Zhao. 2022. "A Novel Ensemble of Arithmetic Optimization Algorithm and Harris Hawks Optimization for Solving Industrial Engineering Optimization Problems" Machines 10, no. 8: 602. https://doi.org/10.3390/machines10080602
APA StyleYao, J., Sha, Y., Chen, Y., & Zhao, X. (2022). A Novel Ensemble of Arithmetic Optimization Algorithm and Harris Hawks Optimization for Solving Industrial Engineering Optimization Problems. Machines, 10(8), 602. https://doi.org/10.3390/machines10080602






