Robot Static Path Planning Method Based on Deterministic Annealing
Abstract
:1. Introduction
2. Artificial Potential Field
2.1. Attractive Potential Function
2.2. Repulsive Potential Function
2.3. Total Potential Function
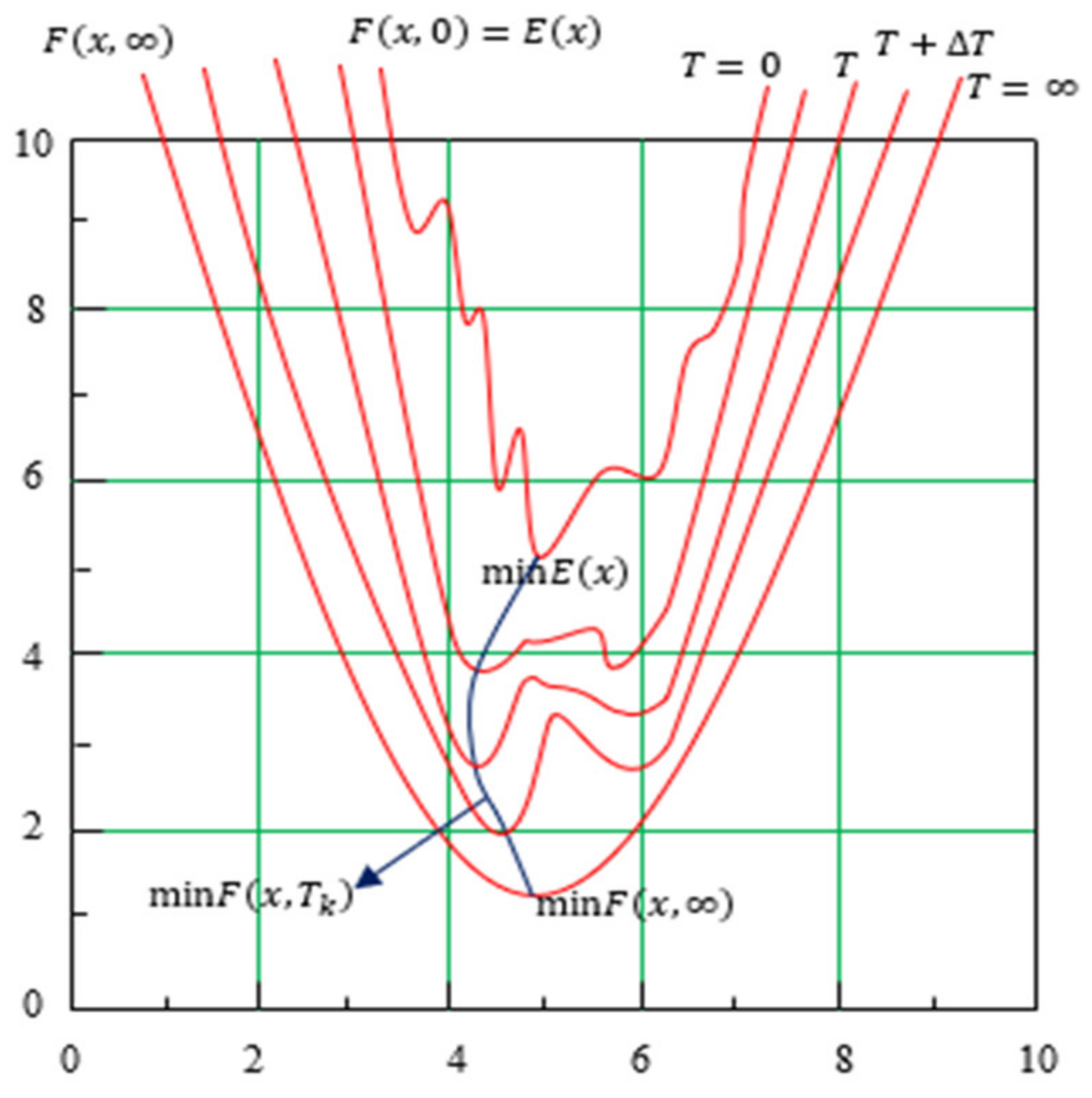
3. Path Planning Approach with Deterministic Annealing
3.1. Deterministic Annealing
| Algorithm 1 Overview of Deterministic Annealing |
| 1. Set a sufficiently large Solve the optimisation problem . Let the optimal solution be ; |
| 2. While |
| 3. ; |
| 4. Take as the initial solution, select an iterative method (such as Newton iteration method, conjugate gradient method or gradient descent method) to solve . Let the optimal solution be ; |
| 5. ; |
| 6. ; |
| 7. End |
| 8. is the optimal solution; |
| 9. Return |
3.2. Deterministic Annealing Based on Artificial Potential Field
| Algorithm 2 DA-APF for local path planning |
| 1. Set , . Here, is large enough; |
| 2. Start annealing. Set , use the conjugate gradient method to obtain the corresponding to each ; |
| 3. While |
| 4. If P Then |
| 5. Execute the gradient descent potential guided strategy to obtain . Let ; |
| 6. If is in the neighbourhood of P under a certain Then |
| 7. If Then |
| 8. Execute the tempering strategy. Let until escape. Update using gradient descent. Let ; |
| 9. Else |
| 10. Let ; |
| 11. If Then |
| 12. Obtain the optimal path . Let ; |
| 13. Let ; |
| 14. End |
| 15. is the optimal or near-optimal path solution; |
| 16. Return |
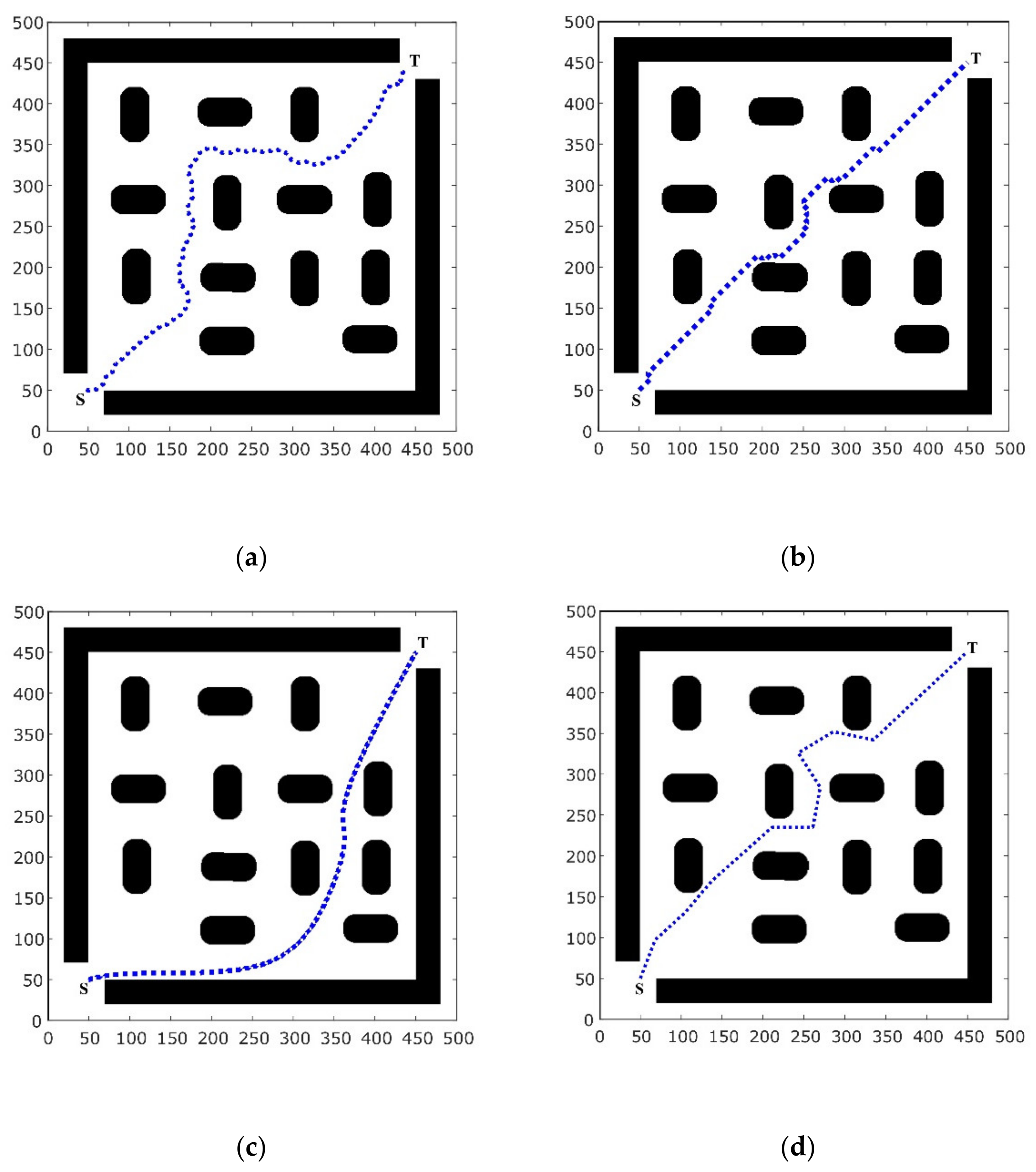
4. Simulation Results
4.1. Environment I
4.2. Environment II
4.3. Environment III
4.4. Environment IV
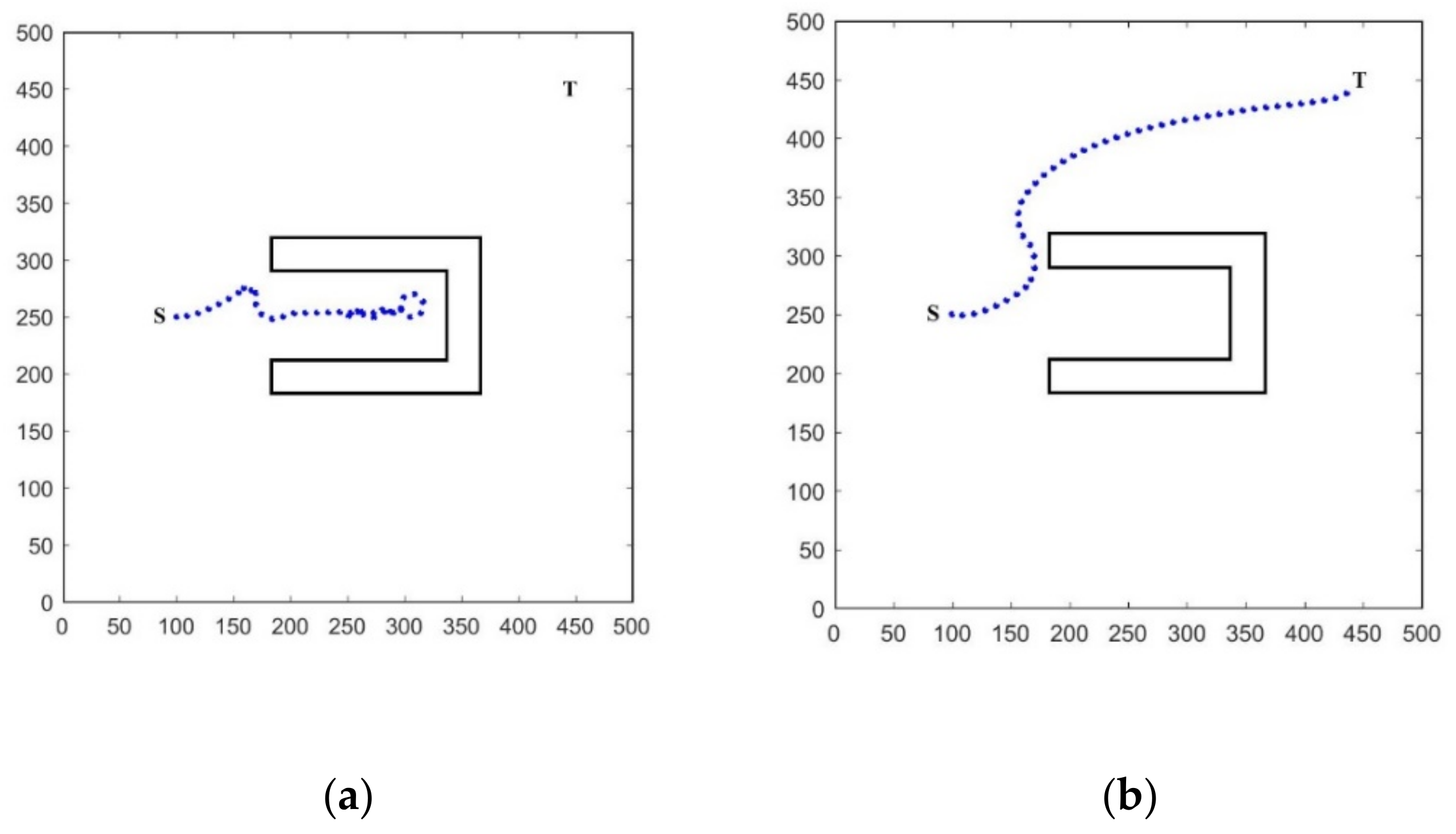
4.5. Further Performance Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tuncer, A.; Yildirim, M. Dynamic path planning of mobile robots with improved genetic algorithm. Comput. Electr. Eng. 2012, 38, 1564–1572. [Google Scholar] [CrossRef]
- Tsai, C.C.; Huang, H.C.; Chan, C.K. Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation. IEEE Trans. Ind. Electron. 2011, 58, 4813–4821. [Google Scholar] [CrossRef]
- Miao, H.; Tian, Y.C. Dynamic robot path planning using an enhanced simulated annealing approach. Appl. Math. Comput. 2013, 222, 420–437. [Google Scholar] [CrossRef] [Green Version]
- Behnck, L.P.; Doering, D.; Pereira, C.E.; Rettberg, A. A modified simulated annealing algorithm for SUAVs path planning. IFAC J. Syst. Control 2015, 48, 63–68. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Liu, H.; Tian, X.; Gao, M. An improved ant colony algorithm for robot path planning. Soft Comput. 2017, 21, 5829–5839. [Google Scholar] [CrossRef]
- Ma, Y.N.; Gong, Y.J.; Xiao, C.F.; Gao, Y.; Zhang, J. Path planning for autonomous underwater vehicles: An ant colony algorithm incorporating alarm pheromone. IEEE Trans. Veh. Technol. 2018, 68, 141–154. [Google Scholar] [CrossRef]
- Abbasi, A.; MahmoudZadeh, S.; Yazdani, A.; Moshayedi, A.J. Feasibility assessment of Kian-I mobile robot for autonomous navigation. Neural Comput. Appl. 2022, 34, 1199–1218. [Google Scholar] [CrossRef]
- Li, G.; Chou, W. Path planning for mobile robot using self-adaptive learning particle swarm optimization. Sci. China Inform. Sci. 2018, 61, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Teli, T.A.; Wani, M.A. A fuzzy based local minima avoidance path planning in autonomous robots. Int. J. Inf. Technol. 2021, 13, 33–40. [Google Scholar] [CrossRef]
- Byrne, S.; Naeem, W.; Ferguson, S. Improved APF strategies for dual-arm local motion planning. Trans. Inst. Meas. Control 2015, 37, 73–90. [Google Scholar] [CrossRef] [Green Version]
- Ma’Arif, A.; Rahmaniar, W.; Vera, M.A.M.; Nuryono, A.A.; Majdoubi, R.; Çakan, A. Artificial potential field algorithm for obstacle avoidance in uav quadrotor for dynamic environment. In Proceedings of the 2021 IEEE International Conference on Communication, Networks and Satellite (COMNETSAT), Purwokerto, Indonesia, 17–18 July 2021; pp. 184–189. [Google Scholar]
- Abdalla, T.Y.; Abed, A.A.; Ahmed, A.A. Mobile robot navigation using PSO-optimized fuzzy artificial potential field with fuzzy control. J. Intell. Fuzzy Syst. 2017, 32, 3893–3908. [Google Scholar] [CrossRef]
- Guerra, M.; Efimov, D.; Zheng, G.; Perruquetti, W. Avoiding local minima in the potential field method using input-to-state stability. Control Eng. Pract. 2016, 55, 174–184. [Google Scholar] [CrossRef] [Green Version]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25 March 1985; pp. 500–505. [Google Scholar]
- Zhang, T.; Zhu, Y.; Song, J. Real-time motion planning for mobile robots by means of artificial potential field method in unknown environment. Int. J. Rob. Res. 2010, 37, 384–400. [Google Scholar]
- Zhu, Q.; Yan, Y.; Xing, Z. Robot path planning based on artificial potential field approach with simulated annealing. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Jian, China, 16–18 October 2006; pp. 622–627. [Google Scholar]
- Weerakoon, T.; Ishii, K.; Nassiraei, A.A.F. An artificial potential field based mobile robot navigation method to prevent from deadlock. J. Artif. Intell. Soft 2015, 5, 189–203. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Yan, J.; Zhang, P. Fixed-wing UAV formation control design with collision avoidance based on an improved artificial potential field. IEEE Access 2018, 6, 78342–78351. [Google Scholar] [CrossRef]
- Szczepanski, R.; Bereit, A.; Tarczewski, T. Efficient local path planning algorithm using artificial potential field supported by augmented reality. Energies 2021, 14, 6642. [Google Scholar] [CrossRef]
- Zappulla, R.; Park, H.; Virgili-Llop, J.; Romano, M. Real-time autonomous spacecraft proximity maneuvers and docking using an adaptive artificial potential field approach. IEEE Trans. Control Syst. Technol. 2018, 27, 2598–2605. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, E. Hybrid path planning using positioning risk and artificial potential fields. Aerosp. Sci. Technol. 2021, 112, 106640. [Google Scholar] [CrossRef]
- Orozco-Rosas, U.; Montiel, O.; Sepúlveda, R. Mobile robot path planning using membrane evolutionary artificial potential field. Appl. Soft Comput. 2019, 77, 236–251. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, H.; Zhang, Y.; Wang, H.; Cao, D.; Xu, N.; Hu, C. A motion planning and tracking framework for autonomous vehicles based on artificial potential field elaborated resistance network approach. IEEE Trans. Ind. Electron. 2019, 67, 1376–1386. [Google Scholar] [CrossRef]
- Sharma, K.; Doriya, R. Coordination of multi-robot path planning for warehouse application using smart approach for iden-tifying destinations. Intel. Serv. Robot. 2021, 14, 313–325. [Google Scholar] [CrossRef]
- Yan, F. Autonomous vehicle routing problem solution based on artificial potential field with parallel ant colony optimization (ACO) algorithm. Pattern Recognit. Lett. 2018, 116, 195–199. [Google Scholar] [CrossRef]
- Guo, J.; Gao, Y.; Cui, G. Path planning of mobile robot based on improved potential field. J. Inf. Technol. 2013, 12, 2188. [Google Scholar] [CrossRef] [Green Version]
- Rose, K.; Gurewitz, E.; Fox, G.C. Statistical mechanics and phase transitions in clustering. Phys. Rev. Lett. 1990, 65, 945–948. [Google Scholar] [CrossRef]
- Wu, Z.; Karimi, H.R.; Dang, C. A deterministic annealing neural network algorithm for the minimum concave cost transportation problem. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4354–4366. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Trans. Conn. Acad. Arts Sci. 1879, 2, 300–320. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef]
- Rose, K.; Gurewitz, E.; Fox, G.C. Vector quantization by deterministic annealing. IEEE Trans. Inf. Theory 1992, 38, 1249–1257. [Google Scholar] [CrossRef]
- Dang, C.; Xu, L. A Lagrange multiplier and Hopfield-type barrier function method for the traveling salesman problem. Neural Comput. 2002, 14, 303–324. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, Q.; Jiang, B.; Karimi, H.R. Solving the production transportation problem via a deterministic annealing neural network method. Appl. Math. Comput. 2021, 411, 126518. [Google Scholar] [CrossRef]
- Wu, Z.; Karimi, H.R.; Dang, C. An approximation algorithm for graph partitioning via deterministic annealing neural network. Neural Netw. 2019, 117, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Wu, Z.; Karimi, H.R.; Jiang, B.; Lu, G. An Approximation Lagrangian-based Algorithm for the Maximum Clique Problem via Deterministic Annealing Neural Network. J. Frankl. Inst. 2022, 359, 6080–6098. [Google Scholar] [CrossRef]
- Molenbruch, Y.; Braekers, K.; Caris, A. Operational effects of service level variations for the dial-a-ride problem. Cent. Eur. J. Oper. Res. 2017, 25, 71–90. [Google Scholar] [CrossRef]
- Baranwal, M.; Parekh, P.M.; Marla, L.; Salapaka, S.M.; Beck, C.L. Vehicle routing problem with time windows: A deterministic annealing approach. In Proceedings of the IEEE 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 790–795. [Google Scholar]
- Patle, B.K.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-star algorithm: An improved A-star algorithm for AGV path planning in a port environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J.; Dai, J.; He, C. Optimal path planning with modified A-Star algorithm for stealth unmanned aerial vehicles in 3D network radar environment. Proc. Inst. Mech. Eng., Part G J. Aerosp. Eng. 2022, 236, 72–81. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Shi, W.; He, Z.; Tang, W.; Liu, W.; Ma, Z. Path planning of multi-robot systems with boolean specifications based on simulated annealing. IEEE Rob. Autom. Lett. 2022, 7, 6091–6098. [Google Scholar] [CrossRef]
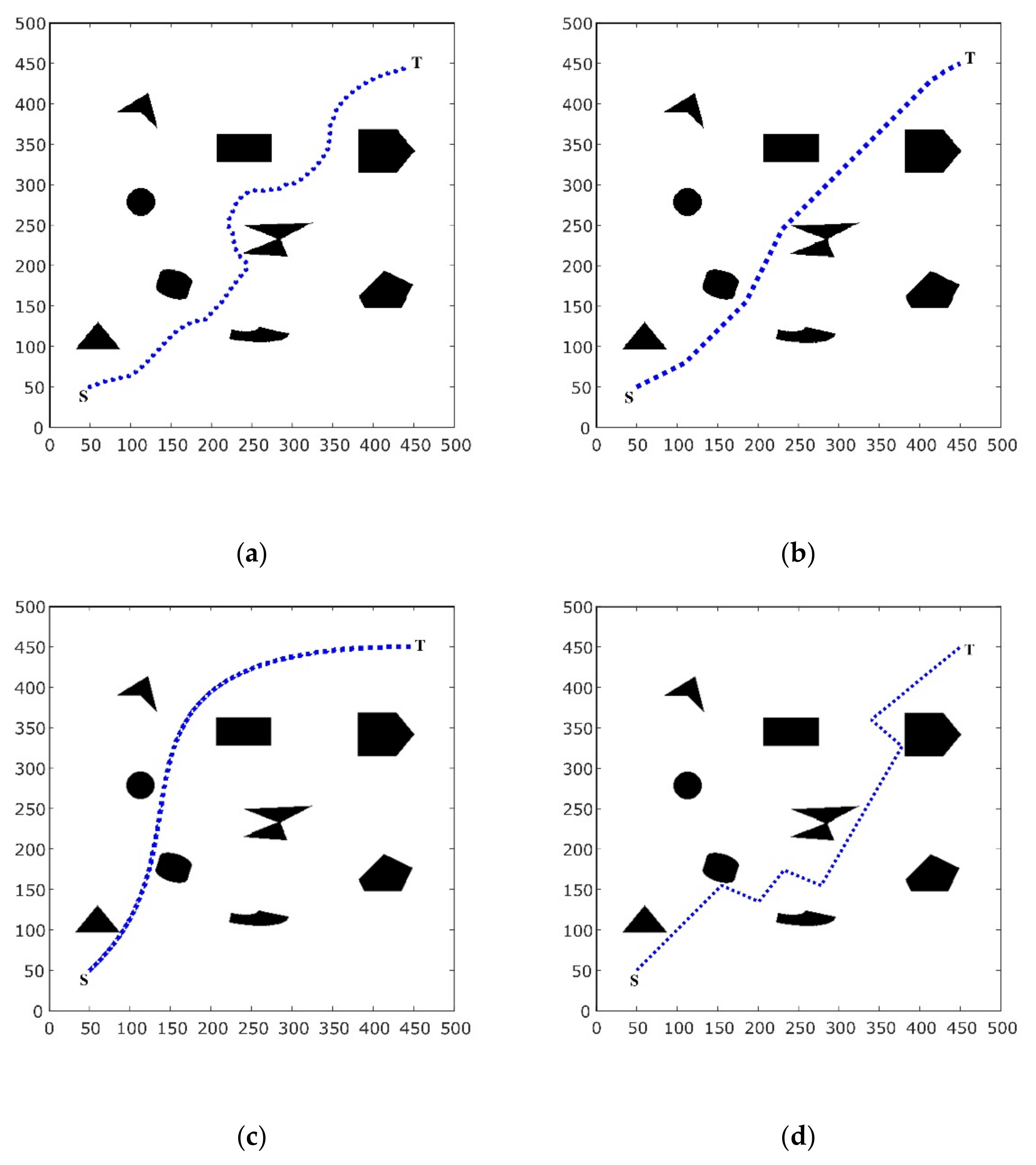
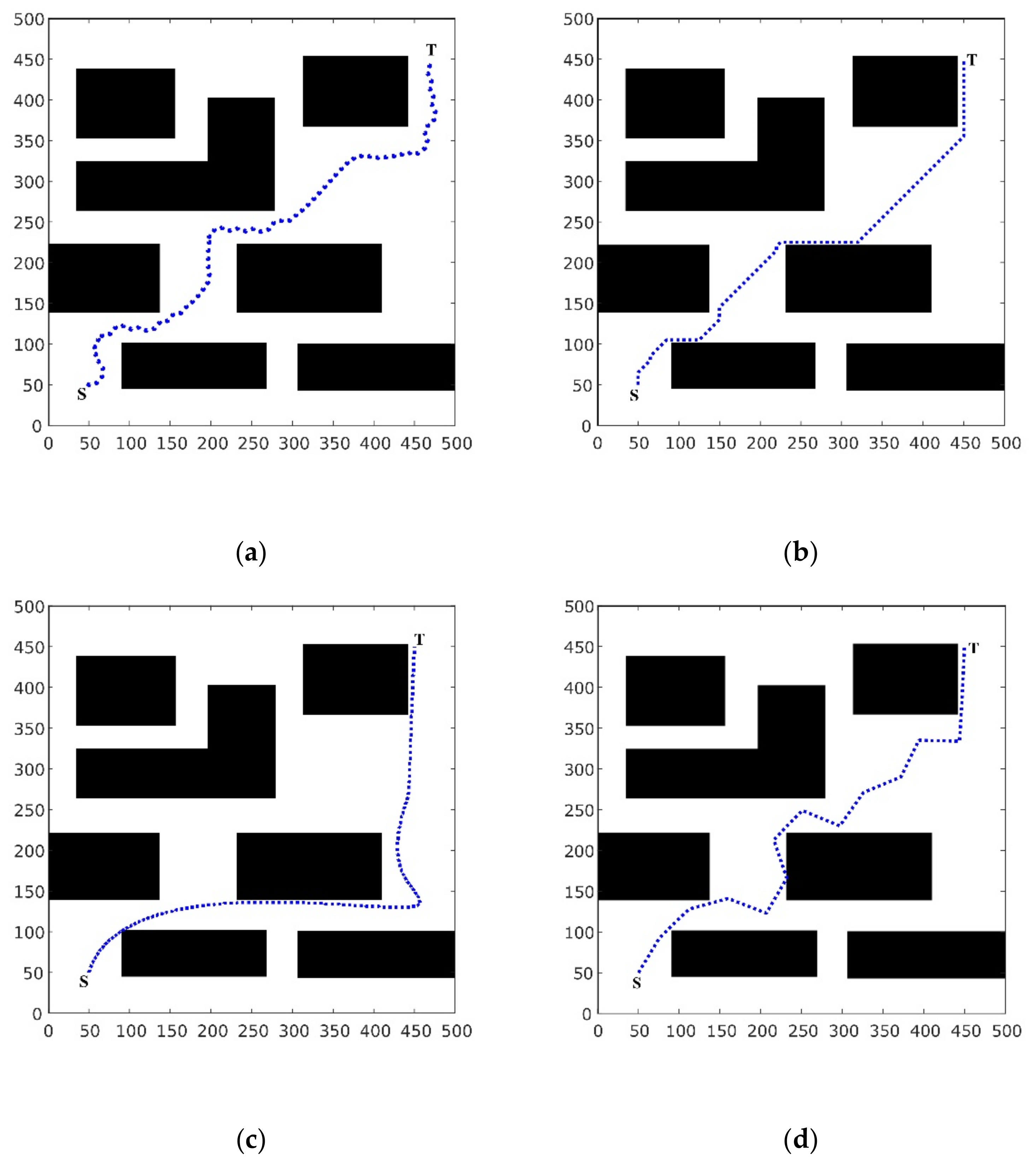
| Algorithms | Time | Path Length | Success Rate/% |
|---|---|---|---|
| DA-APF | 1.57 | 629 | 100 |
| A* | 7.53 | 576 | 100 |
| GA | 2.07 | 710 | 100 |
| SA | 2.08 | 673 | 100 |
| Algorithms | Time | Path Length | Success Rate/% |
|---|---|---|---|
| DA-APF | 1.79 | 712 | 100 |
| A* | 10.18 | 675 | 100 |
| GA | 3.33 | 779 | 84 |
| SA | 1.59 | 763 | 100 |
| Algorithms | Time | Path Length | Success Rate/% |
|---|---|---|---|
| DA-APF | 1.72 | 680 | 100 |
| A* | 6.56 | 651 | 100 |
| GA | 1.81 | 702 | 94 |
| SA | 2.15 | 687 | 100 |
| Algorithms | Time | Path Length | Success Rate/% |
|---|---|---|---|
| APF | 4.15 * | 492 * | 24 |
| DA-APF | 1.12 | 447 | 100 |
| Average Number of Iterations | Success Rate/% | |||
|---|---|---|---|---|
| 9999 | 0.98 | 610 | 100 | |
| 0.97 | 621 | 100 | ||
| 0.96 | 624 | 100 | ||
| 0.95 | 1339 | 80 | ||
| 0.94 | 255 | 0 | ||
| 2000 | 0.98 | 3245 | 40 | |
| 0.97 | 3256 | 10 | ||
| 0.96 | 1738 | 20 | ||
| 0.95 | 476 | 0 | ||
| 0.94 | 230 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Qiu, J.; Yu, H.; Zhang, C.; Wu, Z.; Gao, Q. Robot Static Path Planning Method Based on Deterministic Annealing. Machines 2022, 10, 600. https://doi.org/10.3390/machines10080600
Dai J, Qiu J, Yu H, Zhang C, Wu Z, Gao Q. Robot Static Path Planning Method Based on Deterministic Annealing. Machines. 2022; 10(8):600. https://doi.org/10.3390/machines10080600
Chicago/Turabian StyleDai, Jinyu, Jin Qiu, Haocheng Yu, Chunyang Zhang, Zhengtian Wu, and Qing Gao. 2022. "Robot Static Path Planning Method Based on Deterministic Annealing" Machines 10, no. 8: 600. https://doi.org/10.3390/machines10080600
APA StyleDai, J., Qiu, J., Yu, H., Zhang, C., Wu, Z., & Gao, Q. (2022). Robot Static Path Planning Method Based on Deterministic Annealing. Machines, 10(8), 600. https://doi.org/10.3390/machines10080600







