Abstract
A valve-controlled hydraulic cylinder system has the characteristics of uncertainty and time-variance, and the electro-hydraulic servo unit encounters shock, vibration, and other external interference when working, which seriously affect the stability of the valve-controlled hydraulic cylinder system. Therefore, it is necessary to introduce an active disturbance rejection controller (ADRC) into the electro-hydraulic servo control. However, there are many ADRC parameters, and it is difficult to set these only with expert experience. Therefore, we propose applying the gray wolf optimization algorithm (GWO) to the ADRC, to auto-tune the parameters and find the optimal solution. In addition, the advantages of the GWO in ADRC parameter tuning are proven and analyzed. The simulation and experimental results showed that the GWO algorithm had a faster mean time for parameter tuning and the smallest fitness value (integrated time and absolute error), compared to the particle swarm optimization algorithm and genetic algorithm. Moreover, a valve-controlled cylinder system, after parameter tuning by the gray wolf optimization algorithm, could accurately adjust the parameters of the auto-disturbance rejection controller, with a faster response speed, smaller overshoot, and better anti-disturbance ability.
1. Introduction
Electro-hydraulic servo control systems play an important role in industrial production, military, and even aerospace fields. Their steady-state performance and dynamic performance directly affect the working performance and safety of various devices in the above-mentioned areas [1,2,3,4,5,6]. However, in engineering practice, these systems often face various complex disturbances, such as sudden changes in external forces and changes in system parameters. These interferences will cause deviations in the actions of the system’s actuators and affect production [7].
Focusing on the anti-jamming problem of the control system, researchers have performed research on anti-jamming controllers and parameter tuning algorithms. Lijun Wang linked a single-degree-of-freedom control system with the uncertainties of internal and external factors, used the extended state observer of ADRC to estimate the total disturbance, and combined the backstepping method to improve the nonlinear error feedback control law and improve the tracking of the position signal precision [8]. Chu Zhang’s disturbance decoupling controller, based on linear active disturbance rejection control technology, decomposed the performance requirements of the test acceleration into specifications for no drag and suspension loops. It solved the problem of designing an auto-disturbance rejection controller for a high-precision, towed-free satellite with cubic test quality [9]. Mehrnoosh Kamarzarrin proposed an adaptive control method based on sliding mode control, the coefficients of which were tuned using a combination of the particle swarm optimization algorithm and a support vector machine. Applying this to the control of the pitch angle of wind turbines, the anti-interference effect was improved [10]. Mehran Rahmani proposed a new sliding mode control (NSMC) based on the extended gray wolf optimization algorithm (EGWO), to control a two-degree-of-freedom manipulator, and simulations verified that the modified control method had a good robustness against external disturbances [11]. Lakhdar, C. proposed a novel robust power system stabilizer (PSS) and PSS for an optimal stabilizer (FOPID-PSS). In addition, they used a new meta heuristic optimization bat algorithm (BA), inspired by echolocation behavior, to improve the power system stability. Simulation results showed the effectiveness of BA for FOPID-PSS design [12]. Carrillo-Alarcón, J. C. presented a metaheuristic optimization approach for parameter estimations in arrhythmia classification from unbalanced data. Simulation results showed an accuracy of 99.95%, a sensitivity of 99.87%, a precision of 99.89%, and a specificity of 99.99% [13]. Dahan, F. introduced a hybrid algorithm that combined ant colony optimization (ACO) and the genetic algorithm (GA) to efficiently compose services in the cloud. The experimental results on 15 different real datasets showed the effectiveness of the proposed algorithm for searching for comparable solutions, compared to five competitors [14]. Omar Rodríguez-Abreo presented the use of equations for the dynamic response of a step input in a metaheuristic algorithm for the parametric estimation of a motor model. Tests were carried out with three algorithms (gray wolf optimizer, jaya algorithm, and cuckoo search algorithm), to prove that the benefits could be extended to various metaheuristics. The results showed an improvement for all the algorithms used, achieving the same error as the original method, but with 10 to 50% fewer iterations [15]. With the continuous development of metaheuristic algorithms, their application in engineering is also expanding. In engineering, we often use metaheuristic algorithms to solve practical problems directly or use metaheuristic algorithm to assist in tuning parameters of the controller, to solve practical problems indirectly. There is no doubt that both methods have improved the work efficiency in projects.
It can be seen that the above research conducted in-depth discussions on the tuning methods of a controller and its parameters, and applied this to various working systems to resist the influence of interference and achieved certain results. However, the research on the ADRC and parameter tuning of electro-hydraulic servo systems is not comprehensive [16,17,18]. Therefore, this paper used an auto-disturbance rejection controller to control an electro-hydraulic servo system, and used the gray wolf optimization algorithm to adjust the parameters of the controller, so that the system could minimize the action error caused by interference.
2. Modeling of an Electro-Hydraulic Servo System
The hydraulic cylinder in this study used a double-acting symmetrical cylinder to weaken the influence of nonlinear factors [19]. Assuming that the bulk elastic modulus and temperature of the oil remain unchanged, the pressure in the closed cavity of the hydraulic actuator is equal everywhere, and the internal and external leakage are laminar flow. The natural frequency of the system is lowest when the piston rod is in the neutral position. Based on this position, the basic formula of the valve-controlled cylinder mathematical model can be deduced, as follows:
In this formula, is the flow gain coefficient; is the displacement of the spool, the unit is m; is the flow and pressure coefficient; is the system output pressure, the unit is MPa; is the load flow in m3/s; is the effective area of the actuator, the unit is m2; is the maximum stroke of the cylinder, the unit is mm; is the comprehensive leakage coefficient of the actuator, the unit is m5/N⋅m; is the effective volume modulus, the unit is N/m2; and is the hydraulic cylinder. For an effective viscous damping coefficient, the unit is N⋅m/s; is the equivalent volume of the oil chamber, the unit is m3; and K is the equivalent spring stiffness of the hydraulic cylinder, the unit is N/m. Combine the above three formulas to obtain:
In this formula, is the pressure coefficient of the total flow of the system, , the unit is m5/N⋅m.
In general, the equivalent viscous damping coefficient is very small and can be ignored. Due to:
Therefore, the relevant non-linear influence factors can be ignored, so the system formulas can be simplified. According to Formula (4), the transfer function of the valve-controlled cylinder can be obtained:
In this formula, is the natural frequency of hydraulic pressure, in rad/s; is the damping ratio of hydraulic pressure; is the spring stiffness of hydraulic pressure, in N/m.
And:
The servo valve in this article uses the second-order oscillation link to discuss, and the transfer function is:
In this formula, is the no-load flow of the valve, in L/min; is the flow gain coefficient of the valve; is the natural frequency of the valve, in Hz; and is the damping ratio of the valve.
The frequency response of the servo amplifier is relatively high, and the simplified expression is as follows:
In this formula, is the deviation voltage signal, the unit is V; is the output current signal, the unit is A; and is the voltage-current proportional coefficient.
According to the principle of a displacement sensor, the transfer function is derived as:
Using the above formula, the structure diagram of the position control model is shown in Figure 1
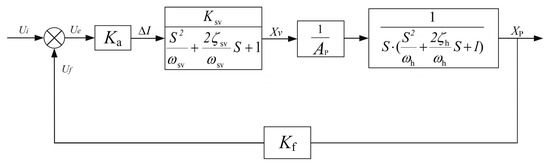
Figure 1.
Structure diagram of the position control model.
From the above figure, the open-loop transfer function of the system can be obtained, as shown in Formula (13).
The closed-loop transfer function for this system is shown in Formula (14).
Therefore, the sensitivity of the feedback system with respect to G(s) is shown in Formula (15).
It is shown that the closed-loop system has some suppression ability for the effects caused by the uptake when the uptake acts on the links of the forward channel surrounded by the feedback loop.
3. Design of Auto-Disturbance Rejection Controller Based on Grey Wolf Algorithm
The gray wolf algorithm belongs to the metaheuristic algorithms. A metaheuristic algorithm is a modification of a heuristic algorithm, which is the product of combining a randomized algorithm with a local search algorithm. The heuristic algorithm is an intuitive or empirically constructed algorithm. The difference between a heuristic algorithm and a metaheuristic algorithm is the presence or absence of a random factor [20]. For the same problem, given an input, the steps of the algorithm are fixed and the output is therefore fixed, and the result remains the same for multiple operations. Therefore, heuristic algorithms do not necessarily guarantee the feasibility and optimality of the resulting solution, and in most cases do not even indicate the degree of approximation between the resulting solution and the optimal solution. A metaheuristic algorithm includes random factors, and these random factors also make the algorithm have some probability of going beyond the local optimal solution to obtain the global optimal solution. Therefore, a metaheuristic algorithm has some advantages in parameter rectification [21].
The unique feature of GWO is that the hierarchy in the wolf pack makes a small group of gray wolves have absolute say, which makes the algorithm have strong convergence performance; it has few parameters, it is easy to implement, and it does not contain specific search parameters [22]. Therefore, GWO is suitable for application in parameter rectification of ADRC.
3.1. Grey Wolf Optimization Algorithm
The gray wolf optimization algorithm is an intelligent algorithm based on the predation of gray wolves. Similar to other intelligent algorithms, the prey represents the optimal solution, and the position of each gray wolf represents a possible solution. In the process of searching for the optimal solution, gray wolves are ranked according to their degree of fitness function value. The gray wolf individuals with the best fitness function value are named α wolves, followed by β wolves, and then δ wolves. The rest are ω wolves, and α, β, and δ wolves are closer to the potential position of the prey. The hierarchy of gray wolves plays an important role in the process of predation, the gray wolves are led by α wolves to surround their prey, β wolves and δ wolves attack the prey, and ω wolves assist in attacking the prey to completion, and finally capture the prey [23].
The mathematical model of the gray wolf optimization algorithm consists of the following parts [24]:
Surround prey:
Formula (16) represents the distance between the gray wolf individual and its prey, and Formula (17) is the position update formula of the gray wolf. Among them, is the current iterative algebra, and are coefficient vectors, and and are the position vector of the prey and the position vector of the gray wolf, respectively. The calculation formulas of A and C are as follows:
Among them, is the convergence factor. As the number of iterations decreases linearly from 2 to 0, the modulus of and takes a random number between 0 and 1.
Track hunting:
Among them, , , and represent the distance between α, β, and δ and other individuals, respectively; , , and are random vectors; X is the current gray wolf position.
Formula (21) defines the step length and direction of ω individuals in the wolf pack toward α, β, and δ, respectively, and Formula (22) defines the final position of ω.
Attack the prey:
When the prey stops moving, the gray wolf completes the hunting process by attacking. In order to simulate approaching prey, the value of a is gradually reduced, so the fluctuation range of A is also reduced. In other words, in the iterative process, when the value of a linearly decreases from 2 to 0, the corresponding value of A also changes in the interval (−a, a). As shown in Figure 2, when the value of A is within the interval, the next position of the gray wolf can be anywhere between its current position and the position of its prey. When < 1, the wolves attack their prey (falling into a local optimum). When > 1, the gray wolf is separated from its prey, hoping to find a more suitable prey (globally optimal).
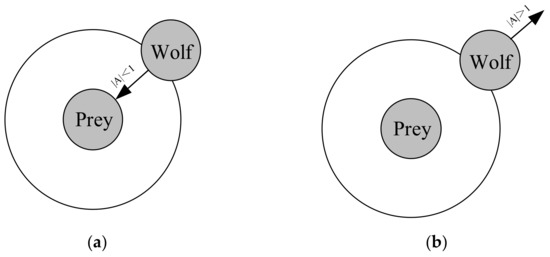
Figure 2.
Attack and hunt for prey: (a) wolves attack their prey; (b) gray wolf separated from prey.
Figure 2 is a schematic diagram of attacking and finding prey.
The process of the gray wolf optimization algorithm is shown in Figure 3:
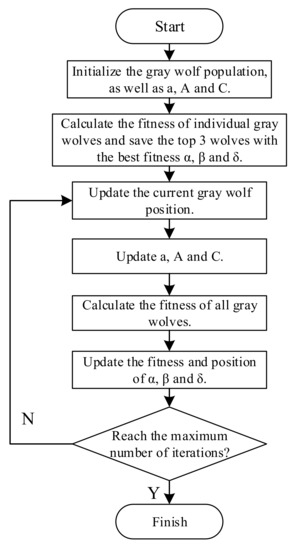
Figure 3.
The optimization flow chart of the gray wolf algorithm.
3.2. Design of the Active Disturbance Rejection Controller
ADRC is a new controller, improved on the basis of a traditional PID. It consists of three parts: tracking differentiator (TD), extended state observer (ESO), and non-linear state error feedback (NLSEF). A TD is a new type of differentiator used to track the target signal obtained, by discretizing and improving the traditional differentiator. Its function is to extract the differential signal from the input signal, to solve the problem of a large overshoot in the system, and to rationally arrange the transition process for the system. ESO eliminates the influence of the total disturbance of the system by estimating and compensating the internal disturbance and external disturbance of the system, which reflects the strong anti-interference performance. NLSEF performs a nonlinear combination of error signals to enhance the dynamic performance of the system [25].
Figure 4 shows the ADRC structure diagram of the electro-hydraulic servo system. In the figure, is the given signal; is the tracking signal of ; is the differential signal of ; is the actual output signal; is the tracking signal of ; is the differential signal of ; is the tracking total disturbance; calculates the control quantity for the nonlinear control law; and is the control quantity output by the active disturbance rejection controller.
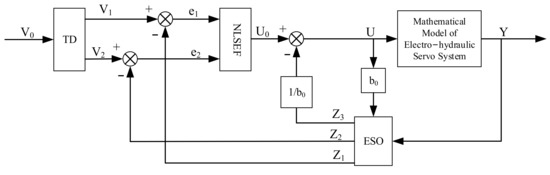
Figure 4.
ADRC structure diagram.
The algorithm of TD is:
The fhan function is:
In Formula (23) and Formula (24), r is the speed factor, which can change the tracking speed of the system and is directly proportional to the tracking speed. However, if r is too large, it will increase the overshoot of the system. Therefore, a smaller r value should be selected when the tracking speed reaches the system requirements. In the formula, h is the filter factor that determines the filter effect.
The algorithm of ESO is:
The fal function is:
where , , , are the gains of ESO; d is the bandwidth; is the bandwidth; , are non-linear factors; and , , , are sampling periods whose values are not necessarily equal. The values of the three parameters , , and are all 0 to 1.
The algorithm of NLSEF is composed of the fst function. The fst function is:
In this formula, is the speed factor, which can change the tracking speed of the system and is proportional to the tracking speed. However, if is too large, it will increase the overshoot of the system. Therefore, when the tracking speed reaches the system requirements, a smaller value of should be selected.
3.3. Parameter Tuning Algorithm Design Based on the Gray Wolf Optimization
The gray wolf algorithm was used to adjust the parameters of the auto-disturbance rejection controller. Its essence is to set and adjust the parameters in each sampling period. The purpose is to find a set of parameters that can make the auto-disturbance rejection controller have the best performance. The basic principle of parameter setting is shown in Figure 5.
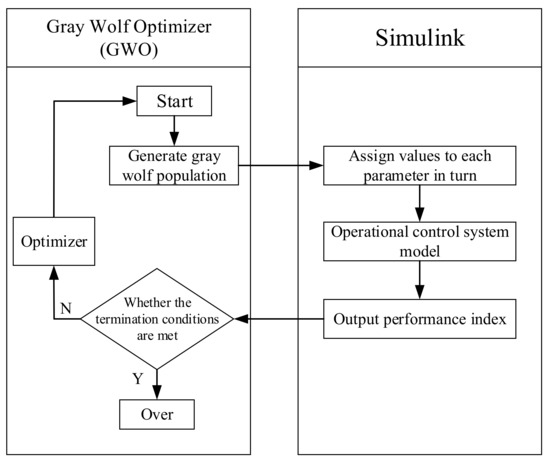
Figure 5.
Basic principle diagram of parameter setting.
3.3.1. Fitness Function
In view of the fact that the parameter tuning of the active disturbance rejection controller can be regarded as a multi-dimensional function optimization problem, the gray wolf algorithm adopts a real number coding method. If the gray wolf population size is n, there are 16 parameters of the controller that need to be tuned, so the dimension of the problem domain is 16. Therefore, the gray wolf population optimized for the parameters of the ADRC can be represented by an n × 16 matrix. The purpose of ADRC parameter tuning optimization is to make the overall system deviation of the control system tend to zero, while ensuring a lower overshoot and faster response speed. However, when evaluating the performance of the control system, it is basically impossible to achieve the optimal performance of all performance indicators at the same time in actual engineering. As each parameter affects the others, when one of them reaches the optimum, the other different performance indexes may be reduced as a result. Parameter tuning is performed using the minimum value of the error output from the Simulink output curve over time. Therefore, in order to ensure the overall performance of the control system, to obtain satisfactory dynamic characteristics of the transition process, and to take into account the control accuracy and convergence speed, the integral of the tune multiplied absolute value of the error (ITAE) criterion was chosen as the fitness function of the self-turbulent controller. As shown in Formula (28) [26]:
The e(t) in the formula represents the deviation of the control system.
The evaluation standard is to integrate the product of the absolute value of the system steady-state error and time, so that the system has a strong stability and short dynamic response time, and can identify control systems with different parameters. The controlled system evaluated by this criterion has the characteristics of a small overshoot, is stable and fast, and can achieve a high level of system performance [27].
3.3.2. Algorithm Implementation
The gray wolf optimization algorithm was used to adjust the 16 parameters of the ADRC. The main idea is shown in Figure 6.
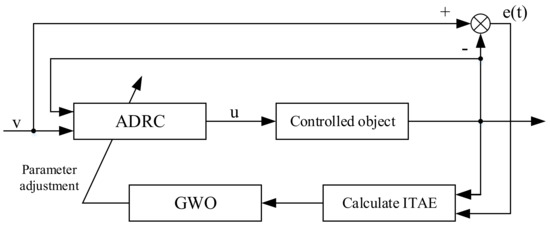
Figure 6.
ADRC control system based on the gray wolf algorithm.
The specific steps are:
- Initialize the parameters of the GWO algorithm. Set the population size to 16, the dimension to 5, the maximum number of iterations to 15, and give the value range of each parameter based on the experience value.
- Initialize the location information of the GWO algorithm. Randomly initialize the position information of the artificial gray wolf optimization algorithm (16 parameters of the auto-disturbance rejection controller to be tuned), and use random initialization for the 16 parameters of the auto-disturbance rejection controller, such as, within the range of values. The mechanism initializes the gray wolf position information in the algorithm. Expressed as: . Among them, i is the i-th gray wolf in the population, and corresponds to an auto-disturbance rejection controller parameter to be tuned.
- The Simulink (and AMEsim) program runs. Assign the value to the Simulink module, run the control system model, calculate the corresponding fitness function value, and find the global optimal position in the initialization phase.
- Iterate the algorithm until the termination condition is met. The population is iterated according to Formula (14) to Formula (20), to select the optimal fitness value and its corresponding location information.
- Whether the stop condition is met: generally, a fixed number of iterations or a fitness function value reaching a certain accuracy is selected as the stopping condition of the algorithm.
- Output the position information corresponding to the optimal fitness value and the change of the fitness value during the iteration process. This positional information is the parameter value of of the active disturbance rejection controller. The change curve of the optimal fitness value is the convergence curve of the GWO algorithm.
4. Simulation Analysis
4.1. Simulink Simulation
In order to verify the effect of the gray wolf optimization algorithm on the parameter tuning of the auto-disturbance rejection controller in the electro-hydraulic servo control system, this research built a simulation model of the auto-disturbance rejection controller in Simulink. The hydraulic servo control system was simplified into a linearized mathematical model and used as a simulation object.
The sampling period of the simulation system was T = 0.001, and the simulation time in Simulink for each iteration was t = 50 s. The parameters of the algorithm are shown in Table 1, Table 2 and Table 3.

Table 1.
Parameters in the Gray Wolf Optimization Algorithm.

Table 2.
Parameters in Particle Swarm Optimization Algorithm.

Table 3.
Parameters in Genetic Algorithms.
Other things being equal, the gray wolf optimization algorithm was compared with the standard PSO and standard GA (That is, the simple genetic algorithm) [28,29,30,31,32,33]. The simulation tests were obtained using the Matlab–Simulink environment.
The 16 parameters of ADRC were divided into eight groups for k-fold cross-validation, i.e., k = 8. The cross-validation flow chart is shown in Figure 7.
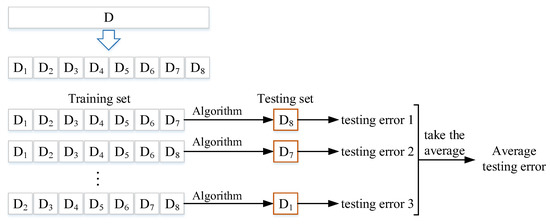
Figure 7.
Flow chart of k-fold cross-validation.
The results of the k-fold cross-validation are shown in Table 4.

Table 4.
The k-fold cross-validation results for each algorithm.
According to Table 4, the GWO algorithm with the smallest average test error was selected as the final parameter rectification algorithm.
The optimization curves of the gray wolf optimization algorithm, particle swarm optimization algorithm, and genetic algorithm are shown in Figure 8.
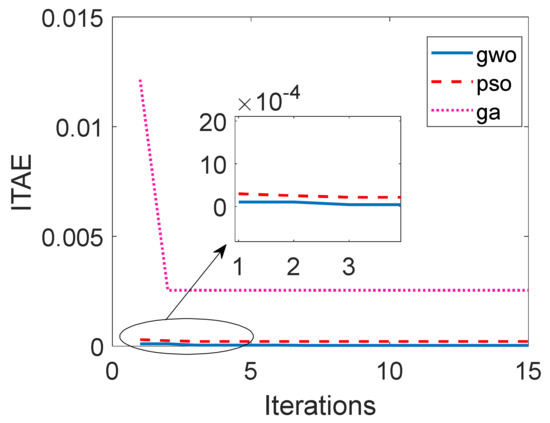
Figure 8.
Comparison chart of the algorithm optimization curves.
It can be seen from Figure 8 that both the gray wolf algorithm and the particle swarm algorithm had obvious changes in the fitness function value at the third iteration; the particle swarm algorithm reached the most optimal fitness function value that it could achieve after the third iteration; in the 11th iteration of the gray wolf algorithm, the fitness function value reached the optimal value. However, the optimal value obtained by the gray wolf algorithm was obviously closer to 0, which was better than the optimal value of the particle swarm algorithm. It can be seen that the gray wolf algorithm had a better optimization performance.
The gray wolf algorithm was used for parameter self-tuning, and the program was used to apply a better set of controller parameters for the ADRC of the electro-hydraulic servo system, and the response curve was obtained as shown in the figure below.
On the premise that the controlled object was determined, the gray wolf optimization algorithm was set up to tune the ADRC controller, and a simulation analysis was carried out. The input source signal adopted a step signal and sine signal, and the simulation time was uniformly set to 20 s. The step time of the input step signal was 1 s, the initial value was 0, the final value was 1, and the sampling time was 0.001 s. The amplitude of the input sine signal was 1, and the frequency was 1 rad/s. The response curve is shown in Figure 9 and Figure 10.
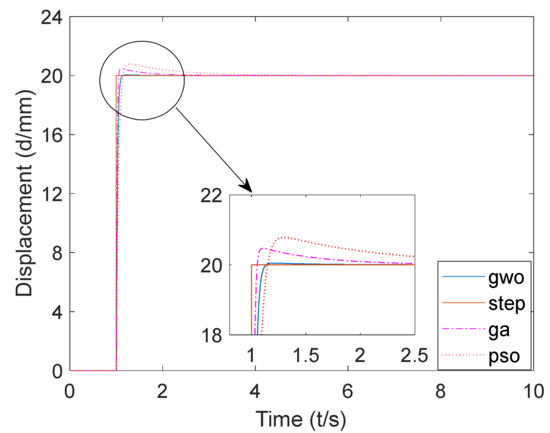
Figure 9.
Simulink simulation step signal response curve.
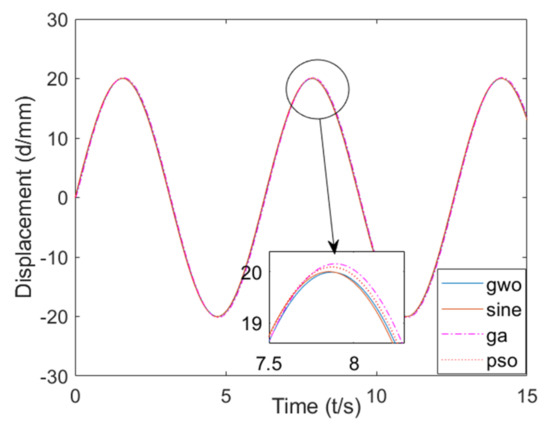
Figure 10.
Simulink simulated sinusoidal signal response curve.
It can be seen from Figure 9 that the steady-state value of the step response based on the GWO algorithm was 1, the rise time was about 0.056 s, the peak time was about 0.198 s, the maximum overshoot was 0.28%, and the adjustment time was about 0.0708 s (Δ0.05). The steady-state value of the step response based on the GA algorithm was 1, the rise time was about 0.0335 s, the peak time was about 0.92 s, the maximum overshoot was 2.45%, and the adjustment time was about 0.041 s (Δ0.05). The steady-state value of the step response based on the PSO algorithm was 0.099 s, the rise time was about 0.096 s, the peak time was about 0.29 s, the maximum overshoot was about 4%, and the adjustment time was about 0.115 s (Δ0.05).
It can be seen from Figure 10 that the phase lag of the sinusoidal response based on the GWO algorithm was about 0.025°, and the amplitude attenuation was about −0.05%. Based on the GA algorithm, the sine response phase lag was about 0.04°, and the amplitude attenuation was about 0.77%. Based on the PSO algorithm, the sine response phase lag was about 0.03°, and the amplitude attenuation was about 0.45%.
It can be seen that the ADRC whose parameters were tuned by the gray wolf algorithm had a fast response speed and a small overshoot, and its performance was fully utilized.
4.2. AMEsim and Simulink Co-Simulation
In order to further verify the simulation results, avoid errors caused by the mathematical model, and also to verify the anti-jamming capability of the ADRC after the algorithm had been tuned, a joint simulation of AMEsim and Simulink was carried out in this paper.
The AMEsim model is shown in Figure 11. This model simplified the hydraulic oil source, the load, and the industrial control computer.
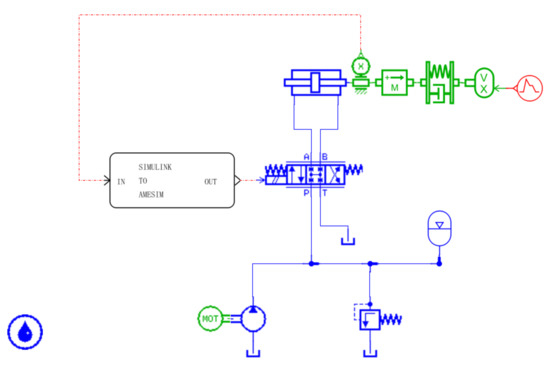
Figure 11.
AMEsim simulation model.
A double rod hydraulic cylinder was used to drive the mass block, to simulate the actual working conditions. The electric motor drives the oil pump, to pump the hydraulic oil into the hydraulic cylinder through the electro-hydraulic servo valve. The piston rod starts to move, pushing the mass block, to produce displacement; the displacement sensor transmits the detected mass movement status to the Simulink control model, and after passing through the corresponding controller, it outputs a control signal to control the electro-hydraulic servo valve.
In order to verify the anti-interference ability of ADRC when there is disturbance in the outside world, this study added a disturbance signal to the load of the AMEsim model and made it output continuously in a loop. The interference signal is shown in Figure 12.
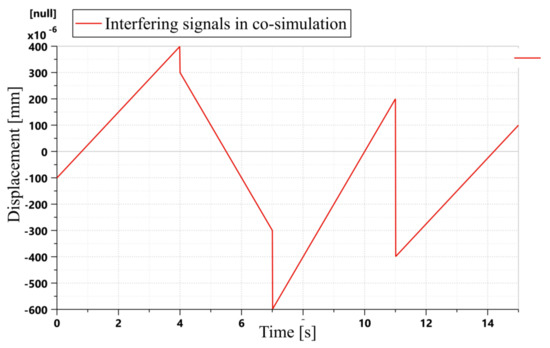
Figure 12.
AMEsim interference signal.
After connecting the interface of AMEsim, we needed to open MATLAB from the tools in AMEsim, connect the interface module to the Simulink model as the target, and use the algorithm to re-tune the parameters.
The input signal in Simulink remained unchanged, and three algorithms were used to set the required parameters in the joint simulation. The joint simulation results are shown in Figure 13 and Figure 14.
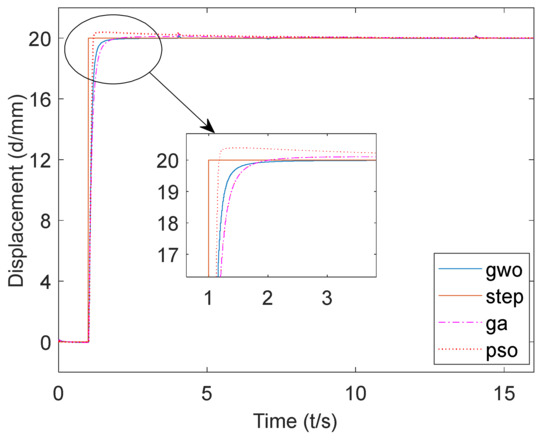
Figure 13.
Co-simulation step signal response curve.
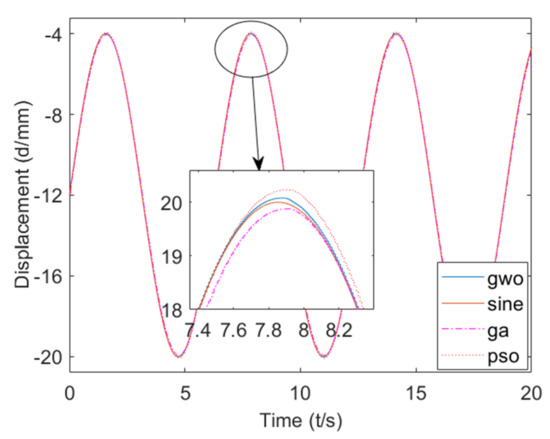
Figure 14.
Co-simulation of sinusoidal signal response curve.
It can be seen from Figure 13 that the steady-state value of the step response based on the GWO algorithm was 1, the rise time was about 0.21 s, the peak time was about 2 s, the maximum overshoot was 0.8%, and the adjustment time was about 0.28 s (Δ0.05). The steady-state value of the step response based on the GA algorithm was 1.005, the rise time was about 0.28 s, the peak time was about 2.1 s, the maximum overshoot was 1.3%, and the adjustment time was about 0.39 s (Δ0.05). The steady-state value of the step response based on the PSO algorithm was 1.01, the rise time was about 0.14 s, the peak time was about 0.5 s, the maximum overshoot was about 1.9%, and the adjustment time was about 0.15 s (Δ0.05).
It can be seen from Figure 14 that the phase lag of the sinusoidal response based on the GWO algorithm was about 0.04°, and the amplitude attenuation was about 0.38%. Based on the GA algorithm, the sine response phase lag was about 0.06°, and the amplitude attenuation was about 0.63%. Based on the PSO algorithm, the sine response phase lag was about 0.068°, and the amplitude attenuation was about 1.16%.
It can be seen that in the presence of an external load and interference, the ADRC controller, after implementing the gray wolf algorithm tuning parameters, had a fast response speed and a small overshoot, and its performance was fully utilized.
5. Experimental Verification
In order to be closer to engineering reality, to simulate the response of the electro-hydraulic servo system to different signals in actual working conditions, and to verify the results of computer simulations, relevant experimental verifications were required.
The experimental environment of the experimental platform was the xPC (xPC Target is developed by Math Works) semi-physical simulation environment. Through the RTW (real-time workshop) in Matlab, combined with Simulink, the system design and hardware devices were combined to achieve the purpose of real-time control. This system used the PC with the Matlab software as the host machine, and the target machine was an industrial computer, and the two communicated via Ethernet. The actuator was a double rod hydraulic cylinder, which was controlled by an electro-hydraulic servo valve and equipped with a displacement sensor, a pressure sensor, and a force sensor, to measure the physical quantities produced in the experiment. The experimental bench equipment is shown in Figure 15 and Figure 16.

Figure 15.
The physical map of the experimental platform.

Figure 16.
The valve-controlled cylinder part of the test bench.
During the experimental verification, it should be noted that since the actuator of the experimental equipment was a double rod hydraulic cylinder, which was not in the middle position at the initial state, the hydraulic cylinder first returned to the middle position before the simulation, and then followed the input signal. In this period of time, the output signal was inevitably affected by the sudden change of the signal at time 0, which made the following curve change significantly.
When the input signal was a step signal, in order to avoid the influence of the subsequent curve following the step signal when the hydraulic cylinder returns to the neutral position, the step time was selected as 10 s, the initial value was 0, and the final value was 1. The following curve is shown in Figure 17.
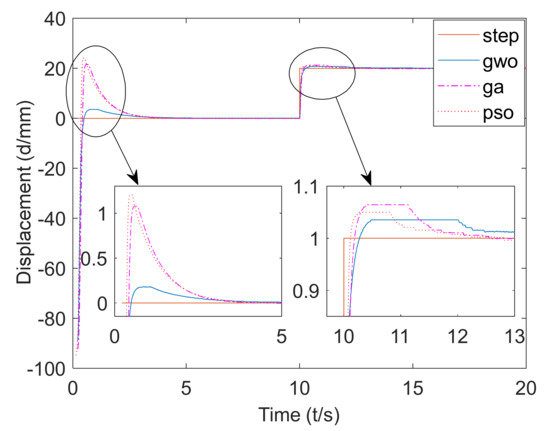
Figure 17.
Experimental curve of the step signal.
It can be seen from Figure 17 that the steady-state value of the step response based on the GWO algorithm was 1, the rise time was about 0.11 s, the peak time was about 0.49 s, the maximum overshoot was 3.5%, and the adjustment time was about 0.17 s (Δ0.05). The steady-state value of the step response based on the GA algorithm was 1, the rise time was about 0.106 s, the peak time was about 0.41 s, the maximum overshoot was 6.4%, and the adjustment time was about 1.22 s (Δ0.05). The steady-state value of the step response based on the PSO algorithm was 0.9961, the rise time was about 0.0587 s, the peak time was about 0.26 s, the maximum overshoot was about 5%, and the adjustment time was about 0.27 s (Δ0.05).
When the input signal was a sinusoidal signal, the amplitude of the input signal was set to 1, the frequency to 1 rad/s, the sampling time to 0, and the simulation time to 20 s. The output result is shown in Figure 18.
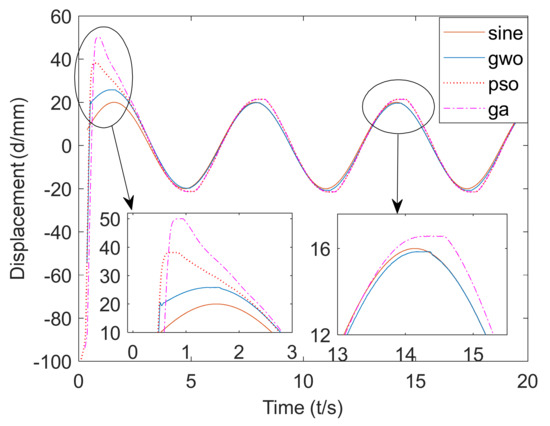
Figure 18.
Experimental curve of the sinusoidal signal.
It can be seen from Figure 18 that the phase lag of the sinusoidal response based on the GWO algorithm was about 0.08°, and the amplitude attenuation was about −1.66%. Based on the GA algorithm, the sine response phase lag was about 0.1° and the amplitude attenuation was about 6.94%. Based on the PSO algorithm, the phase lag of the sinusoidal response was about 0.1° and the amplitude attenuation was about 6.9%.
In addition, when the hydraulic cylinder returns to the neutral position in the first three seconds, the maximum amplitude attenuation of the sinusoidal response based on the GWO algorithm was 28.9%; the maximum amplitude attenuation of the sinusoidal response based on the GA algorithm was 150.0%; and the maximum amplitude attenuation of the sinusoidal response based on the PSO algorithm was 90.8%.
It can be seen that the response speed of the ADRC controller after implementing the gray wolf algorithm tuning parameters was faster, the overshoot was small, and the maximum amplitude generated when returning to the neutral position was also small.
6. Discussion
The three algorithms were used to adjust the parameters of the ADRC separately, and a total of ten experiments were carried out. The average of the numerical results obtained is shown in Table 5.

Table 5.
The numerical results corresponding to each algorithm.
From the previous simulation curves and experimental curves, it can be understood that the ADRC with tuned parameters using the GWO algorithm had a better response. From Table 5, we can see that the parameter setting time of GWO was not the shortest, but its fitness value was the best among the three algorithms. This result corroborates the simulation and experimental results. The parameter tuning time of GWO was less because of its strong convergence performance and having fewer parameters compared to PSO. In addition, GWO algorithms usually generate or approach the best solution with a high probability, which allows them to have a small fitness value [34,35,36,37,38]. Genetic algorithms are based on probabilistic rules, rather than deterministic rules [39,40,41]. This makes their search process more flexible and the influence of parameters on the search effect is as small as possible; therefore, the time spent in the process of parameter adjustment is shorter [42,43,44]. However, since the genetic algorithm is prone to premature convergence, and also prone to inaccuracy when performing encoding [45,46,47], its fitness value was the largest and the corresponding following curve was not ideal.
The parameters corresponding to the experimental following curves are shown in Table 6. The parameters obtained by the three algorithms that differed significantly have been indicated in the table and classified with reference to the results of the output curves.

Table 6.
The ADRC parameters corresponding to the experimental following curve.
As can be seen in Table 6, the three algorithms differed in the values of r, δ, b01, b02, b1, b2, b6. For the ADRC, b01, b02, b1, b0, δ, and hNLSEF are its most important parameters [48,49]. When the disturbance frequency is low, using larger b01, b02, and b1 will increase the output jitter. However, as the disturbance frequency increases, the disturbance can be better suppressed with larger b01, b02, and b1, and no jitter will be generated [50]. Increasing b0 can reduce the jitter in the output curve. However, increasing b0 makes the compensation for the disturbance smaller and the effect of suppressing the disturbance may be discounted [51]. Increasing δ and hNLSEF does not directly compensate for the effects of perturbations, and blindly increasing δ and hNLSEF can also induce jitter. However, larger b01, b02, and b1 in combination with larger δ can lead to better control results [52]. In addition, the jitter caused by excessive hNLSEF can never be solved by increasing b01, b02, and b1, but by increasing b0. In all cases, however, increasing b0 makes the control effect much less effective. This can be overcome by reducing δ, so that the control effect is not overly lost.
7. Conclusions
Three algorithms were used to tune ADRC parameters, and the advantages of the gray wolf algorithm in ADRC parameter tuning were proven. The engineering applications of ADRC are promising, and it has applications in several areas of production and life [53]. The future development trend of ADRC is to simplify the algorithm, improve the single-parameter ADRC algorithm regulation strategy, and improve the control performance and efficiency [54]. In the future, more new metaheuristics will emerge, or existing algorithms will be combined to achieve better performance, or metaheuristics will be applied to more domains to solve their optimization problems [55]. In engineering practice, multiple algorithms can also be used to solve and analyze the same problem, to discover details that may have been overlooked [56].
Author Contributions
Conceptualization, B.G., H.G., W.S. and Y.Y.; writing—original draft preparation, B.G., H.G.; writing—review and editing, B.G., H.G., W.S.; supervision, B.G.; project administration, B.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Heilongjiang Province of China (Grant No. LH2019E064).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gao, B.; Shen, W.; Guan, H.; Zheng, L.; Zhang, W. Research on Multi-Strategy Improved Evolutionary Sparrow Search Algorithm and its Application. IEEE Access 2022, 10, 62520–62534. [Google Scholar] [CrossRef]
- Wenjie, S.; Honghua, T.; Ming, H.; Jing, Y. Electro-hydraulic Position Servo Control System. Chin. Hydraul. Pneum. 2019, 6, 116–121. [Google Scholar]
- Xuchao, Z. Fault diagnosis of hydraulic servo control system for construction machinery. Wirel. Int. Tech. 2018, 15, 125–126. [Google Scholar]
- Rodríguez-Abreo, O.; Velásquez, F.A.C.; de Paz, J.P.Z.; Godoy, J.L.M.; Guendulain, C.G. Sensorless Estimation Based on Neural Networks Trained with the Dynamic Response Points. Sensors 2021, 21, 6719. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Abreo, O.; Garcia-Guendulain, J.M.; Hernández-Alvarado, R.; Rangel, A.F.; Fuentes-Silva, C. Genetic Algorithm-Based Tuning of Backstepping Controller for a Quadrotor-Type Unmanned Aerial Vehicle. Electronics 2020, 9, 1735. [Google Scholar] [CrossRef]
- Junpeng, S.; Lihua, C.; Zhibin, S. The application of fuzzy control strategy in electro-hydraulic servo system. IEEE Int. Conf. Mechatron. Autom. 2005, 4, 2010–2016. [Google Scholar]
- Gao, B.; Shen, W.; Dai, Y.; Ye, Y.T. Parameter tuning of auto disturbance rejection controller based on improved glowworm swarm optimization algorithm. Assem. Autom. 2022, 42, 427–444. [Google Scholar] [CrossRef]
- Wang, L.; Yan, J.; Cao, T.; Liu, N. Manipulator Control Law Design Based on Backstepping and ADRC Methods. In Proceedings of the 2020 Chinese Intelligent Systems Conference, Shenzhen, China, 24–25 October 2021. [Google Scholar]
- Chu, Z.; Jave, H.; Li, D.; Qi, K. Design of an Active Disturbance Rejection Control for Drag-Free Satellite. Microgravity Sci. Technol. 2019, 31, 31–48. [Google Scholar]
- Mehrnoosh, K.; Mohammad, H.R. Intelligent Sliding Mode Adaptive Controller Design for Wind Turbine Pitch Control System Using PSO-SVM in Presence of Disturbance. J. Control Autom. Electr. Syst. 2020, 31, 912–925. [Google Scholar]
- Mehran, R.; Hossein, K.; Mohammad, R. New Sliding Mode Control of 2-DOF Robot Manipulator Based on Extended Grey Wolf Optimizer. Int. J. Control Autom. Syst. 2020, 18, 1572–1580. [Google Scholar]
- Chaib, L.; Choucha, A.; Arif, S. Optimal design and tuning of novel fractional order pid power system stabilizer using a new metaheuristic bat algorithm. Ain Shams Eng. J. 2017, 8, 113–125. [Google Scholar] [CrossRef] [Green Version]
- Carrillo-Alarcón, J.C.; Morales-Rosales, L.A.; Rodríguez-Rángel, H. A Metaheuristic Optimization Approach for Parameter Estimation in Arrhythmia Classification from Unbalanced Data. Sensors 2020, 20, 3139. [Google Scholar] [CrossRef]
- Dahan, F.; Binsaeedan, W.; Altaf, M.; Al-Asaly, M.S.; Hassan, M.M. An efficient hybrid metaheuristic algorithm for qos-aware cloud service composition problem. IEEE Access 2021, 9, 95208–95217. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Álvarez-Alvarado, J.M.; García-Cerezo, A. Metaheuristic Parameter Identification of Motors Using Dynamic Response Relations. Sensors 2022, 22, 4050. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, C.; Zhao, F. Parameter tuning of ADRC and its application based on CCCSA. Nonlinear Dyn. 2014, 76, 1185–1194. [Google Scholar] [CrossRef]
- Lixin, W.; Dingxuan, Z.; Fucai, L.; Fanliang, M.; Qian, L. Active Disturbance Rejection Control for Electro-hydraulic Proportional Servo Force Loading. J. Mech. Eng. 2020, 56, 216–225. [Google Scholar] [CrossRef]
- Zhong, S.; Huang, Y.; Guo, L. A parameter formula connecting PID and ADRC. Sci. China Inf. Sci. 2020, 63, 192203. [Google Scholar] [CrossRef]
- Gao, B.; Shen, W.; Zhao, H.; Zhang, W.; Zheng, L. Reverse Nonlinear Sparrow Search Algorithm Based on the Penalty Mechanism for Multi-Parameter Identification Model Method of an Electro-Hydraulic Servo System. Machines 2022, 10, 561. [Google Scholar] [CrossRef]
- Mistry, S.; Bouguettaya, A.; Dong, H.; Qin, A.K. Metaheuristic optimization for long-term iaas service composition. IEEE Trans. Serv. Comput. 2018, 11, 131–143. [Google Scholar] [CrossRef]
- Mann, P.S.; Singh, S. Improved metaheuristic-based energy-efficient clustering protocol with optimal base station location in wireless sensor networks. Soft Comput. 2019, 23, 1021–1037. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; Velásquez, F.A.C.; Verdin, A.A.O.; Garcia-Guendulain, J.M.; Garduño-Aparicio, M. Estimation of Transfer Function Coefficients for Second-Order Systems via Metaheuristic Algorithms. Sensors 2021, 21, 4529. [Google Scholar] [CrossRef]
- Gao, B.; Shen, W.; Dai, Y.; Wang, W. A Kind of Electro-hydraulic Servo System Cooperative Control Simulation: An Experimental Research. Recent Adv. Electr. Electron. Eng. 2022; to be published. [Google Scholar] [CrossRef]
- Wen, L.; Shaohong, C.; Jianjun, J.; Teibin, W. An lmproved Grey Wolf Optimization Algorithm. Elec. J. 2019, 47, 169–175. [Google Scholar]
- Xiaofeng, Z.; Xiuying, W. Comprehensive Review of Grey Wolf Optimization Algorithm. Comput. Sci. 2019, 46, 30–38. [Google Scholar]
- Nie, Y.; Zhang, Y.; Zhao, Y.; Fang, B.; Zhang, L. Wide-area optimal damping control for power systems based on the itae criterion. Int. J. Electr. Power Energy Syst. 2019, 106, 192–200. [Google Scholar] [CrossRef]
- Marzaki, M.H.; Tajjudin, M.; Rahiman, M.; Adnan, R. Performance of FOPI with error filter based on controllers performance criterion (ISE, IAE and ITAE). In Proceedings of the 10th Asian Control Conference (ASCC), Johor Bahru, Malaysia, 31 May–3 June 2015. [Google Scholar]
- Dongning, C.; Yidan, L.; Chengyu, Y.; Donglin, J.; Kexun, W. Friction Compensation of Proportional Multi-way Valve Based on Modified Viscous Friction LuGre Model. CN Mech. Eng. 2017, 28, 62–68. [Google Scholar]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, L.M. An improved ga and a novel pso-ga-based hybrid algorithm. Inf. Process. Lett. 2005, 93, 255–261. [Google Scholar] [CrossRef]
- Kachitvichyanukul, V. Comparison of Three Evolutionary Algorithms: GA, PSO, and DE. Ind. Eng. Manag. Syst. 2012, 12, 215–223. [Google Scholar] [CrossRef] [Green Version]
- Hu, F.; Lu, Y.; Jin, L.; Liu, J.; Xia, Z.; Zhang, G. Hybrid energy efficiency friendly frequency domain tr algorithm based on pso algorithm evaluated by novel maximizing hpa efficiency evaluation criteria. Energies 2022, 15, 917. [Google Scholar] [CrossRef]
- Dali, A.; Bouharchouche, A.; Diaf, S. Parameter identification of photovoltaic cell/module using genetic algorithm (GA) and particle swarm optimization (PSO). In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015. [Google Scholar]
- Ou, C.; Lin, W. Comparison between PSO and GA for Parameters Optimization of PID Controller. In Proceedings of the 2006 International conference on mechatronics and automation, Luoyang, China, 25–28 June 2006. [Google Scholar]
- Chuei, R.; Cao, Z. Extreme learning machine-based super-twisting repetitive control for aperiodic disturbance, parameter uncertainty, friction, and backlash compensations of a brushless DC servo motor. Neural Comput. Appl. 2020, 32, 14483–14495. [Google Scholar] [CrossRef]
- Harish, G. A hybrid pso-ga algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar]
- Sun, X.; Hu, C.; Lei, G.; Guo, Y.; Zhu, J. State feedback control for a pm hub motor based on gray wolf optimization algorithm. IEEE Trans. Power Electron. 2020, 35, 1136–1146. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.Z.; Mirjalili, S.M. Evolutionary population dynamics and grey wolf optimizer. Neural Comput. Appl. 2015, 26, 1257–1263. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2020, 166, 113917. [Google Scholar] [CrossRef]
- Morris, G.M.; Goodsell, D.S.; Halliday, R.S.; Huey, R.; Hart, W.E.; Belew, R.K. Automated docking using a lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 2015, 19, 1639–1662. [Google Scholar] [CrossRef] [Green Version]
- De Moura Oliveira, P.B.; Freire, H.; Solteiro Pires, E.J. Grey wolf optimization for PID controller design with prescribed robustness margins. Soft Comp. 2016, 20, 4243–4255. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic Algorithm- A Literature Review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Taiyuan, China, 8 November 2019. [Google Scholar]
- Ji, Y.; Liu, S.; Zhou, M.; Zhao, Z.; Guo, X.; Qi, L. A machine learning and genetic algorithm-based method for predicting width deviation of hot-rolled strip in steel production systems. Inf. Sci. 2022, 589, 360–375. [Google Scholar] [CrossRef]
- Deng, C.; Li, H.; Peng, D.; Liu, L.; Zhu, Q.; Li, C. Modelling the coupling evolution of the water environment and social economic system using pso-svm in the yangtze river economic belt, china. Ecol. Indic. 2021, 129, 108012. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Awadallah, M.A.; Faris, H.; Aljarah, I.; Hammouri, A.I. Natural selection methods for grey wolf optimizer. Expert Syst. Appl. 2018, 113, 484–498. [Google Scholar] [CrossRef]
- Moradi, S.; Vosoughi, A.R.; Anjabin, N. Maximum buckling load of stiffened laminated composite panel by an improved hybrid pso-ga optimization technique. Thin-Walled Struct. 2021, 160, 107382. [Google Scholar] [CrossRef]
- Chen, B.; Niu, Y.; Liu, H. Input-to-state stabilization of stochastic markovian jump systems under communication constraints: Genetic algorithm-based performance optimization. IEEE Trans. Cybern. 2021, 99, 1–14. [Google Scholar] [CrossRef]
- Gao, B.; Shen, W.; Guan, H.; Zhang, W.; Zheng, L. Review and Comparison of Clearance Control Strategies. Machines 2022, 10, 492. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Zurita-Bustamante, E.W. On the equivalence between adrc and flat filter based controllers: A frequency domain approach. Control Eng. Pract. 2021, 107, 104656. [Google Scholar] [CrossRef]
- Xiangyang, Z.; Hao, G.; Beilei., Z.; Libo., Z. A ga-based parameters tuning method for an adrc controller of isp for aerial remote sensing applications. ISA Trans. 2018, 81, 318–328. [Google Scholar]
- Jingqing, H. Auto-disturbances-rejection Controller and Its Applications. Control Decis. 1998, 13, 19–23. [Google Scholar]
- Li, W.; Zhang, M.; Deng, Y. Consensus-based distributed secondary frequency control method for ac microgrid using adrc technique. Energies 2022, 15, 3184. [Google Scholar] [CrossRef]
- Yang, J.H.; Fu, L.C. Nonlinear adaptive control for manipulator system with gear backlash. IEEE Conf. Decis. Control 1996, 4, 4369–4374. [Google Scholar]
- Farouki, R.T.; Swett, J.R. Real-time compensation of backlash positional errors in CNC machines by localized feedrate modulation. Int J. Adv. Manuf. Technol. 2022, 119, 5763–5776. [Google Scholar] [CrossRef]
- Peng, W. Research on the Hydraulic Cylinder Friction Test Based on LuGre Model. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2018. [Google Scholar]
- Lijun, F.; Hao, Y. Nonlinear Adaptive Robust Control of Valve-Controlled Symmetrical Cylinder System. J. Beijing Inst. Technol. 2021, 30, 171–178. [Google Scholar]
- Nikoli, M.; Elmi, M.; Macura, D.; Ali, J. Bee colony optimization metaheuristic for fuzzy membership functions tuning. Expert Syst. Appl. 2020, 158, 113601. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
