Automated Identification of Linear Machine Tool Model Parameters Using Global Sensitivity Analysis
Abstract
:1. Introduction
2. Proposed Method
2.1. Starting Point
- A1
- A set of reference (i.e., training) modal parameters , which govern the machine tool’s vibrational behavior, exists. Since there is no significant coupling between modes, the eigenvectors and eigenfrequencies are independent of the structure’s damping. This holds true for weakly damped structures [9].
- A2
- There is a set of parameters such thatmeaning that the model is capable of representing the reference data.
- A3
- Parameter bounds need to be known such that , that is the search space must contain the true and globally valid machine tool parameters , which are to be identified.
- A4
- The machine tool model contains linear damping sources only. Thus, the overall modal damping of a mode i can be expressed aswith being the number of damping sources in the model and being the contribution of damping source i to the overall damping [9].
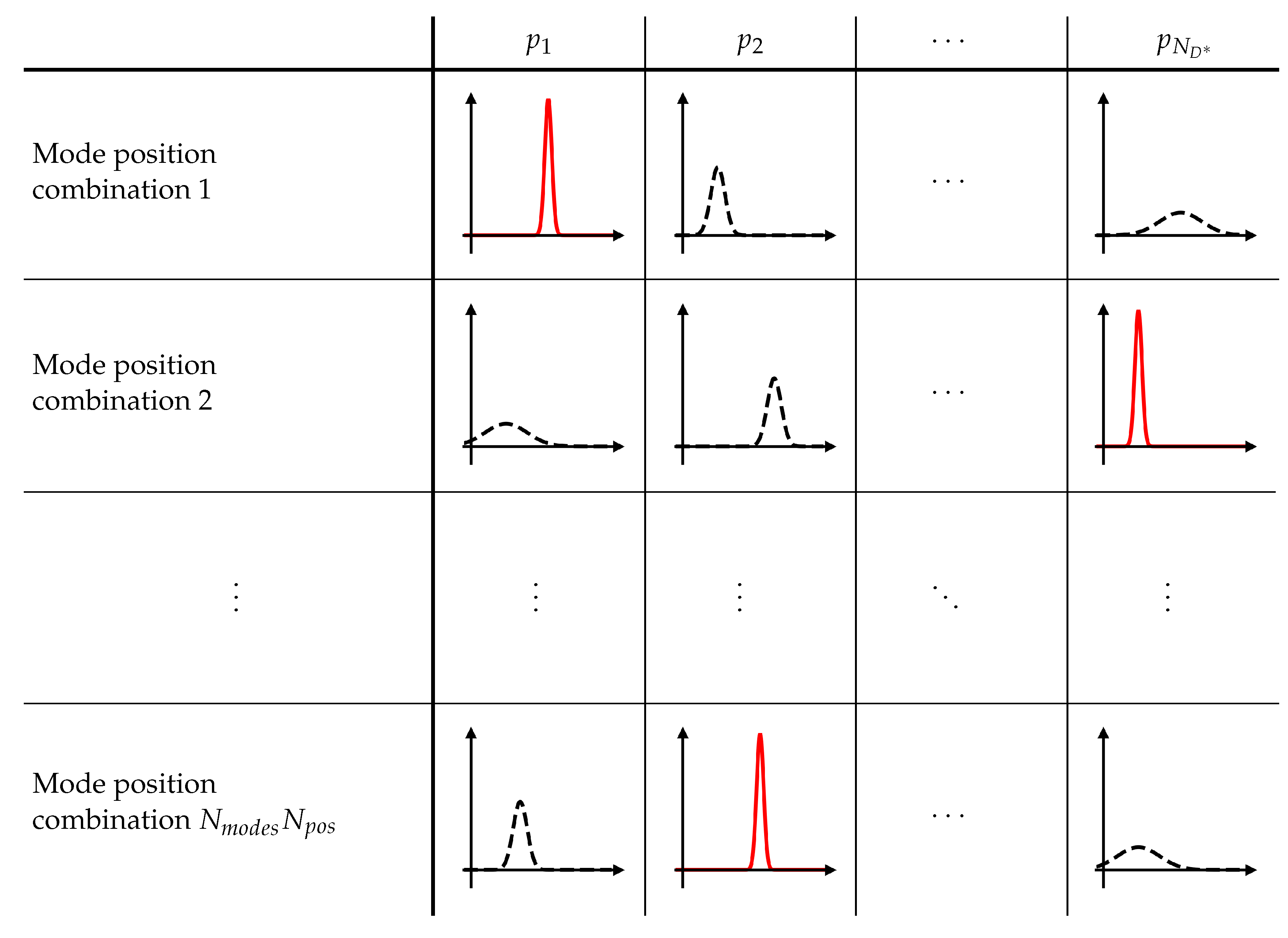
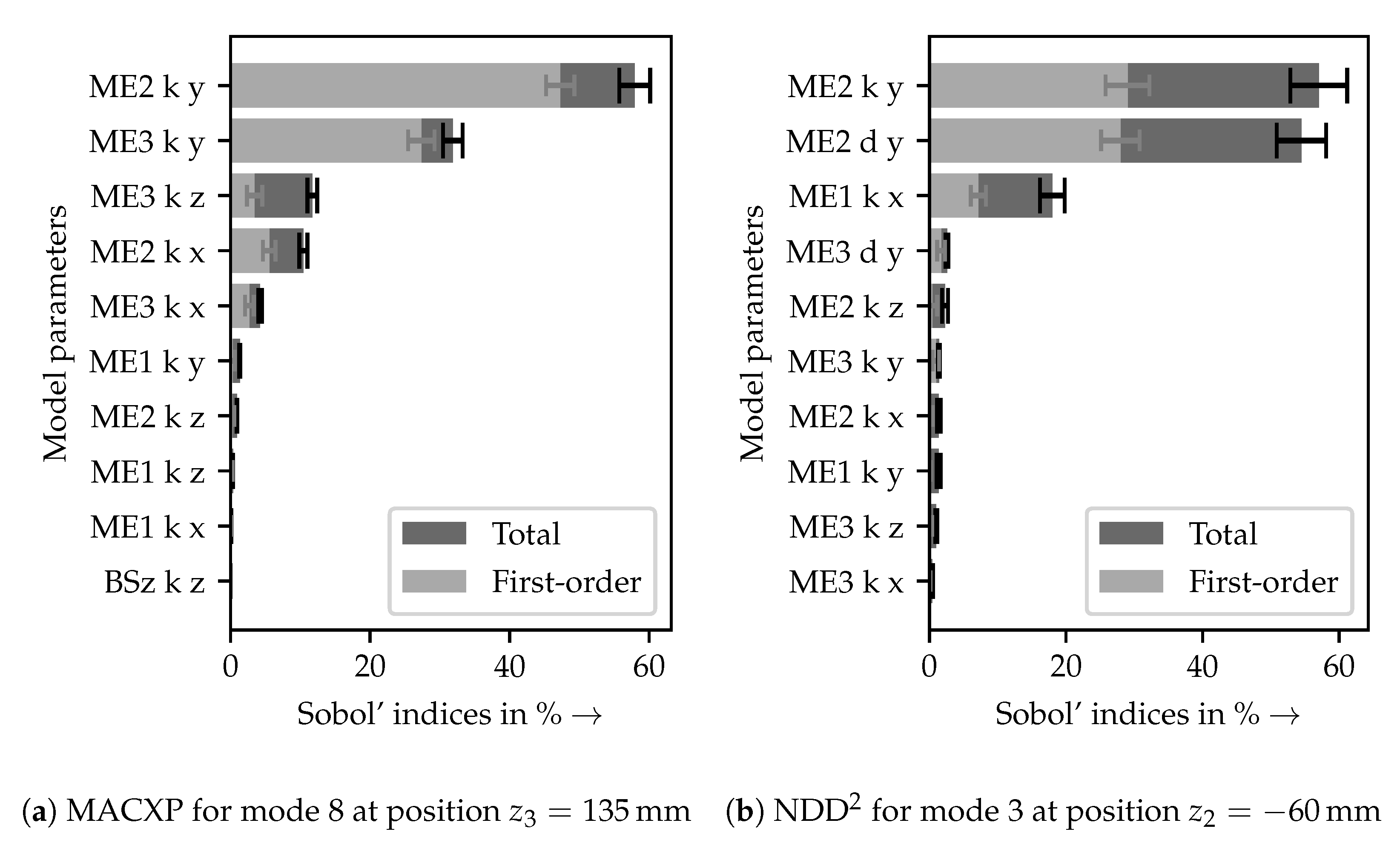
2.2. Global Sensitivity Analysis for Machine Tool Models
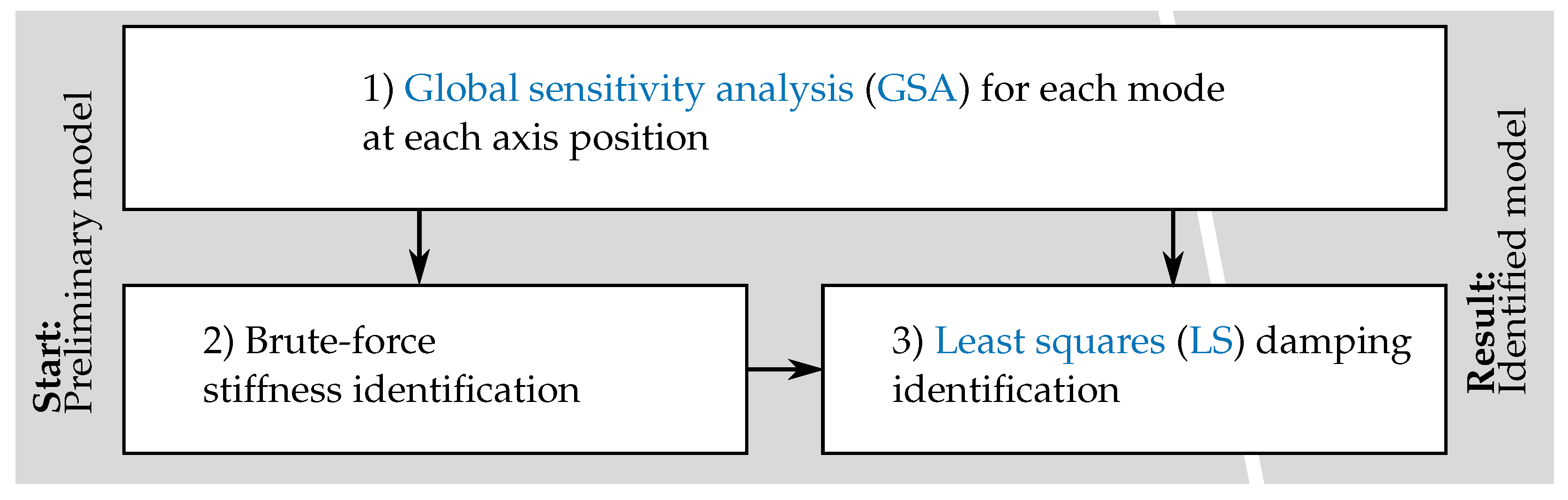
2.3. Identification Procedure
2.3.1. Partitioning of the Overall Identification Problem via GSAs
2.3.2. Stiffness Parameter Identification
2.3.3. Damping Parameter Identification
3. Sensitivity-Guided Parameter Identification
3.1. Machine Tool Structure and Model Description
- The three mounting elements (MEs) ( each)
- The fixed bearing (FB) supporting the BSD ()
- The coupling (CPL) between the motor shaft and the BSD ()
- The BSD ();
- The linear guiding system (LGS) ( used for all four shoes)
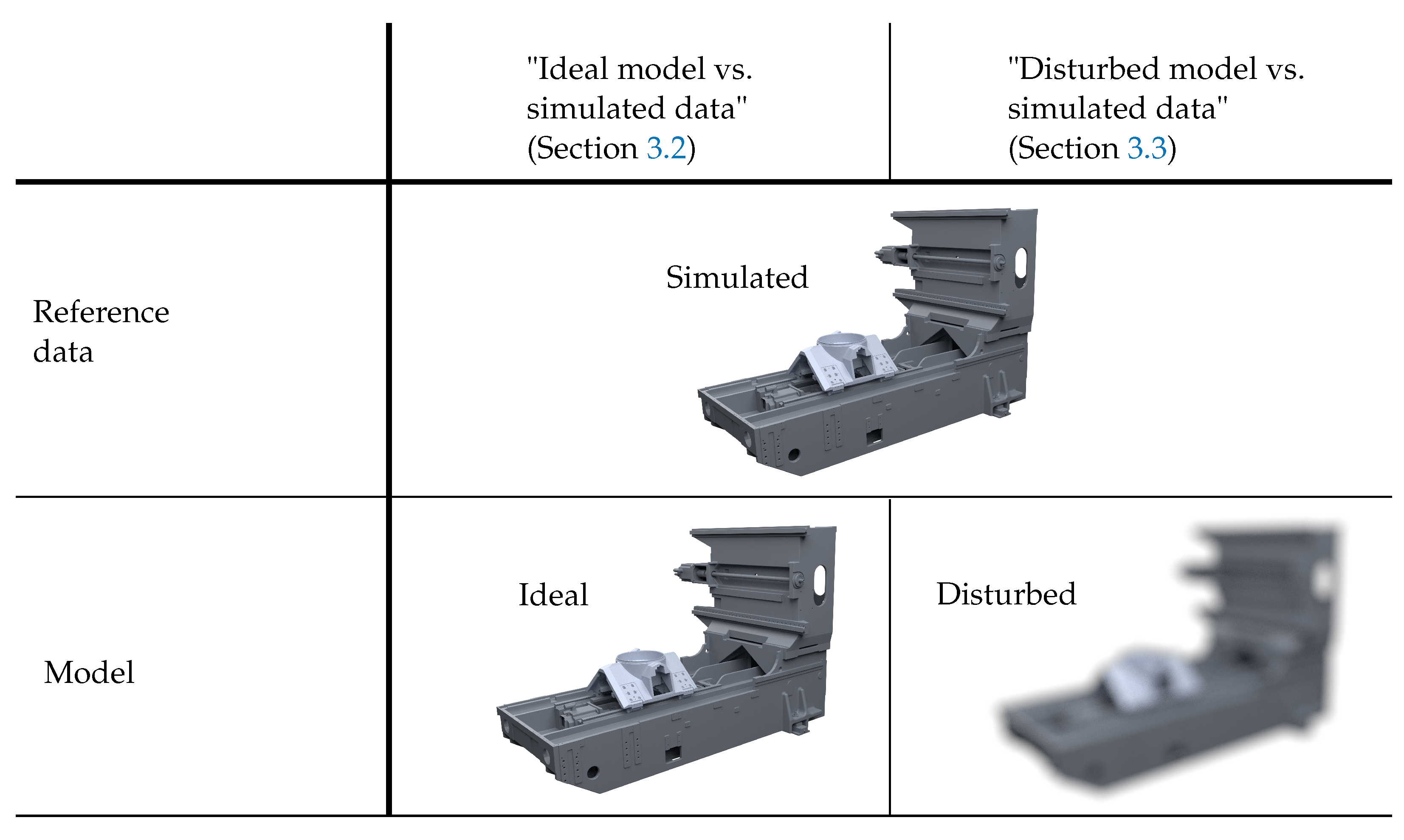
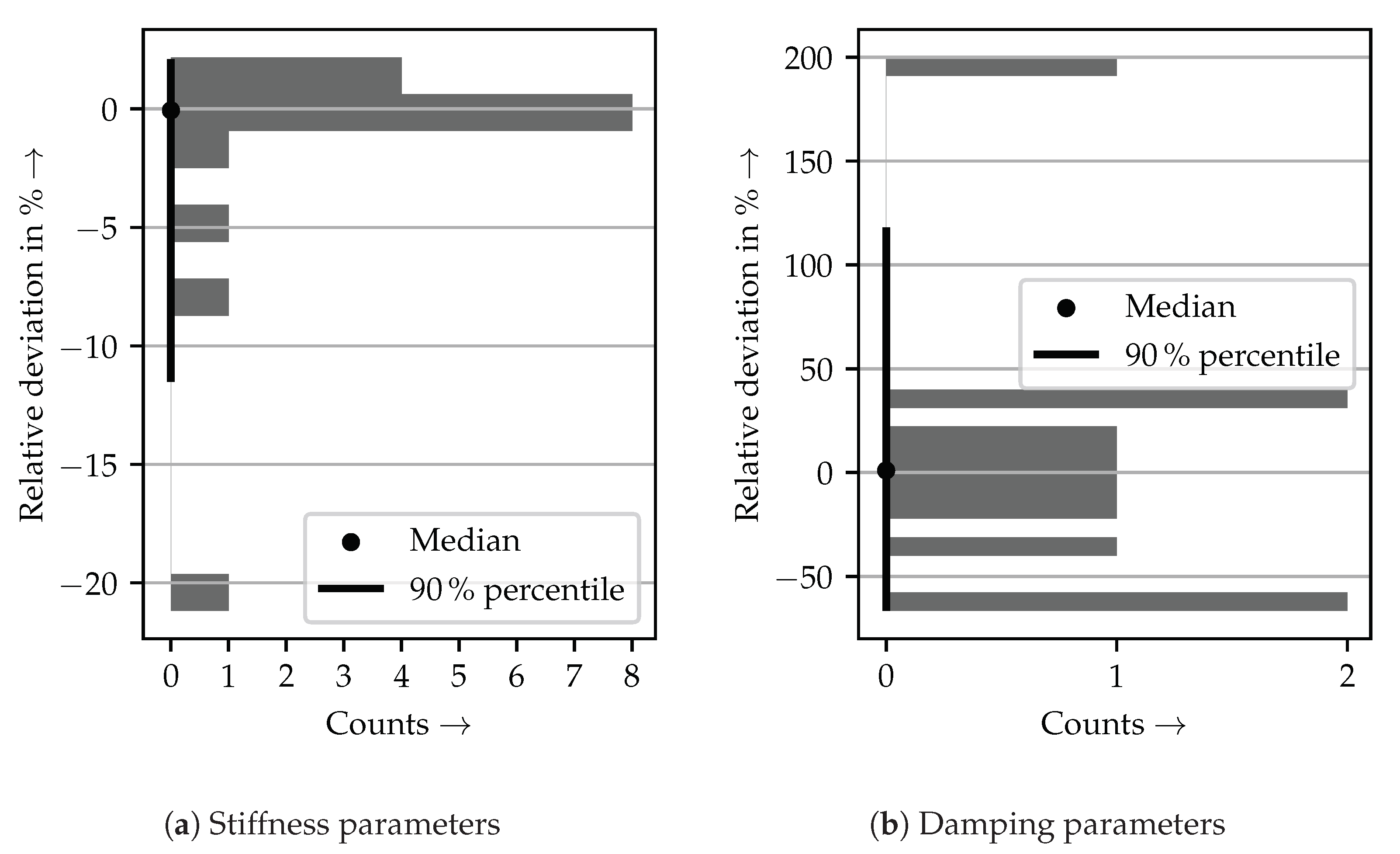
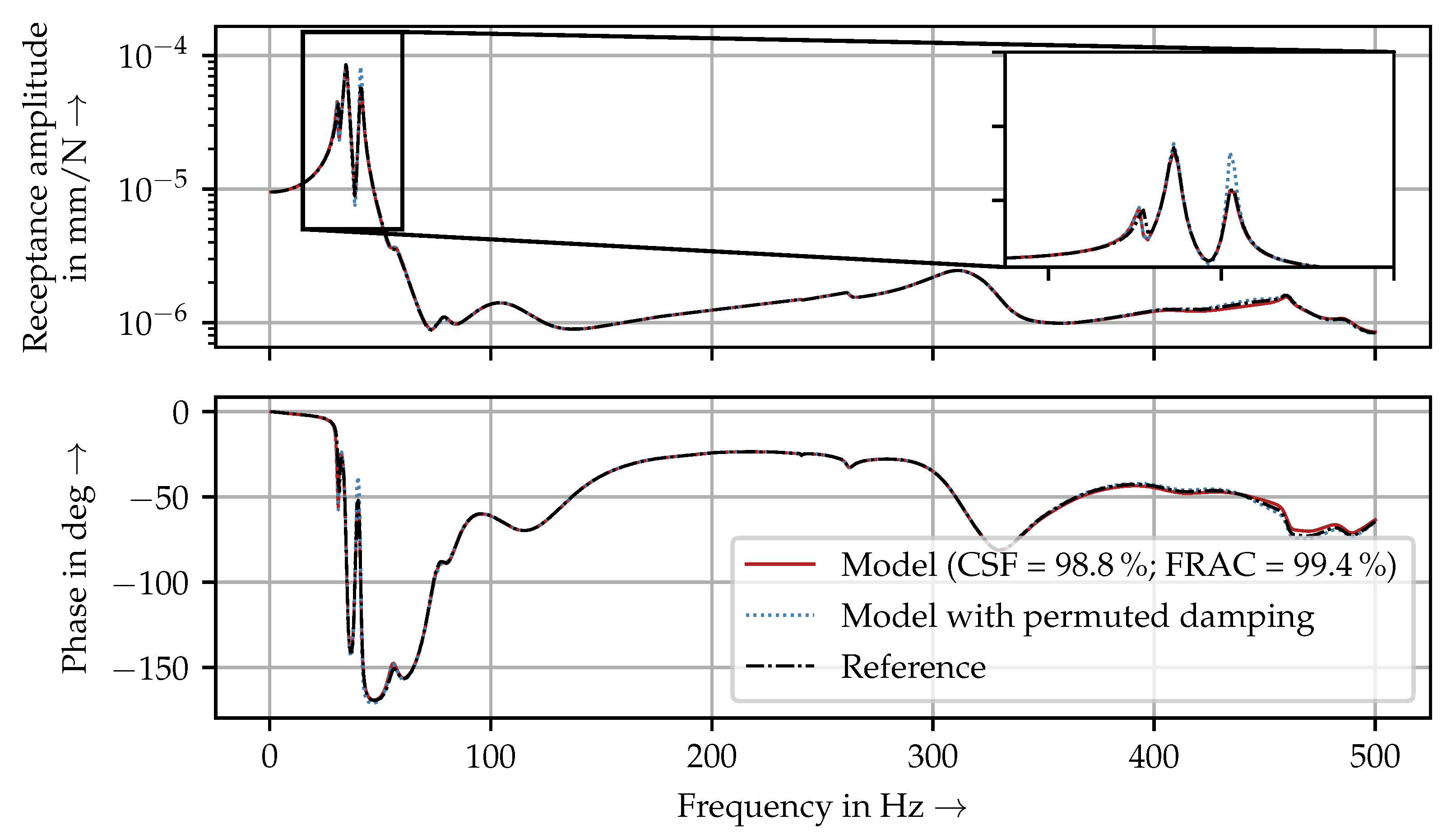
3.2. Parameter Identification of an Ideal Machine Tool Model
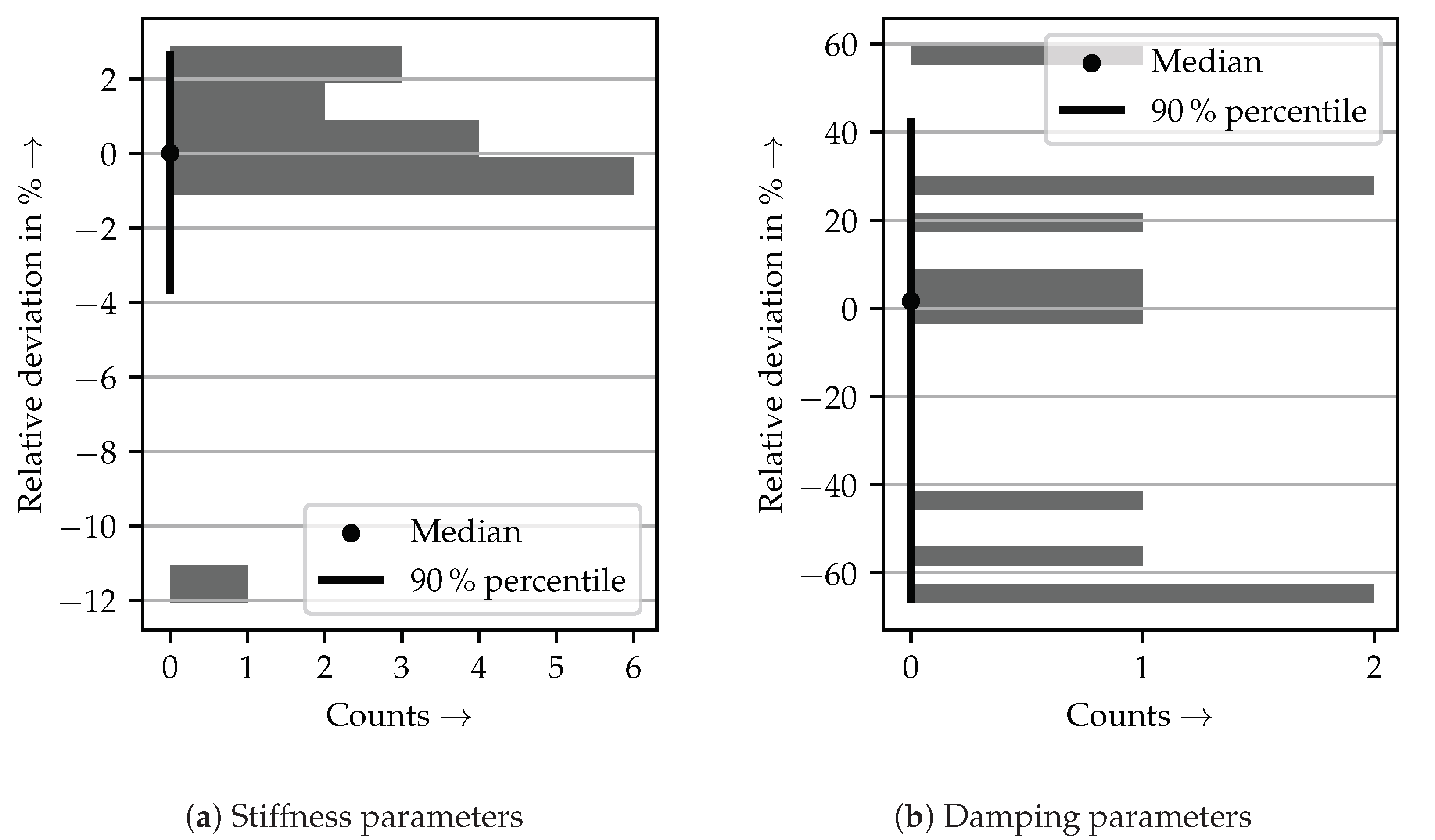
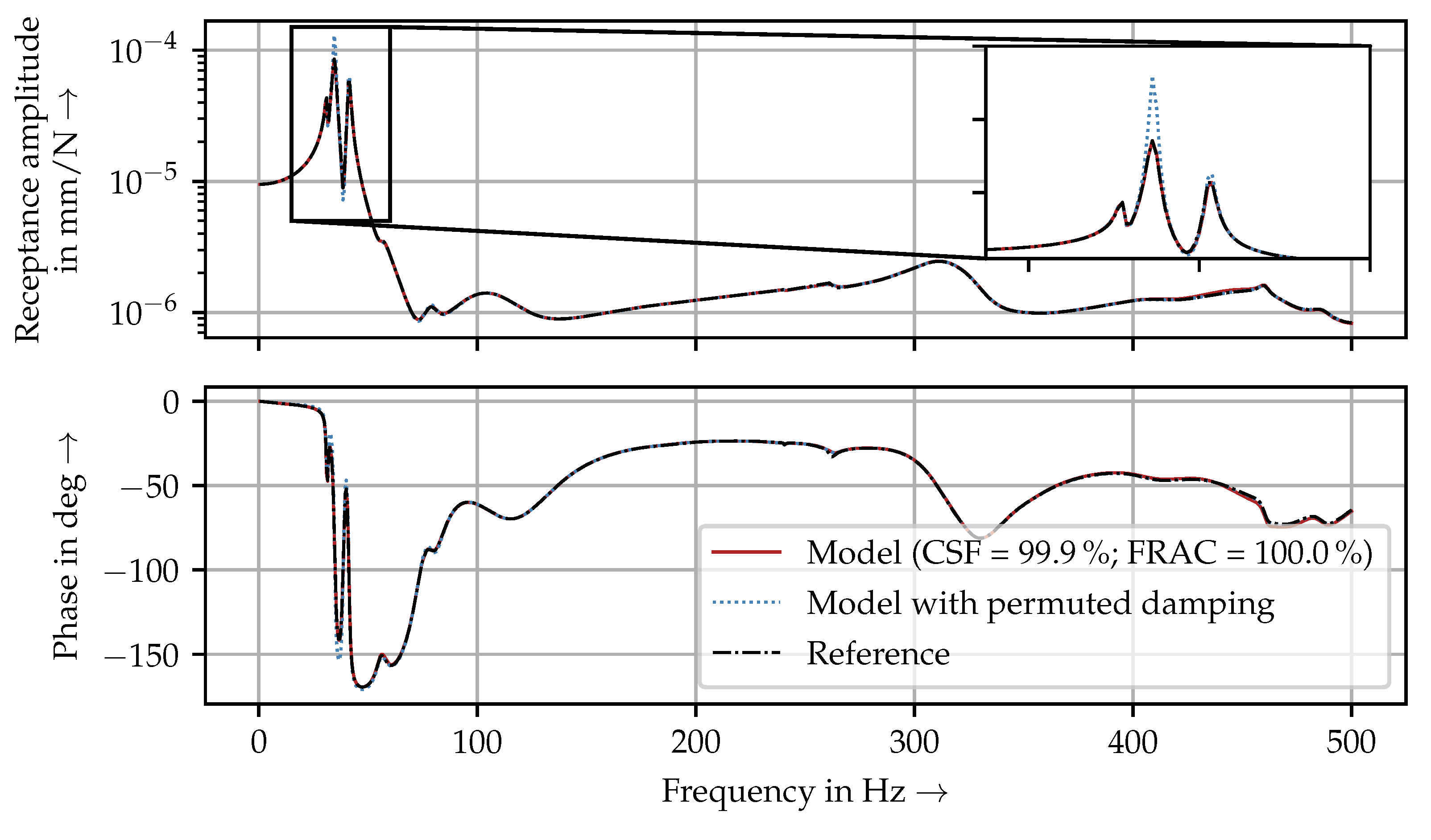
3.3. Parameter Identification of a Disturbed Machine Tool Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | analysis of variance |
| BSD | ball screw drive |
| CPL | coupling |
| CPU | central processing unit |
| CSF | cross-signature scale factor |
| DOF | degree of freedom |
| EMA | experimental modal analyses |
| FB | fixed bearing |
| FEA | finite element analysis |
| FRAC | frequency response assurance criterion |
| FRF | frequency response function |
| GA | genetic algorithm |
| GSA | global sensitivity analysis |
| HDMR | high-dimensional model representation |
| KIDZ | Artificial Intelligence and Digital Twin for Predictive Maintenance of Machine Tools |
| LB | loose bearing |
| LGS | linear guiding system |
| LS | least squares |
| MAC | modal assurance criterion |
| MACXP | extended modal assurance criterion |
| MBS | multibody simulation |
| ME | mounting element |
| MOR | model order reduction |
| NDD | natural damping difference |
| NDD | squared natural damping difference |
| NFD | natural frequency difference |
| PSO | particle swarm optimization |
| SLSQP | sequential least-squares programming |
| StMWi | Bavarian State Ministry for Economic Affairs, Energy and Technology |
| WPT | workpiece table |
References
- Isermann, R. Identifikation Dynamischer Systeme 1; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar] [CrossRef]
- Ellinger, J.; Semm, T.; Benker, M.; Kapfinger, P.; Kleinwort, R.; Zaeh, M.F. Feed Drive Condition Monitoring Using Modal Parameters. MM Sci. J. 2019, 2019, 3206–3213. [Google Scholar] [CrossRef]
- Tseng, G.W.G.; Chen, C.Q.G.; Erkorkmaz, K.; Engin, S. Digital Shadow Identification from Feed Drive Structures for Virtual Process Planning. CIRP J. Manuf. Sci. Technol. 2019, 24, 55–65. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Law, M. Position-Dependent Dynamics and Stability of Machine Tools. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2013. [Google Scholar]
- Zaeh, M.F.; Rebelein, C.; Semm, T. Predictive Simulation of Damping Effects in Machine Tools. CIRP Ann. 2019, 27, 67–77. [Google Scholar] [CrossRef]
- Iglesias, A.; Taner, T.L.; Özsahin, O.; Franco, O.; Munoa, J.; Budak, E. Alternative Experimental Methods for Machine Tool Dynamics Identification: A Review. Mech. Syst. Signal Process. 2022, 170, 108837. [Google Scholar] [CrossRef]
- Ren, W.; Chen, H. Finite Element Model Updating in Structural Dynamics by Using the Response Surface Method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
- Niehues, K. Identification of Linear Damping Models for Machine Tool Structures. Ph.D. Thesis, Technical University of Munich, München, Germany, 2015. [Google Scholar]
- Schwarz, S. Predictive Capability of Dynamic Simulations of Machine Tool Structures. Ph.D. Thesis, Technical University of Munich, München, Germany, 2015. [Google Scholar]
- Rebelein, C. Predictive Simulation of Damping Effects in Mechatronic Machine Tool Structures. Ph.D. Thesis, Technical University of Munich, München, Germany, 2019. [Google Scholar]
- Semm, T.; Spescha, D.; Ceresa, N.; Zaeh, M.F.; Wegener, K. Efficient Dynamic Machine Tool Simulation with Included Damping and Linearized Friction Effects. Procedia CIRP 2020, 93, 1442–1447. [Google Scholar] [CrossRef]
- Apprich, S.; Wulle, F.; Pott, A.; Verl, A. Online Parameter Identification for a Linear Parameter-Varying Model of Large-Scale Lightweight Machine Tool Structures with Pose-Dependent Dynamic Behavior. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 1558–1563. [Google Scholar]
- Zhou, S.; Sun, B.B. Parameter Identification and Optimization of Slide Guide Joint of CNC Machine Tools. IOP Conf. Ser. Mater. Sci. Eng. 2017, 265, 012025. [Google Scholar] [CrossRef]
- Mehrpouya, M.; Graham, E.; Park, S. Identification of Multiple Joint Dynamics Using the Inverse Receptance Coupling Method. J. Vib. Control 2015, 21, 3431–3449. [Google Scholar] [CrossRef]
- Witt, S.T. Integrierte Simulation von Maschine, Werkstück und spanendem Fertigungsprozess. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2007. [Google Scholar]
- Garitaonandia, I.; Fernandes, M.H.; Albizuri, J. Dynamic Model of a Centerless Grinding Machine Based on an Updated FE Model. Int. J. Mach. Tools Manuf. 2008, 48, 832–840. [Google Scholar] [CrossRef]
- Hernandez-Vazquez, J.; Garitaonandia, I.; Fernandes, M.H.; Albizuri, J.; Munoa, J. Comparison of Updating Strategies to Improve Finite Element Models of Multi-Axis Machine Tools. In Proceedings of the 9th International Conference on Structural Dynamics, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Hernandez-Vazquez, J.; Garitaonandia, I.; Fernandes, M.H.; Munoa, J.; Lacalle, L.N. A Consistent Procedure Using Response Surface Methodology to Identify Stiffness Properties of Connections in Machine Tools. Materials 2018, 11, 1220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ellinger, J.; Semm, T.; Zaeh, M.F. Dimensionality Reduction of High-Fidelity Machine Tool Models by Using Global Sensitivity Analysis. J. Manuf. Sci. Eng. 2022, 144, 051010:1–051010:8. [Google Scholar] [CrossRef]
- Semm, T.; Sellemond, M.; Rebelein, C.; Zaeh, M.F. Efficient Dynamic Parameter Identification Framework for Machine Tools. J. Manuf. Sci. Eng. 2020, 142, 081003. [Google Scholar] [CrossRef]
- Semm, T. Position-Flexible Modeling Approach for an Efficient Optimization of the Machine Tool Dynamics Considering Local Damping Effects. Ph.D. Thesis, Technical University of Munich, München, Germany, 2020. [Google Scholar]
- Spescha, D.; Weikert, S.; Wegener, K. Simulation in the Design of Machine Tools. In Reinventing Mechatronics; Yan, X.T., Bradley, D., Russell, D., Moore, P., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 163–177. [Google Scholar] [CrossRef]
- Vacher, P.; Jacquier, B.; Bucharles, A. Extensions of the MAC Criterion to Complex Modes. In Proceedings of the 24th International Conference on Noise and Vibration Engineering, Leuven, Belgium, 20–22 September 2010; pp. 2713–2726. [Google Scholar]
- Imamovic, N. Validation of Large Structural Dynamics Models Using Modal Test Data. Ph.D. Thesis, Imperial College of Science, Technology & Medicine, London, UK, 1998. [Google Scholar]
- Saltelli, A. Global Sensitivity Analysis: The Primer; John Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar] [CrossRef] [Green Version]
- Herman, J.; Usher, W. SALib: An Open-Source Python Library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Semm, T.; Nierlich, M.B.; Zaeh, M.F. Substructure Coupling of a Machine Tool in Arbitrary Axis Positions Considering Local Linear Damping Models. J. Manuf. Sci. Eng. 2019, 141, 071014:1–071014:8. [Google Scholar] [CrossRef]
- Heylen, W.; Lammens, S. FRAC: A Consistent Way of Comparing Frequency Response Functions. In Identification in Engineering Systems; Friswell, M.I., Mottershead, J., Eds.; Univ. of Wales: Swansea, UK, 1996; pp. 48–57. [Google Scholar]
- Haapaniemi, H.; Luukkanen, P.; Nurkkala, P.; Rostedt, J.; Saarenheimo, A. Correlation Analysis of Modal Analysis Results from a Pipeline. In Proceedings of the A Conference and Exposition on Structural Dynamics, Kissimmee, FL, USA, 3–6 February 2003. [Google Scholar]
- Zulaika, J.; Campa, J.; Lopez de Lacalle, N. An Integrated Process–Machine Approach for Designing Productive and Lightweight Milling Machines. Int. J. Mach. Tools Manuf. 2011, 51, 591–604. [Google Scholar] [CrossRef]
- Semm, T.; Rebelein, C.; Zaeh, M.F. Prediction of the Position Dependent Dynamic Behavior of a Machine Tool Considering Local Damping Effects. CIRP J. Manuf. Sci. Technol. 2019, 27, 68–77. [Google Scholar] [CrossRef]
- Kraft, D. A Software Package for Sequential Quadratic Programming; Wiss. Berichtswesen d. DFVLR: Köln, Germany, 1988. [Google Scholar]

| Node | Description |
|---|---|
| N, N | Shoe and rail nodes of the first LGS shoe |
| N, N | Shoe and rail nodes of the second LGS shoe |
| N, N | Shoe and rail nodes of the third LGS shoe |
| N, N | Shoe and rail nodes of the fourth LGS shoe |
| N, N | Nut and shaft nodes of the BSD |
| N, N | Workpiece table (WPT) nodes |
| N, N | Linear encoder bed and WPT nodes |
| N, N | Bed and shaft nodes of the x-axis brake |
| N, N | Bed and shaft nodes of the z-axis brake |
| N, N, N, N, N | Bed nodes |
| N, N, N | ME nodes |
| N, N | FB bed and shaft nodes |
| N, N | Loose bearing (LB) bed and shaft nodes |
| N, N | CPL motor and BSD shaft nodes |
| FRAC in % | CSF in % | MACXP in % | NDD in % | |
|---|---|---|---|---|
| Worst | 84.93 | 91.72 | 99.86 | 4.10 |
| 5% percentile | 86.21 | 92.78 | 99.88 | 1.99 |
| Mean | 94.92 | 97.17 | 99.97 | 0.52 |
| Median | 96.12 | 98.04 | 100.00 | 0.27 |
| FRAC in % | CSF in % | MACXP in % | NDD in % | |
|---|---|---|---|---|
| Worst | 79.17 | 88.43 | 99.86 | 5.48 |
| 5% percentile | 79.41 | 88.78 | 99.89 | 4.73 |
| Mean | 90.21 | 94.19 | 99.98 | 1.07 |
| Median | 91.63 | 95.58 | 100.00 | 0.24 |
| FRAC in % | CSF in % | MACXP in % | NDD in % | |
|---|---|---|---|---|
| Worst | 92.15 | 95.73 | 99.92 | 1.69 |
| 5% percentile | 96.70 | 97.15 | 99.96 | 1.51 |
| Mean | 99.26 | 99.49 | 99.99 | 0.40 |
| Median | 99.85 | 99.91 | 100.00 | 0.25 |
| FRAC in % | CSF in % | MACXP in % | NDD in % | |
|---|---|---|---|---|
| Worst | 97.53 | 97.36 | 88.57 | 40.65 |
| 5% percentile | 98.41 | 98.36 | 89.78 | 39.83 |
| Mean | 99.60 | 99.64 | 98.65 | 6.05 |
| Median | 99.83 | 99.91 | 99.99 | 0.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellinger, J.; Zaeh, M.F. Automated Identification of Linear Machine Tool Model Parameters Using Global Sensitivity Analysis. Machines 2022, 10, 535. https://doi.org/10.3390/machines10070535
Ellinger J, Zaeh MF. Automated Identification of Linear Machine Tool Model Parameters Using Global Sensitivity Analysis. Machines. 2022; 10(7):535. https://doi.org/10.3390/machines10070535
Chicago/Turabian StyleEllinger, Johannes, and Michael F. Zaeh. 2022. "Automated Identification of Linear Machine Tool Model Parameters Using Global Sensitivity Analysis" Machines 10, no. 7: 535. https://doi.org/10.3390/machines10070535
APA StyleEllinger, J., & Zaeh, M. F. (2022). Automated Identification of Linear Machine Tool Model Parameters Using Global Sensitivity Analysis. Machines, 10(7), 535. https://doi.org/10.3390/machines10070535






