APF-DPPO: An Automatic Driving Policy Learning Method Based on the Artificial Potential Field Method to Optimize the Reward Function
Abstract
:1. Introduction
- This work proposes a deep reinforcement learning-based self-driving policy learning method for improving the efficiency of vehicle self-driving decisions, which addresses the problem of difficulty in obtaining optimal driving policies for vehicles in complex and variable environments.
- The ideas of target attraction and obstacle rejection of the artificial potential field method are introduced into the distributed proximal policy optimization algorithm, and the APF-DPPO learning model is established to evaluate the driving behavior of the vehicle, which is beneficial to optimize the autonomous driving policy.
- In this paper, we propose a directional penalty function method combining collision penalty and yaw penalty, which transforms the range penalty of obstacles into a single direction penalty and selectively gives directional penalty by building a motion collision model of the vehicle, and this method effectively improves the efficiency of vehicle decision-making. Finally, the vehicles are trained to learn driving strategies and the resulting models are experimentally validated using TL methods.
2. Research Methods
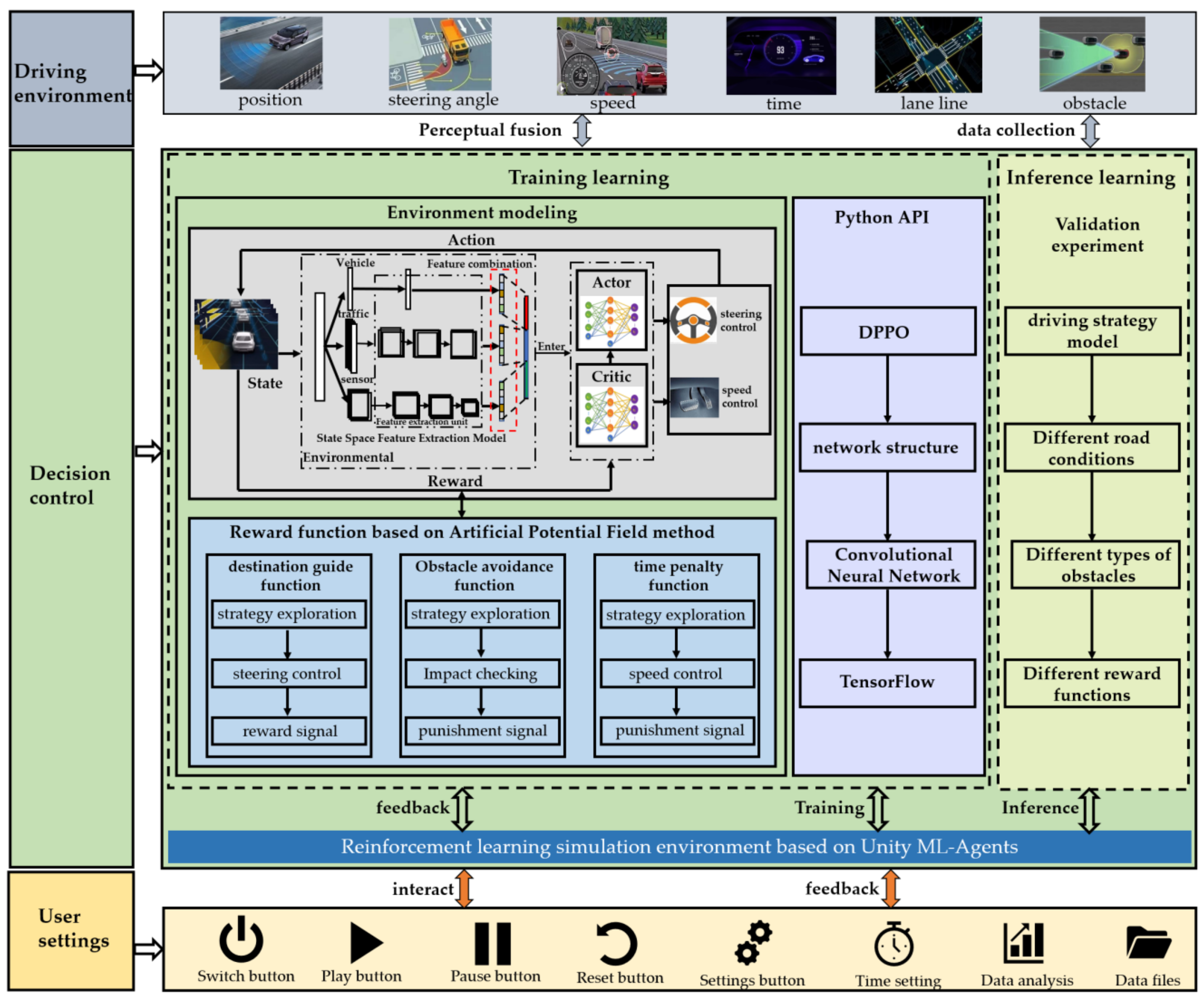
2.1. Overall Framework of the System
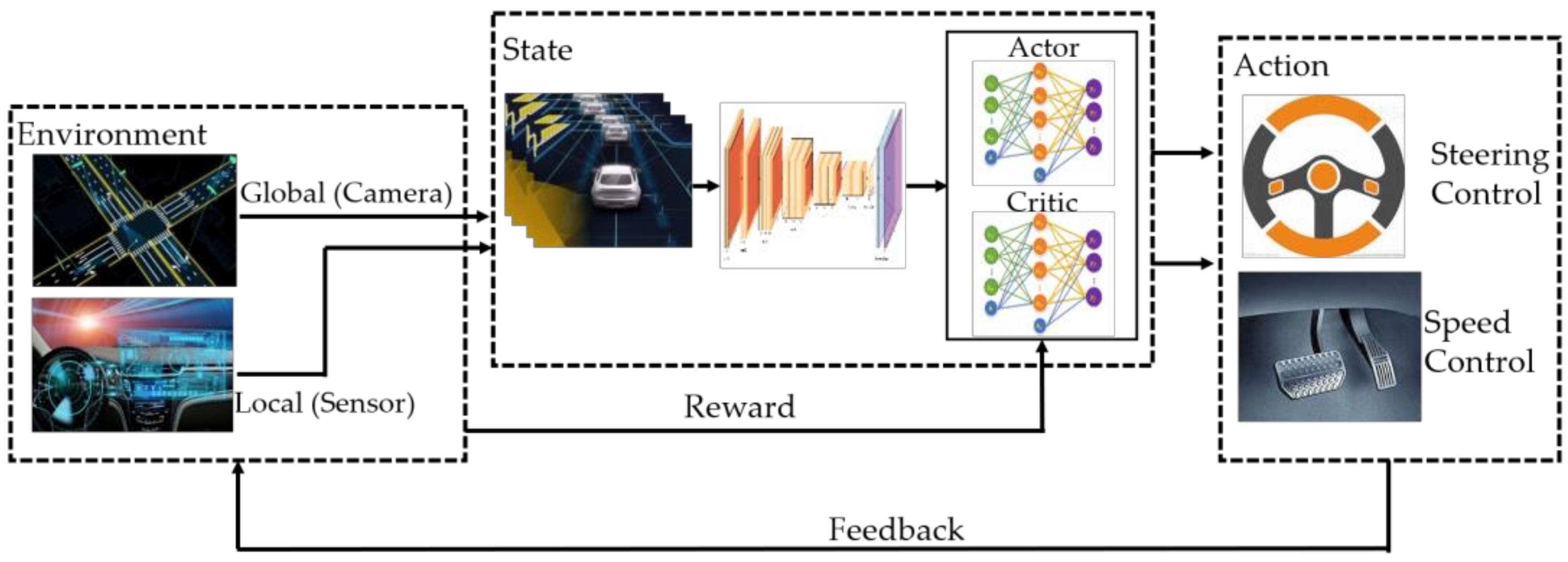
2.2. Modeling of the Automatic Driving Strategy Optimization Problem
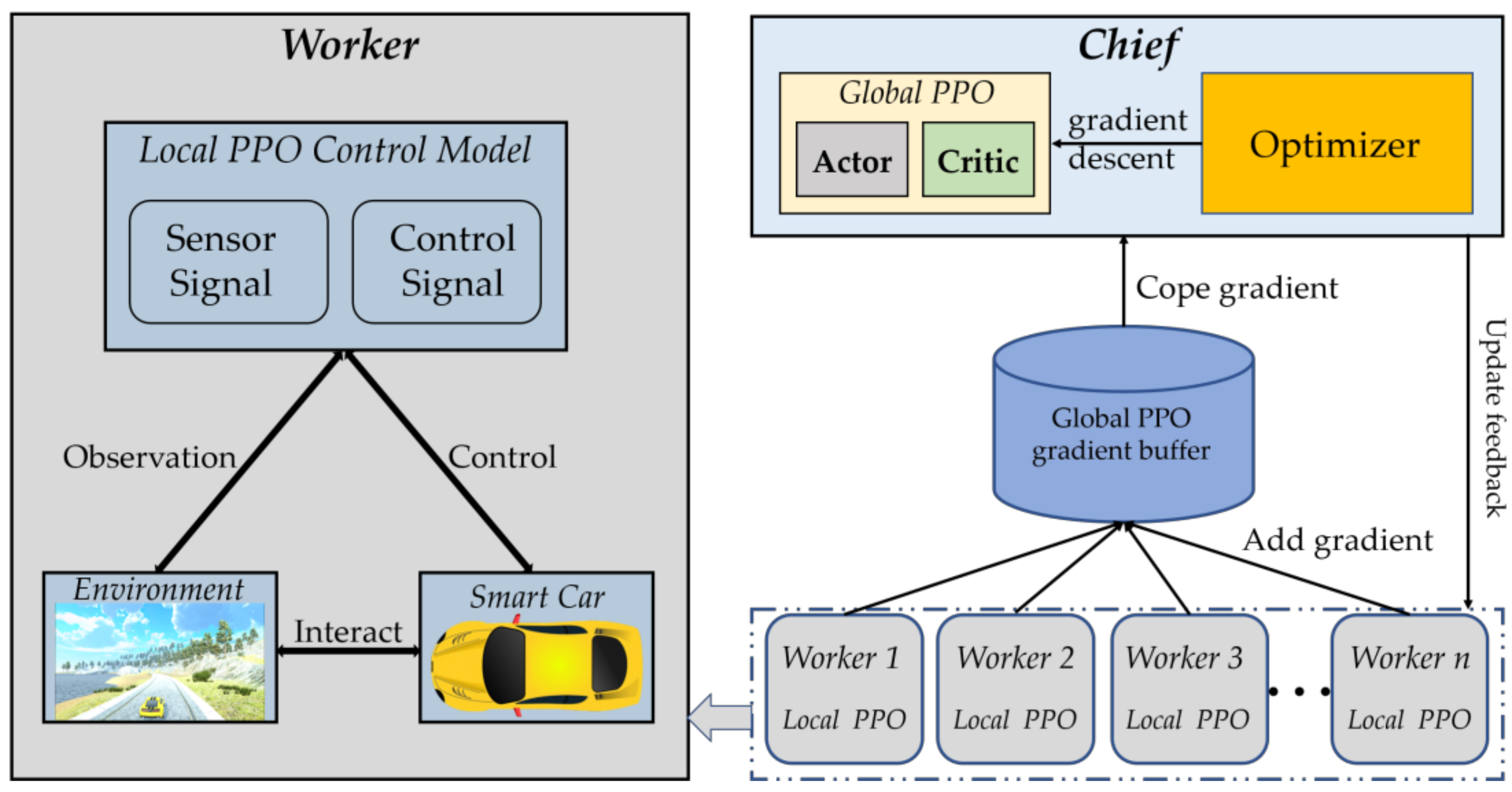
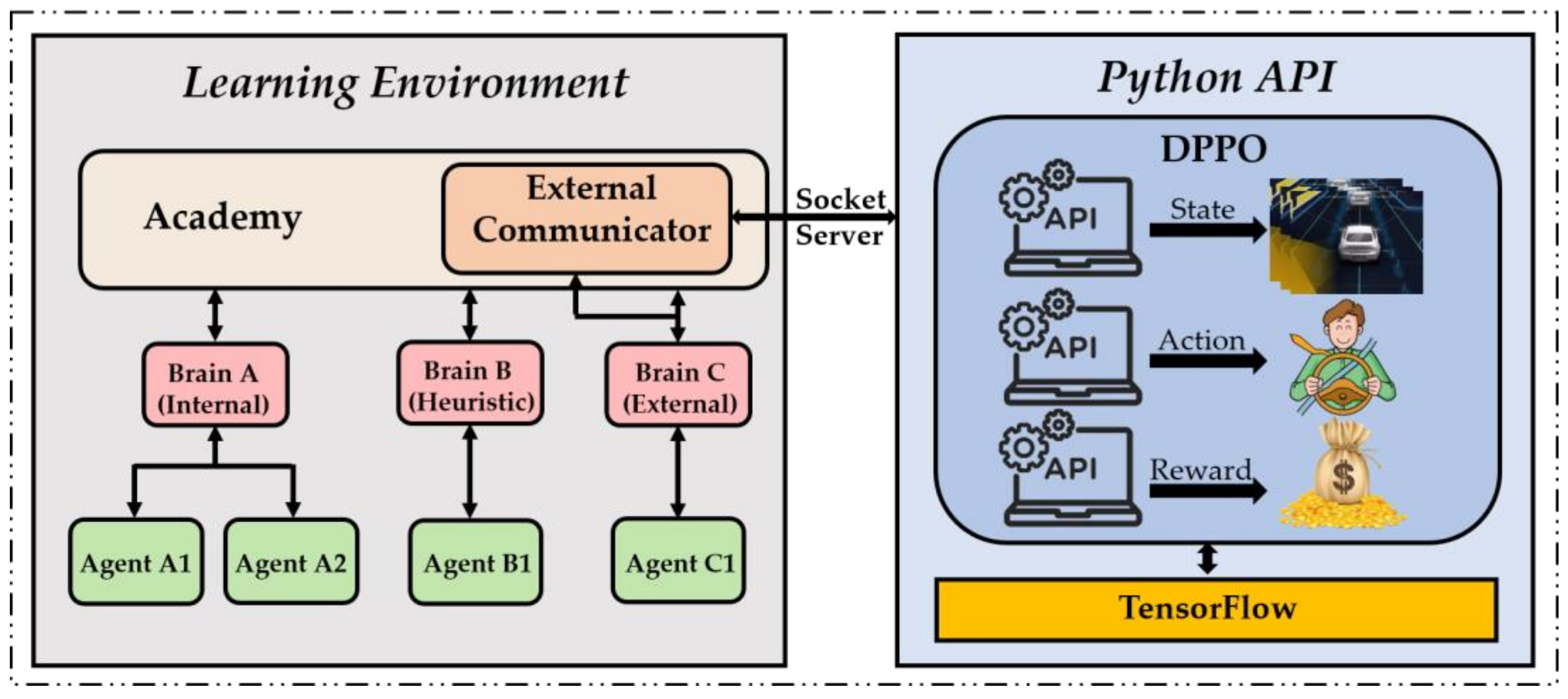
2.3. Distributed Proximal Policy Optimization Algorithm
3. Construction of an Automatic Driving Policy Learning System Based on APF-DPPO
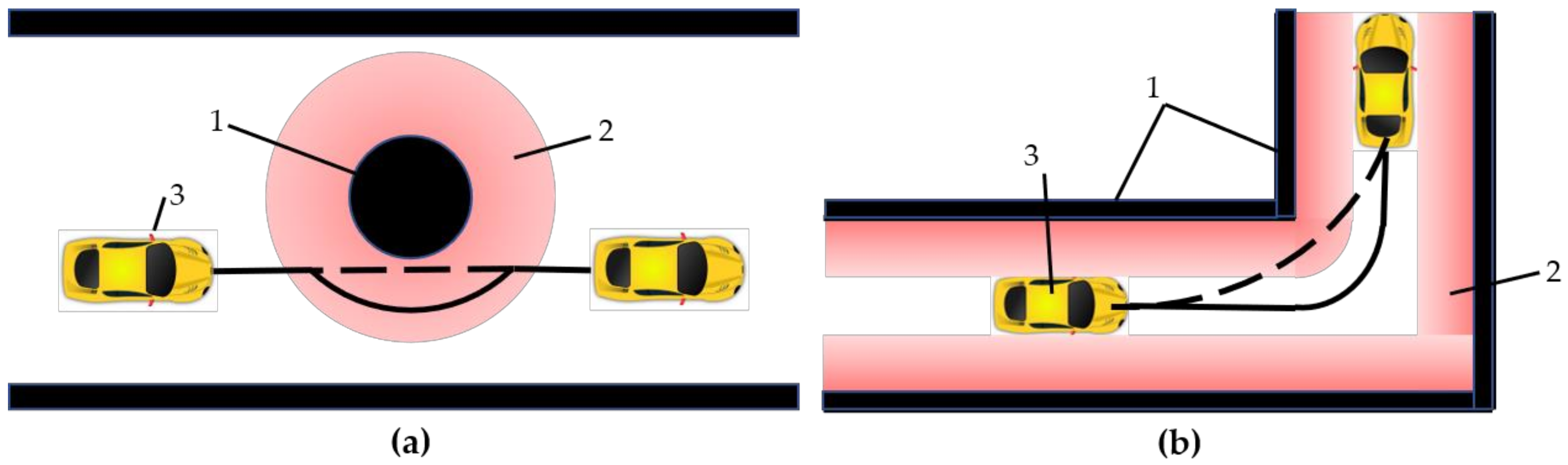
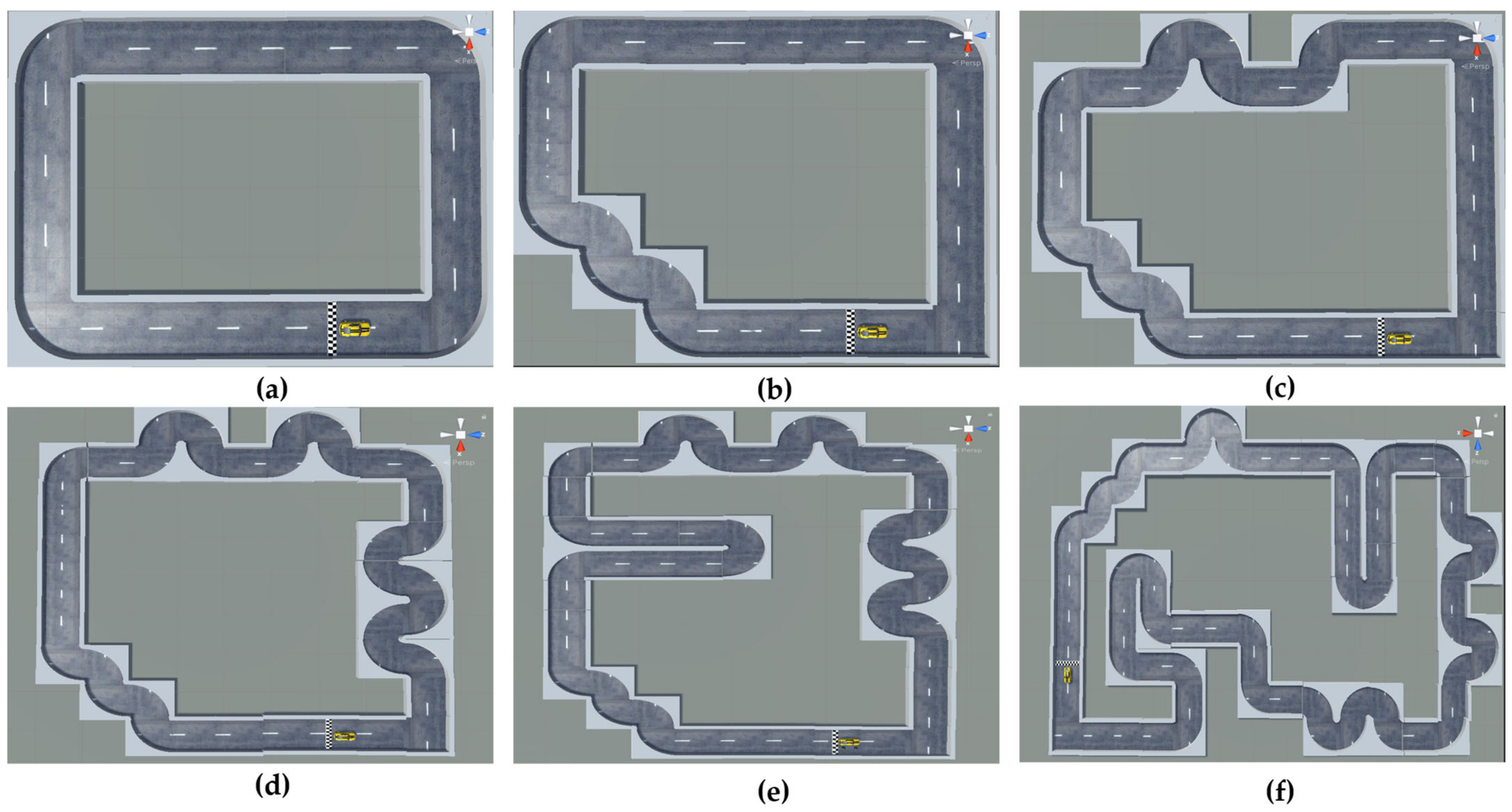
3.1. Introduction to the Simulation Environment
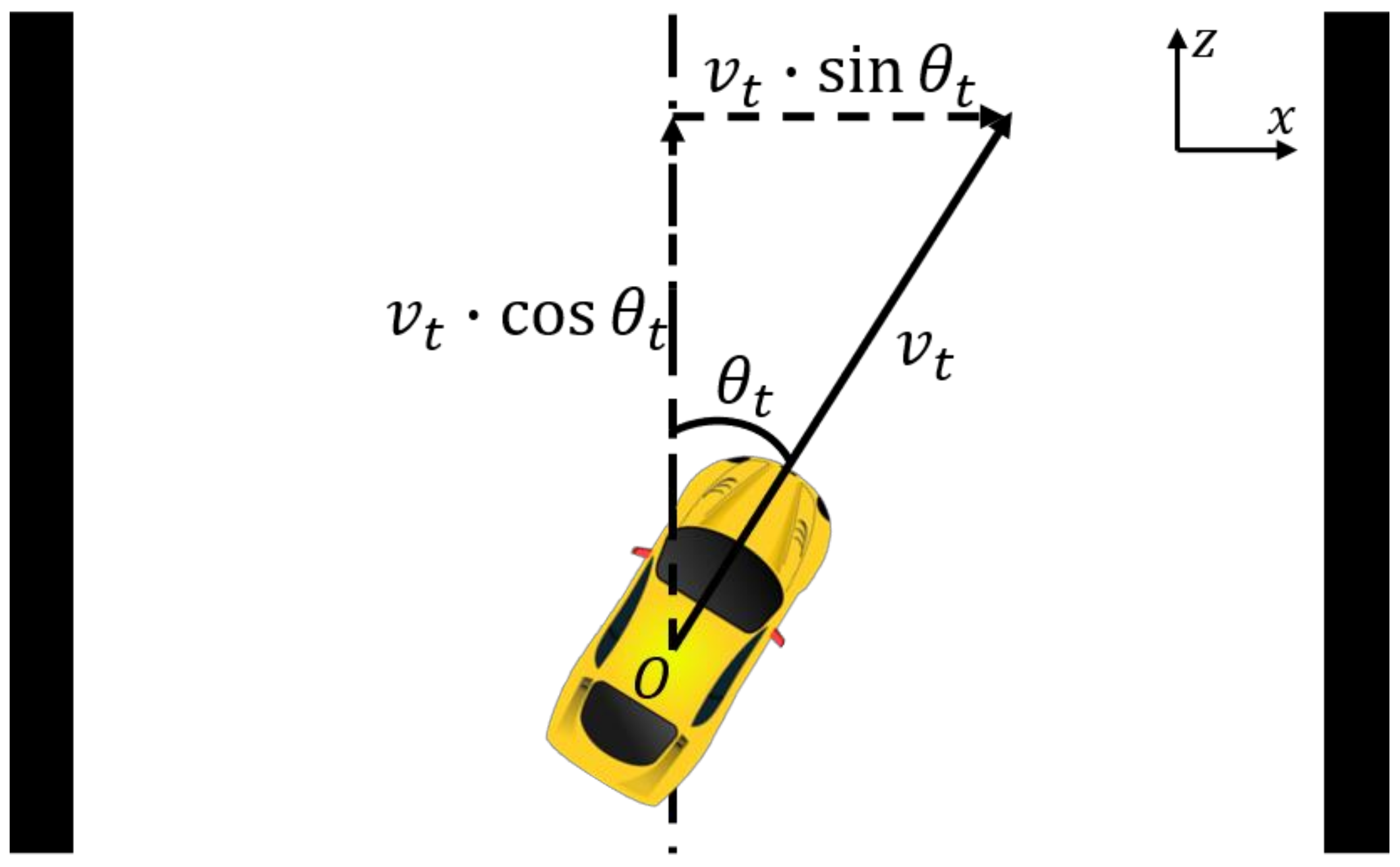
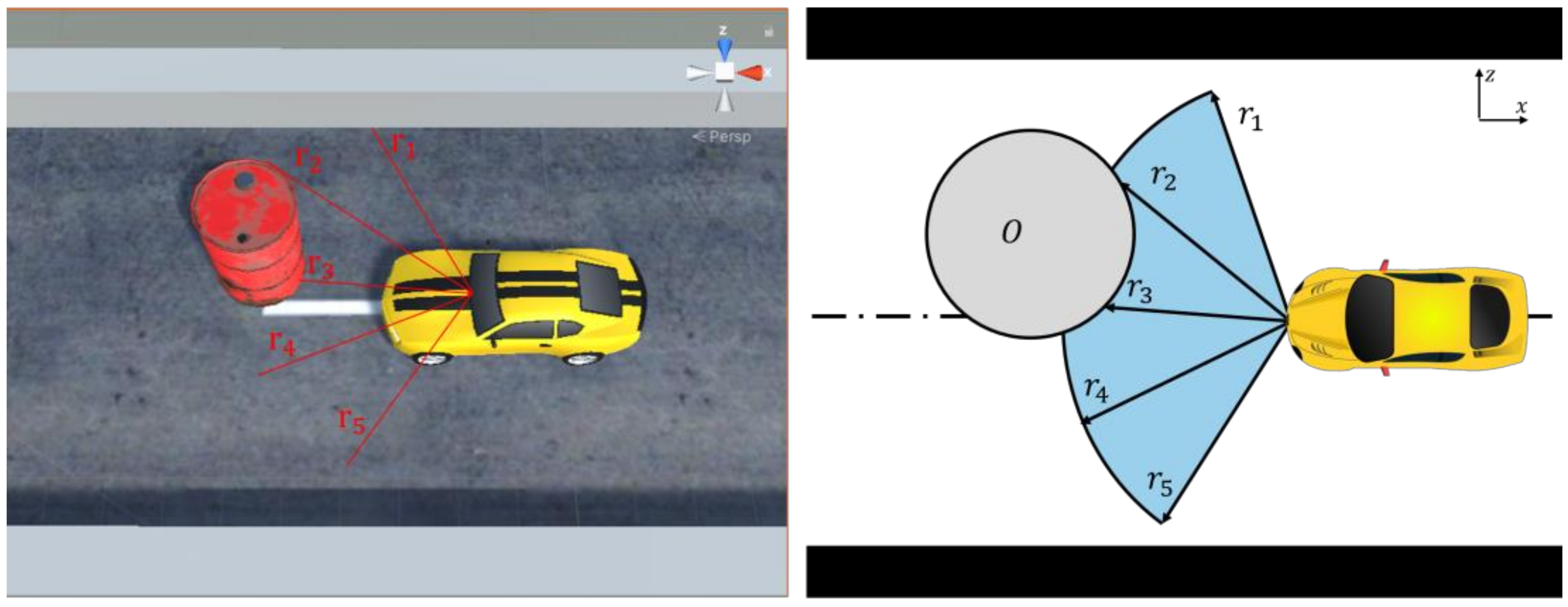
3.2. State Space
3.3. Action Space
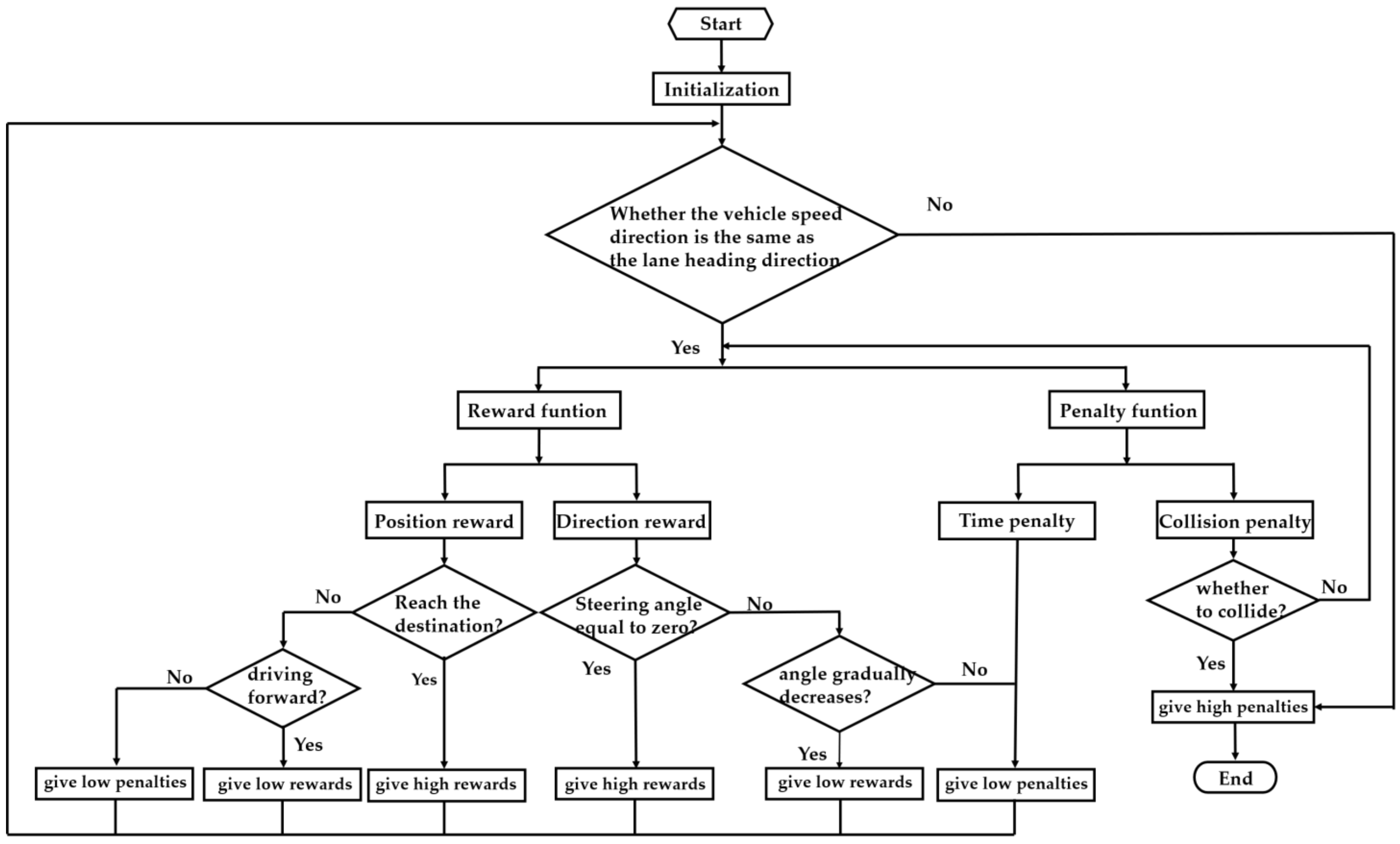
3.4. Optimizing the Reward Function Based on APF-DPPO
3.4.1. Destination Guide Function
3.4.2. Obstacle Avoidance Function Setting
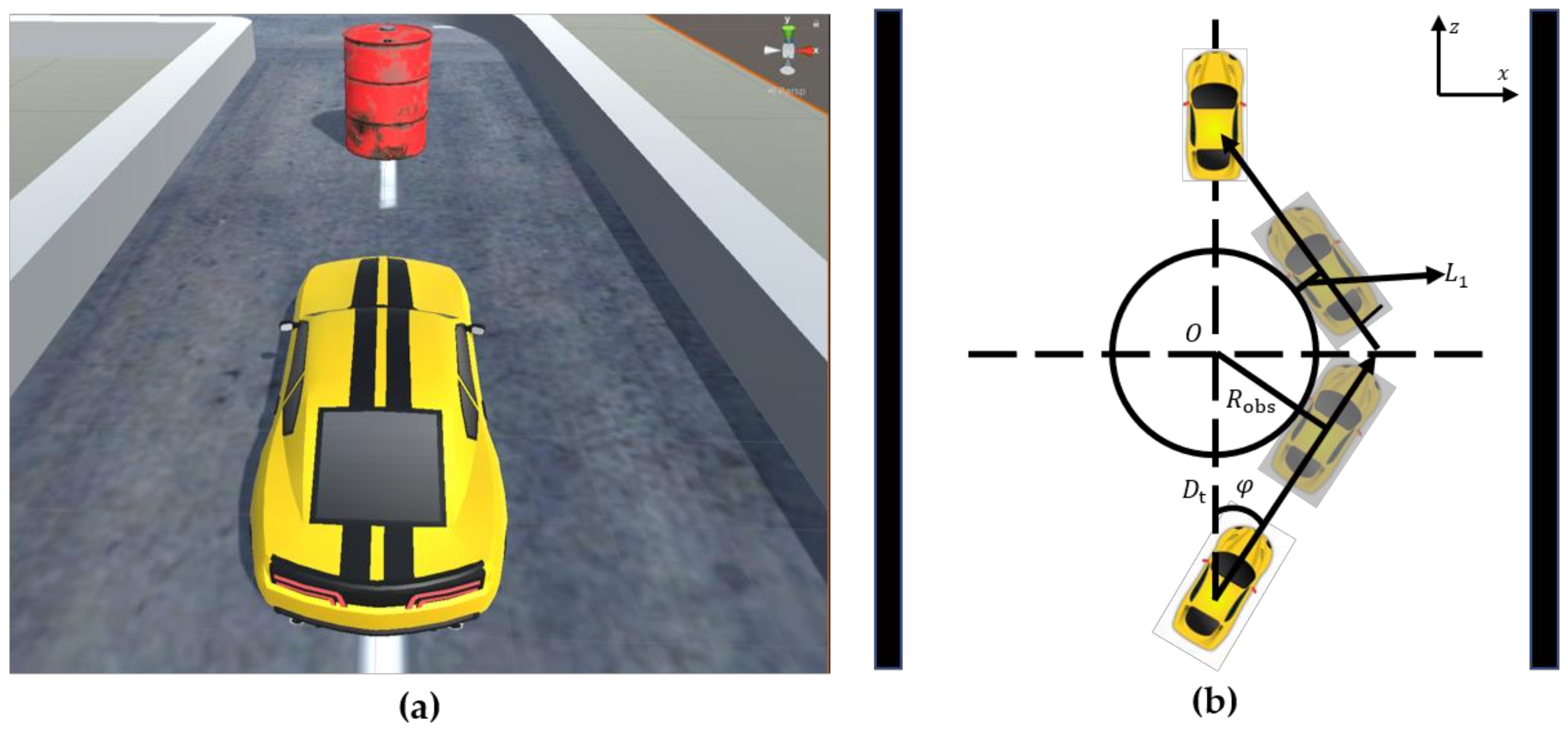
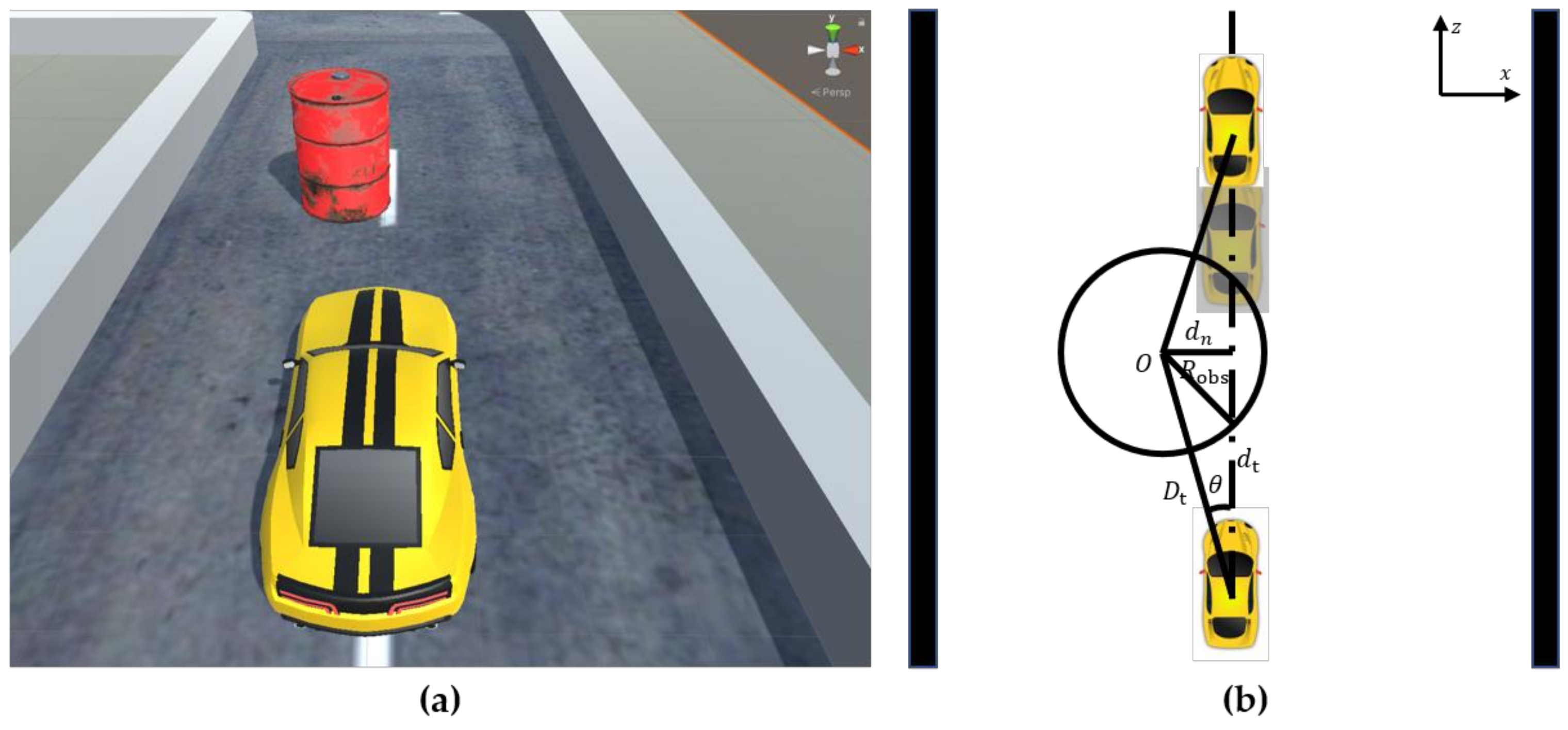
- The vehicle speed direction, obstacle position, and road centerline are collinear, as shown in Figure 8a. A schematic of the driving trajectories of obstacles and virtual vehicles is shown in Figure 8b, where is the center point of the obstacle and is the radius of the obstacle.Figure 8b shows that the vehicle safety domain angle can be obtained according to the trigonometric function relationship, as shown in Equation (14). When the steering angle of the vehicle is less than the safety domain angle , the vehicle has collided with the obstacle in the current state. At this time, the system will impose a maximum penalty on the decision-making direction and end the round. When the steering angle of the vehicle is greater than or equal to the safety domain angle value, the vehicle has collided with the obstacle. The vehicle can autonomously avoid obstacles and continue driving, and the penalty function does not work at this time.where is the distance from the center of the obstacle at the current moment to the center of the virtual vehicle; is the straight-line distance from the center of the virtual vehicle to the body surface along its horizontal axis.
- The vehicle speed direction, obstacle position, and lane centerline are not collinear, as shown in Figure 9a. A geometric schematic of the intersection of the obstacle and the vehicle’s path is shown in Figure 9b, where represents the current coordinate position of the obstacle and is the radius of the obstacle.
3.4.3. Time Penalty Function Setting
3.5. APF-DPPO Algorithm Network Training Process
| Algorithm 1. APF-DPPO algorithm for vehicle autonomous driving decision-making. |
| Input: observation information = [ , , , , , , , ] |
| Initialize |
| Initialize the store memory to capacity |
| Initialize the actor network parameters and critic network parameters |
| For episode = 1, M do |
| Reset the environment and obtain the initial state |
| For epoch t = 1, do |
| Select , , according to |
| Obtain reward and state |
| Collect , |
| Store the transition (, , , ) in |
| Update the state = |
| Compute advantage estimates using generalized advantage estimation |
| After every L steps |
| Update by a gradient method using Equation (3) |
| Update by a gradient method using Equation (6) |
| If the vehicle hits an obstacle |
| Else if the vehicle drives out of the boundary |
| Else if the vehicle travels in the opposite direction |
| Cancel this action |
| If (where is the maximum step) then |
| Finish training |
| End if |
| End for |
| End for |
4. Experiment and Evaluation
4.1. Driving Strategy Learning Program Design
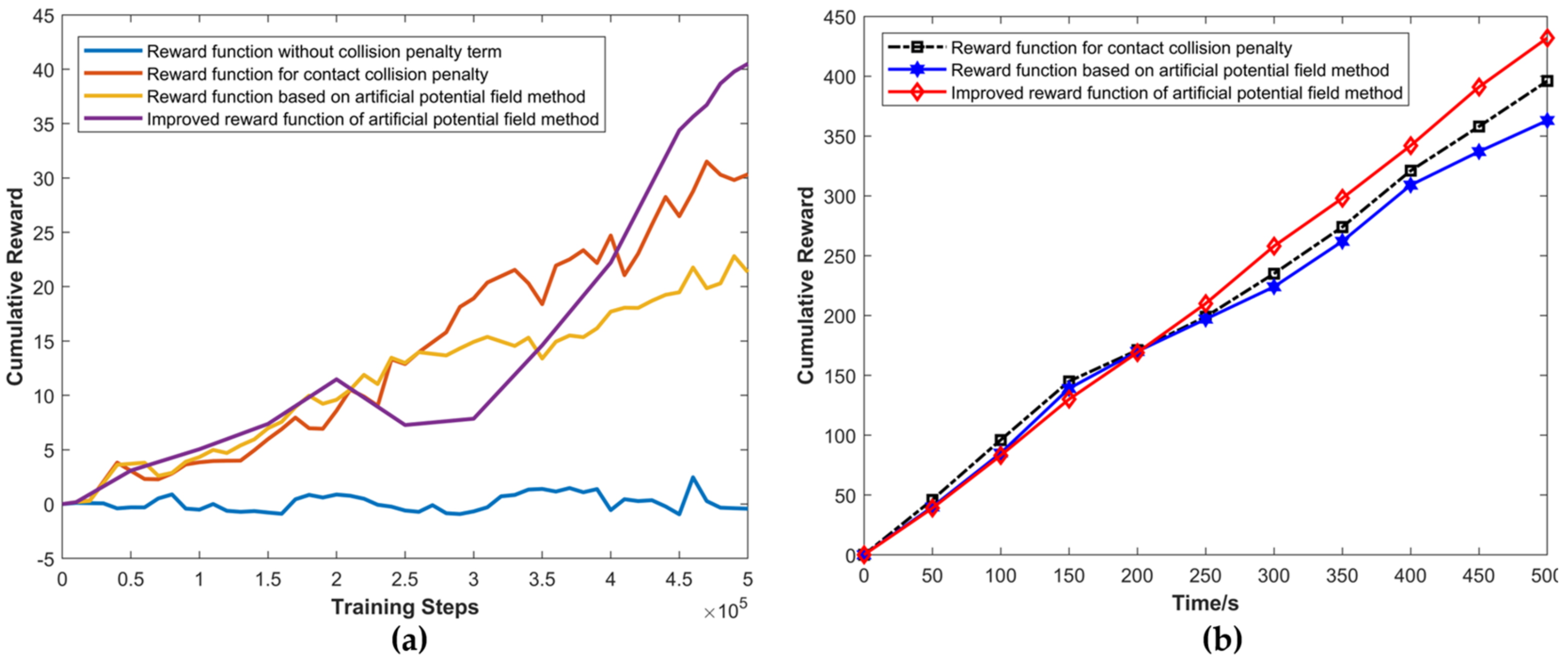
4.2. Data Analysis of Training Results
4.3. Model Validation and Result Analysis Based on Transfer Learning
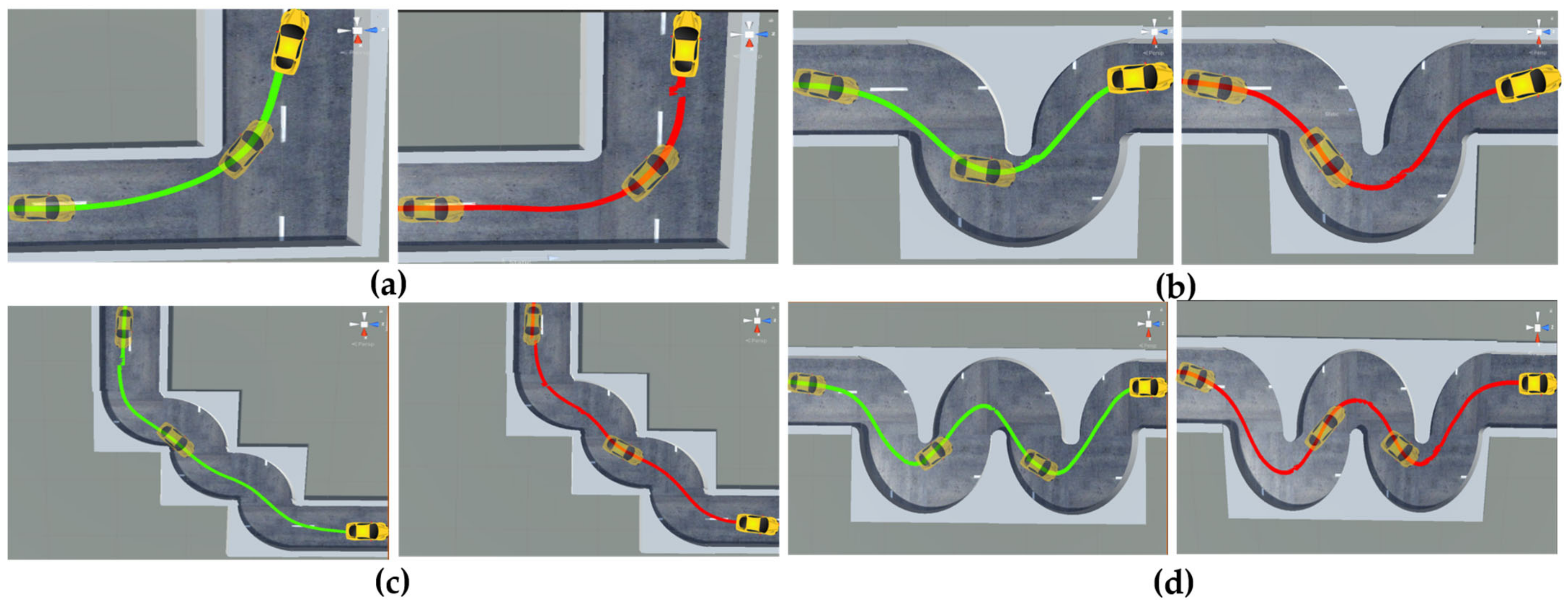
4.3.1. Generalization Performance Experiment of the Autonomous Driving Model in Different Lane Environments
4.3.2. Influence of Different Types of Obstacles on Vehicle Autonomous Driving Decisions
4.3.3. Experiments on the Decision-Making Performance of Autonomous Driving with Different Reward Functions
4.4. Decision Control Effect of Actual Vehicle Autonomous Driving
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, K.; Yan, D.; Yang, F.; Xie, J.; Liu, L.; Du, R.; Xiong, N. Conditional artificial potential field-based autonomous vehicle safety control with interference of lane changing in mixed traffic scenario. Sensors 2019, 19, 4199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, F.; Stern, R.E.; Cui, S.; Monache, M.L.D.; Bhadani, R.; Bunting, M.; Churchill, M.; Hamilton, N.; Haulcy, R.M.; Piccoli, B.; et al. Tracking vehicle trajectories and fuel rates in phantom traffic jams: Methodology and data. Transp. Res. C Emerg. Technol. 2019, 99, 82–109. [Google Scholar] [CrossRef] [Green Version]
- Bifulco, G.N.; Coppola, A.; Loizou, S.G.; Petrillo, A.; Santini, S. Combined Energy-oriented Path Following and Collision Avoidance approach for Autonomous Electric Vehicles via Nonlinear Model Predictive Control. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A survey of autonomous driving: Common practices and emerging technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Erseghe, T.; Ghiani, E.; Murroni, M.; Siano, P.; Silvestro, F. Integration of renewable energy sources, energy storage systems, and electrical vehicles with smart power distribution networks. J. Ambient Intell. Humaniz. Comput. 2013, 4, 663–671. [Google Scholar] [CrossRef]
- Borrelli, F.; Falcone, P.; Keviczky, T.; Asgari, J.; Hrovat, D. MPC-based approach to active steering for autonomous vehicle systems. Int. J. Veh. Auton. Syst. 2005, 3, 265–291. [Google Scholar] [CrossRef]
- Hoel, C.J.; Driggs-Campbell, K.; Wolff, K.; Laine, L.; Kochenderfer, M.J. Combining planning and deep reinforcement learning in tactical decision making for autonomous driving. IEEE Trans. Intell. Veh. 2020, 5, 294–305. [Google Scholar] [CrossRef] [Green Version]
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V.; et al. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 163–168. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, H. A survey of deep RL and IL for autonomous driving policy learning. IEEE Trans. Intell. Transp. Syst. 2021. [Google Scholar] [CrossRef]
- Kargar-Barzi, A.; Mahani, A. H–V scan and diagonal trajectory: Accurate and low power localization algorithms in WSNs. J. Ambient Intell. Humaniz. Comput. 2020, 11, 2871–2882. [Google Scholar] [CrossRef]
- Wei, L.; Changwu, X.; Yue, H.; Liguo, C.; Lining, S.; Guoqiang, F. Actual deviation correction based on weight improvement for 10-unit Dolph–Chebyshev array antennas. J. Ambient Intell. Humaniz. Comput. 2019, 10, 171–1726. [Google Scholar] [CrossRef]
- Fujiyoshi, H.; Hirakawa, T.; Yamashita, T. Deep learning-based image recognition for autonomous driving. IATSS Res. 2019, 43, 244–252. [Google Scholar] [CrossRef]
- Muhammad, K.; Ullah, A.; Lloret, J.; Ser, J.D.; de Albuquerque, V.H.C. Deep learning for safe autonomous driving: Current challenges and future directions. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4316–4336. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Shammah, S.; Shashua, A. Safe, multi-agent, reinforcement learning for autonomous driving. arXiv 2016, arXiv:1610.03295. [Google Scholar]
- Zhu, M.; Wang, Y.; Pu, Z.; Hu, J.; Wang, X.; Ke, R. Safe, efficient, and comfortable velocity control based on reinforcement learning for autonomous driving. Transp. Res. C Emerg. Technol. 2020, 117, 102662. [Google Scholar] [CrossRef]
- Elavarasan, D.; Vincent, P.M. A reinforced random forest model for enhanced crop yield prediction by integrating agrarian parameters. J. Ambient Intell. Humaniz. Comput. 2021, 12, 10009–10022. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, Y.; Qi, Y.; Han, Q. A control method with reinforcement learning for urban un-signalized intersection in hybrid traffic environment. Sensors 2022, 22, 779. [Google Scholar] [CrossRef]
- Leonard, J.; How, J.; Teller, S.; Berger, M.; Campbell, S.; Fiore, G.; Fletcher, L.; Frazzoli, E.; Huang, A.; Karaman, S.; et al. A perception-driven autonomous urban vehicle. J. Field Robot. 2008, 25, 727–774. [Google Scholar] [CrossRef] [Green Version]
- Montemerlo, M.; Becker, J.; Bhat, S.; Dahlkamp, H.; Dolgov, D.; Ettinger, S.; Haehnel, D.; Hilden, T.; Hoffmann, G.; Huhnke, B.; et al. Junior: The stanford entry in the urban challenge. J. Field Robot. 2008, 25, 569–597. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.J.; Lee, M.J.; Hwang, K.H.; Ha, Y.G. End-to-end deep learning-based autonomous driving control for high-speed environment. J. Supercomput. 2022, 78, 1961–1982. [Google Scholar] [CrossRef]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. DeepDriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2722–2730. [Google Scholar]
- Bojarski, M.; Testa, D.D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L.D.; Monfort, M.; Muller, U.; Zhang, J.; et al. End to end learning for self-driving cars. arXiv. 2016, arXiv:1604.07316. [Google Scholar]
- Talaat, F.M.; Gamel, S.A. RL based hyper-parameters optimization algorithm (ROA) for convolutional neural network. J. Ambient Intell. Humaniz. Comput. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.A.; Yogamani, S.; Perez, P. Deep reinforcement learning for autonomous driving: A survey. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4909–4926. [Google Scholar] [CrossRef]
- Jazayeri, F.; Shahidinejad, A.; Ghobaei-Arani, M. Autonomous computation offloading and auto-scaling the in the mobile fog computing: A deep reinforcement learning-based approach. J. Ambient Intell. Humaniz. Comput. 2021, 12, 8265–8284. [Google Scholar] [CrossRef]
- Xia, W.; Li, H.; Li, B. A control strategy of autonomous vehicles based on deep reinforcement learning. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016; pp. 198–201. [Google Scholar]
- Chae, H.; Kang, C.M.; Kim, B.; Kim, J.; Chung, C.C.; Choi, J.W. Autonomous braking system via deep reinforcement learning. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Jaritz, M.; de Charette, R.; Toromanoff, M.; Perot, E.; Nashashibi, F. End-to-end race driving with deep reinforcement learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–26 May 2018; pp. 2070–2075. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal. Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Zhu, L.; Li, J.; Zou, X.; Tang, Y. Collision-free path planning for a guava-harvesting robot based on recurrent deep reinforcement learning. Comput. Electron. Agric. 2021, 188, 106350. [Google Scholar] [CrossRef]
- Cao, X.; Yan, H.; Huang, Z.; Ai, S.; Xu, Y.; Fu, R.; Zou, X. A Multi-Objective Particle Swarm Optimization for Trajectory Planning of Fruit Picking Manipulator. Agronomy 2021, 11, 2286. [Google Scholar] [CrossRef]
- Grewal, N.S.; Rattan, M.; Patterh, M.S. A non-uniform circular antenna array failure correction using firefly algorithm. Wirel. Pers. Commun. 2017, 97, 845–858. [Google Scholar] [CrossRef]
- Li, G.; Yang, Y.; Li, S.; Qu, X.; Lyu, N.; Li, S.E. Decision making of autonomous vehicles in lane change scenarios: Deep reinforcement learning approaches with risk awareness. Transp. Res. C Emerg. Technol. 2022, 134, 103452. [Google Scholar] [CrossRef]
- Lin, G.; Tang, Y.; Zou, X.; Xiong, J.; Li, J. Guava Detection and Pose Estimation Using a Low-Cost RGB-D Sensor in the Field. Sensors 2019, 19, 428. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Yang, Z.; Wu, F.; Zou, X.; Lin, J.; Cao, Y.; Duan, J. YOLO-Banana: A Lightweight Neural Network for Rapid Detection of Banana Bunches and Stalks in the Natural Environment. Agronomy 2022, 12, 391. [Google Scholar] [CrossRef]
- Wang, H.; Lin, Y.; Xu, X.; Chen, Z.; Wu, Z.; Tang, Y. A Study on Long–Close Distance Coordination Control Strategy for Litchi Picking. Agronomy 2022, 12, 1520. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, R.; Lin, Y.; Li, C.; Chen, S.; Yuan, Z.; Chen, S.; Zou, X. Plant Disease Recognition Model Based on Improved YOLOv5. Agronomy 2022, 12, 365. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, Z.; Huang, Z.; Nong, Y.; Li, L. Visual measurement of dam concrete cracks based on U-net and improved thinning algorithm. J. Exp. Mech. 2022, 37, 209–220. [Google Scholar] [CrossRef]
- Jayavadivel, R.; Prabaharan, P. Investigation on automated surveillance monitoring for human identification and recognition using face and iris biometric. J. Ambient Intell. Humaniz. Comput. 2021, 12, 10197–10208. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, M.; Chen, Z.; Wu, C.; Chen, B.; Li, C.; Li, L. Seismic Performance Evaluation of Recycled aggregate Concrete-filled Steel tubular Columns with field strain detected via a novel mark-free vision method. Structures 2022, 37, 426–441. [Google Scholar] [CrossRef]
- Parameswari, C.; Siva Ranjani, S. Prediction of atherosclerosis pathology in retinal fundal images with machine learning approaches. J. Ambient Intell. Humaniz. Comput. 2021, 12, 6701–6711. [Google Scholar] [CrossRef]
- Kochenderfer, M.J. Decision Making Under Uncertainty: Theory and Application; The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Heess, N.; Dhruva, T.; Sriram, S.; Lemmon, J.; Merel, J.; Wayne, G.; Tassa, Y.; Erez, T.; Wang, Z.; Eslami, S.M.A.; et al. Emergence of locomotion behaviours in rich environments. arXiv 2017, arXiv:1707.02286. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Juliani, A.; Berges, V.-P.; Teng, E.; Cohen, A.; Harper, J.; Elion, C.; Goy, C.; Gao, Y.; Henry, H.; Mattar, M.; et al. Unity: A general platform for intelligent agents. arXiv 2018, arXiv:1809.02627. [Google Scholar]





| Observed Variable | Symbol | Description |
|---|---|---|
| Position Variable | Virtual vehicle spatial location | |
| Lane line spatial location | ||
| Obstacle space location | ||
| Vehicle Variable | Virtual vehicle driving speed | |
| Virtual vehicle driving time | ||
| Virtual vehicle steering angle | ||
| Distance Variable | Distance between the obstacle and the virtual vehicle | |
| Distance from vehicle to destination |
| Way to Control | Description | Ranges |
|---|---|---|
| Speed Control | no operation) | [0,1] |
| for no operation) | [0,1] | |
| Steering Control | to turn right) | [−1,1] |
| Parameter | Value |
|---|---|
| Batch Size | 1024 |
| Buffer Size | 10,240 |
| Learning Rate | 3.0 × 10−4 |
| Beta β | 5.0 × 10−3 |
| Epsilon ε | 0.2 |
| Lambda λ | 0.95 |
| Gamma γ | 0.99 |
| Num Epoch | 3 |
| Num Layers | 2 |
| Hidden Units | 1 28 |
| Max Steps | 5.0 × 105 |
| Lane Type | Lane Length/cm | Driving Time/s | Average Reward Value | Pass Rate/% |
|---|---|---|---|---|
| Easy lane | 20 | 131 | 19.6 | 100 |
| Easier lane | 25 | 148 | 24.2 | 100 |
| General lane | 30 | 189 | 28.2 | 100 |
| Difficult lane | 40 | 236 | 37.8 | 100 |
| More difficult lane | 50 | 313 | 47.2 | 100 |
| Particularly difficult lanes | 70 | 445 | 66.8 | 100 |
| Obstacle Type | Vehicle Driving Situation | Completion Rate/% | |
|---|---|---|---|
| Number of Completions | Number of Failures | ||
| Generate punitive feedback No punitive feedback | 77 74 | 3 6 | 96.3 92.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Zhang, P.; Li, C.; Zhou, Y.; Wang, H.; Zou, X. APF-DPPO: An Automatic Driving Policy Learning Method Based on the Artificial Potential Field Method to Optimize the Reward Function. Machines 2022, 10, 533. https://doi.org/10.3390/machines10070533
Lin J, Zhang P, Li C, Zhou Y, Wang H, Zou X. APF-DPPO: An Automatic Driving Policy Learning Method Based on the Artificial Potential Field Method to Optimize the Reward Function. Machines. 2022; 10(7):533. https://doi.org/10.3390/machines10070533
Chicago/Turabian StyleLin, Junqiang, Po Zhang, Chengen Li, Yipeng Zhou, Hongjun Wang, and Xiangjun Zou. 2022. "APF-DPPO: An Automatic Driving Policy Learning Method Based on the Artificial Potential Field Method to Optimize the Reward Function" Machines 10, no. 7: 533. https://doi.org/10.3390/machines10070533
APA StyleLin, J., Zhang, P., Li, C., Zhou, Y., Wang, H., & Zou, X. (2022). APF-DPPO: An Automatic Driving Policy Learning Method Based on the Artificial Potential Field Method to Optimize the Reward Function. Machines, 10(7), 533. https://doi.org/10.3390/machines10070533







