Dynamic Lane Tracking Control of the Commercial Vehicle Based on RMPC Algorithm Considering the State of Preceding Vehicle
Abstract
:1. Introduction
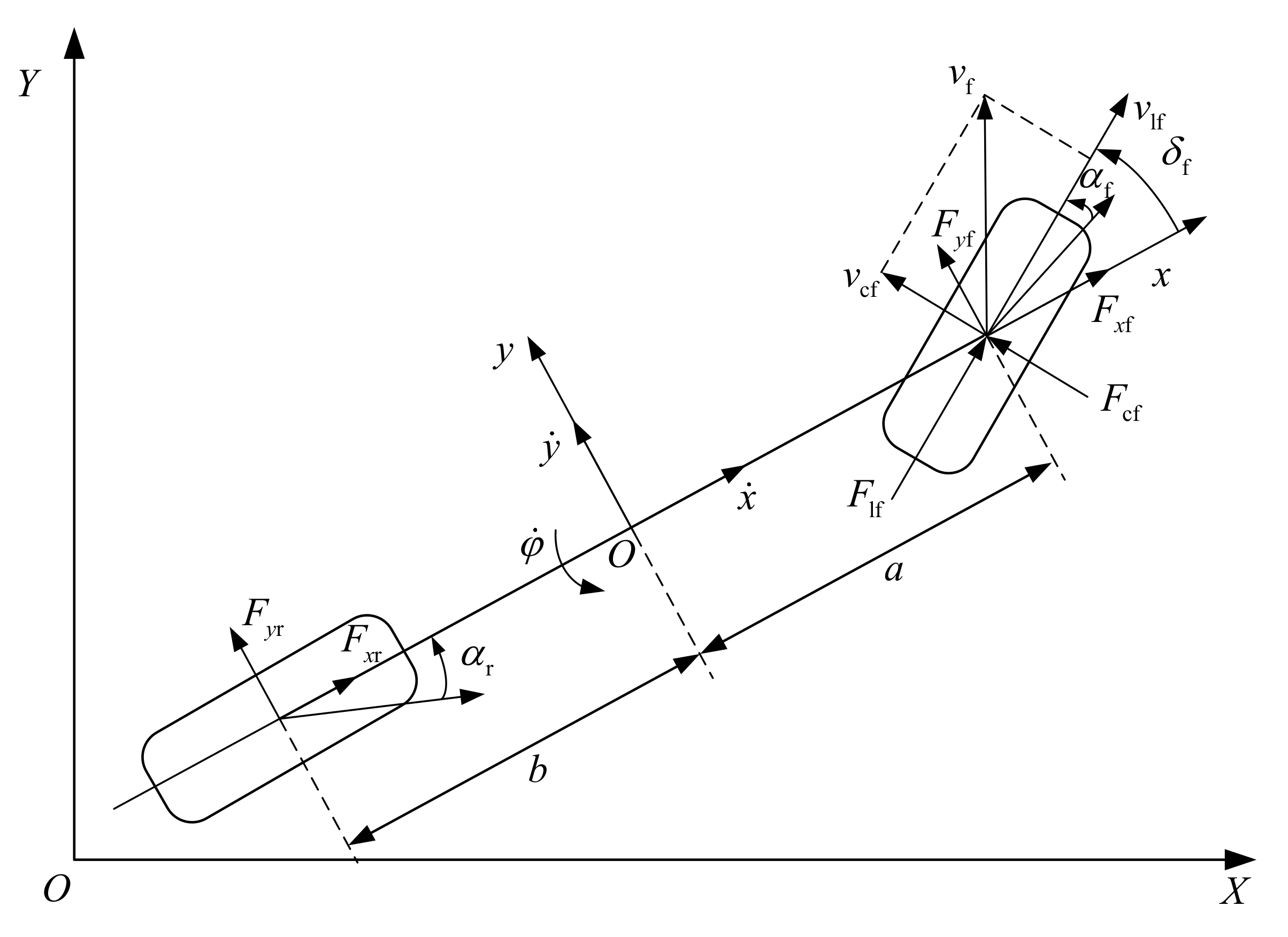
2. Vehicle Dynamics Model
3. Dynamic Lane Tracking Control System
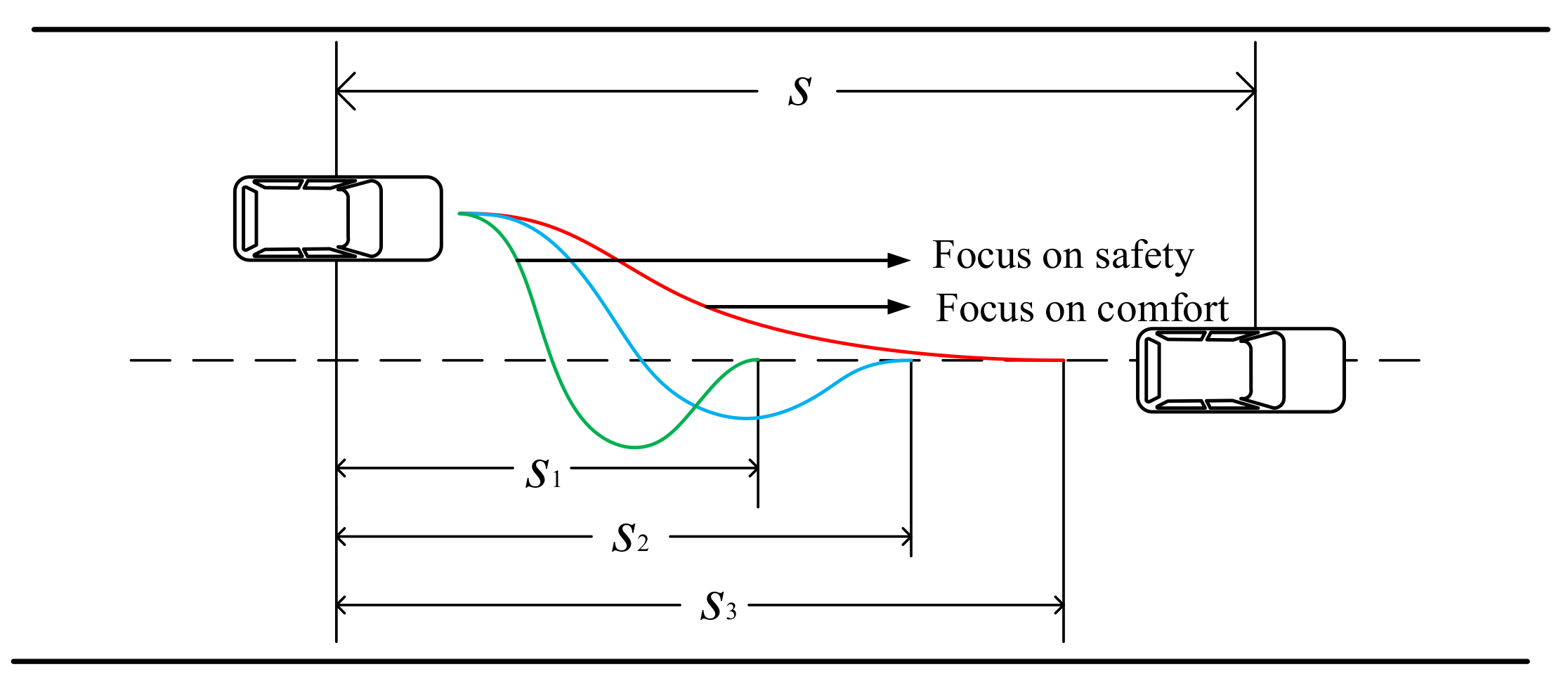
3.1. Dynamic Lane Tracking Control Strategy
3.2. Design of LMI-Based RMPC Controller
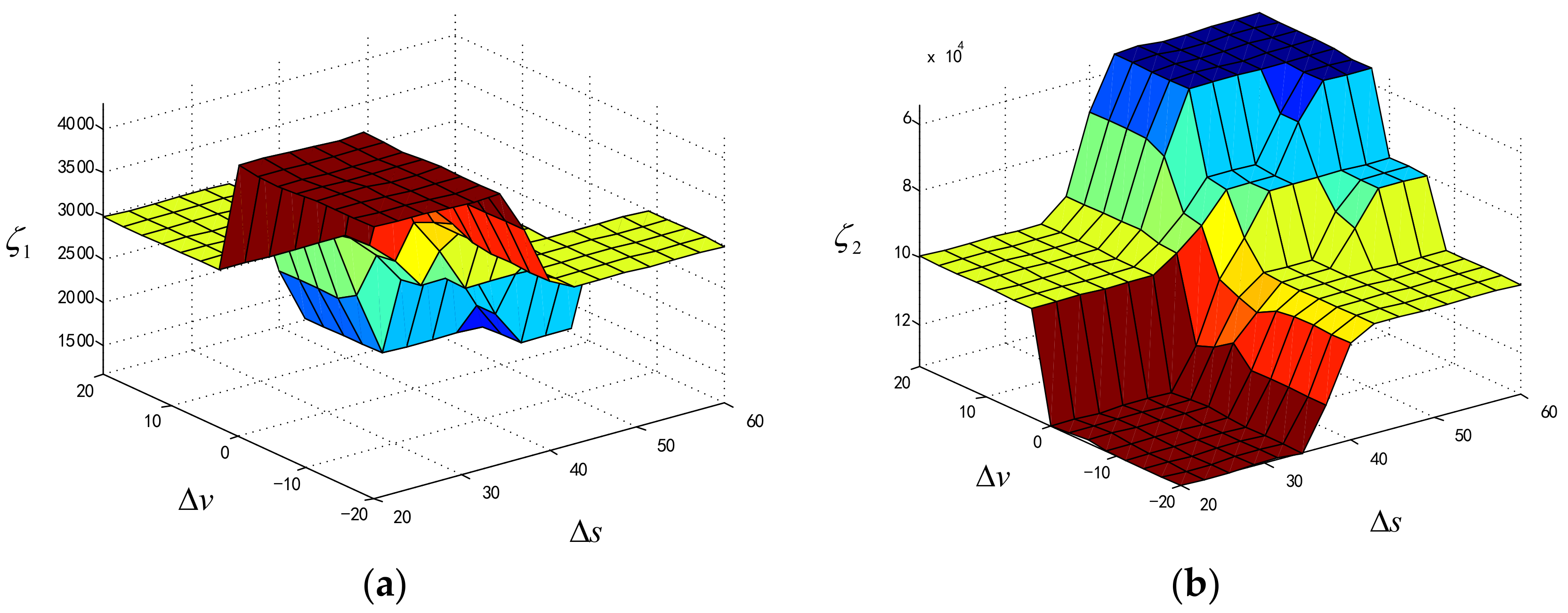
3.3. Design of the Variable Weight Coefficient Matrix of RMPC Based on Fuzzy Theory
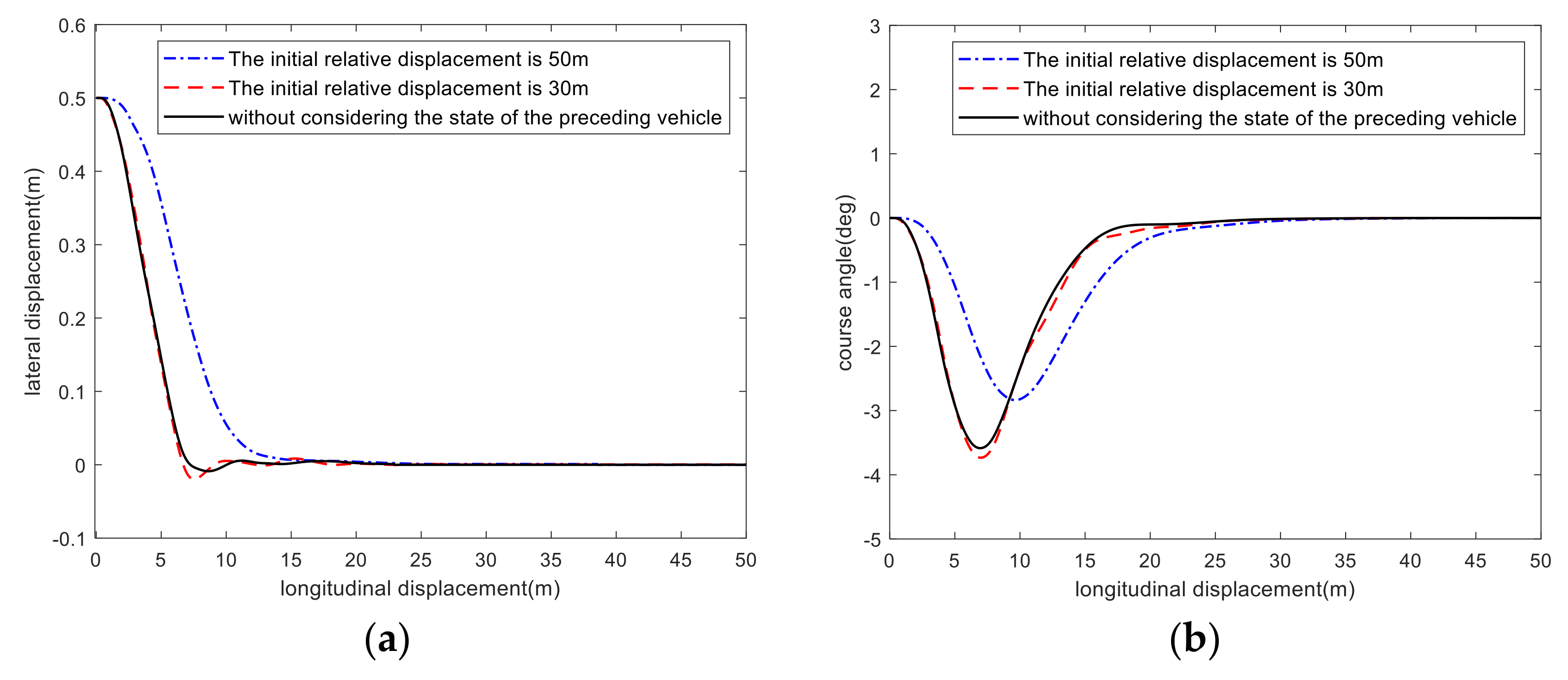
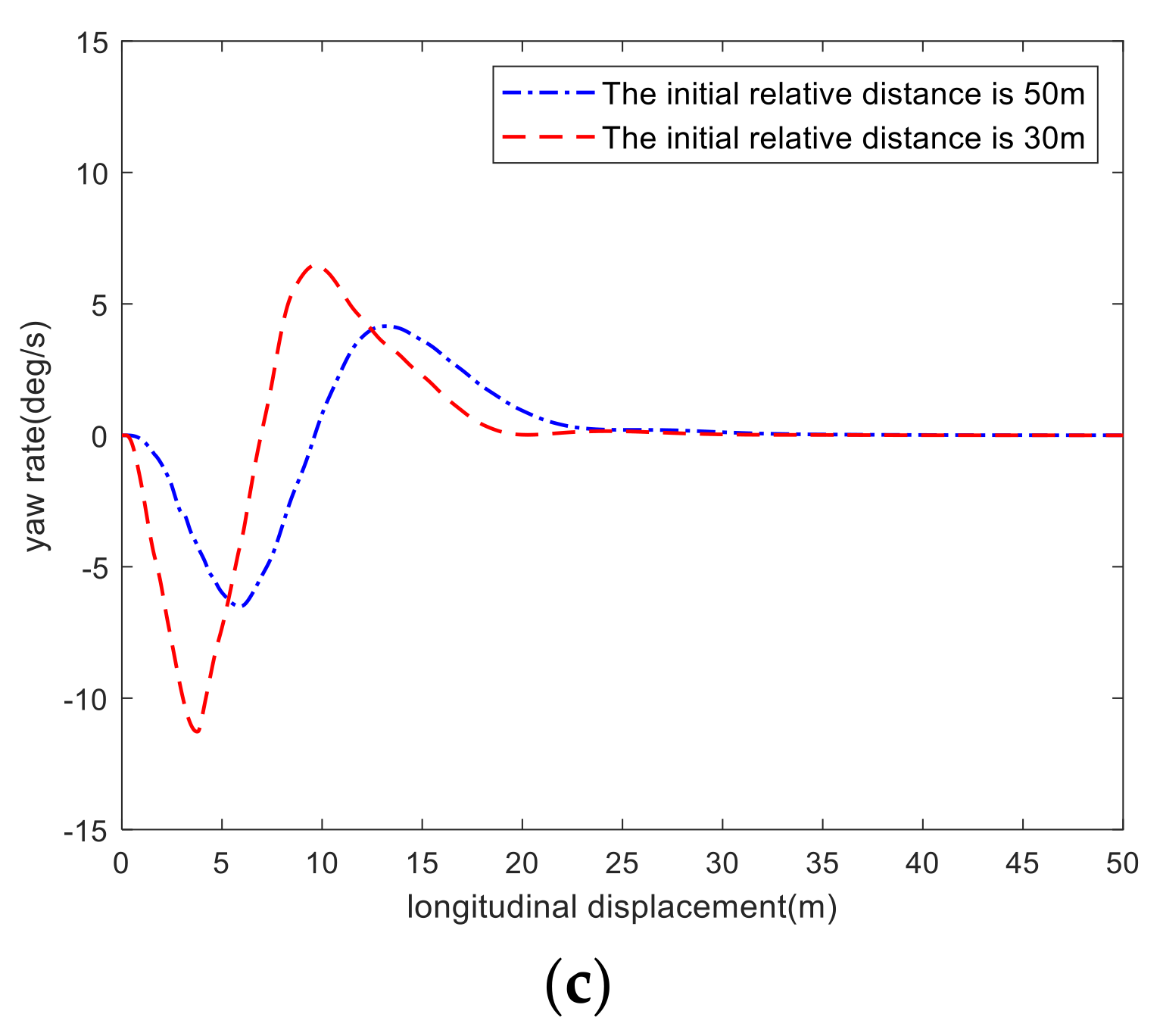
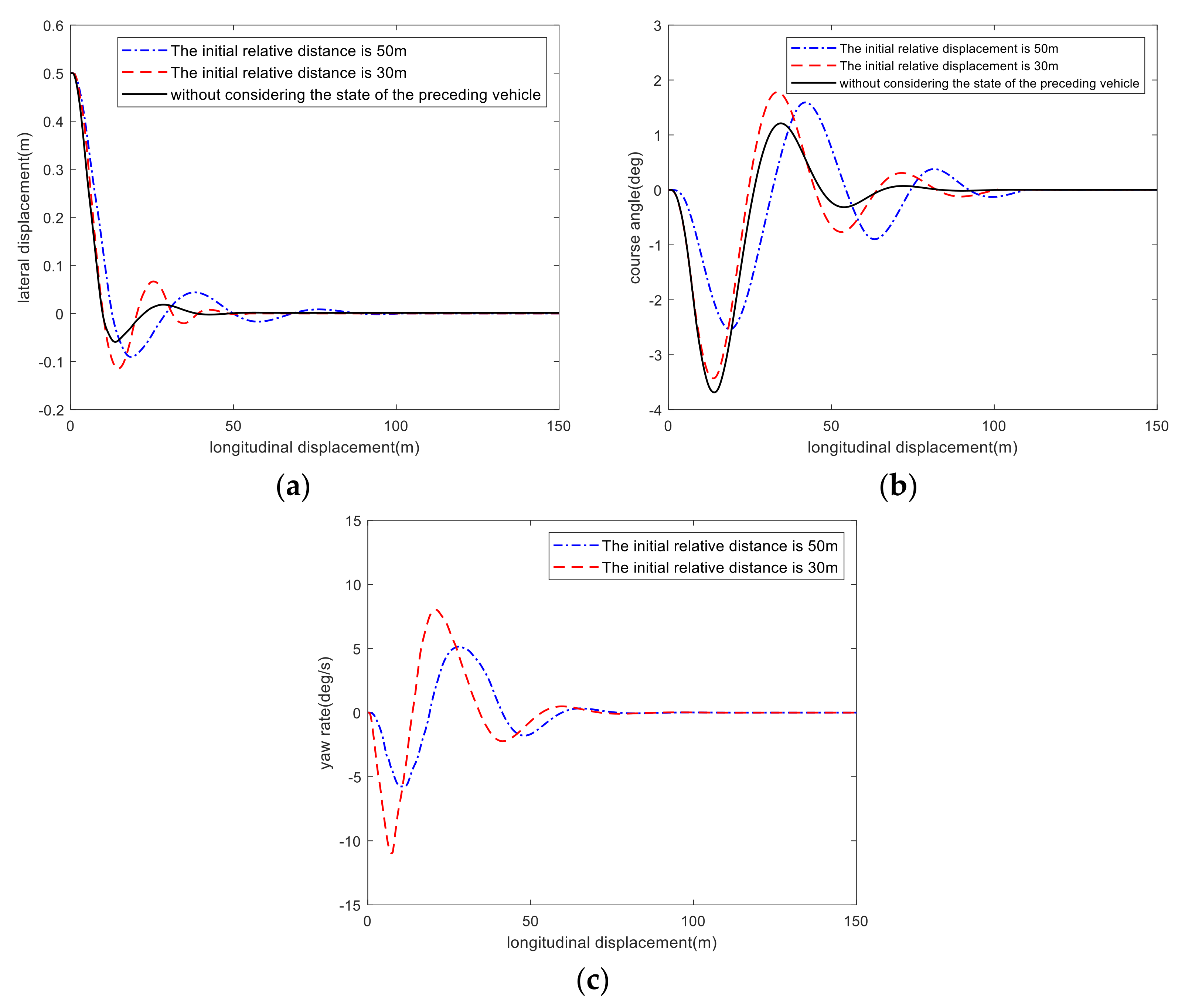
4. Simulation Verification and Result Analysis
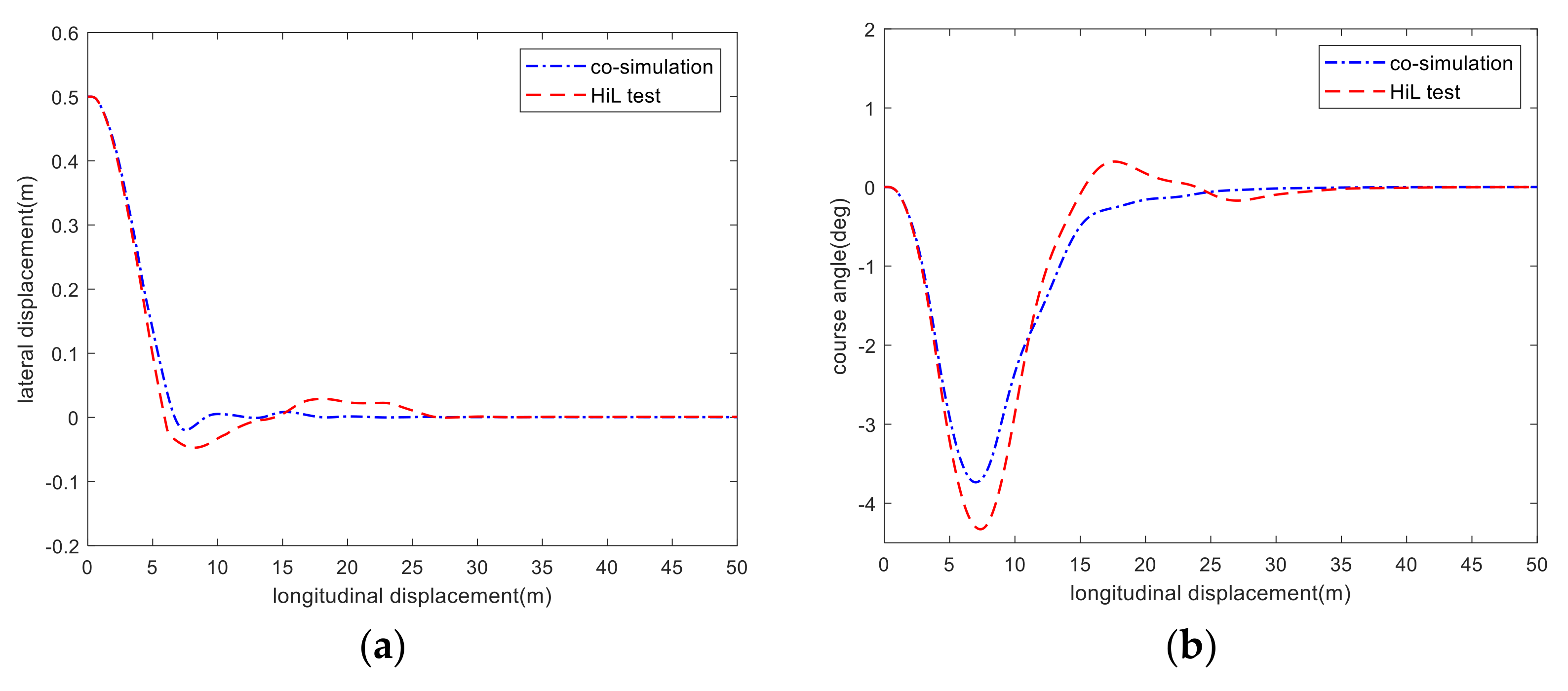
5. Hardware-in-the-Loop Test
6. Conclusions
- (1)
- The 3-DOF vehicle dynamics model of commercial vehicles is established, and the dynamic lane tracking controller based on RMPC is designed. The model predictive control problem is transformed into a ‘min–max’ problem by using LMI theory, which solves the robustness problem caused by model uncertainty and external interference.
- (2)
- A dynamic lane tracking control strategy considering the state of the preceding vehicle is proposed. According to the relative distance, relative speed between the local vehicle and the preceding vehicle, the variable weight coefficients matrix is dynamically adjusted by a fuzzy controller to meet the requirements of safety and comfort in the process of dynamic lane tracking, according to the state of the preceding vehicle.
- (3)
- The results of the co-simulation and HiL test show that the RMPC controller considering the state of preceding vehicle enhances the response speed of lane tracking when the relative distance is short and improves the comfort in the process of lane tracking when the relative distance is long, which demonstrates that the RMPC controller considering the state of preceding vehicle has better environmental adaptability.
- (4)
- The relative distance and relative speed of the preceding vehicle are only considered in this paper. More environmental factors that affect the vehicle’s lane tracking need to be further taken into account to deal with more complex driving scenes, and the robustness and adaptability of the control algorithm can be verified by real vehicle experiments.
Author Contributions
Funding
Conflicts of Interest
References
- Kvári, B.; Hegedüs, F. Bécsi, T Design of a reinforcement learning-based lane keeping planning agent for automated vehicles. Appl. Sci. 2020, 10, 7171. [Google Scholar] [CrossRef]
- Hu, C.; Qin, Y.; Cao, H.; Song, X.; Jiang, K.; Rath, J.J.; Wei, C. Lane keeping of autonomous vehicles based on differential steering with adaptive multivariable super-twisting control. Mech. Syst. Signal Process. 2019, 125, 330–346. [Google Scholar] [CrossRef]
- Lee, J.; Choi, J.; Yi, K.; Shin, M.; Ko, B. Lane-keeping assistance control algorithm using differential braking to prevent unintended lane departures. Control. Eng. Pract. 2014, 23, 1–13. [Google Scholar] [CrossRef]
- Taghavifar, H.; Hu, C.; Taghavifar, L.; Qin, Y.; Na, J.; Wei, C. Optimal robust control of vehicle lateral stability using damped least-square backpropagation training of neural networks. Neurocomputing 2020, 384, 256–267. [Google Scholar] [CrossRef]
- Liu, M.; Deng, X.; Lei, Z.; Jiang, C.; Piao, C. Autonomous lane keeping system: Lane detection, tracking and control on embedded system. J. Electr. Eng. Technol. 2020, 16, 569–578. [Google Scholar] [CrossRef]
- Lin, F.; Wang, S.; Zhao, Y.; Cai, Y. Research on autonomous vehicle path tracking control considering roll stability. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 235, 199–210. [Google Scholar] [CrossRef]
- Dang, T.S.; Duong, D.T.; Le, V.C.; Banerjee, S. A combined backstepping and adaptive fuzzy PID approach for trajectory tracking of autonomous mobile robots. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 156. [Google Scholar] [CrossRef]
- Chen, Z.L.; Li, L.N.; Huang, X.M. Building an autonomous lane keeping simulator using real-world data and end-to-end learning. IEEE Intell. Transp. Syst. Mag. 2018, 12, 47–59. [Google Scholar] [CrossRef]
- Choi, M.; Choi, S.B. MPC for vehicle lateral stability via differential braking and active front steering considering practical aspects. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 459–469. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Liu, Y.G.; Li, W.B.; Guo, H.Q. Virtual fluid-flow-model-based lane-keeping integrated with collision avoidance control system design for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6232–6241. [Google Scholar] [CrossRef]
- Cai, Y.F.; Zang, Y.; Sun, X.Q.; Chen, X.B.; Chen, L. Lane-keeping system of intelligent vehicles based on extension switching control method. China, J. Highw. Transp. 2019, 32, 43–52. [Google Scholar] [CrossRef]
- Swain, S.K.; Rath, J.J.; Veluvolu, K.C. Neural network based robust lateral control for an autonomous vehicle. Electronics 2021, 10, 510. [Google Scholar] [CrossRef]
- Feng, P.F.; Jin, H.Q.; Wang, H.R.; Liu, F. Lane keeping control by considering influences of road adhesion and adaptive time coefficients. China Mech. Eng. 2020, 33, 156–166. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, R.; Zhao, L.; Wang, H.; Wei, Z. Control of chaos in vehicle lateral motion using the sliding mode variable structure control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 776–789. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Liu, L. Review and comparison of path tracking based on model predictive control. Electronics 2019, 8, 1077. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Liu, W.; Chen, G.; Knoll, A. Matrix inequalities based robust model predictive control for vehicle considering model uncertainties, external disturbances, and time-varying delay. Front. Neurorobotics 2021, 14, 110. [Google Scholar] [CrossRef]
- Samuel, M.; Mohamad, M.; Hussein, M.; Saad, S.M. Lane keeping maneuvers using proportional integral derivative (PID) and model predictive control (MPC). J. Robot. Control. 2021, 2, 78–82. [Google Scholar] [CrossRef]
- Mata, S.; Zubizarreta, A.; Pinto, C. Robust tube-based model predictive control for lateral path tracking. IEEE Trans. Intell. Veh. 2019, 4, 569–577. [Google Scholar] [CrossRef]
- Zhao, W.Z.; Luan, Z.K.; Wang, C.Y. Parameter optimization design of vehicle E-HHPS system based on an improved MOPSO algorithm. Adv. Eng. Softw. 2018, 123, 51–61. [Google Scholar] [CrossRef]
- Park, D.; Her, H.; Yi, K. Development of roll stability control of commercial vehicles with environment information. J. Auto-Veh. Saf. Assoc. 2013, 5, 50–55. [Google Scholar] [CrossRef]
- Son, Y.S.; Kim, W.; Lee, S.H.; Chung, C.C. Robust multirate control scheme with predictive virtual lanes for lane-keeping system of autonomous highway driving. IEEE Trans. Veh. Technol. 2014, 64, 3378–3391. [Google Scholar] [CrossRef]
- Marumo, Y.; Yokota, T.; Aoki, A. Improving stability and lane-keeping performance for multi-articulated vehicles using vector follower control. Veh. Syst. Dyn. 2020, 58, 1859–1872. [Google Scholar] [CrossRef]
- Fesharaki, S.J.; Kamali, M.; Sheikholeslam, F.; Talebi, H.A. Robust model predictive control with sliding mode for constrained non-linear systems. IET Control. Theory Appl. 2020, 14, 2592–2599. [Google Scholar] [CrossRef]
- Moradi, S.M.; Ahmad, A.; Mehdi, M. An offline LMI-based robust model predictive control of vehicle active suspension system with parameter uncertainty. Trans. Inst. Meas. Control. 2019, 41, 1699–1711. [Google Scholar] [CrossRef]
- Xie, H.; Dai, L.; Luo, Y.; Xia, Y. Robust MPC for disturbed nonlinear discrete-time systems via a composite self-triggered scheme. Automatica 2021, 127, 109499. [Google Scholar] [CrossRef]
- Salvati, L.; d’Amore, M.; Fiorentino, A.; Pellegrino, A.; Sena, P.; Villecco, F. Development and testing of a methodology for the assessment of acceptability of LKA systems. Machines 2020, 8, 47. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Karimi, H.R. A robust predictive control design for nonlinear active suspension systems. Asian, J. Control. 2016, 18, 122–132. [Google Scholar] [CrossRef]
- Bouzid, A.E.M.; Chaoui, H.; Zerrougui, M.; Elghali, S.B.; Benbouzid, M. Robust control based on linear matrix inequalities criterion of single phase distributed electrical energy systems operating in islanded and grid-connected modes. Appl. Energy 2021, 292, 116776. [Google Scholar] [CrossRef]
- Yang, L.; Yue, M.; Wang, J.; Hou, W. RMPC-based directional stability control for electric vehicles subject to tire blowout on curved expressway. J. Dyn. Syst. Meas. Control. 2019, 141, 041009. [Google Scholar] [CrossRef]
- He, J.; McCarley, J.S.; Kramer, A.F. Lane keeping under cognitive load: Performance changes and mechanisms. Hum. Factors 2014, 56, 414–426. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Chen, Y.; Zhao, Y.; Wang, S. Path tracking of autonomous vehicle based on adaptive model predictive control. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419880089. [Google Scholar] [CrossRef]




| NB | NS | ZO | PS | PB | ||
|---|---|---|---|---|---|---|
| NB | PB | PB | PM | PM | PM | |
| NS | PB | PB | PM | PM | PS | |
| ZO | PN | PB | PM | PS | PS | |
| PS | PM | PM | PS | PS | ZO | |
| PB | PM | PM | ZO | ZO | ZO | |
| Parameters/Unit | Value |
|---|---|
| Vehicle mass/kg | 3950 |
| The wheelbase of vehicle/m | 2.3 |
| The distance from front axle to center of mass/m | 1.38 |
| Rotational inertia of Z-axis/(kg·m²) | 30,857.5 |
| Cornering stiffness of front axle/(N·rad−1) | −85,000 |
| Cornering stiffness of rear axle/(N·rad−1) | −113,700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Hu, Z.; Jiang, H.; Yin, Y.; Yang, Z. Dynamic Lane Tracking Control of the Commercial Vehicle Based on RMPC Algorithm Considering the State of Preceding Vehicle. Machines 2022, 10, 534. https://doi.org/10.3390/machines10070534
Tang B, Hu Z, Jiang H, Yin Y, Yang Z. Dynamic Lane Tracking Control of the Commercial Vehicle Based on RMPC Algorithm Considering the State of Preceding Vehicle. Machines. 2022; 10(7):534. https://doi.org/10.3390/machines10070534
Chicago/Turabian StyleTang, Bin, Zitian Hu, Haobin Jiang, Yue Yin, and Zhengyi Yang. 2022. "Dynamic Lane Tracking Control of the Commercial Vehicle Based on RMPC Algorithm Considering the State of Preceding Vehicle" Machines 10, no. 7: 534. https://doi.org/10.3390/machines10070534
APA StyleTang, B., Hu, Z., Jiang, H., Yin, Y., & Yang, Z. (2022). Dynamic Lane Tracking Control of the Commercial Vehicle Based on RMPC Algorithm Considering the State of Preceding Vehicle. Machines, 10(7), 534. https://doi.org/10.3390/machines10070534






