Abstract
Point cloud is a versatile geometric representation that could be applied in computer vision tasks. On account of the disorder of point cloud, it is challenging to design a deep neural network used in point cloud analysis. Furthermore, most existing frameworks for point cloud processing either hardly consider the local neighboring information or ignore context-aware and spatially-aware features. To deal with the above problems, we propose a novel point cloud processing architecture named TR-Net, which is based on transformer. This architecture reformulates the point cloud processing task as a set-to-set translation problem. TR-Net directly operates on raw point clouds without any data transformation or annotation, which reduces the consumption of computing resources and memory usage. Firstly, a neighborhood embedding backbone is designed to effectively extract the local neighboring information from point cloud. Then, an attention-based sub-network is constructed to better learn a semantically abundant and discriminatory representation from embedded features. Finally, effective global features are yielded through feeding the features extracted by attention-based sub-network into a residual backbone. For different downstream tasks, we build different decoders. Extensive experiments on the public datasets illustrate that our approach outperforms other state-of-the-art methods. For example, our TR-Net performs 93.1% overall accuracy on the ModelNet40 dataset and the TR-Net archives a mIou of 85.3% on the ShapeNet dataset for part segmentation.
1. Introduction
Point cloud is a set of points in 3D space that can be viewed as a representation of object surface. Due to greatly compensating for the lack of spatial structure information of 2D images, point cloud has been extensively used in various fields such as automatic drive [1], virtual reality [2], and intelligent robot technology [3,4]. These contemporary applications usually call for advanced processing methods of point cloud. As is well known, point cloud is unordered and irregular [5], which is distinct from 2D images. All algorithms for point cloud feature extraction, therefore, must be independent of the order of input points and point cloud is a collection of uneven sampling points. On one hand, it makes the relationship between points difficult to be used for extracting features. On the other hand, convolutional neural networks, which have already been applied in image and video processing, are not applicable to be used in point cloud processing directly. This research focuses on shape classification and part segmentation of point cloud, which are two basic and challenging tasks that have received a lot of attention from researchers in point cloud processing.
In the early stages of point cloud research, most researchers usually convert point cloud data into regular 3D voxel grids [6] or a collection of images before feeding them into a convolutional neural network. Voxelization is a simple method of transforming a sparse and uneven point cloud to a conventional grid structure, which can be fed to standard CNNs to extract features. Voxnet [7] vowelizes the point cloud into a volumetric grid that denotes spatial occupancy for each voxel, then uses a standard 3D CNN (Convolutional Neural Network) to predict the categories of objects based on the occupied voxels. For high spatial resolution, it is obvious that sparsely-occupied volumetric grid consumes a lot of memory and incurs vast computational costs. Therefore, several improvements are mentioned to work out the scarcity issue. Kd-net [8] constructs an efficient 3D space division structure using kd-tree [9], along with a deep neural architecture to learn point cloud representations. Analogously, in OctNet [10], 3D CNN is applied to a hybrid grid-octree structure produced from a collection of shallow octrees, which makes it capable of achieving high resolution. The octree structure is effectively encoded using a bit string format, and each voxel’s feature vector is indexed by plain mathematics. OctNet [10] requires substantially less memory and expense for high-resolution point clouds than a baseline network based on dense input grids. Nevertheless, this data conversion not only makes the generated data unnecessarily large, but also introduces quantization artifacts that may overshadow the natural inflexibility of the data.
In recent years, as a groundbreaking work, PointNet [11] directly applied convolutional neural network on the raw point cloud. To extract global features, an MLP (Multi-Layer Perceptron) module and a symmetric function are applied to each point. This method comes up with a useful way for the representation of unstructured point cloud; however, the architecture only deals with independent points without cogitating connections between points in local regions so that local feature is not captured effectively. On the foundation of PointNet, PointNet++ [12] is a hierarchical neural network that exploits local representations by repeatedly applying PointNet with a sampling layer and a grouping layer. In order to better aggregate each point and the matching edges connected to adjacent pairs, DGCNN [13] tries to extend PointNet according to the edge convolutional neural network practical operation (EdgeConv) designed to be applied to edge features. Capitalizing on the advantages of typical CNN practice, PointCNN [14] transforms the given chaotic point set to a latent canonical order by learning a -convolutional operator, and then selects a standard CNN architecture to capture local features.
Transformer has been proved to be effectual in various practical application including machine translation tasks [15,16], computer vision tasks [17,18,19], and graph-based tasks [20]. Nowadays, transformer has been introduced in many specific yields such as remote sensing, cultural heritage, urban environments, and so on. For the purpose of learning the fine-grained local features of point cloud, a variety of attempts for point cloud segmentation have been made to extract spatial relationships between points through applying attention mechanism. The recently successful approaches [21,22,23] further improve semantic segmentation accuracy by ignoring immaterial information and focusing on crucial information. For example in [22], combining transformer with the random sampling algorithm, it is suitable for lightweight point cloud semantic segmentation of large-scale 3D point cloud. However, such approaches have not made it possible to learn more about the structural links between neighboring points.
Inspired by PCT [24] and GRNet [25], we propose a novel architecture TR-Net based on transformer for point cloud processing. In natural language processing, positional encoding module is usually used to express the word order in a sentence. It can show the positional relationship between words at the same time as discriminating the same word in different positions. However, there is no constant order in point cloud data. The raw positional encoding and the input embedding are combined into a coordinate-based input embedding module, which is considered as a viable solution. Because each point has distinct coordinates that describe their spatial placements, it may create distinguishable features. By capitalizing on the idea of PCT [24], we introduce the neighbor embedding strategy to ameliorate the point embedding to enhance the capability of local feature extraction. Furthermore, we employ the encoder-decoder architecture to convert fundamental tasks of point cloud processing as a set-to-set translation issue. The encoder of TR-Net initially embeds the input three-dimensional coordinates into a high dimensional feature space. Then the embedded features are used as input of an attention-based sub-network to learn a semantically abundant representation for each point. It lowers the effect of noise and sharpens attention weights, which is advantageous for downstream tasks. To learn context-aware and spatially-aware features of point cloud, we design a residual neural network which generates global features used for the decoder input. For different specific tasks, the respective decoders have been designed to adaptively respond to task demands. More details about decoder are shown in Section 3.
The major contributions of this work are are summarized as follows:
- We propose a novel network architecture named TR-Net, which directly works on raw point cloud, reducing the memory usage.
- We design a residual backbone with skip connections to learn context-aware and spatial-aware features.
- Extensive experiments demonstrate that the TR-Net achieves state-of-the-art performance on shape classification and part segmentation.
2. Related Work
2.1. Projection-Based Methods
For handling irregular inputs such as point cloud, an intuitive solution is to convert the irregular representation to a regular one. With the success of 2D CNNs in mind, some methods [26,27] use multi-view projections in which 3D point cloud is projected into multiple image planes. Then, in order to generate the final output representations, 2D CNNs are employed to extract feature representations in these image planes, followed by multi-view feature fusion. TangentConv [28] uses a similar method to project local surface geometry onto a tangent plane on each point, resulting in tangent images that can be processed by 2D CNNs. Nevertheless, this approach has a heavy reliance on tangent estimation. For the projection-based frameworks, the geometric information inside the point cloud is collapsed in the projection phase. When creating dense pixel grids on projection planes, these methods may underutilize the sparsity of point cloud.
2.2. Point-Based Methods
PointNet [11] is a pioneering work that deals with point sets directly. PointNet++ [12] learns features from local geometric structures and abstracts local features layer by layer by stacking multiple set abstraction levels. Many networks have been constructed using PointNet [11] because of its simplicity and powerful representation capabilities. Mo-Net [29] has a similar design to PointNet, but it requires a finite collection of moments as input. Point Attention Transformers (PATs) [30] learns high-dimensional features using MLP and represents each point by its own absolute and relative locations with regard to its neighbors. Then, to learn hierarchical features, a permutation invariant, differentiable, and trainable end-to-end Gumbel Subset Sampling (GSS) layer is constructed, which captures relations between points using Group Shuffle Attention (GSA). PointWeb [31], based on PointNet++ [12], adopts Adaptive Feature Adjustment to improve point features in the context of the local neighborhood (AFA). Designed a Structural Relational Network (SRN), Duan et al. [32] employ MLP to exploit structural relational features between distinct local structures. Lin et al. [33] build a lookup table to speed up the inference process for both the input and function spaces learned by PointNet.
2.3. Transformer in NLP
Transformers [16] are first introduced as an attention-based architecture for machine translation in Natural Language Processing (NLP). Furthermore, Transformer models often utilize the encoder-decoder structure and are characterized by both self-attention and cross-attention mechanisms, without any recurrence or convolution operators. It has been proven that transformer models are very helpful to the tasks, which involve long sequences thanks to the self-attention mechanism. The cross-attention mechanism in the decoder learn the attention map of query features by exploiting the encoder information, which makes transformers efficient in generation tasks. By taking the advantages of both self-attention and cross-attention mechanisms, transformers have a mighty capability to handle long sequence input and enhance information communications between the encoder and the decoder. More recently, transformers have began to dominate the tasks that take long sequences as input, while gradually replacing RNNs in many domains.
2.4. Transformer in Vision
Now they begin their journey in computer vision. Multiple studies have introduced attention into computer vision tasks. The pioneering work of ViT [18] based on patch encoding and transformer, which is directly applied on nonoverlapping medium-sized image patches for image classification. Compared to convolutional networks, it achieves an powerful speed-accuracy tradeoff on image classification. While ViT requires large-scale training datasets to perform well, DeiT [19] introduces some training strategies that allow ViT to also be effectual using the smaller training datasets. The results of ViT on image classification are encouraging, however, ViT only focuses on the global patch aggregation without considering its internal interaction. To solve this problem, Transformer-IN-Transformer (TNT) [34] aggregates both patch and pixel-level representations, which is similar to Network In Network (NIN) series [35]. In more detail, each layer of TNT is comprised of two successive blocks, an inner block models the pixel-wise interaction within each patch, and an outer block extracts the global information from patch embeddings. They are linked by a linear projection layer that maps the pixels to their corresponding patch. Therefore, TNT preserves much richer local features at the shallow layer than before.
3. Materials and Methods
In this section, we expound how our TR-Net can be used in some basic tasks of point cloud processing involving shape classification and part segmentation. The design details of TR-Net are also presented systematically.
Let be a sequence of unordered points, with F-dimension, where N represents the number of input points, and is treated as a feature vector containing coordinates in 3D space. In this work, we define and use 3D coordinates as input.
3.1. TR-Net Architecture
The overall architecture of TR-Net is presented in Figure 1, including a neighborhood embedding backbone, an attention-based sub-network, a residual backbone, and decoders for different tasks. TR-Net shares similar principles to Transformer, which initially encodes the input features into a new high dimensional feature space. By this means, the semantic affinities between points are represented for various point cloud processing tasks. It firstly embeds the input coordinates of point cloud into a new space to learn the local neighboring information. The attention-based sub-network is comprised of four stacked offset-attention layers, which makes it better learn semantically abundant and discriminatory representation for each point. Then, we take the output feature of attention-based sub-network into residual backbone to exploit context information of point cloud, followed by a max pooling layer to yield global feature used for downstream tasks.
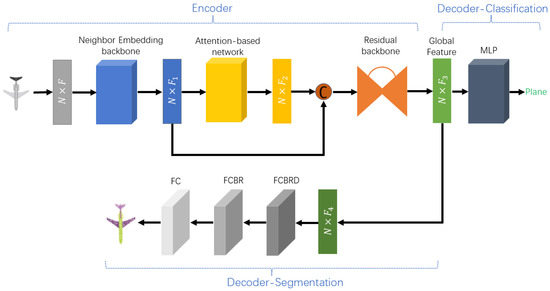
Figure 1.
The architecture of TR-Net. The decoder of TR-Net consists of classification (top branch) and segmentation (bottom branch). C means concatenate operator. FCBR consists of fully connected layer, batch normalization and ReLU. FCBRD stands FCBR followed by a Dropout layer with rate 0.5.
In the classification task. To recognize object categories in point cloud P, the global feature is fed into the classification decoder, which contains MLP layers (1024, 512, 256, ) and dropout operation with a invariable probability of 0.5 to convert global feature to object categories. In addition, we use the activation function LeakyReLU with batch normalization in each layer. Other hyperparameters are chosen in a similar way. The top-scoring category is determined as the category label of this point cloud.
In the part segmentation task. Aiming to segment the point cloud into parts (e.g., cub handle, plane wings; a part hardly request to be contiguous), we need to obtain the specific semantic label for each point. As presented in Figure 1, the global feature created by residual backbone is fed to the part segmentation decoder, which includes three shared full-connected layers to classify each point. In more detail, the first full-connected layer is followed by the activation function ReLU and a dropout layer with probability 0.5. Only the activation function ReLU is applied on the second full-connected layer. Furthermore, all layers are batch normalized.
3.2. Point Cloud Sampling
The raw point cloud data could not represent the relations between neighboring points. So we design a neighborhood embedding backbone that is mainly used for point cloud sampling. However, point embedding is not the same as word embedding in NLP. For word embedding, similar words are placed closer to each other in the embedding space. This approach disregards interactions between points, which is quite important for point cloud learning. To enhance the ability of local feature extraction, we adopt a neighborhood embedding strategy [24] in the locally adjacent points. This module first uses two cascaded 1D convolutional layers, each of which is followed by a universal batch normalization layer and the activation function ReLU to embed point cloud coordinates into a high-dimensional space. To develop the ability of local feature expression, the KNN (K-nearest neighbors) algorithm is utilized to search for the k nearest points on each point during point cloud sampling. Using Euclidean distance, KNN finds an inflexible quantity of neighboring points, then these points will be formed as a k-neighborhood structure. In contrast to coordinate-based point embedding in transform [16], our sampling strategy considers the local neighbor information on each point, thus we can capture point-to-point relations in the local region.
In more detail, we assume the input point cloud P contains N points, which are fed into two convolutional layers to generate corresponding features F. Then, point cloud P is down sampled to by adopting the farthest point sampling (FPS) algorithm. For each sampled point , we assign KNN to its k-nearest neighbors in P, which aggregates the local neighboring features. Finally, we obtain the output features from sampled point cloud P.
3.3. Attention-Based Sub-Network
In Figure 2, the attention-based sub-network is comprised of four stacked offset-attention layers to better learn a semantically abundant and discriminatory representation for each point. The attention mechanism could powerfully capture valuable information by paying different attention to different features, which has performed advantages in various tasks. Self-attention [16], also called intra-attention, is a mechanism for connecting different positions in a sequence together to receive a representation of the sequence. It considers self-geometric information for each individual point to learn self-coefficients. Furthermore, the study in PCT indicates that self-attention ignores the relationship between points which makes it inadequate to learn a semantically abundant and discriminatory representation from the embedded features effectively. Our work draws upon the idea of offset-attention [24] which is advantageous to downstream tasks by diminishing the influence of noise and sharpening the attention weights.
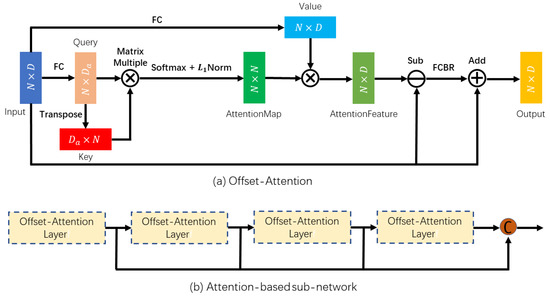
Figure 2.
(a) is the description of offset-attention. (b) is the structure of attention-based sub-network.
Generally, an attention function may be described as a vector that maps a query and a pair of key values to an output, in which the query, key, value, and output are vectors. The output is calculated as a weighted sum of the values, in which the weight assigned to each value is calculated by querying a compatible function with the corresponding key. Specifically, the offset-attention following the terminology in transformer [16] uses Q, K, V to represent the query, key and value metrices, respectively, produced by linear transformations of the input features in Equation (1).
where means 1D-convolution, and they are different with each other.
Then, using the query matrix and the key matrix, the weight of attention is calculated by matrix point product as follows:
There are two widely employed attention functions, which are additive attention and dot-product attention. Dot-product attention is very analogous to algorithm. Additive attention is paid to compute compatibility functions using feed-forward networks with a single hidden layer. Although the theoretical complexity of them is similar, dot-product attention is significantly faster and less space-using by using highly optimized matrix multiplication code in practice. The input involves queries and keys of dimension , and values of dimension . If is too large, dot products may grow rapidly in magnitude and force the softmax function into areas with extremely tiny gradients. To minimize such impact, these weights are normalized to obtain refer to Equations (3) and (4).
It is evident that the normalization in offset-attention is different from traditional self-attention that scales the first dimension by and normalizes the second dimension with softmax. For the sake of normalizing the attention map in the offset-attention mechanism, the softmax operator is used on the first dimension, while a -norm is applied on the second dimension.
Because the input feature and shared matching linear transformation matrices determine the query, key, and value matrices, all of them are independent of order. In addition, both softmax and weighted sum are independent of permutations. As a result, the entire offset-attention process is permutation-invariant which makes it very suitable for the unordered, irregular domain shown by point cloud. Inspired by Laplacian matrix in Graph convolution networks [36], the offset-attention output features are shown in Equation (5). In this stage, we obtain the augmented feature that will be fed to the residual backbone.
where denotes a full-connected layer linear layer with the activation function ReLU.
3.4. Residual Backbone
Traditional deep neural networks may cause a vanishing gradient problem. To address this, we thus design a residual backbone with skip connection following the attention-based sub-network to capture context information in the global space. As shown in Figure 3, the whole convolutional layers are 1D convolution layer. The left convolutional layers are followed by BLM, but the right is BR. It has been proven by Szegedy [37] that the batch normalization could accelerate network convergence and lower the complexity in training stage, thus, a batch normalization layer is used after each 1D convolution. The leakyReLU activation function is chosen to avoid jaggedness problem in gradient direction. A rectified linear unit layer (ReLU) is added after the left BachNorm layer to avoid gradient disappearance. The maximum pooling is to fuse the information of each point in point cloud. Finally, we obtain the output global features with context information as the input of decoder.
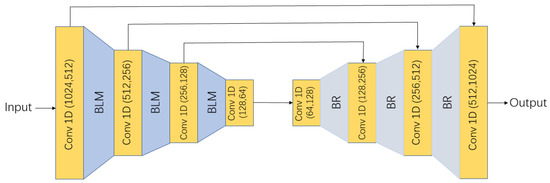
Figure 3.
The architecture of residual backbone. BLM combines BachNorm, LeakyReLU and MaxPooling layers. BR combines BachNorm and ReLU layers.
4. Experiments and Analysis
In this section, to properly evaluate the performance of our network, we cover three public datasets for both shape classification and part segmentation tasks. Then, we show how TR-Net could be trained to execute shape classification and part segmentation. In the end, we compare our model with other existing methods quantitatively and qualitatively.
4.1. Datasets
4.1.1. ModelNet40 Dataset
We evaluate the proposed architecture TR-Net on the opening dataset ModelNet40 [38] for three-dimensional pattern recognition severally. ModelNet40 is offered by Princeton University. There are 12,311 CAD models from 40 object categories, of which 9843 models are used for training and 2468 for testing. The sampling strategy we used is the same as PointNet [11]. For each model, we sample each object to 1024 points uniformly, and the point cloud is realigned to adjust to the unit sphere. Only the 3D spatial coordinates of the sampled points are utilized, while the initial meshes are discarded. At the training process, we extend the data by randomly scaling objects and perturbing the object and point locations. No data augmentation or voting approaches were used during the testing procedure.
4.1.2. ScanObjectNN Dataset
ModelNet40 [38] is the de-facto standard benchmark for point cloud classification; however, owing to its synthetic nature and the rapid evolution of point cloud research, it may not match the requirements of newer approaches. For this purpose, we also make experiments on the ScanObjectNN [39] that is a LiDAR point clouds dataset. ScanObjectNN is a new Real-World data benchmark dataset and classification model based on scanned indoor scene data. It is a new point cloud benchmark that has 15,000 objects divided into 15 classes and 2902 distinct object instances in the actual world. Among them, 12,000 objects are used as the training set and 3000 objects as the testing set. Since objects in real-world scans are often cluttered with background and partially present due to occlusion, this dataset poses a great challenge to existing point cloud classification techniques. In our experiments, we choose the most disturbing variety (PB T50 RS).
4.1.3. ShapeNet Dataset
Point cloud segmentation is often seen as a challenging fine-grained 3D recognition task which is aimed at dividing a 3D object into various meaningful parts. For example, given a 3D scan or a mesh model, the task is to attach part category label (e.g., desk leg, plane wing) to each point. We conducted several experiments on the ShapeNet Parts dataset [40], which involves 16,880 3D models with a training to testing split of 14,006 to 2874. There are 16 object categories and 50 part labels in this dataset; each instance comprises at least two parts and ground truth annotations are labeled on sampled points on the shapes. Following PointNet, 2048 points are sampled from each training model, and greatly sampled point collections are labeled with fewer than six parts. We supplement the input data with random translation in [−0.2, 0.2] and random anisotropic scaling in [0.67, 1.5] during training. We employed a multi-scale testing technique during testing, with scales ranging from [0.7, 1.4] with a 0.1 step.
4.2. Experimental Setup
The experiments were implemented in the server with the Ubuntu 20.04 LTS system. The server GPU was GeForce RTX 2080Ti 12 GB, the CPU was Intel(R) Xeon(R) Silver 4210 CPU @ 2.20 GHz, and the RAM size was 128 GB. The main installation packages required by the executing environment of the program are listed in Table 1.

Table 1.
Main installation packages required by the running environment.
The TR-Net was trained in an end-to-end pattern. For each dataset, we picked 80% as the training set, and we used the remaining 20% as the test set. Following the previous methods [11,12,13], this separation for each dataset is fixed and is not a random procedure. As shown in Table 2, for the ModelNet40 dataset, we used the Adam optimizer. The initial learning rate and weight decay of the network were set to 0.0001 and 0.00005, respectively. We trained the model on ModelNet40 up to 300 epochs with a batch size of 32. The training configuration of ScanObjectNN followed that of ModelNet40. For the ShapeNet dataset, the network parameters were optimized by the SGD method during network training. The initial learning rate we used was 0.1, and the momentum was 0.9. Furthermore, we used cosine annealing to lower the learning rate to 0.001. The batch normalization decay was not used in this work. The model was trained for 300 epochs with a batch size of 24 on ShapeNet dataset. Furthermore, the neighbors of each point is 32 in KNN search.

Table 2.
Hyperparameter settings of our model.
4.3. Results and Analysis
4.3.1. Classification on ModelNet40 Dataset
As shown in Table 3, we compare our proposed TR-Net with a series of previous representative approaches. To quantitatively evaluate the merits of our approach, we choose OA (overall accuracy) and mAcc (mean classification accuracy) as evaluation metrics. As shown in Table 3, experimental results indicate that TR-Net achieves the best result of 90.4% mean class accuracy and the overall accuracy we achieved is 93.1%. Compared to PointNet++ [12] and DGCNN [13], TR-Net makes a 2.4% and 0.2% improvement, respectively. It can be seen that our method demonstrates a clear advantage over other approaches in terms of 3D object classification.

Table 3.
Comparison with other approaches on ModelNet40 classification dataset. OA indicates overall accuracy. mAcc denotes mean class accuracy.
4.3.2. Classification on ScanObjectNN Dataset
In Table 4, we compare our TR-Net with the other state-of-the-art methods on the ScanObjectNN benchmark quantitatively. TR-Net achieves state-of-the-art performance and makes a significant improvement on class mean accuracy (mAcc). For example, we obtain comparable OA compared to GBNet while outperforming it 1.4% mAcc. Furthermore, we observe that our TR-Net produces the smallest gap between mAcc and OA. This phenomenon demonstrates that our approach did not favor one category, demonstrating its robustness.

Table 4.
Classification results on ScanObjectNN dataset.
4.3.3. Part Segmentation on ShapeNet Dataset
We express part segmentation as a per-point classification issue. The mIoU on points is adopted as an evaluation metric. We string along with the identical evaluation scheme as PointNet. To calculate the shape’s mIoU for each shape S in category C, we compute the IoU between ground truth and prediction for each part type in shape S. We count part IoU as 1 if the union of ground truth and prediction points is empty. We average IoUs of all part types to obtain mIoU for that shape. To calculate mIoU for a category, we take the average of mIoUs for all shapes in that category.
The quantitative evaluations of the experimental results are presented in Table 5. Metrics for each category are also provided. We can see that the proposed TR-Net performs better than most of the other methods overall. Our approach achieves the state-of-the-art result with 85.3% part average Intersection-over-Union (mIoU). Compared to PointNet++ and DGCNN, however, we make an improvement of 0.2% and 0.1%, respectively. In addition, we achieve considerable gains in airplane, chair, guitar, laptop and table. These results demonstrate that TR-Net is capable of recognizing a diverse range of fine-grained shapes. The visualization of part segmentation is shown in Figure 4.

Table 5.
Comparison on the ShapeNet part segmentation dataset.
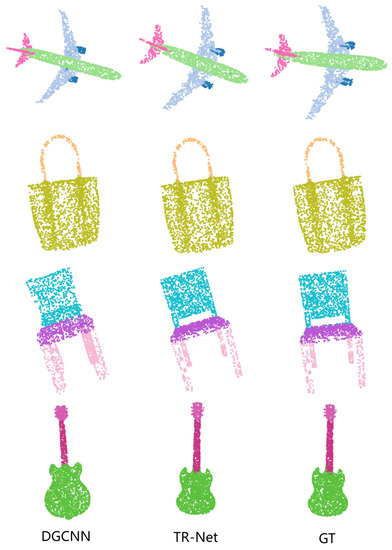
Figure 4.
The visualization of object part segmentation results on the ShapeNet dataset. GT denotes Ground Truth.
4.4. Model Complexity
We now compare the complexity of TR-Net with previous state-of-the-art methods on ModelNet40. The input of model is a sample with 1024 points. As shown in Table 6, our approach achieves the best tradeoff between the model size (number of parameters), FLOPs (floating-point operations required), computational complexity (measured as forward pass time), and the resulting classification accuracy. TR-Net has a relatively low memory requirement with 17Mb parameters and also puts a low load on the processor of only 2.52 GFLOPs, yet obtains high accuracy. These qualities make it well-suited for deployment on mobile devices.

Table 6.
The comparison with different models on complexity, forward time, and accuracy.
5. Ablation Study
To further investigate our proposed approach, we carried out massive experiments on the ModelNet40 dataset. Implementation details remained the same as those given in the experimental section unless otherwise indicated. Without voting strategy, all of the ablative studies were executed.
5.1. Number of Stacked Offset-Attention Layers
There are multiple tasks that have researched the effect of network depth on model performance. We assume that m represents the number of stacked offset-attention layers. As a rule of thumb, we vary the network depth by setting m to 1, 2, 3, 4, 5, and 6. We still adopt OA and mAcc as evaluation metrics. The results of different network depths on the ModelNet40 benchmark are shown in Table 7. At first view, we observe that just increasing the depth cannot always lead to better performance; a proper depth would be an excellent solution. For example, We achieve the best performance with 93.1% OA and 90.4% mAcc when the value of m is 4. The accuracy of the model increases when m is less than 4, and it tends to decrease when m is greater than 4. It is worth noting that we consistently achieve comparable results regardless of the number of hidden layers.

Table 7.
Ablation study: classification accuracy of TR-Net on ModelNet40 test set using m stacked offset-attention layers.
5.2. Number of Neighbors
The setting of neighbors k determines the local neighborhood around each point, which would have an influence on model accuracy. In the phase of this experiment, we still adopt four stacked offset-attention layers in the attention-based sub-network. The quantitative results are displayed in Table 8, and the resulting curves are provided in Figure 5. From the resulting curves with different neighbors, we find that models with more neighbors reach the fitness peak more quickly. When k is set to 32, the best result is obtained. When the value of k is 4, 8, 16 that the neighborhood is smaller, it leads to inadequate local feature extraction. When k is set to 48, 64 that the neighborhood is larger, each offset-attention layer is provided with a great deal of neighborhood data points, many of which may be more distant and less relevant. This may cause too much noise in the processing and thus reduce the accuracy of model. Furthermore, the loss curves are shown in Figure 6. It illustrates that TR-Net with a larger the value of k could converge faster.

Table 8.
Ablation study: classification accuracy of TR-Net on ModelNet40 test set with k neighbors in the definition of local neighborhoods.
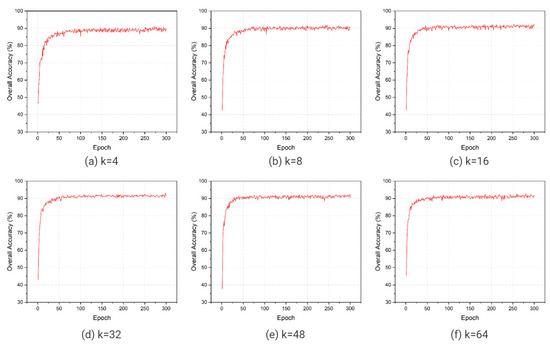
Figure 5.
Six run results (OA) of TR-Net with different neighbors on ModelNet40 test dataset. We use k to denote the number of neighborhood point sets sampled for each point.
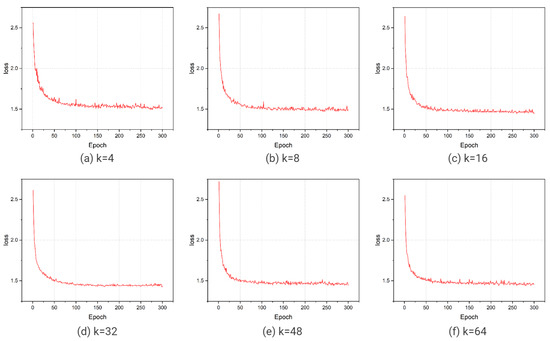
Figure 6.
The loss of TR-Net with different neighbors during each testing phase.
5.3. Component Ablation Study
We only remain the point cloud sampling backbone in TR-Net and test it on the ModelNet40 dataset. The overall accuracy is 91.9%, which is 1.2% less than the base architecture. It indicates that the attention module is effective in improving the accuracy of the network.
6. Conclusions
In this paper, we propose a new architecture named TR-Net, which is based on transformer for learning on point cloud. By adopting the neighborhood embedding strategy and residual backbone, TR-Net could exploit context-aware and spatially-aware features. Experiments show that our approach outperforms voxel-based, MLP-based, and graph-based frameworks and achieves state-of-the-art performance on classification and part segmentation benchmarks. This is due to the fact that the coordinates of point cloud contain spatial location information, and the offset-attention operator sharpens the attention weights to critical information when extracting global features.
Our experiments also suggest that the embedded features can be equally valuable if not more valuable than point coordinates. Developing a practical and theoretically-justified architecture for balancing global and local information in a learning pipeline will require insight from theory and practice in the attention mechanism. Given this, we will think about taking inspiration from image processing and natural language processing. Compared to natural language and 2D image, the available point cloud datasets are very limited nowadays. In the future, we will train it on larger datasets and compare it to other representative frameworks to observe what benefits and limitations it has. Another viable extension is to design a lightweight transformer network that reduces the amount of operations in the reasoning process, making it possible to apply in edge devices.
Author Contributions
Conceptualization, Y.D. and L.L.; methodology, L.L.; software, Y.D.; validation, E.C. and Y.D.; formal analysis, E.C. and Y.D.; investigation, L.L.; resources, E.C.; data curation, Y.D.; writing—original draft preparation, L.L.; writing—review and editing, Y.D.; visualization, E.C. and L.L.; supervision, Y.D.; project administration, L.L.; funding acquisition, E.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Henan Provincial Key Science and Technology Program of China under Grant numbers No. 222102210102.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
We use three publicly available datasets in this study, which are ModelNet40, ScanObjectNN and ShapeNet. ModelNet40 can be found here: https://shapenet.cs.stanford.edu/media/modelnet40_ply_hdf5_2048.zip, accessed on 16 February 2022. ScanObjectNN can be found here: https://hkust-vgd.github.io/scanobjectnn/, accessed on 19 March 2022. ShapeNet can be found here: https://shapenet.cs.stanford.edu/media/shapenet_part_seg_hdf5_data.zip, accessed on 25 March 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zermas, D.; Izzat, I.; Papanikolopoulos, N. Fast Segmentation of 3d Point Clouds: A Paradigm on Lidar Data for Autonomous Vehicle Applications. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 5067–5073. [Google Scholar]
- Rahman, M.M.; Tan, Y.; Xue, J.; Lu, K. Recent Advances in 3D Object Detection in the Era of Deep Neural Networks: A Survey. IEEE Trans. Image Process. 2020, 29, 2947–2962. [Google Scholar] [CrossRef] [PubMed]
- Yi, C.; Lu, D.; Xie, Q.; Liu, S.; Li, H.; Wei, M.; Wang, J. Hierarchical tunnel modeling from 3D raw LiDAR point cloud. Comput.-Aided Des. 2019, 114, 143–154. [Google Scholar] [CrossRef]
- Biswas, J.; Veloso, M. Depth Camera Based Indoor Mobile Robot Localization and Navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1697–1702. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-Shape Convolutional Neural Network for Point Cloud Analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8887–8896. [Google Scholar]
- Le, T.; Duan, Y. PointGrid: A Deep Network for 3D Shape Understanding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9204–9214. [Google Scholar]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Klokov, R.; Lempitsky, V. Escape from Cells: Deep Kd-Networks for the Recognition of 3D Point Cloud Models. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 9, 509–517. [Google Scholar] [CrossRef]
- Riegler, G.; Ulusoy, A.O.; Xie, L.; Geiger, A. OctNet: Learning Deep 3D Representations at High Resolutions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6620–6629. [Google Scholar]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Qi, C.R.; Su, H.; Yi, L.; Su, H.; Guibas, L.J. PointNet plus plus: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. 2019, 5, 146:1–146:13. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution On X-Transformed Points. In Proceedings of the Conference on Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Tu, Z.; Lu, Z.; Liu, Y.; Liu, X.; Li, H. Modeling Coverage for Neural Machine Translation. In Proceedings of the Annual Meeting of the Association-for-Computational-Linguistics, Berlin, Germany, 7–12 August 2016; pp. 76–85. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Su, H.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Mnih, V.; Heess, N.; Graves, A.; Kavukcuoglu, K.; Polosukhin, I. Recurrent Models of Visual Attention. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Hugo, T.; Matthieu, C.; Matthijs, D.; Francisco, M.; Alexandre, S. Training data-efficient image transformers & distillation through attention. arXiv 2020, arXiv:2012.12877. [Google Scholar]
- Huang, J.; Shen, H.; Hou, L.; Kavukcuoglu, K.; Cheng, X. Signed Graph Attention Networks. In Proceedings of the International Conference on Artificial Neural Networks, Munich, Germany, 17–19 September 2019; pp. 566–577. [Google Scholar]
- Chen, C.; Fragonara, L.Z.; Tsourdos, A. GAPNet: Graph Attention based Point Neural Network for Exploiting Local Feature of Point Cloud. arXiv 2019, arXiv:1905.08705. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. RandLA-Net: Efficient Semantic Segmentation of Large-Scale Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11105–11114. [Google Scholar]
- Yang, J.; Dang, J. Semantic segmentation of 3D point cloud based on contextual attention CNN. Ournal Commun. 2020, 7, 195–203. [Google Scholar]
- Guo, M.; Cai, J.; Liu, Z.; Mu, T.; Martin, R.; Hu, S. PCT: Point cloud transformer. Comput. Vis. Media 2021, 2, 187–199. [Google Scholar] [CrossRef]
- Xie, H.; Yao, H.; Zhou, S.; Mao, J.; Zhang, S.; Sun, W. GRNet: Gridding Residual Network for Dense Point Cloud Completion. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 365–381. [Google Scholar]
- You, H.; Feng, Y.; Ji, R.; Gao, Y. PVNet: A Joint Convolutional Network of Point Cloud and Multi-View for 3D Shape Recognition. In Proceedings of the 26th ACM Multimedia Conference, Seoul, Korea, 22–26 October 2018; pp. 1310–1318. [Google Scholar]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view Convolutional Neural Networks for 3D Shape Recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Tatarchenko, M.; Park, J.; Koltun, V.; Zhou, Q. Tangent Convolutions for Dense Prediction in 3D. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3887–3896. [Google Scholar]
- Joseph-Rivlin, M.; Zvirin, A.; Kimmel, R. Momenet: Flavor the Moments in Learning to Classify Shapes. In Proceedings of the IEEE/CVF International Conference On Computer Vision Workshops, Seoul, Korea, 27 October–2 November 2019; pp. 4085–4094. [Google Scholar]
- Yang, J.; Zhang, Q.; Ni, B.; Li, L.; Liu, J.; Zhou, M.; Tian, Q. Modeling Point Clouds with Self-Attention and Gumbel Subset Sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3318–3327. [Google Scholar]
- Zhao, H.; Jiang, L.; Fu, C.; Jia, J. PointWeb: Enhancing Local Neighborhood Features for Point Cloud Processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5550–5558. [Google Scholar]
- Duan, Y.; Zheng, Y.; Lu, J.; Zhou, J.; Tian, Q. Structural Relational Reasoning of Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 949–958. [Google Scholar]
- Lin, H.; Xiao, Z.; Tan, Y.; Chao, H.; Ding, S. Justlookup: One millisecond deep feature extraction for point clouds by lookup tables. In Proceedings of the IEEE International Conference on Multimedia and Expo, Shanghai, China, 8–12 June 2019; pp. 326–331. [Google Scholar]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in Transformer. arXiv 2021, arXiv:2103.00112. [Google Scholar]
- Pang, Y.; Sun, M.; Jiang, X.; Li, X. Convolution in Convolution for Network in Network. IEEE Trans. Neural Netw. Learn. Syst. 2018, 5, 1587–1597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and deep locally connected networks on graphs. In Proceedings of the International Conference on Learning Representations, Munich, Germany, 14–16 April 2014. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A Deep Representation for Volumetric Shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Uy, M.A.; Pham, Q.H.; Hua, B.; Nguyen, D.; Yeung, S. Revisiting Point Cloud Classification: A New Benchmark Dataset and Classification Model on Real-World Data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1588–1597. [Google Scholar]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.C.; Yan, M.Y.; Su, H.; Lu, C.W.; Huang, Q.X.; Sheffer, A.; Guibas, L. A Scalable Active Framework for Region Annotation in 3D Shape Collections. ACM Trans. Graph. 2016, 6, 210:1–210:12. [Google Scholar] [CrossRef]
- Xie, S.; Liu, S.; Chen, Z.; Tu, Z.; Zhang, S.; Sun, W. Attentional ShapeContextNet for Point Cloud Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4606–4615. [Google Scholar]
- Ren, M.; Niu, L.; Fang, Y. 3D-A-Nets: 3D Deep Dense Descriptor for Volumetric Shapes with Adversarial Networks. arXiv 2017, arXiv:1711.10108. [Google Scholar]
- Han, Z.; Shang, M.; Liu, Y.; Zwicker, M. View Inter-Prediction GAN: Unsupervised Representation Learning for 3D Shapes by Learning Global Shape Memories to Support Local View Predictions. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 8376–8384. [Google Scholar]
- Atzmon, M.; Maron, H.; Lipman, Y. Point Convolutional Neural Networks by Extension Operators. ACM Trans. Graph. 2018, 4, 71:1–71:12. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Han, Z.; Liu, Y.; Zwicker, M. Point2Sequence: Learning the Shape Representation of 3D Point Clouds with an Attention-Based Sequence to Sequence Network. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 8778–8785. [Google Scholar]
- Yavartanoo, M.; Kim, E.; Liu, Y.; Lee, K. SPNet: Deep 3D Object Classification and Retrieval Using Stereographic Projection. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; pp. 691–706. [Google Scholar]
- Sfikas, K.; Theoharis, T.; Pratikakis, I. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the Eurographics Workshop on 3D Object Retrieval, Lyon, France, 23–24 April 2017. [Google Scholar]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. 3DmFV: Three-Dimensional Point Cloud Classification in Real-Time Using Convolutional Neural Networks. IEEE Robot. Autom. Lett. 2018, 4, 3145–3152. [Google Scholar] [CrossRef]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. SpiderCNN: Deep Learning on Point Sets with Parameterized Convolutional Filters. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 90–105. [Google Scholar]
- Qiu, S.; Anwar, S.; Barnes, N. Dense-Resolution Network for Point Cloud Classification and Segmentation. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 3812–3821. [Google Scholar]
- Qiu, S.; Anwar, S.; Barnes, N. Geometric Back-Projection Network for Point Cloud Classification. IEEE Trans. Multimed. 2022, 24, 1943–1955. [Google Scholar] [CrossRef]
- Li, J.; Chen, B.; Liu, Y.; Lee, G. SO-Net: Self-Organizing Network for Point Cloud Analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9397–9406. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).