Abstract
Spur shaping cutters, the most versatile gear cutting tools, are used to produce gears that are limited in general cutting cases, such as internal gears and stacked gears. The side clearance angle, which is formed by the profile shifting on the tooth surface, and the rake angle, which increases the cutting efficiency and reduces the wearing of the cutting edge, are designed to create better cutting conditions. However, these cutting angles cause errors in the profile of the cutter edge. In this study, mathematical models of the Isoform® shaping cutter generation method and a model of the cutter edge formed by the conical cutter face were derived to verify the profile error of the cutter edge. A mathematical model to determine the profile error through the corresponding cutter enveloping gear is also proposed. Finally, mathematical models were also derived to correct and reduce the profile error at the major cutter face and the results at the other cutter faces. The numerical results, namely, the profile error curves, show that the corrected cutter has better profile accuracy for the normal usable cutter life.
1. Introduction
Gear shaping is a process that has been widely used for decay and is well developed, especially in fields where it is difficult to achieve results by hobbing, such as manufacturing internal gears and stack gears. A spur gear shaping cutter is a disk-type gear cutting tool that resembles a spur gear in appearance. As shown in Figure 1, the gear shaping cycle comprises the cutting stroke, the returning motion and the indexing motion. The cutting stroke of the spur gear shaping cutter is a linear motion along the cutter’s axis, and its cutting edge forms a cutter enveloping gear [1] during the cutting stroke. To provide appropriate cutting angles for proper cutting conditions, such as the side clearance angle and rake angle, profile shifting along the face width is necessary. Profile shifting also makes the cutter reusable after resharpening. Therefore, the shaping cutter’s parameter needs to be modified on the basis of geometric analysis [1]. Although the modified pressure angle of the cutter enveloping gear is geometrically correct, the curvature of the profile at the pitch circle is slightly incorrect due to the side clearance and rake angles.
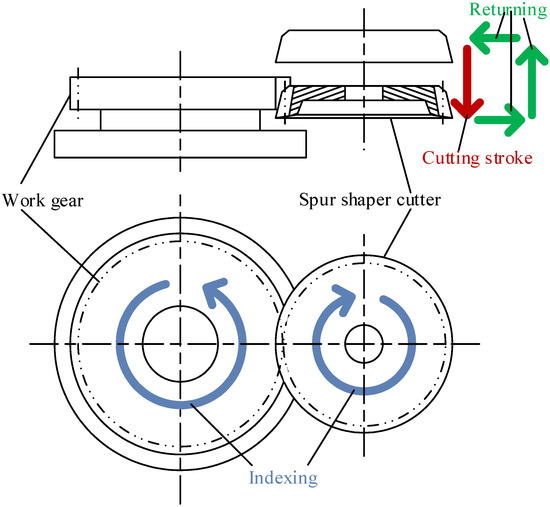
Figure 1.
Motions of the gear shaping cycle.
A shaping cutter is a versatile way to manufacture gears, such as external gears, internal gears and noncircular gears. Its most common application is in manufacturing spur gears. In the past decades, related studies on shaping cutters include those of Mobie et al. [2,3], who developed models for determining cutter offsets to produce nonstandard gears based on equal tooth strength and the method for designing spur gears with shaping cutters; Yoshi et al. [4], who used a spur shaping cutter for finishing gears with arbitrary profiles; Kim and Kim [5], who developed software to design shaping cutters; and Tsai et al. [6], who developed models of spur gears generated by shaping cutters. In studies of elliptical gears manufactured by shaping cutters, Bair [7] developed models for tooth profile generation in elliptical gear manufacturing with shaping cutters and computerized the proposed model, Figliolini and Angeles [8] synthesized elliptical gear generation using a shaping cutter, and Chang and Tsai [9] proposed computerized models for noncircular gears, including the tooth profile and undercut analysis. In the studies of tooth strength and undercutting conditions, Kawalec and Wiktor [10] proposed a model for analyzing the tooth root strength of spur and helical gears manufactured by shaping cutters, Svahn [11] developed the criterion of the undercut condition for shaping gears and improved the undercutting by modifying the basic rack, and Katz et al. [12,13] developed a virtual model for gear shaping that included kinematics, cutter–workpiece engagement, force, elastic deformations and virtual gear metrology.
In addition, Huang and Fong studied helical shaping cutters [14,15,16] based on the Isoform® [17] grinding method, which is focused on the profile correction of helical shaping cutters. In the case of helical shaping cutters, their profile error differs from that of the spur shaping cutters because of their cutter edge types, namely, the plat and the conical cutter faces, respectively. In this study, we modified the mathematical model of the original rack profile to a three-order curve to correct the profile error of a spur shaping cutter. The profile error was reduced by adjusting the second- and third-order coefficients. The results are illustrated as profile error curves that correspond to different resharpened cutter edges.
2. Mathematical Model of the Spur Shaping Cutter
As shown in Figure 2, the Isoform® [17] shaping cutter grinding method is highly accurate and efficient; it also provides a longer cutter life. In the shaping cutter generation process, the grinding wheel reciprocates along the shaping cutter tooth width, and the cutter rocks from side to side against the reciprocating wheel.
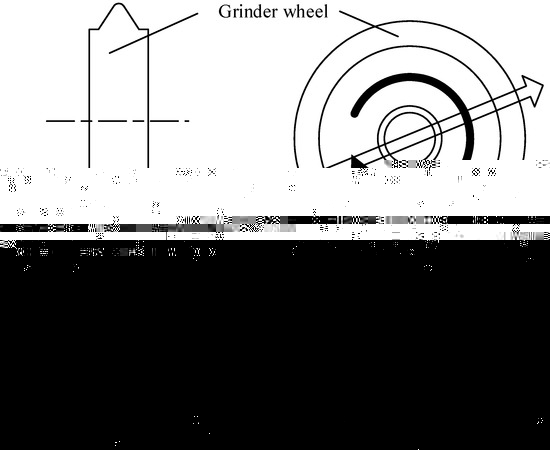
Figure 2.
Isoform® shaping cutter grinding method.
The reciprocating wheel can be considered as an equivalent rack cutter [14,15,16]. The coordinated systems between the shaping cutter and the grinding wheel are shown in Figure 3. Here, the equivalent rack cutter is inclined to the axis of the shaping cutter, which is used to shift the profile of the cutter tooth surface. Figure 3 also shows the relative motion between the equivalent rack and the shaping cutter of an Isoform® shaping cutter. The coordinate system is that of the fixed coordinates, and the coordinate system is rigidly attached to the shaping cutter and rocks from one side to another along the axis; and are the rotating and shifting values during the generating motion along the and axes, respectively. Here, is the pitch radius of the shaping cutter. The coordinate system shifts along . Finally, the coordinate system is rigidly attached to the equivalent rack formed by the reciprocating wheel. It also inclines along to shift the profile of the shaping cutter on the tooth surface.
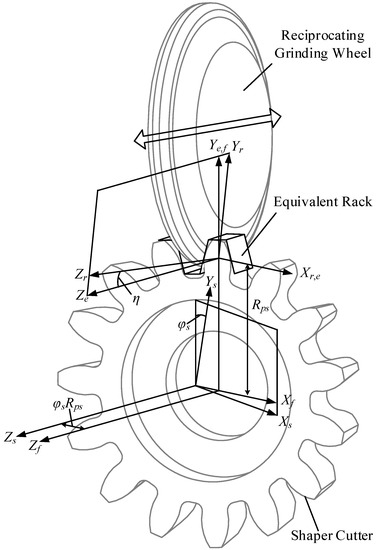
Figure 3.
Coordinate systems for generating a spur shaping cutter.
The profile of the equivalent rack formed by the reciprocating grinding wheel is shown in Figure 4. The coordinate system is attached at the center of the equivalent rack space; and denote the surface variables in the profile and face-width directions on the rack’s surface, respectively; and and depict the tooth space and the normal pressure angle of the equivalent rack, respectively. The position vectors of the rack’s surface are shown in Equation (1) and the unit normal vector of the rack’s surface can be derived by Equation (2), where is the first three elements of . Here, we show only a mathematical model of the right flank, since the left flank is similar. With the coordinate systems , , and shown in Figure 3, the position vectors and unit normal vectors of the equivalent rack can be transformed into the coordinate system of the shaping cutter shown in Equations (3) and (4), respectively. In Equation (3), is the transformation matrix from the equivalent rack coordinate to the spur shaping cutter coordinate . In Equation (4), , the transformation matrix for the normal vectors is the upper-left 3 × 3 sub-matrix of .
where:
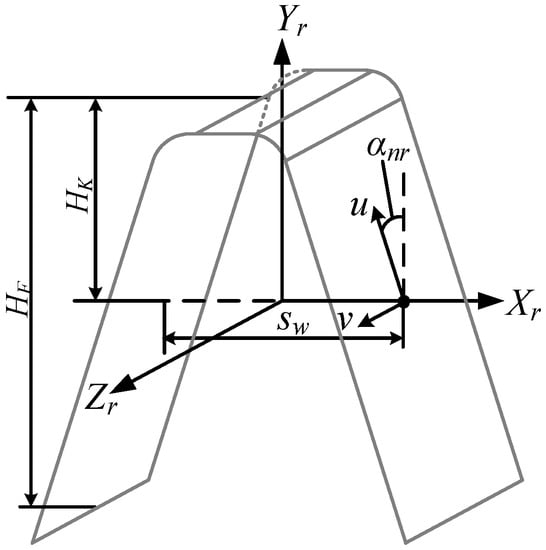
Figure 4.
Profile of the equivalent rack.
Moreover, to derive the tooth surface of the spur shaping cutter, we need the equation of meshing [18,19,20] shown in Equation (5), where depicts the first three elements of . Solving Equations (3) and (5) simultaneously can produce the tooth surface of the shaping cutter.
3. Mathematical Model of the Cutter Edges
Unlike the helical shaping cutter, the spur shaping cutter has a conical cutter face with the rake angle , as shown in Figure 5. Figure 5 also shows the coordinate system for a different resharpened cutter face, , and depicts the distance between the resharpened cutter faces and the original one. A mathematical model of the resharpened cutter face can be derived using Equation (6). Here, is the transformation matrix between the shaping cutter and the resharpened cutter faces. To solve the cutter edge of a spur shaping cutter, the constraint shown in Equation (7) is necessary because it makes the cutter face conical. The cutter edges corresponding to different resharpened positions can be derived by substituting various values of and solving Equations (5)–(7) simultaneously.
where:
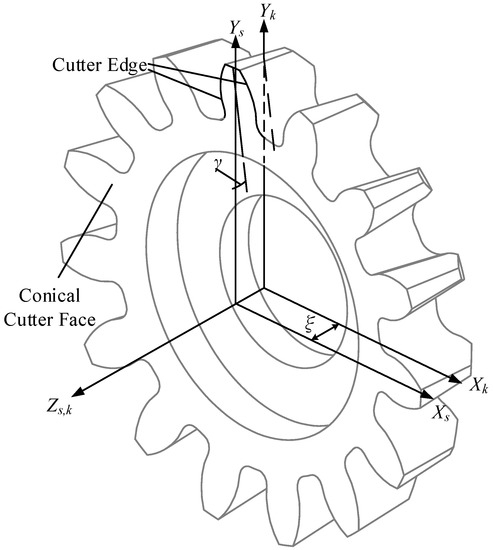
Figure 5.
Cutter edge and conical cutter face of a spur shaping cutter.
4. Profile Error Analysis and Correction
In shaping strokes, the cutter edge sweeps the gear surface of the cutter enveloping gear [1,14,15,16] in space, as shown in Figure 6. The profile of the cutter enveloping gear directly governs the workpiece. Therefore, instead of the cutter edge, the profile of the cutter enveloping gear will be used to determine the profile error of the cutter. The flank of the cutter enveloping gear can be considered as the cutter edge projected on the transverse plane of the spur shaping cutter. Thus, and , which are the respective X- and Y-components of the cutter edge, can be used to determine the profile error. Moreover, in Figure 5, depicts the position corresponding to various resharpened cutter faces. Therefore, by changing and then deriving the corresponding and using the proposed model, the profile of the cutter enveloping gear corresponding to different resharpened cutter faces is derived.
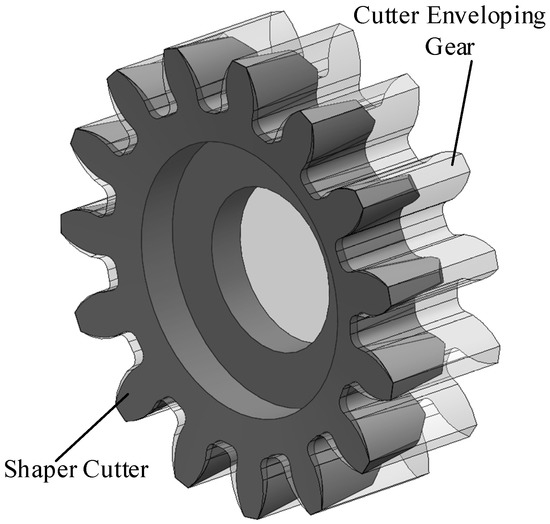
Figure 6.
Spur shaping cutter and cutter enveloping gear.
The spur shaping cutter has a conical cutter face, and the pressure angle of the equivalent rack can be modified by the corresponding geometrical relationships shown below. In Figure 7, shows the desired side clearance angle of the cutter. The side clearance angle relates to the rack cutter pressure angle and the required rack tilting angle shown in Equation (8). In addition, the desired cutter pressure angle related to the required rack tilting angle and the required rack pressure angle are shown in Equation (9). The required parameters and can be derived by solving Equations (8) and (9) simultaneously, which results in Equations (10) and (11), respectively. Note that the determination of the geometrical relationship of the cutter angle was derived in earlier studies [1,14].
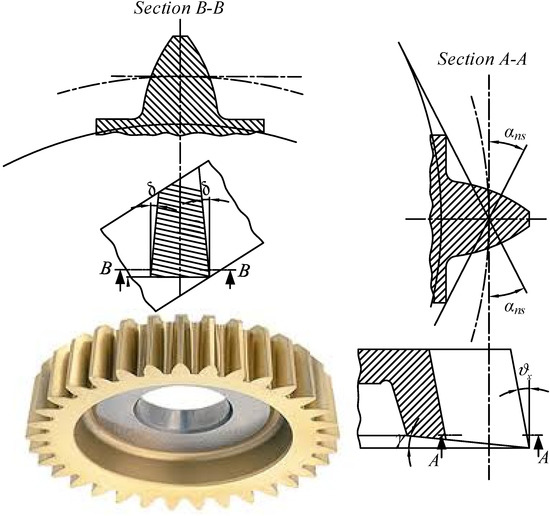
Figure 7.
Cutting angles of a spur shaping cutter.
The profile error of the spur shaping cutter is different from that of the helical shaping cutter because of the difference in the cutter face types. For the helical cutter, even after geometrical modification, the pressure angle is slightly different from what is desired. However, for the spur shaping cutter, the pressure angle of the cutter is correct after geometrical modification. It contains only the curvature and the higher-order curve errors caused by the side clearance angle and rake angle. To reduce the profile of the shaping cutter, the cutter flank of the equivalent rack is replaced by a curve and is related to the coordinate system shown in Figure 8. In Equation (12), depicts the tooth surface of the rack cutter for correcting the cutter profile error, with and as the surface variables. The X- and Y-components of the tooth profile are likewise related in Equation (12). Here, and are the second- and third-order coefficients of the curve. Therefore, can be used to control the curvature of the curve at the pitch circle, while can be used to adjust the third-order curve form. Moreover, is the mathematical model of the rack cutter used to correct the shaping cutter, which is obtained by Equation (13). In Equation (13), is the transformation matrix between the coordinate systems and . We substitute with and re-derive all the corresponding mathematical models, then correct the curvature error by solving and adjusting to reduce the profile error even more.
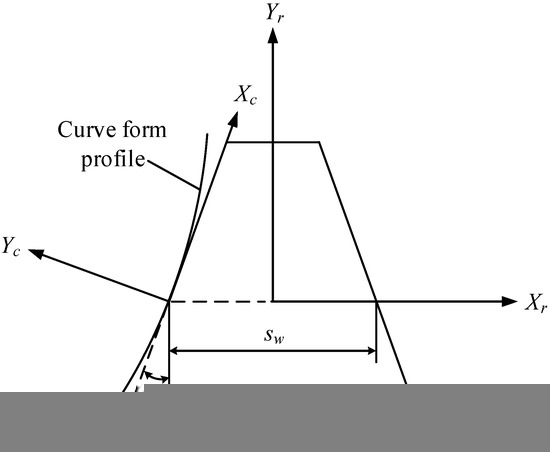
Figure 8.
Profile of the rack for correcting the shaping cutter.
To determine the profile error, the following models should be determined. Figure 9 shows the geometrical model for calculating the error between the actual profile and the theoretical involute. In Figure 9, is the coordinate system of an actual profile and the axis passes through the intersection of the actual profile and the pitch circle. Here, is a certain point on the actual profile and is the tangent point from to the base circle. To calculate the profile error corresponding to the theoretical involute, the latter passes through the intersection of the pitch circle and the axis, which causes the profile error at the pitch circle to be zero. is the corresponding point on the theoretical involute, which starts at on the base circle. The profile error can be determined by . Here, can be derived by Equation (14), where is the radius of the base circle and can be derived by Equation (15), where is the rolling angle of the involute at . Moreover, can be derived by Equation (16), where depicts the value of the involute function obtained by the pressure angle ; can be derived by Equation (17), which is the characteristic of the involute.
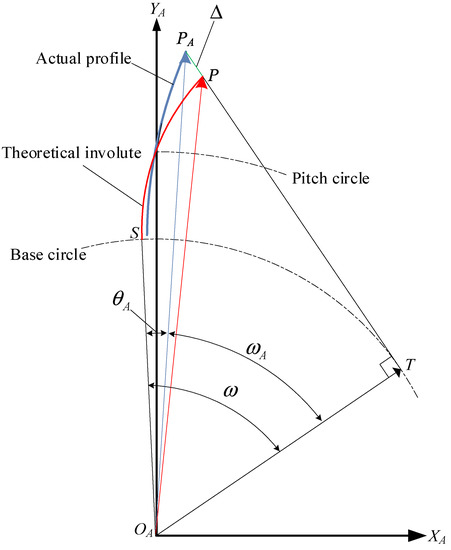
Figure 9.
Determination of the profile error with respect to a theoretical involute.
5. Examples and Discussion
In this section, a numerical example is used to verify the proposed mathematical models for correcting the profile error of the shaping cutter edge. The profile error of each cutter edge varies due to the profile shifting effect caused by the side clearance angle. Here, we used the cutter face at as the major cutter face to correct the profile, in which the profile error of its cutter enveloping gear was reduced to approach zero as much as possible.
The profile error of the cutter edge increases with the number of modules. Normally, internal gears are mostly below Module 3; however, for external gears, Module 4 (or larger) is commonly used. Therefore, as a compromise, we chose DP 7, which is equal to Module 3.6286 mm, as the module of the numerical example. Table 1 shows the design parameters of the numerical example. In Table 1, the cutter parameters are the basic parameter (similar to the spur gear data) and its desired cutting angles; the equivalent rack parameters can be derived using Equations (10) and (11), and the tooth space was chosen as the standard tooth thickness (without profile shifting). The profile error of the uncorrected case is shown in Figure 10. In Figure 10, the error curve is tangential to the Y-axis at the radial positions of the pitch circle, which shows that the pressure angle of the cutter enveloping gear is correct. The maximum profile error of this case is 4.8 μm.

Table 1.
Parameters of the spur shaping cutter and the equivalent rack.
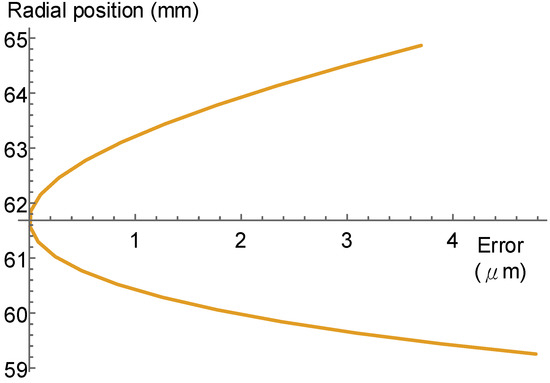
Figure 10.
Cutter edge profile error of the original case of the cutter face, with .
The first step for correction is to correct the curvature at the pitch circle, which can be obtained by . The result is shown in Figure 11. In Figure 11, the profile error near the pitch circle is relatively small, and the profile error is within the sub-micron scale. The maximum profile error is 0.2 μm in this case.
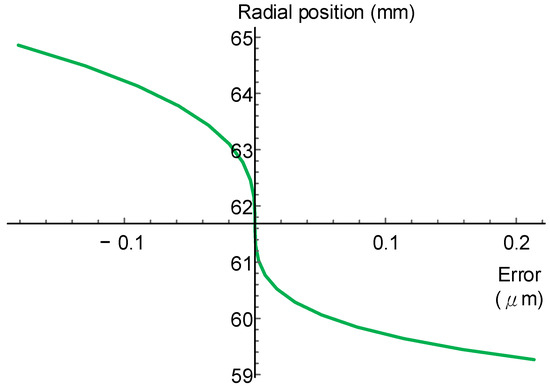
Figure 11.
Cutter edge profile error of the curvature-corrected case of the cutter face, with .
Finally, to reduce the profile error further, we chose . The result is shown in Figure 12. In this case, the maximum profile error is about 0.01 μm, which is usually less than the minimum resolution of a typical gear measuring machine. Figure 13 shows the effects of the proposed model of reducing the profile error step by step on the major cutter edge.
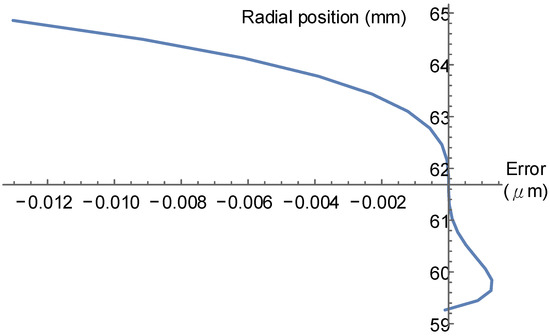
Figure 12.
Cutter edge profile error of curvature and the third-order corrected case of the cutter face, with .
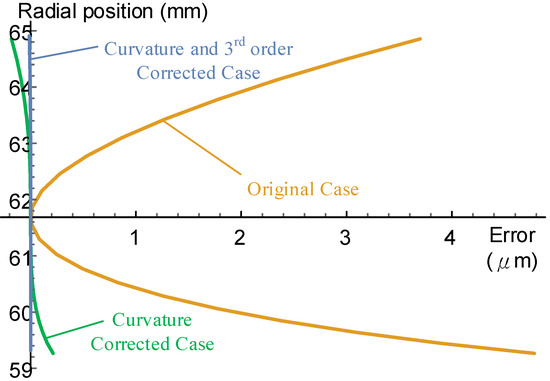
Figure 13.
Comparison of the correction model of the cutter face step by step, with .
The result of the corrected case of the major cutter face approaches zero. To verify the effects of the proposed correcting model on other resharpened cutter faces with positive profile shifting, the results of the corrected and noncorrected cases with the cutter faces and are shown in Figure 14 and Figure 15, respectively. As the results show, after correction, the cutter edges of the shaping cutter perform more accurately in terms of the pressure angle error and form error for positive profile shifting cases.
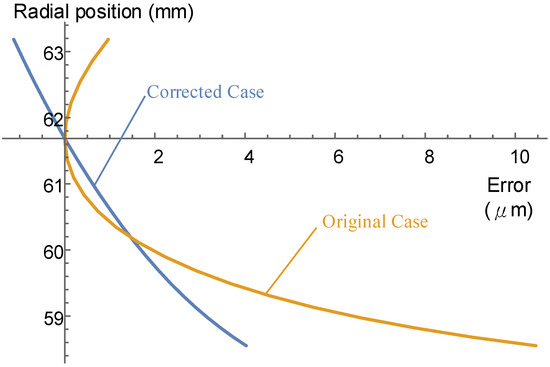
Figure 14.
Comparison of the cutter edge profile error for .
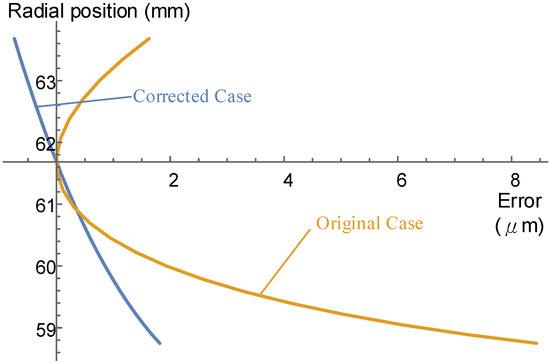
Figure 15.
Comparison of the cutter edge profile error for .
Figure 16 and Figure 17 show the results of the cutter faces and , respectively. In cases of negative profile shifting, after correcting the cutter edge, the shaping cutter still has better form accuracy. For the case of , the pressure angle error of the uncorrected case performs better than that of the corrected case. However, is close to the end of the cutter’s life.
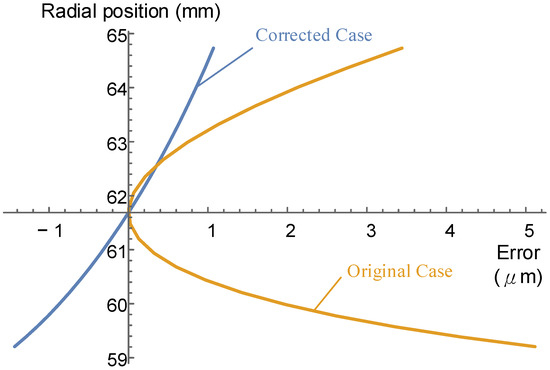
Figure 16.
Comparison of the cutter edge profile error for .
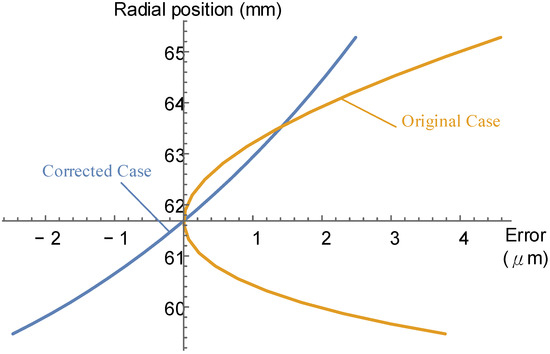
Figure 17.
Comparison of the cutter edge profile error for .
As the results show in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, for the corrected cutter edges, the tilt of the profile error from one side to another corresponds to positive and negative profile shifting. The profile accuracy of the resharpened cutter edges is listed in Table 2 and Table 3, where it is easy to identify the accuracy variations corresponding to the resharpened cutter edges with respect to the original and corrected cases.

Table 2.
Cutter edge profile error of the original case corresponding to the cutter faces.

Table 3.
Cutter edge profile error of the corrected case corresponding to the cutter faces.
6. Conclusions
On the basis of the numerical results, we arrived at the following conclusions:
- (1)
- The proposed model of the spur shaping cutter derives the spur cutter edges of various resharpened cutter faces. The profile error shows that for an uncorrected spur shaping cutter, the pressure angle is correct because the error curve is tangential to the Y-axis of the figure at the pitch circle. However, the curvature at the pitch circle is incorrect.
- (2)
- The proposed model for correcting the spur shaping cutter edges reduces the profile error to approach zero by our second- (curvature) and third-order corrections at the major cutter face. At cutter faces near the major cutter face, the cutter edge profile errors are relatively small with respect to those farther away from the major cutter face. Therefore, for higher accuracy requirements, the major cutter face can be designed slightly behind the first cutter face. In the numerical example, choosing as the first cutter face and as the end of the cutter’s life can be used to manufacture highly accurate workpieces.
- (3)
- The cutter edge profile error forms a convex shape with different sections corresponding to different resharpened spur shaping cutter faces in the uncorrected case, as shown in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. However, for the corrected spur shaping cutter, the form errors of each cutter face are reduced to sub-micron-level accuracy, as shown in Table 3.
Author Contributions
Conceptualization, C.-L.H.; methodology, C.-L.H.; validation, C.-L.H.; data curation, C.-L.H. and Y.-C.W.; writing—original draft preparation, C.-L.H.; writing—review and editing, C.-L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to the Ministry of Science and Technology of Taiwan for its financial support. Part of this work was performed under Contract No. MOST 105-2218-E-150-005.
Conflicts of Interest
The authors declare no conflict of interest.
References
- LORENZ GmbH. Manual for Design and Manufacturing, 3rd ed.; G. Braun GmbH: Ettlingen, Germany, 1980. [Google Scholar]
- Roger, R.N.; Mabie, H.H. Determination of pinion cutter offsets required to produce nonstandard spur gears with teeth of equal strength. Mech. Mach. Theory 1980, 15, 491–506. [Google Scholar]
- Rogers, C.A.; Mabie, H.H.; Reinholtz, C.F. Design of spur gears generated with pinion cutters. Mech. Mach. Theory 1990, 25, 623–634. [Google Scholar] [CrossRef]
- Yoshino, H.; Shao, M.; Ishibashi, A. Design and manufacture of pinion cutters for finishing gears with an arbitrary profile. Int. J. JSME Ser. III 1992, 35, 313–319. [Google Scholar] [CrossRef]
- Kim, J.D.; Kim, D.S. Development of software for the design of a pinion cutter. J. Mater. Process. Technol. 1997, 68, 76–82. [Google Scholar] [CrossRef]
- Tsay, C.B.; Liu, W.Y.; Chen, Y.C. Spur gear generation by shaping cutters. J. Mater. Process. Technol. 2000, 104, 271–279. [Google Scholar] [CrossRef]
- Bair, B.W. Computerized tooth profile generation of elliptical gears manufactured by shaping cutters. J. Mater. Process. Technol. 2002, 122, 139–147. [Google Scholar] [CrossRef]
- Figliolini, G.; Angeles, J. The synthesis of elliptical gears generated by shaper-cutter. ASME J. Mech. Des. 2003, 25, 793–801. [Google Scholar] [CrossRef]
- Chang, S.L.; Tsay, C.B. Computerized tooth profile generation and undercut analysis of noncircular gears manufactured with shaping cutters. ASME J. Mech. Des. 1998, 120, 92–99. [Google Scholar] [CrossRef]
- Kawalec, A.; Wiktor, J. Tooth root strength of spur and helical gears manufactured with gear-shaping cutters. ASME J. Mech. Des. 2008, 130, 034502. [Google Scholar] [CrossRef]
- Svahn, M. The undercut criterion of pinion shaping cutters: And an improvement by modifying the basic rack profile. ASME J. Manuf. Sci. Eng. 2016, 138, 011011. [Google Scholar] [CrossRef]
- Katz, A.; Erkorkmaz, K.; Ismail, F. Virtual model of gear shaping part I: Kinematics, cutter-workpiece engagement, and cutting forces. ASME J. Mech. Des. 2018, 140, 071007. [Google Scholar] [CrossRef]
- Katz, A.; Erkorkmaz, K.; Ismail, F. Virtual model of gear shaping part II: Elastic deformations and virtual gear metrology. ASME J. Mech. Des. 2018, 140, 071008. [Google Scholar]
- Huang, C.L.; Fong, Z.H.; Chen, S.D.; Chang, K.R. Profile correction of a helical gear shaping cutter using the lengthwise-reciprocating grinding method. Mech. Mach. Theory 2009, 44, 401–411. [Google Scholar] [CrossRef]
- Huang, C.L.; Fong, Z.H.; Chen, S.D.; Chang, K.R. Novel third-order correction for a helical gear shaping cutter made by a lengthwise-reciprocating grinding process. ASME J. Mech. Des. 2009, 131, 051008. [Google Scholar] [CrossRef]
- Huang, C.L.; Fong, Z.H. Modified-roll profile correction for a helical gear shaping cutter made by the lengthwise-reciprocating grinding process. ASME J. Mech. Des. 2011, 133, 041001. [Google Scholar] [CrossRef]
- Gleason Works. Gleason Cutting Tools; Gleason Cutting Tools Corporation: Loves Park Illinois, IL, USA, 2000. [Google Scholar]
- Litvin, F.L. Theory of Gearing; NASA Reference Publication, U.S. Government Printing Office: Washington, DC, USA, 1989. [Google Scholar]
- Litvin, F.L. Gear Geometry and Applied Theory; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).