Robust Image Matching Based on Image Feature and Depth Information Fusion
Abstract
:1. Introduction
- A feature point description method that fuses image feature and depth information is proposed, which has the potential to improve the accuracy of feature matching.
- The feature-matching performance of different fusion features constructed based on the proposed method is verified on public RGB-D datasets.
2. Related Work
- (1)
- Image feature extraction and representation
- (2)
- Point cloud feature extraction and representation
- (3)
- Image and point cloud feature fusion
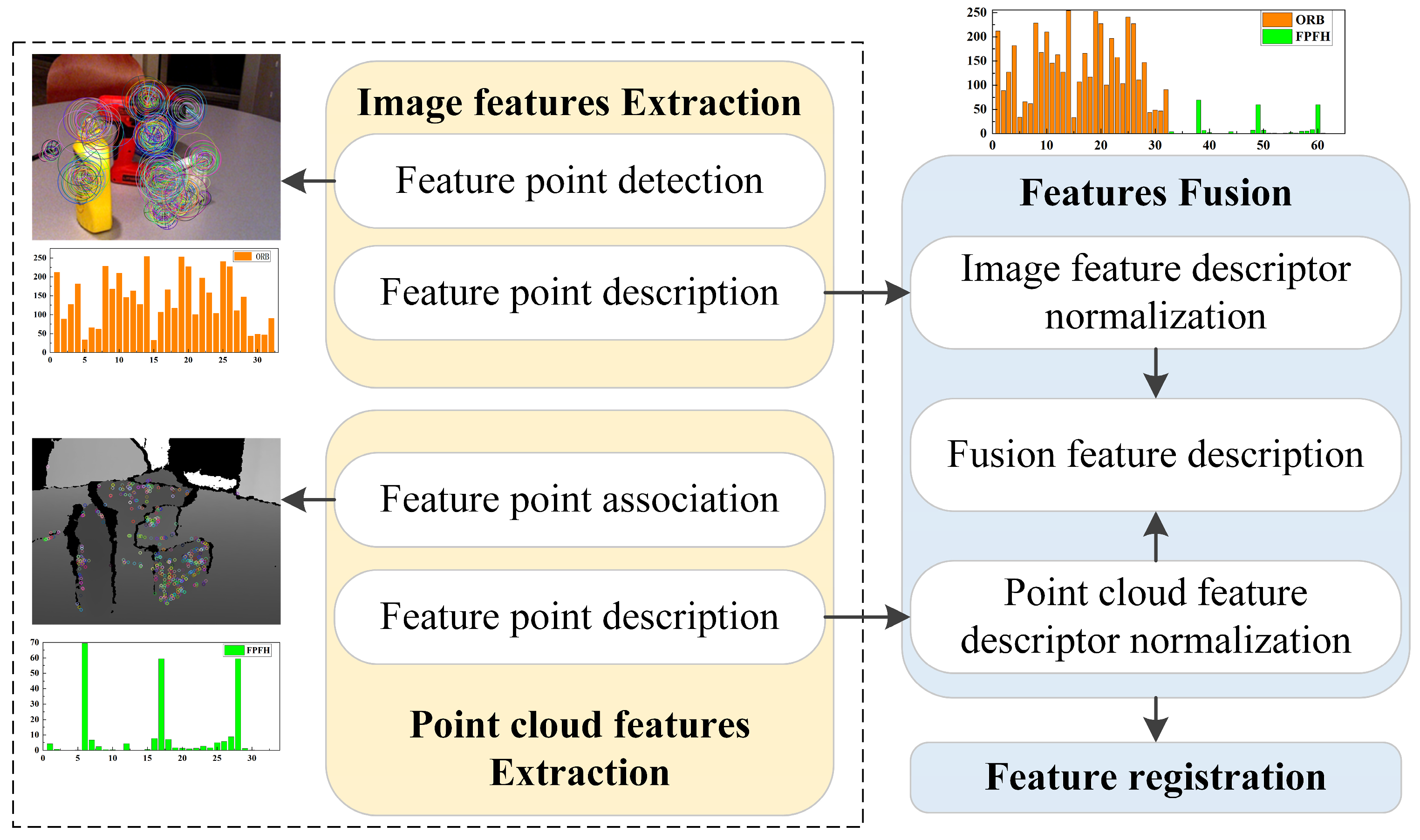
3. Feature Extraction and Matching
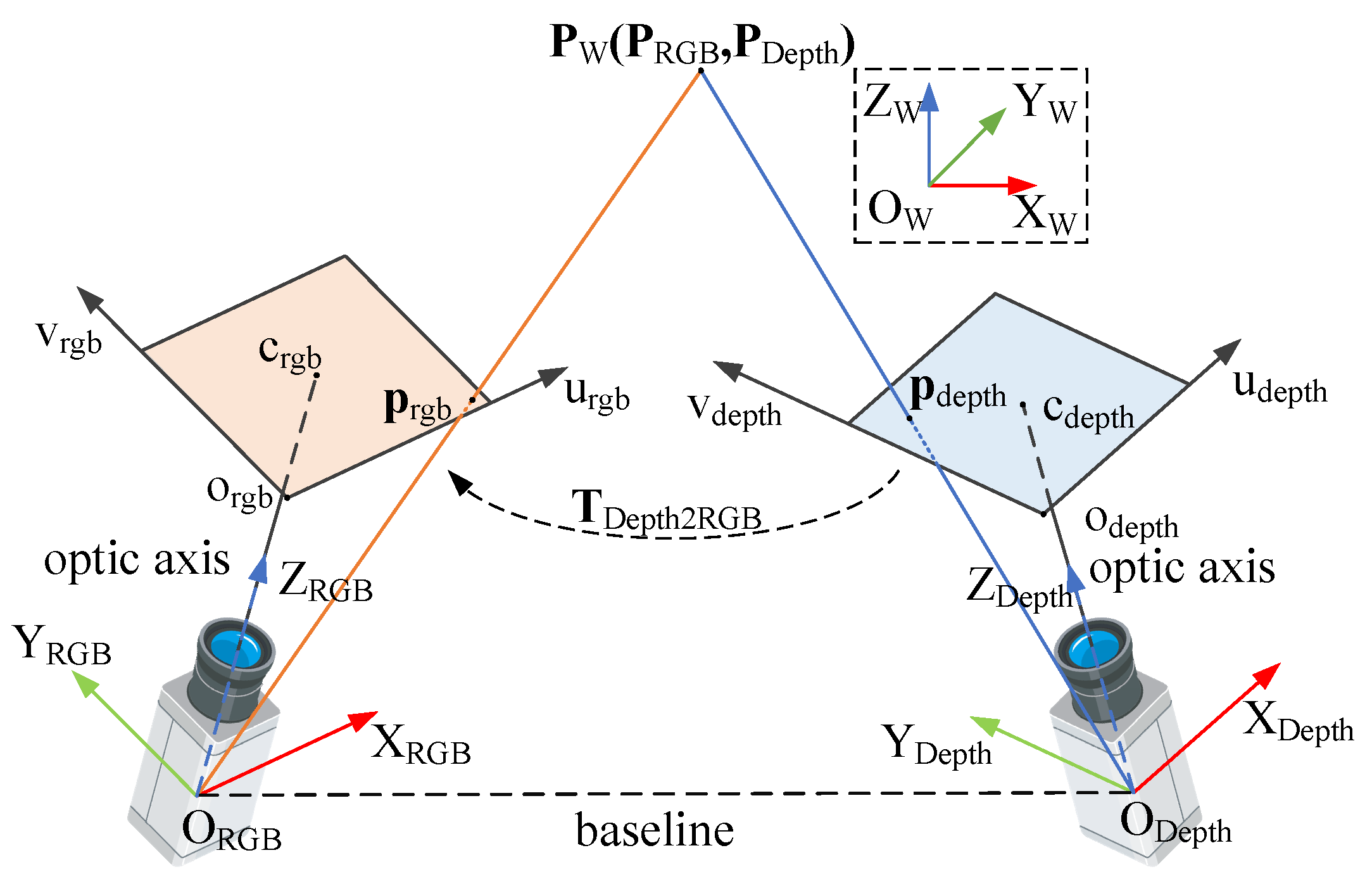
3.1. RGB-D Camera Calibration
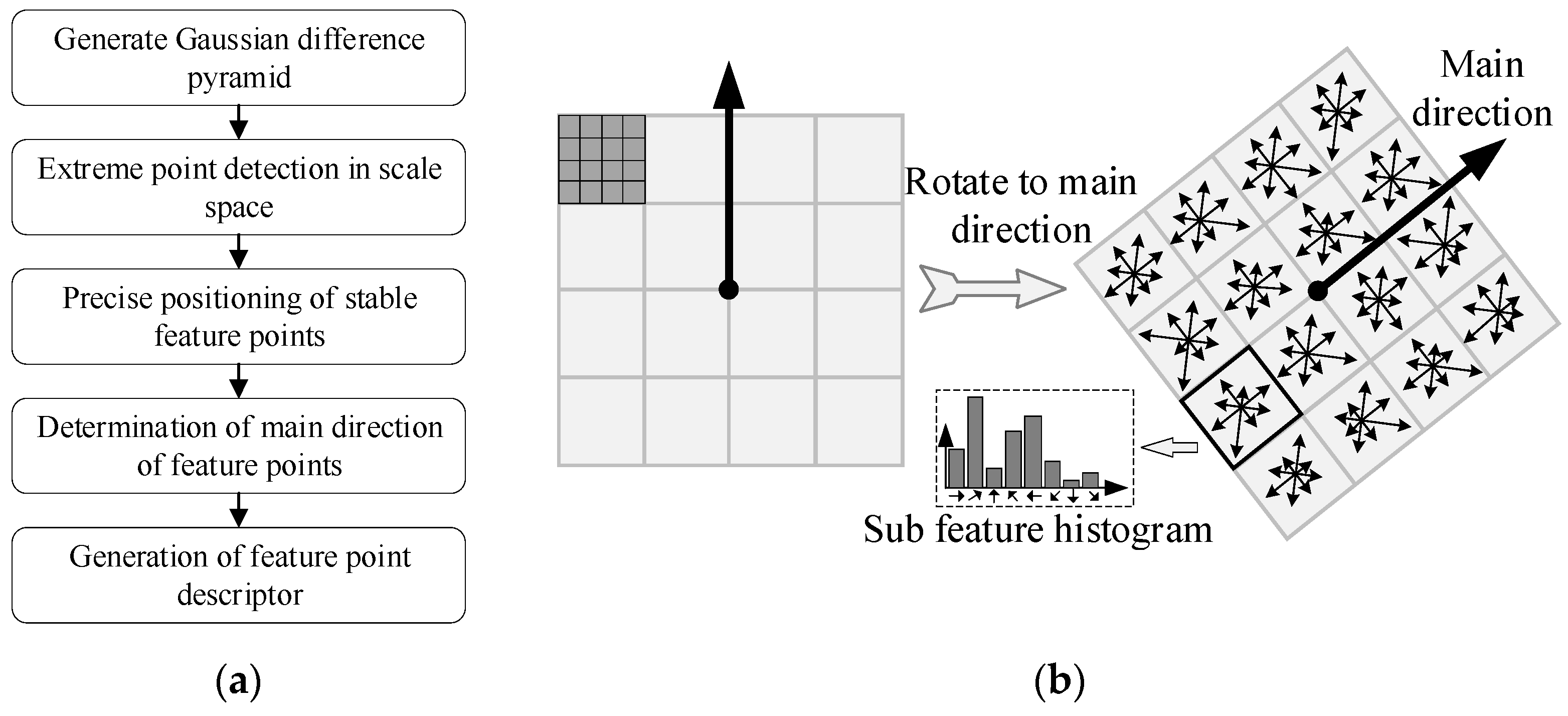
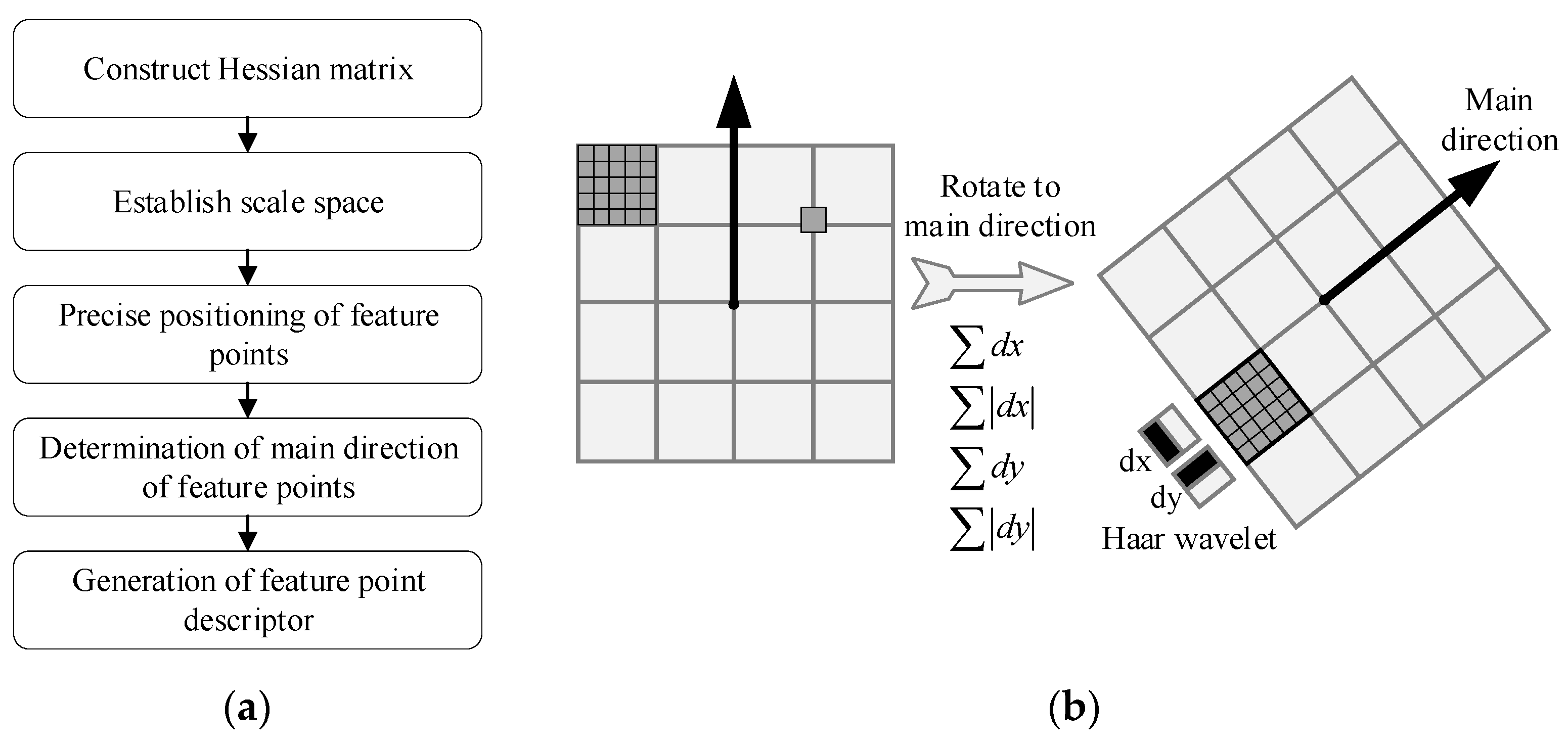
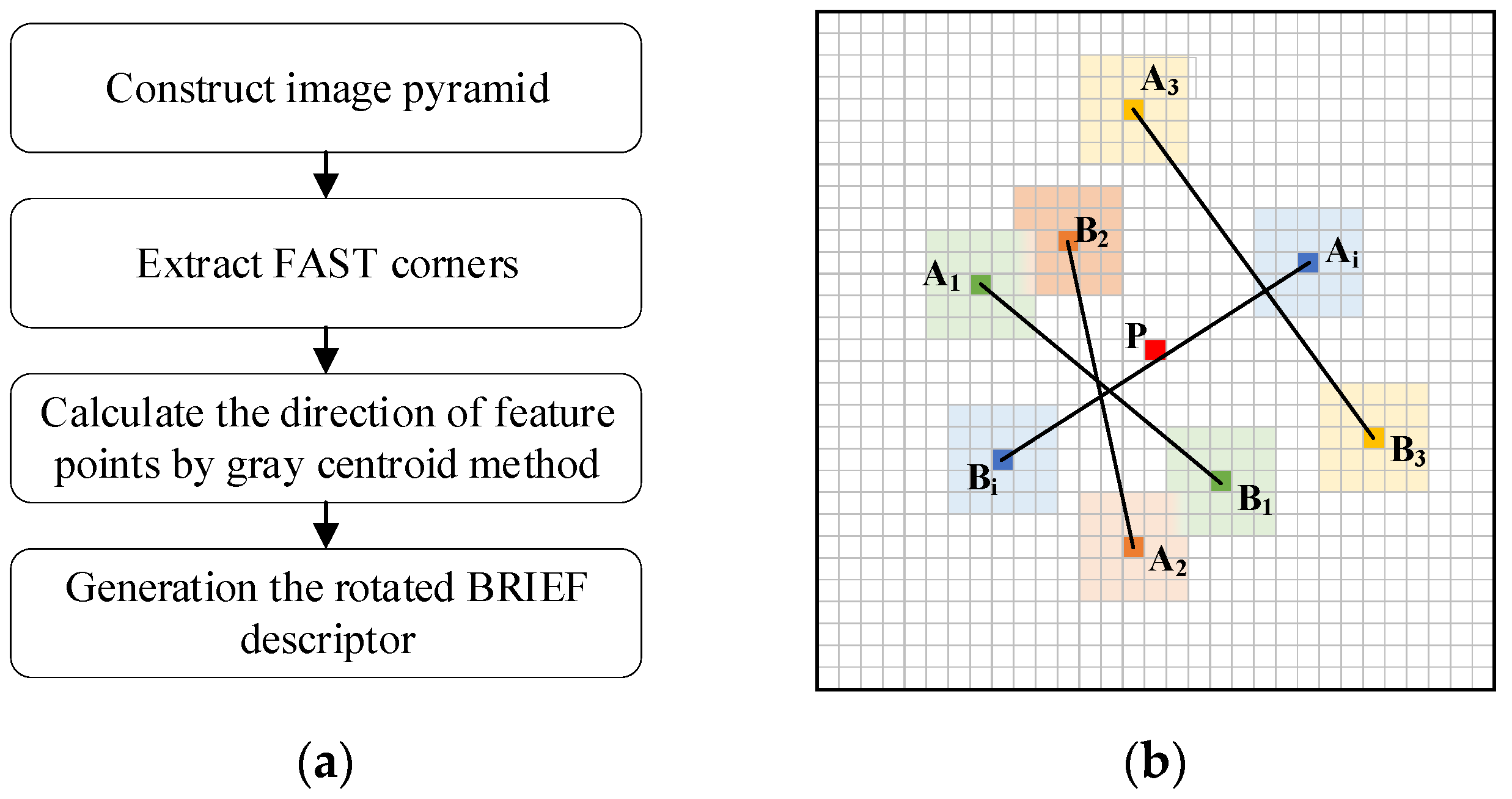
3.2. Feature Extraction from RGB Maps
- (1)
- SIFT
- (12)
- SURF
- (3)
- ORB
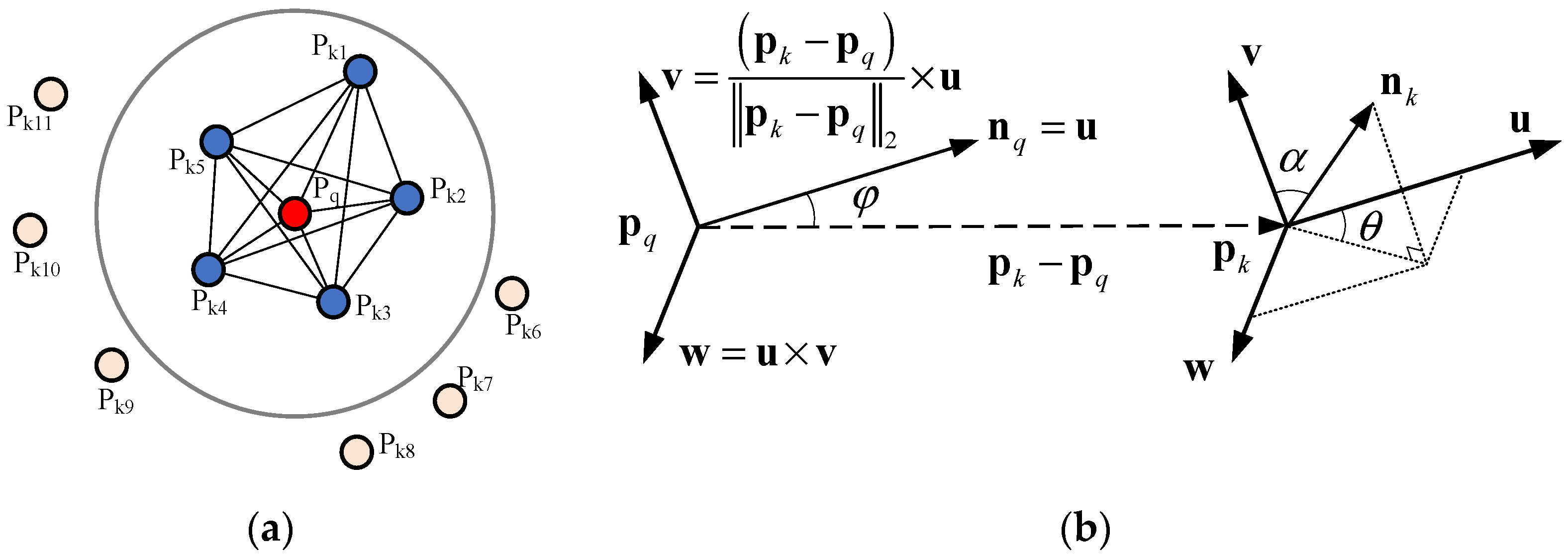
3.3. Feature Extraction from Point Cloud
- (1)
- PFH
- (2)
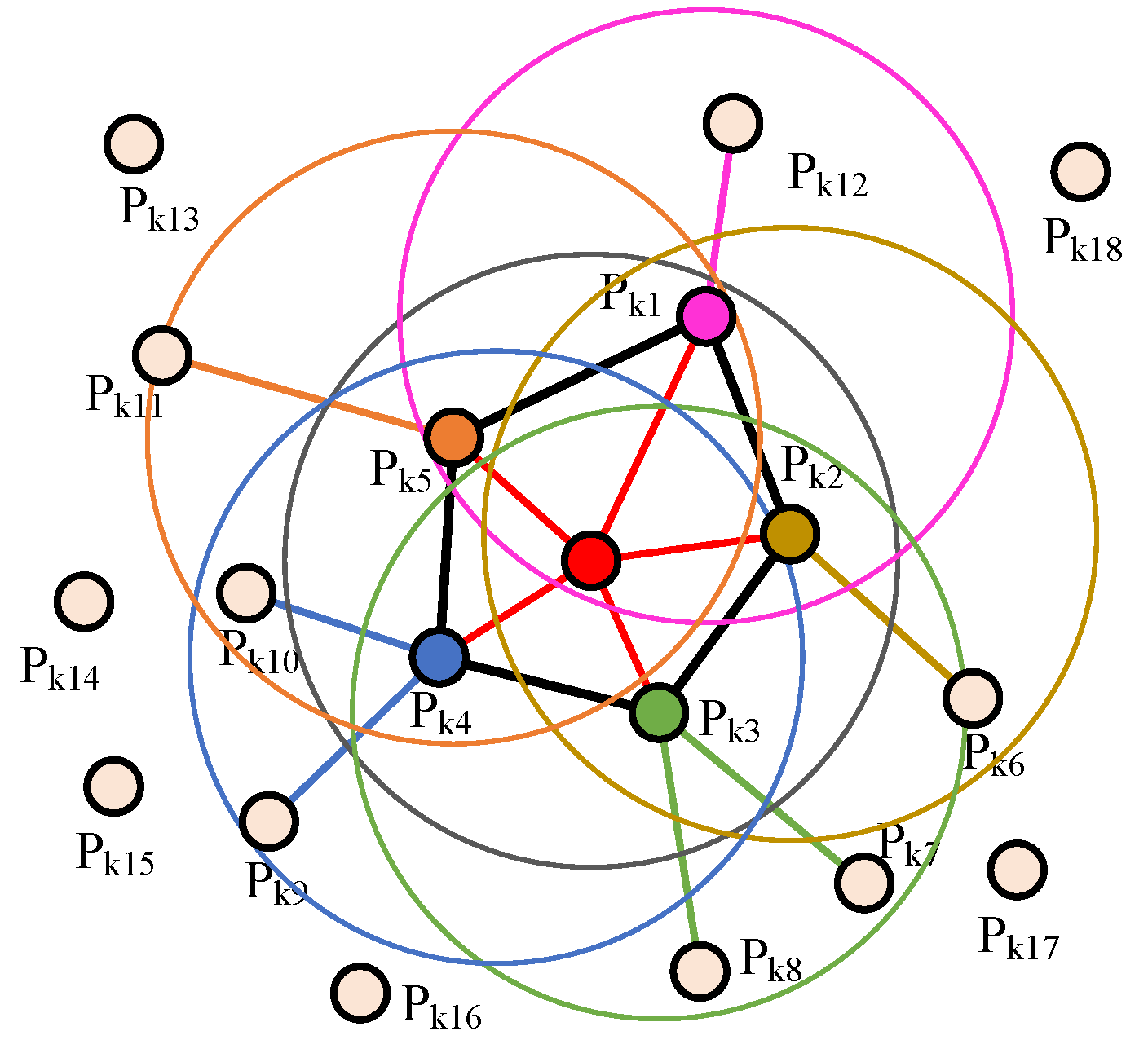
- FPFH
- For each sample point, the three angle eigenvalues are calculated between the point and each point in its K neighborhood, and each angle eigenvalue is divided into 11 intervals, so a 33-dimensional simplified point feature histogram (SPFH) is obtained;
- The K-neighborhood points of each point are calculated to form their SPFH;
- The final FPFH is calculated with the following formula:
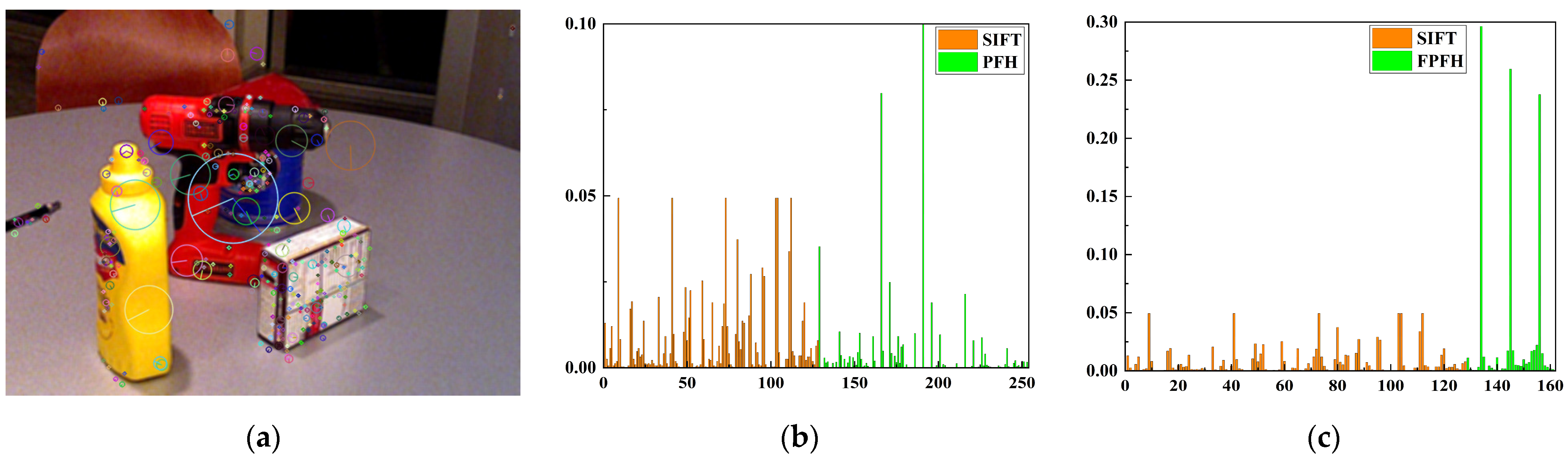
3.4. Feature Fusion
- (1)
- SIFT and SURF feature descriptors, as well as those of PFH and FPFH are floating-point descriptors. For this kind of floating-point feature descriptor, we propose direct splicing of the normalized point cloud feature descriptors after the normalized image feature descriptors to form the fusion feature descriptors SIFTPFH, SIFTFPFH, SURFPFH, and SURFFPFH.
- (2)
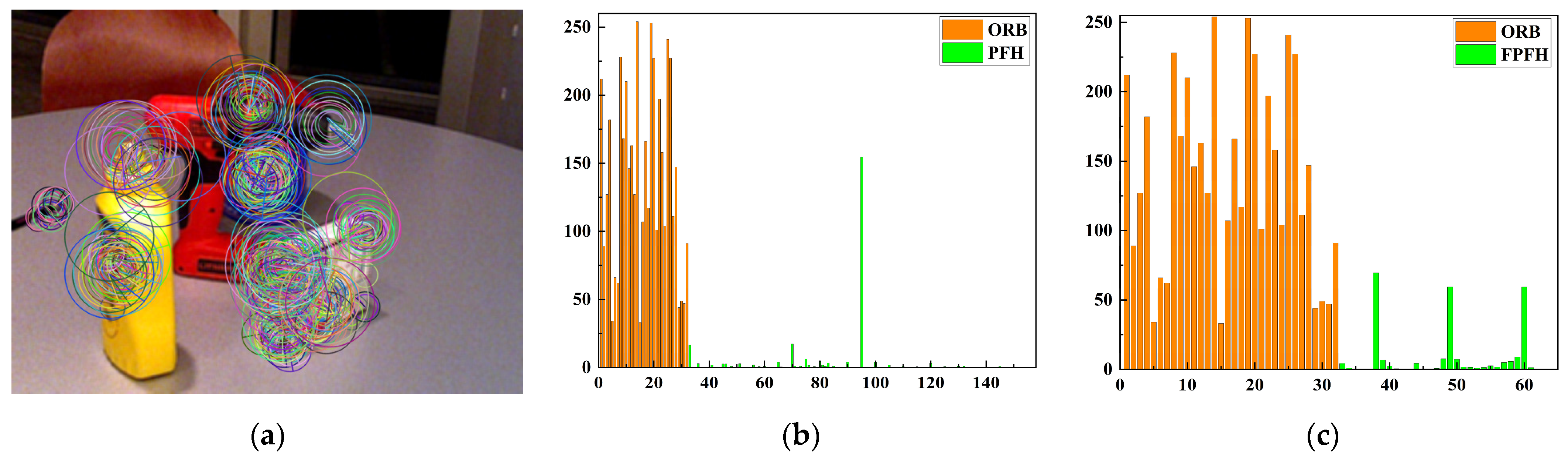
- The image feature descriptor of ORB is a binary string, and the point cloud feature descriptors of PFH and FPFH are floating-point descriptors. In order to maintain the respective feature-description ability of binary descriptors and floating-point descriptors, the data types of the two descriptors are kept unchanged and combined into a tuple, thereby obtaining the fusion feature descriptors of ORBPFH and ORBFPFH. Because the norm of PFH or FPFH is minor, to increase the weight of point cloud features, we usually multiply a coefficient to make the norm of PFH or FPFH after multiplication close to the length of ORB features.
3.5. Feature Matching
4. Experiment and Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Washington, DC, USA, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Washington, DC, USA, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Alahi, A.; Ortiz, R.; Vandergheynst, P. Freak: Fast retina keypoint. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 16–21 June 2012; pp. 510–517. [Google Scholar]
- Johnson, A.E.; Hebert, M. Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 433–449. [Google Scholar] [CrossRef] [Green Version]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing objects in range data using regional point descriptors. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 224–237. [Google Scholar]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef] [Green Version]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Beetz, M. Learning informative point classes for the acquisition of object model maps. In Proceedings of the 2008 10th International Conference on Control, Automation, Robotics and Vision, Hanoi, Vietnam, 17–20 December 2008; pp. 643–650. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Tombari, F.; Salti, S.; Stefano, L.D. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 356–369. [Google Scholar]
- Salti, S.; Tombari, F.; Di Stefano, L. SHOT: Unique signatures of histograms for surface and texture description. Comput. Vis. Image Underst. 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Steder, B.; Rusu, R.B.; Konolige, K.; Burgard, W. NARF: 3D range image features for object recognition. In Proceedings of the Workshop on Defining and Solving Realistic Perception Problems in Personal Robotics at the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taibei, China, 18–22 October 2010. [Google Scholar]
- Guo, Y.; Sohel, F.; Bennamoun, M.; Lu, M.; Wan, J. Rotational projection statistics for 3D local surface description and object recognition. Int. J. Comput. Vis. 2013, 105, 63–86. [Google Scholar] [CrossRef] [Green Version]
- Prakhya, S.M.; Liu, B.; Lin, W. B-SHOT: A binary feature descriptor for fast and efficient keypoint matching on 3D point clouds. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1929–1934. [Google Scholar]
- Shen, Z.; Ma, X.; Zeng, X. Hybrid 3D surface description with global frames and local signatures of histograms. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 1610–1615. [Google Scholar]
- Yang, J.; Cao, Z.; Zhang, Q. A fast and robust local descriptor for 3D point cloud registration. Inf. Sci. 2016, 346, 163–179. [Google Scholar] [CrossRef]
- Srivastava, S.; Lall, B. 3D binary signatures. In Proceedings of the Tenth Indian Conference on Computer Vision, Graphics and Image Processing, Guwahati, India, 18–22 December 2016; pp. 1–8. [Google Scholar]
- Prakhya, S.M.; Lin, J.; Chandrasekhar, V.; Lin, W.; Liu, B. 3DHoPD: A fast low-dimensional 3-D descriptor. IEEE Robot. Autom. Lett. 2017, 2, 1472–1479. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Xiao, Y.; Cao, Z. TOLDI: An effective and robust approach for 3D local shape description. Pattern Recognit. 2017, 65, 175–187. [Google Scholar] [CrossRef]
- Rehman, S.U.; Asad, H. A novel approach for feature extraction from RGB-D data. Technology 2017, 3, 1538–1541. [Google Scholar]
- Zou, Y.; Wang, X.; Zhang, T.; Liang, B.; Song, J.; Liu, H. BRoPH: An efficient and compact binary descriptor for 3D point clouds. Pattern Recognit. 2018, 76, 522–536. [Google Scholar] [CrossRef]
- Quan, S.; Ma, J.; Hu, F.; Fang, B.; Ma, T. Local voxelized structure for 3D binary feature representation and robust registration of point clouds from low-cost sensors. Inf. Sci. 2018, 444, 153–171. [Google Scholar]
- Khan, W.; Phaisangittisagul, E.; Ali, L.; Gansawat, D.; Kumazawa, I. Combining features for RGB-D object recognition. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; pp. 1–5. [Google Scholar]
- Alshawabkeh, Y. Linear feature extraction from point cloud using color information. Herit. Sci. 2020, 8, 28. [Google Scholar] [CrossRef]
- Chen, H.; Sun, D. Feature extraction of point cloud using 2D-3D transformation. In Proceedings of the Twelfth International Conference on Graphics and Image Processing (ICGIP 2020), Xi’an, China, 13–15 November 2021; p. 117200P. [Google Scholar]
- Li, Y.; Luo, Y.; Gu, X.; Chen, D.; Gao, F.; Shuang, F. Point cloud classification algorithm based on the fusion of the local binary pattern features and structural features of voxels. Remote Sens. 2021, 13, 3156. [Google Scholar] [CrossRef]
- Pan, L.; Zhou, X.; Shi, R.; Zhang, J.; Yan, C. Cross-modal feature extraction and integration based RGBD saliency detection. Image Vis. Comput. 2020, 101, 103964. [Google Scholar] [CrossRef]
- Tian, J.; Cheng, W.; Sun, Y.; Li, G.; Jiang, D.; Jiang, G.; Tao, B.; Zhao, H.; Chen, D. Gesture recognition based on multilevel multimodal feature fusion. J. Intell. Fuzzy Syst. 2020, 38, 2539–2550. [Google Scholar] [CrossRef]
- Zhu, X.; Li, Y.; Fu, H.; Fan, X.; Shi, Y.; Lei, J. RGB-D salient object detection via cross-modal joint feature extraction and low-bound fusion loss. Neurocomputing 2021, 453, 623–635. [Google Scholar] [CrossRef]
- Bai, J.; Wu, Y.; Zhang, J.; Chen, F. Subset based deep learning for RGB-D object recognition. Neurocomputing 2015, 165, 280–292. [Google Scholar] [CrossRef]
- Zhang, Z. Flexible camera calibration by viewing a plane from unknown orientations. In Proceedings of the the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 666–673. [Google Scholar]







| Descriptor | Ne | Nm | Te (ms) | Tm (ms) | Ta (ms) | |
|---|---|---|---|---|---|---|
| 1st Img | 2nd Img | |||||
| SIFT | 400 | 400 | 129 | 309 | 19 | 328 |
| SIFTPFH | 400 | 400 | 111 | 848 | 19 | 867 |
| SIFTFPFH | 400 | 400 | 117 | 418 | 15 | 433 |
| SURF | 961 | 991 | 245 | 286 | 31 | 317 |
| SURFPFH | 961 | 991 | 182 | 2425 | 49 | 2474 |
| SURFFPFH | 961 | 991 | 199 | 523 | 31 | 554 |
| ORB | 421 | 433 | 103 | 2 | 11 | 13 |
| ORBPFH | 421 | 433 | 160 | 698 | 9 | 707 |
| ORBFPFH | 421 | 433 | 145 | 108 | 9 | 117 |
| Descriptor | Ne | Nm | Te (ms) | Tm (ms) | Ta (ms) | |
|---|---|---|---|---|---|---|
| 1st Img | 2nd Img | |||||
| SIFT | 400 | 321 | 37 | 309 | 34 | 343 |
| SIFTPFH | 400 | 321 | 26 | 741 | 34 | 775 |
| SIFTFPFH | 400 | 321 | 32 | 433 | 34 | 467 |
| SURF | 1347 | 1169 | 51 | 286 | 49 | 335 |
| SURFPFH | 1347 | 1169 | 29 | 2726 | 65 | 2791 |
| SURFFPFH | 1347 | 1169 | 40 | 562 | 49 | 611 |
| ORB | 347 | 220 | 47 | 2 | 28 | 30 |
| ORBPFH | 347 | 220 | 36 | 378 | 26 | 404 |
| ORBFPFH | 347 | 220 | 38 | 88 | 25 | 113 |
| Descriptor | Failed Nm | MFR | ||||
|---|---|---|---|---|---|---|
| Total frames | 200 | 280 | 300 | 200 | 280 | 300 |
| SIFT | 0 | 0 | 1 | 0% | 0% | 0.33% |
| SIFTPFH | 0 | 3 | 11 | 0% | 1.07% | 3.67% |
| SIFTFPFH | 2 | 20 | 32 | 1% | 7.14% | 10.67% |
| SURF | 0 | 29 | 45 | 0% | 10.36% | 15% |
| SURFPFH | 0 | 25 | 40 | 0% | 8.93% | 13.33% |
| SURFFPFH | 0 | 36 | 53 | 0% | 12.86% | 17.67% |
| ORB | 0 | 36 | 51 | 0% | 12.86% | 17% |
| ORBPFH | 0 | 0 | 1 | 0% | 0% | 0.33% |
| ORBFPFH | 0 | 0 | 0 | 0% | 0% | 0% |
| Descriptor | Failed Nm | MFR | ||||
|---|---|---|---|---|---|---|
| Total frames | 100 | 125 | 150 | 100 | 125 | 150 |
| SIFT | 1 | 10 | 24 | 1% | 8% | 16% |
| SIFTPFH | 8 | 32 | 57 | 8% | 25.60% | 38% |
| SIFTFPFH | 6 | 23 | 48 | 6% | 18.40% | 32% |
| SURF | 16 | 41 | 66 | 16% | 32.80% | 44% |
| SURFPFH | 19 | 44 | 69 | 19% | 35.20% | 46% |
| SURFFPFH | 23 | 48 | 73 | 23% | 38.40% | 48.67% |
| ORB | 11 | 36 | 53 | 11% | 28.80% | 35.33% |
| ORBPFH | 4 | 26 | 46 | 4% | 20.80% | 30.67% |
| ORBFPFH | 2 | 19 | 23 | 2% | 15.20% | 15.33% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Wang, H.; Ning, Q.; Lu, Y. Robust Image Matching Based on Image Feature and Depth Information Fusion. Machines 2022, 10, 456. https://doi.org/10.3390/machines10060456
Yan Z, Wang H, Ning Q, Lu Y. Robust Image Matching Based on Image Feature and Depth Information Fusion. Machines. 2022; 10(6):456. https://doi.org/10.3390/machines10060456
Chicago/Turabian StyleYan, Zhiqiang, Hongyuan Wang, Qianhao Ning, and Yinxi Lu. 2022. "Robust Image Matching Based on Image Feature and Depth Information Fusion" Machines 10, no. 6: 456. https://doi.org/10.3390/machines10060456
APA StyleYan, Z., Wang, H., Ning, Q., & Lu, Y. (2022). Robust Image Matching Based on Image Feature and Depth Information Fusion. Machines, 10(6), 456. https://doi.org/10.3390/machines10060456







