Abstract
With flexure-based micro-positioning stages (MPSs) being in high demand for high-precision applications, the performance and cost of flexure-based MPSs are two issues that urgently need to be addressed. In addition, the current MPSs are being developed toward complex spatial configurations, which further precludes monolithic fabrication. To address the aforementioned issues, modular MPSs using designed standardized modules are introduced in this paper. Firstly, the motivations are described, followed by the modular design. In addition, a new assembly concept analogy with composing compounds is proposed for guiding module assembly, including some proposed planar and spatial configurations. For validation, the static and dynamic performances of modular MPSs with respect to different modules and materials are presented as case studies. The proposed modular MPSs can provide better flexibility and functionality for further applications.
1. Introduction
Unlike rigid-link mechanisms, flexure-based mechanisms possess considerable advantages, including no wear, no friction, no backlash, and no joint assembly [1,2,3]. By virtue of these attributes, compliant mechanisms are widely used in various applications, such as precision alignment [4], ultra-precision grinding operation [5], high-dexterity medical devices [6], and scanning probe systems [7].
At present, the requirements for high precision and low cost should be addressed due to the growing demands for flexure-based MPS [8]. However, compliant MPSs are traditionally manufactured with a monolithic piece of material using the electrical discharging machining (EDM) method [9], which is costly in terms of both time and money [10]. In addition, traditional MPSs are tailored to specific tasks with constant working range, natural frequency, and dimensional size [11]. When a certain compliant beam of MPS is damaged or task requirements are modified, another new monolithic MPS needs to be manufactured to meet the new requirements, which results in non-negligible waste of resources [12]. Most importantly, for the purpose of obtaining multi-functionality, the current flexure-based MPSs are being developed towards complex spatial configurations, which further precludes monolithic fabrication [13]. Therefore, to develop reconfigurable and modular MPSs without degrading performance is worth studying.
From the literature review, it can be observed that the modular method has been increasingly proposed to develop reconfigurable and self-repairable robotic systems [14], while only a few researchers have used it to deal with problems faced by flexure-based mechanisms. C.C. Ng designed a 3-UPU parallel MPS based on a fixed-dimension module and varied-dimension module unit for micro-manufacturing assembly and verified modular architectures which have the same control performance as the monolithic one [15]. J.J. Yu proposed a method to design large displacement flexure-based MPSs based on flexure block modules [16]. J. Wang presented a controller with both redundancy resolution and optimization of null space motion to operate a 5-DOF modular manipulator [17]. B.X. Ding verified the flexibility of the configuration by designing multiple modular MPSs with limited modules [18]. These previous works designed and assembled some modular MPSs, while the principle of how to design and assemble modules was neglected. Modular MPSs are not composed of random modules; they are composed of standardized functional modules to meet certain task requirements under the guidance of assembly methods. Therefore, further studying modular MPSs in terms of design and assembly possesses practical significance for the implementation and application of MPSs.
The main purpose of this paper is to present a modular method for the design, assembly, and simulation of MPSs. Compared with monolithic MPSs, functional requirements (such as dynamic performance, displacement, DOF, etc.) and non-functional requirements (such as upgrading, post maintenance, low cost, etc.) can be achieved easily for modular MPSs. The assembly of modular structure can be regarded as the synthesis of complex organic composites which can be reconfigured into other types by limited modules. Furthermore, self-reconfiguration, reparation, function upgrading, and performance optimization can be realized for modular MPSs by replacing or reassembling modules in an efficient way.
The rest of this paper is organized as follows: Section 2 introduces the research motivations for modular MPSs. Then, design rules and standardization process of modules are introduced in Section 3, and several MPSs with different DOFs are designed under assembly guidance in Section 4. In addition, case studies are conducted in Section 5 to validate the correctness of modular MPSs. Finally, conclusions are made in Section 6.
2. Motivations
In recent years, the modular method has been increasingly proposed for the automotive industry [19], aerospace [20], and home furniture [21]. A modular product can be reconfigured within a limited time, without much more complexity and without buying or manufacturing new modules. Thus, the response to changing user requirements in modular MPSs will be faster than monolithic MPSs. Generally speaking, functional requirements (including DOF, displacement, natural frequency, and resolution) and non-functional requirements (including low cost, post-maintenance and upgrading, and compact size) must be addressed, as shown in Figure 1. As mentioned above, monolithic MPSs are tailored for a specific task, with no function flexibility. However, for the modular method, a product is divided into a number of parts and sub-parts, which can provide the ability to solve different requirements easily by combining with different modules. To clarify this point, the introductions of these requirements are described in the following subsections.
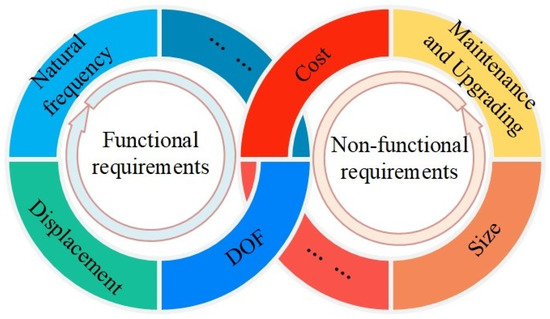
Figure 1.
Performance requirements for an MPS.
2.1. Functional Requirements
Functional requirements, also known as performance indicators, refer to the function that a product must facilitate [22].
For an orientation or positioning application, MPSs with different DOFs are required. However, with the determined monolithic structure, it can only meet the defined task. Furthermore, the XYZ MPS or above DOFs always appear with a complex spatial structure, which further precludes the use of monolithic fabrication. Hence, the modular MPS with reconfigurable characteristics can well adapt the DOF requirements for different tasks.
The dynamic performance of a flexure-based MPS is determined by its natural frequency, which is compromised by the workspace requirements [23]. This means that a high natural frequency for MPSs can only be achieved at the expense of the working range in monolithic MPSs, such as a millimeter-range flexure-based MPSs at a resonant frequency of less than 100 Hz. However, modular MPSs can balance the trade-off between the bandwidth (natural frequency) and working range (stroke) by changing the module material.
The bandwidth indicates responding time, which determines how fast the MPS deals with the input and is related to the axial stiffness and mass. Meanwhile, monolithic MPSs are manufactured by a piece of material, and the system bandwidth is ultimately limited by the physical plant. Based on this, different materials with a high Young’s modulus-to-density ratio are chosen to make non-functional modules for enlarging the bandwidth of modular MPSs.
2.2. Non-Functional Requirements
Non-functional requirements can be related to production, selling, and follow-up service [24].
Time and money are two main factors which need be taken into consideration when manufacturing an MPS. However, monolithic MPSs are mainly made by EMD, which is a time-consuming process. Compared with monolithic MPSs, multiple modules of a modular MPS can be processed at the same time for time saving. In addition, a modular MPS is more suitable for standardization to reduce manufacturing costs due to its strong adaptability and repeatability. Furthermore, a huge expense will be saved because the standard modules are reusable.
Post-maintenance and upgrading reduce the overall cost and ensure the advancement of the product, respectively. From practical experience, some flexure beams will crack first due to different fatigue life, resulting in the failure of the whole system. Nevertheless, monolithic MPSs only can realize maintenance and upgrading by replacing the whole stage, which leads to a huge cost. In contrast, the self-reparation and function upgrading for modular MPSs can be realized by replacing certain modules.
In practical applications, a compact size is required for applications such as cell grasping and medical operations [25]. However, in order to realize micrometer stroke tasks, an MPS needs an amplification mechanism to compensate for the stroke of PZA, which increases the size. A modular MPS can add or remove amplification mechanisms. Thus, the size can be adjusted accordingly. Furthermore, a modular MPS is more suitable to work in a confined space.
3. Modular Design
Modular MPS refers to a product which can fulfill various functions through the combination of distinct blocks. During the literature review, we observed that the working principle of an MPS is a driving force provided by actuators and transmitted by flexible beams acting on the end effector. Ding et al. divided the modules into beam module, connection module, ground module, and amplification module according to planar MPSs [18], but not including three-dimensional MPS. The design process of modular MPSs to have complex spatial structure in this paper is depicted in Figure 2; the modules are classified as follows:
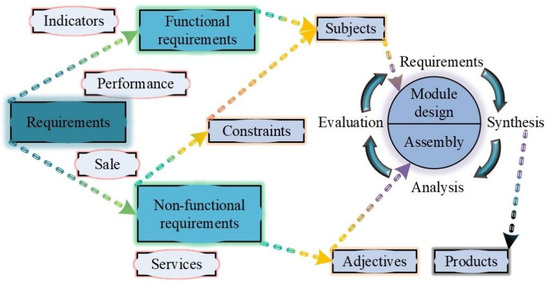
Figure 2.
Design process of modular MPSs.
- Amplification module: Displacement compensation for actuators.
- Transmission module: Flexible beam, core modules of MPS.
- Connection module: Optimizing module assembly.
- Custom module: Increasing flexibility of stages.
Furthermore, details of each module are described in the following subsections.
3.1. Amplification Module
In order to compensate for the displacement of actuator, the lever-type amplifier, the Scott-Russel amplifier, and the bridge-type amplifier are widely used for MPSs. With the advantages of compact size and symmetric structure, the bridge-type amplifier has been attracting increasing attention.
Generally speaking, four bridge-type amplifiers based on rectangular and diamond shapes have been widely adopted for their advantages of compact structure and linear output. The FEA simulation is conducted to compare their performances in terms of magnification, strain, and natural frequency (as depicted in Figure 3). Compared with the rectangular shape, the diamond shape has a larger rotational range (as shown in Figure 3a,b). Meanwhile, compared with maximum strain, rectangular mechanisms are more prone to failure under extreme work conditions. Furthermore, lower natural frequency can result in problems, such as reducing the working bandwidth, increasing structure lagging, and control difficulty for MPS. The double-beam diamond mechanism has two group parallelogram structures, which reduce the parasitic motion and increase the output displacement. To achieve a balanced performance, the double-beam diamond amplification mechanism is adopted to compensate for the PZA displacement.
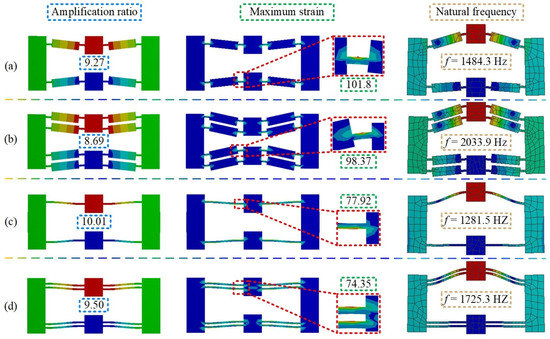
Figure 3.
Simulation of bridge-type amplification mechanisms: (a) single-beam rectangular mechanism; (b) double-beam rectangular mechanism; (c) single-beam diamond mechanism; (d) double-beam diamond mechanism.
3.2. Transmission Module
The transmission module is the core module for modular MPSs, which can be regarded as a translational joint or multiple rotational joints for transmitting force and motion. Flexure-based beams, including distributed compliance beams and lumped compliance beams, are suitable choices for transmission modules [26]. FEA simulation is conducted to compare their performances in terms of working displacement, parasitic displacement, and natural frequency (as shown in Figure 4). Compared with other flexure beams, the distributed single-beam possesses the largest displacement in working direction, which indicates the better flexibility performance. However, the parasitic motion of the flexure-beam significantly deteriorates the precision of MPS. Thus, the lumped double-beam can be selected for high precision tasks for the benefits of lowest parasitic motion and largest natural frequency. Overall, taking all aspects into consideration, the transmission module is designed in a distributed double-beam form.
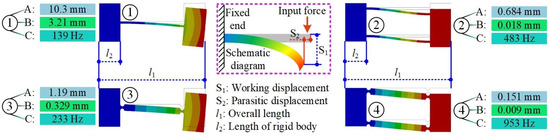
Figure 4.
Comparison of transmission modules. A denotes the working displacement; B denotes the parasitic displacement; C denotes the first mode of beams.
Generally speaking, connection methods include bonding, welding, bolt connection, and so on. The bonding method cannot meet the working requirements under high-frequency, high-speed, and heavy-load conditions. The welding method not only results in modular MPSs changing into monolithic MPSs, but also limits the use of multiple materials. The bolt connection method has the advantage of providing large fastening force between different modules. It is also suitable for standardization with low cost.
During the literature review, we observed that Gandhi et al. proposed an assembly guideline for flexure-based mechanisms [27]. However, the fastening force variation on the bolts deteriorate positioning precision due to the warping deformation of the flexible beam. To prevent this phenomenon, these standard interfaces are arranged in rigid parts on each module (as shown in Figure 5a). Simulations of assembled double-beam transmission modules are depicted in Figure 5b,c. With regard to the simulation results, the deformation of the guiding mechanism mainly appears in compliant beams. Thus, it can be regarded as a monolithic mechanism, without affecting the performance of the flexure beam.
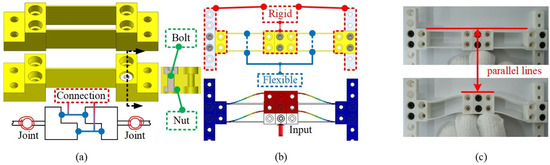
Figure 5.
Schematic of bolt connection: (a) module with standard interface; (b) the connection method; (c) simulation of assembled transmission modules.
3.3. Connection Module
Modular MPSs can be realized by connecting each function module with a standard interface. However, a low ratio in module utilization and poor performance may occur. Therefore, a Z-type connection module (ZTCM) and a T-type connection module (TTCM) with the same volume and mass are introduced to increase flexibility in assembling MPSs. To further validate their pure connection function, comparison studies are performed for the guiding mechanism (as shown in Figure 6a). In addition, the FEA simulations of static and dynamic performance of Z-type and T-type guiding mechanisms are depicted in Figure 6b,c, respectively. The deviations in static and dynamic performance are listed in Table 1. It can be seen that the difference in displacement is 0.01 μm, with 259.3 μm motion range. The maximum difference of natural frequency is 1.8 Hz, which appears in the fifth mode. Hence, the distinction of ZTCM and TTCM can be ignored. Specifically, the function of ZTCM and TTCM is to increase the assembly flexibility without affecting the performance of the MPS.
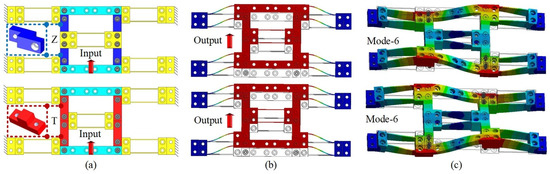
Figure 6.
Comparison of Z-type and T-type connection modules: (a) guiding mechanisms assembled with Z-type and T-type connection modules; (b) static simulation; (c) dynamic simulation.

Table 1.
Deviation between the ZTCM-based mechanism and the TTCM-based mechanism of static performance and dynamic performance.
3.4. Custom Module
A custom module is designed to meet different user requirements. Although minimizing the number of unique parts helps to ensure accurate and repeatable fabrication, the use of custom modules can further expand the diversity of modular configurations, such as developing a planar mechanism into a spatial mechanism.
4. Assembly of Modules
As mentioned above, one of the benefits of using modular architecture is that it can provide a variety of configurations. Assembling a modular MPS is similar to composing a molecular structure, as depicted in Figure 7. Regarding carbon atoms, many inorganic and organic compounds can be composed with hydrogen and oxygen atoms by chemical bonds. Meanwhile, regarding the designed modules with a standardized interface, such as transmission modules, many flexure-based components can be assembled by bolt connections. The C60 is realized by connecting carbon atoms, as for (B2)4. Furthermore, with the difference between 12C and 14C in physical properties, 14C has been widely used in isotope labeling tasks. Meanwhile, the static and dynamic performance can be adjusted by changing transmission modules from B to 1B or 2B. Furthermore, in order to validate the flexibility of the modular method, one-DOF, two-DOF, and three-DOF MPSs are assembled using the aforementioned designed modules.
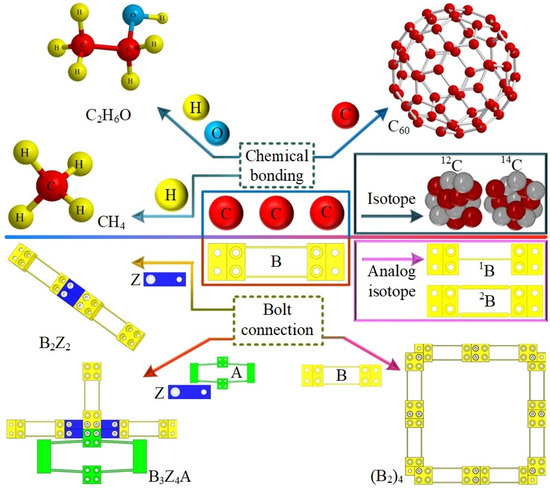
Figure 7.
Assembly of a modular MPS analogy with composing compounds. Z denotes ZTCM; A denotes amplification module; B denotes distributed double-beam transmission module; 1B denotes distributed single-beam transmission module; 2B denotes lumped double-beam transmission module.
4.1. One-DOF Mockups
In practical experience, neither molecules nor modular MPSs can be arbitrarily composed of atoms or modules; they require guidance for combination or assembly. Several one-DOF MPSs with guiding functions are assembled using different modules, as shown in Figure 8. Firstly, the function adjustment of one-DOF MPS can be achieved by the replacement of B, 1B, or 2B. The resolution and motion range are two contradicting indices for PZA-actuated MPS, but this issue can be solved effectively by modular MPSs. For example, the motion range can be enlarged by reconfiguring B2 to B3A to compensate for the PZA displacement with an amplification module; vice versa, the resolution can be enhanced for B3A by removing the amplification module.
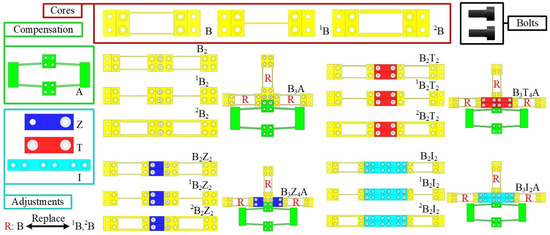
Figure 8.
Assembly of one-DOF MPSs using standard modules.
4.2. Two-DOF Mockups
From the literature review, we observed that two-DOF MPSs play a key role in nanotechnology applications. However, owing to the monolithic structure, the proposed MPS can only meet the specific task.
Some totally decoupled two-DOF parallel MPSs are composed as depicted in Figure 9, involving the basic blocks discussed in Section 4.1. Therefore, the attributes of modular two-DOF MPSs mainly depend on the basic blocks. The function adjustment can be achieved by replacing the transmission modules to meet different tasks.
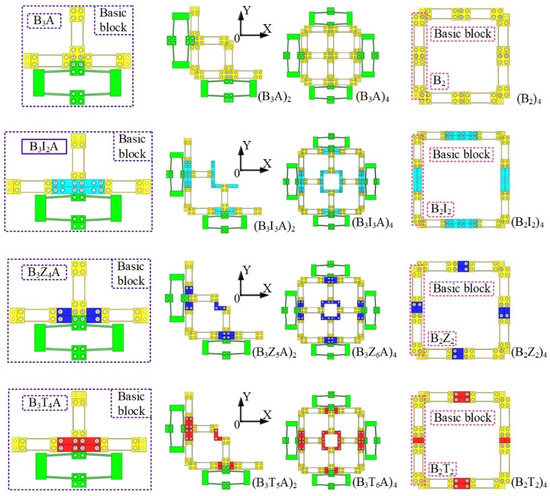
Figure 9.
Assembly of two-DOF MPSs based on basic blocks.
4.3. Decoupled Parallel XYZ MPS Mockup
In recent years, MPSs with complex geometry structures have received much attention. For example, E.U. John designed a XYZ parallel kinematic flexure mechanism with a motion range of 10 mm × 10 mm × 10 mm, guided by a constraint map [28]. However, the monolithic fabrication results in huge cost. Regarding their configuration, a geometric decoupled parallel XYZ MPS with standardized modules is assembled in this subsection. Regarding the assembly of the MPS, the module library, including ground and electromagnetism custom modules, is shown in Figure 10a. Firstly, the function of parallel XYZ MPSs is mainly determined by the B2Z2 basic block; the assembly for the single direction is shown in Figure 10b. According to the static and dynamic requirements, there are nine alternative mechanisms for each single direction. Secondly, with the help of ZTCM and TTCM, the size of an XYZ MPS can be adjusted. Finally, the selection of custom module is based on the size of the ground module and the electromagnetism module.
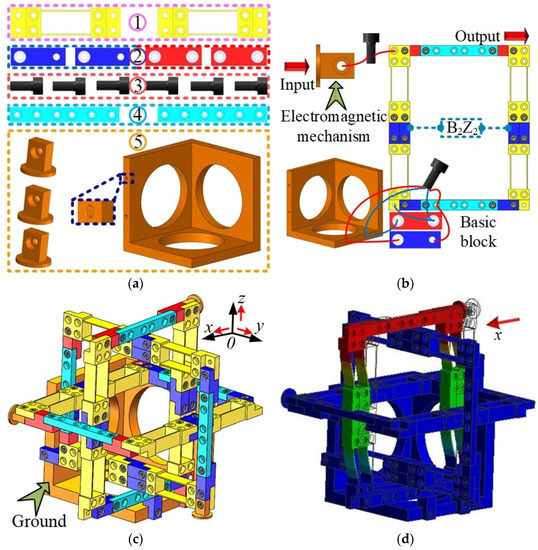
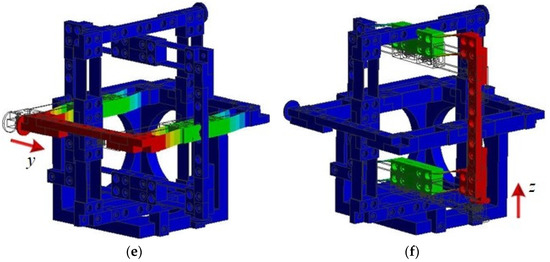
Figure 10.
Flexure-based parallel XYZ MPS: (a) module library; (b) assembly of modules; (c) display of flexure-based XYZ MPS; (d–f) Simulation of XYZ MPS along X, Y, and Z axes, respectively. 1, transmission modules; 2, Z-type and T-type connection modules; 3, bolts; 4, I-type connection modules; 5, ground and electromagnetism custom modules.
4.4. Zθ × θy MPS Mockup
To prevent sensitive objects, such as small and light optical devices from the micro-vibration, a novel compact and modular Zθ × θy MPS based on the well-known tripod parallel configuration is proposed. Regarding the assembly of the MPS, the module library (including column and triangle stage custom modules) is depicted in Figure 11a. The ZTCM-based guiding mechanism is the basic block for assembling the Zθ × θy MPS, which is fixed by the column module, as shown in Figure 11b. In addition, the workspace and the rotation range can be altered by replacing transmission modules.
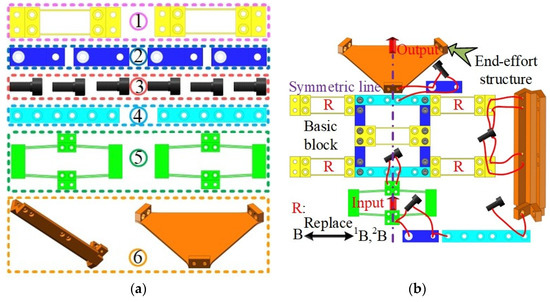
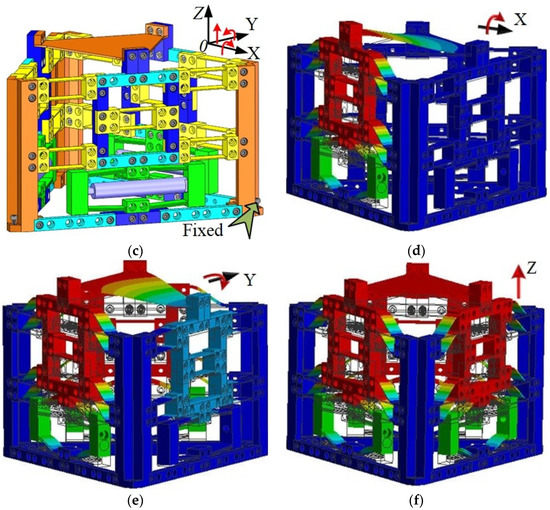
Figure 11.
Flexure-based Zθ × θy MPS: (a) module library; (b) assembly of modules; (c) display of the 3D model of flexure-based Zθ × θy MPS; (d–f) simulation results. 1, transmission modules; 2, Z-type connection modules; 3, bolts; 4, I-type connection modules; 5, amplification modules; 6, column and triangular custom modules.
In addition, the 3D model of Zθ × θy MPS is shown in Figure 11c. When the outputs in three directions are same, the stage can realize translational motion along the Z direction, as shown in Figure 11f, and the stage rotates around the X or Y axis for different output modes, as shown in Figure 11d,e.
5. Case Studies
To verify the feasibility of modular MPS, several totally decoupled parallel XY MPSs are analyzed via ANSYS software. Here, monolithic MPS is named Mon-str, while other modular MPSs with different transmission modules are named (1B3A)4, and (2B3A)4, respectively, as shown in Figure 12. The properties of adopted materials are listed in Table 2. The material of the bolts is 45# steel, while the rest of Mon-str, (B3A)4, (1B3A)4, and (2B3A)4 are made of aluminum alloy AL7075-T651. Further, (B3A)4 can be classified as (B3A)4-AL, (B3A)4-45, or (B3A)4-PLA based on the module materials.
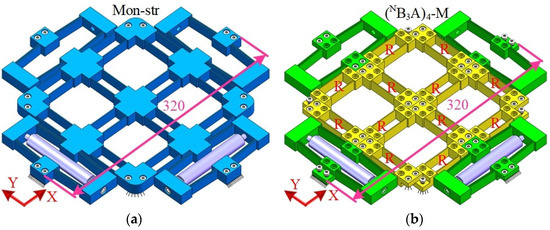
Figure 12.
Two decoupled parallel XY MPSs. N and M are determined by the modules and materials of R, respectively; (a) monolithic XY stage; (b) modular XY stage.

Table 2.
The properties of materials.
5.1. Simulation of Motion Range
The motion range determines the workspace of an MPS. With the same inputting force in the X and Y direction, the FEA simulation results of Mon-str, (B3A)4-AL, (1B3A)4, and (2B3A)4 are shown in Figure 13a,b, respectively. The results listed in Table 3 indicate that the X and Y direction have same output displacement due to the decoupling structure. It can be concluded that with the same materials, Mon-str and (B3A)4-AL have the same displacement, while (1B3A)4 has maximum displacement due to its low stiffness. The motion range of the MPS can be adjusted by changing the materials of modules, compared with (B3A)4, (B3A)4-PLA, and (B3A)4-45. Therefore, modular MPSs can be regarded as another form of monolithic MPSs, and their reconfigurable characteristic lets them adapt to different requirements easily.
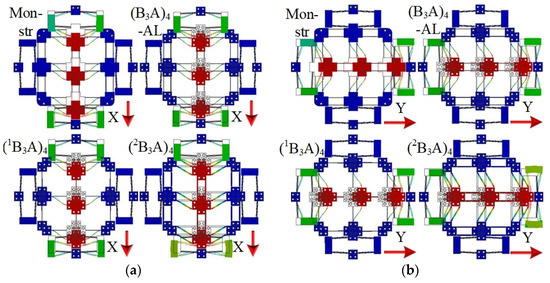
Figure 13.
Displacement simulation results of the XY MPSs: (a) the output along the X axis; (b) the output along the Y axis.

Table 3.
Analysis results of different decoupled parallel XY MPSs.
5.2. Simulation of Harmonic Response
The dynamic response is desired to be as high as possible for designing the flexure-based MPS. Taking the working mode of XY MPS into consideration, the first two resonance frequencies in the X and Y directions are discussed, and obtained frequency results are listed in Table 4. In addition, the six decoupled parallel XY MPSs are analyzed using ANSYS, and the harmonic responses testing from 100 Hz to 250 Hz with 150 steps are plotted in Figure 14.

Table 4.
The natural frequency of different decoupled parallel XY MPSs.
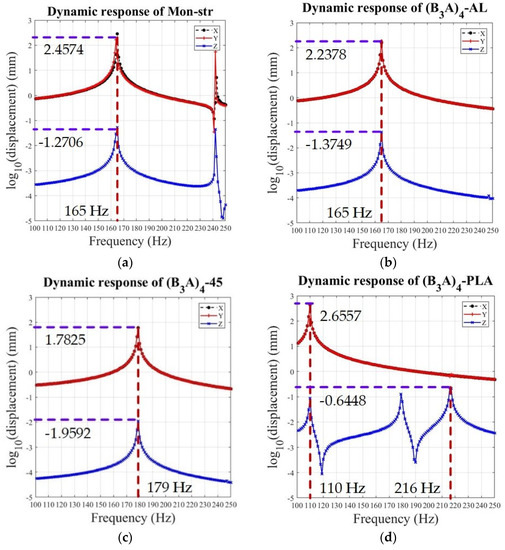
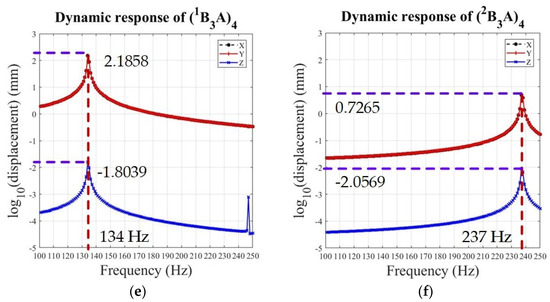
Figure 14.
Comparation of dynamic response of end-effort structure of MPS: (a–f) along the X, Y, and Z axes about Mon-str, (B3A)4-AL, (B3A)4-45, (B3A)4-PLA, (1B3A)4, and (2B3A)4, respectively.
Firstly, when the input frequency is 165 Hz, the displacement in X, Y, and Z axes of Mon-str is larger than (B3A)4-AL, as shown in Figure 14a,b. Hence, with the same structure characteristic, the modular MPS possesses less displacement at the resonant frequency. Next, the harmonic response of (B3A)4 with different materials is depicted in Figure 14b–d, which indicates that a high natural frequency can be achieved by (B3A)4-45, and (B3A)4-PLA is not suitable for tasks requiring high dynamic response. Finally, the simulation results of (B3A)4-AL, (1B3A)4, and (2B3A)4 with different transmission modules are shown in Figure 14b,e,f. The dynamic performance of modular MPS can be improved by using distributed double-beam transmission modules. Considering the above analysis, the dynamic behaviors of modular MPSs can be improved by changing module materials or reconfiguration.
6. Conclusions
This paper employs the modular method to design flexure-based MPSs which can meet various functional and non-functional requirements efficiently. The design process for modular MPSs is described, and four modules with standard interfaces are presented. To validate the flexibility of the modular method, various planar and spatial modular configurations assembled with functional modules are presented. Furthermore, FEA simulation is conducted to investigate the motion range and dynamic performance with decoupled modular parallel XY MPSs. The results demonstrate that monolithic and modular MPSs with the same dimensional parameters exhibit the same performance, and the output displacement and harmonic response of MPSs can be effectively enhanced by changing module materials. In our future work, performances of modular MPSs will be studied by experimental validation.
Author Contributions
S.L.: conception and design of study, acquisition of data, analysis, drafting of the manuscript, critical revision of the manuscript for important intellectual content; B.D.: conception and design of study, methodology, supervision, critical revision of the manuscript for important intellectual content; Y.L.: supervision, critical revision of the manuscript for important intellectual content. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by Huxiang High Level Talent Project of Hunan Province (Grant No. 2019RS1066), the State Key Laboratory of Ultra-precision Machining Technology of Hong Kong Polytechnic University (BBXG), Natural Science Foundation of Jishou University (Jdx20017), National Natural Science Foundation of China (51575544).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict interest.
References
- Ding, B.; Li, Y.; Xiao, X.; Tang, Y.; Li, B. Design and analysis of a 3-DOF planar micromanipulation stage with large rotational displacement for micromanipulation system. Mech. Sci. 2017, 8, 117–126. [Google Scholar] [CrossRef]
- Wang, L.-P.; Jiang, Y.; Li, T.-M. Analytical Compliance Modeling of Serial Flexure-Based Compliant Mechanism under Arbitrary Applied Load. Chin. J. Mech. Eng. 2017, 30, 951–962. [Google Scholar] [CrossRef]
- Pham, M.T.; Yeo, S.H.; Teo, T.J.; Wang, P.; Nai, M.L.S. A Decoupled 6-DOF Compliant Parallel Mechanism with Optimized Dynamic Characteristics Using Cellular Structure. Machines 2021, 9, 5. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Zhong, Y.; Tian, Y.; Zhang, D. Design and analysis of a compact flexure-based precision pure rotation stage without actuator redundancy. Mech. Mach. Theory 2016, 105, 129–144. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, D.; Shirinzadeh, B. Dynamic modelling of a flexure-based mechanism for ultra-precision grinding operation. Precis. Eng. 2011, 35, 554–565. [Google Scholar] [CrossRef]
- Swaney, P.J.; Burgner, J.; Gilbert, H.B.; Webster, R.J. A flexure-based steerable needle: High curvature with reduced tissue damage. IEEE. Trans. Biomed. Eng. 2013, 60, 906–909. [Google Scholar] [CrossRef] [PubMed]
- Schitter, G.; Thurner, P.J.; Hansma, P.K. Design and input-shaping control of a novel scanner for high-speed atomic force microscopy. Mechatronics 2008, 18, 282–288. [Google Scholar] [CrossRef]
- Qian, J.; Li, Y.; Zhuge, L. An investigation on a Novel 3-RCU flexible micromanipulator. Micromachines 2020, 11, 423. [Google Scholar] [CrossRef]
- Chen, W.; Yu, F.; Qu, J.; Chen, W.; Zhang, J. Micro-vision servo control of a multi-axis alignment system for optical fiber assembly. J. Micromech. Microeng. 2017, 27, 045010. [Google Scholar] [CrossRef]
- Jagtap, S.P.; Deshmukh, B.B.; Pardeshi, S. Applications of compliant mechanism in today’s world—A review. J. Phys. Conf. Ser. 2021, 1969, 12013. [Google Scholar] [CrossRef]
- Lateş, D.; Căşvean, M.; Moica, S. Fabrication Methods of Compliant Mechanisms. Procedia Eng. 2017, 181, 221–225. [Google Scholar] [CrossRef]
- Ding, B.; Yang, Z.-X.; Xiao, X.; Zhang, G. Design of Reconfigurable Planar Micro-Positioning Stages Based on Function Modules. IEEE. Access 2019, 7, 15102–15112. [Google Scholar] [CrossRef]
- Soh, S.L.; Ong, S.K.; Nee, A.Y.C. Design for Disassembly for Remanufacturing: Methodology and Technology. Procedia CIRP 2014, 15, 407–412. [Google Scholar] [CrossRef]
- Brunete, A.; Ranganath, A.; Segovia, S.; de Frutos, J.P.; Hernando, M.; Gambao, E. Current trends in reconfigurable modular robots design. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417710457. [Google Scholar] [CrossRef]
- Ng, C.C.; Ong, S.K.; Nee, A.Y.C. Design and development of 3–DOF modular micro parallel kinematic manipulator. Int. J. Adv. Manuf. Technol. 2006, 31, 188–200. [Google Scholar] [CrossRef][Green Version]
- Yu, J.; Xu, P.; Minglei, S.; Shanshan, Z.; Shushing, B.; Guanghua, Z. A New Large-Stroke Compliant Joint & Micro/Nano Positioner Design Based on Compliant Building Blocks; IEEE: Piscataway, NY, USA, 2009. [Google Scholar]
- Wang, J.; Li, Y. Analysis on the interaction between the nonholonomic mobile modular robot and the environment. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 18–22 December 2009; pp. 86–91. [Google Scholar]
- Ding, B.; Yang, Z.; Li, Y. Design of flexure-based modular architecture micro-positioning stage. Microsyst. Technol. 2020, 26, 2893–2901. [Google Scholar] [CrossRef]
- Kern, W.; Rusitschka, F.; Bauernhansl, T. Planning of Workstations in a Modular Automotive Assembly System. Procedia CIRP 2016, 57, 327–332. [Google Scholar] [CrossRef]
- Hwang, J.T. A Modular Approach to Large-Scale Design Optimization of Aerospace Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2015. [Google Scholar]
- Braileanu, P.I. Design of a modular kitchen furniture. J. Ind. Des. Eng. Graph. 2017, 12, 13–20. [Google Scholar]
- Kusiak, A.; Chun-Che, H. Development of modular products. IEEE Trans. Compon. Packag. Manuf. Technol. Part A 1996, 19, 523–538. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Yan, P. Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner. Micromachines 2021, 12, 212. [Google Scholar] [CrossRef]
- Glinz, M. On Non-Functional Requirements. In Proceedings of the 15th IEEE International Requirements Engineering Conference (RE 2007), Delhi, India, 15–19 October 2007; pp. 21–26. [Google Scholar]
- Fifanski, S.K. Flexure-Based Mecano-Optical Multi-Degree-of-Freedom Transducers Dedicated to Medical Force Sensing Instruments; EPFL: Lausanne, Switzerland, 2020. [Google Scholar]
- Choi, K.-B.; Lee, J.J.; Kim, G.H.; Lim, H.J. A compliant parallel mechanism with flexure-based joint chains for two translations. Int. J. Precis. Eng. Manuf. 2012, 13, 1625–1632. [Google Scholar] [CrossRef]
- Gandhi, P.; Sonawale, K.; Soni, V.; Patanwala, N.; Bansode, A. Design for Assembly Guidelines for High-Performance Compliant Mechanisms. J. Mech. Des. 2012, 134, 121006. [Google Scholar] [CrossRef]
- Ustick, J.E. Design, Fabrication, and Experimental Characterization of a Large Range XYZ Parallel Kinematic Flexure Mechanism. Master’s Thesis, University of Michigan, Ann Arbor, MI, USA, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).