Research on Repetition Counting Method Based on Complex Action Label String

Abstract

Smart factories have real-time demands for the statistics of productivity to meet the needs of quick reaction capabilities. To solve this problem, a counting method based on our decomposition strategy of actions was proposed for complex actions. Our method needs to decompose complex actions into several essential actions and define a label string for each complex action according to the sequence of the essential actions. While counting, we firstly employ an online action recognition algorithm to transform video frames into label numbers, which will be stored in a result queue. Then, the label strings are searched for their results in queue. If the search succeeds, a complex action will be considered to have occurred. Meanwhile, the corresponding counter should be updated to accomplish counting. The comparison test results in a video dataset of workers’ repetitive movements in package printing production lines and illustrate that our method has a lower counting errors, MAE (mean absolute error) less than 5% as well as an OBOA (off-by-one accuracy) more than 90%. Moreover, to enhance the adaptability of the action recognition model to deal with the change of action duration, we propose an adaptive parameter module based on the Kalman filter, which improves counting performances to a certain extent. The conclusions are that our method can achieve high counting performance, and the adaptive parameter module can further improve performances.

1. Introduction

1.1. Repetition Counting

The construction of smart factories gives rise to many requirements related to the monitoring of production status, among which the productivity of workers comprises key data. Calculating production efficiency in tradition means it will be performed after workers finish production, which has a lag and cannot meet the needs of rapid response. In order to satisfy the demand above, we came up with a repetitive action counting method based on a decomposition strategy for the real-time statistics of workers’ productivity in the packaging industry.

To complete the counting task of human repetitive movements, the academic community researchers mainly focus on Spatio-temporal information of sequence data, trying to restore the periodic information synchronized with repeated actions from the original data. Finally, post-processing of the periodic information is performed to realize the counting task. The existing methods are classified according to the mode of input, which can be classified as computer-vision or non-computer-vision counting algorithms. Non-machine-vision counting algorithms mainly obtain the number of repetitions by analyzing the data collected from wearable devices [1,2,3]. In addition, the modes of data vary with data acquisition equipment, such as acceleration sequences, angular momentum sequences, and so on. In addition, for the technology route mentioned above, non-machine vision counting algorithms also contain other solutions. For example, one algorithm taking channel state information (CSI) [4] as input, updates the count state with threshold conditions. Moreover, another algorithm employs a linear regression model [5] to fit the relationship between the duration of action and the number of repetitions to generate the counting result of a video. When non-machine vision counting algorithms are applied for some sport-related actions, their counting accuracy can reach 90%, having advantages in processing speed. However, they need to improve performance when dealing with movements with deceptive actions.

Computer-vision repetition counting algorithms use RGB frame sequence as input, which can be divided into three types: ① counting methods based on mapping from motion field to one-dimensional signal [6,7,8,9,10,11], ② self-similarity matrix based counting methods [12,13], ③ counting methods relied on cycle length prediction with deep features [14,15].

The first type estimates the number of repeated actions from the periodic information of time-varying signals [6,7,8]. Pogalin et al. [9] obtained the slice sequence of counting objects by using a tracking algorithm, transform the slice sequence into a one-dimensional time signal by principal component analysis (PCA), and then select the spectral component with the largest amplitude in the signal as the basis for period estimation. This method employs Fourier transform as the tool for spectral analysis. In pursuit of improvement, Runia et al. [10] proposed a method using wavelet transform as a time-frequency analysis tool for one-dimensional signals to deal with motion instability in videos. Furthermore, to accommodate videos with different backgrounds, Yin et al. [11] proposed an energy-based adaptive selection scheme of feature mode to select depth features for videos with different backgrounds.

The second kind of counting method, a part of the unsupervised counting method, obtains the self-similarity matrix by evaluating the similarity of any two frames according to the similarity function and mines the similar action from the self-similarity matrix. Panagiotakis et al. [12] proposed a method that calculates the self-similarity matrix with Euclidean distance as the similarity function and then segmented the periodic clips from the original video based on the self-similarity matrix, an improved MUCOS [16] algorithm is used to complete the period estimation at last. The feature descriptor of this method can be further improved. Dwibedi et al. [13] put forward a method in which an original video is first represented by feature vectors, and then the self-similarity matrix is calculated by the feature vectors of each frame, and finally, the counting result of a video is obtained by processing the self-similarity matrix with a network.

The latter kind of counting algorithm usually utilizes convolutional layers and pooling layers to extract the deep features and then trains classification or regression networks with the deep features for period prediction. Levy et al. [14] introduced a sliding-window strategy to transform the counting problem into a multi-class problem of cycle length. Attributed to the limited number of the period length, this method can be further improved. Zhang et al. [15] proposed an offline processing framework. For more details, anchors of various time lengths are set at different moments of the whole video, and then the depth features extracted by 3D convolutional layers are used to perform iterative regression on the time boundary of anchors to predict the cycle length. In addition, algorithms of temporal action location [17,18,19,20,21,22] can also deal with repetition counting task after simple adjustment.

Aiming at the problem that there are many deceptive actions in the real world, we propose another possible solution based on the action decomposition strategy, which realizes action counting depended on understanding the semanteme of video. The novelty of our method is as follows: firstly, it employs complex action label strings to represent complex actions, and then each complex action will be treated as a sequence of basic actions, thus avoiding the time boundary regression problem of some existing methods. Secondly, to further enhance the performance of the action recognition model, we design an adaptive parameter module based on Kalman filter. In this method, complex actions of counting tasks should be decomposed into several simpler basic actions according to specific rules, and then an online action recognition model will be trained with video samples of basic actions. Meanwhile, each complex action label string is defined in light of the sequence of basic actions, which represents the semantic correspondence between complex actions and simple actions. While counting online, after the online action recognition model has processed some frames, the counting result will be updated only by matching the complex action label string from the model’s output sequence. Moreover, the calling condition of the adaptive parameter module is that when the specific basic action is completed, the module will be called once. Experiments on the video dataset of workers’ repetitive movements in package printing production lines show that the accuracy of the proposed method is above 90%.

1.2. Online Action Recognition

The online action recognition system, as one of the core components of the whole counting system, is a tool to transform the video frames into basic action labels, for which its performance directly determines the accuracy of counting results. The existing methods of online action recognition mainly consist of three ideas:

• The motion information contained in the skeletons sequence is converted into a one-dimensional signal [23], and the fragments of the skeleton sequence are segmented with several thresholds. Finally, the segmented fragments are sent into a classifier to obtain the action labels. Such methods rely on the depth camera or the 2D pose estimation algorithm [24,25,26] to collect the skeleton of people in the scene, which increases the consumption of computing resources.
• Methods based on sliding window process video frames in batches [27], with the next batch having some of the same frames as the last. Those methods may not accommodate the situation where the execution speed of the same action changes dramatically.
• The input video is classified frame by frame, and then historical results over some time are fused to obtain the result of the current moment. The input modes of such methods include RGB frames [28] and optical flow [29], but they cannot effectively take into account both spatial and temporal information at the same time.

In addition, methods to solve the problem of complex action recognition have been proposed in the relevant literature [30,31,32]. The established models have powerful temporal and spatial modeling abilities. However, these models with higher complexity process input videos offline, which require a lot of computing resources. Given the characteristics of the above methods, TSM (Temporal Shift Module) [33] algorithm is adopted to deal with the action recognition task. TSM algorithm, along with the advantages of low delay and high accuracy, is one of the online action recognition algorithms based on the sliding window strategy, which can simultaneously complete the modeling of spatial and temporal information.

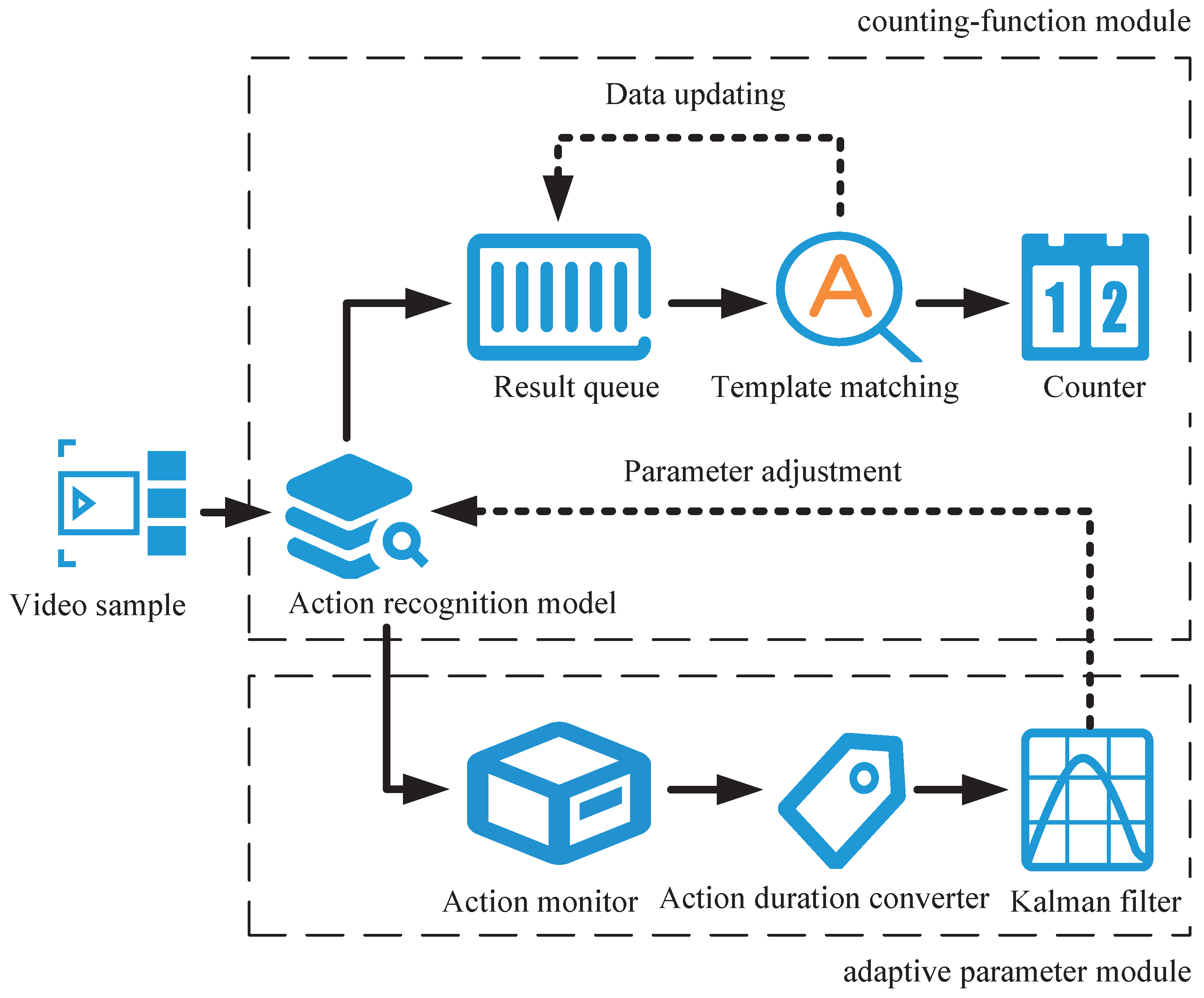
2. Method for Repeating Complex Action Counting

The proposed system consists of two parts: the counting-function module and the adaptive parameter module. Counting-function module firstly transforms visual information into action labels by using an action recognition model and secondly realizes counting under specific semantics by utilizing template matching. Details of the counting-function module are shown in Section 2.1 and Section 2.2. At first, the adaptive parameter module reuses output information from the action recognition model to obtain the action duration, and then it generates a new value of action duration according to the trend of change of it; it then uses the new value to perform parameter estimation based on the Kalman filter, finally, the new value of the adaptive parameter is set to the result of the filtering. Details of the adaptive parameter module are illustrated in Section 3.2. Figure 1 is the complete framework of our entire system.

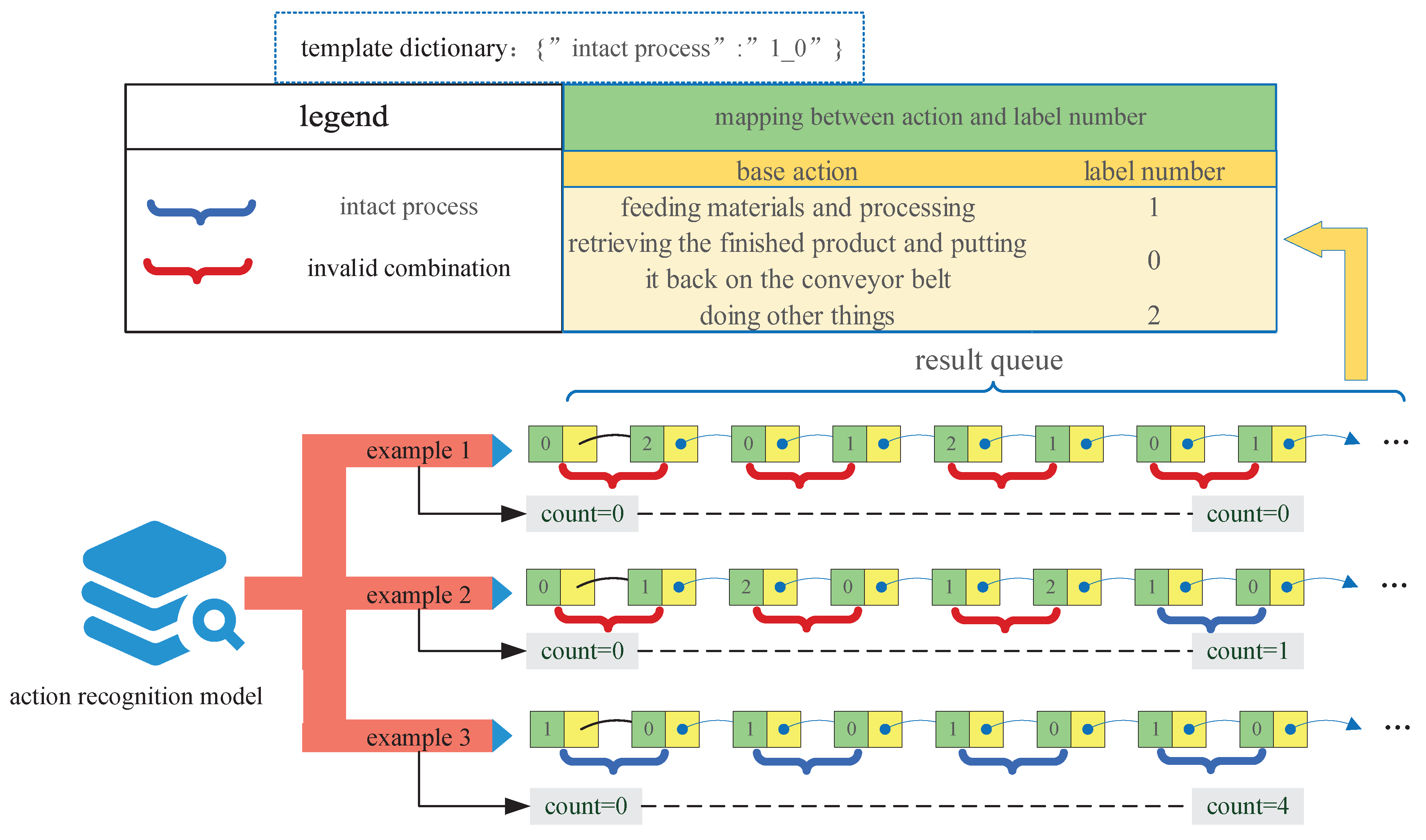
2.1. Decomposition Strategies for Complex Actions

A complex human action is usually composed of several more simple basic actions. As long as the basic actions are recognized, the counting of complex actions can be accomplished according to the sequence of simple actions. Therefore, a decomposition strategy for human complex actions is proposed in this paper, which converts the repetitive action counting problem into online action recognition and template matching.

A complete processing action, especially those on the package printing production line, can be divided into several beats (simple actions) based on semantics. Basic principles of the decomposition of complex actions include the following:

• In order to make it easier for the online action recognition system to distinguish basic actions, the keypoints [34] of the human limbs involved in each basic action of a complex action should possess motion tracks that are markedly different.
• The time span of different basic actions should be equal to the greatest extent for the sake of setting the parameters of the online action recognition system, named historical result length.
• Of all the complex actions that need to be counted, any two complex actions cannot have semantic–subsumption relations.
• For a complicated movement, each basic motion, due to explicit semantic and basic actions with the same semantic cannot appear continuously, because the latter basic action will lead to the online action recognition model’s output without changing. As a result, the counting module may not be able to perceive it, and eventually bring about an error-counting result.

Based on the decomposition strategy mentioned above, actions on the semi-automated package printing production line can be decomposed into two beats: ① feeding materials and processing, ② retrieving the finished product and putting it back on the conveyor belt. Figure 2 shows the key gestures of two beats of book packaging and album punching in the printing factory. Because the time span of the two beats is basically equal, as a consequence, through action decomposition, the requirement for the Spatio-temporal modeling ability of the online action recognition model is lower.

2.2. Counting Principle

Video frame sequence after processing by the action recognition model will obtain label numbers, which reflect the sequence of each basic action. After inserting the label number to the end of the result queue, we can count the number of complex action label strings in it to know how many complex actions have happened.

A complex action label string, a simple and efficient semantic model that a computer can easily parse, uses basic actions to describe complex actions. In this paper, a complex action label string is constructed with the label number of basic actions, which is consistent with the counterpart in the basic action dataset used to train the online action recognition model. The construction steps are as follows: firstly, we need to permutate label numbers following the time order, and secondly use a non-numeric character to join label numbers up. In practice, the underscore character is chosen as the joining character of the complex action label string. This character is to facilitate the computer to parse out basic actions that make up the complex action. Without this connector, when the number of basic actions exceeds ten, the parsing result will be ambiguous. Ultimately, the name of each complex action combined with its respective complex action label string will generate a key-value pair of a template dictionary.

Action counting adopts the template matching of complex action label strings. Template matching applied to counting will execute if the output of the online action recognition algorithm changes. When it happens, the latest label number is inserted at the end of the result queue, a data structure that stores the historical results generated by the online action recognition model, and then template matching is performed. As illustrated in Figure 3, our counting principle can be stated as follow: ① We are supposed to select a complex action label string from the template dictionary and then we split it with the underscore character (join character) to obtain a basic action label number sequence that will be used for making the template queue for matching. ② A fragment with the same length as the template queue is cut from the result queue for a match. If all elements of the two queues are equal, the match succeeds. If the match fails, the head of the fragment to be matched should move backward one step until the match succeeds. If the head of the fragment moves to the end of the result queue without a successful match, or the length of the result queue is shorter than the template queue, the matching of the current complex action label string is ended, and then it is necessary to select another complex action label string and perform the above process until all key-value pairs in the template dictionary are iterated. Eventually, the state of the counting variable corresponding to the identified complex action is updated, while the elements in the result queue of completing the matching are cleared.

3. Optimization of Online Action Recognition Algorithm

3.1. Primary Optimization Strategy

Although the TSM algorithm owns excellent performance, it needs to be optimized in terms of noise. Label number jumping suppression as well as invalid action elimination constitute the optimizing strategies of the online action recognition system. The former strategy’s solution is to adjust the historical result length of the TSM algorithm for different stations, while the latter is to eliminate invalid actions based on the previous step.

Historical result length for which its value is relevant to the action duration of a specific station is a parameter that controls the sensitivity of the TSM model, and its default value is 12 (frames), about 0.5 s. However, during the experiment, it was found that no matter whether the historical result length is too large or too small, the performance of the TSM model will degrade. When the historical result length is too large, it will lead to reduced sensitivity of the TSM model, resulting in failing to identify actions within a short time span. On the other hand, when the historical result length is too small, it will make the label number jump repeatedly. During manual adjustment, we find that the optimal value is the multiplication of the shortest time span of the basic action at the current station by the frame rate of the video.

The elimination of invalid action is a mechanism for verifying the validity of basic actions. In the time of the test of untrimmed videos, it was found that the accuracy of the TSM model is low in recognizing actions in the category of doing other things, probably owning to the number of samples in this class being too small. As can be observed, the time span of action named “doing other things” is usually larger than the historical result length of each station. Therefore, the rule of eliminating invalid actions is that if an action of doing other things has a time span smaller than the historical result length, it will be deleted from the result queue.

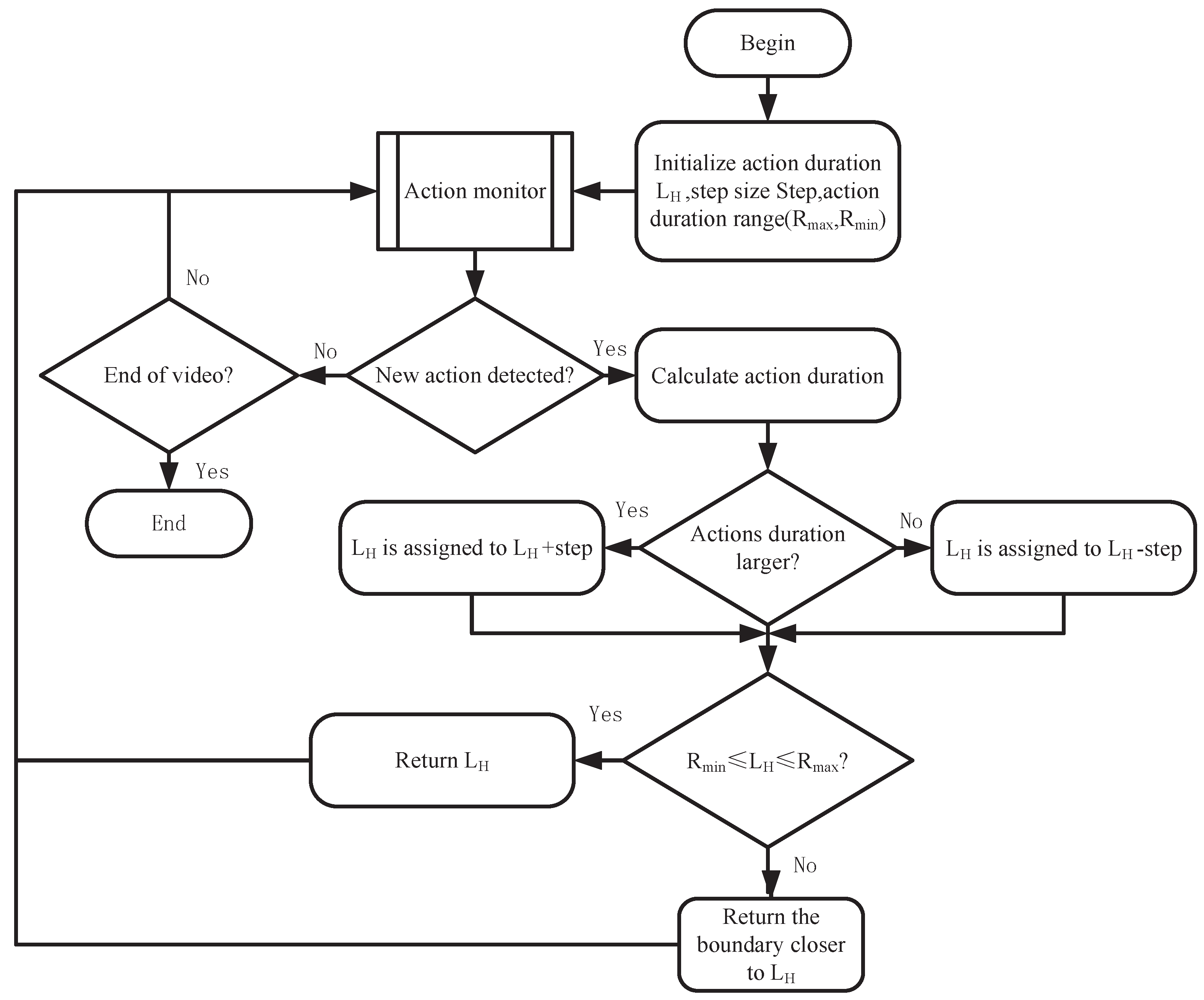
3.2. Optimization Strategy Base on Adaptive Parameter Strategy

In the real world, the durations of a group of repeated actions are usually centered on the average and fluctuate within a certain range. The model of TSM has a parameter—historical result length related to action duration—that will affect the accuracy of action recognition. In order to keep the performance of the action recognition model excellent, we propose an adaptive parameter module based on Kalman filtering to estimate and adjust the historical result length dynamically, realizing the improvement of robustness of the action recognition model.

3.2.1. Kalman Filter Design

The Kalman filter is an algorithm that uses the linear system state equation to estimate the system state optimally with observation data as input. The observation data contains a lot of noise, while the Kalman filter can estimate the state from a series of data with measurement noise. Therefore, we choose to use the Kalman filter algorithm to complete the online estimation of the action duration.

Figure 4 is a scatter plot of action durations of test videos. As can be seen, most action durations are concentrated around the mean and fluctuate around it. We develop a Kalman filter based on the distribution of action durations above.

The key steps of the Kalman filter are as follows:

• Calculate the a priori estimate: we take the action duration into account in our research. The unit of action duration is the frame (that is, the number of frames that the action lasts). Since our system has no external input, the state transition equation of the system can be given by the following:

  $${\widehat{X_t}}^{-}=F\widehat{X_{t-1}}$$

  (1)

  where ${\widehat{X_t}}^{-}$ and $\widehat{X_{t-1}}$ denote the prior estimate at time t and the optimal estimation at time $t-1$, respectively. Moreover, F denotes the state transition matrix. Since it is assumed that the action maintains a uniform speed during the execution process, we obtain $F=1$. Therefore, the state transition equation of the system can be given by the following.

  $${\widehat{X_t}}^{-}=\widehat{X_{t-1}}$$

  (2)
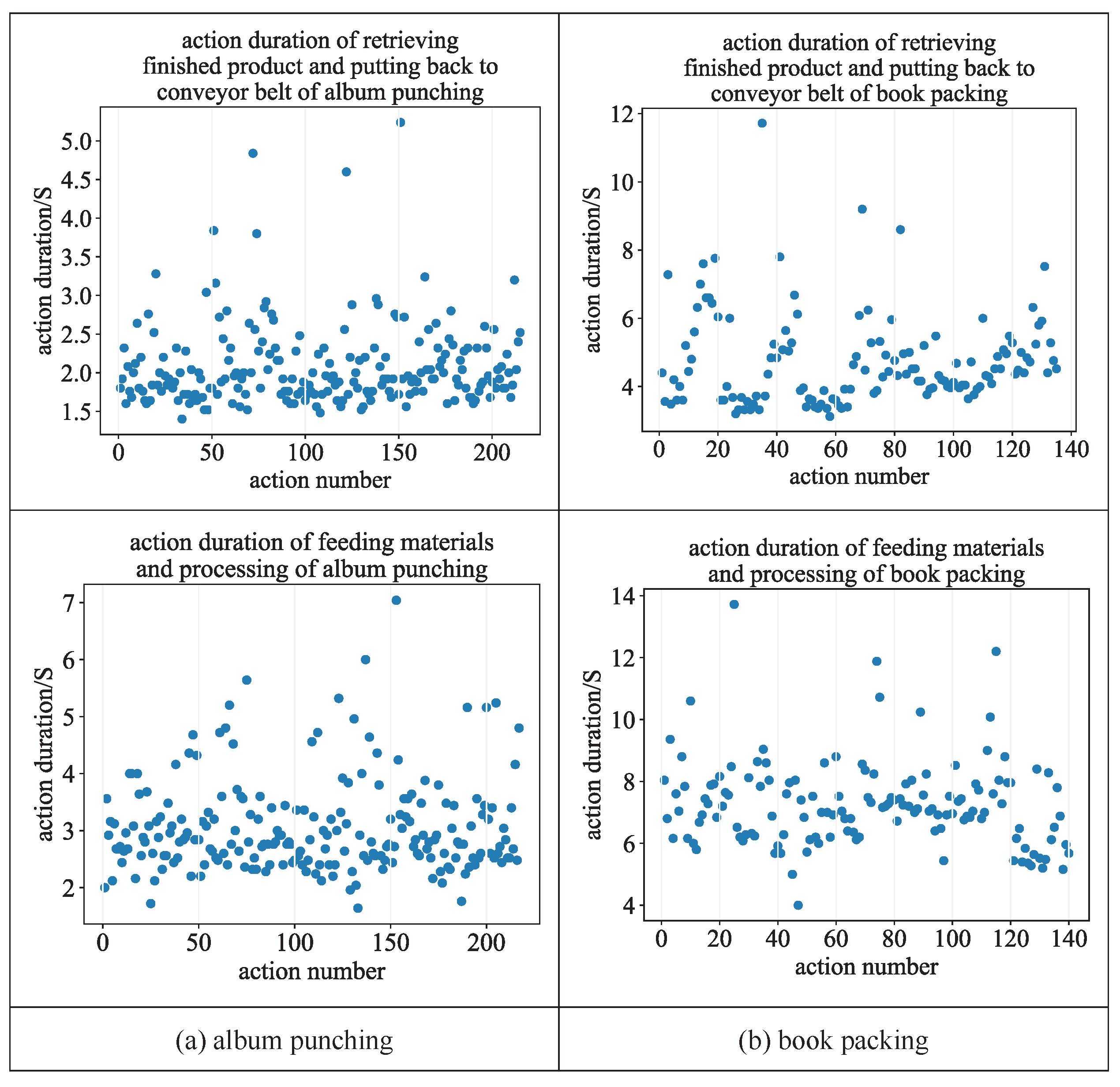
• Calculate prior estimate covariance: The calculation method of prior estimate covariance is as follows:

  $${P_t}^{-}=F{P}_{t-1}{F}^T+Q$$

  (3)

  where ${P_t}^{-}$ is the optimally estimated covariance at time $t-1$, and Q is the process noise covariance. We sort the action durations of feeding materials and processing, removed 5% of the data at the beginning and end, and obtained the mean and variance of the action durations by Gaussian distribution fitting. The mean of Q is set to zero, and the variance is the same as the variance of the action durations of feeding materials and processing.
• Update the Kalman gain as follows:

  $$K_t={P_t}^{-}{H}^T\left(H{P_t}^{-}{H}^T+R\right)$$

  (4)

  where $K_t$ is the Kalman gain at time t, and ${P_t}^{-}$ is the a priori estimated covariance at time t. H is the measurement matrix, and R is the measurement noise covariance. Since the action duration can be obtained from action monitor, we obtain $H=1$.
• Revise the following estimate:

  $$\widehat{X_t}={\widehat{X_t}}^{-}+K_t\left(Z_t-{\widehat{X_t}}^{-}\right)$$

  (5)

  where $Z_t$ is the observed value of the action duration.
• Update posterior estimate covariance:

  $$P_t=\left(1-K_t\right){P_t}^{-}$$

  (6)

  where $P_t$ is the posterior estimate covariance at time t.

The relationship between the steps above is shown in Figure 5.

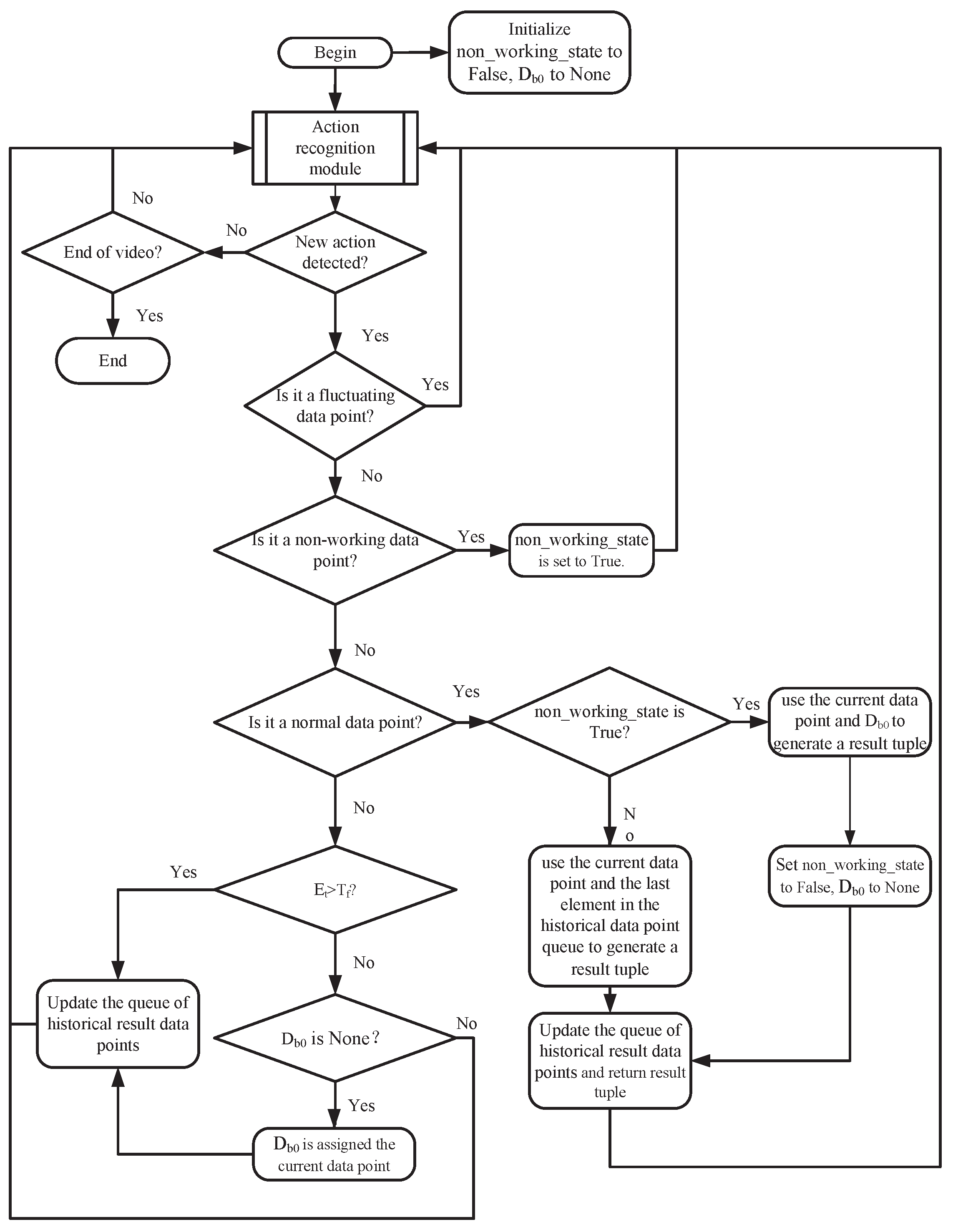
3.2.2. Action Monitor Design

The principle of the action monitor is based on the reuse of the outputs of the action recognition model. The relevant information consists of the label number and the moment when the label number appears. The output of the action monitor is defined with its format, $(label\_number, frame\_number)$, which is named as result tuple. A result tuple is called a data point. Data points are divided into four categories: fluctuating data points, non-working data points, normal data points, and disturbed data points. The judgment conditions for the four data points are as follows:

• Fluctuating data point: Fluctuating data point refers to a data point for which its difference between the frame number of the current data point and the last data point in the historical data point queue is less than the fluctuation threshold;
• Non-working data point: Non-working data point refers to a data point for which its category corresponds to non-processing action (do other things). Note that the non-working data points and fluctuating data points have an intersection, but they do not conflict in the working process.
• Normal data point: A normal data point is a data point for which its action duration is greater than the fluctuation threshold and for which its label number is different from the label number of the last element in the historical data point queue;
• Disturbed data point: A disturbed data point is a data point for which its action duration is greater than the fluctuation threshold and for which its label number is the same as its counterpart of the last element in the historical data point queue.

The flow chart of the action monitor is shown in Figure 6. Note that $E_t$ and $T_f$ are the action durations of current action and fluctuation threshold, respectively.

The resultant tuple’s format is as follows: $\left(start, end, label\_number\right)$, where $start$ and $end$ are the start frame number and end frame number of the action respectively. $label\_number$ is the label number of current action. The calculation method to $start$ is as follows:

$$start=D_{pre}\left[frame\_number\right]-\frac{L}{2}$$

(7)

where $D_{pre}$ is the previous data point, L is the fixed value of historical result length, and $D_{pre}\left[frame\_number\right]$ means to obtain $frame\_number$ of $D_{pre}$. Similarly, we obtain the following:

$$end=D_{cur}\left[frame\_number\right]-\frac{L}{2}$$

(8)

where $D_{cur}$ is the current data point.

3.2.3. Action Duration Converter Design

In the real world, the durations of actions sometimes fluctuate violently. If the results from action monitor are directly used as the observation value of the Kalman filter, the output of the Kalman filter will fluctuate too violently to make the counting-function module work steadily. In order to make the adaptive parameter more stable, the results from the action monitor need to be further transformed. According to the trend of results from the action monitor, we adjust the parameter $L_H$ of the action duration converter step by step to achieve the smoothing of results from the action monitor. The flow chart of the action duration converter is shown in Figure 7.

4. Framework of Counting Algorithm

The key component of the counting algorithm is composed of two stages: The first stage is basic action recognition, and the second is complex action label string matching. The first stage is completed by the TSM algorithm, and the label number of basic actions is obtained from RGB frames in the video stream. When the output of the TSM model changes, the new label number is inserted at the end of the result queue and then the second stage begins. In the second stage, it is essential to traverse all key-value pairs in the template dictionary. Every round of matches needs to implement such a process: take out a complex action label string, and then search for it in the result queue, finally update the state of the corresponding counting variable and the result queue. In addition, the adaptive parameter module will be updated frame by frame, according to the label number output from the action recognition model. The complete processing routine of the algorithm is shown in Algorithm 1.

Algorithm 1: Counting the repetitive movements of videos.

5. Experiments

5.1. Dataset

To meet the data requirements of TSM model training, we design and build an action recognition data set concerning the package printing production line, which contains three actions named: ① feeding materials and processing, ② retrieving the finished product and putting it back on the conveyor belt and ③ doing other things respectively. The first two categories correspond to the normal operation, and the last one is relevant to the maintenance of the equipment during production. The sample number of each category is as follows: feeding materials and processing: 1079, retrieving the finished product and putting it back on the conveyor belt: 1080, do other things: 162. The training set, validation set, and test set samples are stratified and randomly sampled from each category in a 7:2:1 ratio. All samples of the action recognition dataset are video clips containing only a single basic action, which are segmented from the original video according to the basic action definitions. The test samples of the comparison experiments in Section 5.3.2 and Section 5.4 are as follows: ten videos of book packaging (for which its time span is large) and eleven videos of picture album punching (for which its time span is small). The processing cycle of book packaging is about 3 s, while that of picture album punching is around 12 s. Most of the test videos were between one and five minutes. These videos are different from the samples in the basic action dataset because they are all original videos that have not been segmented, containing multiple basic actions. In addition, there is no intersection between test videos and the samples in the basic action dataset.

5.2. Evaluation Metrics

5.2.1. Evaluation Metrics of Action Counting

Referring to the literature [15], we employ MAE (mean absolute error) and OBOA (off-by-one accuracy) as evaluation metrics of counting accuracy:

$$\mathrm{MAE}=\frac{1}{M}\sum _{k=1}^M\frac{\left|C_k-\widehat{C_k}\right|}{C_k}$$

(9)

$$\mathrm{OBOA}=\frac{1}{M}\sum _{k=1}^M\left[\left|C_k-\widehat{C_k}\le 1\right|\right]$$

(10)

where M is the number of video samples participating in the test, and $C_k$ is the ground truth of a sample, which is determined by manual counting result. $\widehat{C_k}$ represents the number of repetitions predicted by the counting algorithm. MAE can directly reflect the counting error, while OBOA pertains to the sample’s proportion with the error number within one.

5.2.2. Evaluation Metrics of Action Monitor

We use tIOU to evaluate the performance of the action monitor in the action monitoring task, whose calculation method is as follows:

$$tIOU=\frac{I\left(P_g,P_p\right)}{U\left(P_g,P_p\right)}$$

(11)

$P_g$ represents the ground truth of the start and end time of an action, and $P_p$ represents the predicted result of the start and end time of an action. Similarly, the mean tIOU of the same semantic actions can be given by the following:

$$Mea{n}_{tIOU}=\sum _{i=1}^M\frac{I\left(P_{g_i},P_{p_i}\right)}{U\left(P_{g_i},P_{p_i}\right)}$$

(12)

where M is the number of video samples participating in the test.

5.3. Details and Results of Modules

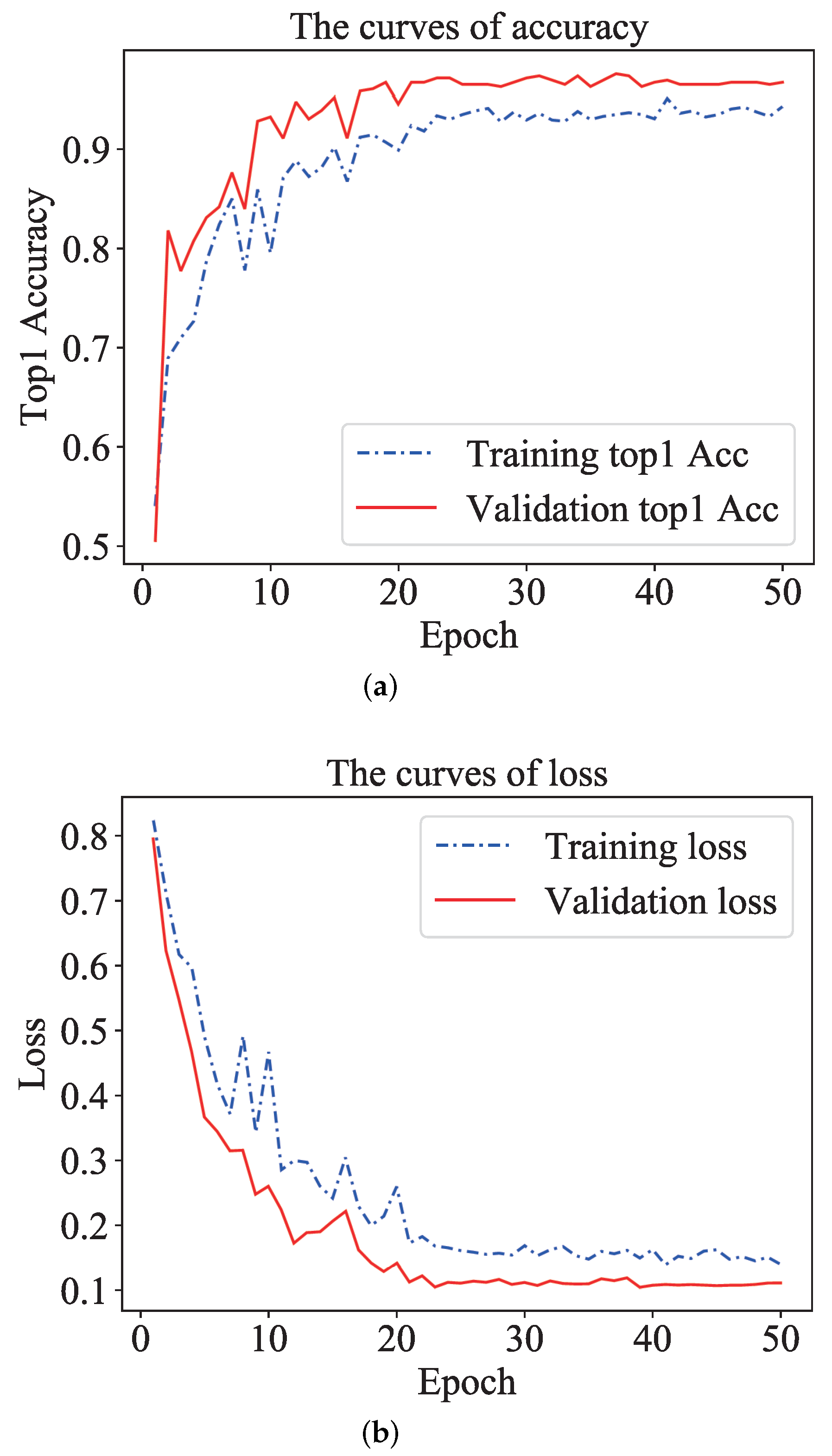
5.3.1. Details of TSM Model Training

The training TSM model uses an RTX2080 GPU with 11 GB of memory. The whole computer is equipped with a Xeon E5-2620 V4 CPU and 64 GB memory. The TSM model with the temporal shifting modules only shifts 1/8 channels of the feature map, for which its input mode is RGB, uses cross entropy as the loss function to evaluate the loss between prediction results and ground truths. Other crucial parameters are set as follows: Batch size: 16, initial learning rate: 0.0001, and the learning rate is attenuated to 0.1 times every ten epochs. Moreover, the SGD optimizer is used to run 50 epochs in the whole process. Due to the small number of samples in the dataset, the dropout is set to 0.8. The top one accuracy and loss curves are shown in Figure 8 respectively. The trained model is slightly underfitting, mainly due to the movement patterns of the actions belonging to the class named do other things varies and the regularity of them is weak.

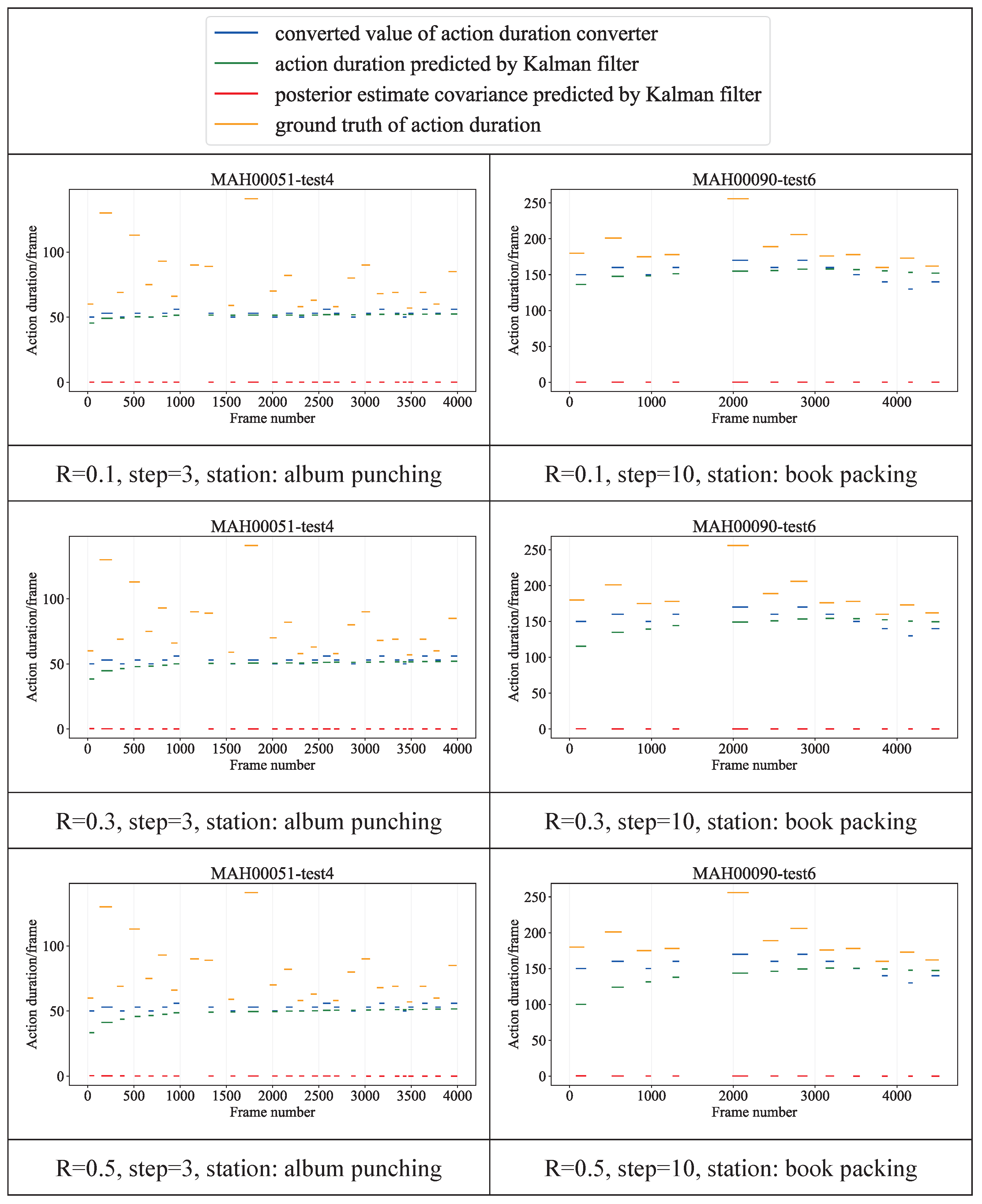
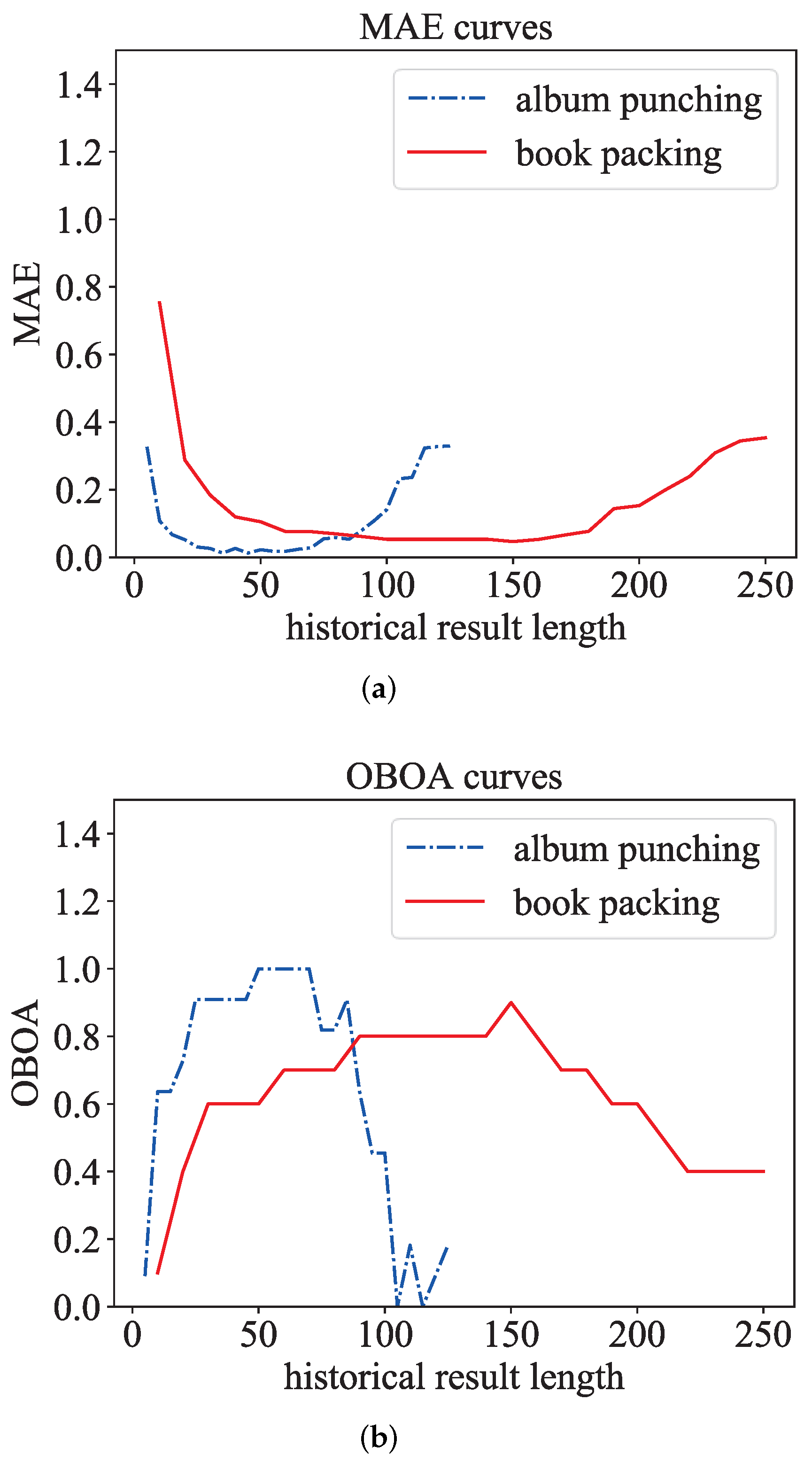
5.3.2. Details and Results of Adaptive Parameter Module

The initial values of the adaptive parameter module need to be set as follows:

• Action monitor: $non\_working\_state$: False, $D_{b0}$: None; L and $T_f$ needed to be set to different values at different stations, album punching: L: 25, $T_f$: 10; book packing: L: 150, $T_f$: 50;
• Action duration converter: album punching: $R_{max}$: 70, $R_{min}$: 50, Step: 3; book packing: $R_{max}$: 200, $R_{min}$: 100, Step: 10;
• Kalman filter: F: 1, H: 1, $Q\sim N\left(0,4.41\right)$, $X_0$: 0, $P_0$: 1, R: 0.4.

As shown in

Table 1. Performance of action monitor.

Action	Station	Mean tIOU
Feeding materials and processing	Album punching	0.57
	Book packaging	0.57
Retrieving the finished product and putting it back on the conveyor belt	Album punching	0.48
	Book packaging	0.49

, it can be seen that the location accuracy of the action named feeding materials and processing is higher. The reason for this phenomenon is that workers often need to adjust machines after processing some samples. Therefore, in this paper, we choose the action duration of feeding materials and processing as input of the Kalman filter.

Figure 9 shows the results of the adaptive parameter module, consisting of the results of the Kalman filter, the ground truths of the action durations, and the predicted results of the action monitor under the condition that the step is fixed and the observation noise R takes different values.

As shown in Figure 9, the predicted results of the action monitor can go in the same direction as the ground truths of the action duration in most cases. In addition, the results from the Kalman filter are usually below the ground truths of the action duration, so basic actions are less likely to be missed. When the deceptive actions have little effect on the action recognition model, we should make the result of the Kalman filter as small as possible, so as to ensure the detection ability of the action recognition model for actions with a small time span to the greatest extent. As R increases, the results of the Kalman filter converge to the predicted results of the motion monitor slower. Meanwhile, the results of the Kalman filter become smoother, which will make the whole system more stable.

Figure 10 shows the results of the adaptive parameter module, consisting of the results of the Kalman filter, the ground truths of the action duration, and the predicted results of the action monitor under the condition that the observation noise R is fixed and the step takes different values.

As shown in Figure 10, as the step increases, the predicted results of the motion monitor fluctuate more violently, and the results of the Kalman filter also fluctuate.

5.4. Experiments and Result Analysis

5.4.1. Optimization Strategy Experiment

Aiming at confirming the property of two optimization strategies mentioned in Section 3.2, we conducted two optimization strategy comparison experiments. ① default setting compared with label number jumping suppression strategy, ② based on label number jump suppression strategy, comparing the cases whether the invalid action elimination strategy is adopted or not.

Table 2. Performance of optimization strategy experiment.

Setting	Station	MAE	OBOA
TSM Default Setting	Album Punching	0.052	0.727
	Book Packaging	0.589	0.200
LNJS	Album Punching	0.105	0.364
	Book Packaging	0.047	0.900
LNJS&IAE	Album Punching	0.026	1.0
	Book Packaging	0.047	0.900

shows the results of the comparison experiment of the two optimization strategies. The results in the area of the first two rows of the first column are all the evaluation results of the comparison experiment of the first optimization strategy. As can be seen, the performance of the book packaging process is improved significantly, while the performance of album punching degrades. The main reason lies in that there are some misjudgments, so in the case without the invalid action elimination strategy, count omissions occur. When not optimized, since label jumping compensates for part of counting missing, these metrics are superior to those being optimized by the first strategy. As demonstrated in Figure 11, the phenomenon of label jumping at both stations is suppressed well.

Note that LNJS and IAE is the abbreviation for label number jumping suppression and invalid action elimination respectively.

The relationship between historical result length and counting accuracy is shown in Figure 12. The reasons why the historical result affects the counting accuracy are as follows: taking an MAE curve as an example, with the increasing length of historical results, counting accuracy improves due to a decrease in the influence of invalid actions before the historical result length reaches the first extreme point. However, when the historical result length exceeds the rational range, the historical results of the basic actions with larger time spans will result in the fact that the basic actions with smaller time spans will not be recognized by the TSM algorithm, thus leading to counting accuracy decreases. The reasons above can also obtain the trend of OBOA curves.

The results tell us that the invalid action elimination strategy has an obvious effect on the improvement of the album punching station. However, it makes no sense with the book packaging station. The main reason is that when the basic action of this station is misjudged as doing other things, it usually sustains only a short time, so its initial prediction result is annihilated by historical results, which is not shown as the recognition result of basic action. Figure 13 shows one of the results of this trial.

In summary, since the label number jumping suppression strategy suppresses the environmental noise and the invalid action elimination strategy cleans up the invalid base action, MAE is decreased by 0.542, and OBOA is increased by 0.7 compared with the algorithm without any optimization strategy. The results illustrate that the above two optimization strategies contribute to the performance improvement of the counting algorithm in this paper.

5.4.2. Comparison Experiment

We compare the performance of the algorithm with adaptive parameter module and its variant without adaptive parameter module.

Table 3. Comparison of the performance between the algorithm with adaptive parameter and the algorithm without adaptive parameter.

Algorithm	Station	MAE	OBOA
Algorithm without adaptive parameter module	Album Punching	0.026	1.0
	Book Packaging	0.047	0.900
Algorithm with adaptive parameter module	Album Punching	0.022	1.0
	Book Packaging	0.047	0.900

is the performance of algorithms containing and not containing the adaptive parameter module. As shown in the table, the adaptive parameter module plays a positive role in improving the counting accuracy. The counting accuracy of the book packaging station does not change, which lies in the fact that the time span of the actions of book packaging is large, so the time span of interfering actions is also large; moreover, the adaptive parameter module lacks sufficient adjustment capability to eliminate the impact generated by deceptive actions.

6. Conclusions

Distinct from existing semantically independent counting methods, our method uses template matching to realize counting based on semantic understanding. It establishes a semantic mapping relationship between video frames and action labels by using an online action recognition model. The interference factors in the input are corrected by the action recognition model. In addition, the counting principle of this method has clear logic and good interpretability, which plays a positive role in the accuracy of the final result. The contrast experiment reveals that the method proposed in this paper has a lower counting error for the test samples. In addition, the adaptive parameter module contributes to improving counting accuracy to a certain degree.

The online action recognition model is a key component of the algorithm. We take the TSM algorithm into consideration, but it can be replaced with another counterpart according to specific movements. Moreover, it should be noted that our method is only suitable for the actions that can be decomposed according to our decomposition principles, so other action counting problems may not be solved by the method in this paper.