Steering and Speed Control System Design for Autonomous Vehicles by Developing an Optimal Hybrid Controller to Track Reference Trajectory

Abstract

In this paper, a longitudinal and lateral control system of an autonomous vehicle is presented by developing a novel hybrid trajectory tracking algorithm. In this proposed method, the longitudinal control system is developed based on the curvature information of the reference path. The autonomous vehicle modifies the desired speed according to the estimated size and types of the reference trajectory curves. This desired speed is integrated into the PID controller to maintain an optimal speed of the vehicle while following the given path. The lateral control system is designed based on feedforward (preview control) and feedback (LQR) controllers to reduce lateral errors between the trajectory and autonomous vehicle. The feedforward and the feedback controllers generate precise steering angles to eliminate orientation and lateral errors caused by the curvature of the trajectory and external disturbances. The effectiveness of the proposed method is evaluated by comparing simulation and experimental results with different trajectory tracking algorithms on simulated and experimented paths. It is proven that the proposed algorithm is capable of significantly minimizing lateral errors on sharp curves compared to other path tracking methods.

1. Introduction

Autonomous vehicles are one of the most popular research topics currently. Autonomous driving offers comfortable, efficient, and safe transportation. In recent years, technologies have dramatically advanced, therefore, autonomous vehicle’s computational power has increased, whereas sensing and computing time are reduced [1]. Autonomous vehicles have to understand and have cooperation with some major functions, such as localization and mapping, perception, trajectory generation, and control for automated driving [2]. Reference trajectory tracking is one of the fundamental issues of autonomous vehicle control and navigation systems. The main objective of the trajectory tracking system is to generate control commands to follow the predefined path by considering the autonomous vehicle’s relevant motion constraints. Various trajectory tracking methods exist in the literature. Three types of widely used path tracking methods are geometric methods (pure pursuit, Stanley controller), optimal control based methods (LQR, optimal preview control), and model based methods (PID, MPC, sliding mode control, fuzzy logic controller). This section describes a review of some path tracking algorithms which are already being tested for trajectory tracking of autonomous vehicles.

Several geometric and kinematic path tracking controllers are used for autonomous vehicle path tracking purposes; among them, the pure pursuit controller [3] is probably the most simple and widely used path tracking controller [4].

The pure pursuit calculates a certain distance, which is known as the look-ahead distance, at every time step in the reference trajectory to compute the steering angle ($\delta$) of the autonomous vehicle [5].

An adaptive pure pursuit algorithm is proposed in [6], where it is integrated with the PID controller to reduce tracking error at low curvature path.

A comparative study has been conducted among the Stanley, the quadratic dynamic, and the pure pursuit controllers under discontinuous paths and stochastic actuation, where the performance of the pure pursuit outperformed other controllers.

However, it suffers mainly from corner-cutting (neglects curvature information) and significant lateral error if look-ahead distance is high and from severe oscillations when it is assumed too small [7]. The Stanley is another effective geometric steering controller. Look-ahead distance is not required in this controller, and it considers the dynamics model and instantaneous velocity of the autonomous vehicle [8]. The Stanley controller was led by the Stanford University team to win the DARPA Grand Challenge 2005. It has a non-linear feedback function, which calculates steering command from the front wheel axle of the vehicle based on lateral errors [9]. However, it suffers from external disturbances and generates more lateral errors in the curved path [10]. The Stanley controller is not robust under a discontinuous path compared to other controllers [2]. The linear quadratic regulator (LQR) is one of the popular optimal control based methods, which is mainly a state feedback controller. It has versatile applications as a control system from flight control to robotics, as its implementation is simple. A generalized version of the LQR control system is proposed in [11] for solving aircraft full tracking problems in aviation with the presence of different uncertain physical disturbances. The LQR controller is integrated with a particle swarm optimization (PSO) method for autonomous passenger vehicles trajectory tracking in various dynamic conditions [12]. The LQR controller suffers when sharp curves are present in the reference path. Optimal preview controller (OPC) is capable of effectively developing the path tracking performance as the future information of the reference trajectory is available in this closed-loop control system [13,14]. Therefore, the OPC is widely used in autonomous vehicles for trajectory tracking. The original studies, concepts, models, and some potential applications of the preview controller are explained thoroughly in [15,16,17]. The classical Riccati equation is extensively used in the OPC design based on the LQR control theory [18,19,20,21]. Particularly, [22,23] presented a novel discrete-time system for preview control by utilizing the information of the fusion estimation theory. Subsequently, the Riccati equation method was further developed for the preview controller in [24,25] for linear descriptor systems.

The OPC shows poor tracking performance when the error is external and discontinuous [20,26]. Some researchers have focused on the fuzzy logic controller (FLC) to overcome autonomous trajectory tracking problem of mobile robots [27]. The FLC is easier to design, robust, inexpensive, and easily operated because human driving behaviors are interpreted linguistically in this technique [28]. Therefore, the FLC has been used broadly over the last few decades for mobile robot path tracking like vehicle parking [29]. A simple FLC is designed in [30], where very few fuzzy rules are applied for path tracing of wheeled mobile robot, whereas [31] enhances a complex adaptive fuzzy technique to generate appropriate automatic steering and velocity command for the autonomous vehicle. To handle vehicle and environmental uncertainties, fuzzy logic based technique is a good solution for the trajectory tracking of mobile robots [32].

The FLC is appropriate to control nonlinear applications because no explicit dynamics model is required in this technique [33]. A novel hybrid path tracking algorithm is proposed by combining a neural network and the FLC for a nonholonomic mobile robot in [34]. However, rough membership function parameters and rules base adjustment of a fuzzy controller usually produces steady-state error and takes more computational time [32]. Recently, there have been more studies done on the model predictive control (MPC) method to improve path tracking accuracy of autonomous mobile robots [35,36]. The MPC is able to forecast future trajectory information and decide the optimal control actions accordingly for autonomous vehicles. It reduces the lateral error between the given trajectory and the anticipated path by applying the vehicle dynamics model to generate the appropriate steering angle of the vehicle by online optimization [37]. A nonlinear model predictive control (NMPC) technique is applied on two different vehicles by controlling the combination of braking as well as steering [38]. A novel real-time trajectory tracking MPC algorithm is proposed in [39] for an autonomous vehicle at low speed. For high-speed vehicle path tracking, Ref. [40] presented a novel MPC scheme by considering tire slip angle constraint for controlling front steering angle to follow a path on slippery roads. Ref. [41] investigated trajectory tracking stability at high speed. Based on the system features, it can be seen that linear and nonlinear MPC have to solve the optimization problem iteratively at each control step, which may lead to heavy computation load, and optimization may fail if the initial values are improper [37]. Therefore, it is very challenging for real-time implementation [38]. Authors in [42] proposed a novel two-level optimization method of scheduling and trajectory planning for connected automated vehicles (CAVs) to improve the traffic efficiency of conflict zones and reduce the travel delay and fuel consumption of CAVs, which provides new opportunities and challenges for the optimization and management of traffic conflict zones. In paper [43], simulation results of an unconventional principle of the vehicle power flow transmission is presented where a combined hydro-mechanical transmission with hydrostatic units and torque converter in parallel lines with mechanical components are used. This novel method can be used in commercial vehicles and mobile working machines. A unique method is proposed in [44] to develop a prototype of a variable message sign (VMS) reading system using machine learning techniques. In this project, advanced driver assistance system (ADAS) devices perceive the environment by using machine learning methods and provide assistance to the driver for his comfort or safety. Authors in [45] developed a deep neural network (DNN) based model to estimate longitudinal–lateral dynamics of an autonomous vehicle where it predicts accurate vehicle states in real time.

The purpose of the aforementioned trajectory tracking controllers is to reduce the lateral error between the autonomous vehicle and the reference trajectory. However, the problem arises for most of the path-tracking controllers while the autonomous vehicle moves through a sharp curve in the reference path [46]. Driving through a sharp curve of the trajectory is always dangerous if the speed and steering angle are not appropriately adjusted for the vehicle. In the real world, if a driver wants to stay in the path and go through the sharp curve safely, he must be able to reduce speed and control the steering wheel simultaneously. A similar principle should be used for autonomous vehicle while tracking reference trajectory.

Therefore, a novel path tracking strategy is proposed in this paper, where the main contribution is to reduce the lateral errors and tracking errors of the autonomous vehicle, especially while going through sharp curves, by developing a hybrid longitudinal and lateral control system. The longitudinal control design is based on the geometrical curvature information and is integrated with the PID controller for speed control purposes. The desired speed of the vehicle is generated from the vehicle current speed and curvature profile of the road. Furthermore, the feedforward optimal preview control is applied to solve lateral errors of the trajectory by controlling the steering angle of the vehicle, especially caused by curvatures of the road. The LQR will be applied to decrease the errors caused by environmental and external disturbances. The architecture overview of the proposed method is shown in Figure 1. The tracking performance of the proposed algorithm is evaluated through the average root mean square errors. The effectiveness of the proposed method is tested and verified by simulation and experimental results. The goals of this paper are as follows:

• Analyze the given GPS trajectory,
• Identify the current position of the vehicle in the reference path,
• Determine sharp curves position information from the reference path,
• Calculate the desired velocity for each sharp curve,
• Calculate the appropriate steering angle for each sharp curve,
• Adjust speed and steering angle with respect to sharp curves to follow the reference trajectory precisely.

The rest of this paper is organized as follows. The dynamic model of the vehicle is presented in Section 2, and Section 3 broadly explains the design of the proposed path tracking controller. Section 4 describes the performance of the proposed method and verifies experimental results with different trajectory tracking algorithms. Section 5 concludes the paper with possible future research directions.

2. Vehicle Dynamic Model

It is useful to describe the vehicle dynamic bicycle model with the kinematic bicycle model by considering the reference path. The kinematics of the vehicle can be illustrated in Equations (2)–(4) according to the geometry relationship as shown in Figure 2. Parameters of the vehicle are shown in

Table 1. Vehicle model parameters considered from [47,48,49].

Parameter	Value	Description
M	1155.0 kg	Vehicle mass
W	1.6 m	Width of vehicle
I	1466.35 kgm${}^2$	Vehicle yaw moment inertia
WB	2.6 m	Wheel base
TR	0.33 m	Tyre radius
TW	0.21 m	Tyre width
$l_f$	1.165 m	Distances of front tire from the C.G of the vehicle
$l_r$	1.165 m	Distances of rear tire from the C.G of the vehicle
$C_f$	162,835.82 N/rad	Cornering stiffness of front tyre
$C_r$	162,835.82 N/rad	Cornering stiffness of rear tyre

.

$$m{a}_y=F_{xf}sin\left({\delta }_f\right)+F_{yf}cos\left({\delta }_f\right)+F_{yr}$$

(1)

$$\dot{x_o}=vcos(\psi +\beta )$$

(2)

$$\dot{y_o}=vsin(\psi +\beta )$$

(3)

$$\dot{\psi }=r$$

(4)

where longitudinal and lateral coordinates ($\dot{x_o}$ and $\dot{y_o}$) are situated at the center of gravity (C.G); $\psi$, $\dot{\psi }$, and $\beta$ are the yaw angle, the yaw rate, and the sideslip angle of the vehicle, respectively. The longitudinal velocity of CoG is v. Assuming that the curvature of the path is small, for this reason, it generates small variances of yaw angle and sideslip angle of the vehicle. Therefore, the kinematic model can be illustrated as

$$\dot{x_o}=v$$

(5)

$$\dot{y_o}=v(\psi +\beta )$$

(6)

$$\dot{\psi }=r$$

(7)

It is difficult to track the trajectory using only the kinematic model of the vehicle when the speed of the vehicle is increased and the curvature of the path varies. In this case, a dynamic model of the vehicle must be developed that considers the dynamic effects and motion of the vehicle for precisely tracking the reference trajectory. The longitudinal velocity of the vehicle is assumed to be constant; then according to Newton’s Law, the dynamics of the vehicle could be illustrated as follows:

$$a_y=v\dot{\beta }+v\dot{\psi }$$

(8)

where $a_y$ is the initial acceleration at the C.G in the direction of the y axis. Two terms contribute to $a_y$: the acceleration $v\dot{\beta }$ along the y axis and the centripetal acceleration $v\dot{\psi }$.

Therefore, lateral angular motion equation of the vehicle can be expressed as

$$mv(\dot{\beta }+\psi )=F_{yf}+F_{yr}.$$

(9)

The equation of the yaw dynamics in the z axis can be expressed as

$$I_z\dot{\psi }=l_f{F}_{yf}-l_r{F}_{yr}$$

(10)

where $l_f$ and $l_r$ are the distances of the front tire and the rear tire, respectively, from the C.G of the vehicle; $F_{yf}$ and $F_{yr}$ are the front and rear lateral tire forces, and $F_{yf}$ and $F_{yr}$ are defined as

$$F_{yf}=C_f{\alpha }_f$$

(11)

$$F_{yr}=C_r{\alpha }_r$$

(12)

where $C_f$ and $C_r$ are the cornering stiffness of the front and rear tires. The front and rear tire sideslip angles of vehicle ${\alpha }_f$ and ${\alpha }_r$ are computed as follows:

$${\alpha }_f=\frac{\beta +l_f\dot{\psi }}{v}$$

(13)

$${\alpha }_r=\frac{\beta -l_r\dot{\psi }}{v}$$

(14)

Substituting Equations (11)–(14) into Equations (9) and (10), the vehicle lateral and yaw dynamics can be determined. The lateral dynamic equation can be written as

$$\dot{\beta }=-\frac{(C_f+C_r)\beta }{mv}-v\dot{\psi }-\frac{(l_f{C}_f-l_r{C}_r)\dot{\psi }}{mv}+\frac{C_f}{m}\delta .$$

(15)

Similarly, the yaw rate updated equation can be expressed as

$$\dot{\dot{\psi }}=-\frac{(l_f{C}_f-l_r{C}_r)\beta }{I_{z}v}-\frac{(l_f^2{C}_f+l_r^2{C}_r)\dot{\psi }}{I_{z}v}+\frac{l_f{C}_f}{I_z}\delta .$$

(16)

Therefore, the vehicle lateral state space model can be defined from Equations (6), (7), (15), and (16) and can be written as

$$\begin{array}{cc}\hfill \frac{d}{dt}\left[\begin{array}{c}{y}_o\\ \psi \\ \beta \\ \dot{\psi }\end{array}\right]& =\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{(C_f+C_r)}{mv}& 0& -v-\frac{(l_f{C}_f-l_r{C}_r)}{mv}\\ 0& 0& 1& 0\\ 0& -\frac{(l_f{C}_f-l_r{C}_r)}{I_{z}v}& 0& -\frac{(l_f^2{C}_f+l_r^2{C}_r)}{I_{z}v}\end{array}\right]\hfill \\ \hfill & \left[\begin{array}{c}{y}_o\\ \psi \\ \beta \\ \dot{\psi }\end{array}\right]+\left[\begin{array}{c}0\\ \frac{C_f}{m}\\ 0\\ \frac{l_f{C}_f}{I_z}\end{array}\right]{\delta }_f\hfill \end{array}$$

(17)

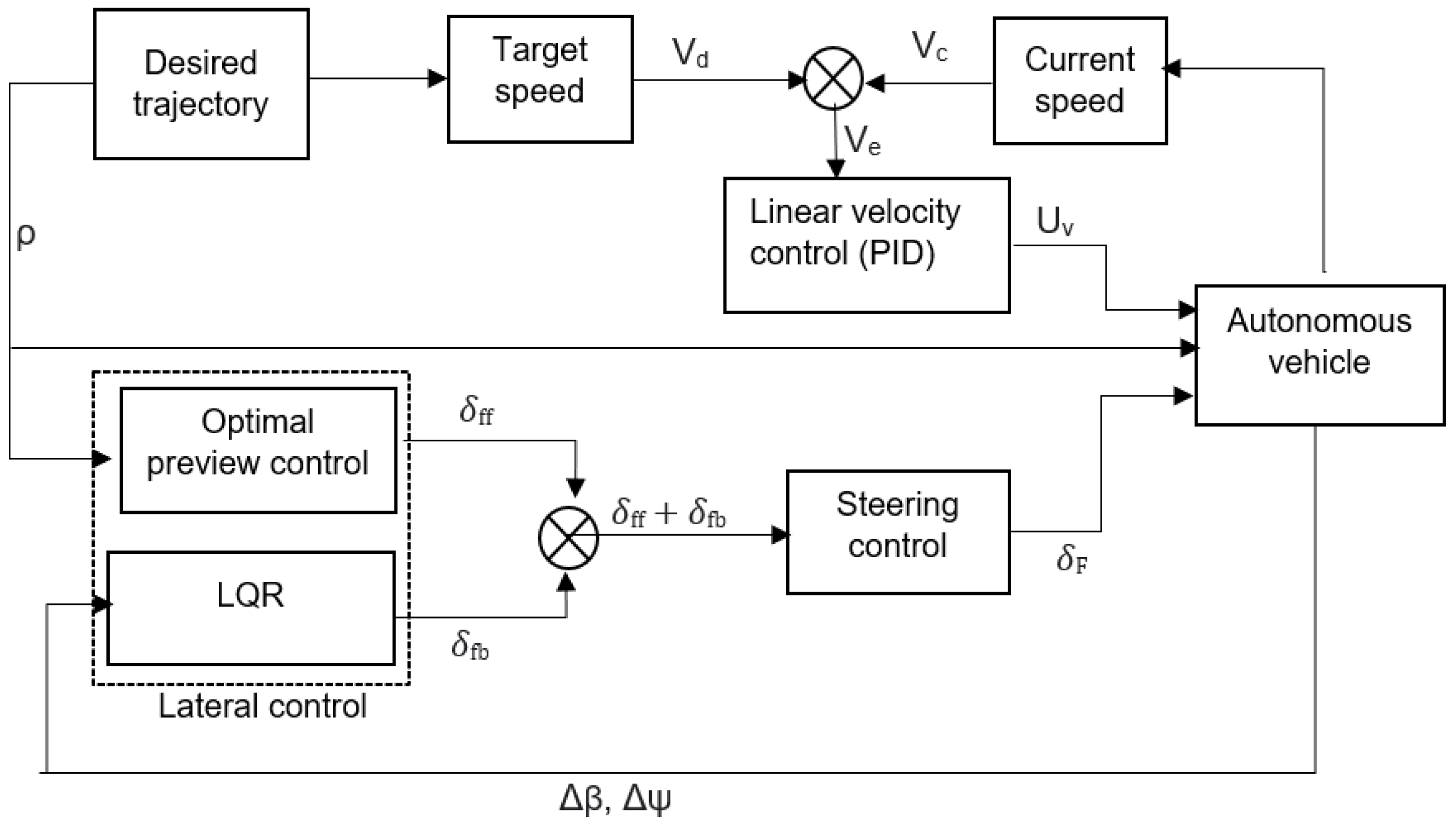
3. Trajectory Tracking Controller Design

For the last three decades, extensive research has been done on the navigation and motion control of autonomous vehicles, but some limitations still exist. The path tracking problem is one of the vital challenges that need to be solved for autonomous navigation. Trajectory tracking controllers calculate the optimal commands for the autonomous vehicle to follow a reference path as accurately as possible. The desired speed (v) and the desired vehicle orientation ($\theta$) commands are required to achieve good tracking performance. In this section, the proposed trajectory tracking algorithm will be developed.

3.1. Longitudinal Speed Controller

A longitudinal controller is designed to generate appropriate velocity commands for autonomous vehicles while tracking the given trajectory. Human driving behavior should exist in the controller so that it can make proper decisions and reduces its speed based on uncertain curvatures of the path. Therefore, curve analysis is one of the important parts for the autonomous vehicle [35] to control the vehicle’s velocity appropriately, as it will keep the lateral errors to a minimum.

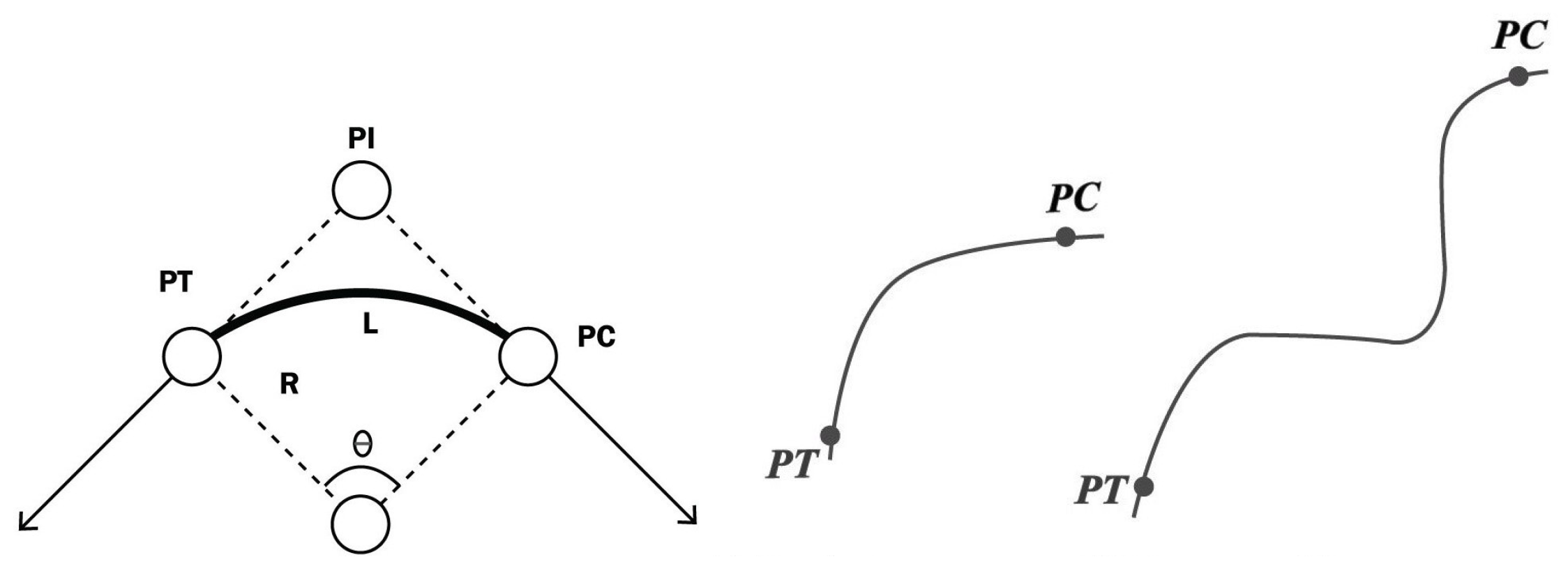
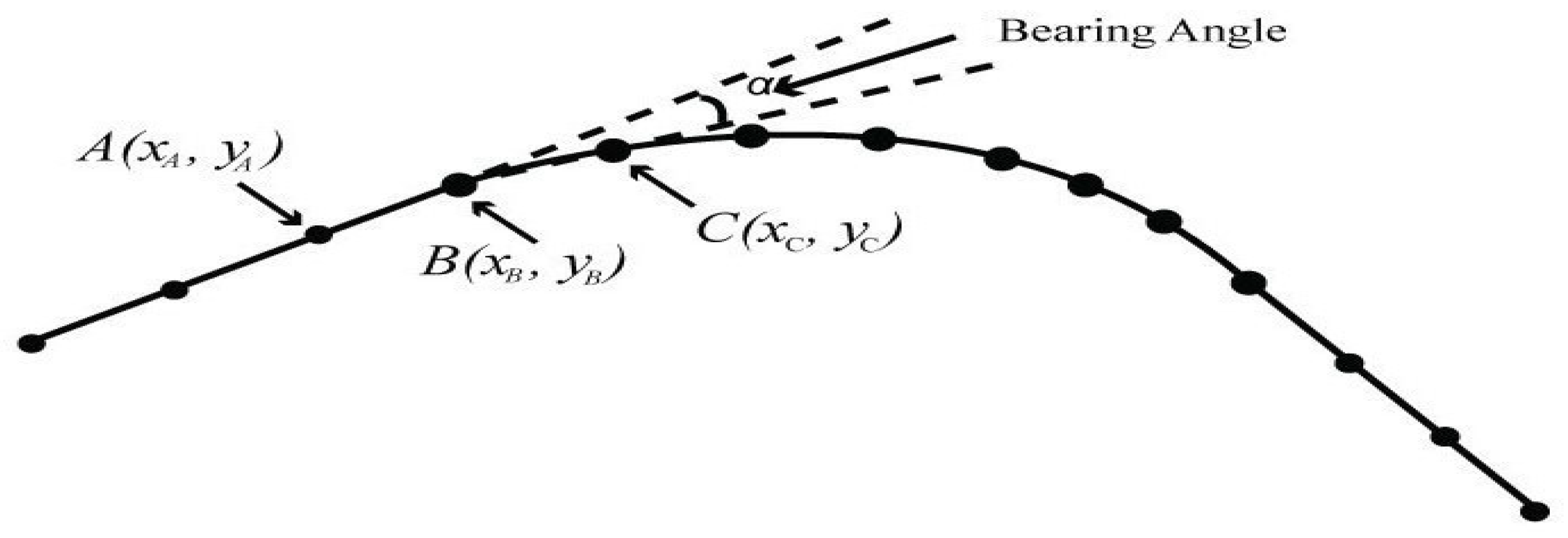
3.1.1. Sharp Curve Estimation

To determine sharp curves, all of the curves need to be identified from the reference GPS path to generate optimal speed of the autonomous vehicle for each curve. A first step is localizing the curves starting and ending points, which are known as points of tangency (PT) and points of curvature (PC), respectively. When PT and PC points are defined, the characteristics of the curves can be computed as illustrated in Figure 3, where curve length, point of intersection, central angle, and radius are presented by the symbols of L, PI, $\theta$, and R, respectively. A curve can be defined as sharp or dangerous when it has a larger central angle or smaller radius, whereas a larger radius or smaller central angle depicts a less dangerous curve [26]. The severe curve location deserves more attention when the vehicle has to reduce speed for keeping small lateral errors.

After identifying PT and PC in a curve, there is an important step to compute the bearing angle between two consecutive segments AB and BC formed from three points (A, B, and C), as shown in Figure 4, and $\alpha$ can be expressed as

$$\begin{array}{cc}\hfill \alpha =& co{s}^{-1}\{\frac{(x_B-x_A)(x_C-x_B)}{\sqrt{{(x_B-x_A)}^2+{(y_B-y_A)}^2}}+\hfill \\ \hfill & \frac{(y_B-y_A)(y_C-y_B)}{\sqrt{{(x_C-x_B)}^2+{(y_C-y_B)}^2}}\}\times \frac{180}{\pi }\hfill \end{array}$$

(18)

where $x_A$, $x_B$, and $x_C$ are the x coordinates of points A, B, and C, respectively, and $y_A$, $y_B$, and $y_C$ are the y coordinates of points A, B, and C, respectively.

When the bearing angle $\alpha$ is computed, it is essential to determine a threshold value, and this threshold value will define whether point B is assumed to be part of a curvature or not. If the bearing angle $\alpha$ is smaller than the defined threshold, point B is not a part of the curve, whereas if $\alpha$ is higher than the threshold value, center point B is a part of the curve. Therefore, defining the right threshold value is an important step, as the identification of the curve depends on it. In this paper, the threshold value is chosen as $1.{25}^{\circ }$, and this threshold value is evaluating from [26], where different curvature identification threshold values were tested in order to choose the right threshold value. Curves can be classified as simple or compound based on [26,46], shown in Figure 3. A simple curve has one segment between two points, whereas, the compound curve has at least two consecutive segments that are separated by a specific distance between each other. From the geometric information of each curve with its starting (PT) and ending point (PC), one can compute the central angle ($\theta$), radius (R), and length (L) of each curve as follows:

$$R=\sqrt{{(x_{PC}-x_O)}^2+{(y_{PC}-y_O)}^2}$$

(19)

$$C=\sqrt{{(x_{PT}-x_{PC})}^2+{(y_{PT}-y_{PC})}^2}$$

(20)

$$\theta =2\times si{n}^{-1}\left(\frac{C}{2R}\right)\times \frac{180}{\pi }$$

(21)

$$L=\frac{\theta ·\pi }{180}\times R$$

(22)

In this work, only dangerous curves are considered to reduce vehicle speed. Therefore, according to [46], dangerous curves are categorized when their radius is from 5 to 18 m or in a range of angles between ${30}^{\circ }$ and ${180}^{\circ }$. The curve driving scenario is presented in Figure 5.

3.1.2. Speed Control Algorithm for Sharp Curves

In this paper, the longitudinal speed controller is designed according to the derivation of the trajectory curvature $K_{traj}$ and the vehicle curvature $K_{vehicle}$. The autonomous vehicle is calculating $K_{traj}$ and $K_{vehicle}$ iteratively while tracking the reference trajectory. The curvature of the trajectory and vehicle can be determined iteratively as

$$K=\frac{\mathsf{\Delta }\theta }{\mathsf{\Delta }L}$$

(23)

where K, $\theta$, and L are the curvature, central angle, and length of the trajectory. Based on the present curvature, the curvature function f($K_{traj}$, $K_{vehicle}$) value is used to generate appropriate speed reduction in a dangerous curve for the autonomous vehicle during the movement. From Equation (24), we get the new desired velocity $V_d$ by subtracting the curvature function from the current velocity $V_c$, which is preventing cutting corner error of the vehicle while following the trajectory.

$$V_d=V_c-f(K_{traj},K_{vehicle})$$

(24)

$$V_e=K_d-V_c$$

(25)

The calculated velocity error $V_e$ from Equation (25) is fed into the PID controller to adjust the position of the throttle pedal to maintain the optimal speed precisely. The PID velocity controller equation can be written as

$$U_v=k_p{V}_e+K_i\sum V_e\mathsf{\Delta }t+K_d\frac{\mathsf{\Delta }{V}_e}{\mathsf{\Delta }t}$$

(26)

where $U_v$, $K_p$, $K_i$, and $K_d$ are the control output, proportional control gain, integral control gain, and derivative control gain, respectively.

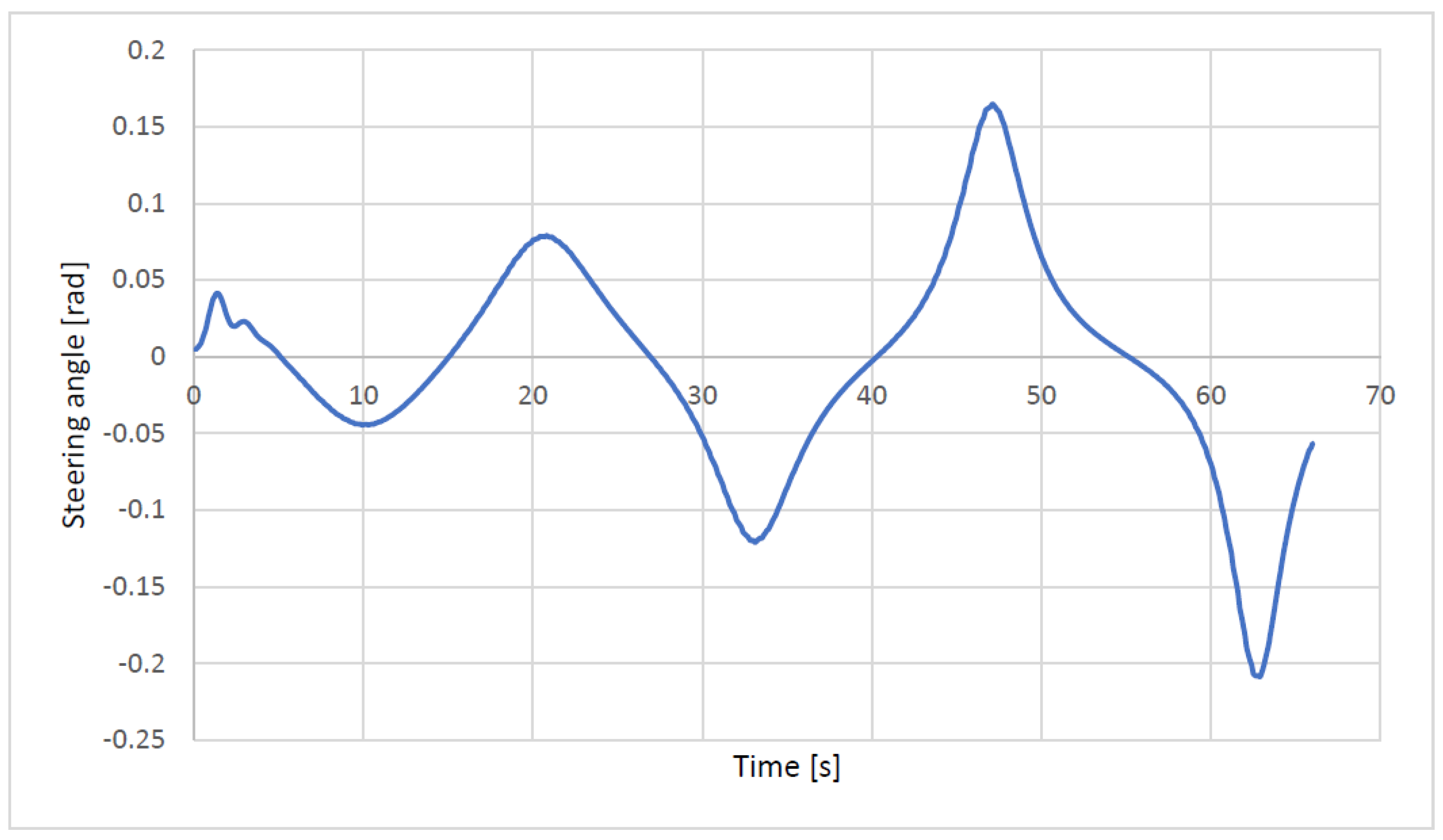
3.2. Lateral Controller

According to the dynamics model of the vehicle, a preview (feedforward) control and the LQR (feedback) control strategy is applied to generate an appropriate steering angle for autonomous vehicles. The preview controller is applied to reduce interference from trajectory curvature as the preview information of the reference path is used in this controller. In contrast, the LQR is designed to eliminate the real-time lateral deviation and orientation error caused by external disturbances and has a better adaptability with the changes in longitudinal speed while following the given trajectory.

3.2.1. Optimal Preview Controller

The purpose of the optimal preview (feedforward) controller is to remove the lateral error generated by the curvature of the path. In this algorithm, preview information about the trajectory curvature of the path is required, which can be determined from the reference GPS path or obtained from road geometry. The feedforward control can be defined as $C_{ff}$ and expressed in Equations (27) and (28).

$$C_{ff}=\frac{C_f{C}_r{(l_f+l_r)}^2+(l_r{C}_r-l_f{C}_f)m{v}^2}{C_f{C}_r(l_f+l_r)}$$

(27)

$${\delta }_{ff}=C_{ff}·\rho$$

(28)

where ${\delta }_{ff}$ is the feedforward control input, and $\rho$ is the information of the reference curvature radius. The lateral error produced by the curvature of the trajectory can be reduced by the preview controller. However, this controller can not always maintain zero lateral error due to external disturbances. Therefore, it is important to design a feedback controller for external disturbances that is able to eliminate lateral error.

3.2.2. Optimal LQR Controller

In this proposed method, the objective of the LQR controller is to generate appropriate steering angles to eliminate the lateral error between the reference path and the actual path that is generated by external disturbances. Therefore, the curvature of the trajectory is not considered here, and the longitudinal velocity is assumed to be constant. The state-space model of the vehicle dynamics can be expressed as

$$\dot{x}=Ax+U{\delta }_{fb}$$

(29)

where $x=[y_0,\psi ,\beta ,\dot{\psi }]$, and ${\delta }_{fb}$ is feedback steering control command. The state-space model needs to be discretized by using the discretization method because digital discrete control input is used in the LQR controller where the discretized sample time is 0.01 s. Therefore, the discrete lateral dynamics model can be written as

$$x(k+1)=A_{d}x+U_d{\delta }_{fb}$$

(30)

The state-space variables ($A_d,U_d$) are controllable, therefore, the optimal steering control command can be expressed as

$${\delta }_{fb}=-Kx\left(k\right)$$

(31)

where K is the optimal control gain and K is expressed in Equation (32)

$$K={(R+U_d^{T}P{U}_d)}^{-1}{U}_d^{T}P{A}_d.$$

(32)

The objective cost of the control command can be minimized by Equation (33) and the matrix P can be solved by applying the algebraic Riccati equation (Equation (34)).

$$J=\sum _{n=1}^{\infty }{x}^T\left(k\right)Qx\left(k\right)+{\delta }_{fb}^T\left(k\right)R{\delta }_{fb}^T\left(k\right)$$

(33)

$$P=A_d^{T}P{A}_d-A_d^{T}P{U}_d{(R+U_d^{T}P{U}_d)}^{-1}{U}_d^{T}P{A}_d+Q$$

(34)

where

$$Q=\left[\begin{array}{cccc}{q}_1& 0& 0& 0\\ 0& q_2& 0& 0\\ 0& 0& q_3& 0\\ 0& 0& 0& q_4\end{array}\right]$$

where Q is the diagonal state cost matrix and it minimizes bad performance (e.g., minimizes large differences between the reference position of the vehicle and where the vehicle actually is in the world); $R=\left[1\right]$ is the input cost matrix, which is minimizing control effort. This LQR proposed method controls the turning parameter of the vehicle. Therefore, the turning parameter can be chosen as $q_2=q_3=q_4=0$. Now there is only a single parameter that is used for turning purposes. Finally, the steering angle input ${\delta }_F$ is generated by combining the feedforward control command and feedback control command.

$${\delta }_F={\delta }_{ff}+{\delta }_{fb}$$

(35)

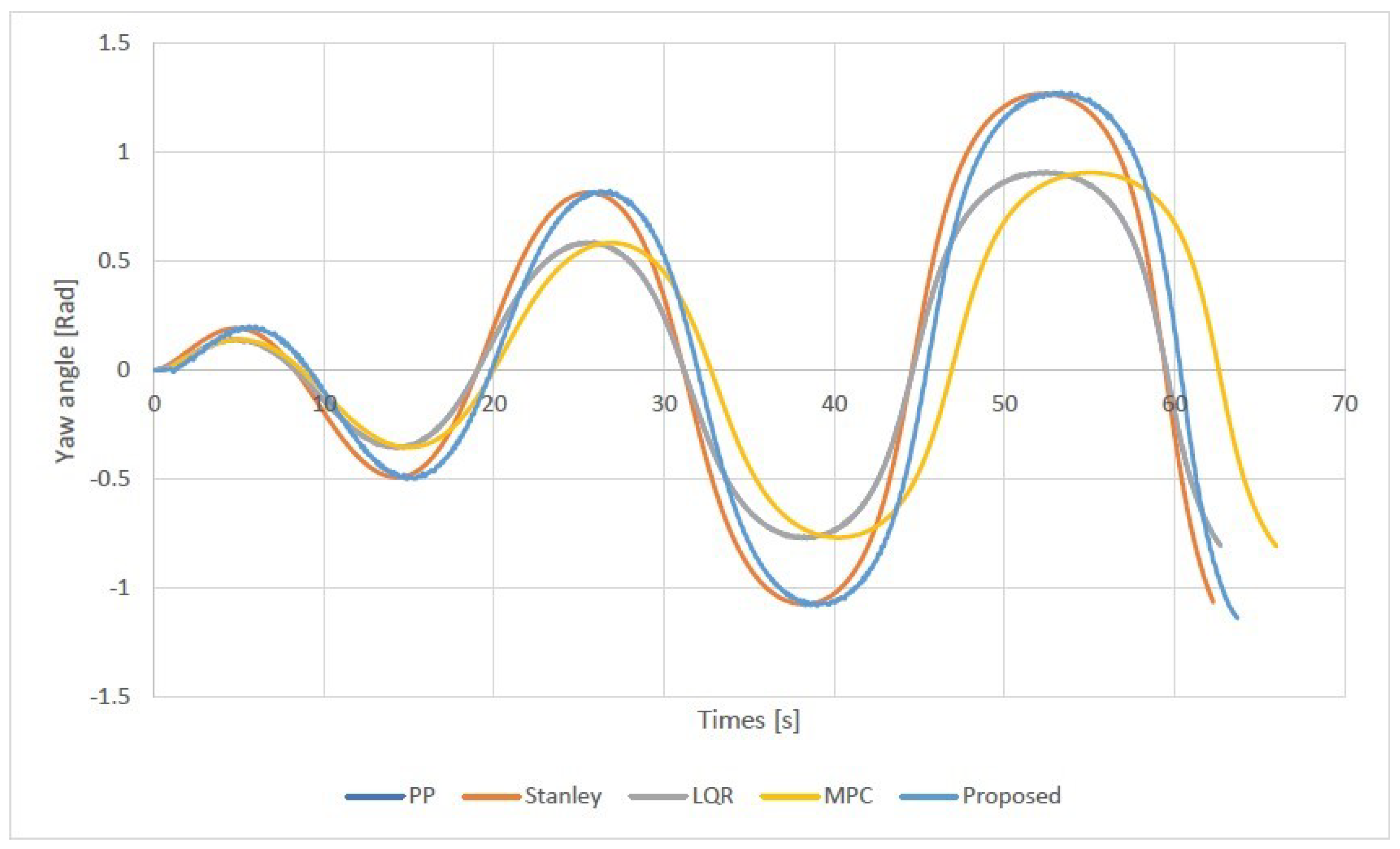
4. Experimental Results and Discussion

In this section, different tracking control methods are performed on simulated and real dataset trajectories. The aim is to show and compare how path tracking accuracy is improved when the proper speed of the vehicle is considered for each segment in the reference trajectory. Two paths (one is created and one is real) are considered for the experiments. Each path has various lengths and curve characteristics, and these paths are created by using the python cubic splines.

• Simulated path: There are 750 continuous points and five normal curves identified in the simulated path. Total distance of this trajectory is approximately 3.95 km, and the maximum speed limit is 20 km/h for the entire path.
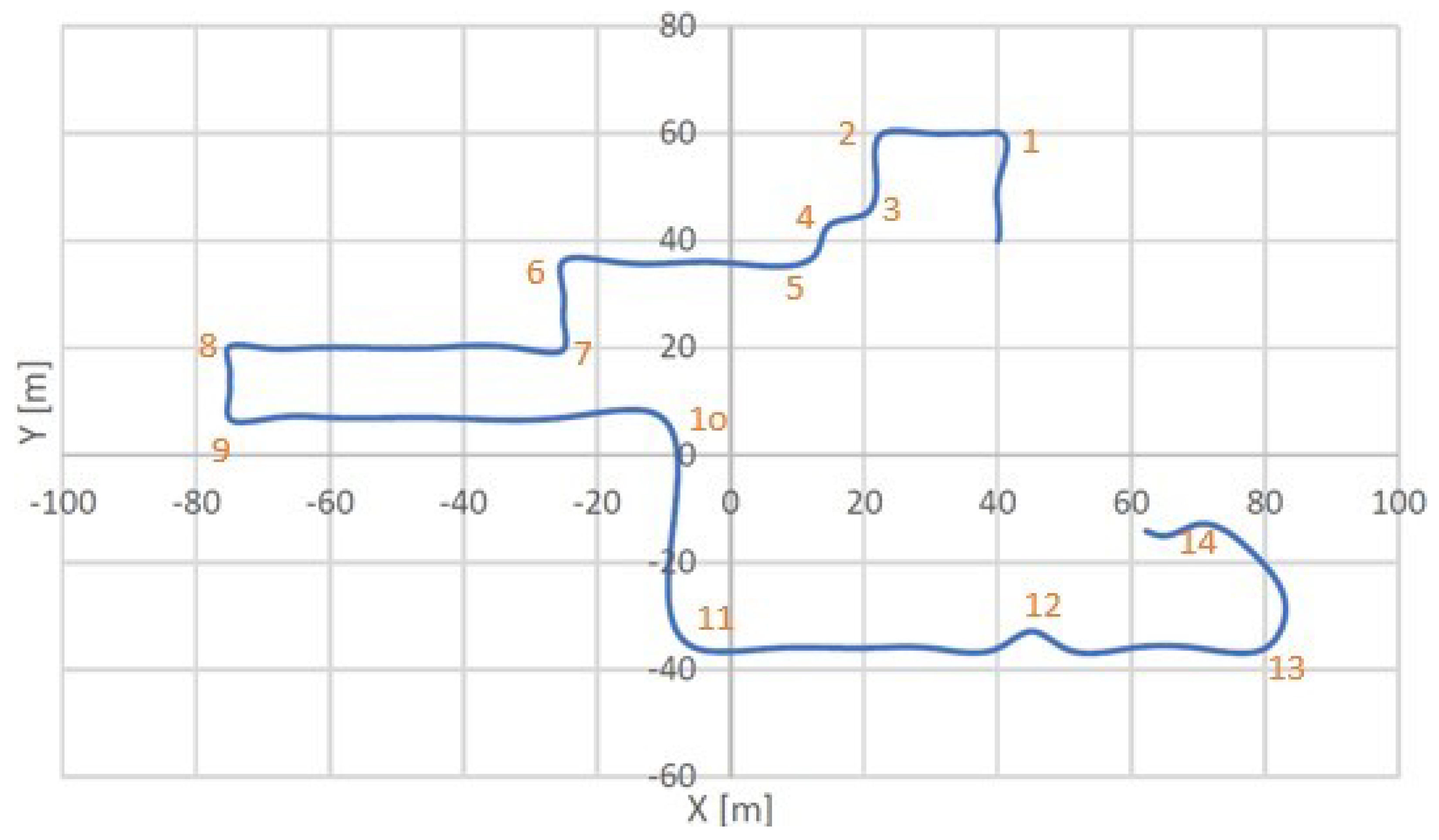
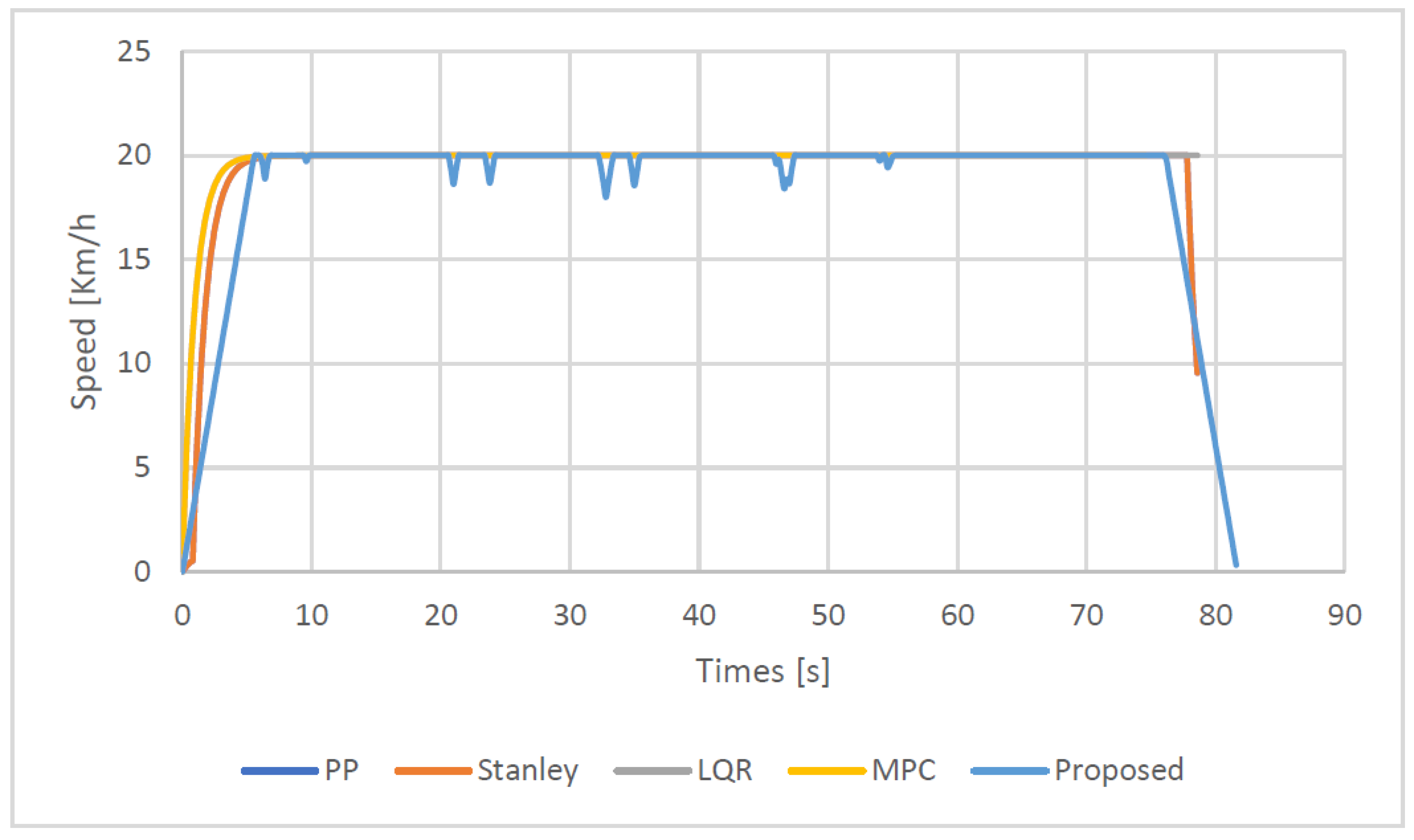
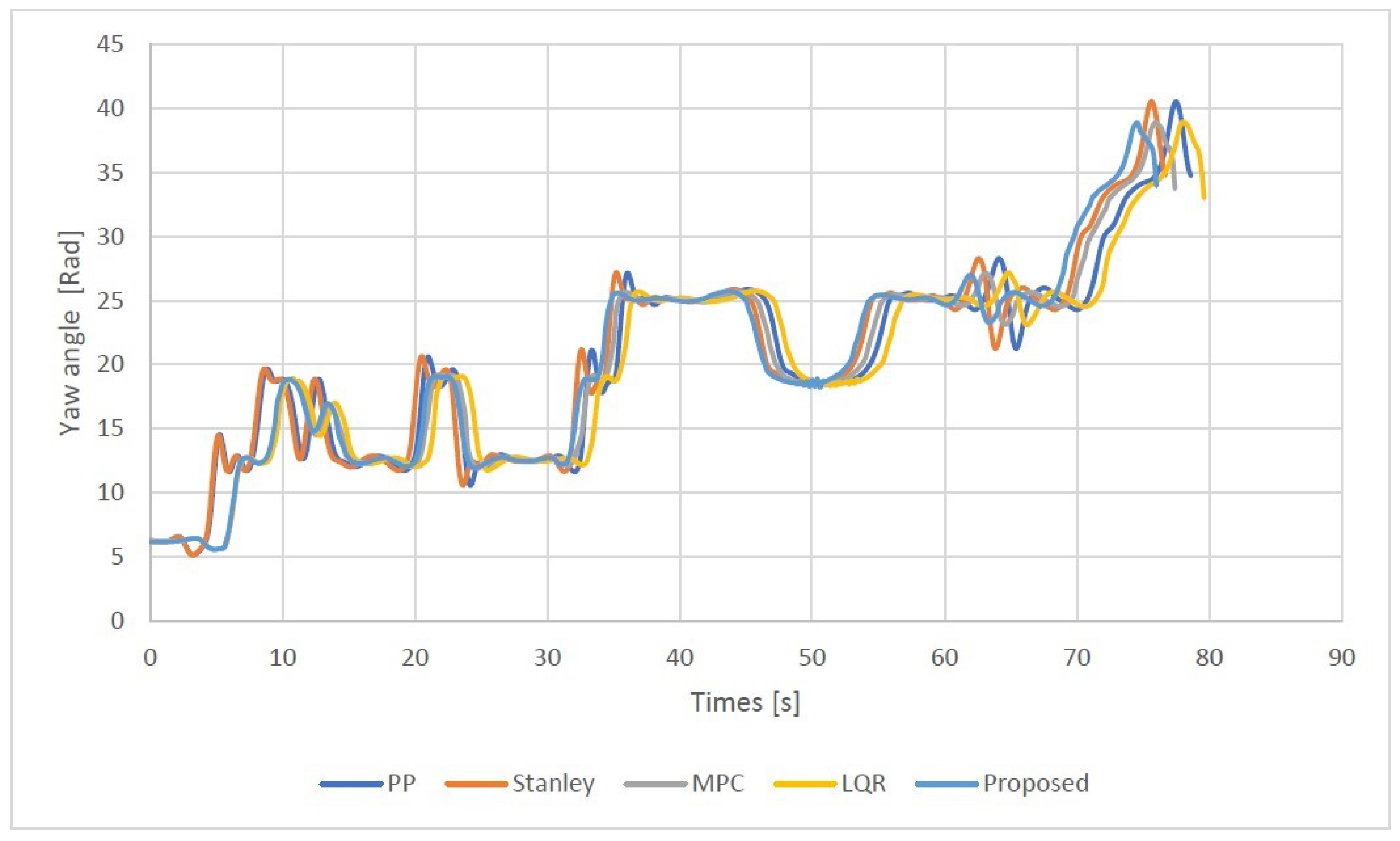
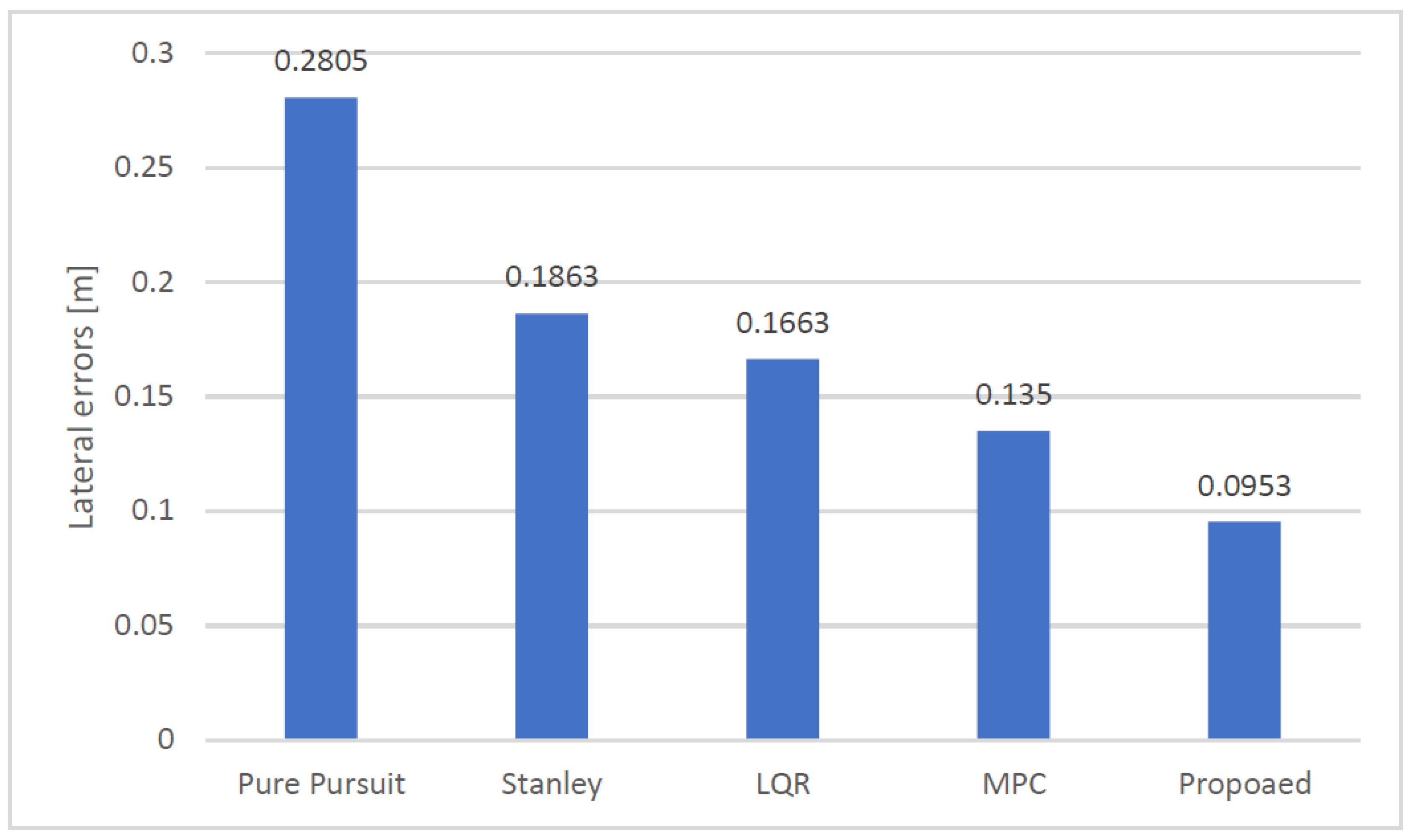
• Real dataset: The total distance of the reference path (traveled path) is approximately 4.2 km, and the maximum speed is 20 km/h for the entire path. There are 1094 segment points determined after the preprocessing and analyzing of given GPS data. Fourteen sharp curves (dangerous curves) are detected in this trajectory with different geometric characteristics.

The performance of the proposed algorithm is compared with the different steering control methods: (1) the pure pursuit, (2) the Stanley, (3) the LQR, and (4) the MPC. In order to compare the performance, first one needs to calculate the root mean square error ($E_{rms}$) for five algorithms per each trajectory, which is expressed in Equation (36) as

$$E_{rms}=\sqrt{\frac{\sum {(L_d\left(t\right)-L_c\left(t\right))}^2}{S_t}}$$

(36)

where the desired and current vehicle location are represented by $L_d$ and $L_c$, respectively. The lateral error can be computed from the difference between $L_d$ and $L_c$, whereas $S_t$ is the total sampling number calculated every 380 ms. The average root mean square error ($\overline{E_{rms}}$) is calculated as

$$\overline{E_{rms}}=\frac{1}{N}\sum E_{rms}$$

(37)

Path tracking algorithm performance are compared in the simulated trajectory where all the curves are simple, shown in Figure 6. As the curves of the trajectory are normal, all the algorithms can appropriately follow the path with constant speed, as can be seen in Figure 7, and the variations of the yaw angle are almost similar, shown in Figure 8. Even our proposed method tracks the simulated trajectory with constant speed because there are no sharp or dangerous curves present in the path.

Table 2. Error comparison at every curve of the simulated trajectory. Results are presented in meters.

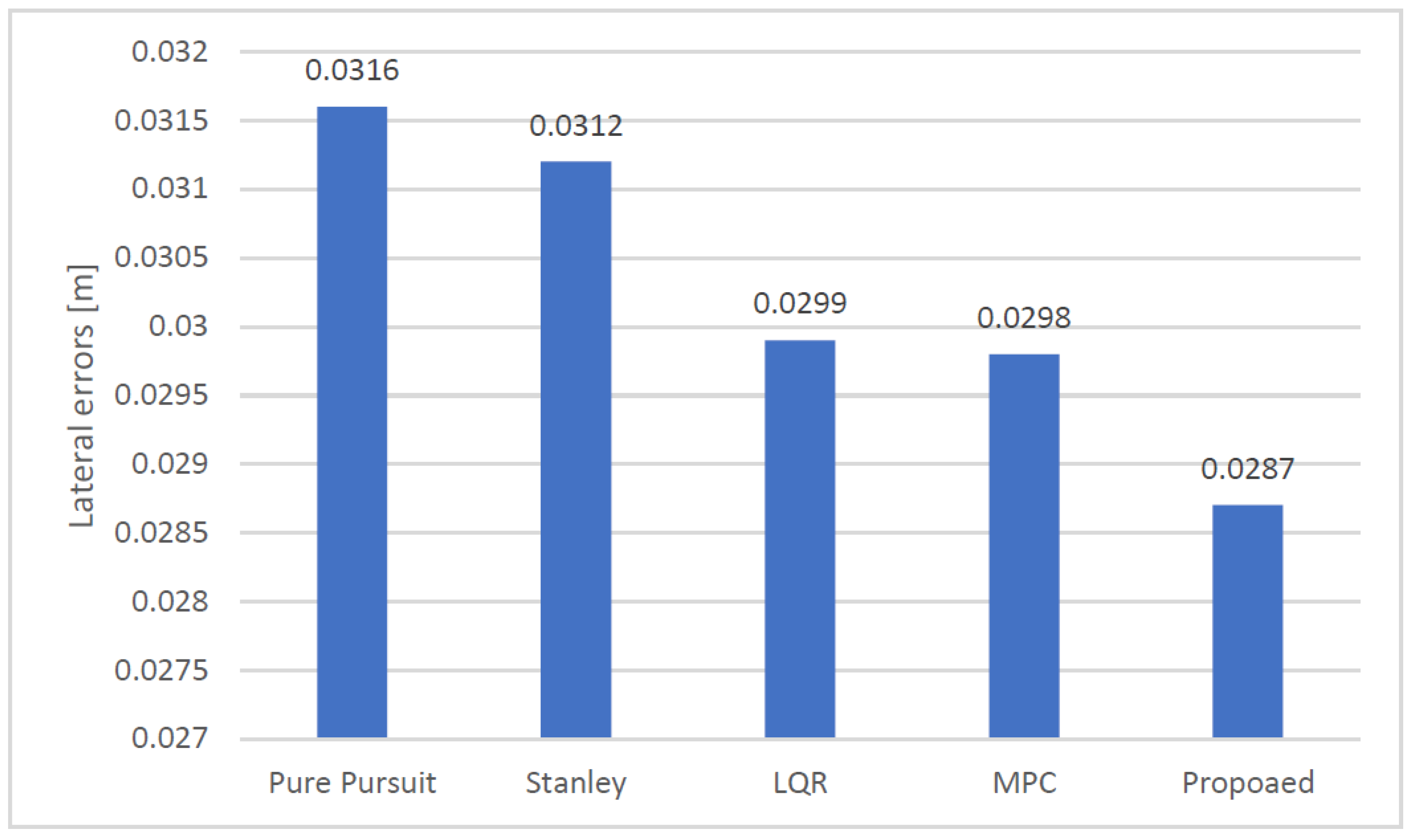
Curve	PP	Stanley	LQR	MPC	Proposed
1	0.0201	0.0192	0.0163	0.0182	0.0156
2	0.0238	0.0231	0.0199	0.0193	0.0185
3	0.0310	0.0309	0.0306	0.0301	0.0291
4	0.0431	0.0428	0.0421	0.0415	0.0404
5	0.0404	0.0403	0.0403	0.0403	0.0396
Average	0.0316	0.0312	0.0299	0.0298	0.0287
Travel time	63 s	63 s	63 s	63 s	63 s

shows that most of the controller’s lateral errors are the smallest in the simulated path. From Figure 9, it can be seen that the proposed algorithm has the smallest lateral error among all the controllers. The proposed method is controlling the steering angle precisely shown in Figure 10 without reducing the speed of the vehicle when the curvatures are simple. In this simulated trajectory there is no sharp curves; for this reason, none of the controllers need to reduce the speed of the vehicle. Therefore, all of the path tracking controllers took the same amount of time to reach the destination.

Experimental Results

In order to verify the performance of the proposed algorithm, an autonomous vehicle is tested with the GPS trajectory shown in Figure 11. The experimental trajectory with all identified sharp curves is presented in Figure 12.

Now we are analyzing and comparing the real dataset based trajectory tracking performance shown in Figure 13, where fourteen dangerous curves are present. The blue line is the reference trajectory; the orange line represents the pure persuit test result; the grey, gold, blue, and green lines represent the test results of the Stanley, LQR, MPC, and the proposed algorithm, respectively. The test results comparison at the dangerous curves are shown in Figure 13. From the test results it is clear that the curvature is an important factor for path tracking algorithms; therefore, it requires special attention for controlling autonomous vehicles while traveling through the curvatures of the path. The proposed algorithm is able to reduce the speed of the vehicle depending on the curvatures of the trajectory. When the value of the curvature is high, the reduction of the speed is also high in the proposed method to ensure that the autonomous vehicle is able to follow the trajectory successfully. Figure 14 shows the speed adjustment of the vehicle depending on the sharp curves of the road, whereas Figure 15 represents the yaw angle comparison for different trajectory tracking controllers. Figure 16 represent the steering angle of the proposed method.

Table 3. Root mean square errors comparison in sharp curves of the proposed trajectory dataset. Results are presented in meters.

Curve	PP	Stanley	LQR	MPC	Proposed
1	0.1915	0.1403	0.1384	0.0504	0.0905
2	0.2341	0.1619	0.1398	0.0992	0.0910
3	0.2096	0.1534	0.1275	0.0549	0.0531
4	0.1101	0.1041	0.1007	0.0481	0.0467
5	0.1305	0.1253	0.1131	0.0918	0.0685
6	0.5039	0.3580	0.3169	0.2727	0.1553
7	0.6321	0.3337	0.2744	0.2809	0.1561
8	0.6909	0.3824	0.3410	0.2901	0.1624
9	0.6911	0.3773	0.3305	0.2903	0.1631
10	0.0873	0.0851	0.0822	0.0814	0.0752
11	0.0817	0.0803	0.0813	0.0883	0.0747
12	0.1544	0.1032	0.0949	0.0621	0.0533
13	0.0909	0.0906	0.0871	0.0710	0.0651
14	0.1192	0.1126	0.1008	0.1098	0.0801
Average	0.2805	0.1863	0.1663	0.1350	0.0953
Travel time	78 s	79 s	79 s	78 s	82 s

represents the lateral errors for all of the controllers that are obtained from the different sharp curves of the trajectory. The improvement of the proposed method is shown in Figure 17 when considering speed regulations in dangerous curves. From Figure 17, it can be noticed that the pure pursuit controller has the largest average root mean square error (0.28 m), whereas the proposed algorithm shows the smallest tracking error (0.09 m), which is 19 cm less than the pure pursuit method. The LQR and the MPC represents good tracking performance with average lateral errors of 0.17 m and 0.13 m, respectively. However, the LQR and MPC controller tracking errors are aprroximately 8 cm, about 5 cm higher than the proposed method. It is clearly seen from Table 3 that all the largest lateral tracking errors are present in the dangerous curves. Therefore, speed regulation plays an important role in the path tracing of autonomous vehicles while passing through sharp curves.

Overall, the performance of the proposed method shows significant improvements (at least 5 cm less error) than all the trajectory tracking methods. A visual representation of lateral tracking error (root mean square error) is shown in Figure 17, where it can be noticed that the proposed algorithm is able to decrease errors by reducing the speed in the sharp curves of the trajectory. However, the proposed method took more time compared to the other path tracking controllers. When sharp curves appear in the trajectory, the proposed method reduces the velocity to track the reference path properly; therefore, it takes 82 s to complete the trajectory tracking.

5. Conclusions

In this paper, a novel hybrid real-time trajectory tracking controller is proposed based on the curvature information of the reference trajectory to control the speed, and feedforward and feedback information is used to generate the appropriate steering angle of the vehicle. From the experimental results, it can be noticed that the proposed algorithm is able to follow the trajectory successfully. The performance of the proposed method shows significant reduction of tracking errors compared to other controllers. The contributions of the proposed method are to estimate the upcoming sharp curves type and compute the appropriate speed and steering angle for each curve to control the autonomous vehicle, which is the desired goal of any autonomous vehicle in real driving scenarios. When the curvatures of the path are normal, then the vehicle is traveling with constant speed by properly controlling the steering angle. However, if the upcoming curvatures are sharp, the vehicle then reduces the speed before arriving at them and reaches the desired speed and steering angle to minimize lateral errors. This better serves the tracking performance of the vehicle especially during cornering maneuvers, whereas most of the existing trajectory tracking controllers face problems during cornering maneuvers.

Future work will combine the control system of the vehicle with a vision system and neural network in order to develop perception capabilities of autonomous vehicles. The stereo sensor information with a semantic segmentation method and neural network will allow us to: (1) detect traffic signs and the speed limit of the road to control the speed of the autonomous vehicle accordingly; (2) recognize the path properly when GPS data are not available; and (3) identify lane markings on the trajectory by developing boundary detection algorithms.