Effect of the Gap Matching Relation on the Pressure Pulsation Characteristics at Blade’s Surface of the Multiphase Pump
Abstract
:1. Introduction
2. Computational Model
3. Numerical Simulation Method and Boundary Conditions
3.1. Turbulence Model
3.2. Grid Division and Boundary Conditions
3.3. Experimental Study
3.4. Experimental Verification
4. Result Analysis
4.1. Method of the Pressure Pulsation Analysis
4.1.1. Pressure Pulsation Coefficient
4.1.2. Fast Fourier Transform
4.2. Effect of the Gap Matching Relation on the Pressure Pulsation Characteristics at Blade’s Surface of the Multiphase Pump
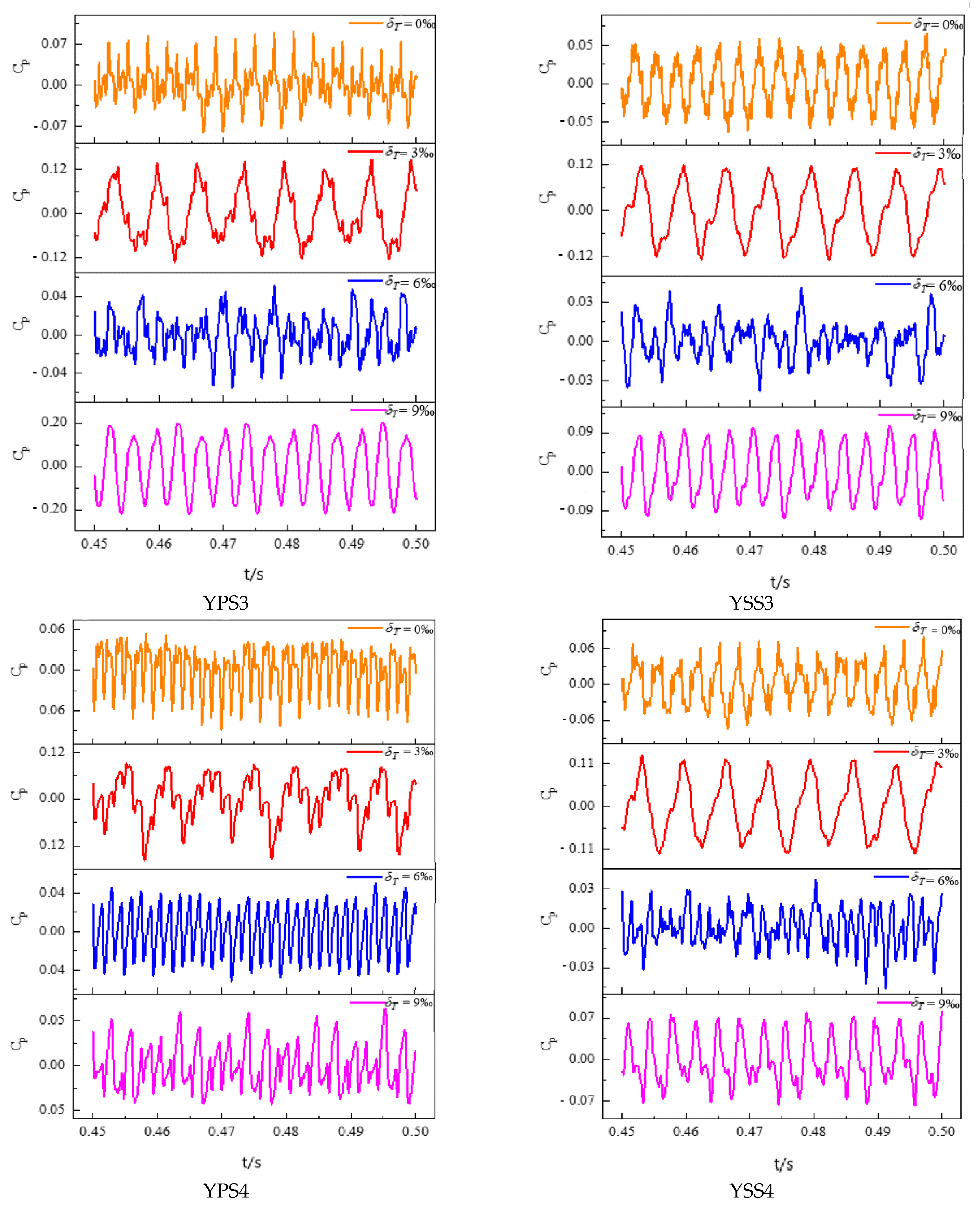
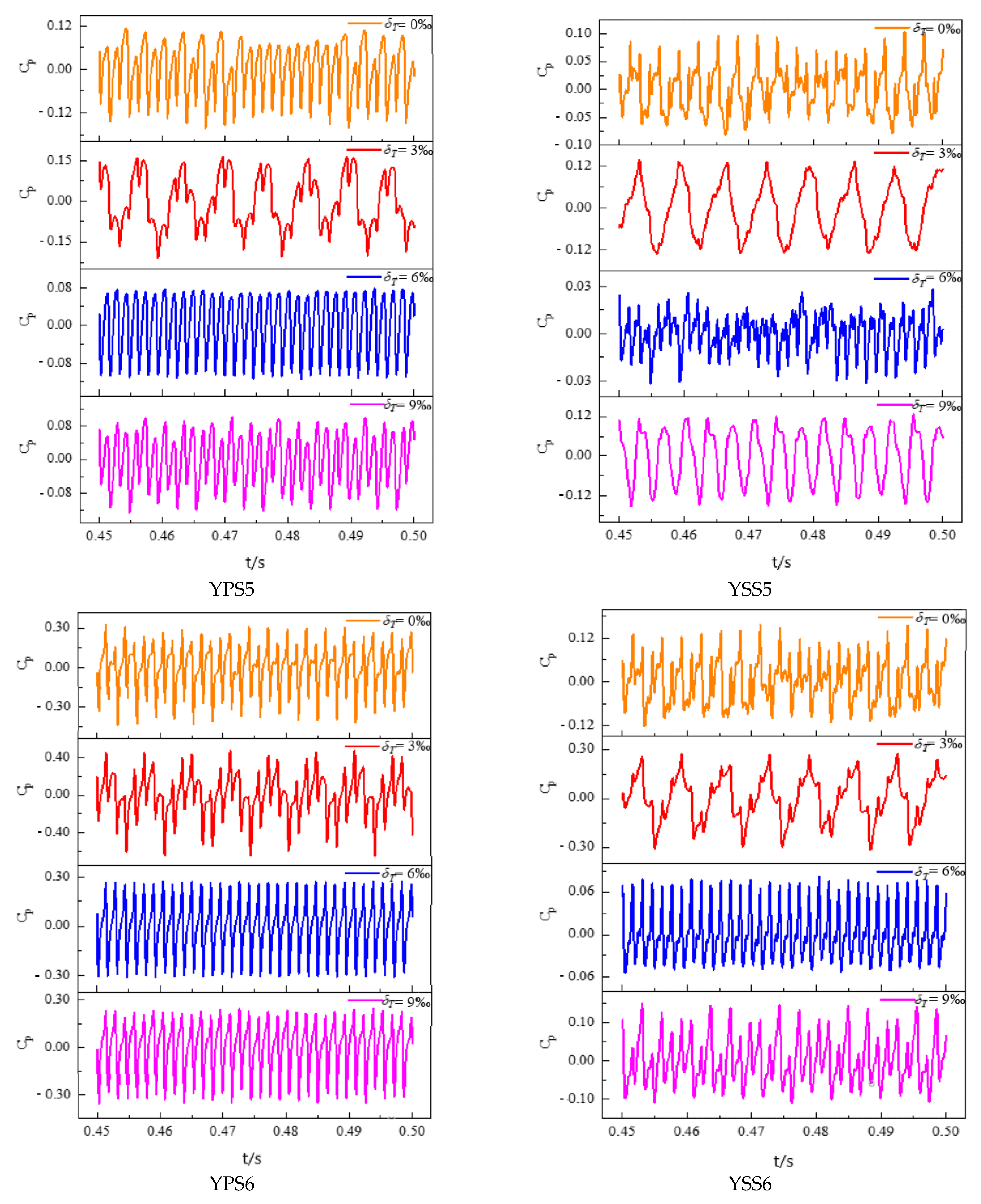
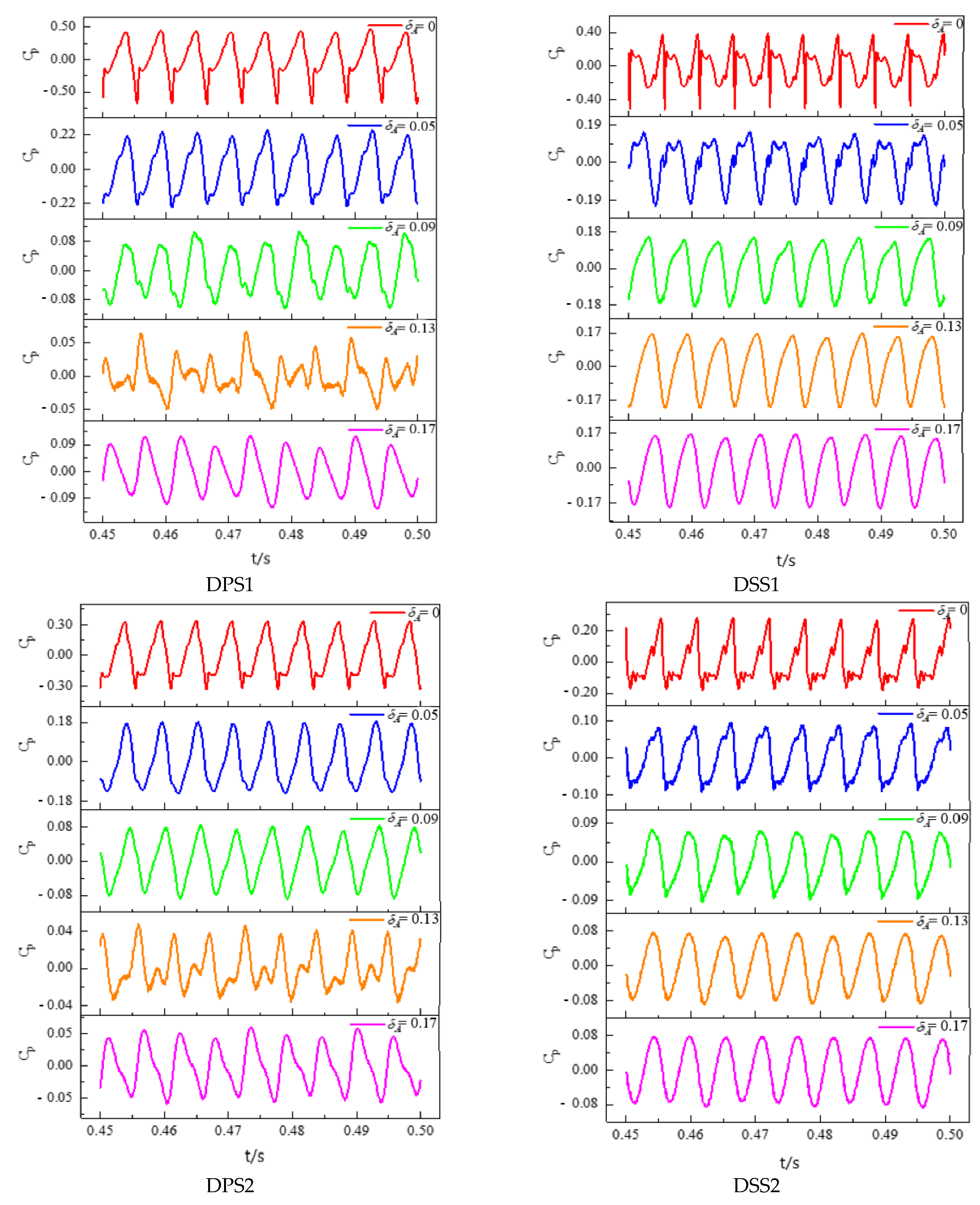
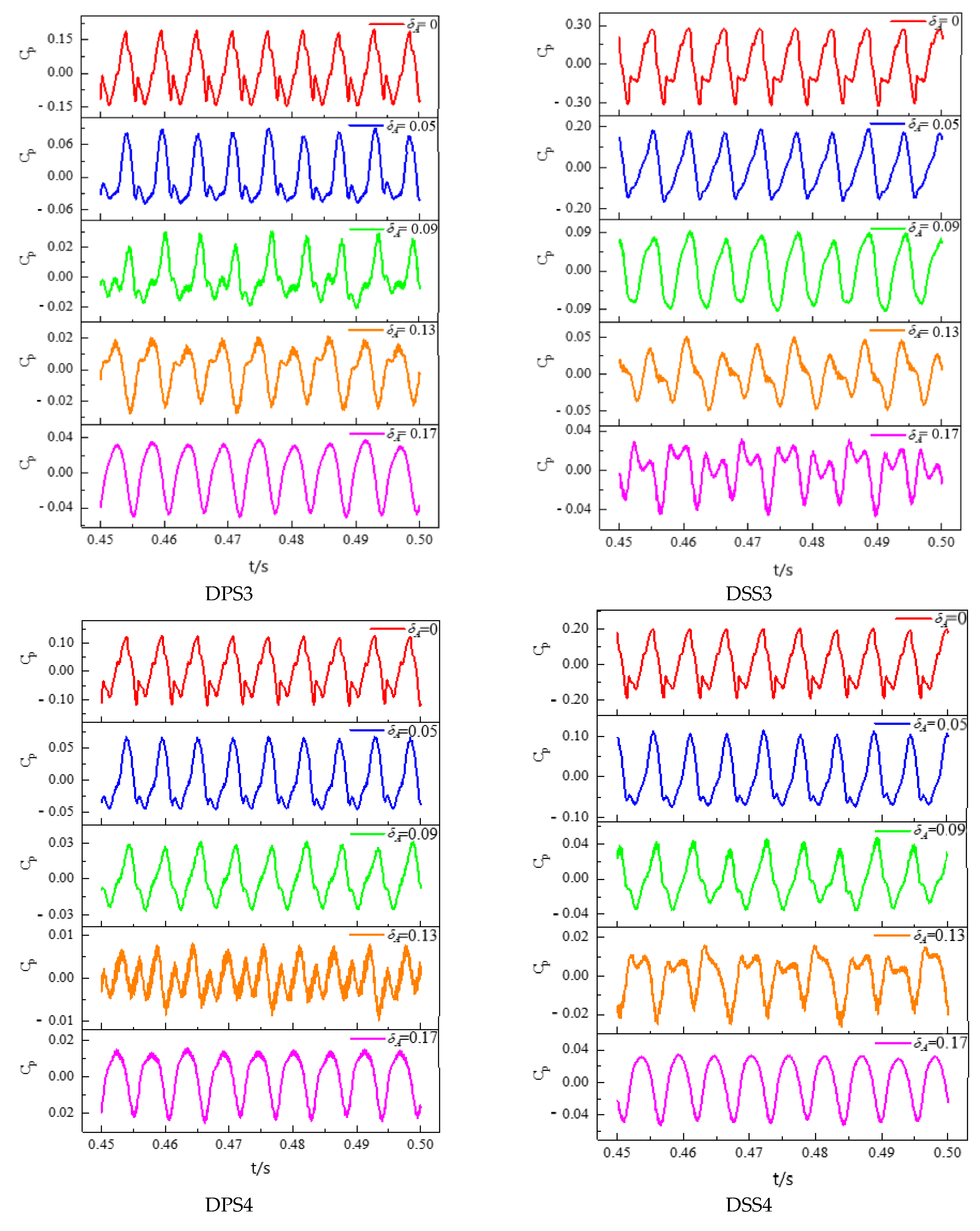
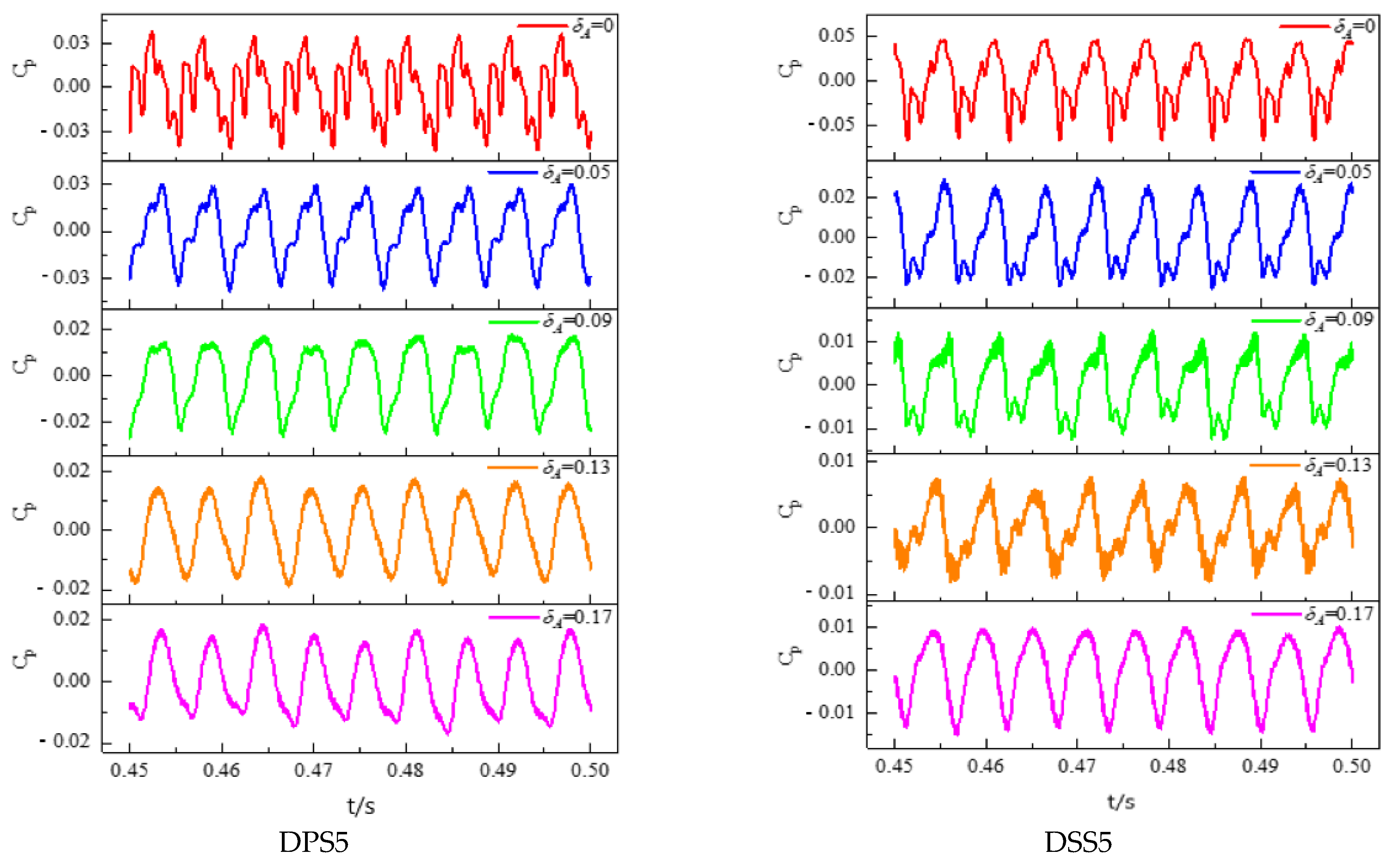
4.2.1. Time Domain Characteristics Analysis
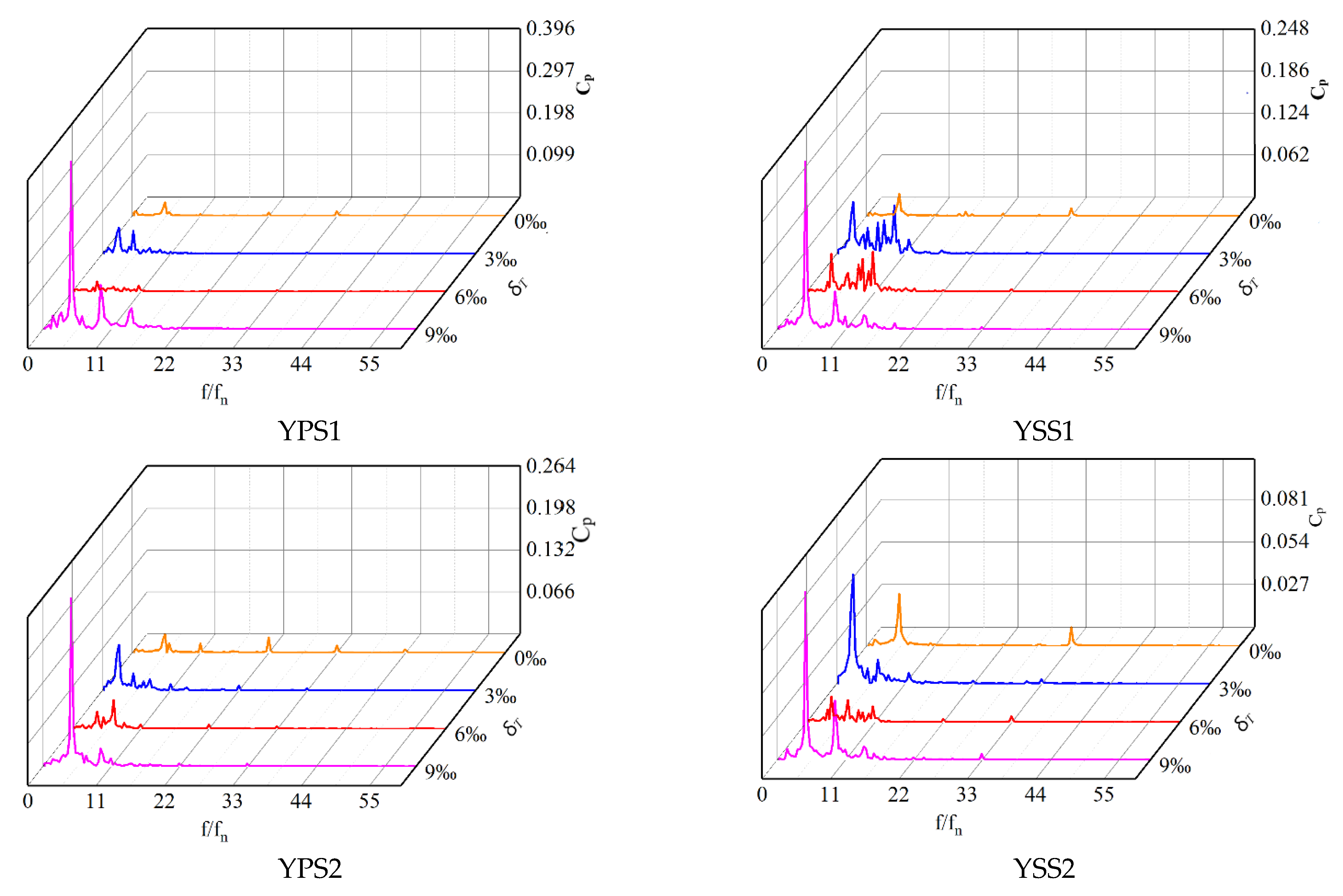
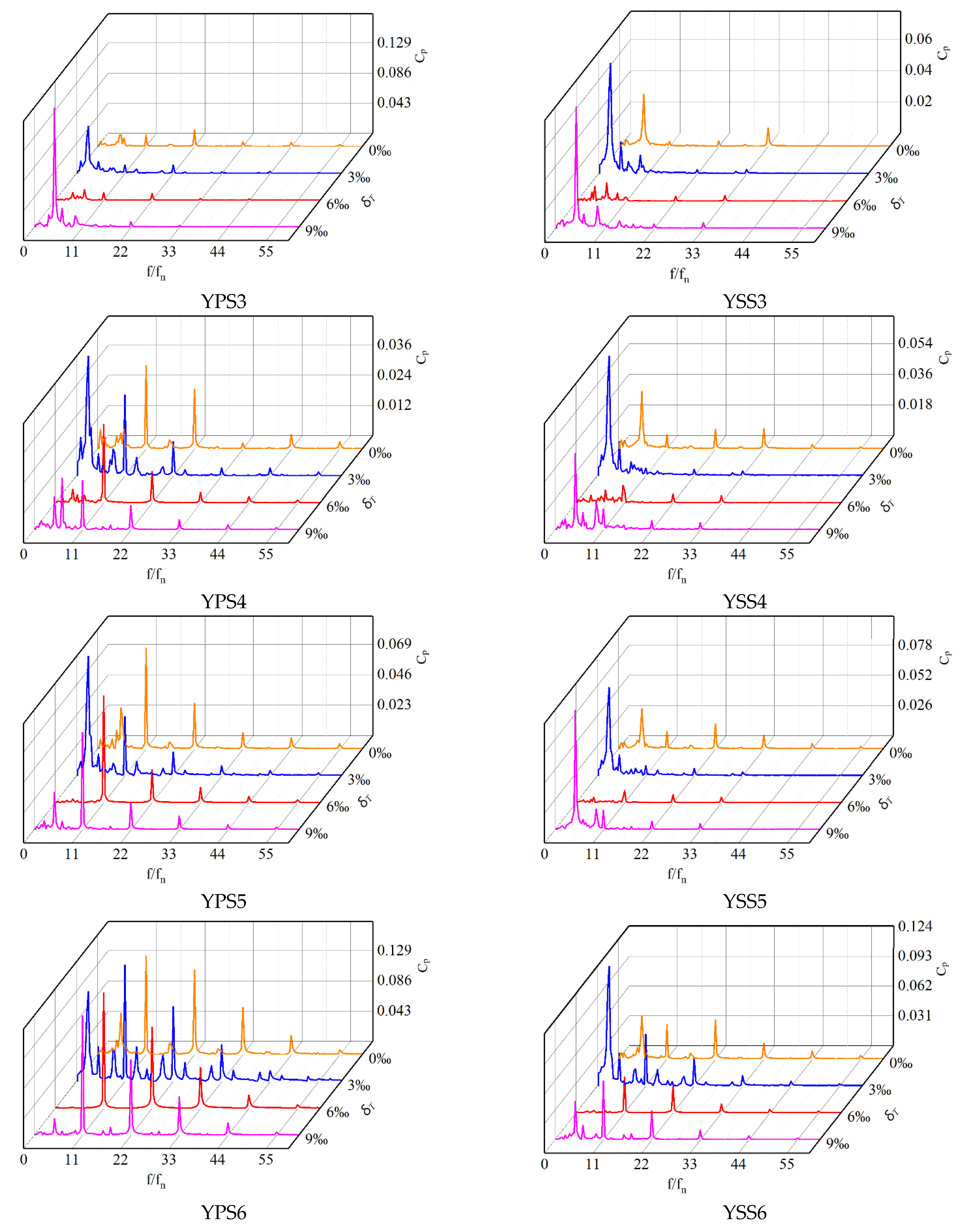
4.2.2. Frequency Domain Analysis
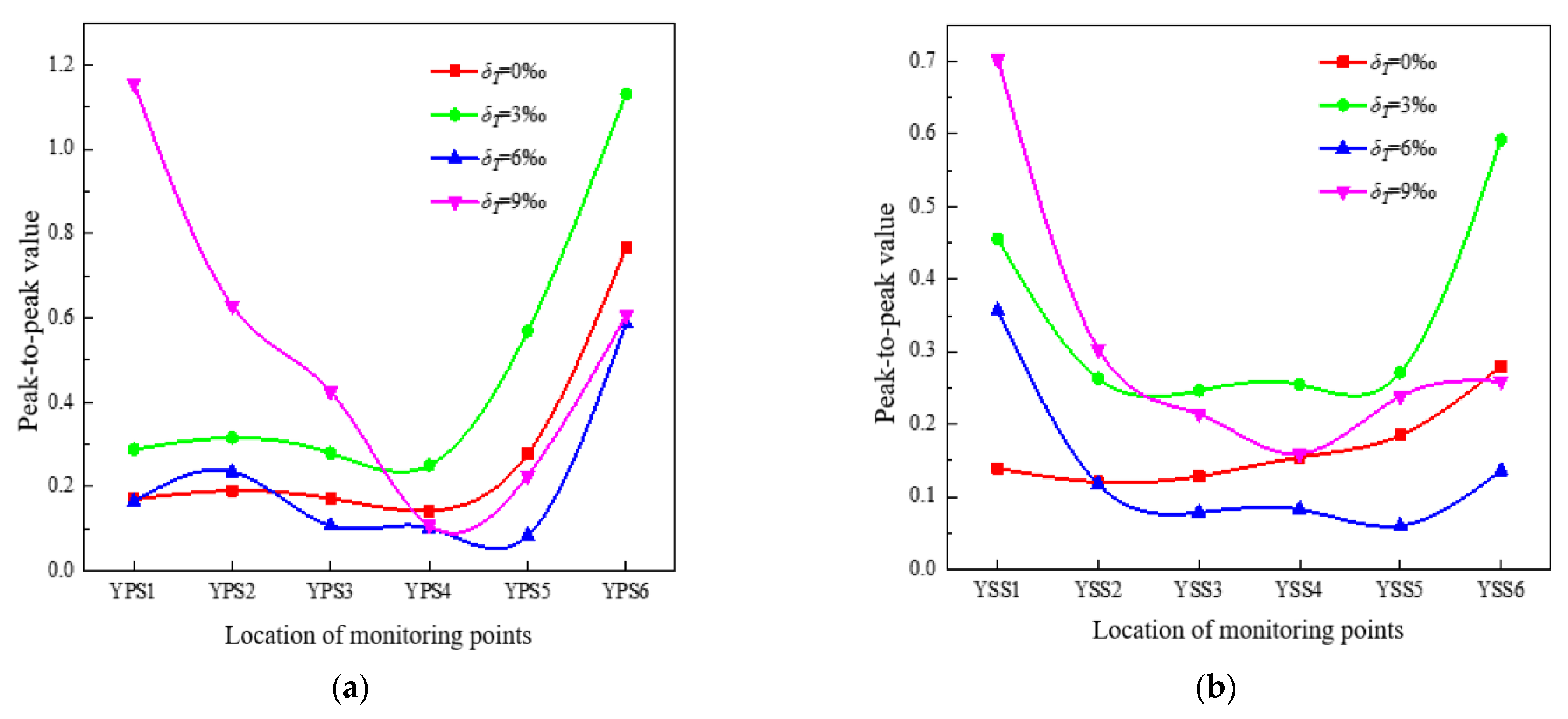
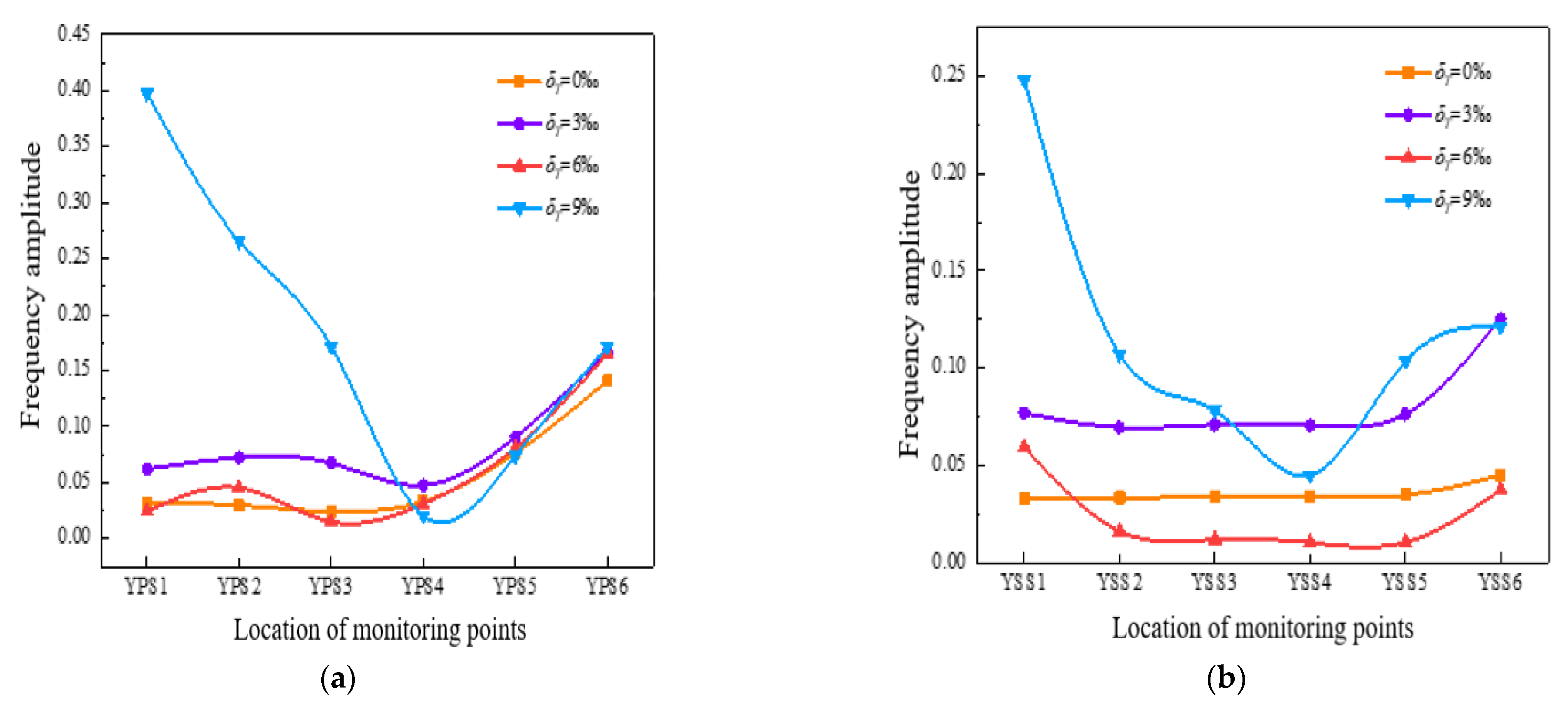
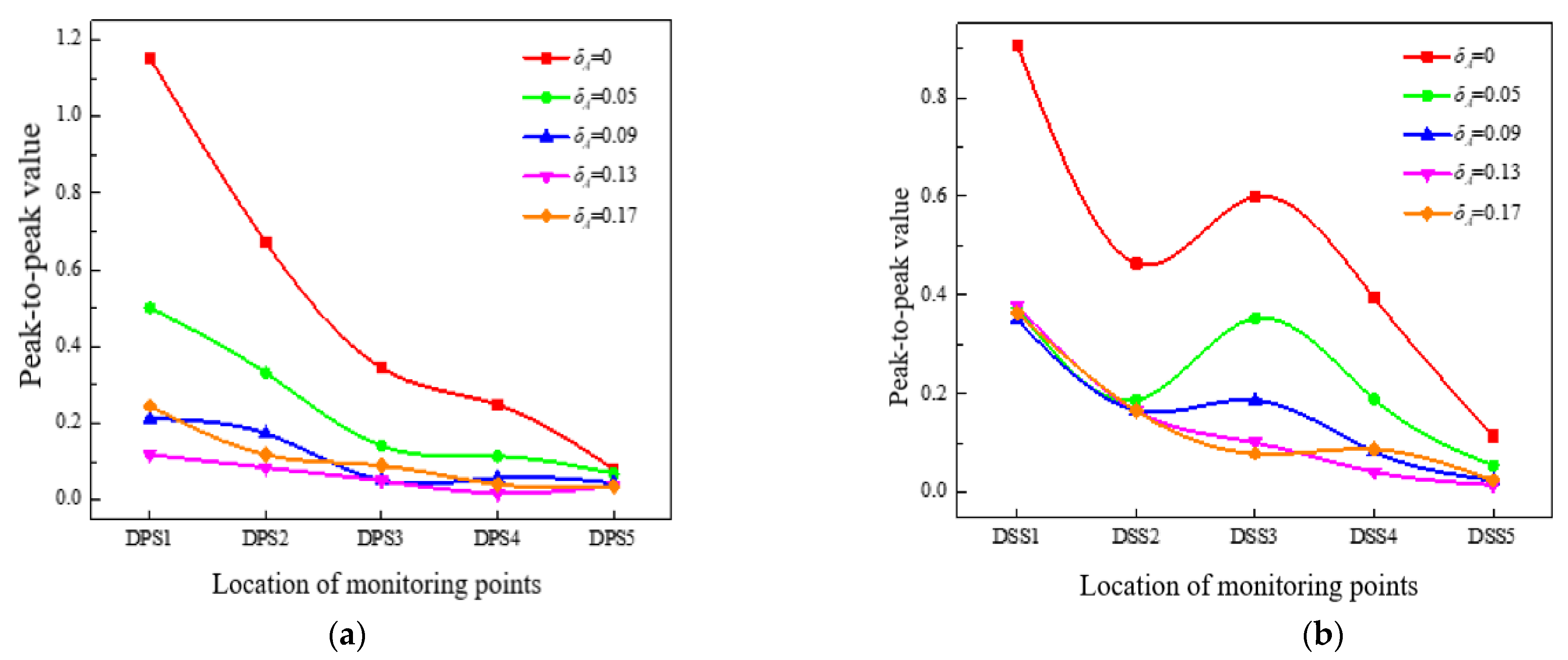
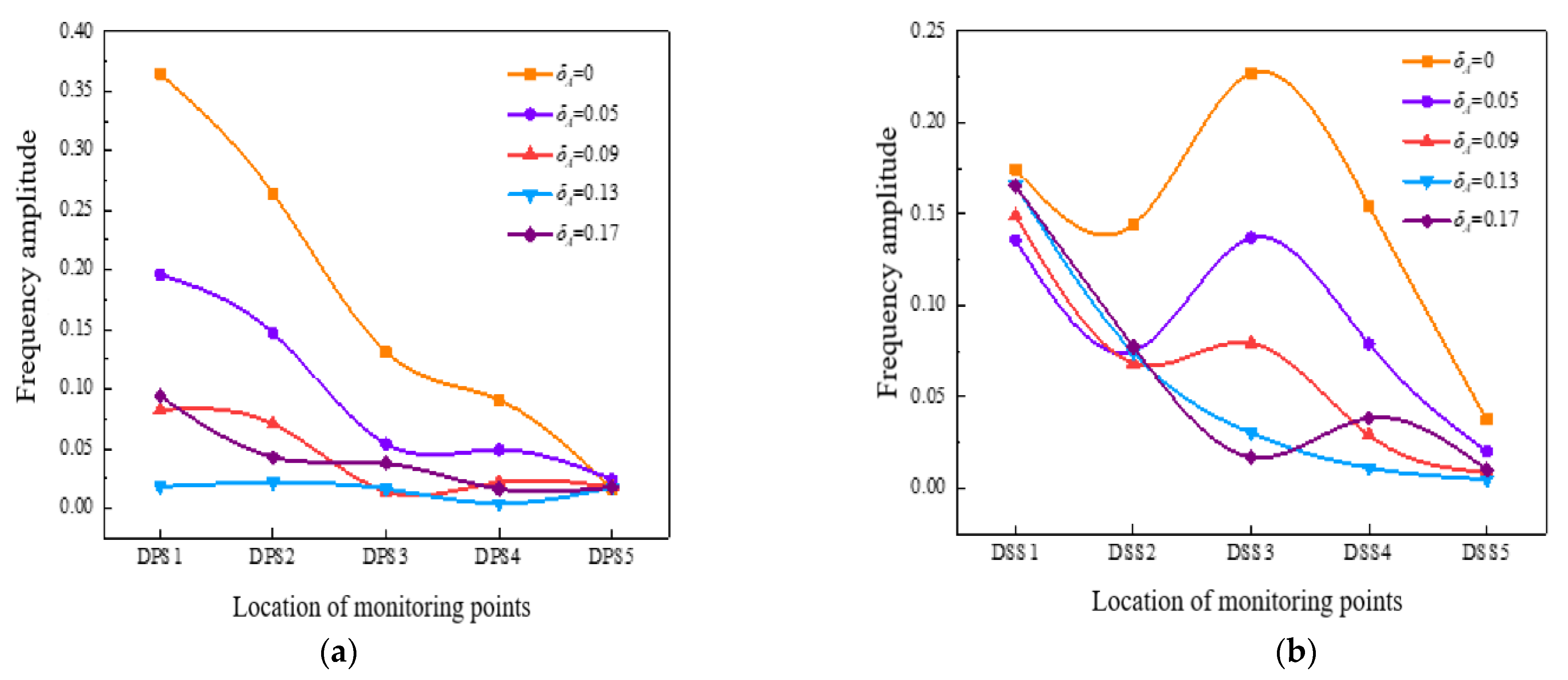
4.2.3. Analysis of the Pressure Pulsation Peak-to-Peak Value and the Dominant Frequency Amplitude Coefficient
4.3. Effect of the Gap Matching Relation on the Pressure Pulsation Characteristics of the Diffuser
4.3.1. Time Domain Characteristics Analysis
4.3.2. Frequency Domain Analysis
4.3.3. Analysis of the Pressure Pulsation Peak-to-Peak Value and the Dominant Frequency Amplitude Coefficient
5. Conclusions
- (1)
- The pressure pulsation regularity of the monitoring points in the first half of the impeller blade’s suction surface was better than the pressure surface, while the pressure pulsation regularity was opposite from the middle to the outlet of the blades. This may be due to the larger influence of the tip leakage flow on the mainstream area near the second half of the blades. As the monitoring points moved towards the outlet of the impeller, the closer to the diffuser, the stronger the rotor-stator interaction. Therefore, the regularity of the pressure pulsation at the monitoring points was better, and 11 similar peaks and troughs appeared in a rotating cycle at the impeller outlet monitoring points, corresponding to 11 diffusers.
- (2)
- On the pressure surface of the impeller, the size of peak-to-peak value and the dominant frequency amplitude coefficient and their variation range along the flow direction were greater than those on the suction surface. What’s more, the vibration amplitude in the middle of the impeller blades was the smallest. On the whole, the existence of tip clearance greatly changed the pressure pulsation in the impeller. In the diffuser, the variation of the pressure pulsation peak-to-peak value and the dominant frequency amplitude coefficient with different axial clearance coefficients were similar. Additionally, the peak-to-peak value decreased with the increase of the ACC, and the dominant frequency amplitude of the monitoring points was most sensitive to the change of the ACC at the inlet of the diffuser pressure surface.
- (3)
- The pressure pulsation in the diffuser fluctuated periodically, and the fluctuation period was the same as the number of impeller blades, which indicated that the main reason for the pressure pulsation inside the diffuser was the interference of the impeller rotation. As the increase of the ACC, the pressure pulsation amplitude coefficient of the monitoring points gradually decreased. What’s more, for the same working condition monitoring points, the pressure coefficient of the pressure surface was greater than the suction surface. With the increase of the ACC and the direction from the diffuser inlet to the outlet, the amplitude of the dominant frequency pulsation was gradually smaller.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Williams, A.; Althaus, F.; MacIntosh, H.; Loo, M.; Gowlett-Holmes, K.; Tanner, J.E.; Sorokin, S.J.; Green, M. Characterising the invertebrate megafaunal assemblages of a deep-sea (200–3000 m) frontier region for oil and gas exploration: The Great Australian Bight, Australia. Deep-Sea Res. Part II 2018, 157–158, 78–91. [Google Scholar] [CrossRef]
- Falcimaigne, J.; Brac, J.; Charron, Y.; Pagnier, P.; Vilaginès, R. Multiphase pumping: Achievements and perspectives. Oil Gas Sci. Technol. 2017, 57, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Xu, Q.; Chang, L. Numerical study on the effect of gas void fraction on the performance of deep-sea multiphase pump. J. Eng. Thermophys. 2021, 42, 1479–1485. [Google Scholar]
- Shi, Y.; Zhu, H.; Zhang, J.; Zhang, J.; Zhao, J. Experiment and numerical study of a new generation three-stage multiphase pump. J. Pet. Sci. Eng. 2018, 169, 471–484. [Google Scholar] [CrossRef]
- Li, C.; Luo, X.; Feng, J.; Sun, H.; Zhu, G.J.; Xue, G. Investigation on the influence of inlet gas volume fraction on the performance of deep-sea multiphase pump. Chin. J. Hydrodyn. 2020, 35, 248–257. [Google Scholar]
- Ma, X.; Ni, P.; Jia, W. Influence of rotating speed on performance of helico-axial oil-gas multiphase pump. J. Gansu Sci. 2015, 27, 128–130. [Google Scholar]
- Liu, M.; Tan, L.; Cao, S. Analysis on the influence of rotating speed on the performance of helic-axial multiphase pump. Energies 2018, 11, 1048. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.Y.; Tan, L. Correlation between radial force and flow patterns in rotodynamic multiphase pump. J. Hydroelectr. Eng. 2019, 38, 90–101. [Google Scholar]
- Tremante, A.; Moreno, N.; Rey, R.; Noguera, R. Numerical turbulent simulation of the two-phase flow (liquid/gas) through a cascade of an axial pump. J. Fluids Eng. Trans. ASME 2002, 124, 371–376. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, S.; Zhu, H.; Yang, K.; Qiang, R. Numerical investigation of compessible flow in a three-stage helico-axial multiphase pump. Thansaction Chin. Soc. Agric. Mach. 2014, 45, 89–95. [Google Scholar]
- Xu, Y.; Cao, S.L.; Reclari, M.; Wakai, T.; Sano, T. Multiphase performance and internal flow pattern of helico-axial pumps. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 32029. [Google Scholar] [CrossRef]
- Saadawi, H.N. Operating multiphase helicoaxial pumps in series to develop a satellite oil field in a remote desert location. SPE Proj. Facil. Constr. 2008, 3, 1–6. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.; Li, Y.; Cheng, X. Flow characteristics analysis for the whole flow passage of a multiphase rotodynamic pump. J. Mech. Eng. 2019, 55, 168–174. [Google Scholar] [CrossRef] [Green Version]
- Serena, A.; Bakken, L.E. Design of a multiphase pump test laboratory allowing to perform flow visualization and instability analysis. In Proceedings of the 2015 American Society of Mechanical Engineers (ASME), San Diego, CA, USA, 28 June–2 July 2015. [Google Scholar]
- Serena, A.; Bakken, L.E. Flow visualization of unsteady and transient phenomena in a mixed-flow multiphase pump. In Proceedings of the 2016, American Society of Mechanical Engineers (ASME), Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Chang, L.; Yang, C.; Zhang, X. Experimental study on pressurization property of three-stage centrifugal multiphase pump on gas-liquid two-phase flow conditions. J. Eng. Thermophys. 2021, 42, 1233–1237. [Google Scholar]
- Yu, Z.; Zhu, B.; Cao, S. Interphase force analysis for air-water bubbly flow in a multiphase rotodynamic pump. Eng. Comput. 2015, 32, 2166–2180. [Google Scholar] [CrossRef] [Green Version]
- Guangtai, S.; Zhiwen, W.; Kun, L. Analysis of turbulent flow intensity and dissipation characteristics of an oil-gas multiphase pump in its compression stages. J. Eng. Therm. Energy Power 2018, 36, 115–121. [Google Scholar]
- Shi, G.T.; Luo, K.; Wang, Z.W.; Liu, Y. Study on load distribution characteristics of axial flow multiphase pump. Water Resour. Power 2018, 36, 175–178. [Google Scholar]
- Guangtai, S.; Zhiwen, W. Pressurization performance of multiphase pump impeller in different regions. J. Drain. Irragation Mach. Eng. 2019, 37, 13–17. [Google Scholar]
- Zhang, Y.; Zhang, J.; Zhu, H.; Cai, S. 3D Blade hydraulic design method of the rotodynamic multiphase pump impeller and performance research. Adv. Mech. Eng. 2014, 6, 803972. [Google Scholar] [CrossRef]
- Zhongku, L. Characteristics of Vortex and Pressure Fluctuation in Tip Clearance of a Multiphase Pump. Master’s Thesis, Xihua University, Chengdu, China, 2020. [Google Scholar]
- Kong, X.; Lv, Y.; Gao, J. Research on multi-stage compressible simulation of helico-axial multiphase pump. China Pet. Mach. 2016, 44, 77–81. [Google Scholar]
- Pang, J.; Liu, X.; Zeng, Y. Restraining effect of bearing structure on oil mist escaping of hydrogenerator unit. J. Drain. Irragation Mach. Eng. 2021, 39, 1020–1026. [Google Scholar]
- Zhang, D.; Wang, H.; Shi, W.; Pan, D.; Shao, P. Experimental investigation of pressure fluctuation with multiple flow rates in scaled axial flow pump. Thansaction Chin. Soc. Agric. Mach. 2014, 45, 139–145. [Google Scholar]
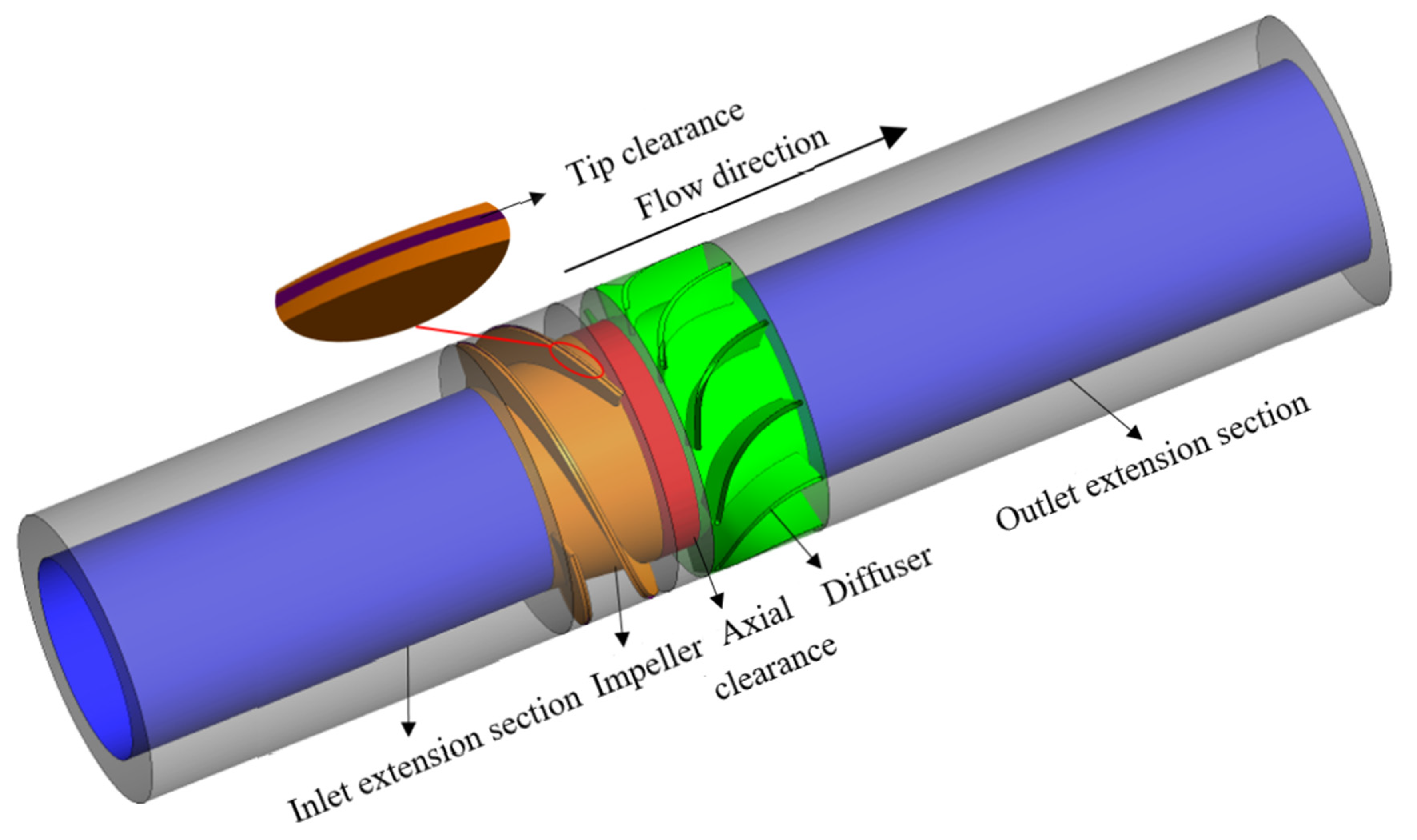
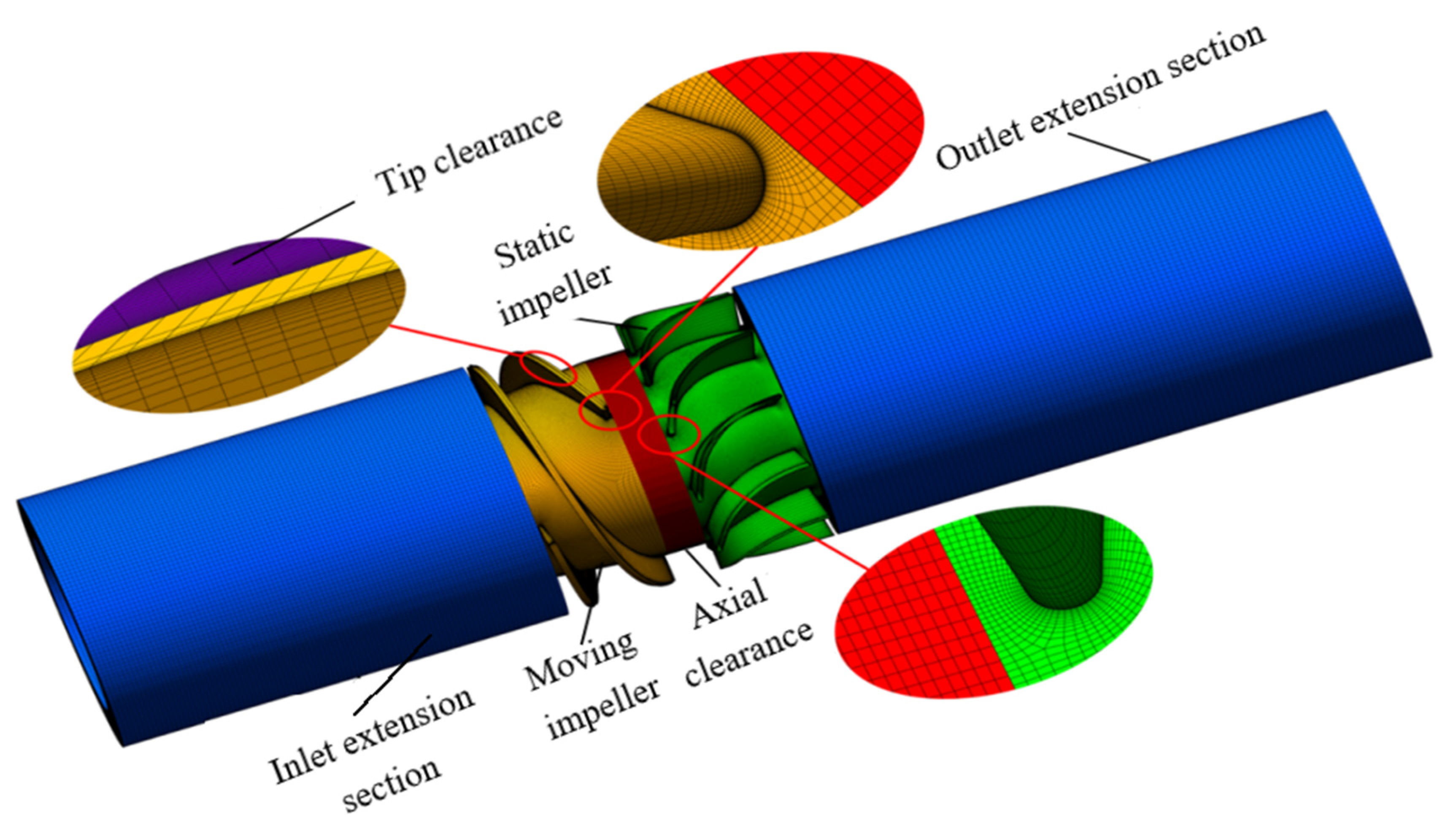
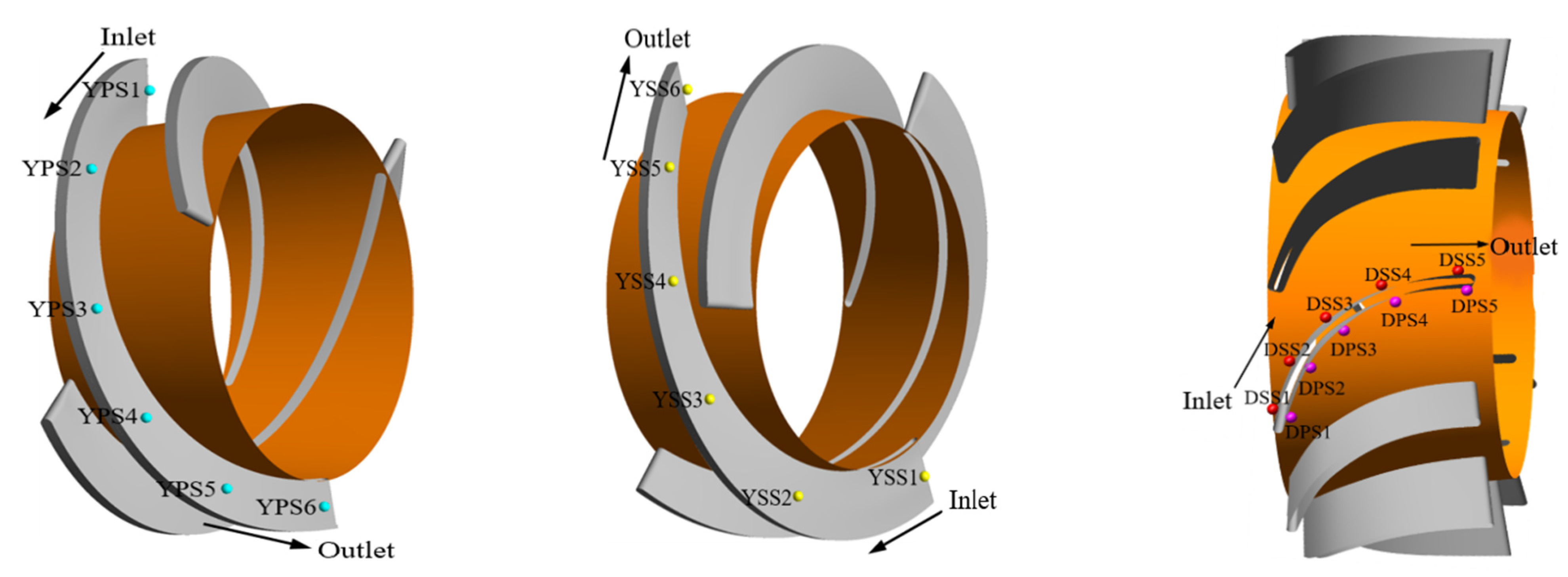






| Parameters | Symbol | Unit | Value |
|---|---|---|---|
| Design flow rate | Q | m3/h | 90 |
| Design rotating speed | n | rpm | 3600 |
| Number of impeller blades | Zi | (–) | 3 |
| Number of diffuser blades | Zd | (–) | 11 |
| Outer diameter | Di | mm | 161 |
| Parameters | Impeller | Diffuser |
|---|---|---|
| Number of impeller blades | 3 | 11 |
| Outer diameter (mm) | 161 | 161 |
| Inlet hub ratio | 0.7 | 0.78 |
| Blade inlet angle(hub/shroud) (o) | 9.05/6 | 0/0 |
| Blade outlet angle(hub/shroud) (o) | 27.05/24 | 35/35 |
| Axial length (mm) | 60 | 66 |
| Instrument | Range | Precision | Unit |
|---|---|---|---|
| Inlet pressure gauge | 0–0.8 | 0.3 class | Mpa |
| Outlet pressure gauge | 0–1 | ±0.2% | Mpa |
| Water flow meter | 0–140 | ±0.5% | m3/h |
| Air flow meter | 0–60 | 1.5 class | m3/h |
| Torquemeter | 0–50 | 0.2 class | N·m |
| Parameters | Value | Unit |
|---|---|---|
| Camera speed | 4000 | fps |
| Shutter speed | 1/80,000 | s |
| Resolution | 1240 × 1240 | ppi |
| Sensitivity | 40,000 | (–) |
| Memory | 8 | GB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Zhu, Z.; Wang, B.; Wen, H. Effect of the Gap Matching Relation on the Pressure Pulsation Characteristics at Blade’s Surface of the Multiphase Pump. Machines 2022, 10, 418. https://doi.org/10.3390/machines10060418
Shi G, Zhu Z, Wang B, Wen H. Effect of the Gap Matching Relation on the Pressure Pulsation Characteristics at Blade’s Surface of the Multiphase Pump. Machines. 2022; 10(6):418. https://doi.org/10.3390/machines10060418
Chicago/Turabian StyleShi, Guangtai, Zheyu Zhu, Binxin Wang, and Haigang Wen. 2022. "Effect of the Gap Matching Relation on the Pressure Pulsation Characteristics at Blade’s Surface of the Multiphase Pump" Machines 10, no. 6: 418. https://doi.org/10.3390/machines10060418
APA StyleShi, G., Zhu, Z., Wang, B., & Wen, H. (2022). Effect of the Gap Matching Relation on the Pressure Pulsation Characteristics at Blade’s Surface of the Multiphase Pump. Machines, 10(6), 418. https://doi.org/10.3390/machines10060418






