Abstract
Many consumers and scholars currently focus on driving assistance systems (DAS) and intelligent transportation technologies. The distance and speed measurement technology of the vehicle ahead is an important part of the DAS. Existing vehicle distance and speed estimation algorithms based on monocular cameras still have limitations, such as ignoring the relationship between the underlying features of vehicle speed and distance. A multi-cue fusion monocular velocity and ranging framework is proposed to improve the accuracy of monocular ranging and velocity measurement. We use the attention mechanism to fuse different feature information. The training method is used to jointly train the network through the distance velocity regression loss function and the depth loss as an auxiliary loss function. Finally, experimental validation is performed on the Tusimple dataset and the KITTI dataset. On the Tusimple dataset, the average speed mean square error of the proposed method is less than , and the average mean square error of the distance is . On the KITTI dataset, the average velocity mean square error of our method is less than . In addition, we test in different scenarios and confirm the effectiveness of the network.
1. Introduction
With the rapid economic growth, the global vehicle ownership increases rapidly, leading to more serious traffic safety problems. The application of advanced driver assistance systems allows the driver to be aware of possible hazards in advance, effectively increasing the comfort and safety of vehicle driving. Accurate calculation of the distance and speed between vehicles is a basic requirement for driver assistance systems.
Scene depth velocity information is a very important role in many contemporary topics and there are many typical algorithms in current research: single-radar sensor, camera sensor, stereo image, wireless sensing, multi-sensing fusion, etc.
Radar can achieve speed and range measurement of target vehicles, but it detects obstacles by transmitting optical fibers, and light reflection can also cause misjudgment in harsh environments, especially rain, snow, and water mist on foggy days [1]. In addition, the refresh rate of LIDAR is low, and it is difficult to perceive objects ahead quickly in a single scene at high speed. The camera sensor is another key part of a typical sensor configuration that can be used in normal rain and snow conditions, as it can obtain high-pixel environmental information as well as fine-texture structure information. Therefore, many researchers have started with a monocular sensor to explore the depth estimation algorithm.
In wireless sensors, many scholars have also conducted research. Ciccarese et al. [2] combined the potential of antenna array processing with cooperative strategies using vehicle-to-vehicle and vehicle-to-infrastructure communications and defined a novel algorithm with asynchronous updates triggered by beacon packet reception and capable of reaching the angle estimation goal. This algorithm achieves high localization accuracy even in sparse scenarios, outperforming competitors, while maintaining lightweight communication and low computational complexity. Shin et al. proposed [3] a prediction algorithm of vehicle speed based on a stochastic model using a Markov chain with speed constraints. The Markov chain generates the velocity trajectory stochastically within speed constraints. The constraints are estimated by an empirical model that takes into account the road geometry and is organized by the intuitive form of matrices. The experimental results show a root mean square error of 3.8041 over a prediction range of up to 200 . Stereo images take up too many computational resources compared to image sensors, even though the accuracy rate is improved.
Meanwhile, deep learning has recently achieved great success in many vision applications, such as object detection [4,5], optical flow estimation [6,7], and depth estimation [8,9]. Considering economic efficiency and environmental adaptability, many researchers have started with monocular cameras and explored their estimates of distance and speed using deep learning methods. In addition, some researchers explore the connection between the optical stream information and the monocular depth [10]. Ma [11] and Christoph [12] achieved impressive results by adding stereo video sequences to the optical flow algorithm. However, the use of stereoscopic video can lead to very high computational costs. Therefore, the use of monocular cameras with different cues has been proposed to estimate the speed and distance of vehicles in a real-time scene. For example, surveillance cameras can be used to analyze traffic flow and vehicle speed in real-time by fixing camera settings and road constraints [13]. However, the estimation becomes unstable in dynamic scenes. Thus, the actual depth of the vehicle as well as the speed mapped to reality through image time cues is difficult to obtain. Until the current study, studies on monocular velocity estimation using multiple complex cues, including vehicle target tracking, dense depth information, and optical flow information to regress the relative velocity of other vehicles, were few [14]. In the present study, we design the network systematically by combining the distance regression model and optical flow estimation network. To enable the network to accurately focus on the traffic prediction for each vehicle, a vehicle-centric vehicle bounding box extraction module is used to reduce the unbalanced motion caused between the stationary background and the moving vehicles. We focus more on the intrinsic connection between geometric cues and deep features.
The main contributions of this study are as follows:
- The inter-vehicle distance and relative speed estimation network is systematically designed.
- The intrinsic connection between geometric cues and deep features is investigated.
- Geometric features are expanded and incorporated into the attention mechanism.
- The results show that the speed and distance measurement results are significantly improved.
The remainder of this paper is structured as follows: Section 2 introduces the related work, Section 3 introduces the multi-cue fusion method and explores the relationship between deep features and the network, Section 4 introduces the proposed algorithm on two datasets, Tusimple and KITTI, and Section 5 presents the conclusion and future work.
2. Related Work
Traditional depth estimation uses binocular images for matching [15], but this method suffers from a slow computation speed and low accuracy. Deep neural network has become one of the most widely used depth estimation techniques. Generally, it can be roughly divided into the following categories: learning-based stereo-matching, supervised monocular depth estimation [16], and unsupervised monocular depth estimation. In Table 1, we list the model structure and main contributions of some typical algorithms. Although they contribute significantly to the monocular depth velocity algorithm, they neglect the underlying vehicle geometry features.

Table 1.
Algorithm model comparison.
In traditional methods, the Markov random field model [24,25] is usually used to predict the monocular depth. Saxena et al. [26] trained, in a supervised manner, to model the relationship between the depth features of the image and the image target to predict the image depth from monocular images. Karsch et al. [27] proposed the use of nonparametric depth to estimate the depth of monocular images and videos, and it can also realize the transformation from stereo images to 3D images. Meanwhile, the structure of motion (SFM) algorithm [28,29,30] was commonly used to estimate the depth information of objects in monocular images.
In 2014, Eigen et al. [17] used two deep convolutional neural networks to estimate the depth of monocular images. Subsequently, Eigen et al. [31] used a multiscale approach to obtain the pixel set features of the image for depth prediction, which can improve the accuracy of the network. In addition, Atapour et al. [32] used a joint training of pixel-level semantic information and depth information to estimate the depth of objects in the scene. Moukari et al. [33] studied four different depth networks, where the depth map can be obtained using multiscale features in the network. Qi et al. [34] applied the uncertainty method to monocular depth. Zhe et al. [35] applied 3D detection to monocular depth estimation to achieve distance recovery.
Supervised monocular depth estimation requires the use of a large amount of manually labeled data to train the model, leading to a high cost of true depth acquisition. In 2016, Garge et al. [36] proposed an unsupervised framework based on deep convolutional neural networks using stereo image pairs for training, without pre-training. Godard et al. [37] proposed a consistency loss for left- and right-image parallax using polar line geometric constraints on binocular images to improve the accuracy and robustness of monocular depth estimation. Zhou et al. [38] established a visual correspondence between different instances and used the inter-instance consistency relationships as supervised signals to train convolutional neural networks. Subsequently, Zhou et al. [39] addressed the problem of new view synthesis by synthesizing the same scene obtained from any viewpoint to obtain a new image based on the highly correlated appearance of the same instance in different views. Inspired by these approaches, an unsupervised learning framework based on binocular images and image reconstruction loss [40] is widely used in monocular depth estimation.
Relevant studies on monocular velocity estimation algorithms are relatively few. Most of them rely on the distance information of the target ahead and then estimate the velocity by the rate of change of the distance. However, the existence of distance errors causes the superposition of speed estimation errors, thereby obtaining inaccurate speed information. To obtain the relative velocity between the self-vehicle and the vehicle in front, Christoph et al. [12] regressed the velocity of the vehicle directly from monocular sequences that exploited several cues, such as the motion features of Flownet [41] and the depth features of Monodepth. In addition, the authors of [42] used geometric constraints and optical flow features to jointly predict the velocity and distance of the vehicle. Although these works achieved the expected performance, they predicted the state of each vehicle separately and neglected to explore the relationship between neighboring vehicles. The authors of [43] proposed a global relative constraint loss that requires the states between vehicles to reduce the error.
These research results show that the use of monocular cameras for distance and speed measurement work still has many unresolved problems. The two main factors are as follows: one is the difficulty of obtaining distance through monocular cameras, and the other is that the current ranging algorithms are imperfect, resulting in less accurate monocular ranging and speed measurement than expected. To solve these problems, a multi-clue fusion distance and speed model is proposed to estimate the distance and speed of the vehicle ahead.
3. Method
The coordinate system of the camera is defined as follows: the z-axis is forward along the optical axis of the camera, the x-axis is parallel to the image to the right, and the y-axis is parallel to the bottom of the image. The specific perspective view is shown in Figure 1.
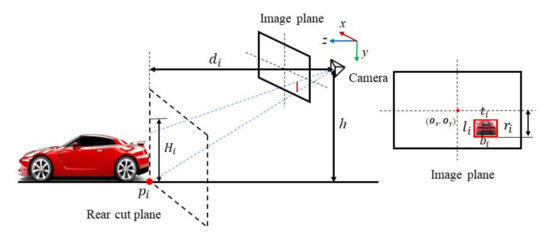
Figure 1.
Perspective projection of the vehicle. In the above picture, is the vehicle’s pickup point, denotes the distance to the previous vehicle, denotes the camera height and , represent the size of the vehicle frame.
The cropped vehicle target bounding box, , is used as the input of the ranging and speed measurement network, and each bounding box consists of four image coordinates: left, top, right, and bottom. The overall algorithm flowchart is shown in Figure 2.
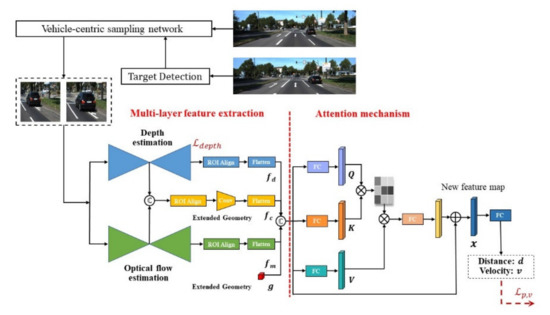
Figure 2.
Algorithm flowchart. The target detection part is used to extract the vehicle detection frame in the video and input it into the speed measurement and ranging network. The algorithm used for target detection is the general Yolo3 [44] algorithm.
3.1. Geometric Cues and Odometry Models
Many current ranging algorithms rely on additional information, such as vanishing points and lane lines, but vanishing points and lane lines are susceptible to the influence of road quality and surrounding references. Therefore, we explore the relationship between geometric cues and ranging models to estimate the distance to the vehicle ahead.
According to the pinhole camera model, the distance of the vehicle ahead can be solved in two ways: one is solved assuming that the height or width of the vehicle is known, and the other is solved based on the vehicle’s grounding point.
The distance based on the vehicle height and width is shown in Equation (2):
and the distance based on the vehicle pickup point is shown in Equation (3):
where indicate the focal length of the camera, are the actual vehicle height and width, respectively, are the coordinates of the left, right, top, and bottom of the vehicle bounding box, respectively, and is the coordinate of the camera optical axis in the y-axis direction under the camera plane.
Each approach has its limitations. The distance based on the vehicle height and width requires the actual width of the vehicle. In addition, the other approach needs to assume that the road surface is always level.
Therefore, the two ranging algorithms can be fused and used to improve the accuracy and stability of vehicle distance estimation in Equation (4), where , , and are obtained directly from the geometric features through the camera intrinsic parameters, bounding box parameters, and camera height, respectively. are the actual height and width information of the vehicle, respectively, depending only on the characteristics of the vehicle. These vehicle features can be learned by a large number of training samples. Therefore, to learn these parameters and features, they are extracted using a deep neural network, and the distance geometric feature vector obtained is represented by . , , and can be used to measure the confidence level of each partial distance estimation. is shown in Equation (5):
In summary, the specific method for the forward vehicle distance, , estimation is as follows: The depth features and other different sizes are unified to the same size by ROI align, and then spread to obtain the depth feature vector, . Finally, the vehicle deep feature vector, , together with the geometric cue, , form the depth estimation network.
Thus, the model for distance regression can be expressed as follows:
where is the depth network, is the feature extraction network, is the ROI align module, Flatten is the spreading operation, is the depth feature vector, is the deep feature vector, is the distance geometry feature vector, and is the fully connected layer.
The loss function, , of the depth network is as follows:
where denotes the loss function of image reconstruction, denotes the smoothness loss of parallax, denotes the front-to-back consistency loss, , , and b are the corresponding coefficients, is the image reconstruction parameter, and SSIM is the image structure similarity formula.
3.2. Geometric Cues and Speed Models
Solving the speed directly by distance leads to the superposition of errors because the distance has errors, thereby resulting in inaccurate speed information. Therefore, the speed of the vehicle ahead is estimated directly using geometric cues. In addition, because distance and speed information are directly related, distance information is introduced as an aid to improve the accuracy and stability of speed estimation. According to the basic theory of relative velocity and distance of vehicles, is the following is obtained:
where is the distance that the vehicle moves between the two frames.
To obtain the velocity component in the lateral direction of the vehicle ahead, the coordinates of the pixel point at the center of the vehicle target frame are used, as well as the inverse perspective projection of the camera.
where is the lateral velocity of the vehicle ahead, and is the longitudinal velocity of the vehicle ahead. indicate the offset of the optical axis concerning the coordinate center of the projection plane, and and are the projection image coordinates of and , respectively.
The analysis results show that the speed information of the vehicle ahead is directly related to several parameters, such as the center point of the bounding box, the change of height, the offset of the camera optical axis, the focal length, and the position of the camera. These parameters can be directly obtained by the inherent parameters of the camera, the target bounding box information, and the height of the camera, so the distance geometric vector, , can be expanded to obtain the expanded geometric vector, , for speed estimation, as follows:
where are directly related to the coordinates, so the geometric cue can be translated as follows:
The motion of the vehicle is analyzed from the pixel perspective, indicating that the relative velocity information of the vehicle is the displacement of each pixel at time interval. This displacement information can be obtained through the optical flow network. The feature vector is used to represent the extracted optical flow information.
In summary, the final model for velocity regression can be expressed as follows:
where is the encoder of the deep network, is the encoder of the optical flow network, is the deep feature vector of the vehicle, is the optical flow feature vector, is the expanded geometric feature vector, and is the fully connected layer.
The regression model for velocity contains the parameters required for the distance regression model, as follows:
The attention mechanism can be viewed as a resource allocation system that reallocates the original equally allocated features according to the importance of the features, which are achieved in neural networks by assigning different weights. Thus, the self-attention mechanism is improved based on the proposed framework, as shown in Figure 3. The self-attention mechanism adjusts the previously obtained depth features, deep features, optical flow features, and geometric features, and it generates an attention map. It forces the model to focus on stable and geometrically meaningful features and can self-adjust without any manual settings to capture the long-term correlation and global correlation, thereby generating better attention-guided maps from a wide range of spatial region features as well as features with different information for joint vehicle speed and distance estimation.
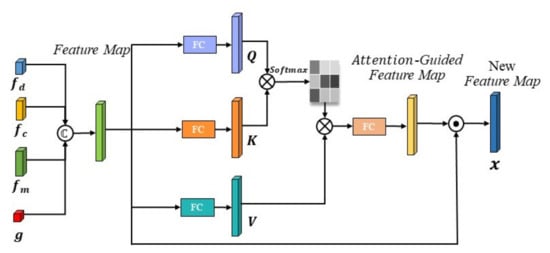
Figure 3.
Attention fusion module.
The final regression model for distance velocity is obtained as follows:
The fusion of depth features, , deep features, , optical flow features, , and geometric features, , by this attention fusion module is shown in Figure 3. Firstly, using the obtained features, , the vectors Q and K are obtained by linear transformations and , respectively, and the similarity of the inner product of the vectors Q and K is calculated as follows:
Then, for the obtained feature , the vector V is obtained by linear transformation again, and the inner product is calculated with the vector S to obtain the associated feature vector F:
Finally, the associated feature vector F is fused with the original feature vector through the fully connected layer , to obtain the final feature vector :
The loss function, , used in the distance and velocity regression is regressed on distance and velocity using MSE loss, as follows:
where , , is the loss function of distance, and is the loss function of velocity.
4. Experimental Validation of Distance–Velocity Estimation Network
In this section, experiments are conducted on the proposed distance–velocity estimation network. We evaluate the performance metrics of the proposed network on the Tusimple velocity dataset and the original KITTI dataset. Some evaluation metrics for distance and speed estimation are presented, as well as experiments comparing the performance of this proposed network with previous networks.
Evaluation metrics:
- Abs relative difference (AbsRel):
- 2.
- Squared relative difference (SqRel):
- 3.
- Root mean square error (RMSE):
- 4.
- Root mean square logarithmic error (RMSlog):
- 5.
- Accuracy:
The three different thresholds are generally used in the accuracy metrics to measure the accuracy of the network.
- 6.
- Mean squared error (MSE):
The overall MSE of the three distances was used as the final metric:
where represents the distance of the vehicle ahead, and represents the distance of the vehicle in the next frame.
4.1. Experimental Validation of the Tusimple Dataset
In the Tusimple speed estimation challenge rule, the vehicles are initially divided into three groups according to their relative distances. The data distribution of the Tusimple dataset is statistically distributed to obtain the distribution of samples at different distances: near distance (d < 20 m), about 12% of the samples, medium distance (20 m < d < 45 m) about 65% of the samples, and long distance (d > 45 m), about 23% of the samples. Related information is shown in Table 2.

Table 2.
Distribution of the number of vehicles labeled in the Tusimple dataset.
The results of the distance estimation were not provided in the Tusimple speed challenge. Thus, the focus is placed on the comparison of the speed results. The evaluation results are shown in Table 3.

Table 3.
Quantitative results of distance velocity estimation on the Tusimple dataset.
The comparison results of different networks on speed metrics at different distances are shown in Table 3. The table shows that the proposed network achieved the best results in terms of the MSE of speed at each distance. Though the target frame of long-distance vehicles is insufficiently rich in deep information, leading to a significant increase in distance and speed estimation errors, the proposed network still achieved good results.
The proposed distance–velocity estimation network on the Tusimple test set yielded a mean velocity MSE of , a 42% reduction compared with [42] (full) and a 23% reduction compared with [35]. In terms of distance, the mean distance MSE obtained was , which is 44% lower than that in [34] (full) and 23% lower than that in [27]. The distance verification results are shown in Table 4.

Table 4.
Quantitative results of distance estimation for the Tusimple dataset.
The inference was performed on the test set using the network trained on the Tusimple dataset to visualize the prediction effect of the proposed network. Figure 4 and Table 5 show the results of the predicted values of the proposed network in terms of cross-longitudinal distance and velocity compared with the labels.

Figure 4.
Qualitative visualization results for the Tusimple dataset. Figures (a–d) are typical feature maps extracted from the Tusimple dataset.

Table 5.
Predicted distance velocity estimates obtained corresponding to Figure 4.
4.2. Experimental Validation of KITTI Dataset
4.2.1. Analysis of Performance Indicators
The speed estimation results of the network on the KITTI dataset are shown in Table 6.

Table 6.
Quantitative results of speed estimation for the KITTI dataset.
Table 6 shows that the MSE of the proposed network for medium distance velocity was reduced by 59.7% compared with [27], proving the effectiveness of multiple features for distance and velocity estimation.
Table 7 shows the quantitative results of different networks on each metric, and the proposed network had a 13% difference in error on the AbsRel metric compared with the method in [34], with only a 0.9% difference with the DORN method on the RMS metric. However, a 15.5% and a 13% improvement were found in the SqRel and RMSlog metrics, respectively. The accuracy was almost the same as other excellent networks. The proposed network achieved excellent results in distance estimation.

Table 7.
Quantitative results of distance estimation for the KITTI dataset.
4.2.2. Qualitative Visualization Analysis
The results were also visualized on the test set of the KITTI dataset to visualize the prediction effect of the proposed network. Figure 5 and Table 8 compare the prediction results of the proposed network with the labeling results in terms of horizontal and vertical distance and speed.

Figure 5.
Qualitative visualization results on the KITTI dataset. Figures (a–d) respectively represent the vehicle ahead, the oncoming vehicle, the multi-vehicle in front, and the multi-vehicle in the opposite direction.

Table 8.
Qualitative results obtained from predictions corresponding to Figure 5.
As shown in the table, the distance and speed in the longitudinal direction are shown on the left side of the brackets, and the distance and speed in the lateral direction are shown on the right side. After the statistical Table 8, the network can reach an average relative error of 2.1% in terms of distance and 2.6% in terms of relative speed obtained from the KITTI dataset. The proposed network can maintain high accuracy and stability for multiple targets, as well as for the prediction of the oncoming traffic situation.
4.2.3. Visualization Analysis under Different Working Conditions
This section visualizes and analyzes different working conditions separately to clearly show the effect of the range and speed measurement network. The selected video clip scenes are as follows: forward following scene, containing 291 frames of images, lateral incoming scene, containing three targets with 56 frames of images, and opposite incoming scene, containing 17 frames of images.
Figure 6 shows the prediction results of the forward-following scenario. The red box is the obtained bounding box of the target vehicle, and the prediction is performed for each frame to obtain the real-time distance and speed variation of the target vehicle in the forward-following scenario, as shown in Figure 7.

Figure 6.
Prediction results of the target vehicle in the forward-following scenario. The green font represents the true values, which are the longitudinal lateral distance and longitudinal lateral velocity; the blue represents the predicted values, which are the longitudinal lateral distance and longitudinal lateral velocity.
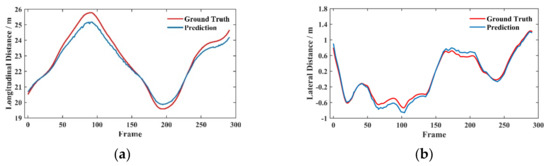
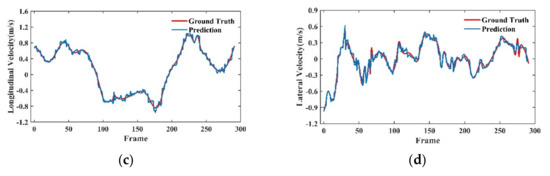
Figure 7.
Real–time variation curve of distance and speed of the target vehicle in the forward-following scenario. (a) Longitudinal distance, (b) Lateral distance, (c) Longitudinal velocity, (d) Lateral velocity.
Figure 7a,b show that the predicted value and the actual value of the longitudinal distance and the transverse distance are offset at some moments. The maximum offset on the longitudinal distance is around 1 m, and the offset on the transverse distance is around 0.2 m. In addition, the predicted result has the same trend as the actual value, and the change is relatively smooth, indicating that the network has high accuracy and robustness in the prediction result on the distance. Figure 7c,d show that the predicted value always fluctuates up and down near the actual value in the transverse and longitudinal velocities, and a better result can be obtained for the case of violent vehicle movement. Although the predicted velocity curve has some fluctuations, the magnitude of the fluctuations is maintained within a small range.
Figure 8 shows the prediction results of the lateral incoming vehicle scene. Figure 9 shows the real-time variation curves of the distance and speed of the target vehicle under the lateral incoming traffic scenario.

Figure 8.
Prediction results of the target vehicle in the lateral incoming vehicle scenario.
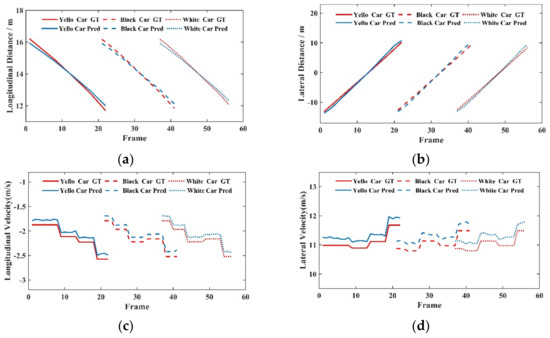
Figure 9.
Real-time variation curves of the distance and speed of the target vehicle under the lateral incoming traffic scenario. (a) Longitudinal distance, (b) Lateral distance, (c) Longitudinal velocity, (d) Lateral velocity.
Figure 9a,b show that the prediction effect of the network on vehicles with farther lateral distances decreases in the longitudinal and lateral distances. Figure 9c,d show the predicted effect of the vehicle on longitudinal and lateral speeds. The error gradually decreases as the vehicle moves to the front of the self-propelled vehicle. In the transverse longitudinal distance, the slope of the distance prediction curve is different from that of the actual value curve, resulting in a bias between the predicted and actual results. The two reasons for the error in the lateral speed are as follows: on the one hand, the lateral incoming car belongs to a more difficult scene than the following car, which cannot be easily learned by the; on the other hand, the amount of data trained for this scene is relatively small, thereby increasing the error. Through the calculation, the error on the lateral speed is around 2% and that on the longitudinal speed is around 4%, which is still in a very low range.
Figure 10 shows the prediction results of the lateral incoming car scenario. The red box is the boundary box of the obtained target vehicle. Figure 11 shows the real-time distance and speed change of the target vehicle in the lateral incoming car scenario.

Figure 10.
Prediction results of the target vehicle in the opposite direction traffic scenario. The green font represents the true values, which are the longitudinal lateral distance and longitudinal lateral velocity; the blue represents the predicted values, which are the longitudinal lateral distance and longitudinal lateral velocity.
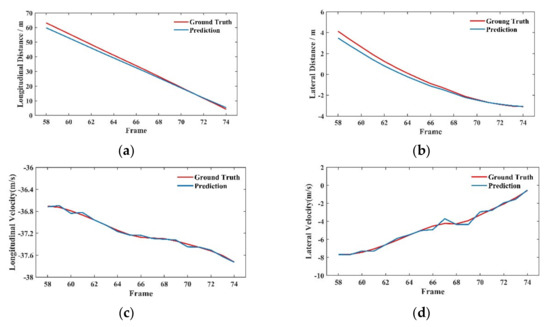
Figure 11.
Real–time variation curve of the distance and speed of the target vehicle in the opposite direction of incoming traffic scenario. The red lines represent the true values, (a-d) are the longitudinal transverse distance and longitudinal transverse velocity.
Figure 11a,b show that the network’s prediction effectiveness decreases for long-distance vehicles at longitudinal and lateral distances. This finding is due to the small target frame obtained from the long-range vehicle volume and the insignificant parameter variation, which leads to the reduced effectiveness of the network for long-range target prediction. However, the error gradually decreases as the target vehicle continues to approach the self-vehicle. Figure 11c,d show that the predicted value fluctuates up and down around the actual value in the transverse longitudinal velocity. This finding is due to the fast speed of incoming traffic in the opposite direction, and the fluctuations are elevated compared with the following scenario, but still remain small.
The analysis of the prediction effect of the network under different scenarios indicates that the network has a high prediction accuracy for medium- and close-range targets. Although the prediction accuracy for long-range and lateral farther targets is reduced, it still has a good prediction effect.
In addition to this, the model in this paper is also capable of running in real time, with each vehicle-centric patch running on a single TITAN XP with an inference time of 38 ms. The time consumption results for the different layers are shown in Table 9.

Table 9.
Time consumption statistics for different layers.
5. Discussion and Conclusions
The main focus of this study was a monocular camera-based distance and speed measurement method for forwarding vehicles in autonomous driving scenarios. The proposed algorithm in this paper enables end-to-end training of a monocular ranging and speed measurement model for ADAS systems. The main work was divided into the following parts.
1. Training process and dataset preparation: Firstly, the target frame parameters of the vehicle were obtained using a typical target detection algorithm. Then, the detected target frame was expanded so that some background information around the target frame could be preserved. Next, the previous frame was sampled and cropped using a vehicle-centric sampling strategy to deal with unbalanced motion distributions and perspective effects to obtain the image pairs for network input. Finally, the extracted image pairs from the Tusimple dataset and the KITTI dataset were used to train the network, and the distance and speed labels of the dataset were extracted and transformed to obtain the distance and speed labels of the targets.
2. We proposed a neural network-based multi-feature fusion distance and speed regression model. Firstly, by deriving the geometric relationship between the target frame information and the information between distance and speed, the information required in the distance and speed estimation was obtained to solve the problems existing in the current distance and speed measurement algorithm. By introducing depth features of images, optical flow features, deep features of vehicles, and geometric features obtained from target frame parameters and camera parameters, the fusion of multiple features was achieved, the accuracy of distance and speed estimation was improved, and a multi-feature distance and speed regression model based on neural network was presented. The attention mechanism was used to fuse different feature cues. The distance and speed information of the vehicle ahead was obtained by constructing distance and speed loss and adding depth loss as an auxiliary loss to regress the distance and speed.
3. On the Tusimple dataset, the mean squared error of the mean velocity of this method was less than , and the mean squared error of the distance was . The relative velocity estimation performance of this method was better than the existing techniques in all distance ranges. On the KITTI dataset, the mean speed mean squared error of this method was less than , and the method achieved the best results in most of the metrics and obtained fewer outliers in terms of distance. In addition, the prediction effect plots of the KITTI test set were visualized and the robustness of the model in the KITTI test set was verified. Figure 6, Figure 7, Figure 8 and Figure 9 show the lateral incoming traffic scenario, and the comparison curve with the true value shows that the error was also within a small range. Figure 10 and Figure 11 show the opposite direction incoming vehicle scenario in the KITTI dataset. From the real-time true value curves of the distance and speed of the target vehicle, it can be seen that the distance error became smaller and smaller as the vehicle came closer and closer, and the speed fluctuation in the horizontal and vertical directions also became smaller and smaller. In summary, the algorithm in this paper has a good effect at medium and long distance, and also has a good performance in other working conditions, which directly proves that the model has a certain generalization ability and is suitable for multi-scene working conditions.
Author Contributions
Conceptualization, S.S. and H.Z.; methodology, C.Q., N.Z. and C.S.; software, C.Q., S.S. and F.X.; validation, C.Q., F.X. and S.S.; formal analysis, C.S., H.Z. and H.X.; investigation, N.Z., S.S. and C.Q.; resources, H.Z. and F.X.; data curation, C.Q., H.Z. and N.Z.; H.X. provided suggestions for the revision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National key research and development program under 2021YFB2500704, in part the by Grant Science and Technology Development Plan Program of Jilin Province under Grant 20200401112GX, in part by the Industry Independent Innovation Ability Special Fund Project of Jilin Province under Grant 2020C021-3.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to express their gratitude to the editors and the anonymous reviewers for their insightful and constructive comments and suggestions, which have led to this improved version of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hasirlioglu, S.; Riener, A.; Huber, W.; Wintersberger, P. Effects of Exhaust Gases on Laser Scanner Data Quality at Low Ambient Temperatures. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017. [Google Scholar]
- Fascista, A.; Ciccarese, G.; Coluccia, A.; Ricci, G. Angle of Arrival-Based Cooperative Positioning for Smart Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2880–2892. [Google Scholar] [CrossRef]
- Shin, J.; Sunwoo, M. Vehicle Speed Prediction Using a Markov Chain With Speed Constraints. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3201–3211. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. Adv. Neural Inf. Process. Syst. 2015, 28, 28,1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fischer, P.; Dosovitskiy, A.; Ilg, E.; Häusser, P.; Hazırbaş, C.; Golkov, V.; van der Smagt, P.; Cremers, D.; Brox, T. FlowNet: Learning Optical Flow with Convolutional Networks. arXiv 2015, arXiv:1504.06852. [Google Scholar]
- Sun, D.; Yang, X.; Liu, M.Y.; Kautz, J. PWC-Net: CNNs for Optical Flow Using Pyramid, Warping, and Cost Volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Bian, J.; Li, Z.; Wang, N.; Zhan, H.; Shen, C.; Cheng, M.M.; Reid, I. Unsupervised Scale-consistent Depth and Ego-motion Learning from Monocular Video. Adv. Neural Inf. Process. Syst. 2019, 32, 49–65. [Google Scholar]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep Ordinal Regression Network for Monocular Depth Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles in Computer Vision & Pattern Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Ma, W.C.; Wang, S.; Hu, R.; Xiong, Y.; Urtasun, R. Deep Rigid Instance Scene Flow. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Vogel, C.; Schindler, K.; Roth, S. 3D Scene Flow Estimation with a Piecewise Rigid Scene Model. Int. J. Comput. Vis. 2015, 115, 1–28. [Google Scholar] [CrossRef]
- Tran, M.T.; Dinh-Duy, T.; Truong, T.D.; Ton-That, V.; Do, T.N.; Luong, Q.A.; Nguyen, T.A.; Nguyen, V.T.; Do, M.N. Traffic Flow Analysis with Multiple Adaptive Vehicle Detectors and Velocity Estimation with Landmark-Based Scanlines. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Kampelmühler, M.; Müller, M.G.; Feichtenhofer, C. Camera-based vehicle velocity estimation from monocular video. arXiv 2018, arXiv:1802.07094. [Google Scholar]
- Hirschm, H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Shen, C.; Dai, Y.; Van Den Hengel, A.; He, M. Depth and surface normal estimation from monocular images using regression on deep features and hierarchical CRFs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth Map Prediction from a Single Image using a Multi-Scale Deep Network. In Proceedings of the 28th Conference on Neural Information Processing Systems (NIPS), Montreal, Canada, 8–13 December 2014. [Google Scholar]
- Lee, J.H.; Heo, M.; Kim, K.R.; Kim, C.S. Single-Image Depth Estimation Based on Fourier Domain Analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Li, J.; Klein, R.; Yao, A. Two-Streamed Network for Estimating Fine-Scaled Depth Maps from Single RGB Images. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper Depth Prediction with Fully Convolutional Residual Networks. In Proceedings of the 2016 Fourth international conference on 3D vision (3DV), Stanford, CA, USA, 25–28 October 2016. [Google Scholar]
- Hu, J.; Ozay, M.; Zhang, Y.; Okatani, T. Revisiting Single Image Depth Estimation: Toward Higher Resolution Maps with Accurate Object Boundaries. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G. Deep Convolutional Neural Fields for Depth Estimation from a Single Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Xu, D.; Ricci, E.; Ouyang, W.; Wang, X.; Sebe, N. Multi-Scale Continuous CRFs as Sequential Deep Networks for Monocular Depth Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Rajagopalan, A.N.; Chaudhuri, S.; Mudenagudi, U. Depth Estimation and Image Restoration Using Defocused Stereo Pairs. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1521–1525. [Google Scholar] [CrossRef] [PubMed]
- Saxena, A.; Chung, S.; Ng, A. Learning Depth from Single Monocular Images. Adv. Neural Inf. Process. Syst. 2005, 18, 1161–1168. [Google Scholar]
- Saxena, A.; Sun, M.; Ng, A.Y. Make3D: Learning 3D Scene Structure from a Single Still Image. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 824–840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karsch, K.; Liu, C.; Kang, S.B. Depth Extraction from Video Using Non-parametric Sampling. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Song, S.; Chandraker, M.; Guest, C.C. High Accuracy Monocular SFM and Scale Correction for Autonomous Driving. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 730–743. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Chandraker, M. Robust Scale Estimation in Real-Time Monocular SFM for Autonomous Driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications (Texts in Computer Science); Springer Science and Business Media: New York, NY, USA, 2010. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture. In Proceedings of the International Conference on Computer Vision (ICCV), Santiago, Chile, 7-13 December 2015. [Google Scholar]
- Atapour-Abarghouei, A.; Breckon, T.P. Monocular Segment-Wise Depth: Monocular Depth Estimation Based on a Semantic Segmentation Prior. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019. [Google Scholar]
- Moukari, M.; Picard, S.; Simon, L.; Jurie, F. Deep multi-scale architectures for monocular depth estimation. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018. [Google Scholar]
- Song, C.; Qi, C.; Song, S.; Xiao, F. Unsupervised Monocular Depth Estimation Method Based on Uncertainty Analysis and Retinex Algorithm. Sensors 2020, 20, 5389. [Google Scholar] [CrossRef] [PubMed]
- Zhe, T.; Huang, L.; Wu, Q.; Zhang, J.; Pei, C.; Li, L. Inter-Vehicle Distance Estimation Method Based on Monocular Vision Using 3D Detection. IEEE Trans. Veh. Technol. 2020, 69, 4907–4919. [Google Scholar] [CrossRef]
- Garg, R.; Bg, V.K.; Carneiro, G.; Reid, I. Unsupervised CNN for Single View Depth Estimation: Geometry to the Rescue; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Brostow, G.J. Unsupervised Monocular Depth Estimation with Left-Right Consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhou, T.; Krahenbuhl, P.; Aubry, M.; Huang, Q.; Efros, A.A. Learning Dense Correspondence via 3D-guided Cycle Consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhou, T.; Tulsiani, S.; Sun, W.; Malik, J.; Efros, A.A. View Synthesis by Appearance Flow. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Yin, Z.; Shi, J. GeoNet: Unsupervised Learning of Dense Depth, Optical Flow and Camera Pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. FlowNet 2.0: Evolution of Optical Flow Estimation with Deep Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017.
- Song, Z.; Lu, J.; Zhang, T.; Li, H. End-to-end Learning for Inter-Vehicle Distance and Relative Velocity Estimation in ADAS with a Monocular Camera. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Huang, K.C.; Huang, Y.K.; Hsu, W.H. Multi-Stream Attention Learning for Monocular Vehicle Velocity and Inter-Vehicle Distance Estimation. arXiv 2021, arXiv:2110.11608. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Mousavian, A.; Anguelov, D.; Flynn, J.; Kosecka, J. 3D Bounding Box Estimation Using Deep Learning and Geometry. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).