Experimental Validation in a Controlled Environment of a Methodology for Assessing the Dynamic Behavior of Railway Track Components
Abstract
1. Introduction
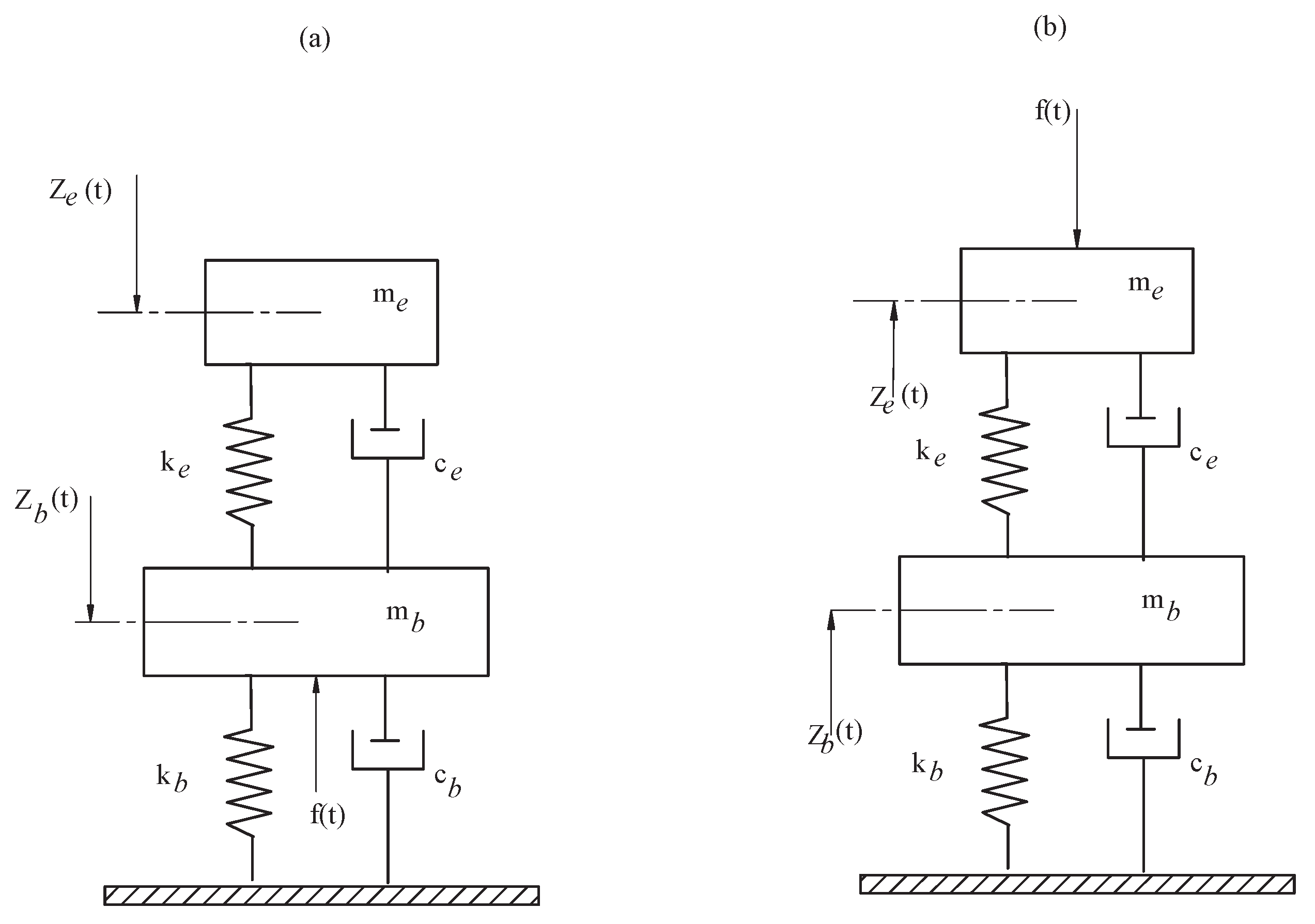
2. Description of the Mass-Elastomer System Model
3. Methodology for Assessing the Dynamic Behavior of Railway Tracks
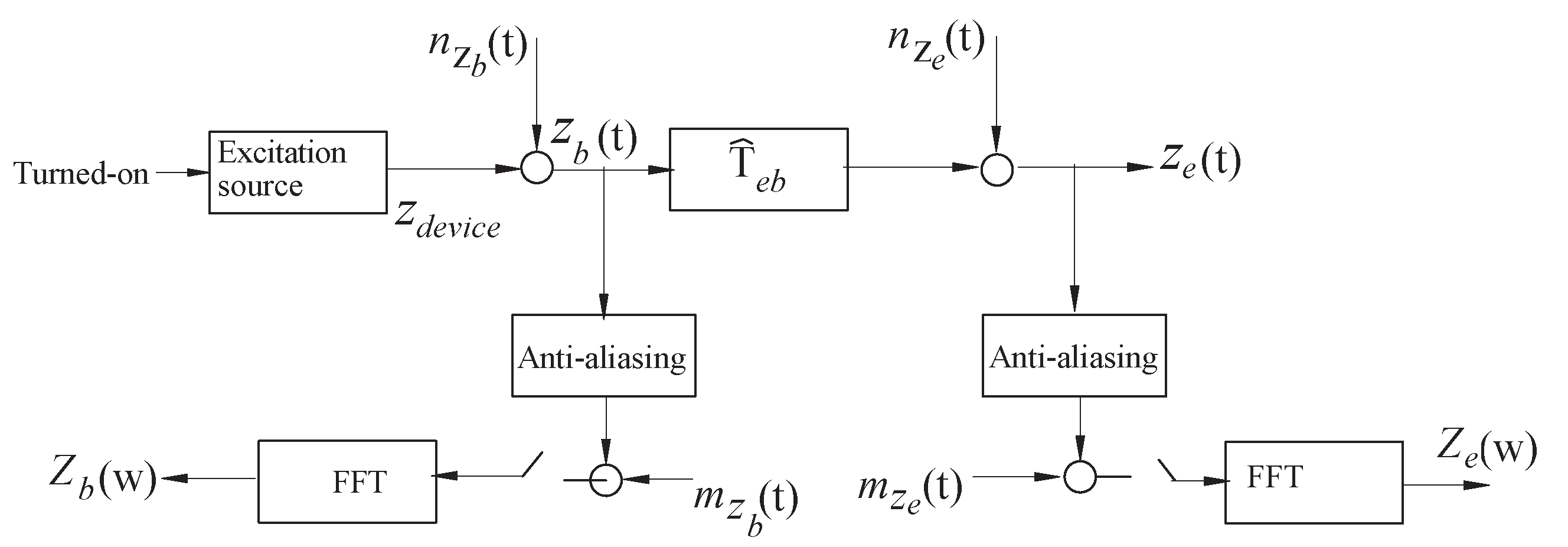
4. Experimental FRF Determination of the Mass-Elastomer System
The Input Excitation Analysis Method
5. Experimental Results
- Apply the peak-amplitude method to determine the transmissibility curve.
- Specific frequencies by shaker.
- Sine sweep by shaker.
- Maximum amplitude frequency estimation.
- Numerical analysis of the standardized parameters and .
- Development of an approximate curve that relates to the maximum amplitude of the vibratory response.
- Use the SNR for estimate transmissibility by the unbalanced mass device.
- Apply the spectral analysis method for the measurements of the input and output signals.
- Define the signal-to-noise ratio for different excitation parameters.
- Find the error, , to estimate the transmissibility, based on the SNR due to background noise.
- Determine the excitation parameters of the unbalanced mass sweep rate , unbalanced mass me, and excitation frequency of the mass-elastomer system.
- Define , the standardized parameter of the maximum peak frequency as a function of the natural frequency of the system.
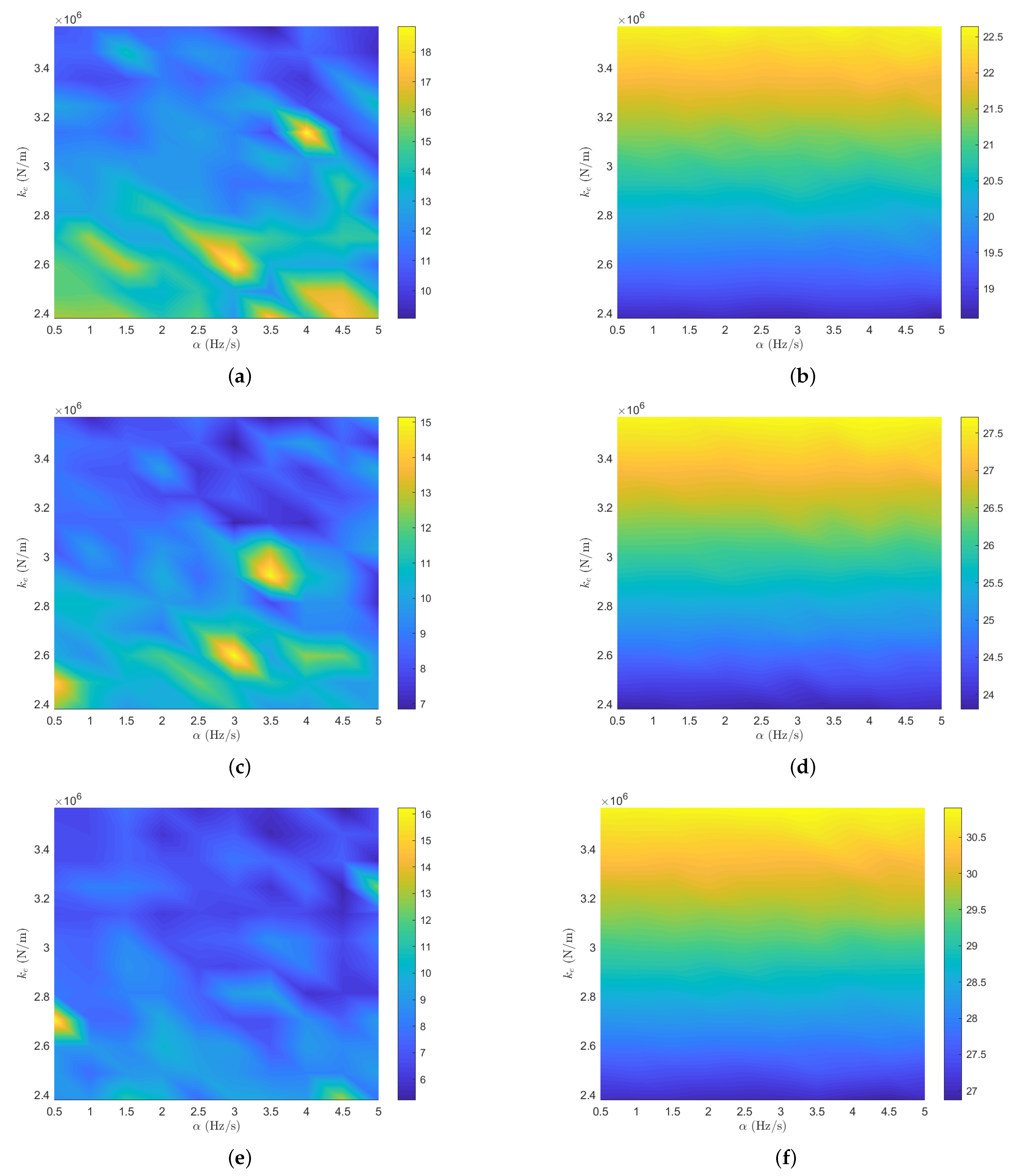
- Determine the stiffness, , of the railway elastomeric component and its damping factor, , to validate the methodology.
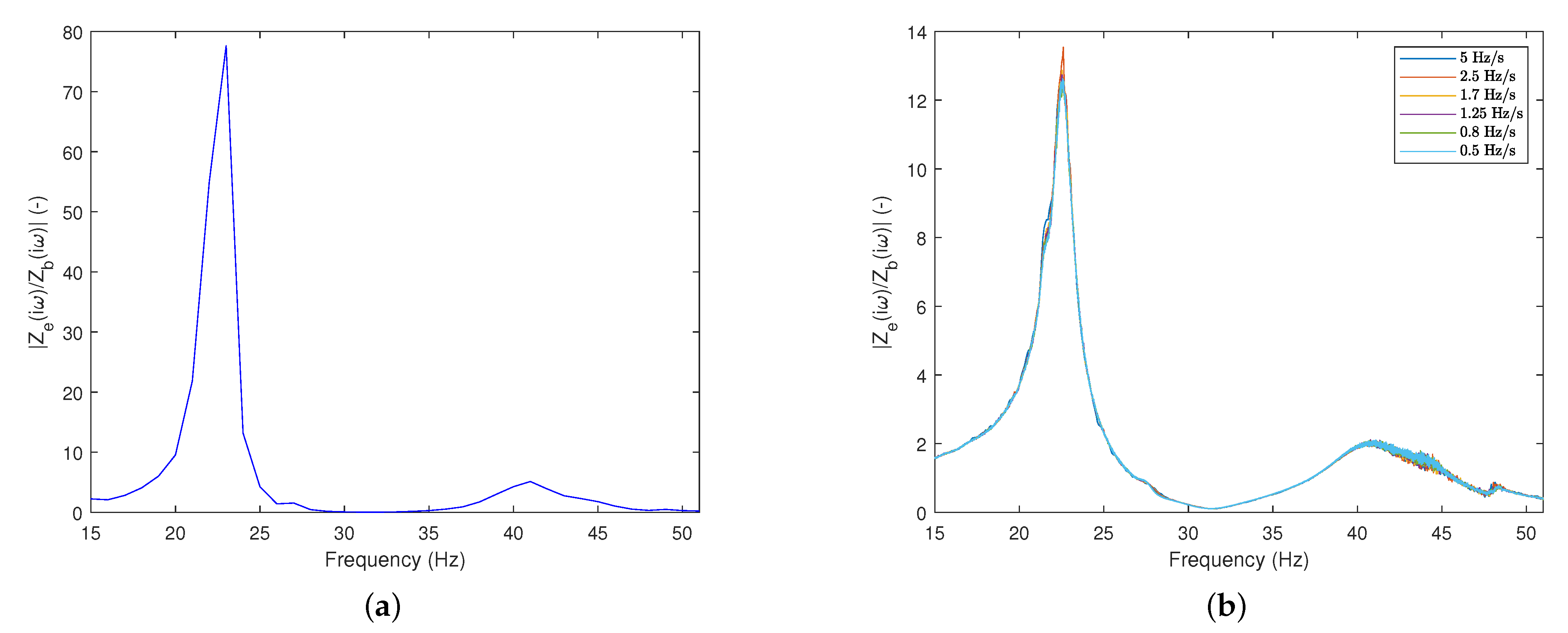
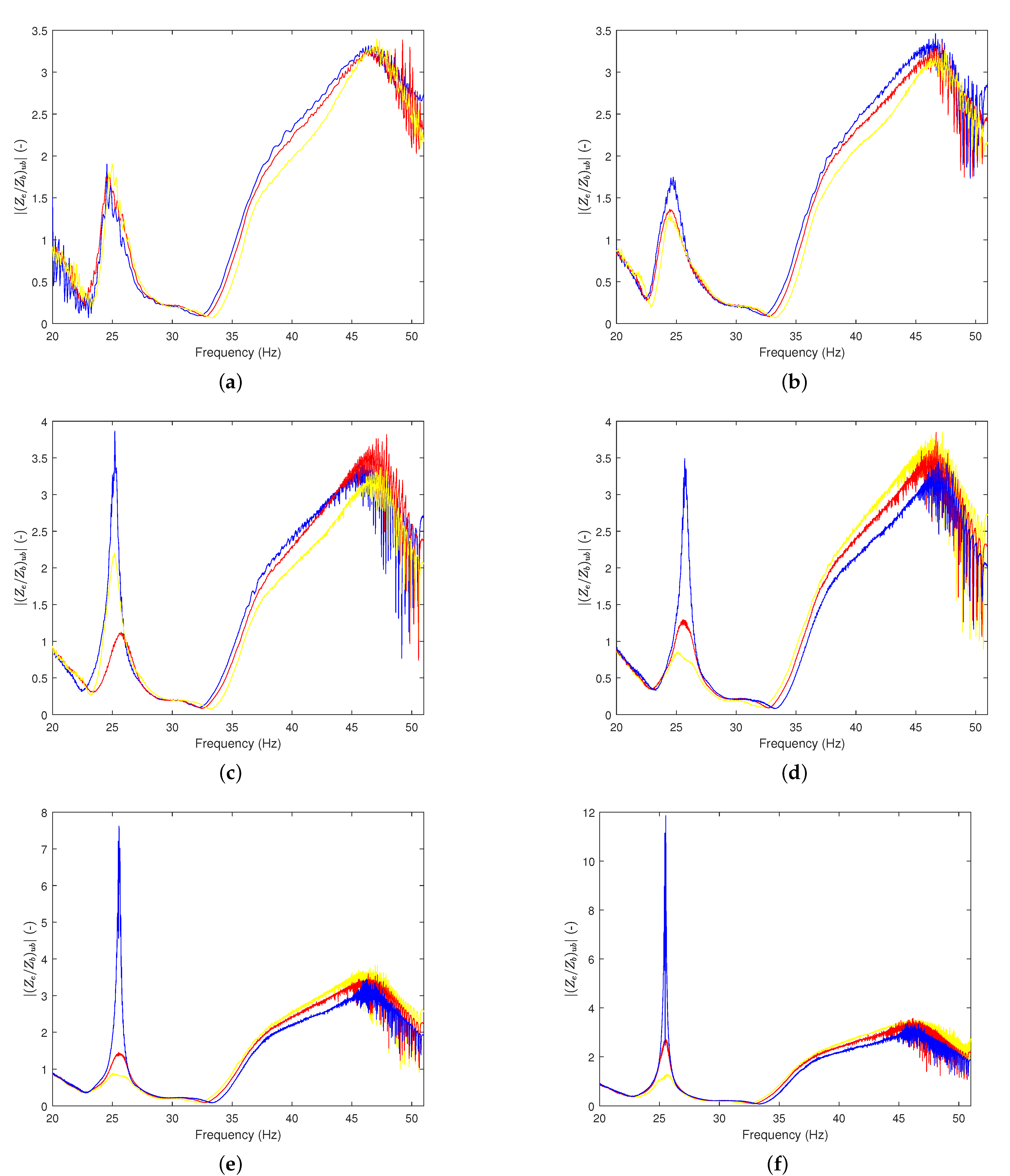
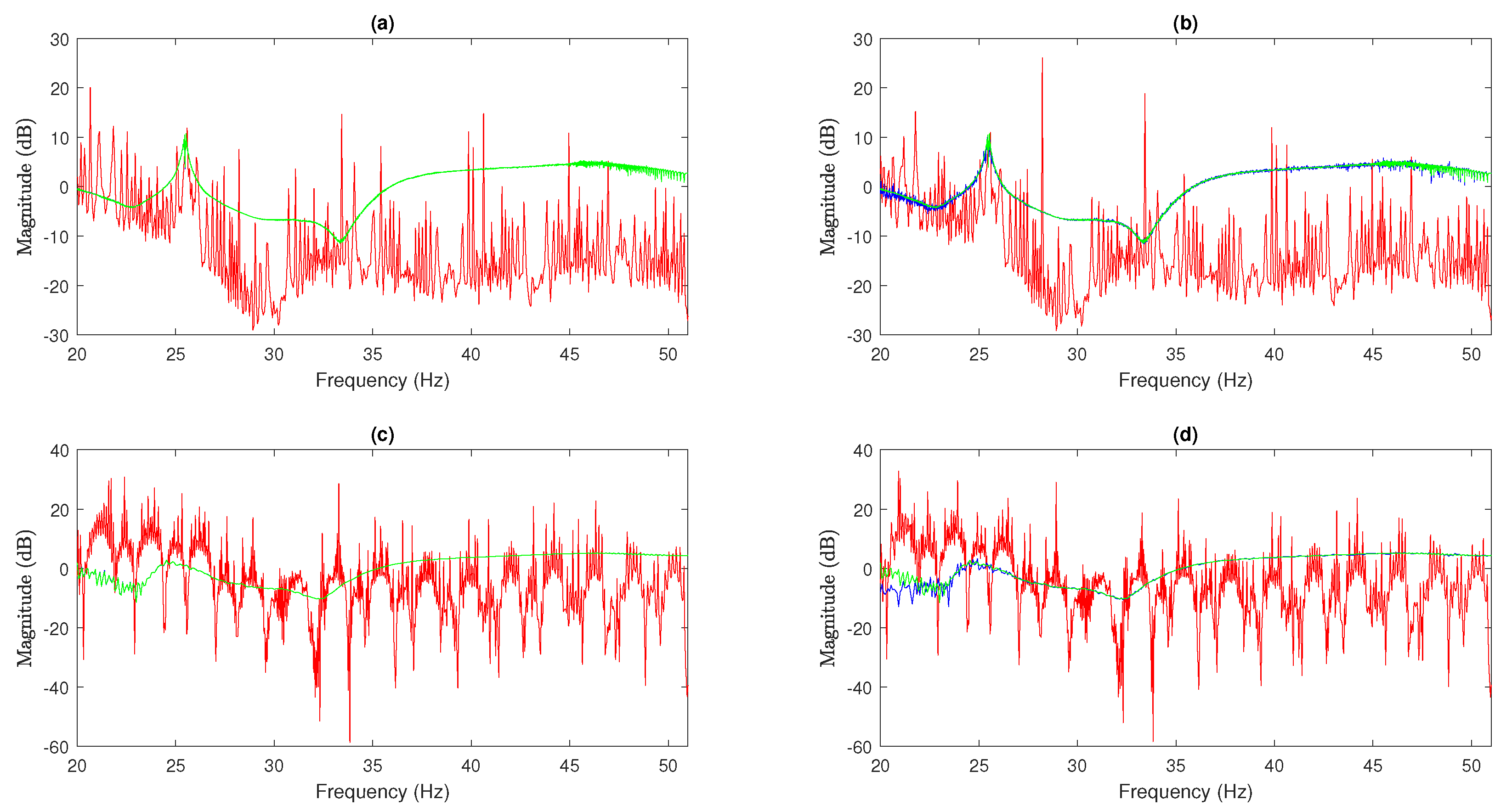
5.1. Apply Peak-Amplitude Method to Determine the Transmissibility Curve
5.2. Maximum Amplitude Frequency Estimation
5.3. Use the SNR to Estimate Transmissibility by the Unbalanced Mass Device
6. Conclusions
- (1)
- In the test with the unbalanced mass device, a better signal-to-noise ratio and slower sweep rate can effectively improve the estimate of transmissibility. The FRF estimation error decreased as the signal-to-noise ratio increased. The location of the unbalanced mass in the largest position of the rotating disc of the unbalanced mass device showed a decrease in the FRF estimation error.
- (2)
- In the laboratory test, different background noise conditions demonstrated the dependence on the sweep rate to achieve the best steady-state condition using the unbalanced mass device.
- (3)
- By obtaining the stiffness of the elastomeric material, the damping factor using the shaker with frequency–frequency excitation, and sine sweep, as well as the unbalanced mass device, the background noise effects of the FRF were experimentally validated.
- (4)
- The methodology was validated in the laboratory with the characterization of the elastomeric material for railway applications to determine the dynamic parameters of stiffness and damping factor using the unbalanced mass device.
- (5)
- The methodology is useful for reducing setup time in cases where several different samples need to be tested, such as quality control tests in the manufacturing process.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FRF | Frequency Response Functions |
| PSD | Power Spectral Density |
| SNR | Signal-to-Noise Ratio |
References
- Shi, J.; Wen, S.; Zhao, X.; Wu, G. Sustainable development of urban rail transit networks: A vulnerability perspective. Sustainability 2019, 11, 1335. [Google Scholar] [CrossRef]
- Reina, S.; Arcos, R.; Clot, A.; Romeu, J. An Efficient Experimental Methodology for the Assessment of the Dynamic Behaviour of Resilient Elements. Materials 2020, 13, 2889. [Google Scholar] [CrossRef]
- Zbiciak, A.; Kraśkiewicz, C.; Oleksiewicz, W.; Lipko, C. Viscoelastic dynamic models of resilient elements used in railway tracks. MATEC Web Conf. 2016, 86, 01015. [Google Scholar] [CrossRef]
- Oregui, M.; Molodova, M.; Núñez, A.; Dollevoet, R.; Li, Z. Experimental investigation into the condition of insulated rail joints by impact excitation. Exp. Mech. 2015, 55, 1597–1612. [Google Scholar] [CrossRef]
- Oregui, M.; Li, Z.; Dollevoet, R. An investigation into the modeling of railway fastening. Int. J. Mech. Sci. 2015, 92, 1–11. [Google Scholar] [CrossRef]
- Arlaud, E.; D’Aguiar, S.C.; Balmes, E. Receptance of railway tracks at low frequency: Numerical and experimental approaches. Transp. Geotech. 2016, 9, 1–16. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Lv, Q.; Jiao, H.; Xiao, X.; Jin, X. Measuring, modelling and optimising an embedded rail track. Appl. Acoust. 2017, 116, 70–81. [Google Scholar] [CrossRef]
- ISO 7626-2; Mechanical Vibration and Shock. Experimental Determination of Mechanical Mobility. Part 2: Measurements Using Single Point Traslation Excitation with an Attached Vibration Exciter. ISO: Geneva, Switzerland, 2015.
- Ding, D.; Liu, W.; Li, K.; Sun, X.; Liu, W. Low frequency vibration tests on a floating slab track in an underground laboratory. J. Zhejiang Univ.-Sci. A 2011, 12, 345–359. [Google Scholar] [CrossRef]
- Yaroshevich, N.; Zabrodets, I.; Yaroshevich, T. Dynamics of Starting of Vibrating Machines with Unbalanced Vibroexciters on Solid Body with Flat Vibrations. Appl. Mech. Mater. 2016, 849, 36–45. [Google Scholar] [CrossRef]
- Wang, L. Vibration characterization of fully-closed high speed railway subgrade through frequency: Sweeping test. Soil Dyn. Earthq. Eng. 2016, 88, 33–44. [Google Scholar] [CrossRef]
- Beijen, M.; Heertjes, M.; Voorhoeve, R.; Oomen, T. Evaluating performance of multivariable vibration isolators: A frequency domain identification approach applied to an industrial AVIS. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 3512–3517. [Google Scholar]
- Weijtjens, W.; De Sitter, G.; Devriendt, C.; Guillaume, P. Operational modal parameter estimation of MIMO systems using transmissibility functions. Automatica 2014, 50, 559–564. [Google Scholar] [CrossRef]
- Beijen, M.A.; Voorhoeve, R.; Heertjes, M.F.; Oomen, T. Experimental estimation of transmissibility matrices for industrial multi-axis vibration isolation systems. Mech. Syst. Signal Process. 2018, 107, 469–483. [Google Scholar] [CrossRef]
- Beijen, M.; Heertjes, M.; Voorhoeve, R.; Oomen, T. Estimating transmissibility functions in industrial vibration isolation systems by combining floor and shaker excitations. In Proceedings of the 36th Benelux Meeting on Systems and Control, Spa, Belgium, 28–30 March 2017; p. 70. [Google Scholar]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Pauwels, S.; Michel, J.; Robijns, M.; Peeters, B.; Debille, J. A New MIMO Sine Testing Technique for Accelerated High Quality FRF Measurements. In Proceedings of the 24th International Modal Analysis Conference, St. Louis, MI, USA, 30 January–2 February 2006. [Google Scholar]
- Gloth, G.; Sinapius, M. Analysis of swept-sine runs during modal identification. Mech. Syst. Signal Process. 2004, 18, 1421–1441. [Google Scholar] [CrossRef]
- Roy, N.; Girard, A. Revisiting the effect of sine sweep rate on modal identification. In Proceedings of the 12th European Conference Space Structures, Materials & Environmental Testing, Noordwijk, The Netherlands, 20–23 March 2012. [Google Scholar]
- Roy, N.; Violin, M.; Cavro, E. Sine sweep effect on specimen modal parameters characterization. Adv. Aircr. Spacecr. Sci. 2018, 5, 187–204. [Google Scholar]
- Lollock, J. The effect of swept sinusoidal excitation on the response of a single-degree-of-freedom oscillator. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002; p. 1230. [Google Scholar]
- Girard, A.; Bugeat, L. Effect of Sine Sweep Rate on Modal Parameter Identification. In Proceedings of the 5th International Symposium on Environmental Testing for Space Programmes, Noordwijk, The Netherlands, 15–17 June 2004; Volume 558, pp. 153–156. [Google Scholar]
- Orlando, S.; Peeters, B.; Coppotelli, G. Improved FRF estimators for MIMO Sine Sweep data. In Proceedings of the ISMA 2008 International Conference on Noise and Vibration Engineering, Leuven, Belgium, 15–17 September 2008; pp. 229–241. [Google Scholar]
- Lalanne, C. Mechanical Shock; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Arcos Villamarín, R.; Sans Garcia, J.; Romeu Garbí, J.; Razquin, C.; Cardona Gonyalons, J.; Oregui, M. Methodology for the experimental evaluation of frequency response functions in the frame of railway-induced or construction-induced groundbourne vibration. In Proceedings of the EuroRegio 2016, Porto, Portugal, 13–15 June 2016; Sociedade Portuguesa de Acústica: Lisboa, Portugal, 2016. [Google Scholar]
- Ciulli, E.; Forte, P. Nonlinear response of tilting pad journal bearings to harmonic excitation. Machines 2019, 7, 43. [Google Scholar] [CrossRef]
- Trethewey, M.W.; Sommer, H.J., III. Application of a pure moment exciter for measurement of moment-rotational DOF frequency response functions. Proc. SPIE Int. Soc. Opt. Eng. 2002, 4753, 1153–1158. [Google Scholar]
- Cveticanin, L.; Zukovic, M.; Balthazar, J.M. Dynamics of Mechanical Systems with Non-Ideal Excitation; Springer: Berlin, Germany, 2018. [Google Scholar]
- Mituletu, I.C.; Gillich, G.R.; Maia, N.M. A method for an accurate estimation of natural frequencies using swept-sine acoustic excitation. Mech. Syst. Signal Process. 2019, 116, 693–709. [Google Scholar] [CrossRef]
- Markert, R.; Seidler, M. Analytically based estimation of the maximum amplitude during passage through resonance. Int. J. Solids Struct. 2001, 38, 1975–1992. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, in SI Units, Global Edition; Pearson: London, UK, 2017. [Google Scholar]
- Ewins, D. Basics and state-of-the-art of modal testing. Sadhana 2000, 25, 207–220. [Google Scholar] [CrossRef][Green Version]
- Reina, S.; Arcos, R.; Romeu, J. Experimental study of a methodology for the dynamic characterization of systems using unbalanced mass excitation. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; Institute of Noise Control Engineering: Madrid, Spain, 2019; Volume 259, pp. 7424–7433. [Google Scholar]
- Arcos Villamarín, R.; Cardona Gonyalons, J.; Torres, R.; Turiel, I. RECYTRACK Project: Elastomeric eco-friendly material based on end-of-life tires blended with organic bind resin for railway applications. J. Mech. Eng. Autom. 2014, 4, 165–171. [Google Scholar]
- Diego, S.; Casado, J.; Carrascal, I.; Ferreño, D.; Cardona, J.; Arcos, R. Numerical and experimental characterization of the mechanical behavior of a new recycled elastomer for vibration isolation in railway applications. Constr. Build. Mater. 2017, 134, 18–31. [Google Scholar] [CrossRef]
- Reina, S.; Arcos Villamarín, R.; Romeu Garbí, J.; Clot, A. Optimización de los parámetros para la determinación experimental de la receptanciaa partir de una excitación armónica con barrido logarítmico en frecuencia. In Proceedings of the XXII Congreso Nacional de Ingeniería Mecánica, Madrid, Spain, 19–21 September 2018; pp. 1253–1261. [Google Scholar]
- Pintelon, R.; Schoukens, J. Measurement of frequency response functions using periodic excitations, corrupted by correlated input/output errors. IEEE Trans. Instrum. Meas. 2001, 50, 1753–1760. [Google Scholar] [CrossRef]
- Shin, K.; Hammond, J. Fundamentals of Signal Processing for Sound and Vibration Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chandra, N.H.; Sekhar, A. Swept sine testing of rotor-bearing system for damping estimation. J. Sound Vib. 2014, 333, 604–620. [Google Scholar] [CrossRef]
- ISO 10846-2: 1997; Acoustics and Vibration–Laboratory Measurement of Vibro-Acoustic Transfer Properties of Resilient Elements–Part 2. ISO: Geneva, Switzerland, 1997.

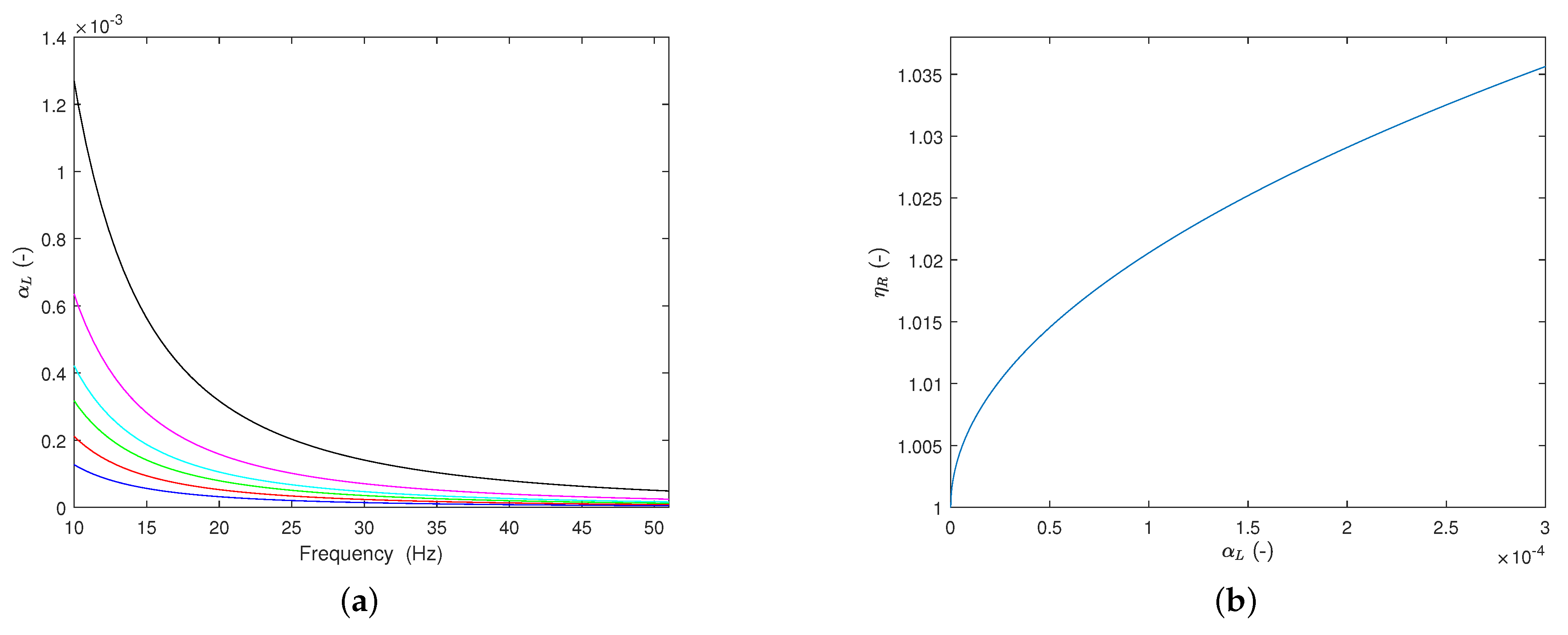

| me [kg m] | ||||||
|---|---|---|---|---|---|---|
| 0.25 × 10 | 0.615 | 0.366 | 0.249 | 0.141 | 0.095 | 0.076 |
| 0.45 × 10 | 0.480 | 0.310 | 0.194 | 0.124 | 0.089 | 0.057 |
| 0.65 × 10 | 0.419 | 0.235 | 0.149 | 0.118 | 0.075 | 0.043 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reina, S.; Ayabaca, C.; Venegas, D.; Zambrano, I.; Venegas, W.; Vila, C.; Ordoñez, V. Experimental Validation in a Controlled Environment of a Methodology for Assessing the Dynamic Behavior of Railway Track Components. Machines 2022, 10, 394. https://doi.org/10.3390/machines10050394
Reina S, Ayabaca C, Venegas D, Zambrano I, Venegas W, Vila C, Ordoñez V. Experimental Validation in a Controlled Environment of a Methodology for Assessing the Dynamic Behavior of Railway Track Components. Machines. 2022; 10(5):394. https://doi.org/10.3390/machines10050394
Chicago/Turabian StyleReina, Salvatore, Cèsar Ayabaca, Diego Venegas, Iván Zambrano, William Venegas, Carlos Vila, and Victor Ordoñez. 2022. "Experimental Validation in a Controlled Environment of a Methodology for Assessing the Dynamic Behavior of Railway Track Components" Machines 10, no. 5: 394. https://doi.org/10.3390/machines10050394
APA StyleReina, S., Ayabaca, C., Venegas, D., Zambrano, I., Venegas, W., Vila, C., & Ordoñez, V. (2022). Experimental Validation in a Controlled Environment of a Methodology for Assessing the Dynamic Behavior of Railway Track Components. Machines, 10(5), 394. https://doi.org/10.3390/machines10050394






