Abstract
Underwater robotic gliders exploit gravity and buoyancy for long-distance cruising with ultra-low energy consumptions, making them ideal for open ocean surveying operations. However, the gliding-based motion generation principle also prevents their maneuverability, limiting their use in the short distances that are usually encountered in harbors or coastal scenarios. In this work, an innovative underwater glider robot is developed, enabling maneuverability through the introduction of an efficiently actuated caudal fin with bidirectional turning capabilities. In addition, modular actuator units, based on soft actuated materials, are integrated to control pitch angle by dynamically shifting the center of mass from the center of buoyancy. As a result, the high energy efficiency feature of the gliders is maintained, while high maneuverability is also achieved. The design concept, modeling of key components, and framework for control are presented, with the prototyped glider tested in a series of bench and field trials for validation of its motion performance.
1. Introduction
Measuring water temperature, salinity, conductivity, the direction of sea currents, and mapping of the seafloor are just a few of the many operations performed today using unmanned underwater vehicles (UUVs) [1,2]. Such submersible robots can be operated remotely or autonomously. They are usually employed to assist with a range of activities, ranging from oceanographic studies in deep-sea explorations to oceanic warfare [3,4]. Recent review studies summarize the advancements in autonomous underwater vehicles (AUVs) [4,5,6]. These studies highlighted the usefulness of such robotic systems and numerous differences in their operating principles. While earlier designs were mostly bulky, with the advances in functional materials, sensors, and batteries, AUVs transitioned to become more efficient and accessible [7,8]. Historically, AUVs with wings that glide by utilizing water buoyancy were first reported with far superior efficiency over surface floating vehicles or propeller-based underwater vehicles [9]. Since then, a number of gliders were designed and tested [10,11,12,13].
Nevertheless, existing actuating methods for the buoyancy and direction adjustment of underwater gliders rely on traditional mechanisms that incorporate geared pumps, hydraulic cylinders, steering engines, and worm-gears with drum-like mechanisms [14,15,16,17,18,19]. To date, only a handful of designs have come forward with innovative methods of actuation [20,21]. Indicatively, these actuation mechanisms rely on adjusting buoyancy and the center of mass by dynamically changing the shape of the glider body or gliding in various directions by shifting their internal structures and components. This resulted in limited maneuverability within confined spaces. Besides, most existing designs use at least three different mechanisms to adjust the center of mass, buoyancy, and direction of gliding, respectively. The resulting more complex mechanism, larger size, and heavier mass are not conducive to more efficient use of energy and cabin space. Therefore, it is a good research direction to find a modular actuator that can meet the various driving requirements of gliders and reduce the number of actuation mechanisms.
In this work, an innovative AUV glider design that couples the control of the buoyancy with the center of mass is introduced, thus reducing actuating mechanisms, compared with previous designs (Figure 1). In previous researches of soft actuators, soft bellow muscle has been successfully used in the field of soft robotic joints actuation [22,23,24,25,26]. In this work, a combination of several bellow muscles with different layouts in the mechanism design has been discussed, which did not become the previous researches’ crucial point. Design of the main driven mechanisms is achieved by utilizing linearly contracting soft muscle modules, powered by a peristaltic pump, and using two instances of those to realize the actuation of the entire glider. Specifically, one instance of the actuator module is used for the simultaneous adjustment of buoyancy and center of the mass of the gilder, and the other is used for the actuation of the caudal fin for turning. By incorporating an arrangement of hydraulically powered, soft bellowed actuators into the AUV glider body, a new control model for buoyancy and direction adjustment has been arranged for underwater gliders. The actuator modules are designed to conserve valuable space within the shell of the glider by acting, at the same time, as the actuation mechanism and compartments where the liquid is stored. Finally, connecting the muscle actuation mechanism with the steering of the fin provides the glider with the ability to maneuver rapidly and effectively in a narrow radius, mimicking the tail movement of fish and robot fish designs alike [27,28,29].
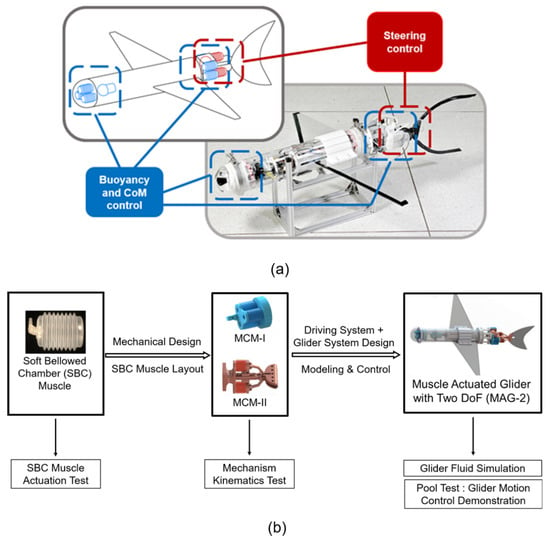
Figure 1.
System design concept and research methodology schematic. (a) The concept of a modularized design glider coupling the buoyancy with the center of mass control and using a caudal fin to steer. (b) Research methodology schematic diagram.
2. Principle of Operation for the MAG-2
The conceptual design of the muscle actuated glider with two DoF (MAG-2) presented in this paper is shown in Figure 2. The glider replaces traditional buoyancy control mechanism of the gliders and tail steering actuation mechanism of fish-like underwater robots with new actuation mechanisms that make use of soft materials. In this way, space is preserved, and the structural complexity of the glider decreases. The main actuating component introduced in this glider is a linear soft bellowed chamber (SBC) muscle, as shown in Figure 2 and Figure 3. Due to the bellowed design and selected material properties, the SBC is able to increase and decrease in length along its main axis when the internal pressure is increased or decreased under the operation of a hydraulic pump. The MAG-2 takes advantage of the SBC’s ability to vary its volume and generate forces. These two motion control mechanisms (MCM) are incorporated into the glider in two distinct modes; one is designed to control buoyancy by varying its volume, and the other generates steering by pushing/pulling the fin of the glider (Figure 2).
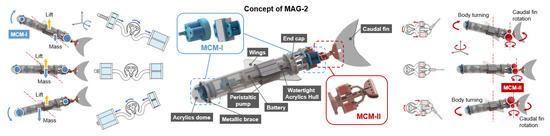
Figure 2.
Concept of MAG-2 glider, with MCM-I and MCM-II controlling the pitch and turning, respectively.
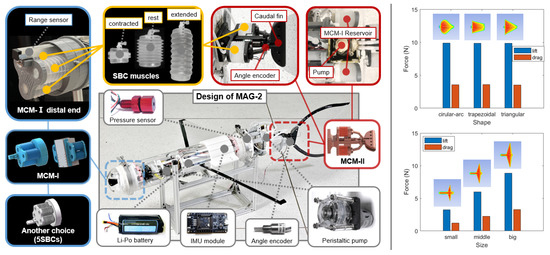
Figure 3.
(Left) Design of the proposed MAG-2, with system components and details of the MCM-I and MCM-II mechanisms. (Right) Simulation results of wings of different shapes, but the same size. Simulation results of wings of different sizes, but with the same shape.
The first motion control mechanism (MCM-I) performs buoyancy control for the glider. It involves one set of three SBCs at the distal end of the glider and two sets of two SBCs near the rear end, both stacked in parallel formation to each other (Figure 2—in blue). A closed-loop hydraulic system is formed with the presence of a peristaltic pump in between the two sets of SBCs. This creates a coupled system for the center of mass (CoM) of the glider with water buoyancy. At glider equilibrium, i.e., the glider is parallel to the seafloor and zero-buoyant, the distal and rear sets of SBCs share identical volume of liquid (water) and, thus, mass/density. To descend, the peristaltic pump pushes liquid from the rear SBCs to the distal ones, growing them in length, thus shifting the CoM from the center of buoyancy. Reversely, to ascend, the same pump pushes the liquid back to the rear SBCs, shifting the CoM to the opposite side of the center of buoyancy. Taking advantage of this seesaw-like motion, energy consumption is minimized, and shell space is preserved, compared to traditional mechanisms that require multiple motors, heavy rigid linkages, and dedicated reservoirs to control buoyancy.
The second motion control mechanism (MCM-II) performs steering of the glider through a hinged, fish-like tail. An antagonistic pair of SBCs is linked to a closed-loop hydraulic system that is powered by a single peristaltic pump (Figure 2—in red). One end of each SBC is mounted, with a rigid linkage to the left and right sides of the rigid tail. To maneuver the glider, the pump is powered, sending liquid that increases the length of one SBC, while drawing liquid away from the other that decreases in length. This antagonism of SBCs drives the rigid linkage, creating a moment that turns the tail. As a result, the glider utilizes this simple fish-tail inspired slider-crank linkage mechanism to achieve tight turns, at short distances, with low energy consumption.
3. System Design of the MAG-2
The proposed MAG-2 body takes the shape of a torpedo, with the addition of a hinged caudal fin perpendicular to the ground at the rear and two wings fixed at the midsection of the robot horizontally, as shown in Figure 1. The glider is 123 cm in length and 12 cm in diameter, with the side wings spanning 100 cm and the tail spanning 35 cm.
3.1. Overall System Layout
Coupled control of pitch and buoyancy. Unlike most conventional gliders, where two mechanisms are employed to regulate the buoyancy and pitch angle separately, the proposed MCM-I mechanism changes both quantities with a single degree of freedom (DOF) deformation. This results in a substantial simplification in mechanisms and control algorithms, since only one regulation quantity is necessary to control descending and ascending.
Design of the watertight compartment. To circumnavigate the space constraints, the active portion of the MCM-I is placed close to the nose of the glider. This placement achieves pitch regulation of high sensitivity and range, while a passive reservoir, exposed to the surrounding water, is placed near the rear of the glider, as shown in Figure 2. On the other hand, the MCM-II is entirely exposed in ambient water, with only electrical connections for power and control being stored inside the shell. To better regulate the glider’s density, all compartments are water-sealed. A clear acrylic tube, of 5 mm in thickness, is used for the MCM-I and front section of the glider body. The front dome is capped with metallic plates and braces, having only electrical wires and two tube lines for liquids (to and from the MCM-I sections) pass through small orifices that are sealed with silicone. One peristaltic pump, driving the MCM-I, is placed within the sealed compartment, along with a battery, electronics, and sensors. The passive sections of the MCM-I and entire MCM-II mechanism are placed in the same unsealed section of the glider within ambient water.
Weight balancing and roll/pitch adjustment. Having pitch angle and buoyancy be controlled by a single DOF mechanism requires the MCM-I’s sufficient control of the glider to be well-balanced, in terms of weight. To achieve this, the three heavier objects, i.e., two pumps and one battery, are distributed evenly across the shell, with the battery pack placed in the center and pumps placed with one to the front and one in the back, so that, statically, the glider’s center of mass is located as close to its center (lengthwise). In addition, to retain the rolling angle of the glider, according to the caudal fin angle, all the heavy components are further placed close to the bottom of the shell. This arrangement allows for lighter objects (electronics, etc.) to be housed on in higher spaces. The volume of the shell is designed to be slightly positively buoyant, and additional ballasts are placed to achieve neutral buoyancy. These additional weights are placed at the bottom of the shell to improve rolling stability. As a result, the glider can be adjusted to be positive- or negative- buoyant on demand by changing swapping ballasts. The balanced weight of the glider is 8.7 kg.
3.2. Modularized Actuation Mechanisms
Modular stacking design using SBC units. In the design of MAG-2, all actuation mechanisms are realized by stacking modular and identical SBC units. This substantially reduces system design iterations and makes specific adjustments convenient by selecting the required number of SBC units within the design framework. In mechanisms design, seven SBCs are applied for the MCM-I, and two SBCs are applied for the MCM-II. In other scenarios, different number of SBCs and networks can be chosen to meet different requirements. For instance, when a larger amount of adjustment is required, five SBCs can be chosen, to connect in parallel, to serve as reservoirs in the front part of MCM-I, rather than the three in this glider (Figure 3).
The soft bellow muscles (i.e., SBCs) used in the glider are lightweight, durable, and offer a large deformation range that achieves sufficient attitude control. The design and performance characteristics of the SBCs are described, in detail, in the authors’ previous work [28]. Such soft muscles produce linear elongational motions, up to 300%; when pressurized by liquid or gas, they can generate pushing/pulling forces several hundreds of times of their own weight and remain passive in radial directions [29]. The SBCs are fabricated using blow-molding techniques with excellent repeatability, making them ideal for the modularized stacking design in this work.
MCM-I for diving control. For the MCM-I diving control mechanism, two clusters of SBCs are formed as reservoirs to each other during operation, but they are placed in different topological patterns to fit the available spaces in the shell. Specifically, the frontal section has three SBCs, stacked in parallel, in the tip dome; the rear section has four SBCs split into two groups of two each, placed behind the pump driving MCM-II. Hydraulic tubes connect the two sections, passing through the peristaltic pump in the middle section (Figure 3).
MCM-II for turning control. The design of the MCM-II is centered around the hinged caudal fin, driven by two antagonistic SBCs that are connected to the driving pump by tubes. To minimize the lateral deformation of the actuator, motion constraints, in the form of rigid caps, are placed at each SBC’s ends, such that they only produce linear elongations when pressurized. The caudal fin is actuated by a rigid linkage mechanism, in order to achieve bilateral turning.
3.3. Valve-Free Efficient Actuation
The MCMs are actuated by peristaltic pumps (G928, Grothen), where bilateral actuation is achieved by a single pump, eliminating the requirement of hydraulic valves. Each peristaltic pump achieves forward and backward pumping, as well as locking, offering adequate control options in this application. During operation, the opposing groups of SBCs in the MCM act as reservoirs for the liquid and, through tubes, form an internal circulation system. This closed-form system is important to the operation of the glider, as it ensures the purity of fluids running inside the SBCs. More importantly, removing valves from the hydraulic loop reduces liquid resistance, hence improving the flow rate and increasing the overall speed of operation. Considering the limited space within the shell and requirement for high operational efficiency makes peristaltic pumps an ideal replacement for traditional membrane pump-valve systems.
The electronics used in the actuation system include a micro control unit (MCU) (STM32F103ZET6, ST) as the main microcontroller of the glider, inertial measurement unit (IMU) (HI229, Hipnuc) (to identify pitch, raw, and yaw angles), displacement transducers (KSF-70, Miran Tech) to measure the SBC displacement, encoder (GTDAS31136, WXXY) to measure the fin angle, and hydraulic pressure sensor (MS5837, Rovmaker) to provide depth information. A two-channel electronic speed controller (Dual Brushed ESC, Private Factory) is used to control the two peristaltic pumps using pulse width modulation (PWM) signals transmitted from MCU. The entire system is powered by a 4S lithium-polymer (Li–Po) battery (16.8 V, 266 Wh), regulated with a step-down module (EV60-K24012, Eveps).
3.4. Wings and Tails
The wings and tails (caudal fin) are important features of the glider design that help the interaction with ambient water in motion generation and attitude control.
In this work, a triangular shape wing design is adopted, which is commonly used by conventional gliders. The pattern and size of the wing are investigated through finite methods modelling (FEM) simulations (Ansys Fluent), as well as experimental validations. In all the performed simulations, both the attack angle and velocity are set up as constants, respectively. As shown in the upper right part of Figure 3, wings with different shapes can obtain almost the same lift and drag forces if their effective area is kept constant. However, as shown in the lower right part of Figure 3, larger wings produce better lift to drag ratios, compared to smaller ones. In this work, the wings are manufactured by using acrylic sheets in a larger size (experimental validation is provided in Section 5) to theoretically achieve higher lift-drag ratio and glide longer distances.
For the caudal fin design, a crescent shape is adopted from previous works in biomimetic fish with caudal fin propulsion [30]. Such a shape exhibits effective turning performances for turns over 180 degrees. It is noted that other tail designs and sizes could contribute to the enhancement of glider steering; however, they require investigation that goes beyond the scope of this article.
4. Modeling and Control
Mathematical models are derived to capture the working principle of the proposed actuator modules and, thus, control the MAG-2′s motion underwater. The models depict each of the three pillars of the glider design: a single SBC, the MCM-I nose actuation, and the MCM-II tail actuation. Based on those models, a cascaded controller, with an inner and outer layer that can be used to control the motion of the glider, was developed.
4.1. Model of Single SBC
The SBC is the smallest unit component of the actuators. The relationship between the length of the SBC and volume of the liquid inside is demonstrated by (1). As shown in Figure 4a, the inner radius (Rin) of the SBC and outer radius Rout of the SBC at the initial state are constants, and so is the half of the height (hi) of the bellow ring at the initial state. The change of that height (Δh) is a variable, and so is the radius (R’out) of the SBC at the end state. According to their geometrical relationship, the volume of the liquid a single bellow can obtain is Vbellow:
After leaving the initial state, the out radius of the bellow transformed to be R’out:
Considering that the SBC used consists of N bellow rings, the volume of water inside was changed to be V’SBC:
This equation will be validated by comparing it with the experimental measurements.
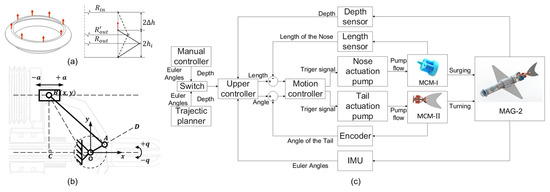

Figure 4.
Modeling and control of the MAG-2. (a) Model of a single SBC actuator, (b) model of the MCM-II mechanism, (c) control diagram of the system.
4.2. Model of the MCM-I for Buoyancy Adjustment
The nose part of the MCM-I is used to adjust the buoyancy and CoM. It is the opening and closing of the peristaltic pump that causes the change in the volume of water and mass of the nose part. Assuming the rate of pumping flow is constant (, the relationship between the pumping time ( and change in volume of water (ΔV) can be obtained:
According to the basic physical theory, the change in the mass (Δm) could be obtained:
4.3. Model of the MCM-II for Tail Turning
The principle of the MCM-II mechanism can be simplified as a slider-crank linkage mechanism. As shown in Figure 4b, points and are on the follower part, points and represent are the two endpoints of the driving part, point is the projection of point B on the horizontal line, point is on the extension line of ray , and points and represent point and when the muscle is not deformed. Define , which is the transmission angle of the mechanism, when acute or right, and is the supplementary angle of transmission angle when obtuse. Resulting from the design, are constant values. According to geometric relation, the relation between muscle deformation () and tail deflection angle () can be obtained as follows:
where
Equations are experimentally validated in Section 5.
4.4. Cascaded Motion Controller for the MAG-2
A motion controller was developed based on the models derived for the MCMs (Figure 4c). The controller takes a cascaded approach, with an inner layer regulating the liquid pressures in each MCM and outer layer regulating the main glider attitude and diving. Both layers are feedback control loops using on-board sensory feedback information.
4.4.1. Inner Layer Controller: Single Pump-SBC Actuation
Each MCM is controlled by a separate pressure control loop, as shown in Figure 4. The slave controller, overseeing both loops, generates the pump control signals and regulates the liquid pressure to each MCM.
Based on the physical model of SBCs, the relationship between the length of the SBC and liquid intake is quasi-linear. Therefore, for a single SBC, applying a positive trigger signal to the peristaltic pump can increase the liquid intake, elongating the SBC accordingly. Conversely, a negative trigger signal contracts the SBC. For simple, but intuitive, control, a binary control law in the slave controller is implemented. This was proven highly effective (as is experimentally observed in Section 5), mainly due to the very low operating speeds of each component, allowing sufficient time for the controller to settle in each command cycle. To achieve closed control, the nose structure is equipped with three SBCs and a distance sensor to measure their liner deformations. The tail structure, composed of the two antagonistic SBCs, incorporates a rotary encoder, which is installed on the tail shaft. This provides the angle of rotation of the tail used in the control feedback loop.
4.4.2. Outer Layer Controller: Diving and Turning Control
The outer loop controller regulates the diving and turning of the glider, based on the sensory feedback provided from the whole glider body gesture. As the forward motion of the glider is produced by diving and lifting, an inertia measurement unit (IMU) is mounted inside the shell to measure the actual body orientation. This IMU provides gesture feedback on both the pitch and turning angle, while the MCM-I executes the glider’s rotation motion. In parallel, tracking of the diving and turning depth in autonomous gliding is performed with a depth sensor. This sensor is exposed to the liquid, so as to achieve real-time depth measurements and feedback. The master controller utilizes the depth and orientation information to determine the desired elongation of the MCM-I and desired angle of the MCM-II tail and cascades it to the inner loop slave controllers for execution.
Both autonomous and manual control operations are enabled for the glider. Due to liquid attenuation, no radio frequency can reach the glider when operating in a tether-free mode. Therefore, an autonomous algorithm was developed for the glider to execute a fixed number of descending–ascending cycles by reaching certain depths and/or setting the caudal fin to certain angles for turning. On the contrary, in manual operation the glider works in tethered mode. In this mode, an operator provides the steering commands manually to both the outer and inner controllers. As the scope of this work is primarily focused on the proof-of-concept of the glider design, the majority of the experimental results are obtained using the manual mode. A demonstration of autonomous gliding and turning is provided in the Supplementary Video S1 and will be further explored in future work.
5. Experimental Validation
5.1. Experimental Performance of the SBC Actuators
The first group of experiments was focused on testing the performance of a single SBC actuator and validating the derived mathematical models. Experiments were conducted to examine the relationship between the length of the SBC and volume of water within the SBC. This was achieved by monitoring the pumping time and water volume in the SBCs, respectively. A dedicated experimental platform was developed for these experiments (Figure 5a), where the SBC was fixed on one end, and a laser range sensor (Panasonic HG-C1100) was used to measure its linear displacement. A peristaltic pump (G928, Grothen) was employed to pump water in via a syringe. The liquid displacement and volume were monitored at the syringe. The experiment was repeated for five trials, with the SBC actuator deforming in free space, without external loads being applied to it. The results of this experiment are shown in Figure 5b. In the SBC length-to-water volume graph, the data and fitting results are in good agreement, demonstrating an RMS of 4.4 mL, R = 0.997. This indicates that nonlinear effects are negligible, and the results are consistent with (3). In the pumping time to the SBC length graph (Figure 5c), the data also present a good relationship, with R = 0.99. This indicates that controlling the pumping time could yield a linear actuator deformation output. From both experiments, the efficacy of integrating the range sensor to monitor the SBC length and volume is also demonstrated.
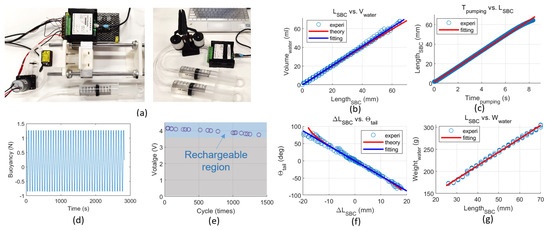
Figure 5.
Bench test results, with the test apparatus, energy consumption test, and SBC actuator test results, as well as the tail MCM-II test, shown. (a) Bench test apparatuses. The left one is used to explore the relationship between the length of the SBS (LSBC) and volume of the contained water (Vwater), pumping time (Tpumping), and weight of the contained water (Wwater). The results are shown in subfigures (b), (c), and (g), respectively. The right one was used to explore the relationship between the change of the length of SBC (∆L_SBC) and rotation angle of the tail (θtail), and the result is shown in subfigure (f). During the endurance test, the buoyancy states of the gilder were recorded timely and shown as the subfigure (d). The voltage of the Li–Po battery is also recorded and shown as the subfigure (e). Besides, the different colors in (e) represents the different times of the tests.
5.2. Experimental Performance of the MCM-I Nose Mechanism
Experiments were also conducted to test the MCM-I mechanism on: (a) its relationship with the SBC displacement and (b) the mass change of the nose that adjusts the buoyancy levels. Similar to the previous experiments, displacement of the SBC was measured using the range sensor, while the weight change of the MCM-I nose section was measured by an electric scale. The experiment was repeated five times. In each trial, the water was pumped into the nose of the SBCs, and the length displacement, as well as the mass changes, were recorded. The results are shown in Figure 5g, where the experimental data presents a linear relation, with R = 0.996, validating the theoretical model of Section 4.
5.3. Experimental Performance of the MCM-II Caudal Fin
To obtain the relationship between the volume of water and rotation angle of the caudal fin, experiments were conducted on the components of the glider prototype. To prepare the experiment, the SBC muscles were filled with equal amount of liquid, but were set at opposite directions. Two syringes were used to measure the volume of water supplied to each SBC (Figure 5a). After priming the SBCs, the syringes were simultaneously actuated, and the tail angle was measured using a goniometer. The test was repeated five times, altering the angle of the tail from zero (neutral position) degrees to a set of predetermined values by pushing and pulling the syringes at opposite directions with equal water displacements. Rotating angles, as well as water displacements, were recorded and presented in Figure 5f. The data were fitted to be a line with an average RMS error of 4.04° and R = 0.996, while the line function was . The experimental results are in agreement with the analytically-derived model (8), indicating the quasi-linear relationship between the water volume and tail angle.
5.4. Energy Efficiency Experiment
To estimate the number of dive-lift cycles that the proposed glider can reach with a fully-charged battery, an energy consumption experiment was conducted, where the MCM-I section was actuated at different time intervals in fully-powered cycles, using a fully-charged battery pack. The voltage of the Li–Po battery was measured and recorded before and after the experiment to calculate the power storage between battery voltage and capacity. Figure 5e shows the recorded data, where, after about 1250 actuating cycles, the voltage was reduced from 16.8 to 15.2 V. For the MCM-I, the more the amount of adjustment, the longer the pump working time, which means more energy consumption. With the conservative operation condition set at 80% of the maximal amount of adjustment, determined from actual field tests in a swimming pool, the estimated number of cycles that can be performed on a full charge is over 1000. Considering the battery power is 266 Wh, the average power consumption is estimated to be 0.177 Wh/cycle. As the pump consumes the vast majority of energy in the system, this test provides a ballpark estimation of the glider’s capability for efficient underwater gliding. It is noted that traveled distance is not an adequate method to examine the efficiency of a glider. This is because the glider only consumes energy to initiate the descent or ascent. After reaching the powered tipping point, the glider basically uses buoyancy to travel unpowered. Thus, the depth and gliding angle are directly related and, within a single energy cycle, an infinite number of traveled distances can be measured.
5.5. Field Tests of the MAG-2
To demonstrate the performance of the MAG-2, in realistic settings, the prototype is placed in an open pool to perform a series of field tests. The pool used in these experiments measured 1.6 m in depth and 20 m in length. Four groups of experiments are conducted to test the relationship between the gliding performance and the: (1) wing size, (2) nose filling condition of MCM-I, (3) turning at different tail angles, and (4) autonomous gliding and turning at fixed depth ranges and caudal fin angles.
Data measurements were taken in the field, both from external and from on-board the glider sensors, for all experiments. An aerial drone provided external measurements, by means of aerial photographs and video recordings (Figure 6d), while, inside the pool, footage was recorded with an underwater camera. Results analysis was performed on the data obtained from an on-board IMU sensor, angle encoder, and depth sensor, recording the measurements synchronously. Using those sensing modalities, the glider motion trajectory was traced. In particular, the recorded video footage was analyzed using an opensource software called Tracker. The pool tiles (0.25 by 0.125 m each) and lines on the pool floor were used to calibrate the cameras, so as to provide accurate reference distances (Figure 6a) and orientation angles.
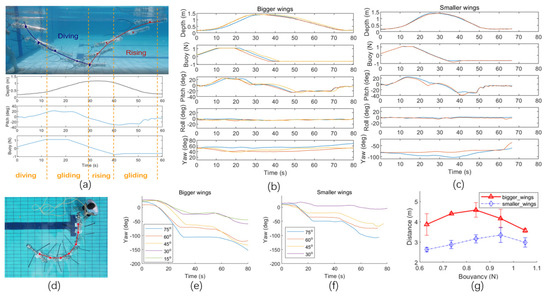
Figure 6.
Field test results. The MAG-2 was tested in the pool with turning, gliding, different wing size, and different MCM-I control conditions. (a) The tracking result, with the tracker and corresponding recorded states data. The state data were recorded during tests with different size wings, and the result is shown in subfigures (b,c). Besides, different colors here represent different times of tests. (d) The tracking result from the aerial view. During the tail angle turning tests, with different wings, the yaw angle of the gilder (in the world coordinate) was recorded timely, and results are shown in subfigures (e,f). The distance that the glider can reach in one cycle was recorded, with different control strategies and wings, and the result is shown in subfigure (g).
Both the manual control (tethered) and autonomous gliding (untethered) modes were tested in the pool. In the manual control mode, the data, collected by the on-board sensors, were transmitted with the aid of a tether to a workstation located outside the pool. In the autonomous control mode, the data were stored on a solid drive (SD) memory card, while the glider was cruising underwater. The obtained experimental results are shown in Figure 6.
Wing size test: Two pair of wings, smaller and bigger, were mounted to the rear section of the hull, for comparison of the gliding performances. The data recorded is shown in Figure 6b,c,g, with the average traveled distance for a full descending–ascending cycle of the glider being 37% longer for the bigger size than the smaller wing size.
Nose filling condition of MCM-I: Following the previous experimental results, a pair of rear-mounting bigger size wings were used to compare different nose filling strategies for the forward gliding distance. Five different testing conditions were explored in filling, with liquid, the MCM-I nose at 100%, 90%, 80%, 70%, and 60% of its maximum volume capacity of 210 mL, which corresponds to the 1.05 N, 0.45 N, 0.84 N, 0.735 N, and 0.63N buoyancy forces applied on the glider. Each condition was repeated for three full gliding cycles. The results are shown in Figure 6g, where a maximum mean cycle distance of 4.58 m was obtained at 0.84 N nose filling. It was discovered that, with the pump operating at a constant speed, larger buoyancy force can be applied, but the filling time is prolonged, and the nose becomes extremely heavy, thus affecting the pitch angle of the glider.
Tail angle turning test: Turning experiments were conducted at different tail angles, in order to test the influence of the tail angle on the glider steering performance. Note that the caudal fin is not used to propel the glider, nor for active turning (although it has the capability to do so). Instead, the glider descended with the caudal fin forming certain angles. This resulted in steering while descending and ascending. A total of five different angles (15, 30, 45, 60, and 75 degrees) were examined, and the obtained results are shown in Figure 6e,f, where the maximum steering angle (yaw angle) achieved 190 degrees of glider rotation at 75 degrees tail angle, indicating the efficacy of caudal fin steering.
Autonomous gliding and turning: In the final experiment, the glider was set to autonomous mode and operated tether-free. A series of continuous gliding cycles were conducted at a maximum depth of 1.5 m, with the glider covering, on average, a distance of 6 m per diving cycle. Autonomous steering experiments, also conducted at the same depth and footage, were recorded with an underwater camera. This experimental footage is included in the Supplementary Video S1.
6. Conclusions and Future Work
In this work, an innovative design for an underwater glider robot with modular actuators was developed, offering high maneuverability, utilizing a biomimetic caudal fin for turning. The efficacy of the proposed coupled control of pitch and buoyancy with one actuator was demonstrated. With this method, the control of every motion direction was implemented via stacked modules of identical soft muscle units. The design concept enabled the entire underwater robot to be actuated, by means of two peristaltic pumps for bidirectional and proportional control of the 3-DOF body motions, resulting in a highly maneuverable glider design.
The design concept and modeling of key components, as well as the control framework and prototyping details, have been presented. A prototype MAG-2 was fabricated and tested in a series of bench and field tests. The 4.8 kg MAG-2 prototype, driven by two peristaltic pumps and nine SBC muscles, could perform both manually controlled and autonomous gliding scenarios, achieving an impressively small turning radius of 0.7 m; additionally, it has a low energy consumption, with an estimated over 1000 dives per charge with its on-board battery pack, proving the design concept to be both maneuverable and efficient, thus offering an alternative to underwater glider designs and controls.
Future directions include the optimization of the wing design for improved efficiency and hydrodynamics, design iterations of the MCM sections for improved performance, and adding navigation to the glider for long-distance field tests. Besides, SBC muscles actuators are of great research value. In the future, research will be implemented to stack the muscle units in different ways to meet more driving requirements, such as rotation and screw motions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/machines10050381/s1, Video S1: Supplementary video.
Author Contributions
Conceptualization, B.W., Y.C., S.L., J.Y. and Z.W.; Data curation, B.W., Y.W., Y.L. and S.P.; Funding acquisition, Y.W. and Z.W.; Investigation, B.W.; Methodology, B.W., Y.W. and X.L.; Project administration, B.W. and Y.C.; Resources, Z.W.; Software, B.W.; Supervision, S.L., J.Y., P.P. and Z.W.; Validation, B.W., Y.C., Y.W., Y.L., S.P. and S.W.; Writing—original draft, B.W., Y.C., Y.W. and P.P.; Writing—review & editing, B.W., Y.W., P.P. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was jointly supported by Shenzhen Science, Tech. & Innovation Commission Grant ZDSYS20200811143601004, NSFC Grant 51975268, 52015021, Guangdong Natural Science Fund—2021A1515110658, Guangdong Provincial Key Lab of Human-Augmentation and Rehabilitation Robotics in Universities, Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), and SUSTECH-Taizhou Innovation Fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, X.; Shang, J.; Luo, Z.; Tang, L.; Zhang, X.; Li, J. Reviews of power systems and environmental energy conversion for unmanned underwater vehicles. Renew. Sustain. Energy Rev. 2012, 16, 1958–1970. [Google Scholar] [CrossRef]
- Button, R.W.; Kamp, J.; Curtin, T.B.; Dryden, J. A Survey of Missions for Unmanned Undersea Vehicles; National Defense Research Institute: Santa Monica, CA, USA, 2009; Volume 223. [Google Scholar]
- Gafurov, S.A.; Klochkov, E.V. Autonomous unmanned underwater vehicles development tendencies. Procedia Eng. 2015, 106, 141–148. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, A.; Dwivedy, S.K.; Robi, P.S. Advancements in the field of autonomous underwater vehicle. Ocean Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Petillot, Y.R.; Antonelli, G.; Casalino, G.; Ferreira, F. Underwater robots: From remotely operated vehicles to intervention-autonomous underwater vehicles. IEEE Robot. Autom. Mag. 2019, 26, 94–101. [Google Scholar] [CrossRef]
- Wadoo, S.; Kachroo, P. Autonomous Underwater Vehicles: Modeling, Control Design and Simulation; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Simetti, E.; Casalino, G.; Torelli, S.; Sperinde, A.; Turetta, A. Floating underwater manipulation: Developed control methodology and experimental validation within the TRIDENT project. J. Field Robot. 2014, 31, 364–385. [Google Scholar] [CrossRef]
- PowerVision, Inc. PowerRay. Available online: https://www.powervision.me/en/product/powerray (accessed on 3 September 2021).
- Rudnick, D.L. Ocean Research Enabled by Underwater Gliders. Annu. Rev. Mar. Sci. 2016, 8, 519–541. [Google Scholar] [CrossRef]
- Sherman, J.; Davis, R.E.; Owens, W.B.; Valdes, J. The autonomous underwater glider “Spray”. IEEE J. Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Eriksen, C.C.; Osse, T.J.; Light, R.D.; Wen, T.; Lehman, T.W.; Sabin, P.L.; Ballard, J.W.; Chiodi, A.M. Seaglider: A long-range autonomous underwater vehicle for oceanographic research. IEEE J. Ocean. Eng. 2001, 26, 424–436. [Google Scholar] [CrossRef] [Green Version]
- Webb, D.C.; Simonetti, P.J.; Jones, C.P. SLOCUM: An underwater glider propelled by environmental energy. IEEE J. Ocean. Eng. 2001, 26, 447–452. [Google Scholar] [CrossRef]
- Xue, D.Y.; Wu, Z.L.; Wang, Y.H.; Wang, S.X. Coordinate Control, Motion Optimization and Sea Experiment of a Fleet of Petrel-II Gliders. Chin. J. Mech. Eng. 2018, 31, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Thon, J.; Thon, C.; Tan, X. Miniature underwater glider: Design, modeling, and experimental results. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4904–4910. [Google Scholar]
- Petritoli, E.; Leccese, F.; Cagnetti, M. A high accuracy buoyancy system control for an underwater glider. In Proceedings of the IEEE International Workshop on Metrology for the Sea: Learning to Measure Sea Health Parameters (MetroSea), Bari, Italy, 8–10 October 2018; pp. 257–261. [Google Scholar]
- Ribeiro, G.A.; Pinar, A.; Wilkening, E.; Ziaeefard, S.; Mahmoudian, N. A multi-level motion controller for low-cost underwater gliders. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1131–1136. [Google Scholar]
- Mitchell, B.; Wilkening, E.; Mahmoudian, N. Developing an underwater glider for educational purposes. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3423–3428. [Google Scholar]
- Yu, J.C.; Zhang, A.Q.; Jin, W.M.; Chen, Q.; Tian, Y.; Liu, C.J. Development and experiments of the sea-wing underwater glider. China Ocean Eng. 2011, 25, 721–736. [Google Scholar] [CrossRef] [Green Version]
- Williams, A. Design of a Low-Cost Open-Source Underwater Glider. engrXiv 2018. [Google Scholar] [CrossRef]
- Ranganathan, T.; Aravazhi, S.; Mishra, S.; Thondiyath, A. Design and analysis of a novel underwater glider-robuoy. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2089–2094. [Google Scholar]
- Yu, P.; Wang, T.; Zhou, H.; Shen, C. Dynamic modeling and three-dimensional motion simulation of a disk type underwater glider. Int. J. Nav. Arch. Ocean Eng. 2018, 10, 318–328. [Google Scholar] [CrossRef]
- Krieg, M.; Sledge, I.; Mohseni, K. Design considerations for an underwater soft-robot inspired from marine invertebrates. Bioinspiration Biomim. 2015, 10, 065004. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Yang, X.; Zhang, X.; Hu, H. Water hydraulic soft actuators for underwater autonomous robotic systems. Appl. Ocean Res. 2021, 109, 102551. [Google Scholar] [CrossRef]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft robotics: Review of fluid-driven intrinsically soft devices; manufacturing, sensing, control, and applications in human-robot interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z. Mechanoreception for soft robots via intuitive body cues. Soft Robot. 2020, 7, 198–217. [Google Scholar] [CrossRef]
- Tan, Q.; Chen, Y.; Liu, J.; Zou, K.; Yi, J.; Liu, S.; Wang, Z. Underwater Crawling Robot with Hydraulic Soft Actuators. Front. Robot. AI 2021, 8, 688697. [Google Scholar] [CrossRef]
- Marchese, A.D.; Onal, C.D.; Rus, D. Autonomous soft robotic fish capable of escape maneuvers using fluidic elastomer actuators. Soft Robot. 2014, 1, 75–87. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Hu, H. Biological inspiration: From carangiform fish to multi-joint robotic fish. J. Bionic Eng. 2010, 7, 35–48. [Google Scholar] [CrossRef]
- Yu, J.; Tan, M.; Wang, S.; Chen, E. Development of a biomimetic robotic fish and its control algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 1798–1810. [Google Scholar] [CrossRef]
- Gupta, S.; Ng, T.; Shen, Z.; Wang, Z. Development of High Performance Mechanical Robotic Fish. In Proceedings of the Advanced Maritime Engineering Conference (AMEC) & Pan Asian Association of Maritime Engineering Societies (PAAMES) Meeting, Busan, Korea, 9–12 October 2018; The Society of Naval Architects of Korea (SNAK): Daejeon, Korea, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).