Dynamic Scaling of a Wing Structure Model Using Topology Optimization
Abstract
:1. Introduction
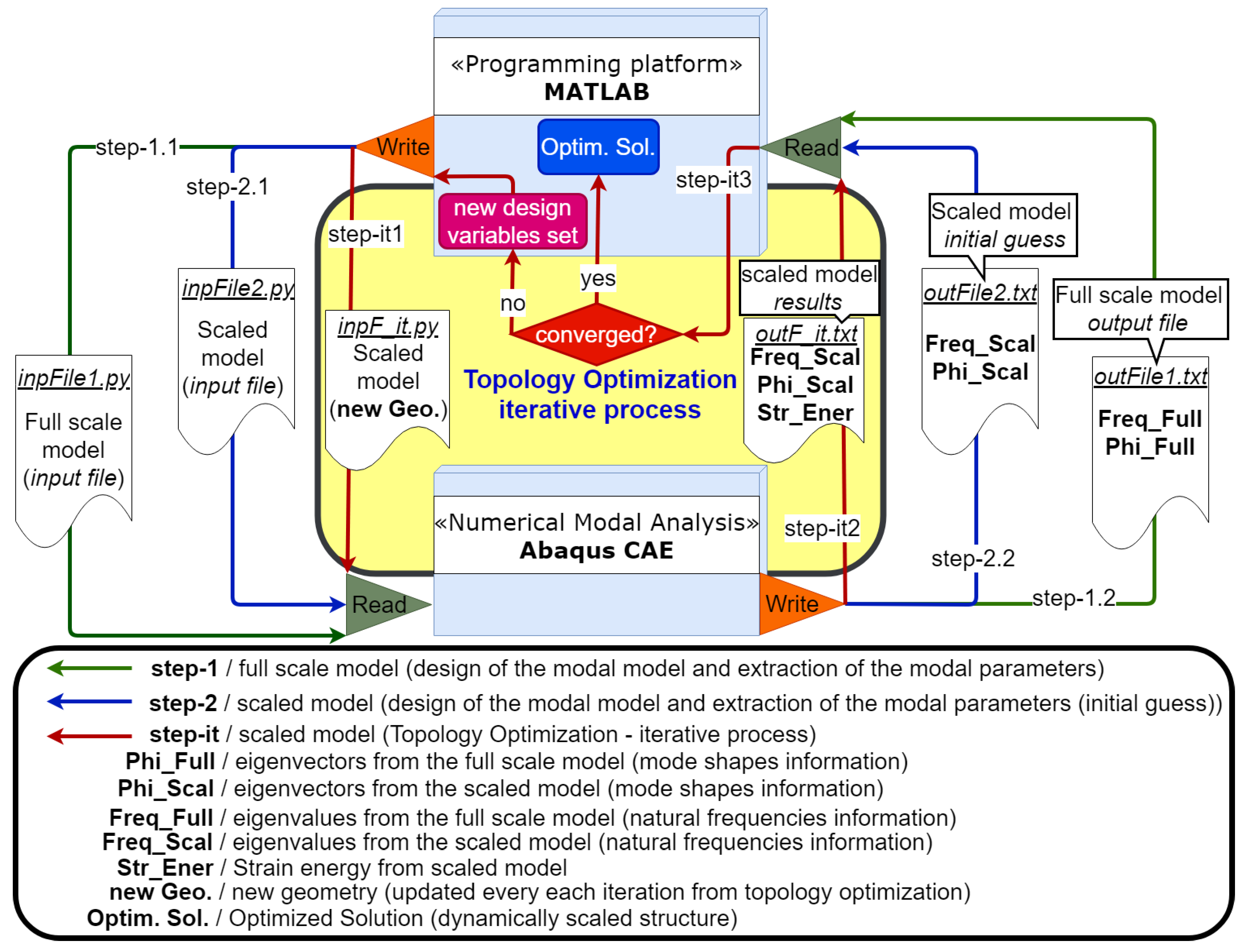
2. Dynamic Scaling Methodology
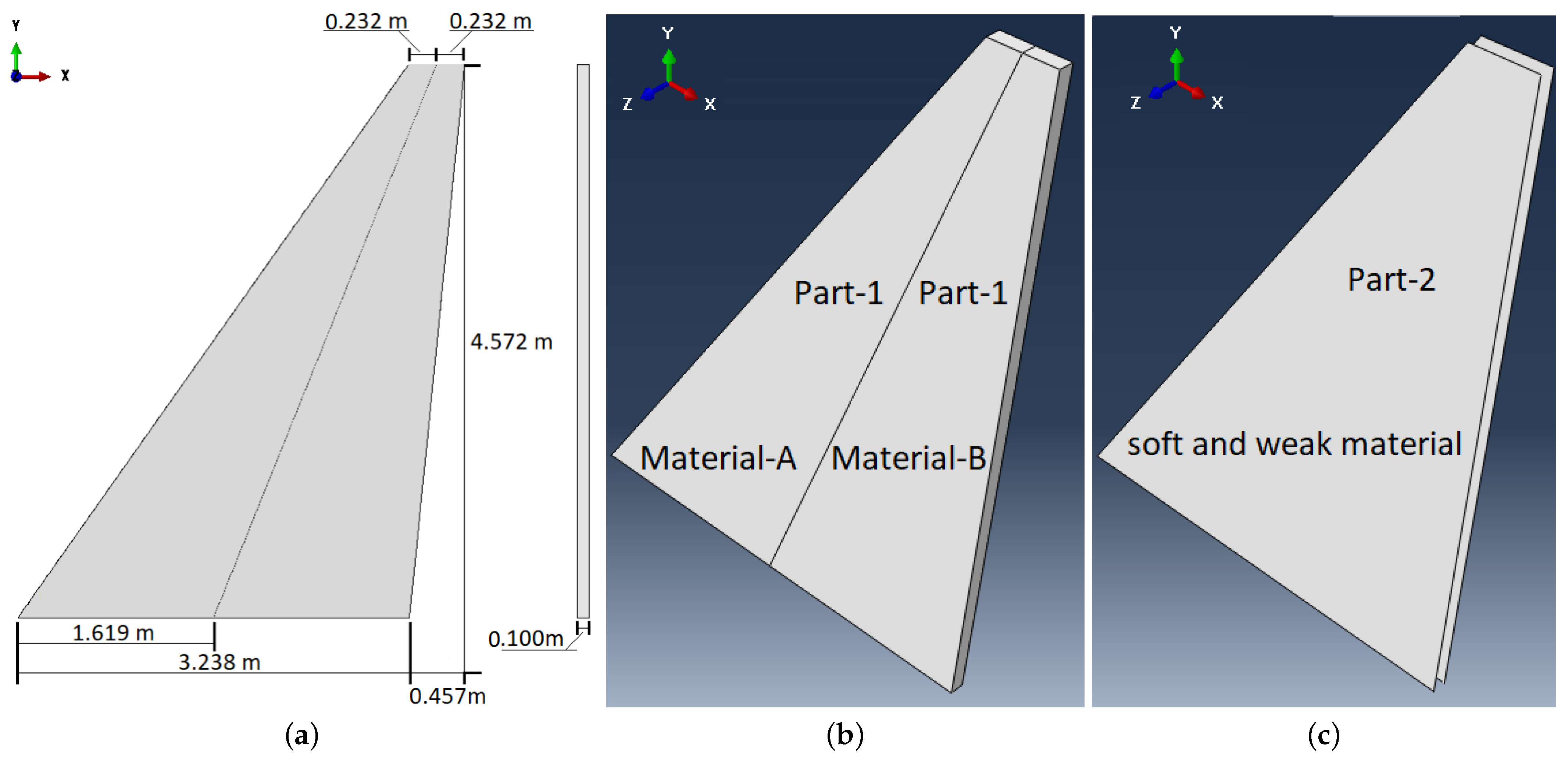
2.1. Full Scale Model
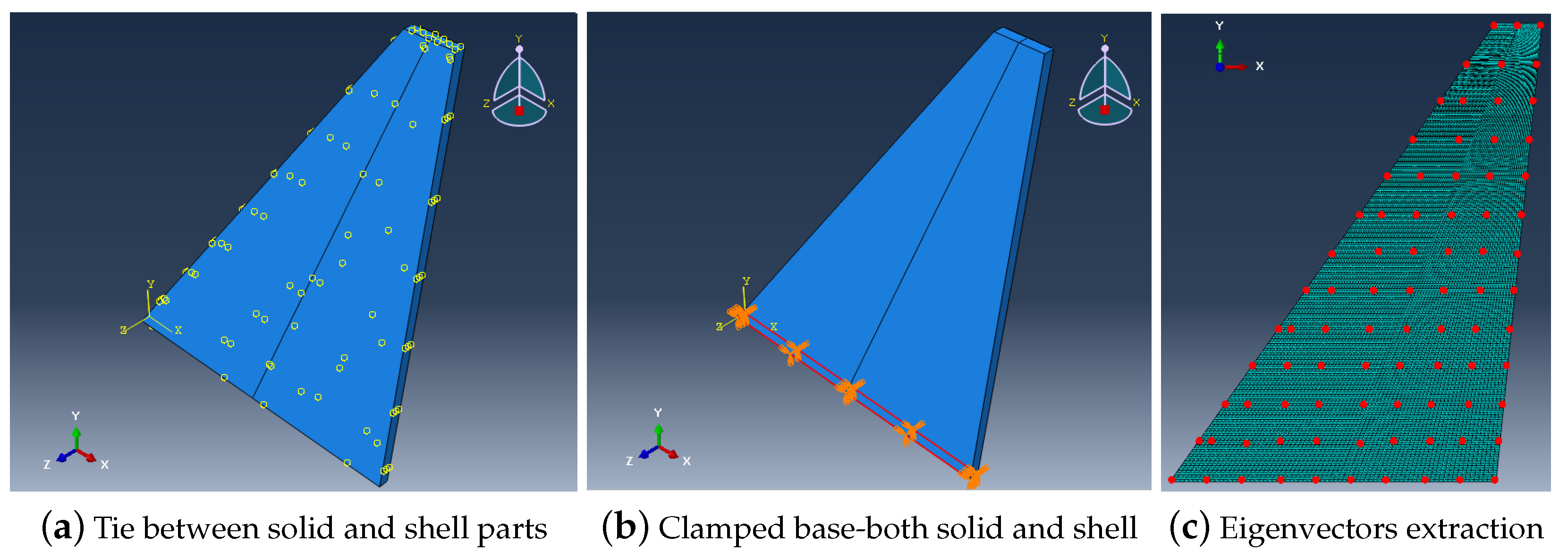
2.2. Scaled Model
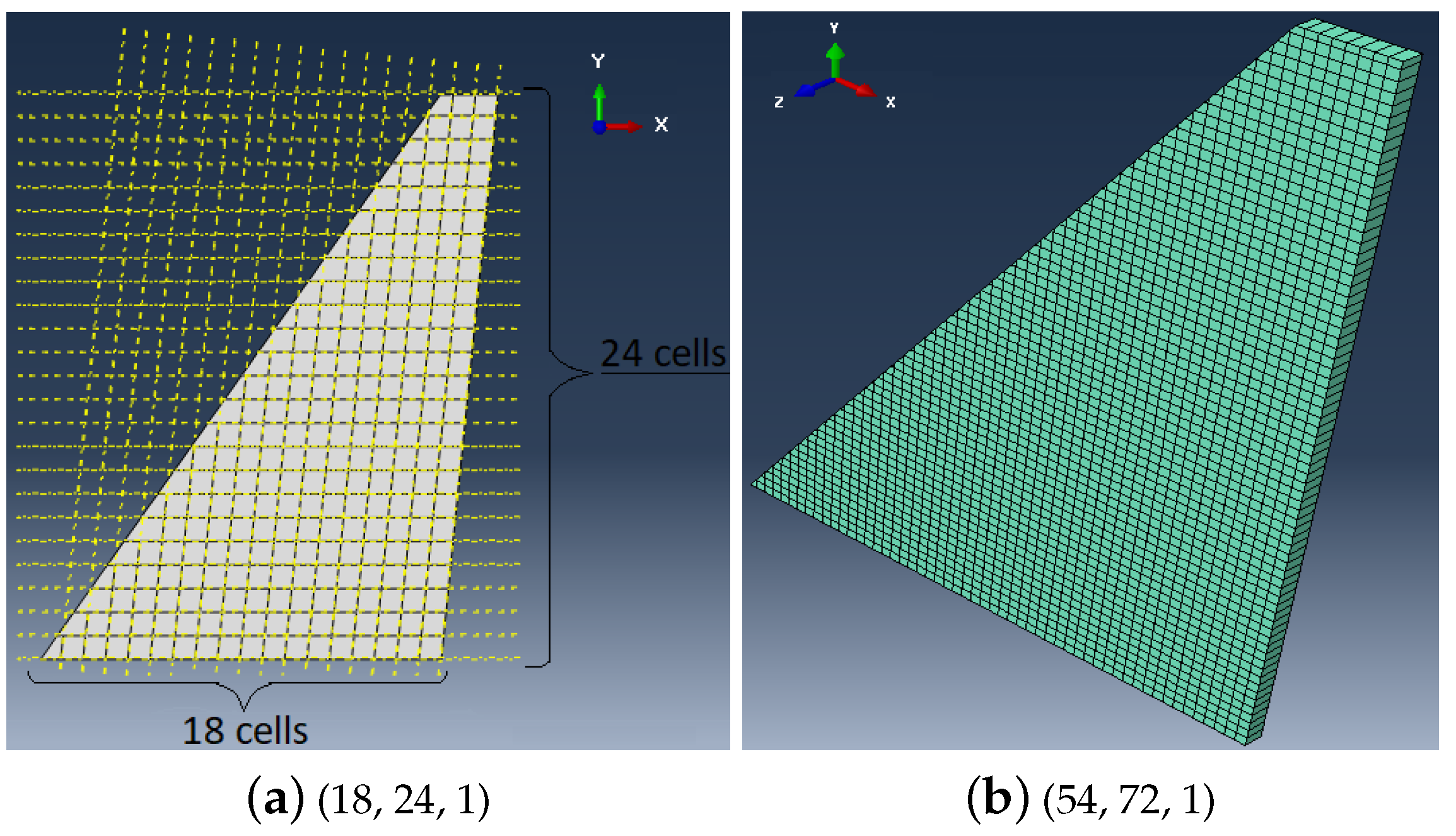
2.3. Topology Optimization
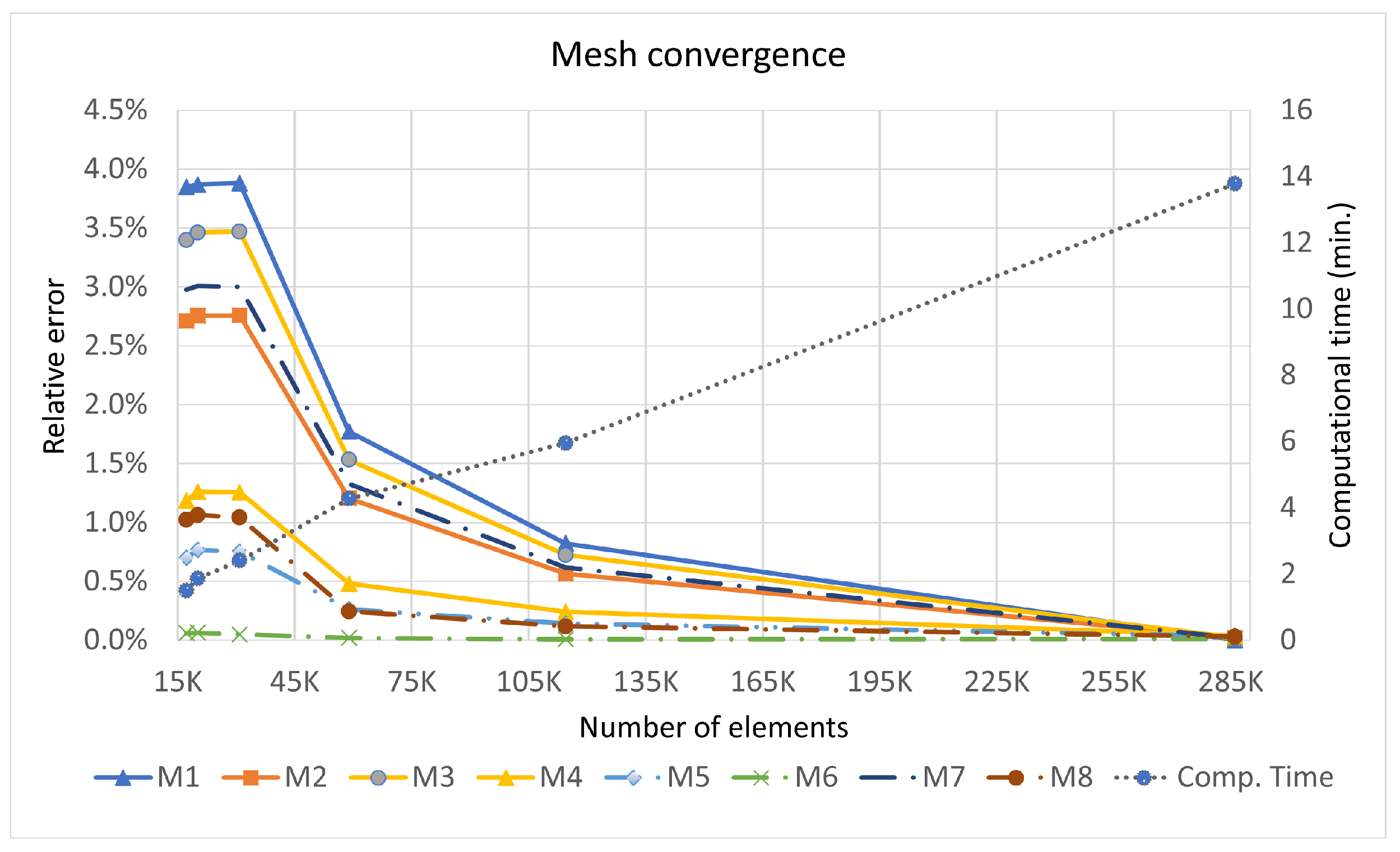
3. Results
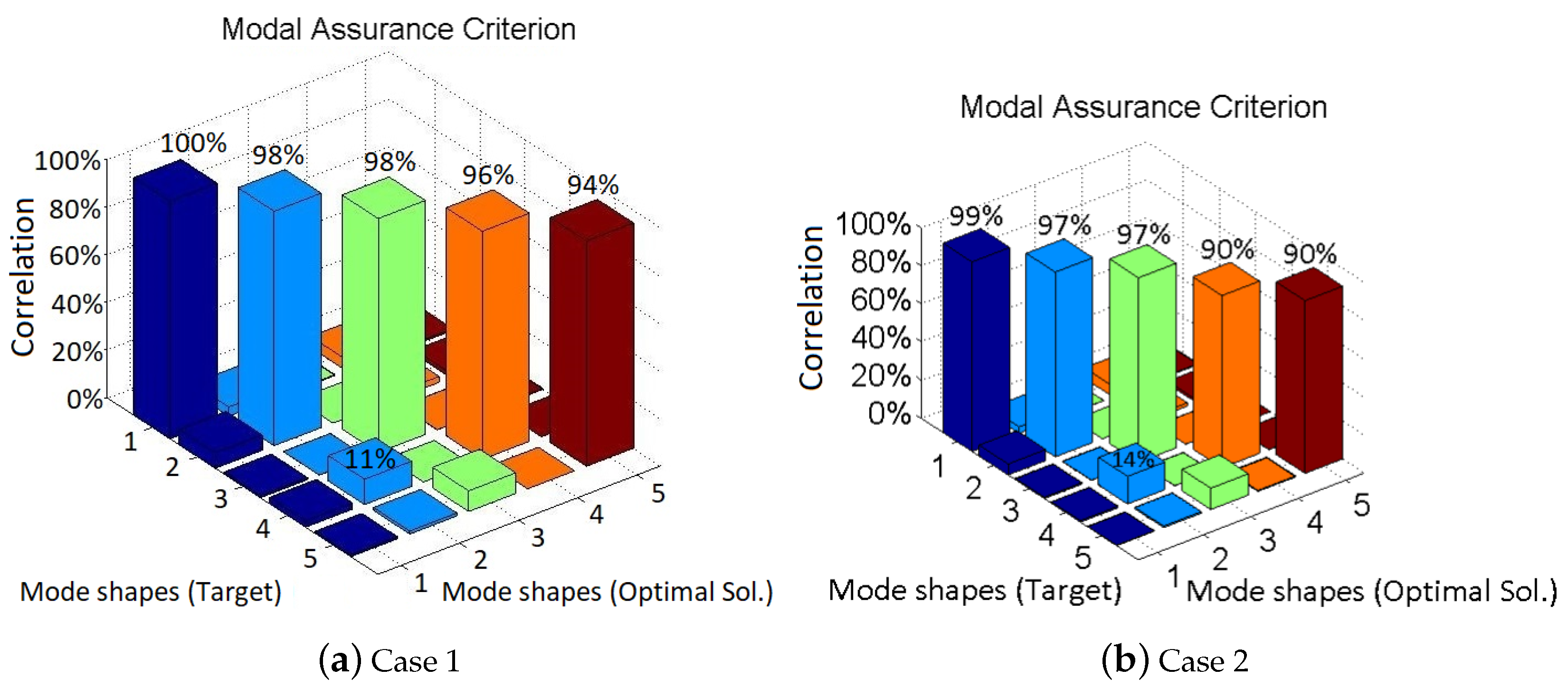
3.1. Material Influence Test Case
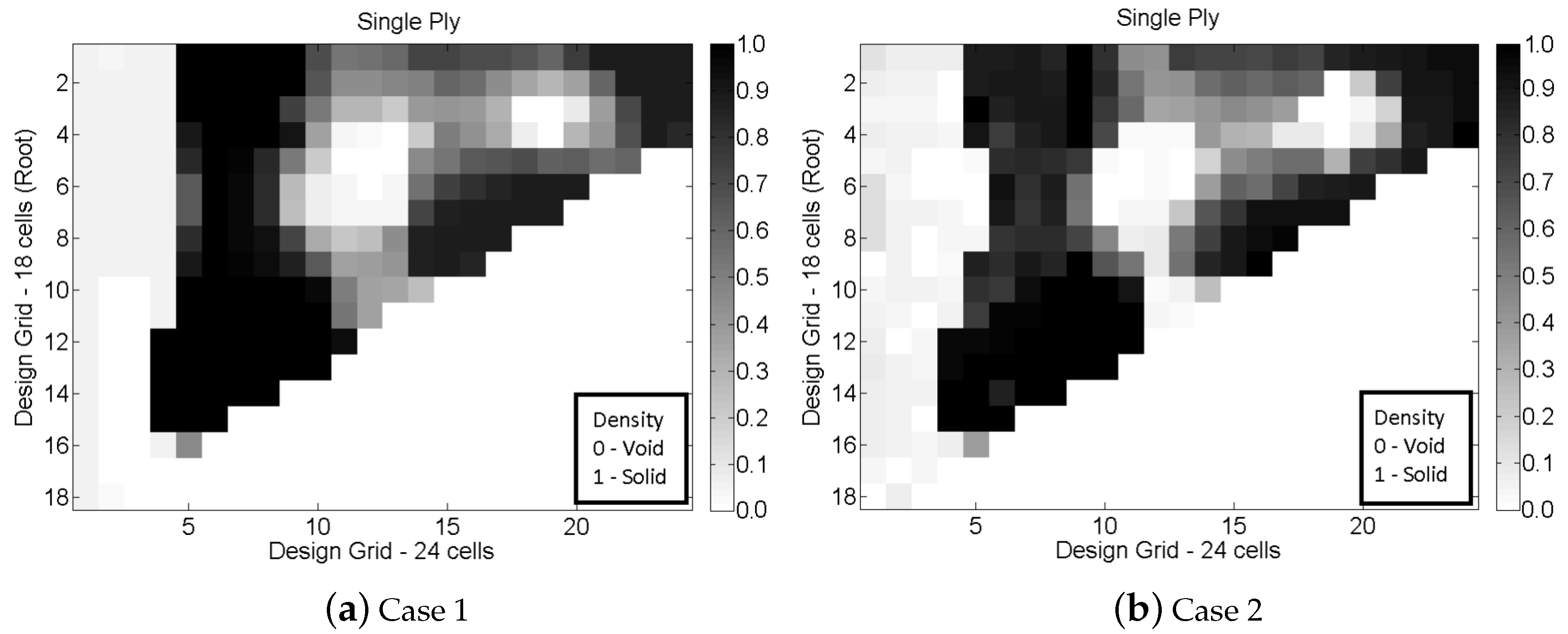
3.2. Design Space Test Case
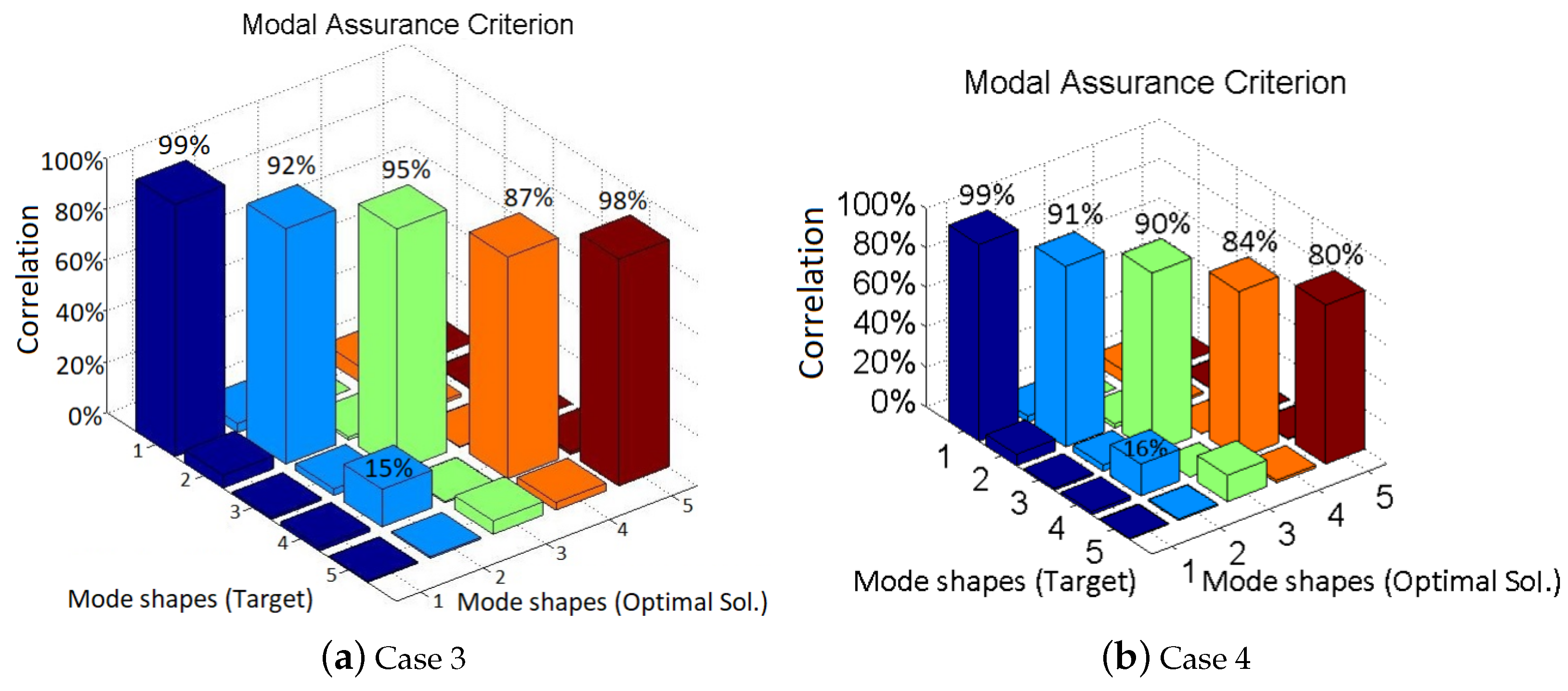
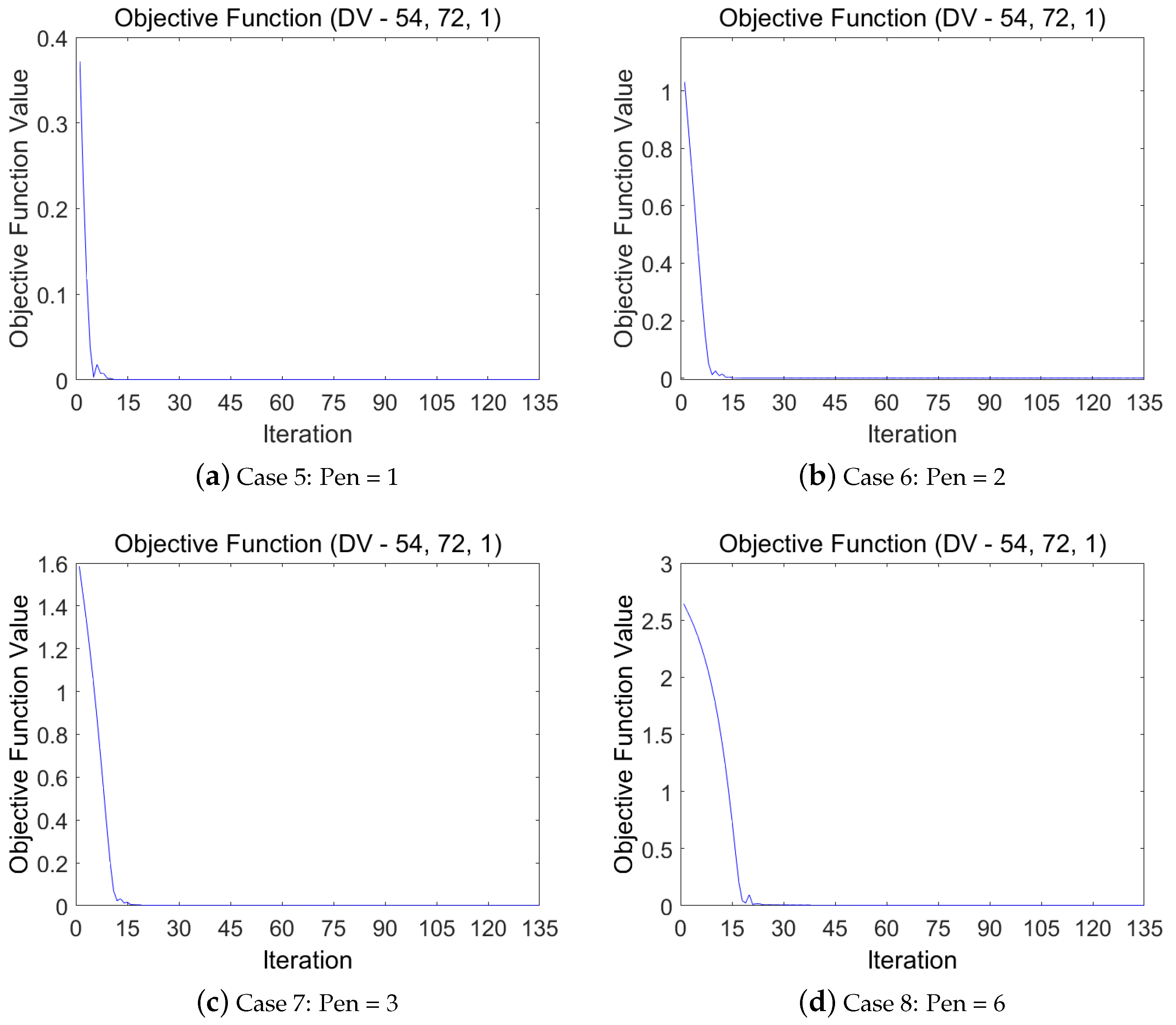
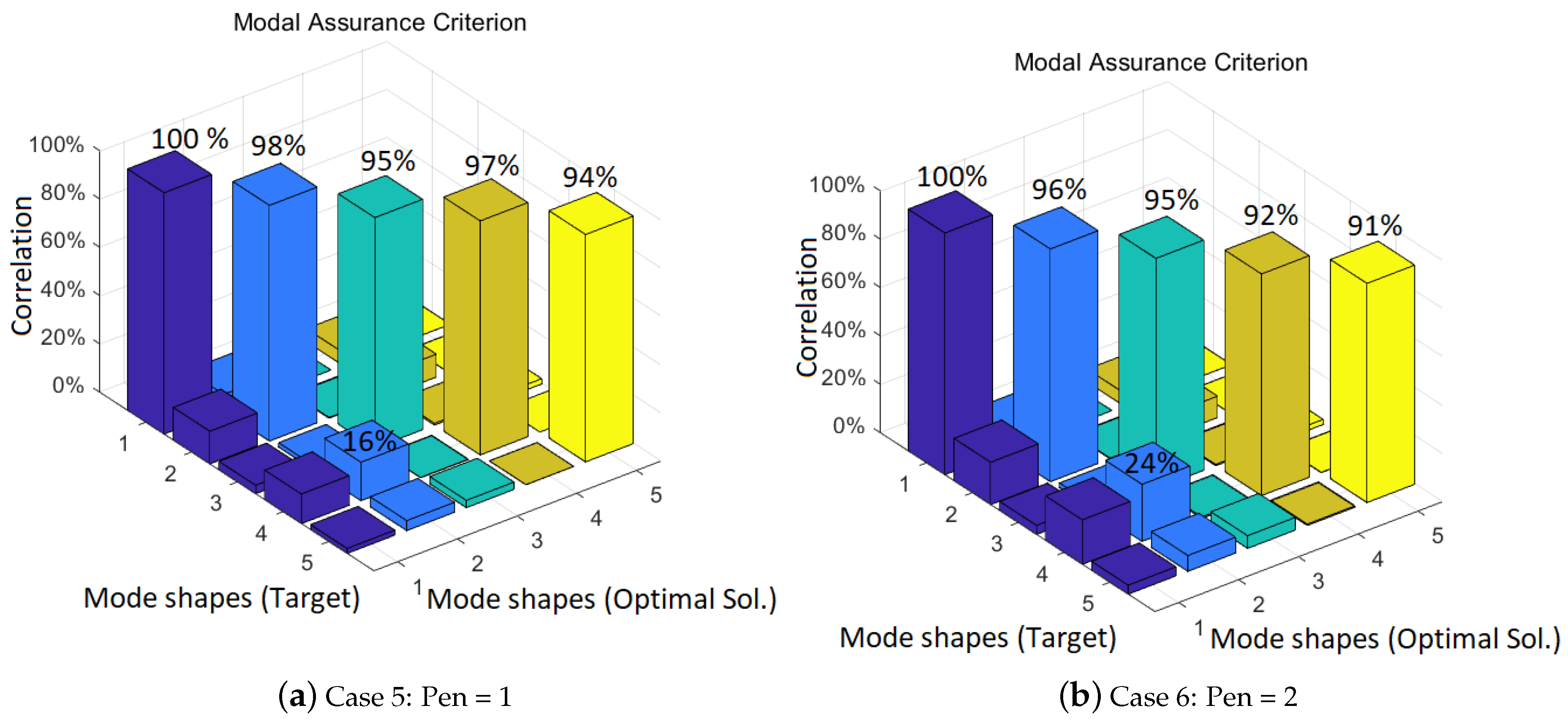
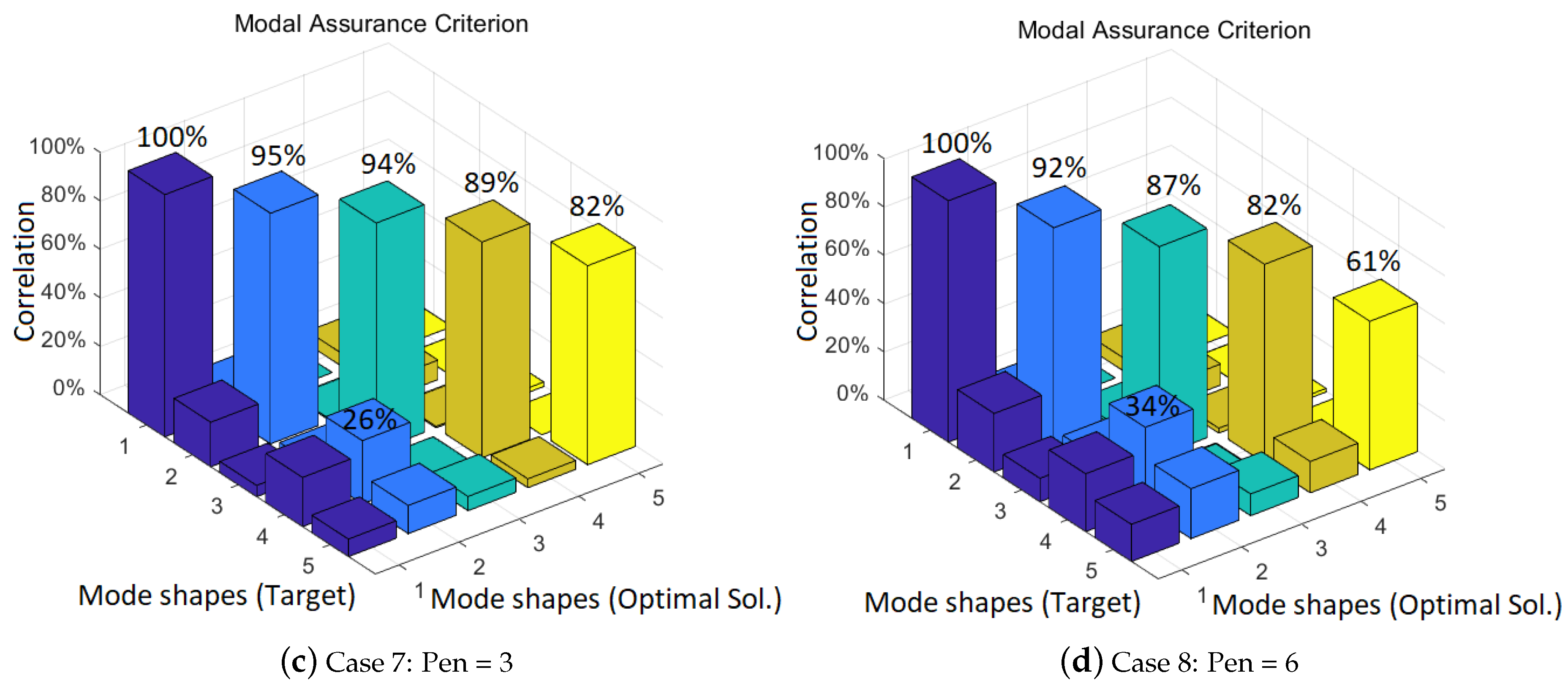
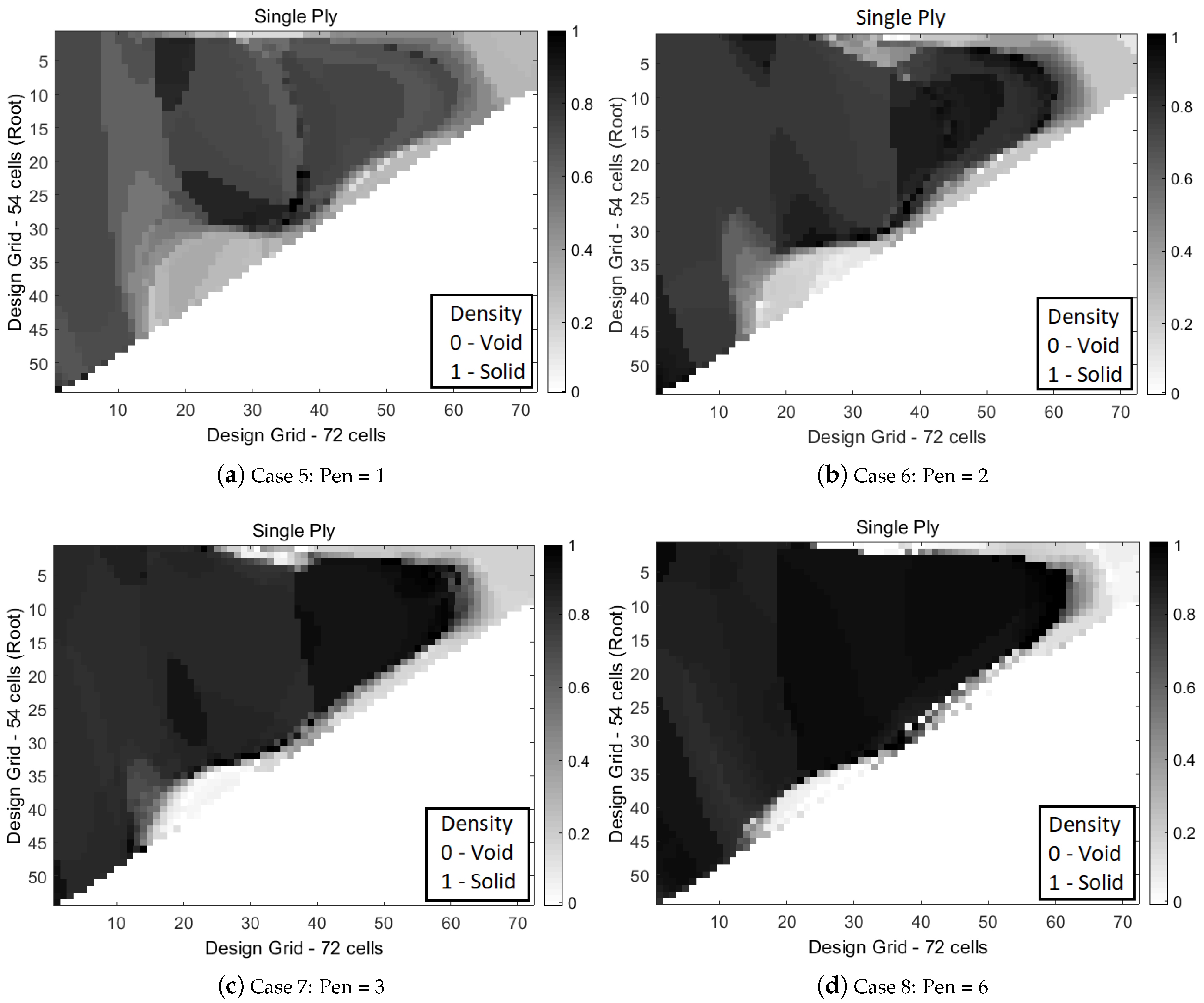
3.3. Penalization Factor Test Case
4. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okonkwo, P.; Smith, H. Review of evolving trends in blended wing body aircraft design. Prog. Aerosp. Sci. 2016, 82, 1–23. [Google Scholar] [CrossRef]
- Cavallaro, R.; Demasi, L. Challenges, Ideas, and Innovations of Joined-Wing Configurations: A Concept from the Past, an Opportunity for the Future. Prog. Aerosp. Sci. 2016, 87, 1–93. [Google Scholar] [CrossRef]
- Papageorgiou, A.; Tarkian, M.; Amadori, K.; Ölvander, J. Multidisciplinary Design Optimization of Aerial Vehicles: A Review of Recent Advancements. Int. J. Aerosp. Eng. 2018, 2018, 4258020. [Google Scholar] [CrossRef]
- Zhu, W. Models for wind tunnel tests based on additive manufacturing technology. Prog. Aerosp. Sci. 2019, 110, 100541. [Google Scholar] [CrossRef]
- Sobron, A.; Lundström, D.; Krus, P. A Review of Current Research in Subscale Flight Testing and Analysis of Its Main Practical Challenges. Aerospace 2021, 8, 74. [Google Scholar] [CrossRef]
- Casaburo, A.; Petrone, G.; Franco, F.; De Rosa, S. A Review of Similitude Methods for Structural Engineering. Appl. Mech. Rev. 2019, 71, 030802. [Google Scholar] [CrossRef] [Green Version]
- Georgiou, G.; Vio, G.A.; Cooper, J.E. Aeroelastic tailoring and scaling using Bacterial Foraging Optimisation. Struct. Multidiscip. Optim. 2014, 50, 81–99. [Google Scholar] [CrossRef]
- He, S.; Guo, S.; Liu, Y.; Luo, W. Passive gust alleviation of a flying-wing aircraft by analysis and wind-tunnel test of a scaled model in dynamic similarity. Aerosp. Sci. Technol. 2021, 113, 106689. [Google Scholar] [CrossRef]
- Bond, V.L.; Canfield, R.A.; Suleman, A.; Blair, M. Aeroelastic Scaling of a Joined Wing for Nonlinear Geometric Stiffness. AIAA J. 2012, 50, 513–522. [Google Scholar] [CrossRef]
- Wan, Z.; Cesnik, C.E.S. Geometrically Nonlinear Aeroelastic Scaling for Very Flexible Aircraft. AIAA J. 2014, 52, 2251–2260. [Google Scholar] [CrossRef] [Green Version]
- Ricciardi, A.P.; Canfield, R.A.; Patil, M.J.; Lindsley, N. Nonlinear Aeroelastic Scaled-Model Design. J. Aircr. 2016, 53, 20–32. [Google Scholar] [CrossRef]
- Mas Colomer, J.; Bartoli, N.; Lefebvre, T.; Martins, J.R.R.A.; Morlier, J. An MDO-based methodology for static aeroelastic scaling of wings under non-similar flow. Struct. Multidiscip. Optim. 2021, 63, 1045–1061. [Google Scholar] [CrossRef]
- Spada, C.; Afonso, F.; Lau, F.; Suleman, A. Nonlinear aeroelastic scaling of high aspect-ratio wings. Aerosp. Sci. Technol. 2017, 63, 363–371. [Google Scholar] [CrossRef]
- Afonso, F.; Coelho, M.; Vale, J.; Lau, F.; Suleman, A. On the Design of Aeroelastically Scaled Models of High Aspect-Ratio Wings. Aerospace 2020, 7, 166. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, M.; Tao, Y.; Li, J.; Li, D.; Zhang, Y.; Yuan, C.; Sang, W.; Zhang, B. Research on analytical scaling method and scale effects for subscale flight test of blended wing body civil aircraft. Aerosp. Sci. Technol. 2020, 106, 106114. [Google Scholar] [CrossRef]
- Banazadeh, A.; Hajipouzadeh, P. Using approximate similitude to design dynamic similar models. Aerosp. Sci. Technol. 2019, 94, 105375. [Google Scholar] [CrossRef]
- French, M.; Eastep, F.E. Aeroelastic model design using parameter identification. J. Aircr. 1996, 33, 198–202. [Google Scholar] [CrossRef]
- Stanford, B. Topology Optimization of Low-Speed Aeroelastic Wind Tunnel Models. AIAA Scitech 2021 Forum 2021. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Zhu, J.H.; Zhang, W.H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, W.; Quan, D.; Shi, G.; Tang, L.; Hou, Y.; Breitkopf, P.; Zhu, J.; Gao, T. From Topology Optimization Design to Additive Manufacturing: Today’s Success and Tomorrow’s Roadmap. Arch. Comput. Methods Eng. 2020, 27, 805–830. [Google Scholar] [CrossRef]
- Goh, G.; Agarwala, S.; Goh, G.; Dikshit, V.; Sing, S.; Yeong, W. Additive manufacturing in unmanned aerial vehicles (UAVs): Challenges and potential. Aerosp. Sci. Technol. 2017, 63, 140–151. [Google Scholar] [CrossRef]
- Klippstein, H.; Diaz De Cerio Sanchez, A.; Hassanin, H.; Zweiri, Y.; Seneviratne, L. Fused Deposition Modeling for Unmanned Aerial Vehicles (UAVs): A Review. Adv. Eng. Mater. 2018, 20, 1700552. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef] [Green Version]
- Allaire, G.; Dapogny, C.; Estevez, R.; Faure, A.; Michailidis, G. Structural optimization under overhang constraints imposed by additive manufacturing technologies. J. Comput. Phys. 2017, 351, 295–328. [Google Scholar] [CrossRef] [Green Version]
- Lazarov, B.S.; Wang, F.; Sigmund, O. Length scale and manufacturability in density-based topology optimization. Arch. Appl. Mech. 2016, 86, 189–218. [Google Scholar] [CrossRef] [Green Version]
- Gaynor, A.T.; Guest, J.K. Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Struct. Multidiscip. Optim. 2016, 54, 1157–1172. [Google Scholar] [CrossRef]
- Deaton, J.D.; Kolonay, R.M.; Reuter, R.A.; Kobayashi, M.H. Validation of Topology Optimized Lifting Surfaces using 3-D Printing. In Proceedings of the 17th International Forum on Aeroelasticity and Structural Dynamics (IFASD), Como, Italy, 25–28 June 2017. [Google Scholar]
- Pastor, M.; Binda, M.; Harčarik, T. Modal Assurance Criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Stolpe, M.; Svanberg, K. An alternative interpolation scheme for minimum compliance optimization. Struct. Multidiscip. Optim. 2001, 22, 116–124. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Tsai, T.; Cheng, C.C. Structural design for desired eigenfrequencies and mode shapes using topology optimization. Struct. Multidiscip. Optim. 2001, 47, 673–686. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- MatWeb, Material Property Data. Property Search. Available online: http://www.matweb.com/search/PropertySearch.aspx (accessed on 21 May 2021).
- Silva, M.; Mateus, A.; Oliveira, D.; Malça, C. An alternative method to produce metal/plastic hybrid components for orthopedics applications. Proc. Inst. Mech. Eng. Part J. Mater. Des. Appl. 2017, 231, 179–186. [Google Scholar] [CrossRef]
- Zhan, J.; Tamura, T.; Li, X.; Ma, Z.; Sone, M.; Yoshino, M.; Umezu, S.; Sato, H. Metal-plastic hybrid 3D printing using catalyst-loaded filament and electroless plating. Addit. Manuf. 2020, 36, 101556. [Google Scholar] [CrossRef]
- Chen, L.; Huang, J.; Lin, C.; Pan, C.; Chen, S.; Yang, T.; Lin, D.; Lin, H.; Jang, J. Anisotropic response of Ti-6Al-4V alloy fabricated by 3D printing selective laser melting. Mater. Sci. Eng. A 2017, 682, 389–395. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; John Wiley & Sons: Baldock, UK, 2009. [Google Scholar]


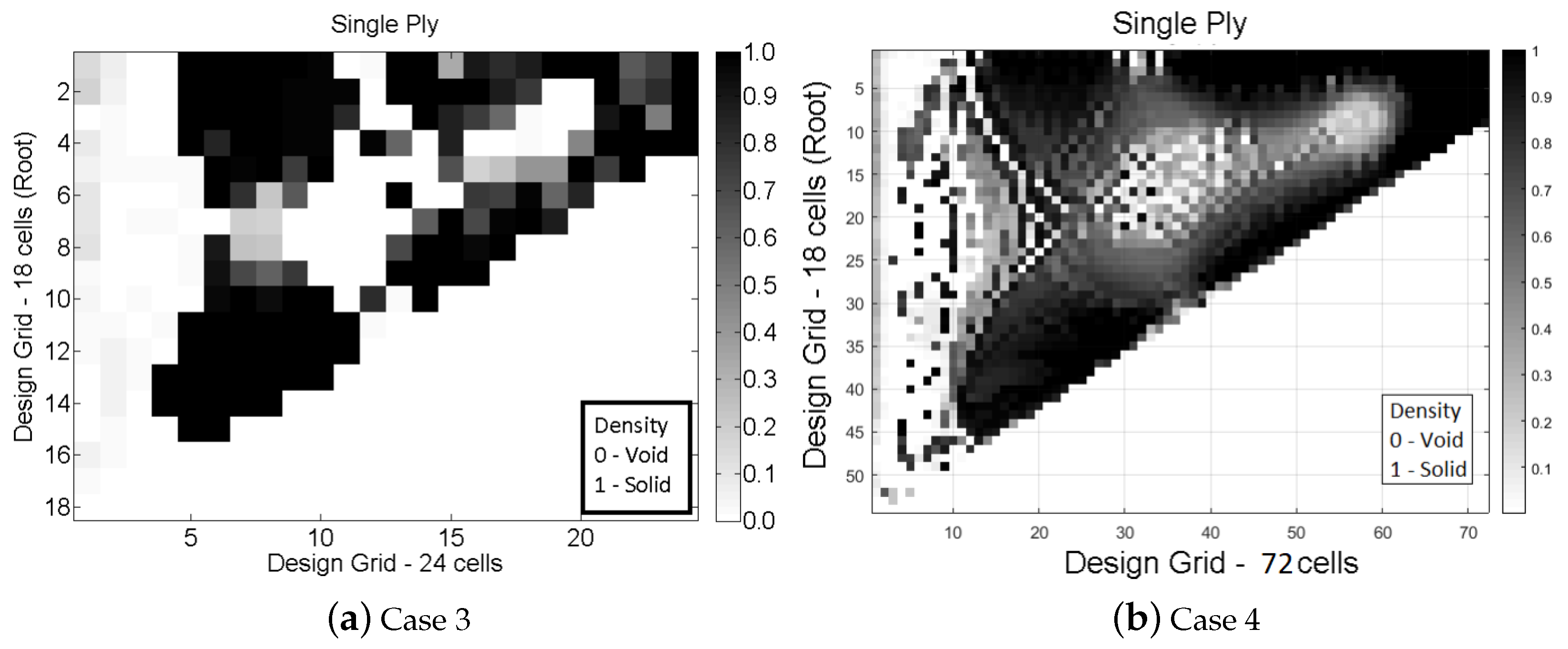

| Case 1 | Case 2 | ||||||
|---|---|---|---|---|---|---|---|
| Material Property | Target | Scaled Model | Difference [%] | Target | Scaled Model | Difference [%] | |
| Density | 2400 | 2700 | 11 | 2400 | 2700 | 11 | |
| Part-1, Solid A | Elasticity modulus | 14 | 14 | ||||
| Poisson Ratio | 0.33 | 0.30 | 9 | 0.33 | 0.30 | 9 | |
| Density | 2200 | 2700 | 19 | 2000 | 2700 | 26 | |
| Part-1, Solid B | Elasticity modulus | 6 | 21 | ||||
| Poisson Ratio | 0.36 | 0.30 | 17 | 0.36 | 0.30 | 17 | |
| Density | 2200 | 1800 | 18 | 1210 | 1800 | 33 | |
| Part-2, Shell | Elasticity modulus | 39 | 60,506 | ||||
| Poisson Ratio | 0.36 | 0.33 | 8 | 0.36 | 0.33 | 8 | |
| Case 1 | Case 2 | |||||
|---|---|---|---|---|---|---|
| Target F [Hz] | Obtained F [Hz] | Relative Error [%] | Target F [Hz] | Obtained F [Hz] | Relative Error [%] | |
| Mode 1 | 61.00 | 61.06 | 0.01 | 59.24 | 58.90 | 0.06 |
| Mode 2 | 263.77 | 264.76 | 0.04 | 257.61 | 257.54 | 0.00 |
| Mode 3 | 378.81 | 381.53 | 0.07 | 368.66 | 368.77 | 0.00 |
| Mode 4 | 656.28 | 655.54 | 0.01 | 643.87 | 640.55 | 0.05 |
| Mode 5 | 918.68 | 917.47 | 0.01 | 897.06 | 891.73 | 0.06 |
| Target | Scaled Model | Difference [%] | ||
|---|---|---|---|---|
| Density | 2400 | 2700 | 13 | |
| Part-1, Solid A | Elasticity modulus | 17 | ||
| Poisson | 0.33 | 0.30 | 9 | |
| Density | 1800 | 2700 | 50 | |
| Part-1, Solid B | Elasticity modulus | 133 | ||
| Poisson | 0.36 | 0.30 | 17 | |
| Density | 1210 | 1800 | 49 | |
| Part-2, Shell | Elasticity modulus | 60,506 | ||
| Poisson | 0.36 | 0.33 | 8 |
| Case 3 | Case 4 | ||||
|---|---|---|---|---|---|
| Target F [Hz] | Obtained F [Hz] | Relative Error [%] | Obtained F [Hz] | Relative Error [%] | |
| Mode 1 | 52.31 | 52.72 | 0.87 | 51.94 | 0.71 |
| Mode 2 | 234.32 | 235.43 | 0.47 | 235.51 | 0.50 |
| Mode 3 | 321.93 | 324.67 | 0.85 | 321.07 | 0.27 |
| Mode 4 | 592.69 | 595.44 | 0.46 | 593.84 | 0.19 |
| Mode 5 | 786.21 | 785.53 | 0.09 | 791.05 | 0.61 |
| Target | Scaled Model | Difference [%] | ||
|---|---|---|---|---|
| Density | 2400 | 4430 | 46 | |
| Part-1, Solid A | Elasticity modulus | 47 | ||
| Poisson | 0.33 | 0.342 | 4 | |
| Density | 1800 | 4430 | 59 | |
| Part-1, Solid B | Elasticity modulus | 74 | ||
| Poisson | 0.36 | 0.342 | 5 | |
| Density | 1210 | 1210 | 0 | |
| Part-2, Shell | Elasticity modulus | 0 | ||
| Poisson | 0.36 | 0.33 | 8 |
| Case 5: Pen = 1 | Case 6: Pen = 2 | Case 7: Pen = 3 | Case 8: Pen = 6 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Target | Obtained | Relative | Obtained | Relative | Obtained | Relative | Obtained | Relative | |
| NF [Hz] | F [Hz] | Error [%] | F [Hz] | Error [%] | F [Hz] | Error [%] | F [Hz] | Error [%] | |
| Mode 1 | 52.31 | 52.58 | 0.52 | 52.47 | 0.31 | 52.42 | 0.21 | 52.67 | 0.68 |
| Mode 2 | 234.32 | 234.61 | 0.12 | 234.67 | 0.15 | 234.87 | 0.23 | 236.63 | 0.98 |
| Mode 3 | 321.93 | 322.79 | 0.27 | 322.47 | 0.17 | 322.61 | 0.21 | 323.22 | 0.40 |
| Mode 4 | 592.69 | 591.37 | 0.22 | 592.27 | 0.07 | 593.74 | 0.18 | 592.33 | 0.06 |
| Mode 5 | 786.21 | 787.46 | 0.16 | 786.57 | 0.04 | 787.84 | 0.21 | 795.34 | 1.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, É.; Sohouli, A.; Afonso, F.; da Silva, R.G.A.; Suleman, A. Dynamic Scaling of a Wing Structure Model Using Topology Optimization. Machines 2022, 10, 374. https://doi.org/10.3390/machines10050374
Oliveira É, Sohouli A, Afonso F, da Silva RGA, Suleman A. Dynamic Scaling of a Wing Structure Model Using Topology Optimization. Machines. 2022; 10(5):374. https://doi.org/10.3390/machines10050374
Chicago/Turabian StyleOliveira, Éder, Abdolrasoul Sohouli, Frederico Afonso, Roberto Gil Annes da Silva, and Afzal Suleman. 2022. "Dynamic Scaling of a Wing Structure Model Using Topology Optimization" Machines 10, no. 5: 374. https://doi.org/10.3390/machines10050374
APA StyleOliveira, É., Sohouli, A., Afonso, F., da Silva, R. G. A., & Suleman, A. (2022). Dynamic Scaling of a Wing Structure Model Using Topology Optimization. Machines, 10(5), 374. https://doi.org/10.3390/machines10050374







