Numerical and Experimental Analysis for the Dynamics of Flawed–Machining Rod–Disk Rotor with Inner Misalignment
Abstract
:1. Introduction
2. Static Features of Flawed Rod–Disk Rotor with Inner Misalignment
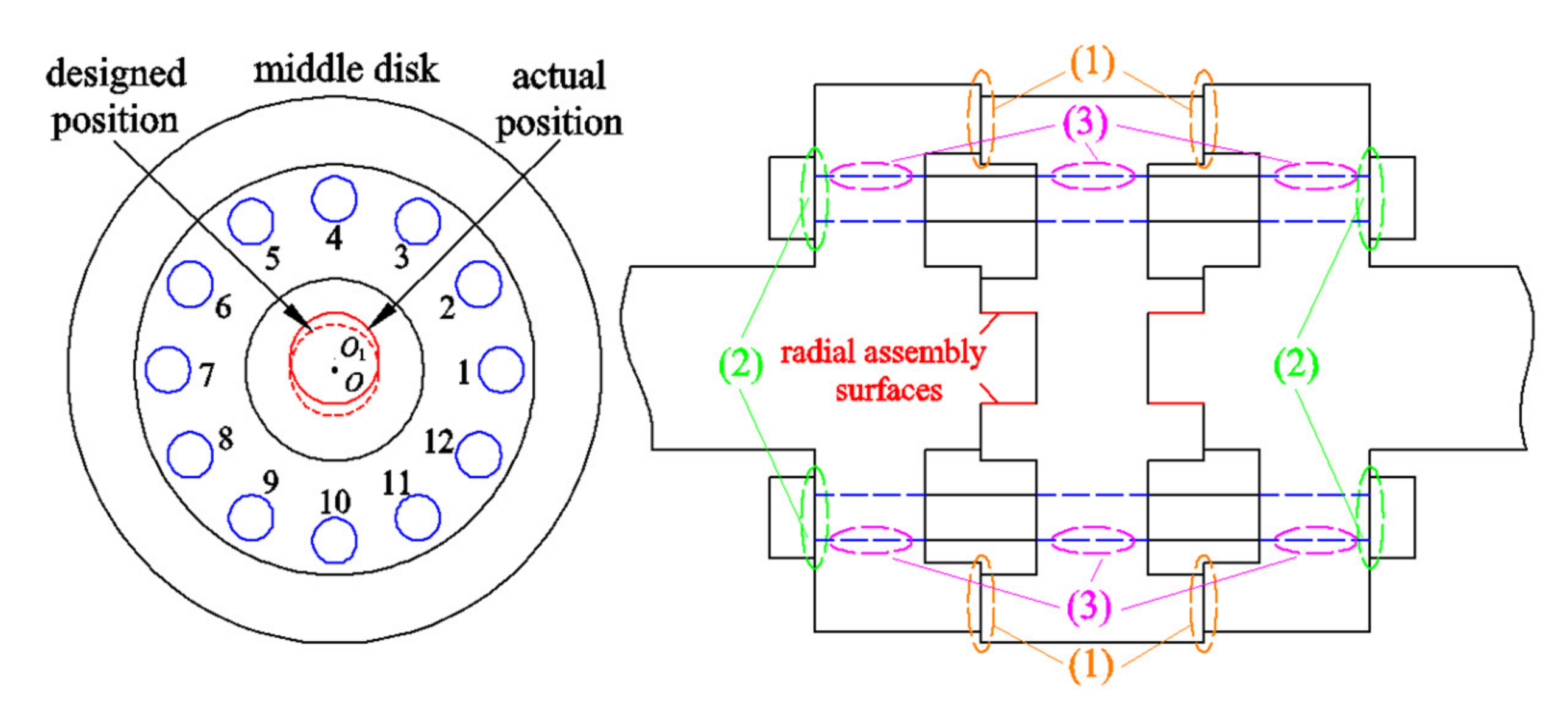
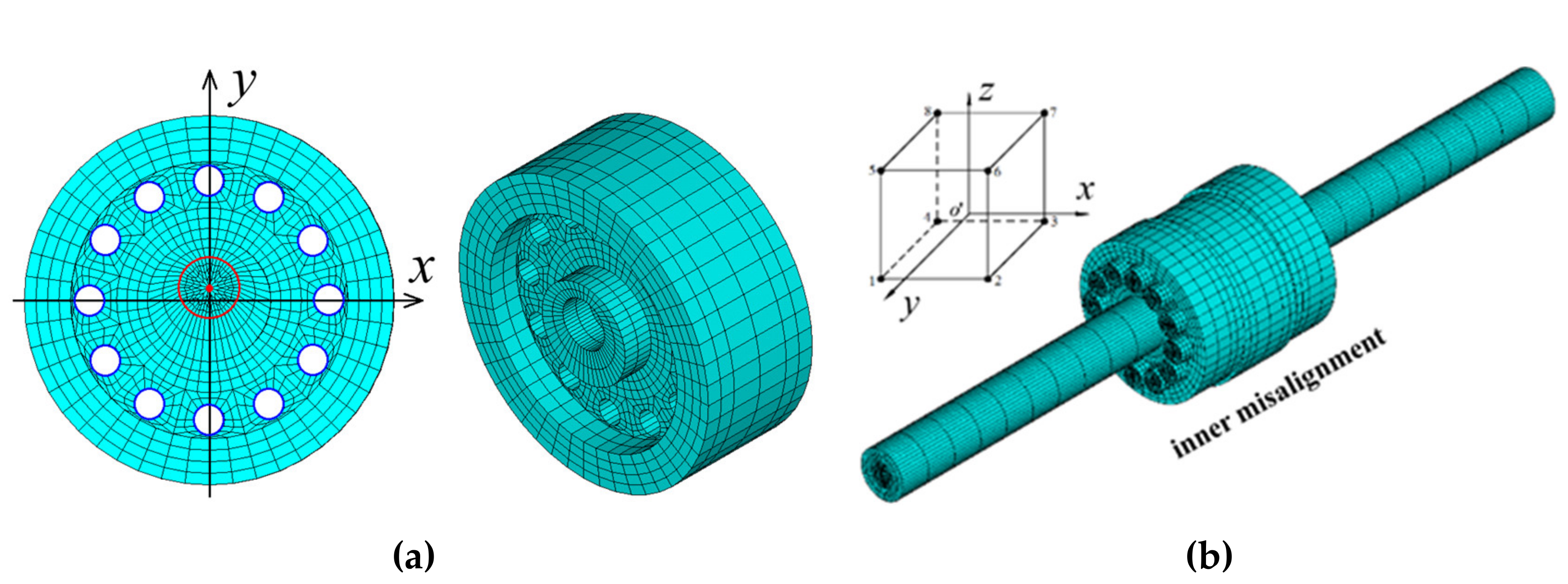
2.1. Inner Misalignment and Static Solution
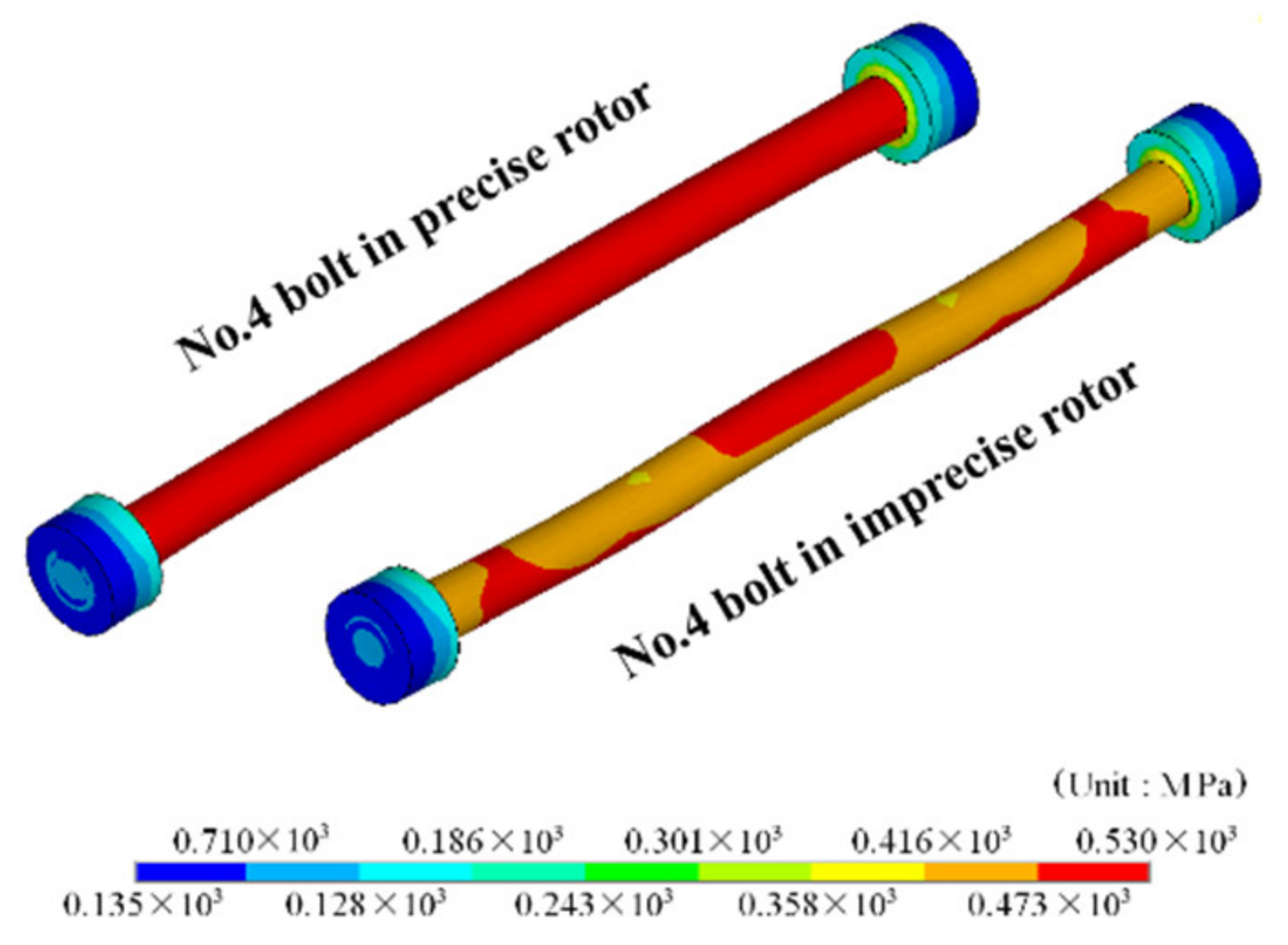
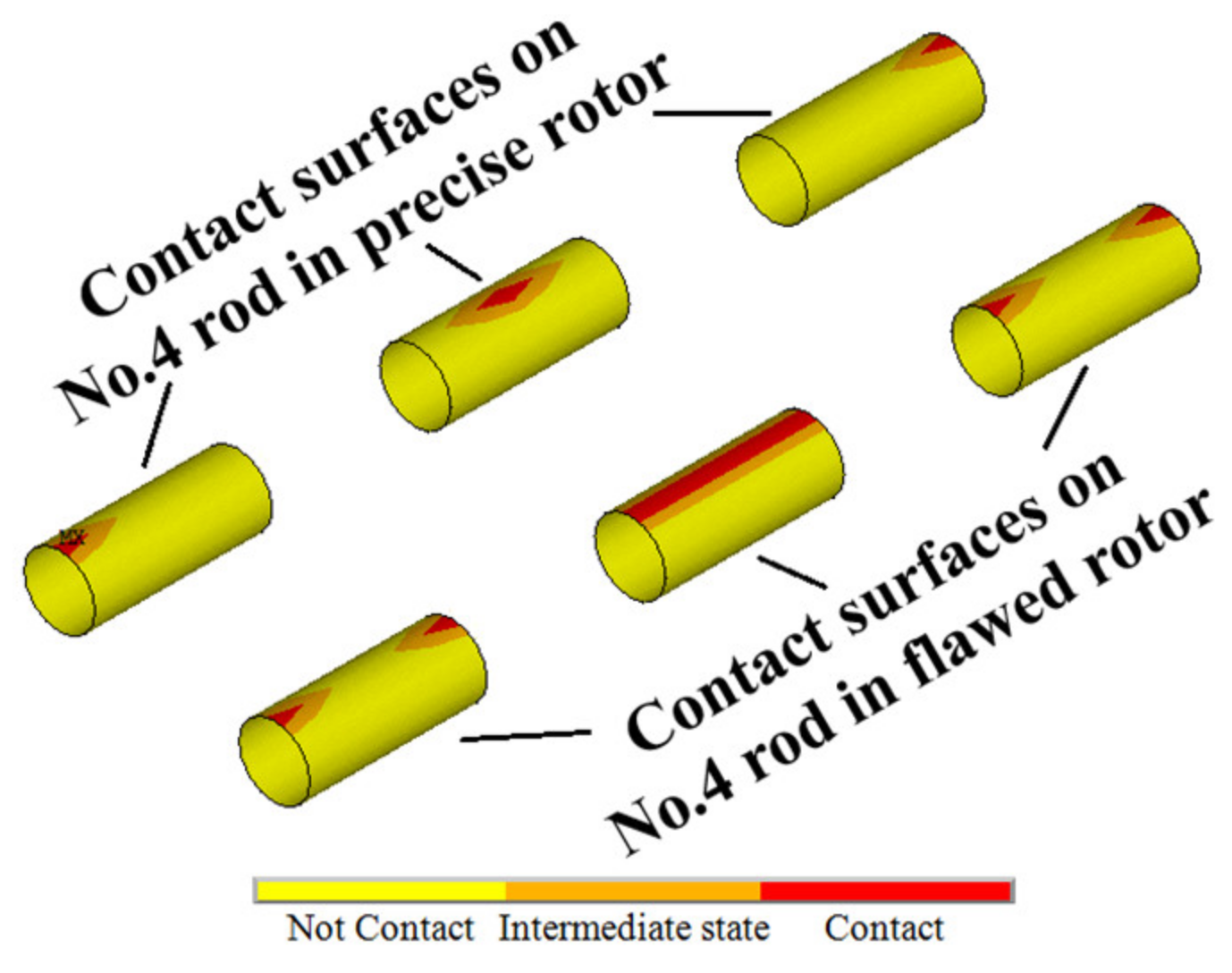
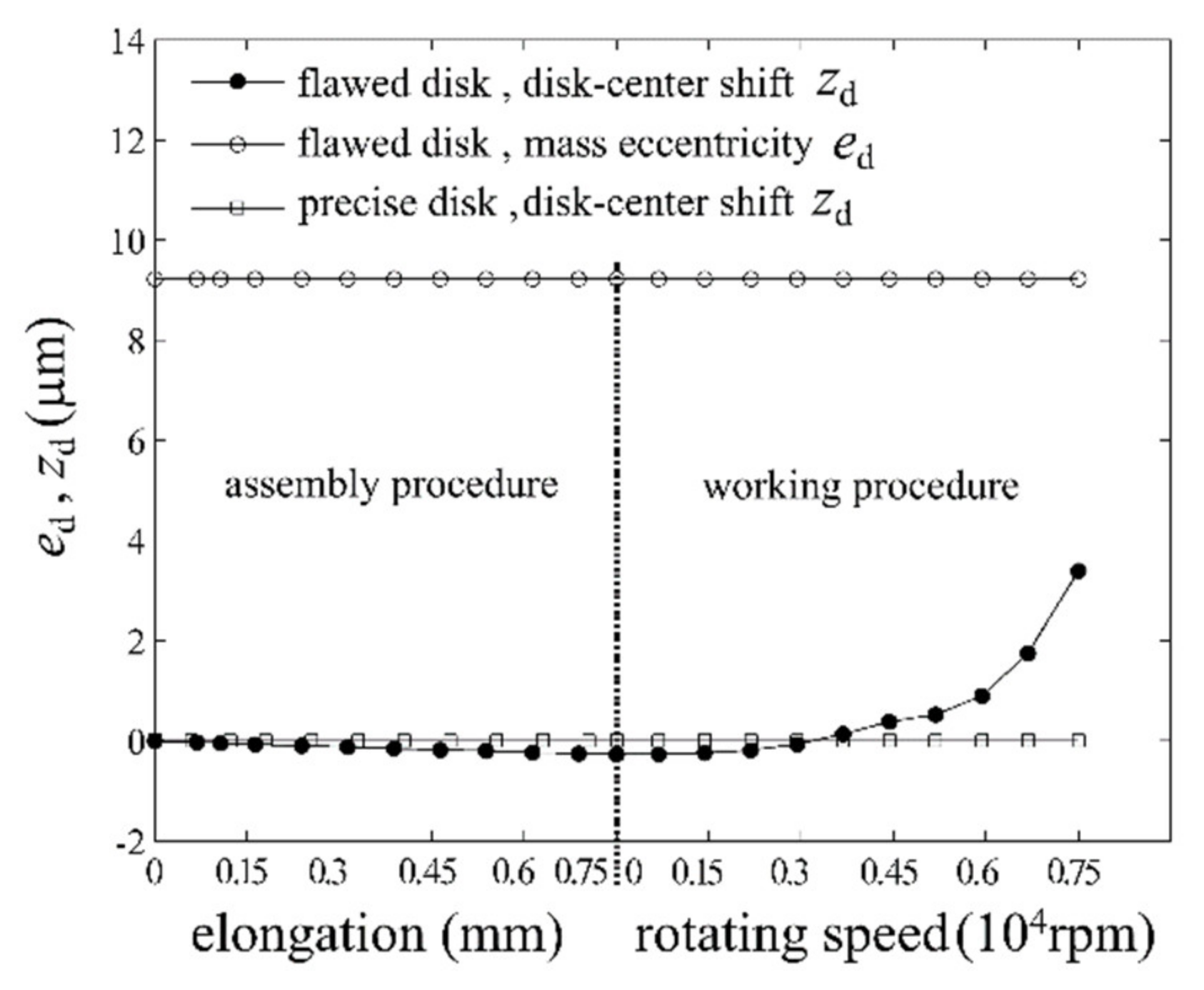
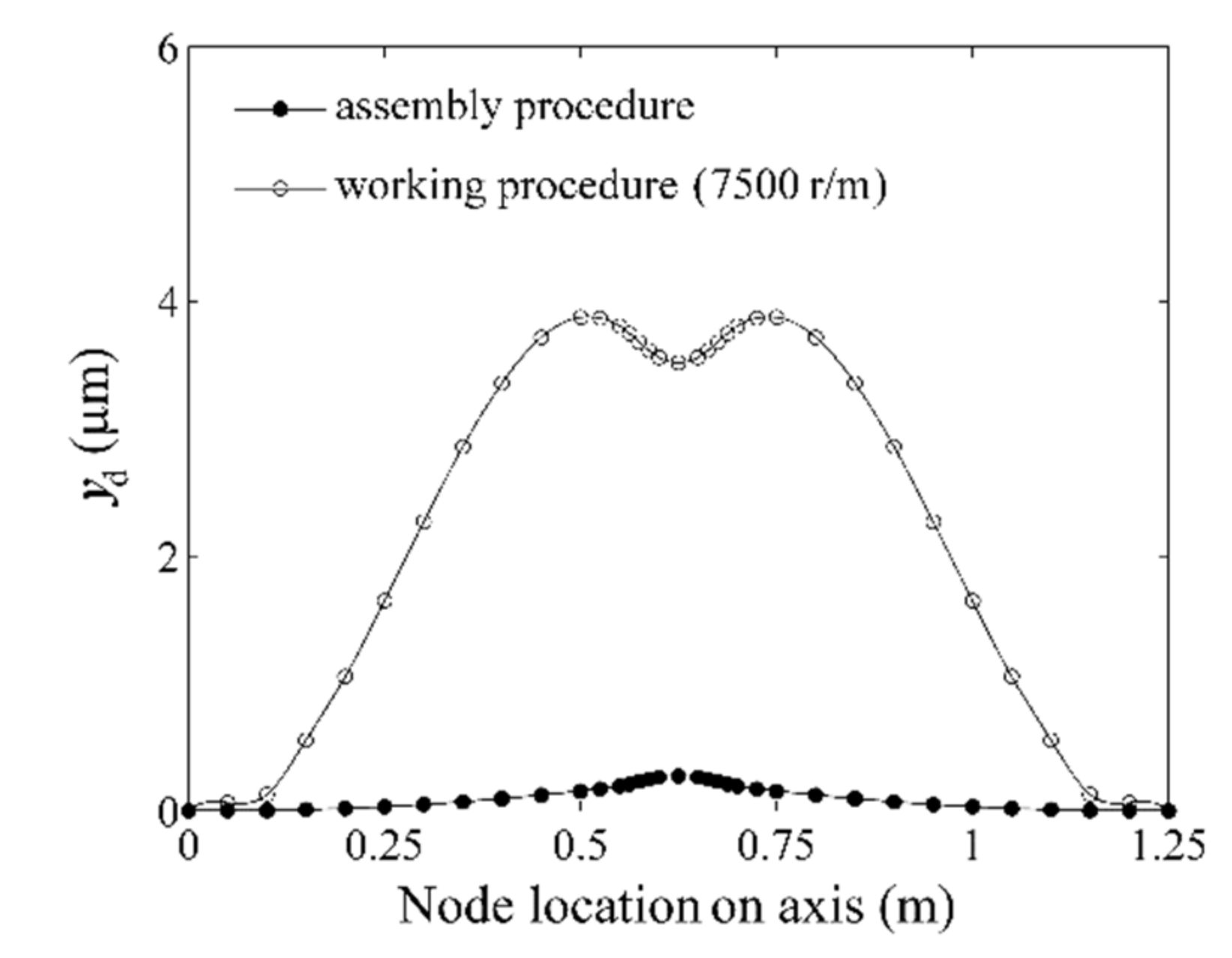
2.2. Static Analysis of the Flawed Rod–Disk Rotor
3. Nonlinear Equations and Solving Algorithm
4. Dynamic Features of Flawed Rod–Disk Rotor System
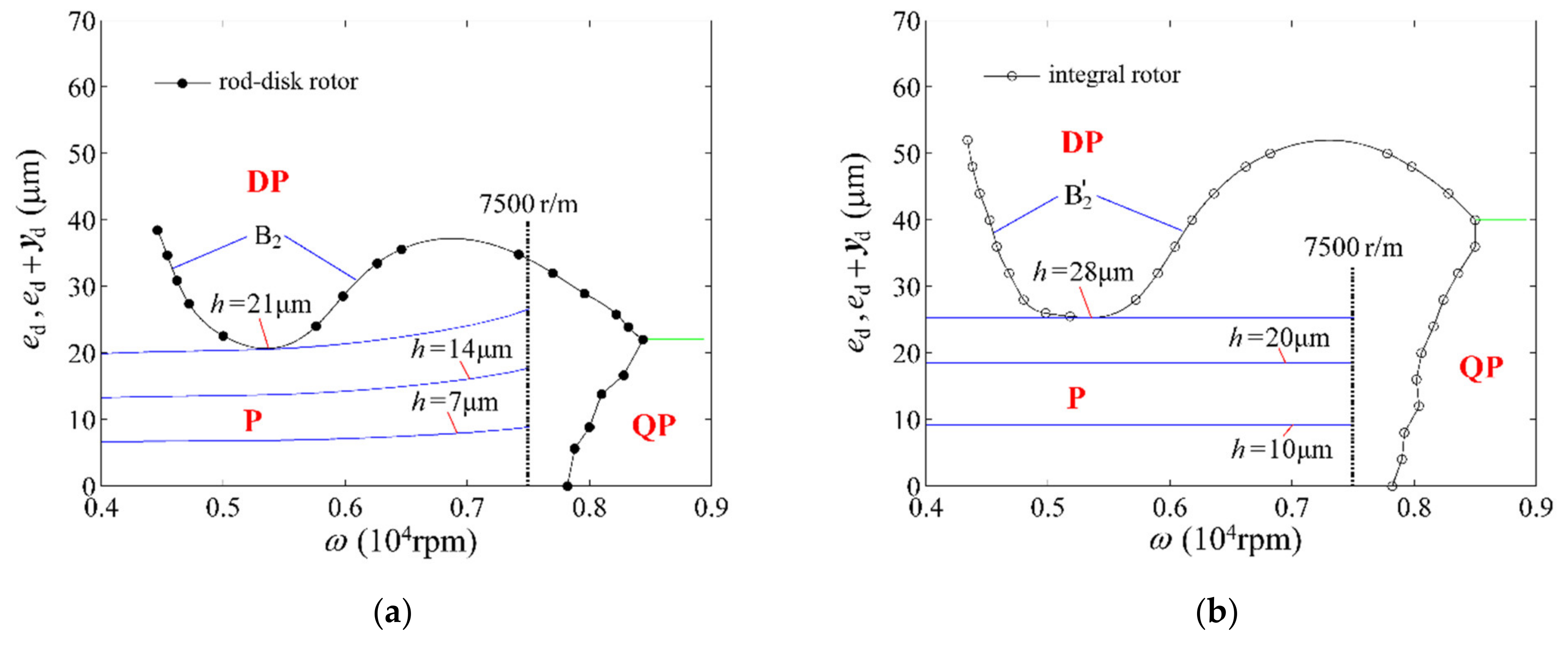
4.1. Global Stability Features
4.2. Nonlinear Vibration
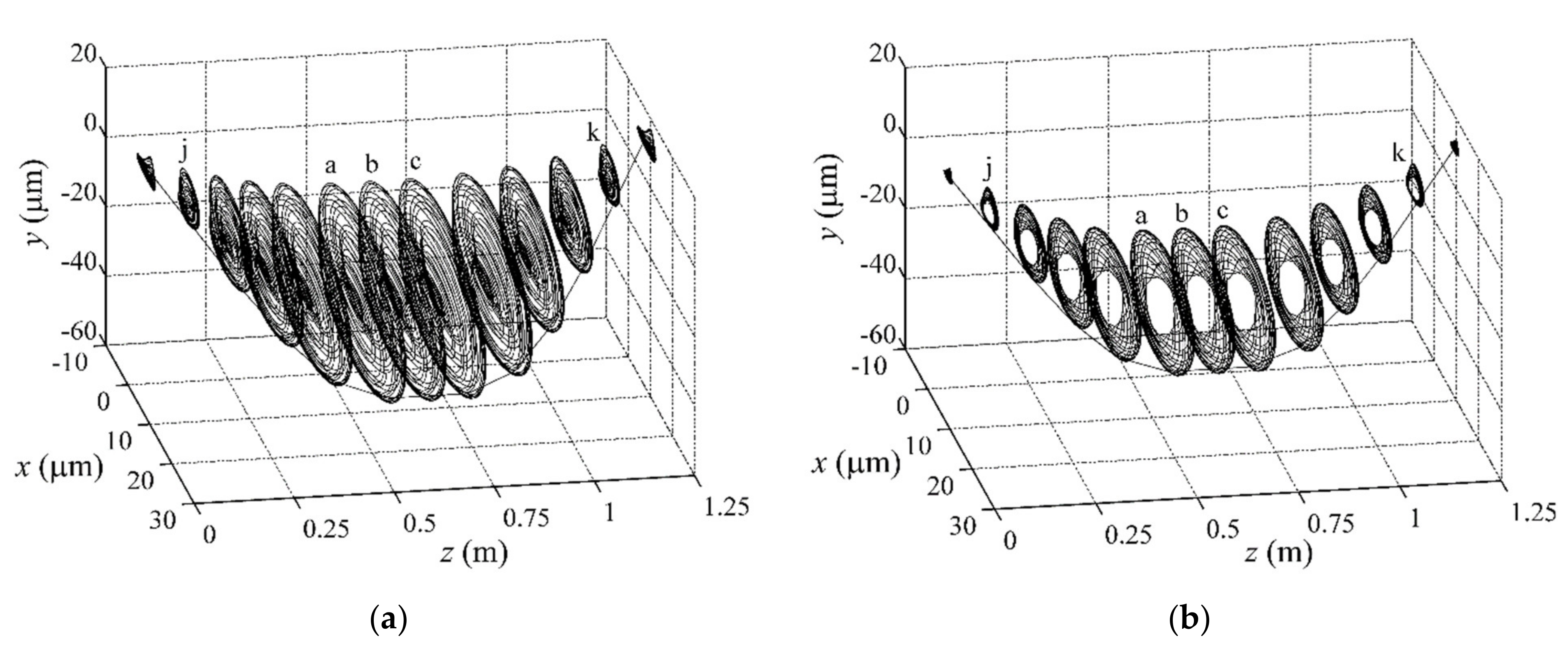
4.3. Dynamic Motions
4.4. Centration Tolerance
4.5. Uneven Tightening
5. Experiment about the Flawed Rod–Disk Rotor System
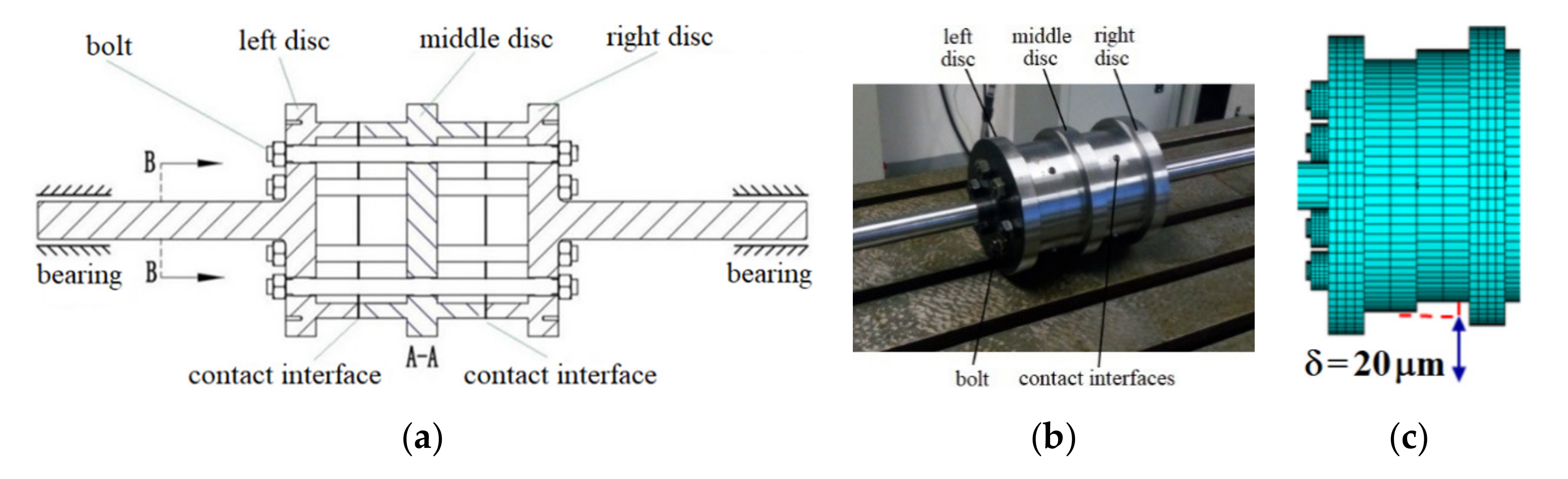
5.1. Structure and Inner Misalignment of the Rod–Disk Rotor System
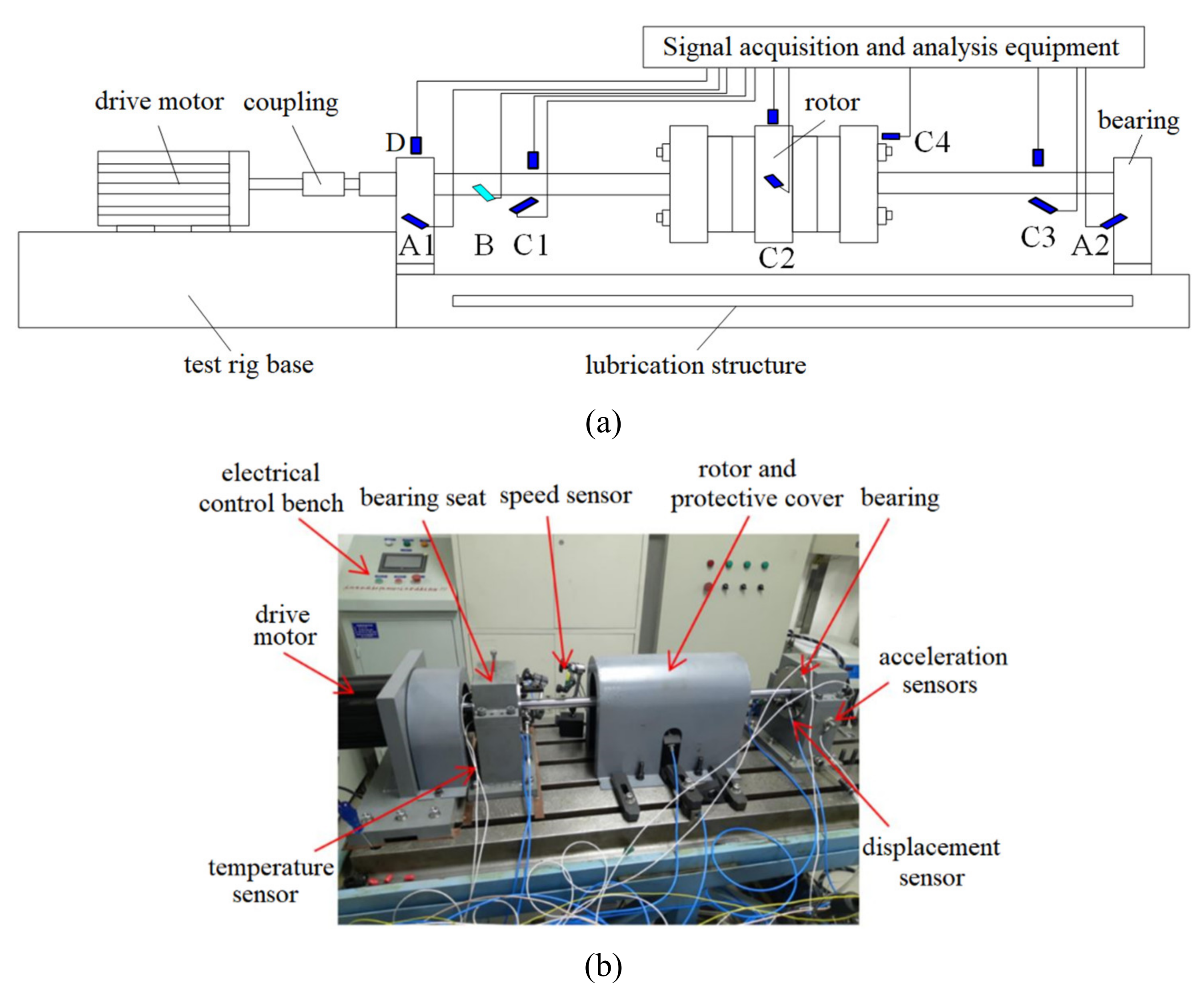
5.2. Test Rig System and Its Sensor Arrangement
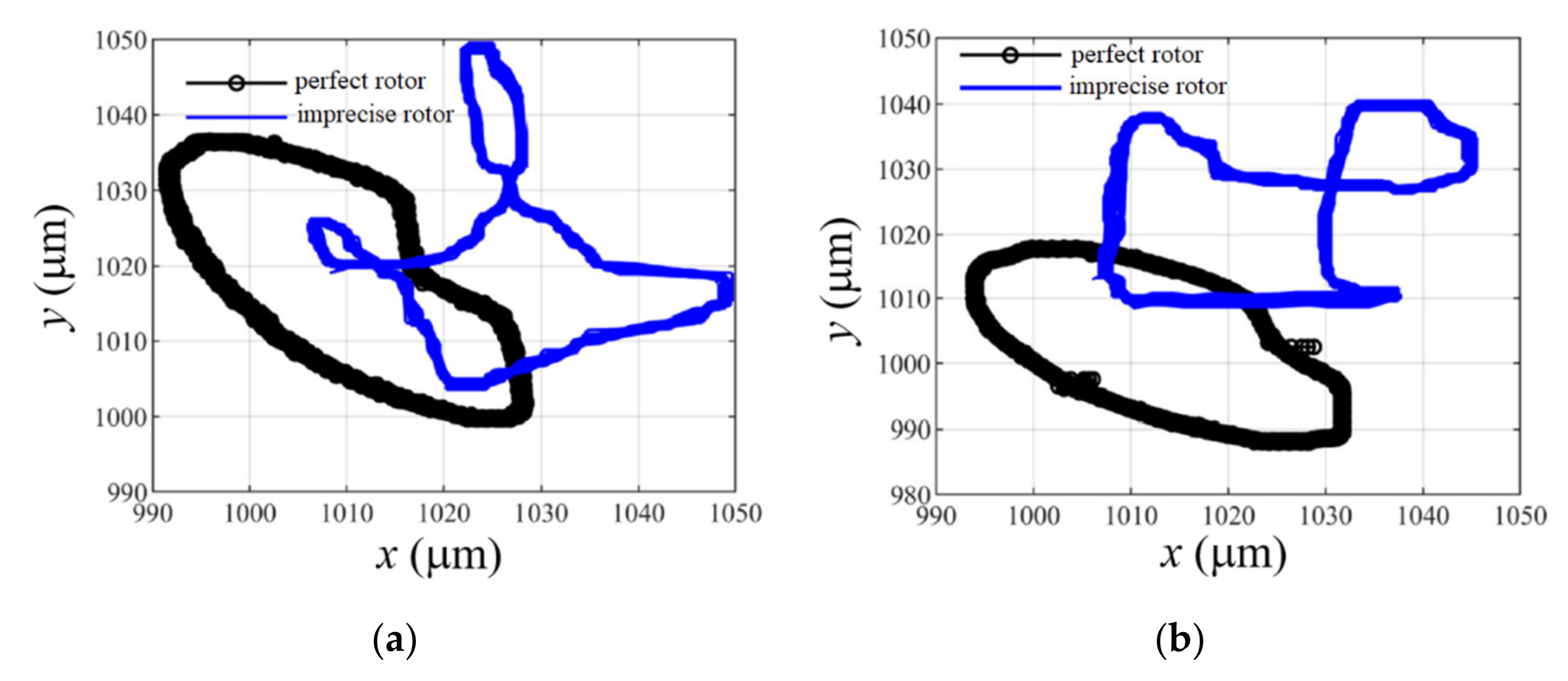
5.3. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| u | displacement vector | zd | disk–center shift | KR | stiffness matrix of t rotor |
| Q | force vector | ed | mass eccentricity of disk | MR | mass matrix |
| W | potential energy due to contact | yd | rotor bending | GR | gyroscope matrix |
| Δ | penalty factor | λ | excitation parameter | g | gravity force vector |
| η | Lagrangian multiplier | fc | balance vector | fb | oil film force |
| b | contact constraints | F | unbalance excitation vector | P | transformation matrix |
References
- Zhang, Y.; Fang, B.; Kong, L.; Li, Y. Effect of the ring misalignment on the service characteristics of ball bearing and rotor system. Mech. Mach. Theory 2020, 151, 103889. [Google Scholar] [CrossRef]
- Dal, A.; Karaçay, T. Effects of angular misalignment on the performance of rotor–bearing systems supported by externally pressurized air bearing. Tribol. Int. 2017, 111, 276–288. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, Z.; Yang, Y.; Li, F.; Chen, Y. Nonlinear vibrations of a dual–rotor–bearing–coupling misalignment system with blade–casing rubbing. J. Sound Vib. 2021, 497, 115948. [Google Scholar] [CrossRef]
- Kumar, P.; Tiwari, R. Dynamic analysis and identification of unbalance and misalignment in a rigid rotor with two offset discs levitated by active magnetic bearings: A novel trial misalignment approach. Propuls. Power Res. 2021, 10, 58–82. [Google Scholar] [CrossRef]
- Lu, K.; Jin, Y.L.; Huang, P.F.; Zhang, F.; Zhang, H.P.; Fu, C.; Chen, Y.S. The applications of POD method in dual rotor–bearing systems with coupling misalignment. Mech. Syst. Signal Process. 2021, 150, 107236. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Li, J.; Lu, H.; Ma, H. Feature extraction method based on NOFRFs and its application in faulty rotor system with slight misalignment. Nonlinear Dyn. 2019, 99, 1763–1777. [Google Scholar] [CrossRef]
- Abdou, K.M.; Saber, E. Effect of rotor misalignment on stability of journal bearings with finite width. Alex. Eng. J. 2020, 59, 3407–3417. [Google Scholar] [CrossRef]
- Srinivas, R.; Tiwari, R.; Kannababu, C. Model based analysis and identification of multiple fault parameters in coupled rotor systems with offset discs in the presence of angular misalignment and integrated with an active magnetic bearing. J. Sound Vib. 2019, 450, 109–140. [Google Scholar] [CrossRef]
- Sawalhi, N.; Ganeriwala, S.; Tóth, M. Parallel misalignment modeling and coupling bending stiffness measurement of a rotor-bearing system. Appl. Acoust. 2019, 144, 124–141. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Li, M. Nonlinear dynamics of unsymmetrical rotor-bearing system with fault of parallel misalignment. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Yang, Y.; Lu, K.; Gu, F. Nonlinear vibration analysis of a rotor system with parallel and angular misalignments under uncertainty via a Legendre collocation approach. Int. J. Mech. Mater. Des. 2019, 16, 557–568. [Google Scholar] [CrossRef]
- Pennacchi, P.; Vania, A.; Chatterton, S. Nonlinear effects caused by coupling misalignment in rotors equipped with journal bearings. Mech. Syst. Signal Process. 2012, 30, 306–322. [Google Scholar] [CrossRef] [Green Version]
- Verma, A.K.; Sarangi, S.; Kolekar, M.H. Experimental Investigation of Misalignment Effects on Rotor Shaft Vibration and on Stator Current Signature. J. Fail. Anal. Prev. 2014, 14, 125–138. [Google Scholar] [CrossRef]
- Tapia, J.C.; Silva, J.J.; Fonseca, L.; Heredia, O.; Mata, J.L. Design of a mechatronic system for fault detection in a rotor under misalignment and unbalance. IEEE Lat. Am. Trans. 2015, 13, 1899–1906. [Google Scholar] [CrossRef]
- Mogal, S.P.; Lalwani, D.I. Experimental investigation of unbalance and misalignment in rotor bearing system using order analysis. J. Meas. Eng. 2015, 3, 114–122. [Google Scholar]
- Ma, H.; Wang, X.L.; Niu, H.Q.; Wen, B. Oil-film instability simulation in an overhung rotor system with flexible coupling misalignment. Arch. Appl. Mech. 2015, 85, 893–907. [Google Scholar] [CrossRef]
- Simo, J.; Laursen, T. An augmented lagrangian treatment of contact problems involving friction. Comput. Struct. 1992, 42, 97–116. [Google Scholar] [CrossRef]
- Wang, X.; Yamaguchi, A. Characteristics of hydrostatic bearing/seal parts for water hydraulic pumps and motors. Part 1: Experiment and theory. Tribol. Int. 2002, 35, 425–433. [Google Scholar] [CrossRef]
- Malgol, A.; Vineesh, K.P.; Saha, A. Investigation of vibration characteristics of a Jeffcott rotor system under the influence of nonlinear restoring force, hydrodynamic effect, and gyroscopic effect. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 105. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Analytical Study of Nonlinear Vibration in a Rub-Impact Jeffcott Rotor. Energies 2021, 14, 8298. [Google Scholar] [CrossRef]
- Shanmugam, A.; Padmanabhan, C. A fixed–free interface component mode synthesis method for rotordynamic analysis. J. Sound Vib. 2006, 297, 664–679. [Google Scholar] [CrossRef]
- Shen, Z.; Chouvion, B.; Thouverez, F.; Beley, A. Enhanced 3D solid finite element formulation for rotor dynamics simulation. Finite Elem. Anal. Des. 2021, 195, 103584. [Google Scholar] [CrossRef]










| Variables | Value | |
|---|---|---|
| Bearings | bearing diameter | 80 mm |
| bearing width | 80 mm | |
| radial clearance | 0.18 mm | |
| oil lubricant viscosity | 0.018 Pa⋅s | |
| Rods | number of rods | 12 |
| length of rods | 250 mm | |
| diameter of rods | 10 mm | |
| elongation | 750 μm |
| Part | Parameter | Value |
|---|---|---|
| Rotor | Diameter of shaft | 25 mm |
| Length of shaft | 900 mm | |
| Diameter of disks | 154 mm | |
| Length of left disk | 50 mm | |
| Length of middle disk | 80 mm | |
| Length of right disk | 50 mm | |
| Number of rods | 6 | |
| Length of rods | 205 mm | |
| Diameter of rods | 10 mm | |
| Elongation | 200 μm | |
| Diameter of circumference for rods | 88 mm | |
| Bearings | Bearing diameter | 25 mm |
| Span of bearing | 771 mm | |
| Bearing width | 15 mm | |
| Radial clearance | 200 μm | |
| Oil lubricant viscosity | 0.018 Pa⋅s |
| Types of Model | Structure | Element | DOF Number | Advantage | Disadvantage |
|---|---|---|---|---|---|
| rigid rotor model | rigid shaft and disks | mass point | few | 1. can describe basic dynamic features; 2. has high calculating efficiency | 1. has over structure simplification; 2. has obvious difference with real complicated rotors |
| Jeffcott rotor model | flexible shaft and rigid disks | beam element | |||
| 1D rotor model | flexible shaft and rigid disks | beam element | some | ||
| integral 3D rotor model | flexible shaft and disks | 3D element | large | can describe integral rotor structure fully | cannot consider assembly process |
| combined 3D rotor model | flexible parts are combined | 3D element | 1. can describe integral rotor structure fully; 2. can consider assembly process | has low calculating efficiency |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Liu, Y. Numerical and Experimental Analysis for the Dynamics of Flawed–Machining Rod–Disk Rotor with Inner Misalignment. Machines 2022, 10, 355. https://doi.org/10.3390/machines10050355
Jin X, Liu Y. Numerical and Experimental Analysis for the Dynamics of Flawed–Machining Rod–Disk Rotor with Inner Misalignment. Machines. 2022; 10(5):355. https://doi.org/10.3390/machines10050355
Chicago/Turabian StyleJin, Xin, and Yi Liu. 2022. "Numerical and Experimental Analysis for the Dynamics of Flawed–Machining Rod–Disk Rotor with Inner Misalignment" Machines 10, no. 5: 355. https://doi.org/10.3390/machines10050355
APA StyleJin, X., & Liu, Y. (2022). Numerical and Experimental Analysis for the Dynamics of Flawed–Machining Rod–Disk Rotor with Inner Misalignment. Machines, 10(5), 355. https://doi.org/10.3390/machines10050355





