1. Introduction
With the widespread application of bearings in manufacturing machinery and equipment, bearing faults may cause serious equipment and personnel safety issues. Therefore, bearing fault issues have been attracting increasing attention. Generally, bearing condition detection includes two sequential processes of feature extraction and fault diagnosis [
1]. Fault feature extraction is a reference to system health and decision-making, on which many researchers have done a lot of research [
2,
3]; thus, it plays an important role in system monitoring. For the monitoring system of large equipment, the collection of signals needs to obey the Nyquist sampling theorem, making the amount of signals collected huge [
4] and challenging the transmission and storage equipment of the system. Meanwhile, due to the limitations of environmental factors, the signal obtained by the sensor needs to be transmitted and stored to the analysis system for further analysis, which requires the efficient and high-quality transmission of data. As an effective method, compressed sensing (CS) can effectively relieve the storage pressure of the system and reduce the cost of signal processing. Meanwhile, the large compression rate also makes CS more attractive [
5].
CS is a theory for data compression and recovery, which is proposed by Donoho [
6]. Generally, time of transmission will be greatly extended when the amount of data is large. According to the theory of CS, the original signal, which is sparse in a certain domain, often contains a lot of redundant data, which has little effect on the dynamic features of the original signal. Therefore, important data containing dynamic properties can be kept in the signal compression process, making the length of the compressed signal much shorter than the original signal. The advantage of CS is that the compressed signal not only reduces the requirements for hardware, but also improves the efficiency of data transmission.
In recent years, CS has been extensively used in many industries, such as medicine [
7], imaging [
8], and underwater communications [
9]. In mechanical fault diagnosis, many scholars have proposed various methods based on CS theory [
10,
11]. In CS theory, the random Gaussian matrix is extensively adopted as a measurement matrix to satisfy restricted isometric property (RIP) condition to the greatest extent [
12,
13]. CS reconstruction algorithms, such as matching pursuit (MP) [
14], basis pursuit (BP) [
15], and iterative thresholding (IT) [
16], have been developed and utilized by many scholars. Regarding dictionary selection, on the one hand, wavelet dictionary [
17], Fourier dictionary [
18], and discrete cosine dictionary [
19] are traditional dictionaries. On the other hand, there are also dictionaries that are constructed by the different signal characteristics, such as Symlet dictionary and Daubechies dictionary [
20]. Even so, it is still difficult for traditional dictionaries to represent noise signals sparsely. Therefore, a self-adaptive dictionary that can be constructed by the characteristics of the signal is needed. In the method of mining data characteristics, the modes of dynamic mode decomposition (DMD) contain fruitful dynamic information. Compared with the traditional dictionaries, the constructed DMD dictionary has the characteristics of the signal and is more self-adaptive. Meanwhile, it is theoretically considered that the DMD dictionary has a great potential to represent the original signal.
DMD [
21] is an equation-free and data-driven frequency analysis method, based on singular value decomposition (SVD) and Koopman spectrum analysis, which combines the nonlinear dynamic systems and measured results of complex systems with the recognized method in dynamic system theory [
22]. Compared with the application of traditional fault feature extraction methods in bearing signals [
23,
24], DMD has a good application prospect in bearing fault diagnosis. The DMD method decomposes the signal, which is rich in mechanical properties [
25], into a series of single-frequency and non-orthogonal modes with inherent dynamic characteristics, the reconstructed signal formed by the filtered mode matrix and time matrix can describe the dynamic characteristics of the original signal well. Each decomposed mode corresponds to an eigenvalue, the real part represents the growth rate, and the imaginary part represents corresponding frequency.
It has been proven that CS can compress and reconstruct the signal perfectly and relieve the pressure of equipment transmission and storage, while DMD can decompose original signal and obtain fruitful temporal and spatial coherency. Therefore, DMD and CS can complement each other. This idea has been fully reflected in previous studies [
26,
27,
28] and is called compressed dynamic mode decomposition (CDMD). CDMD considers two hypotheses, namely known and unknown full-state data. If full-state data is known, the data can be compressed, based on CS, and then decomposed by DMD. Then, the compressed mode can be calculated. Finally, the full-state modes of data, obtained through combing the full-state data and compressed modes, are utilized to characterize the flow field.
This paper puts forward compressed sensing, based on adaptive dynamic mode decomposition (ADMD-CS), adopting the frame of CS, in which the DMD dictionary is based on the specific dynamic modes obtained from adaptive truncated rank dynamic mode decomposition (ADMD). The original signal can be compressed through the DMD dictionary constructed by ADMD and efficiently reconstructed, in order to reduce the storage space and improve transmission efficiency. Different from previous combination of CS and DMD [
28], ADMD-CS focuses on the representation of the current signal via modes obtained from ADMD. By concatenating the dominant modes obtained from ADMD, as well as the modes that have the largest inner product with the fundamental frequency and multiple frequency, the DMD dictionary can be built. The best truncated rank is selected automatically by the improved particle swarm algorithm (IPSO), which can improve DMD decomposition accuracy effectively. Due to the fundamental and multiple frequency, which can be estimated by [
29], the new dictionary is utilized to represent the original signal based on the fact that deviation exists between actual and ideal signals, and it is also used to extract the fault frequency under the noise background. The deviation is based on the power ratio of the low-rank matrix to the noisy signal [
30].
The main structure of this article is as follows:
Section 2 introduces CS, DMD theory, and the construction process of the DMD dictionary. IPSO and error indexes are also included. In
Section 3, the validity of the DMD dictionary and ADMD-CS is proven by processing the simulation signal. In
Section 4, the effectiveness of ADMD-CS in the experimental signal is verified. The last section draws a conclusion to this paper.
3. Application of ADMD-CS in the Simulation Experiment
In this section, ADMD-CS is applied to the bearing simulation signal model established by Randall [
43]. Due to the structural characteristics of the bearing, when the inner and outer rings of the bearing rotates relatively, the rolling elements will be subjected to different alternating loads, due to the different position. When the bearing faults, the bearing will generate an instantaneous impact signal and vibrate at its own inherent frequency.
Supposed that
is the sampling time interval,
is the natural oscillation frequency function of the bearing,
is the amplitude of the
-th impulse response, and
is the background noise with zero mean, the model of the simulation signal can be expressed as:
where
is the
-th impact energy,
and
are initial phases,
is the modulation frequency,
is the attenuation coefficient (relevant to the bearing system),
is the lag time caused by fluctuations, and
is a constant.
The parameter in Formula (32) is shown in
Table 1. The fault frequencies of the inner ring, outer ring, rolling element, and cage are
,
,
, respectively. Take the fault signal of the inner ring as an example. The sampling frequency is selected as
= 6 kHz, and the number of sampling points is
= 5000. At the same time, Gaussian white noise is taken into consideration, so as to make SNR reach 3dB. Haar dictionary, Fourier dictionary, and discrete cosine dictionary are employed for comparison, in order to verify the superiority of the AMDM-CS. Firstly, the historical signal is generated through a simulation signal model and decomposed with ADMD; we take the order of Hankel matrix
= 2048. Then, the best truncated rank is selected,
= 32, by the IPSO, and the manual truncated rank is selected when the energy of the eigenvalue is up to 90% of the total energy of all eigenvalues. Next, a new mode matrix is generated, and modes corresponding to the fault and multiple frequencies are picked out, according to Formula (26). Finally, the first mode matrix is concatenated with filtered modes to form a DMD dictionary, where each column represents a mode (an atom). At last, we get a dictionary with 91 atoms. The current signal is generated when 3 dB noise is added to the historical signal. The simulation bearing fault signal is shown in
Figure 5. The parameters of the bearing simulation signal are shown in
Table 1.
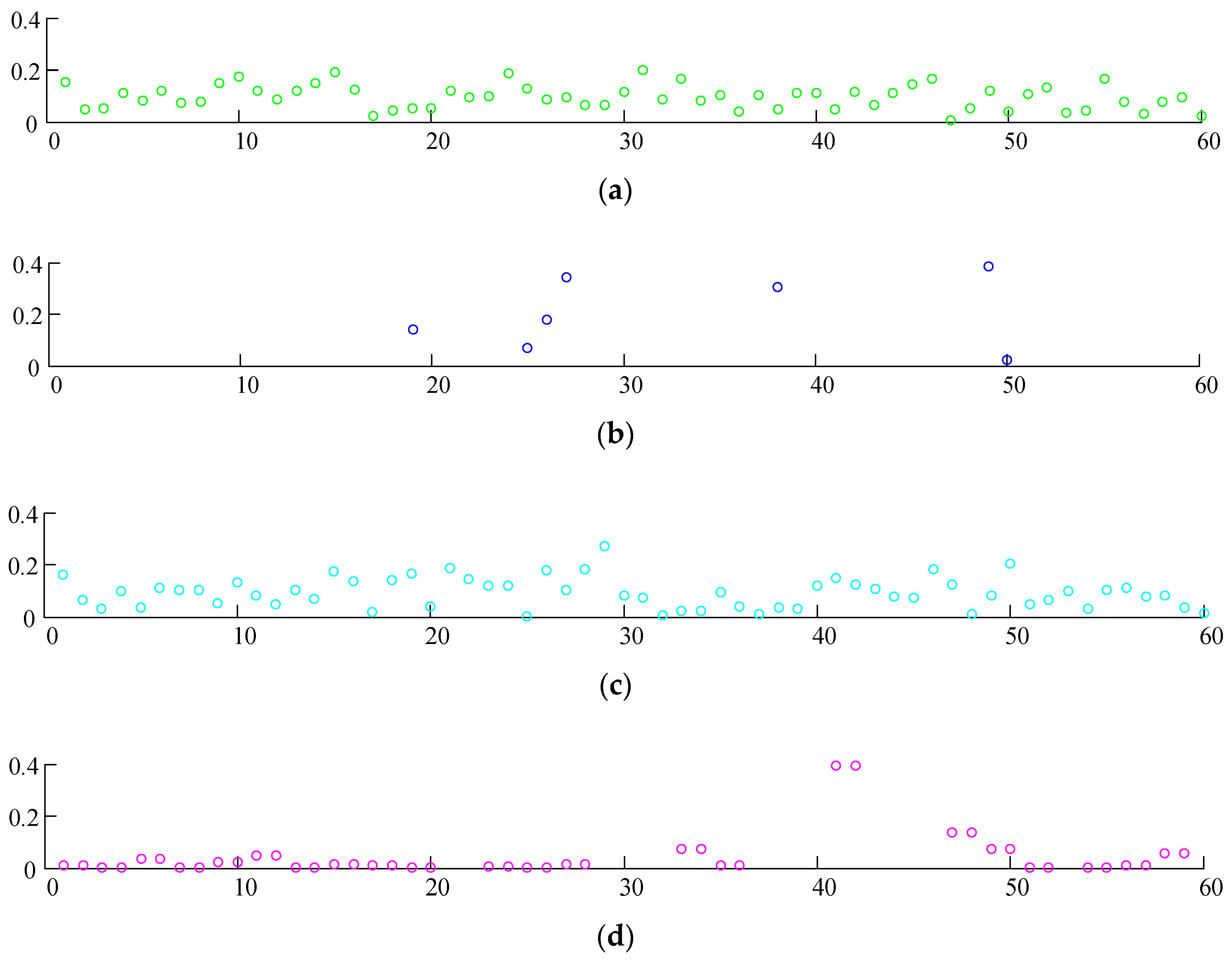
To verify the sparsity of the DMD dictionary, it is compared with traditional dictionaries. The sparse coefficients of each dictionary are shown in
Figure 6.
As shown in
Figure 6, the sparsity of the sparse coefficients of each dictionary is relatively small. For the first three dictionaries, because they are stable and not designed for the signal, the dictionary owns a wide range of frequency. In addition, the signal contains noise, and their coefficients are not zero. The DMD dictionary is composed of the main modes containing the dynamic characteristics of the signal, so its coefficients are also non-zero. What is different is that its coefficient distribution is more regular, and there would be more elements close to zero than in other dictionaries. In other words, this coefficient vector is sparser. Furthermore, DMD modes are rich in signal characteristics, and they are more self-adaptable to signals. According to the estimation of the low-rank matrix in [
30], the estimated power ratio of the noise-free signal to the noisy signal is 0.4511, and the signal represented by the DMD dictionary has a power ratio of 0.4594, with a difference of 0.0083. It can be considered that the DMD dictionary represents the original signal well.
In actual application scenarios, the signal needs to be preprocessed and compressed in the sending module, then reconstructed in the receiving module. As mentioned above, there are many recovery algorithms for signals, typically including the L1, OMP, and IT algorithms. In order to select efficient and high-quality recovery algorithms, these three typical algorithms are compared in
Figure 7. Then, the reconstruction time and quality of the recovery signal processed by the DMD dictionary are compared, and the quality is measured by RMSE and CORR, as proposed in Formulas (28) and (29). The reconstructed time and quality of each algorithm are shown in
Figure 7.
As shown in
Figure 7 and
Table 2, among these three algorithms, the reconstructed time of the IT and OMP algorithms is much shorter than that of L1 algorithm, and the reconstructed time of the IT algorithm is almost equivalent to the OMP algorithm. In terms of reconstructed quality, the reconstructed quality of the IT algorithm is slightly lower than the other two algorithms (reconstruction quality of the OMP and L1 algorithms are too close, and their curves overlapped). However, the IT algorithm has higher signal requirements than other algorithms. Therefore, from the perspective of factors such as reconstruction time and quality, the OMP algorithm is the most suitable among three algorithms and has a wide range of applicability. It can be used as the reconstruction algorithm for experimental data.
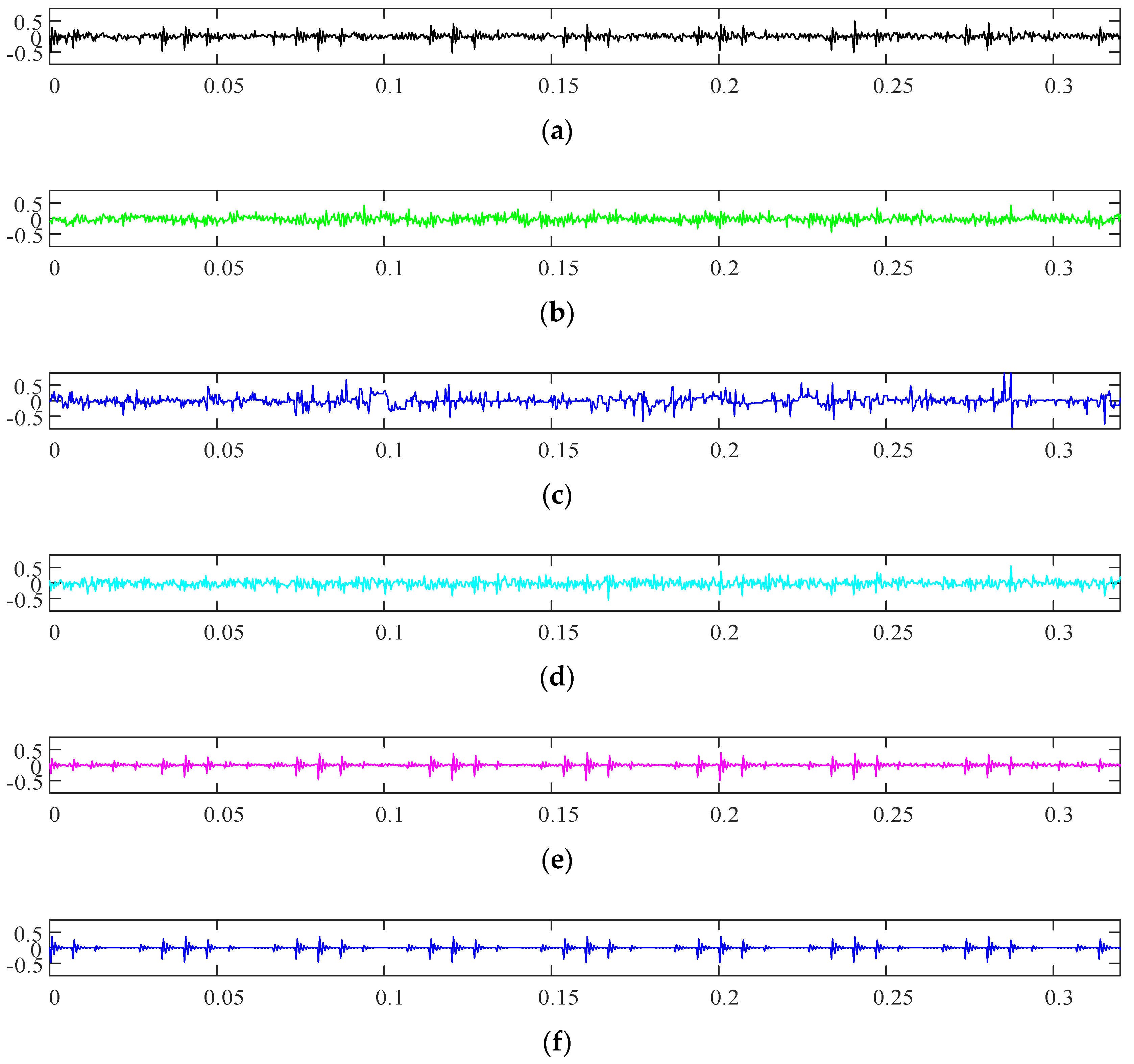
After the compression of the original signal, the simulation signal is reconstructed by the OMP algorithm; the reconstructed signals are shown in
Figure 8. The CORR and RMSE of each reconstructed signal to the noisy signal and no-noise signal are shown in
Table 3.
In
Figure 8, the reconstructed signal (e), via the DMD dictionary, is compared with (a), and most of the noise in (e) is removed; it is even similar to the noise-free signal (f). This is proven in
Table 3 by the CORR and RMSE of the noise-free signal. Due to the wide frequency range of dictionary atoms and existence of noise, traditional dictionaries are not sparse enough in their respective domain; the noise is retained in the reconstruction process and even causes signal distortion. The DMD dictionary is composed of main modes containing signal characteristics, so useful components can be retained during the reconstruction process, and noises can be removed effectively, as well. As shown in
Table 3, the correlation between the ADMD-CS reconstructed signal and noisy signal is better than other reconstructed signals. For the noiseless signal, the CORR and RMSE of ADMD-CS reconstructed signal are also better than other reconstructed signals. It could be conducted that ADMD-CS has a good denoising effect, and the DMD dictionary has good adaptability.
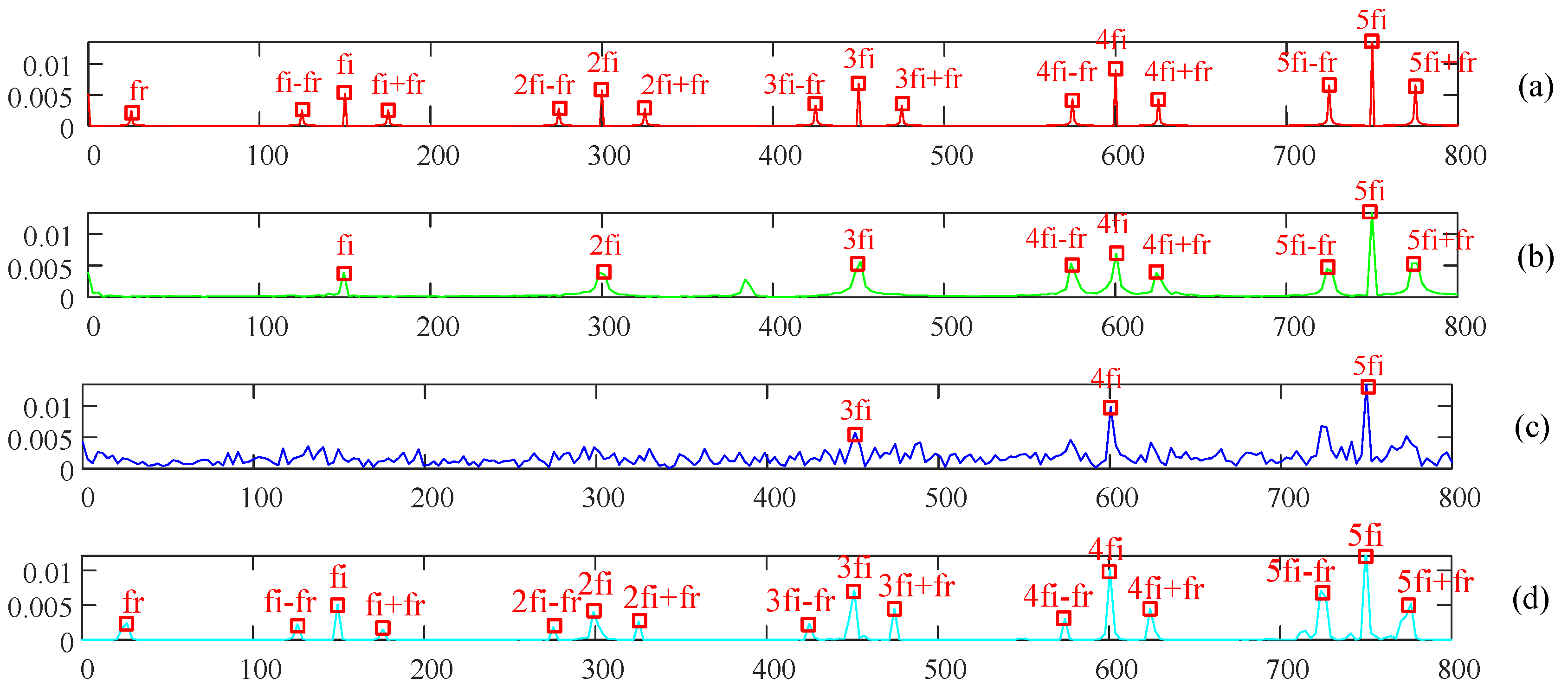
In order to judge the performance of the proposed method in denoising, ADMD-CS is compared with traditional denoising methods, such as SVD and EMD, in the frequency domain. Frequency domains of various methods are shown in
Figure 9.
As shown in
Figure 9 and
Table 4, compared with the traditional denoising methods, ADMD-CS has better effect than traditional methods in extracting the fault frequency by qualitative and quantitative indexes. The traditional SVD can remove plenty of noise; the low-energy fault frequencies submerged in the noise also can be removed, and the SNR of the recovered signal is −0.3188. The EMD method decomposes the signal into some intrinsic mode functions (IMFs). Each IMF contains noise consequently, but only those noises in unnecessary IMF are removed during the reconstructed process. Those IMFs containing fault features, needed to reconstructed original signal, are still accompanied by noise. As a result, the fault frequency is submerged in the noise background and cannot be distinguished. SNR of the recovered signal by EMD is −1.6664. ADMD-CS uses the faulty atoms of the historical signal to extract useful components. The noise is less in each atom, compared to the original signal. Each atom corresponds to a single frequency; after the power is enhanced in frequency domain, the noise is further suppressed, so as to achieve the purpose of denoising and extracting the fault frequency. ADMD-CS can effectively remove the noise in the original signal; the obtained reconstructed signal is purer, and the characteristic and multiple frequencies can be clearly displayed. Meanwhile, its SNR is 0.3017, which is higher than that of SVD and EMD, consistent with the results shown in
Figure 9, indicating that ADMD-CS has excellent performance in feature extraction and noise reduction.
In actual application scenarios, CS is adopted as the transmission method, and the signal transmission cost and storage space are greatly reduced, compared with other traditional methods that need to collect and transmit a large amount of data. Signals reconstructed by traditional SVD, EMD, and ADMD-CS were saved as “.xls” format files, respectively; the file sizes were 99, 99, and 33.5 kb, respectively, and the size of the original signal was 99 kb, which is shown in
Table 5. From the perspective of storage, the storage space of the signal processed by the traditional methods is almost unchanged, while the storage space of ADMD-CS is greatly reduced, with the reduction being about two-thirds of that of the traditional methods, and the CR is 66.16%. The effect of denoising is better than traditional methods, and it could be seen that the advantages of ADMD-CS are more obvious. Signal analysis and processing are often carried out after the signal transmits to the processing system. Compared to traditional fault feature extraction methods, ADMD-CS can be carried out in the signal sending module, which reduces the pressure on the signal receiving module.
4. Application of Algorithm in Experimental Data
The actual fault signal is more complex than the simulation signal and easily interfered by noise during the transmission process. To verify the effectiveness of ADMD-CS in the experimental signal, the method is applied to the experimental signal data of rolling bearings, as published by Cincinnati University [
44].
The structure of the Cincinnati University test bench is shown in
Figure 10. Four Rexnord ZA-2115 double-row bearings were mounted on a 2000 rpm shaft, which was driven by an AC motor via sever rub belts. Each row of the bearing had
= 16 rolling elements. The bearing pitch and rolling element diameter were
= 28.15 mm and
= 3.31 mm, respectively. The contact angle of bearings was
= 15.17°. The vibration signal was collected by a high-sensitivity quartz ICP accelerometer, installed in the bearing box, and the signal was recorded via a NI DAQ Card 6062E.
The sixth channel of the first data set was employed, sampling frequency was set as
= 20 kHz, and number of data points was set as
= 20480. The rotation and fault frequencies were calculated as
= 33.3 Hz and
= 296.63 Hz. We take the order of the Hankel matrix:
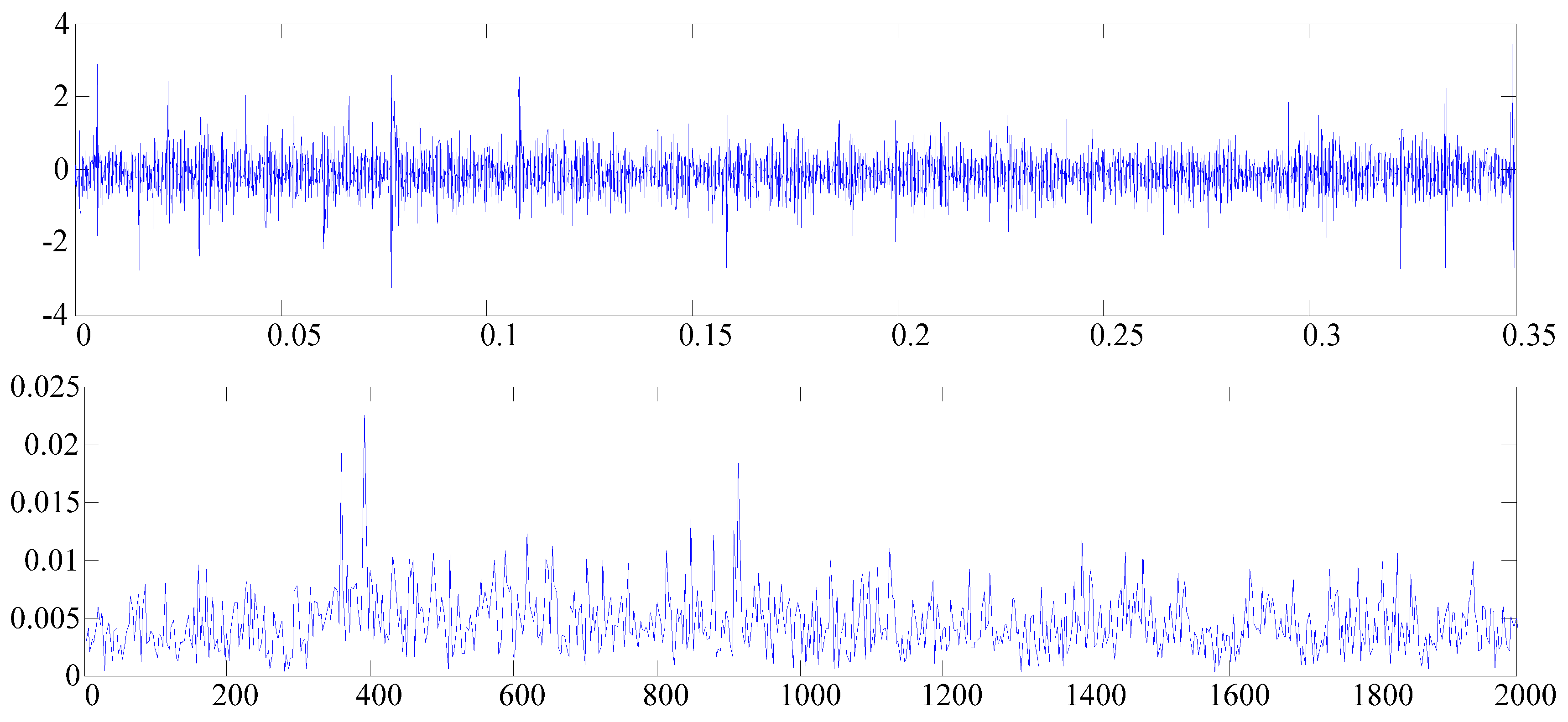
= 7000. The time domain and frequency domain of the signal are shown in
Figure 11.
As shown in
Figure 11, only a few prominent spikes could be observed in the frequency domain. The fault frequency of the signal was submerged in noise and could not be distinguished; ADMD-CS was, thence, adopted to represent the original signal. The historical signal was decomposed by ADMD, and a new dictionary could be constructed via DMD modes—a total of 565 atoms were obtained. According to the literature [
30], it is estimated that the measured signal power ratio is 0.3185, power ratio expressed by the DMD dictionary is 0.2589, difference is 0.0596, difference is small, and estimation is considered to be suitable. The signal is then reconstructed through the OMP algorithm.
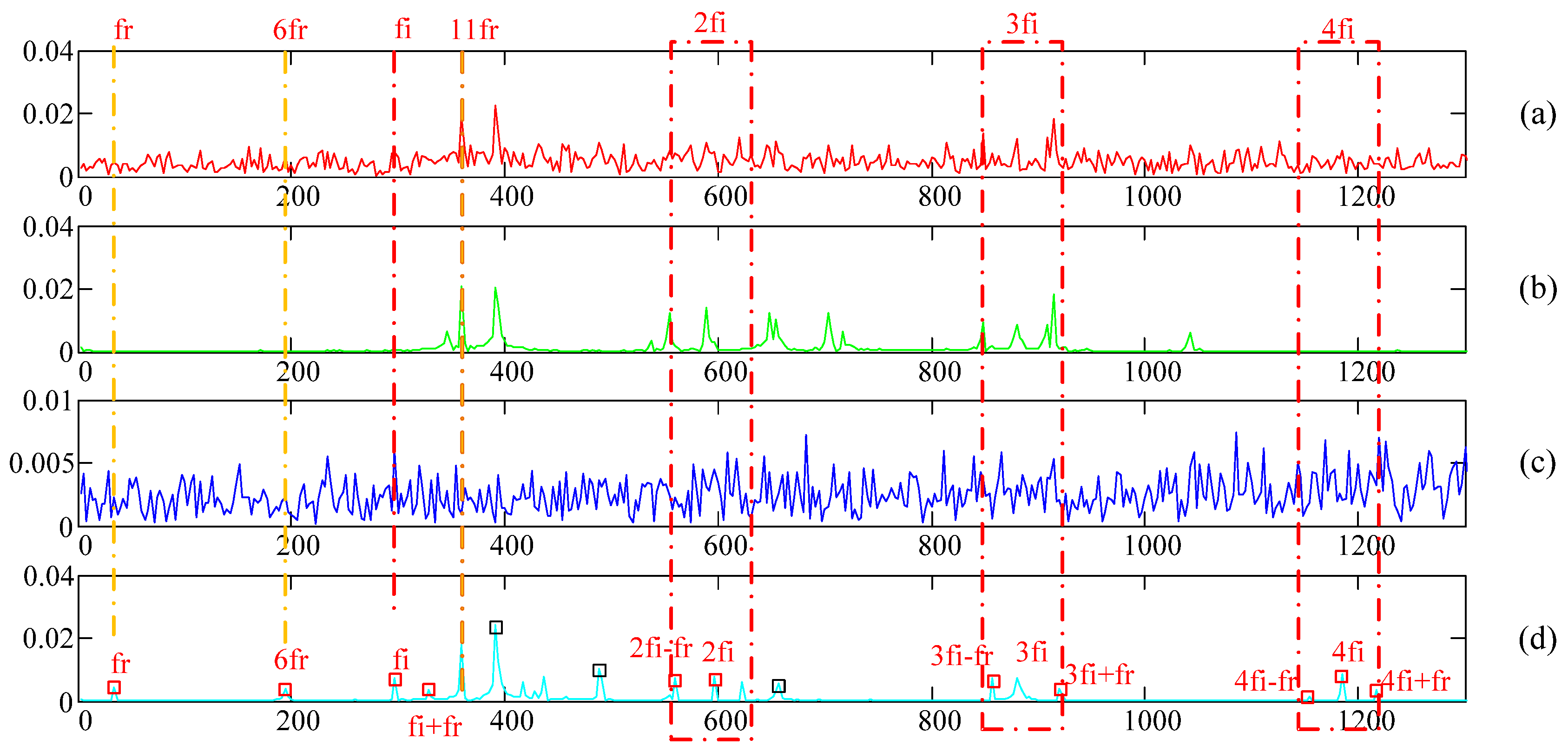
To verify the effectiveness of the proposed method in noise reduction, the signal recovered by ADMD-CS was compared with the signal recovered by traditional SVD and EMD in the frequency domain. Additionally, the frequency domains of the different methods are shown in
Figure 12.
Though the comparison of the three methods in
Figure 12 and
Table 6, it can be easily found that, though SVD can remove plenty of noise, the low-frequency fault component submerged in the noise was also removed as noise, and only the part of the fault frequency with strong energy was retained. While EMD decomposes the signal into several IMFs, noise exists in each IMF. When some IMFs containing fault features are used for reconstruction, the noise in each IMF is not removed, and it is even brought into the reconstructed signal, in turn, resulting a lot of noise in frequency domain, making it difficult to distinguish and extract the fault frequency. ADMD-CS approximates the original signal by using the fault frequency modes obtained by the ADMD of the historical signal. The frequency range narrows when the dictionary is constructed, and the noise is further suppressed in the frequency domain because of enhanced power. The reconstructed signal is purer, making it possible to extract the fault frequency submerged in the noise. However, we should notice that, though the noise of the signal is suppressed, to a certain extent, and fault frequency is extracted successfully, there are still some unknown components in the frequency domain. To be honest, ADMD-CS has a better performance in fault extraction than the SVD and EMD methods. The SNR of the reconstructed signals processed by ADMD-CS was 0.8407, while that processed by SVD and EMD were 0.6193 and 0.2920, respectively, which also verifies that ADMD-CS has an excellent noise reduction performance. In addition, the traditional signal collection and transmission methods in actual application scenarios put great pressure on the collection and storage system. As can be seen from
Table 7, ADMD-CS has better compression performance and CR is 59.08%. ADMD-CS compresses and reconstructs the signal based on CS, which not only alleviates the collection and storage space, but also performs preliminary signal processing, consequently reducing the pressure for subsequent further analysis; it has certain application potential in actual application scenarios.
5. Conclusions
As an equation-free and data-driven frequency analysis method, based on SVD and Koopman spectrum analysis, ADMD can describe dynamic features of the original system. Therefore, the modes obtained from ADMD can be constructed as a self-adaptive dictionary to represent the original signal, while selecting a suitable dictionary is a key problem of CS theory. As a mutual complement, by combining these two features from DMD and CS, ADMD-CS is proposed, based on CS and ADMD.
In this paper, a self-adaptive dictionary, based on ADMD, is constructed; the original signal is reconstructed based on the actual situation, where there is an error between the ideal and actual signals. Firstly, the historical signal is decomposed by ADMD; then, the best truncated rank is selected through IPSO, and the energy modes are obtained. Simultaneously, the fault modes are picked out through inner product, with fundamental and multiple frequencies. Finally, the DMD dictionary is built up through concatenating the two mode matrices. Compared with traditional dictionaries, the DMD dictionary demonstrates a good effect on representing the original signal. The CORR between reconstructed signal and noise signal was 0.8109, and, between the reconstructed and non-noise signals, it was 0.9278; the RMSE was 0.0659 and 0.0351, respectively. Compared with the traditional denoising method of SVD and EMD, ADMD-CS has the better denoising effect. In this paper, SNR is used as a quantitative indicator of denoising performance. It was found that the SNR of the simulation and experimental signals processed by ADMD-CS was higher than that of traditional denoising methods, which were 0.3017 and 0.8407, respectively. The storage space of signal processed by ADMD-CS was quite smaller than the traditional methods, and the CR of the simulation and experimental signals were 66.16% and 59.08%, respectively. The main contributions of this paper are as follows:
- (1).
A new fitness function of the IPSO algorithm is defined, namely a synthetic envelope kurtosis characteristic energy difference ratio. Additionally, a better decomposition effect can be achieved by using optimized target parameters.
- (2).
A nonlinear dynamic inertia weight is used to optimize the traditional PSO algorithm, which is out of local search, and adaptively selects the truncated rank and threshold value to obtain a better decomposition effect and accurately extract fault features.
- (3).
Combined ADMD with CS to form a new method, namely ADMD-CS. It compresses and reconstructs the signal to achieve the goal of reducing storage space and improving transmission efficiency.
- (4).
Enhance the power of the mode in the frequency domain and use OMP to suppress the noise to obtain a better reconstructed signal.
Both DMD and CS have been widely used in their respective communities. This paper proposes the method of ADMD-CS for constructing an adaptive dictionary, signal transmission, and fault extraction. By applying ADMD-CS to simulation and experimental signals, the effect of representing the original signal and noise reduction are proved. The DMD dictionary is formed by energy and fault modes, and the truncated rank determines how many atoms there are in the energy mode matrix. The power of the modes is enhanced in the frequency domain to suppress noise. Though ADMD-CS outperforms traditional dictionaries and denoising methods, and noise has been better processed, there are still several unidentified components in the signal. In addition, the deviation of two power ratios in the experimental and simulated signals is a problem that should be paid attention to. SNR will influence this ratio; as a result, the performance of the extract fault features may be influenced. With different SNR in the signal, research on effect of this ratio and how to shrink this deviation will be our future work. Moreover, we will further analyze the signals collected in large equipment and further optimize them by using methods such as compression sampling matching tracking algorithm, so as to apply them to practical industrial production as soon as possible.