Analysis of the Static Performance of a Cableless Aerostatic Guideway
Abstract
:1. Introduction
2. The Mathematical Model of Air Film Flow
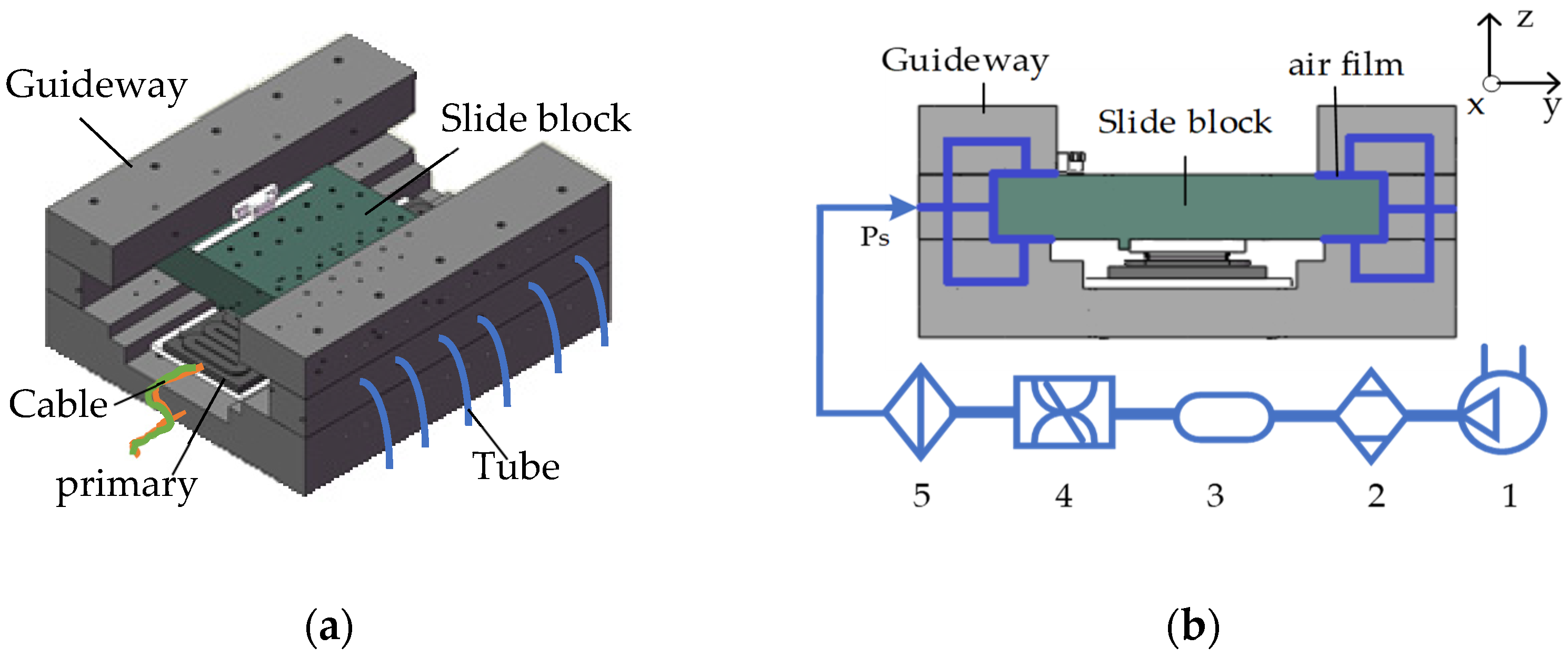
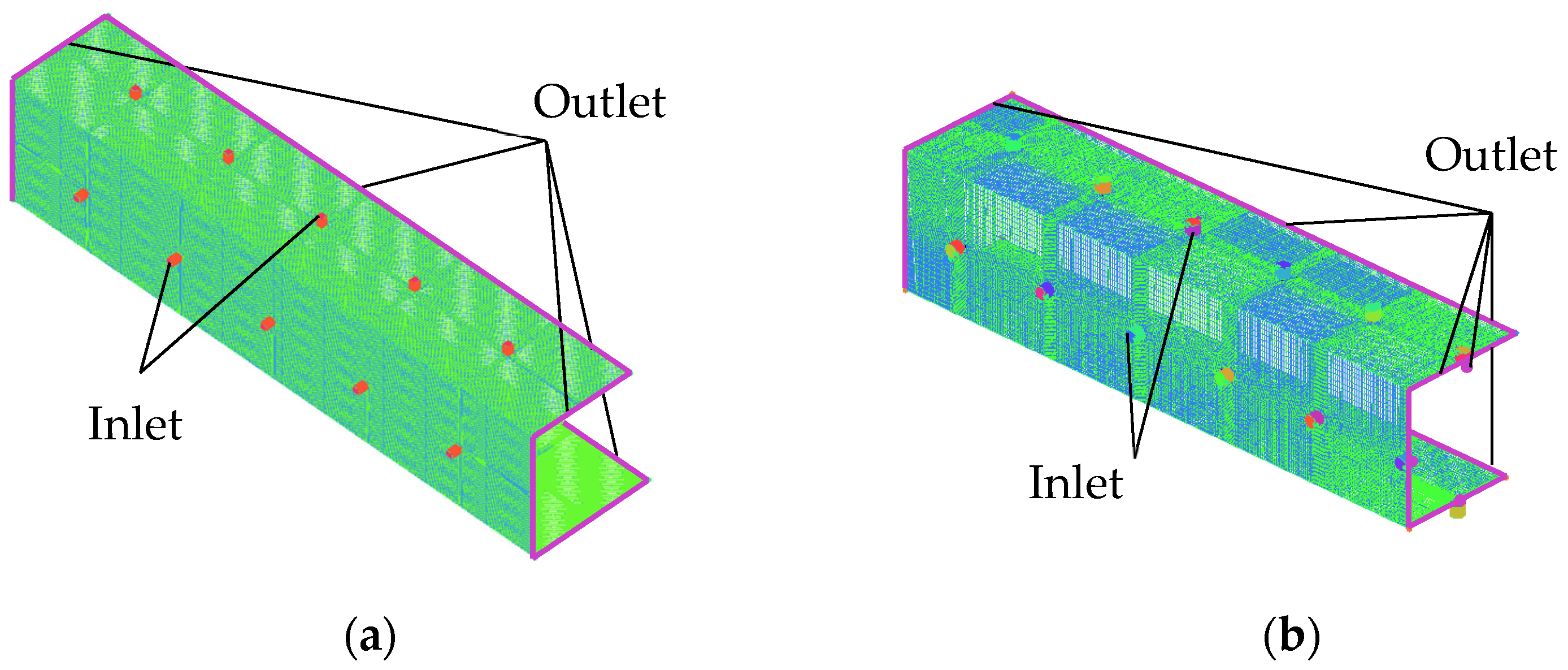
2.1. The Structure and Operational Principle of the Aerostatic Guideway
2.2. The Governing Equations of the Fluid Flow
- The flow is isothermal, the gas viscosity is constant, and the air is an ideal gas.
- The flow is parallel to the wall and only changes in the direction of the vertical wall.
- There is no pressure gradient in the flow direction and no chemical action on the wall.
- The inertia force is too small relative to the damping force and gravity, and the effect of the fluid inertia force is ignored.
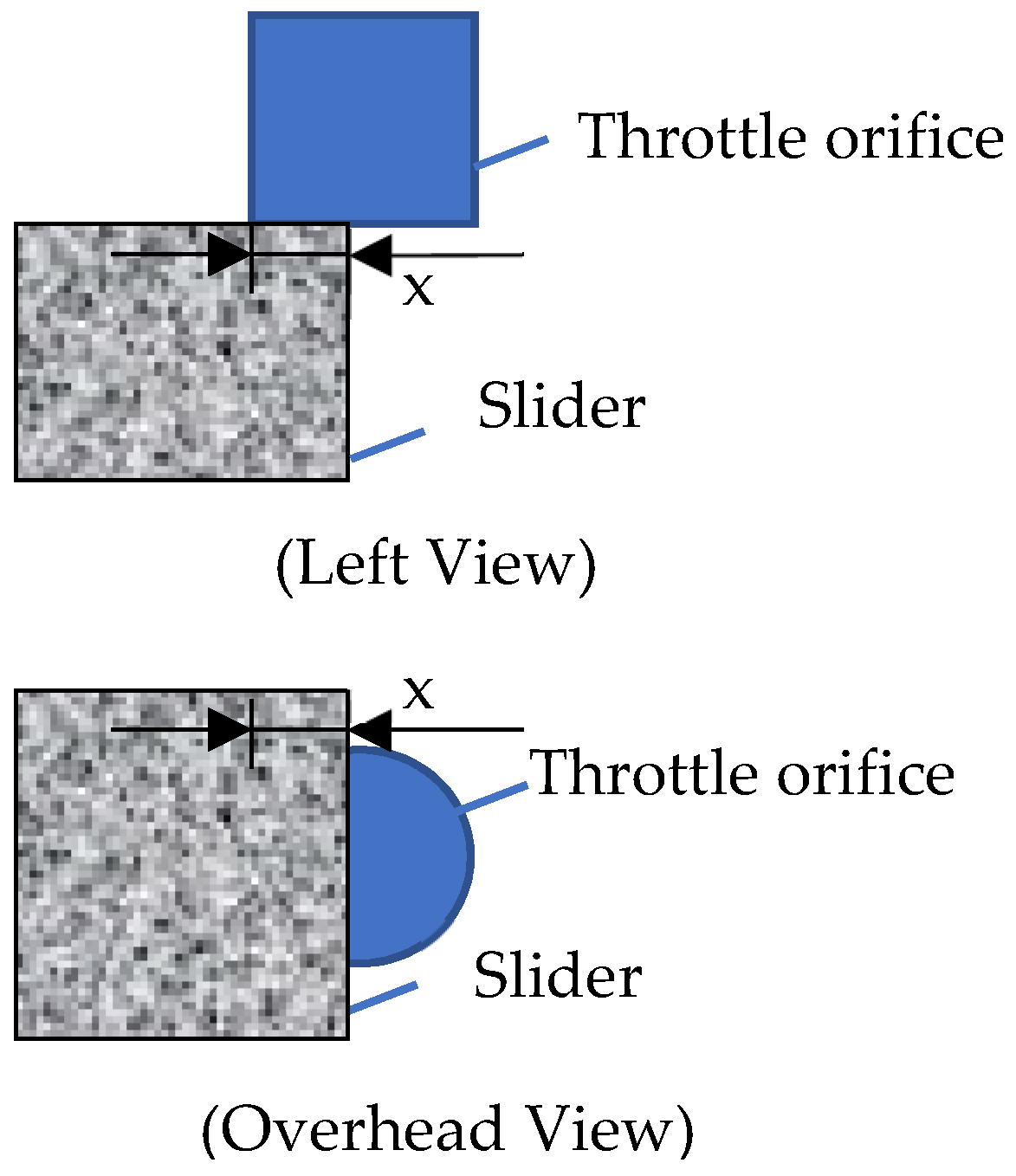
2.3. Boundary Conditions
- Pressure boundary condition
- Temperature boundary condition
- Symmetric boundary conditions
3. Results and Discussion
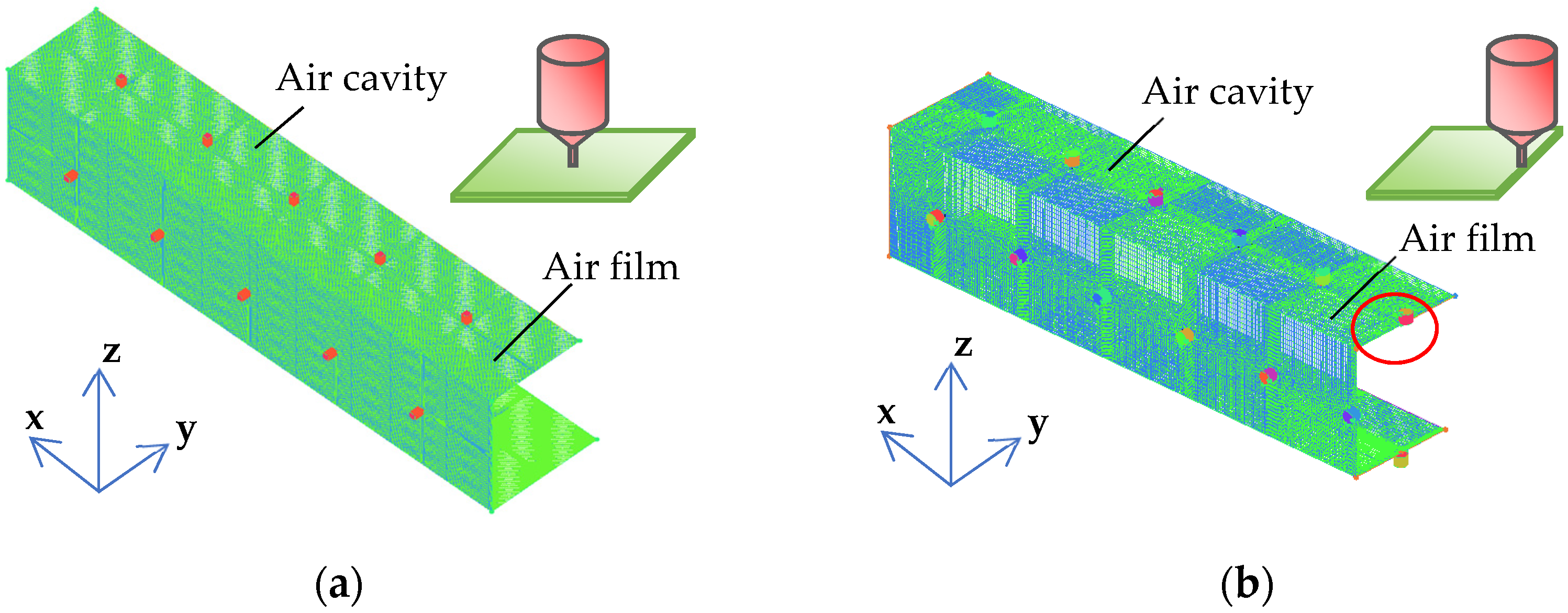
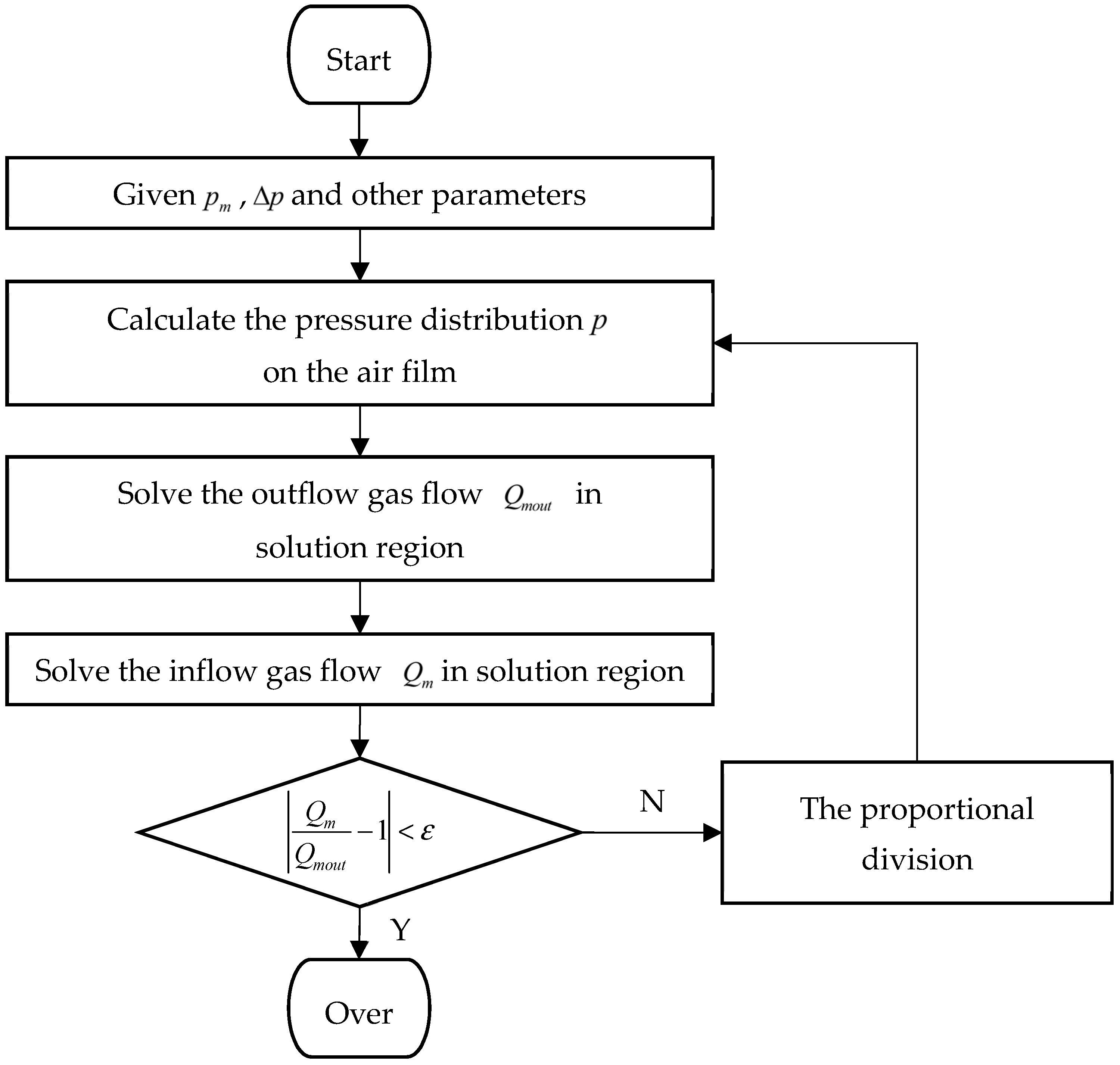
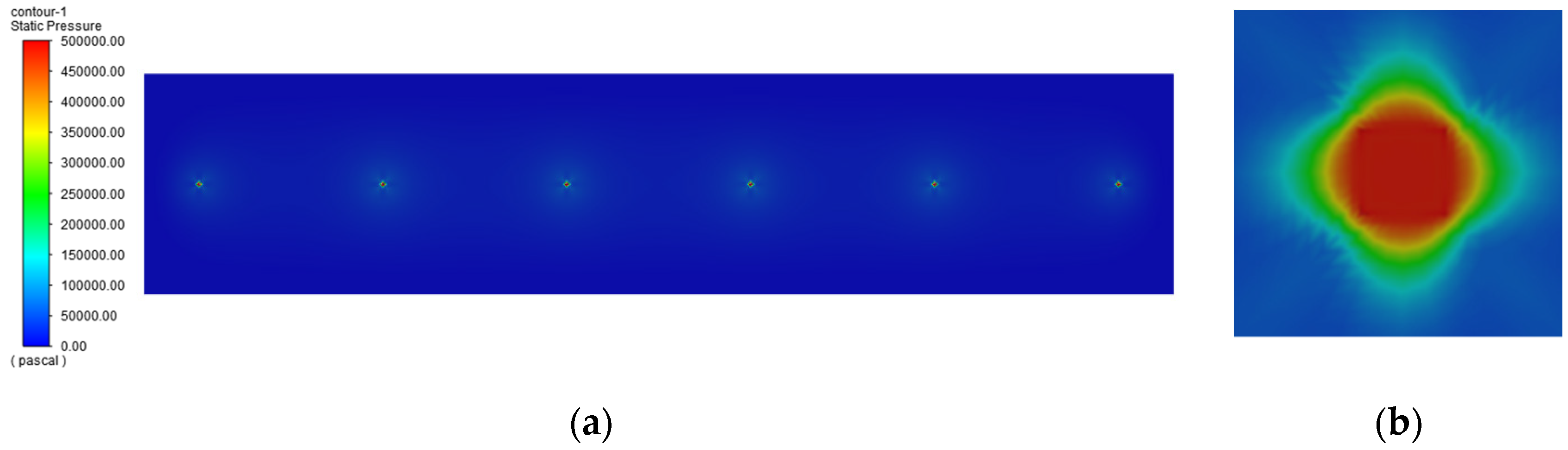
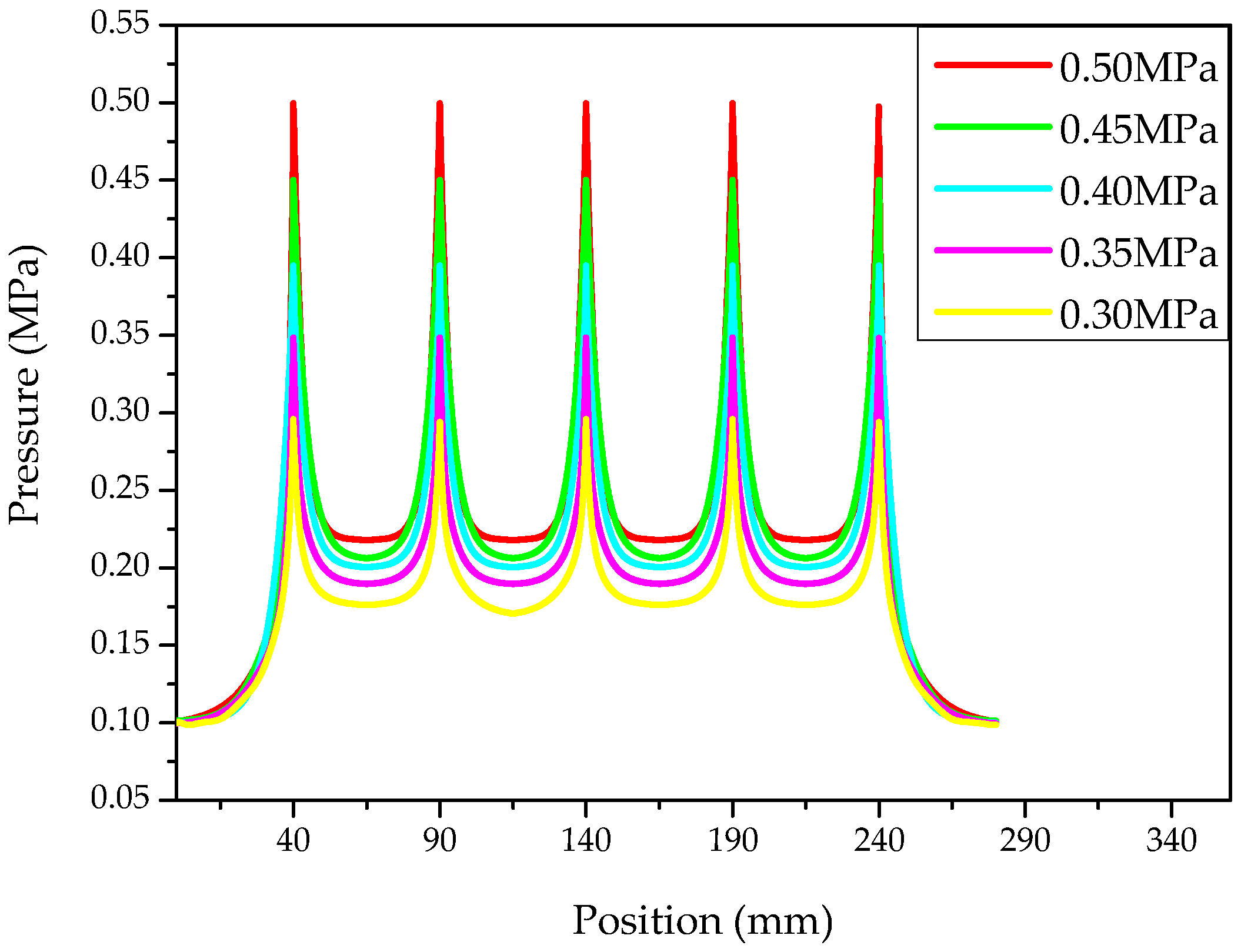
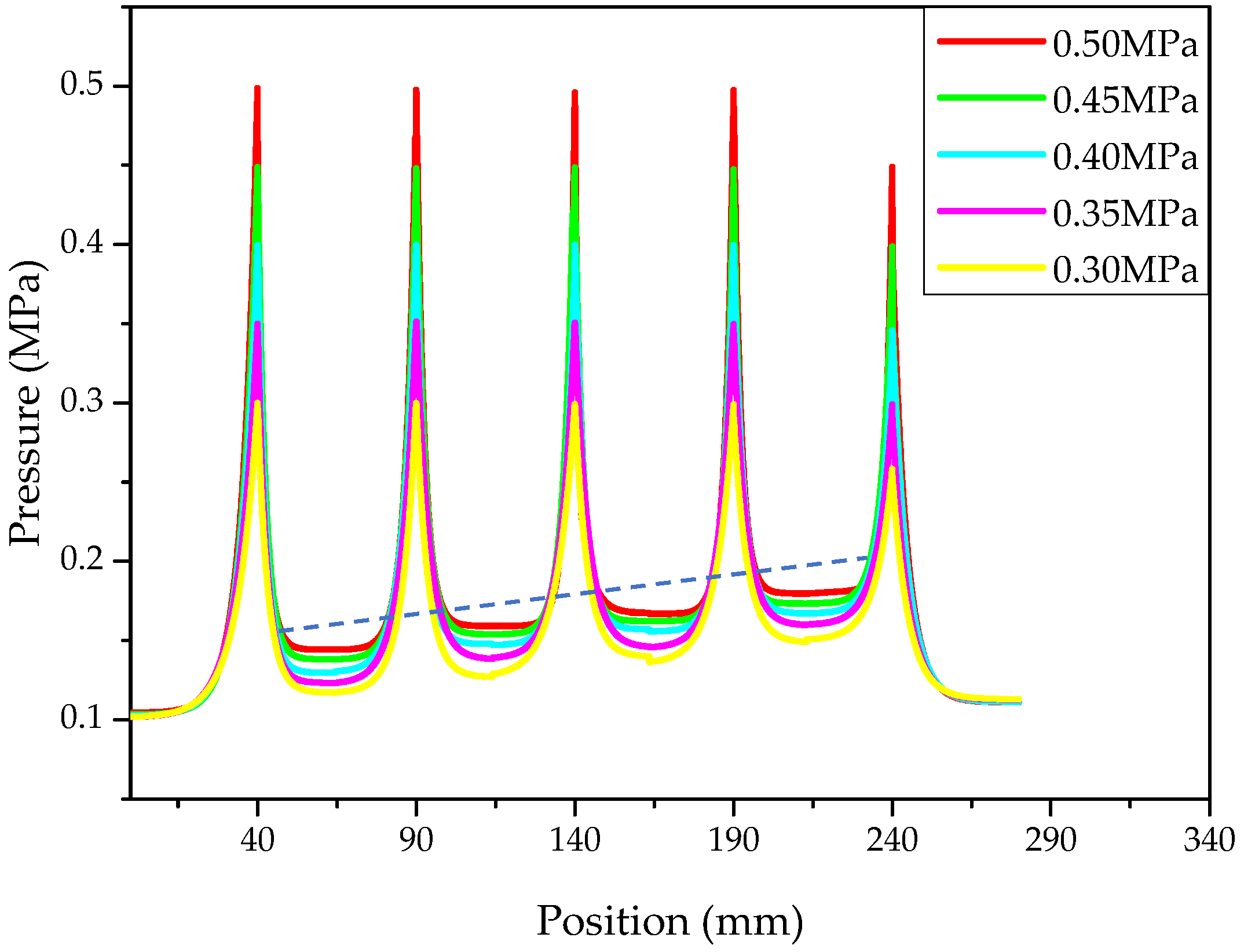
3.1. The Calculation and Analysis of the Pressure Distribution of Air Film
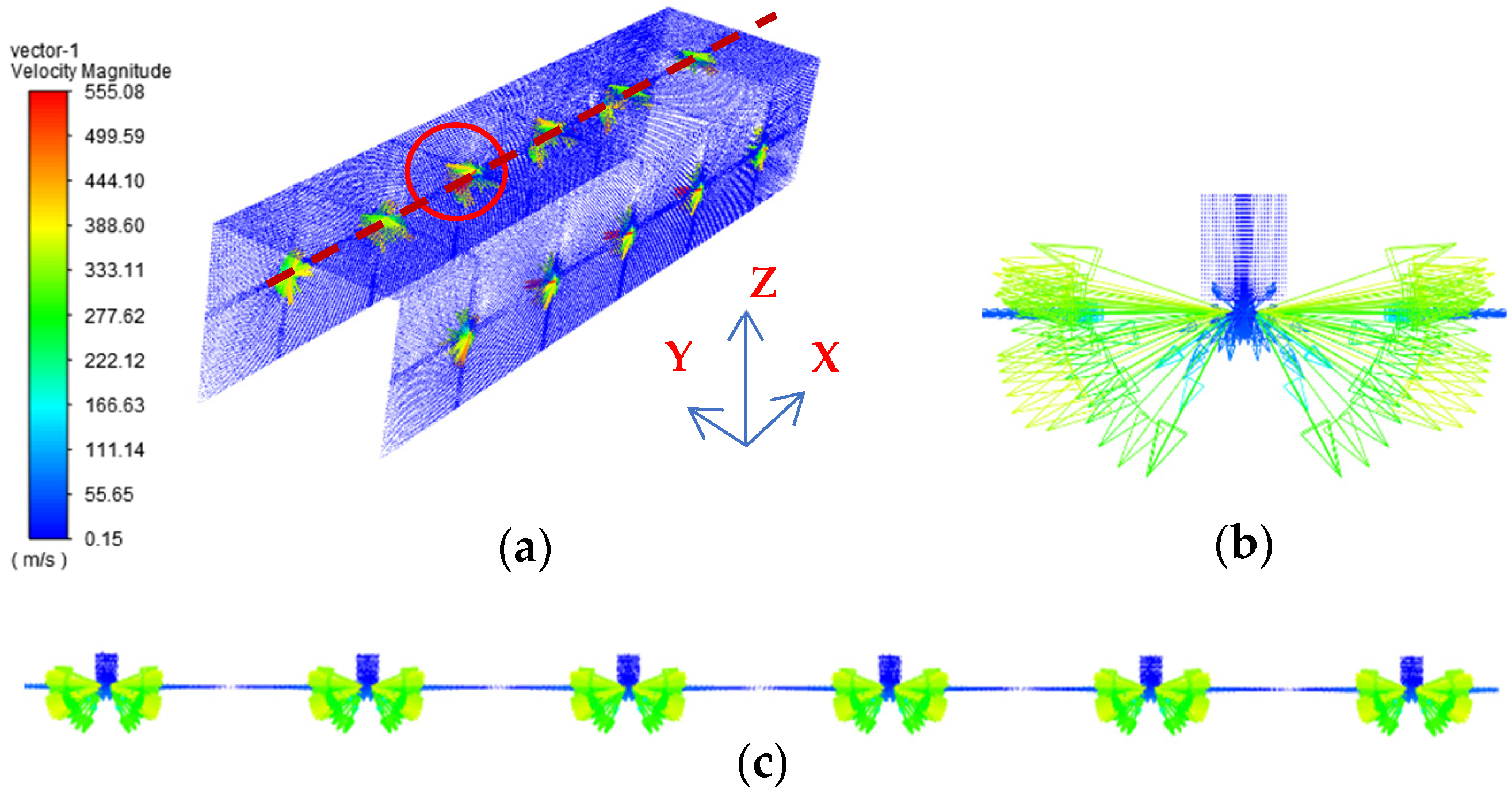
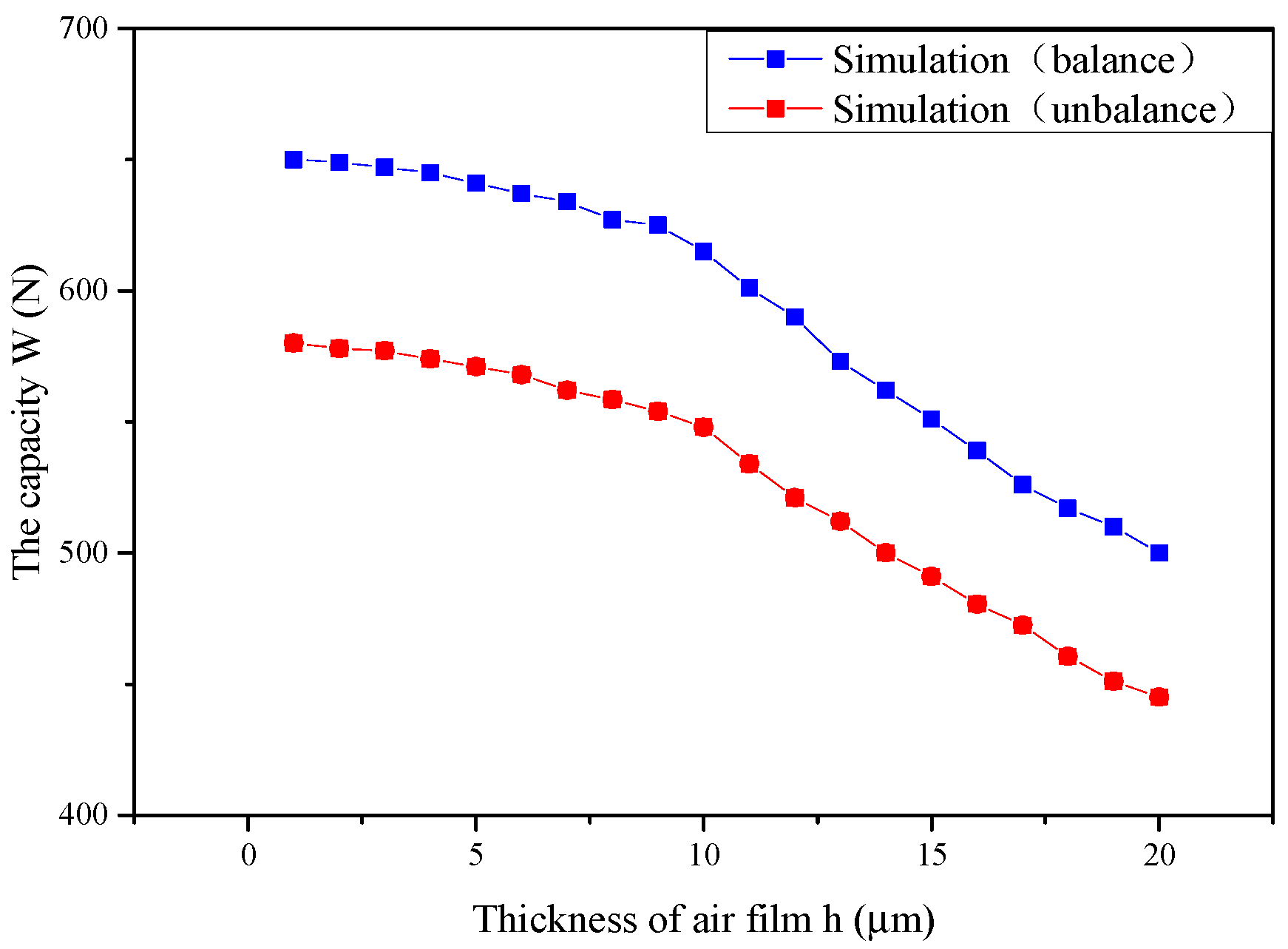
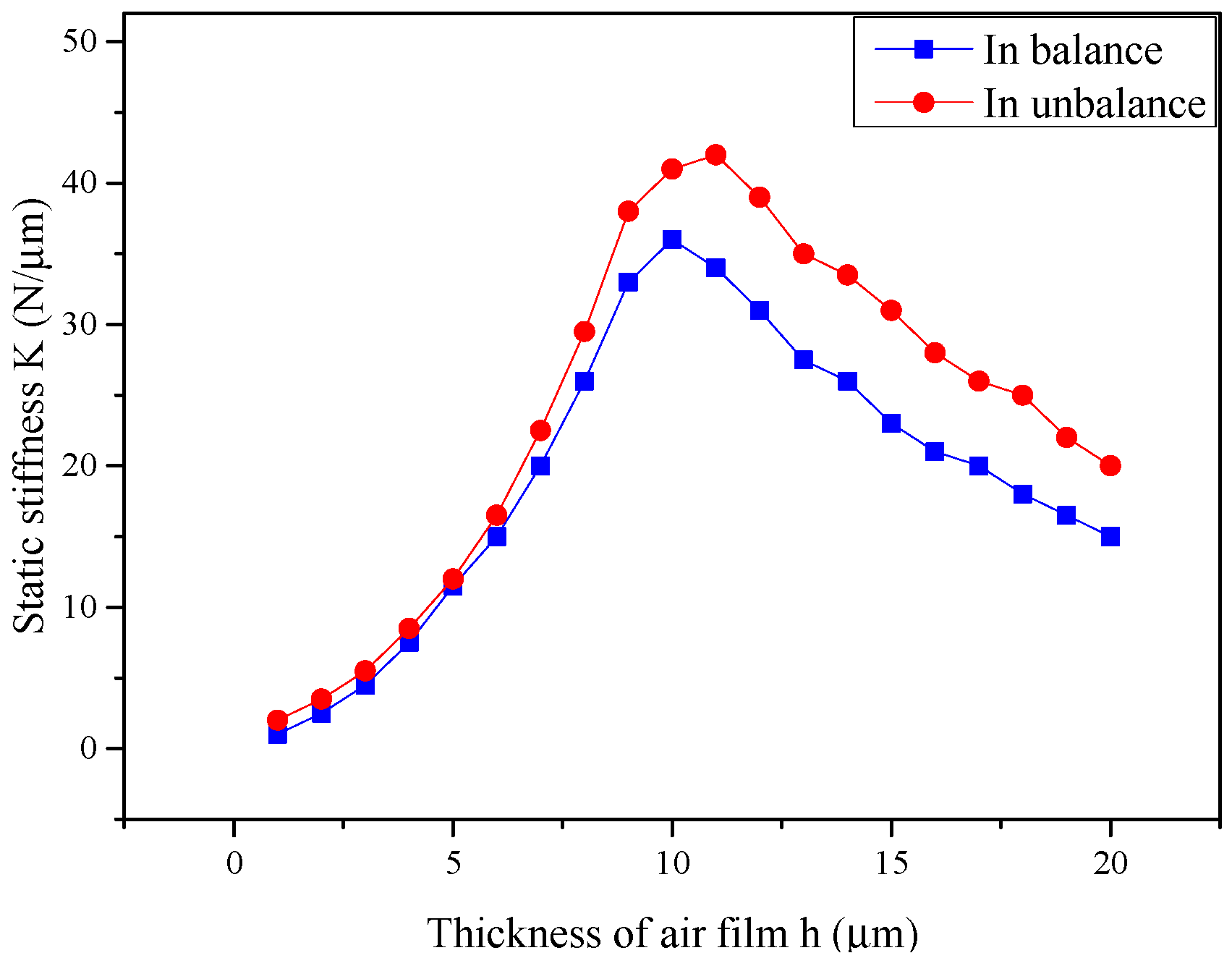
3.2. The Analysis of the Static Performance of the Aerostatic Guideway
4. Verification of Experimental Results
4.1. Equipment and Method
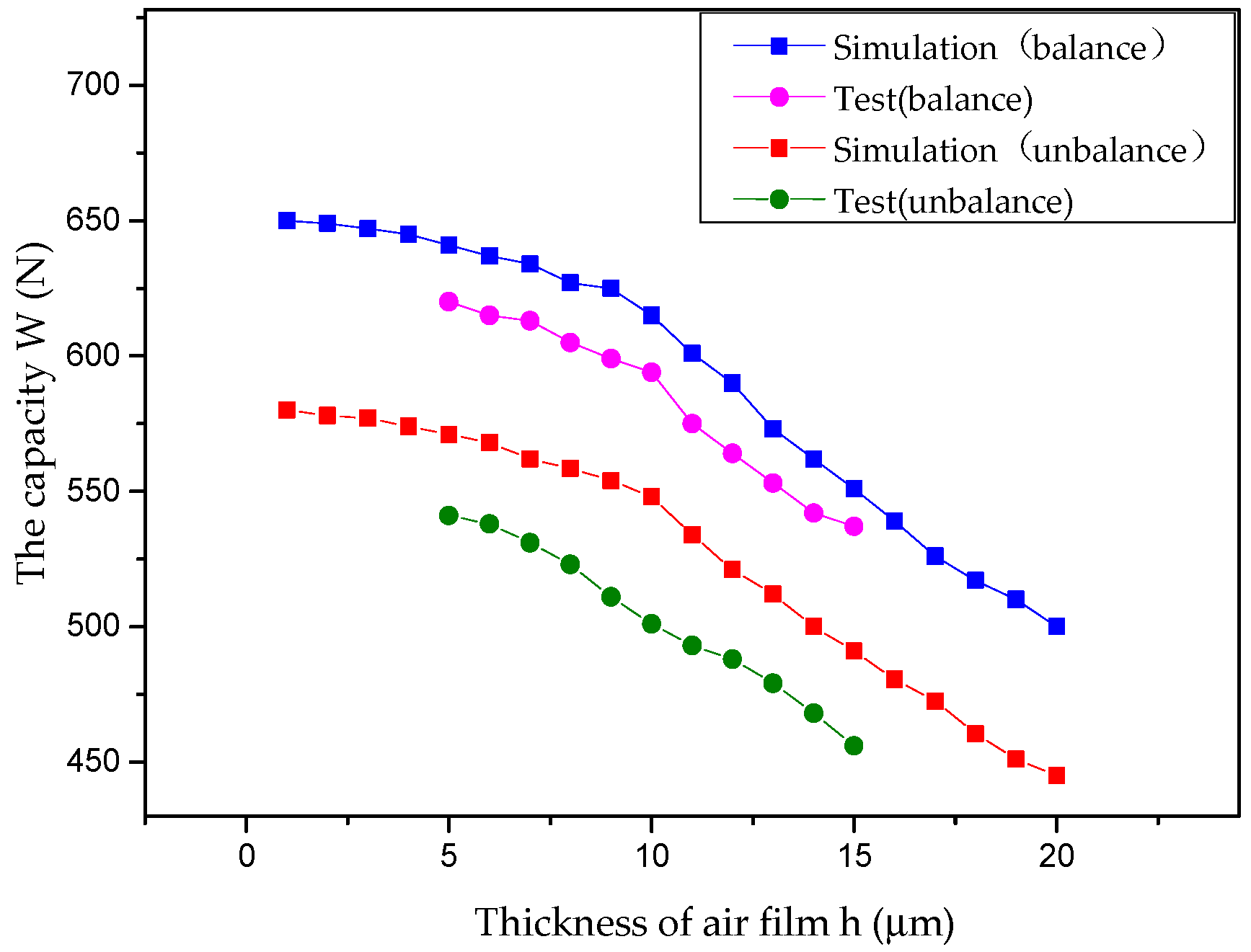
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shinno, H.; Hashizume, H.; Yoshioka, H.; Komatsu, K.; Shinshi, T.; Sato, K. X-Y-θ Nano-Positioning Table System for a Mother Machine. CIRP Ann.-Manuf. Technol. 2004, 53, 337–340. [Google Scholar] [CrossRef]
- Akhondzadeh, M.; Vahdati, M. Study of variable depth air pockets on air spindle vibrations in ultra-precision machine tools. Int. J. Adv. Manuf. Technol. 2014, 73, 681–686. [Google Scholar] [CrossRef]
- Chen, G.D.; Sun, Y.Z.; Zhang, F.H.; Lu, L.H.; Chen, W.Q.; Yu, N. Dynamic Accuracy Design Method of Ultra-precision Machine Tool. Chin. J. Mech. Eng. 2018, 31, 8. [Google Scholar] [CrossRef] [Green Version]
- Leach, R.K.; Flack, D.R.; Hughes, E.B.; Jones, C.W. Development of a new traceable areal surface texture measuring instrument. Wear 2009, 266, 552–554. [Google Scholar] [CrossRef]
- Marsh, E.; Schalcosky, D.; Couey, J.; Vallance, R. Analysis and performance of a parallel axis flatness measuring instrument. Rev. Sci. Instrum. 2006, 77, 2693. [Google Scholar] [CrossRef] [Green Version]
- Bos, E.; Moers, T.; Van Riel, M. Design and verification of an ultra-precision 3D-coordinate measuring machine with parallel drives. Meas. Sci. Technol. 2015, 26, 085904. [Google Scholar] [CrossRef]
- Chen, G.; Ju, B.; Fang, H.; Chen, Y.; Yu, N.; Wan, Y. Air bearing: Academic insights and trend analysis. Int. J. Adv. Manuf. Technol. 2020, 106, 1191–1202. [Google Scholar] [CrossRef]
- Zhou, Y.; Zong, W.; Tan, Q.; Hu, Z.; Sun, T.; Li, L. End Effect Analysis of a Slot-Less Long-Stator Permanent Magnet Linear Synchronous Motor. Symmetry 2021, 13, 1939. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Trivella, A.; Viktorov, V.; Visconte, C. CFD Analysis of a Simple Orifice-Type Feeding System for Aerostatic Bearings. Tribol. Lett. 2015, 58. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zou, D.; Ta, N.; Rao, Z. Numerical research of pressure depression in aerostatic thrust bearing with inherent orifice. Tribol. Int. 2018, 123, 385–396. [Google Scholar] [CrossRef]
- Miyatake, M.; Yoshimoto, S. Numerical investigation of static and dynamic characteristics of aerostatic thrust bearings with small feed holes. Tribol. Int. 2010, 43, 1353–1359. [Google Scholar] [CrossRef]
- Charki, A.; Diop, K.; Champmartin, S.; Ambari, A. Numerical simulation and experimental study of thrust air bearings with multiple orifices. Int. J. Mech. Sci. 2013, 72, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Eleshaky, M.E. CFD investigation of pressure depressions in aerostatic circular thrust bearings. Tribol. Int. 2009, 42, 1108–1117. [Google Scholar] [CrossRef]
- Chen, D.; Huo, C.; Cui, X.; Pan, R.; Fan, J.; An, C. Investigation the gas film in micro scale induced error on the performance of the aerostatic spindle in ultra-precision machining. Mech. Syst. Signal Process. 2018, 105, 488–501. [Google Scholar] [CrossRef]
- Chen, D.; Dong, L.; Pan, R.; Fan, J.; Cheng, Q. Coupling effects of the impact factors in micro-scale on the performance of aerostatic guideway. Ind. Lubr. Tribol. 2018, 70, 846–855. [Google Scholar] [CrossRef]
- Li, Y.; Han, D. Influences of the geometrical parameters of aerostatic thrust bearing with pocketed orifice -type restrictor on its performance. Tribol. Int. 2007, 40, 1120–1126. [Google Scholar] [CrossRef]
- Gao, S.; Cheng, K.; Chen, S.; Ding, H.; Fu, H. CFD based investigation on influence of orifice chamber shapes for the design of aerostatic thrust bearings at ultra-high speed spindles. Tribol. Int. 2015, 92, 211–221. [Google Scholar] [CrossRef]
- Chen, Y.S.; CCChiu Cheng, Y.D. Influences of operational conditions and geometric parameters on the stiffness of aerostatic journal bearings. Precis. Eng. 2010, 34, 722–734. [Google Scholar] [CrossRef]
- Cui, H.L.; Wang, Y.; Wang, B.R.; Yang, H.; Xia, H. Numerical Simulation and Experimental Verification of the Stiffness and Stability of Thrust Pad Aerostatic Bearings. Chin. J. Mech. Eng. 2018, 31, 23. [Google Scholar] [CrossRef] [Green Version]
- Belforte, G.; Colombo, F.; Raparelli, T.; Trivella, A.; Viktorov, V. Comparison between grooved and plane aerostatic thrust bearings: Static performance. Meccanica 2010, 46, 547–555. [Google Scholar] [CrossRef] [Green Version]
- Shi, B.J.; Yang, T.Y. Simplified model of Reynolds equation with linearized flow rate for ultra-thin gas film lubrication in hard disk drives. Microsyst. Technol. 2010, 16, 1727–1734. [Google Scholar] [CrossRef]
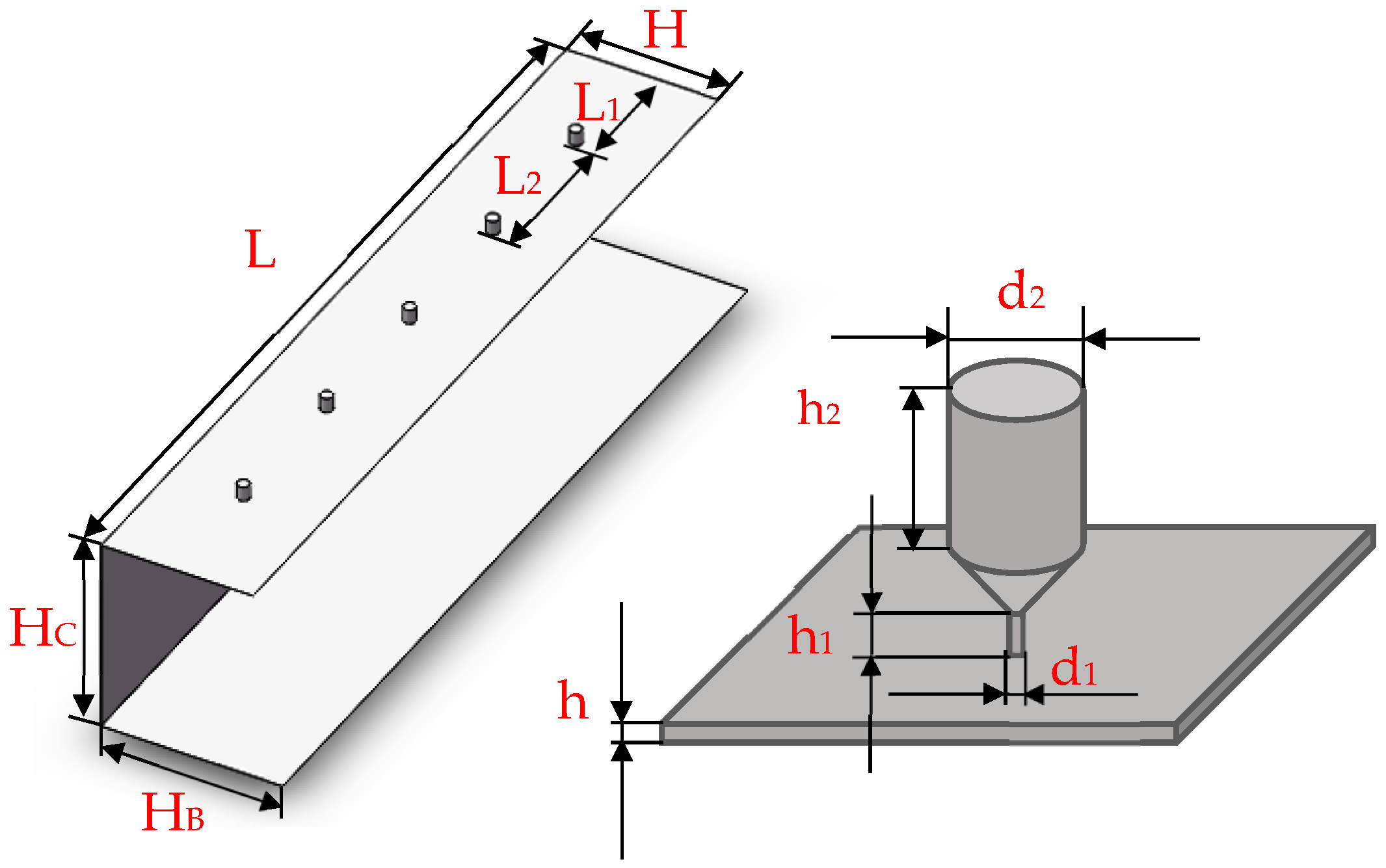

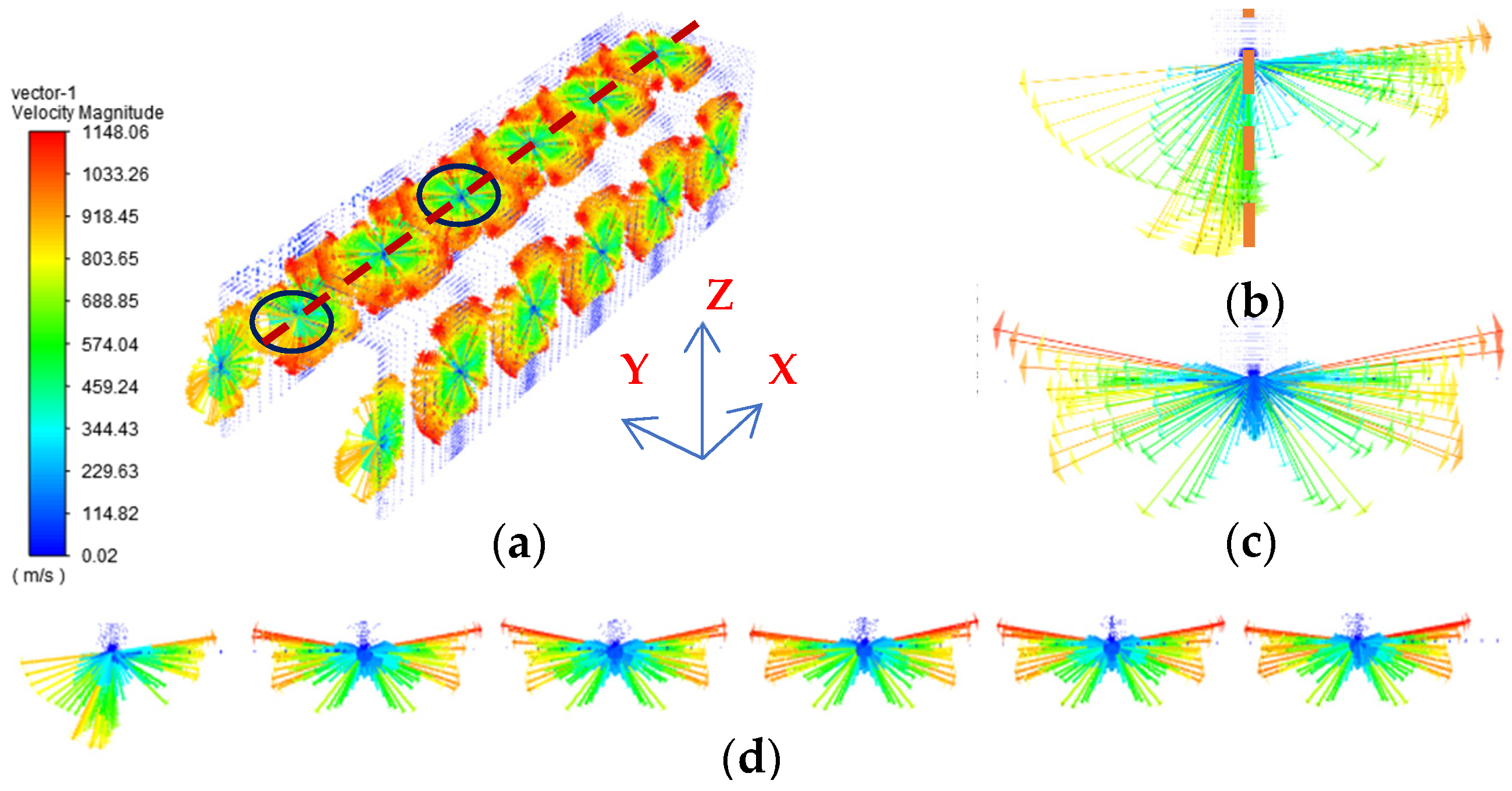


| Aerostatic Guideway | Designed Value |
|---|---|
| The length of air film L | 280 mm |
| The breadth of air film HC | 66 mm |
| The breadth of air film HA | 56 mm |
| The breadth of air film HB | 61 mm |
| The distance from the edge of air film to the nearby orifice L1 | 40 mm |
| The distance between orifices L2 | 50 mm |
| The diameter of air cavity d2 | 4 mm |
| The height of air cavity h2 | 5 mm |
| The average thickness of air film h | 10 μm |
| The diameter of orifice d1 | 0.1 mm |
| The height of orifice h1 | 0.5 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Hu, Z.; Sun, T.; Zhao, X.; Zhang, J.; Zong, W. Analysis of the Static Performance of a Cableless Aerostatic Guideway. Machines 2022, 10, 308. https://doi.org/10.3390/machines10050308
Zhou Y, Hu Z, Sun T, Zhao X, Zhang J, Zong W. Analysis of the Static Performance of a Cableless Aerostatic Guideway. Machines. 2022; 10(5):308. https://doi.org/10.3390/machines10050308
Chicago/Turabian StyleZhou, Yue, Zhenjiang Hu, Tao Sun, Xuesen Zhao, Junjie Zhang, and Wenjun Zong. 2022. "Analysis of the Static Performance of a Cableless Aerostatic Guideway" Machines 10, no. 5: 308. https://doi.org/10.3390/machines10050308
APA StyleZhou, Y., Hu, Z., Sun, T., Zhao, X., Zhang, J., & Zong, W. (2022). Analysis of the Static Performance of a Cableless Aerostatic Guideway. Machines, 10(5), 308. https://doi.org/10.3390/machines10050308







