A New Trajectory Tracking Control Method for Fully Electrically Driven Quadruped Robot
Abstract
:1. Introduction
- (1)
- The trajectory tracking controller of a quadruped robot is often analyzed on the basis of a kinematic model, and the dynamic characteristics are not studied. Therefore, the accuracy of trajectory tracking is difficult to be further improved.
- (2)
- Trajectory tracking often adopts a simple closed-loop control strategy, which is difficult to be further popularized for quadruped robots with underactuated, multi-variable, strong coupling and nonlinear characteristics.
- (3)
- A large number of scholars have carried out research on the trajectory tracking control of quadruped robots, often focusing on the trajectory tracking of the robot trunk centroid, ignoring the impact of the accuracy of the quadruped robot leg trajectory tracking control on the overall control of the robot.
- (4)
- The MPC algorithm is an effective method to solve the trajectory tracking problem of unmanned vehicles, but whether it can meet the real-time performance requirements of quadruped robot trajectory tracking control needs to be further verified.
- (1)
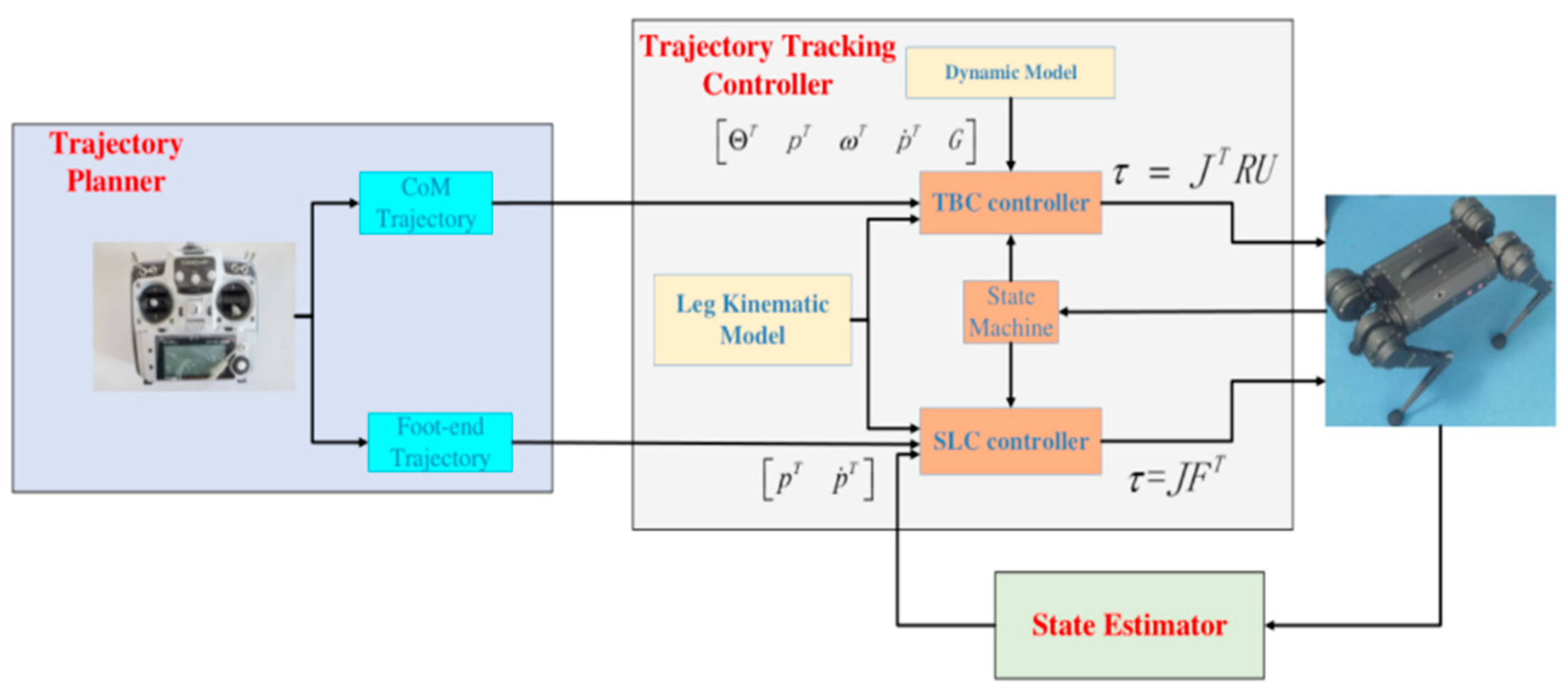
- In the TBC, the trunk dynamic model of the quadruped robot is established and based on this model, a trajectory tracking method based on model predictive control theory is designed. Firstly, the dynamic model is discretized to obtain the state space equation. Secondly, the optimization objective function and constraints are established, and the solution of the future control quantity is transformed into the optimal solution of quadratic programming. Finally, the optimal solution is applied to the system.
- (2)
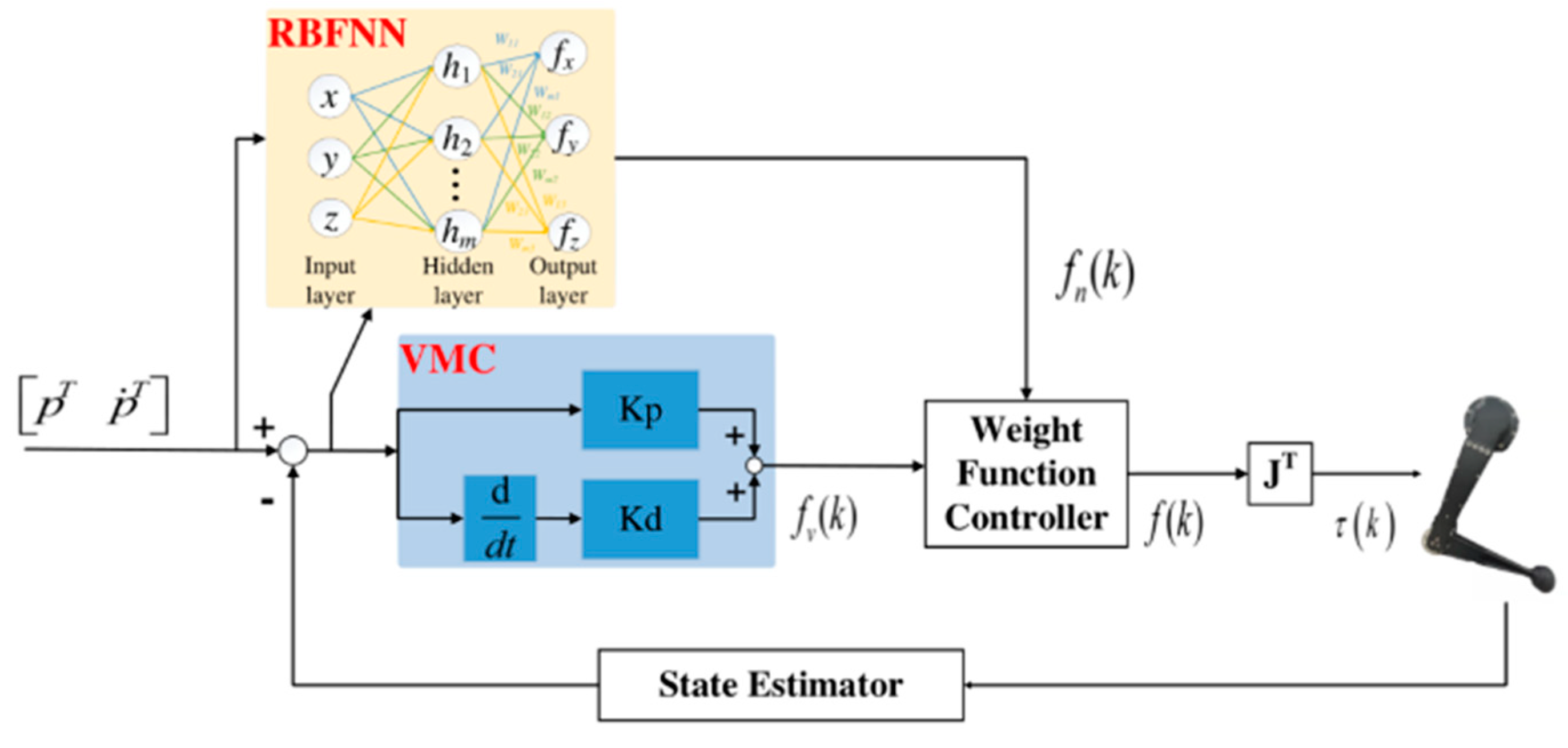
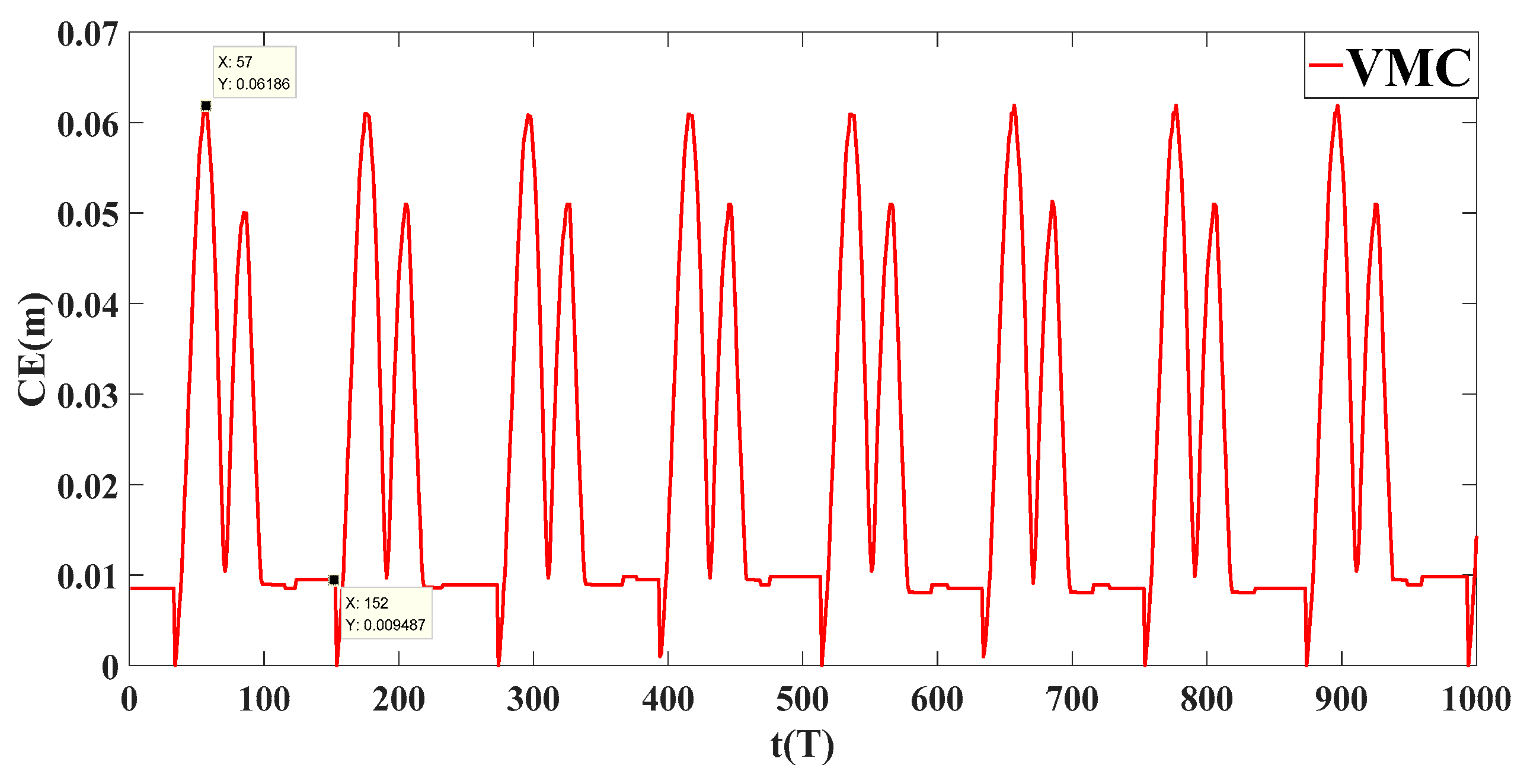
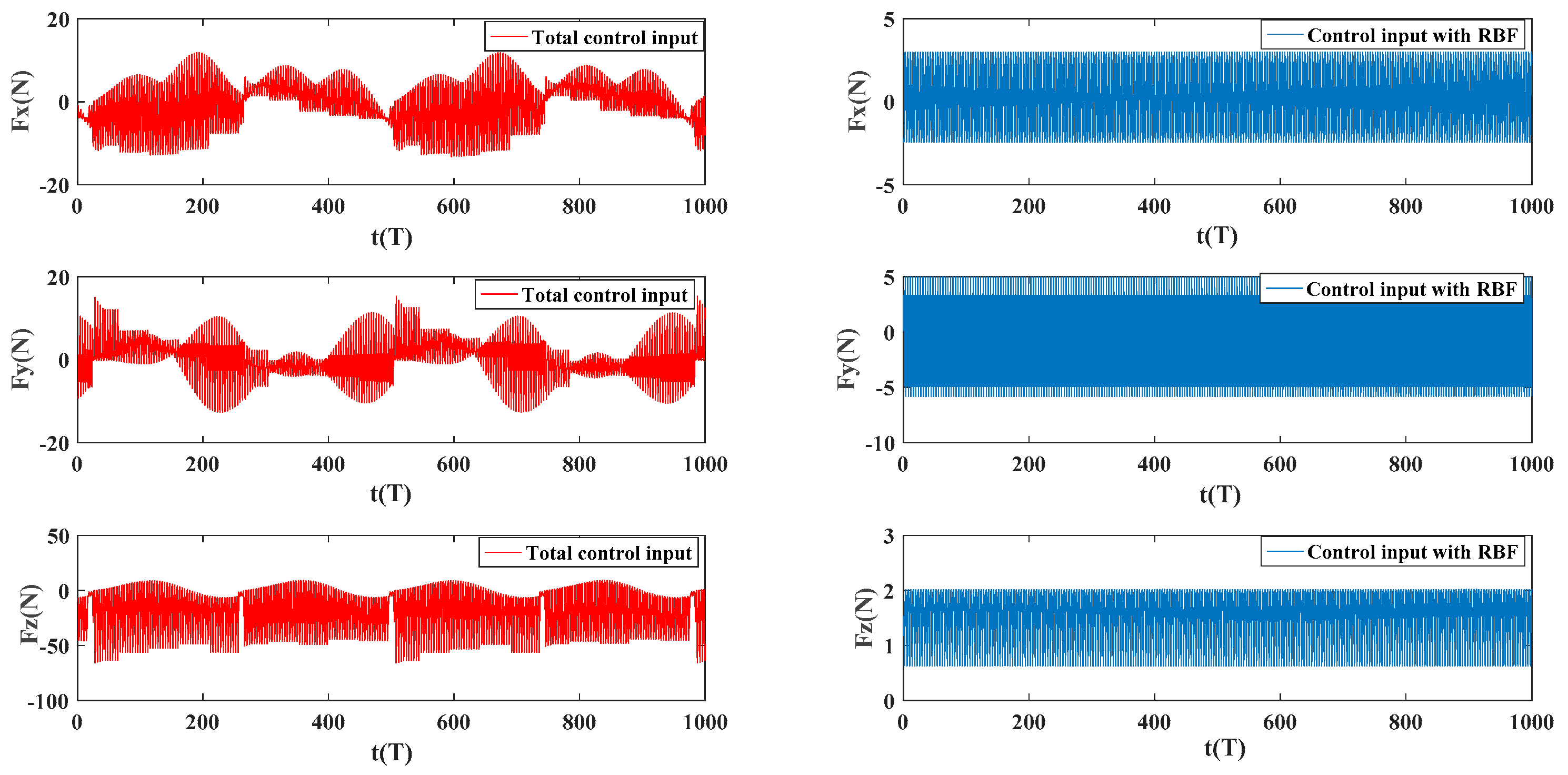
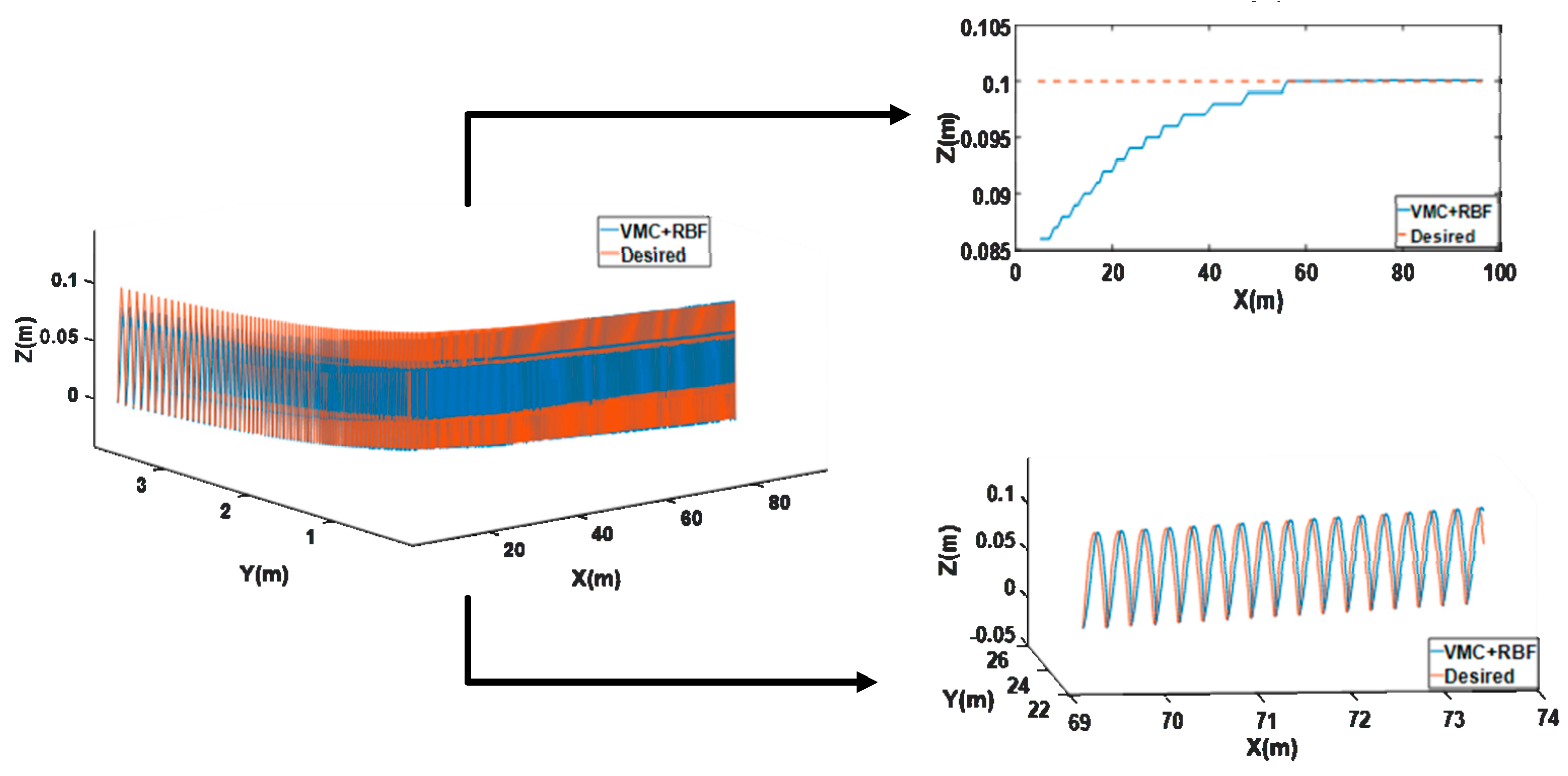
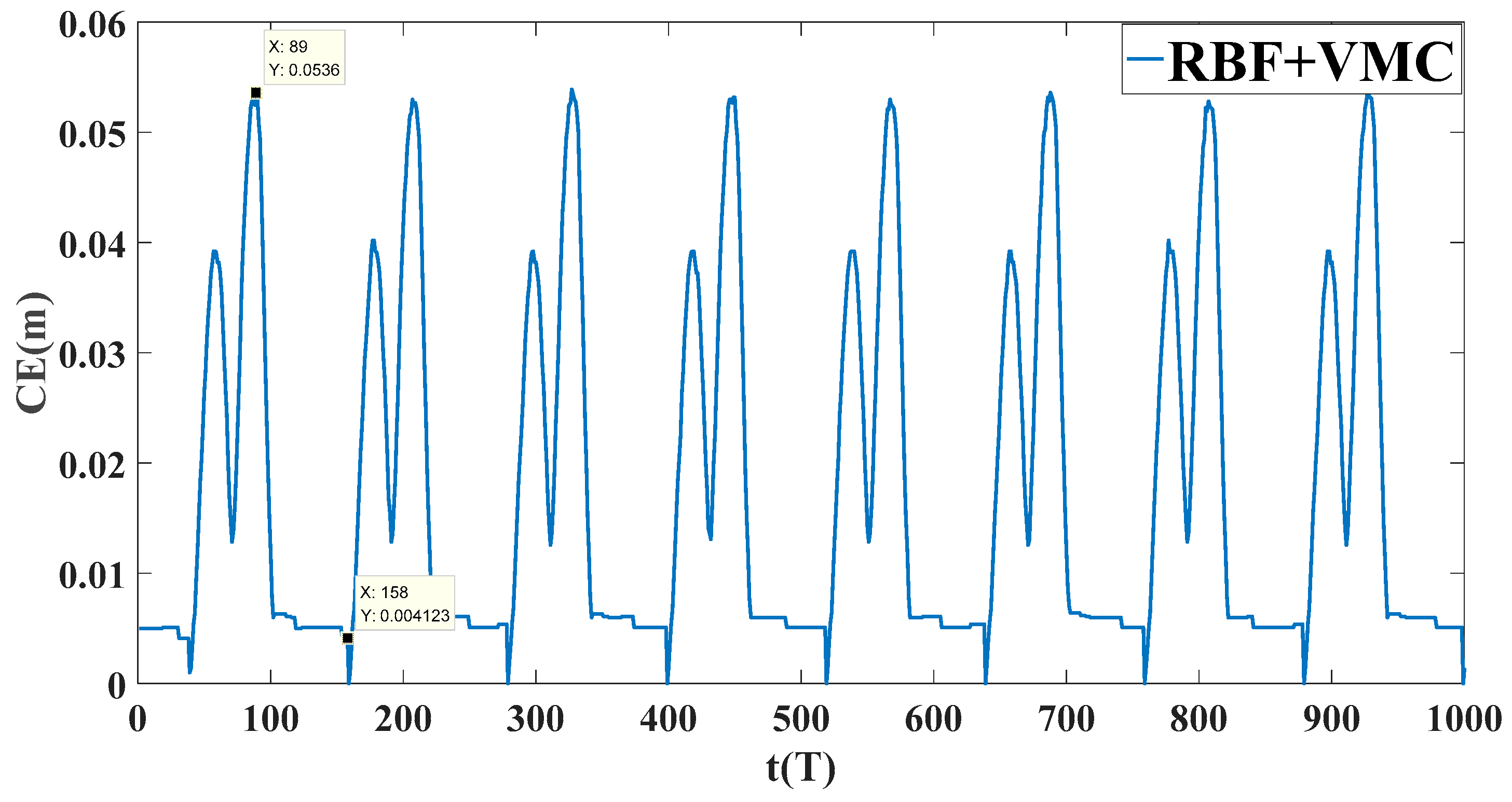
- In the SLC, a virtual model control method based on radial basis function neural networks (RBFNN) is designed. This control method uses the imaginary components to connect internal and external points, in order to generate virtual force to drive the foot-end to track the desired trajectory of the robot; at the same time, a supervise controller was designed based on RBFNN and online learning, optimizing the supervision of learning parameters of the controller, by weighting function to coordinate the two foot-end power output of the controller. The function of the two controllers is to ensure that the quadruped robot has good response characteristics while reducing the deviation during trajectory tracking by tracking the desired trajectory.
2. Mathematical Model
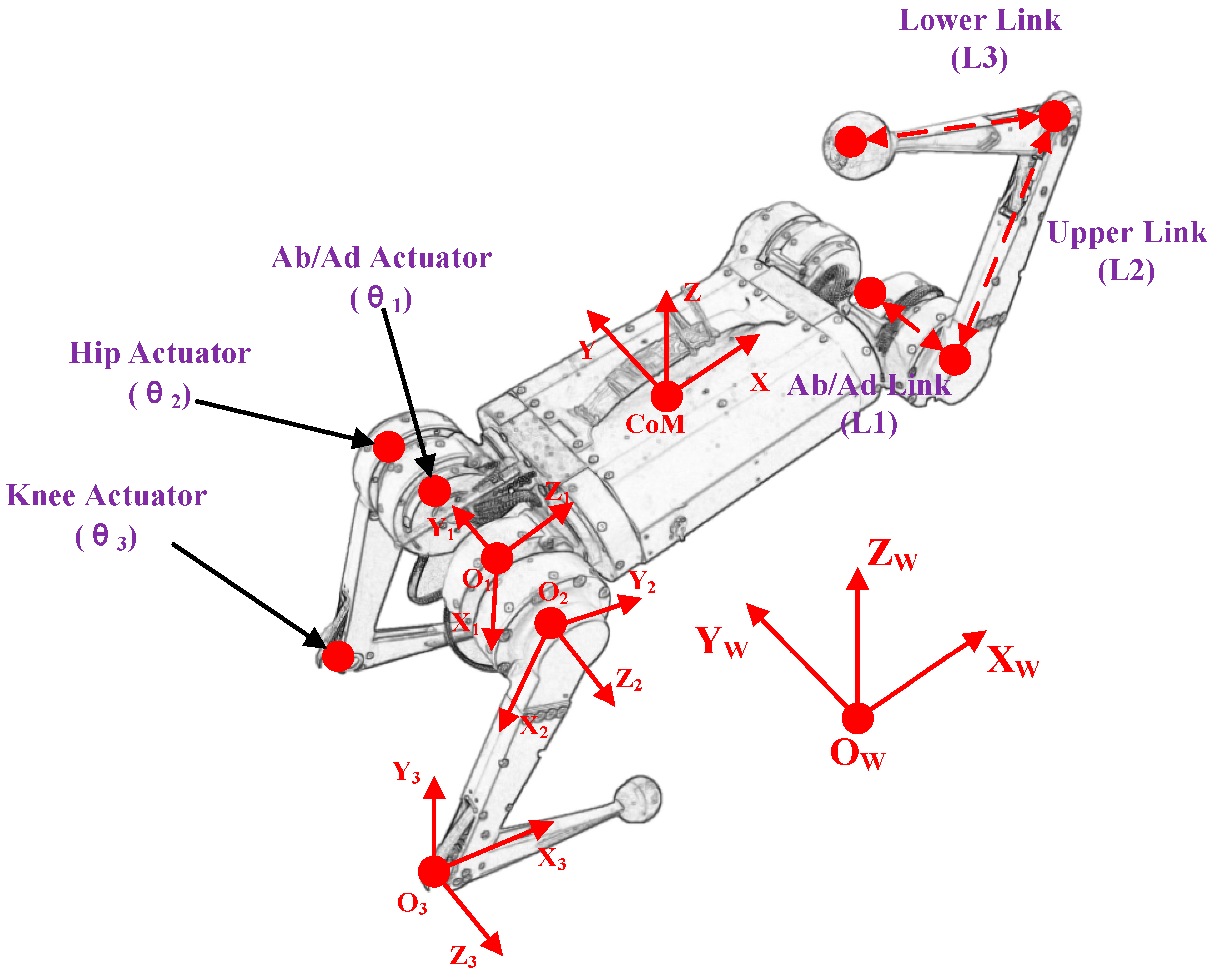
2.1. Leg Kinematic Model
2.2. Dynamic Model
3. Control Design
3.1. Foot-End Trajectory Planning
3.2. Design of TBC
3.2.1. Prediction Equation
3.2.2. Optimization Solution
3.3. Design of SLC
3.3.1. Virtual Model Control
3.3.2. RBFNN Supervision Control
3.3.3. Weight Function Controller
4. Experimental Results
4.1. Quadruped Robot Experimental Platform
4.2. Initial Value Training of RBFNN Controller
4.3. COM Trajectory Tracking Experiment
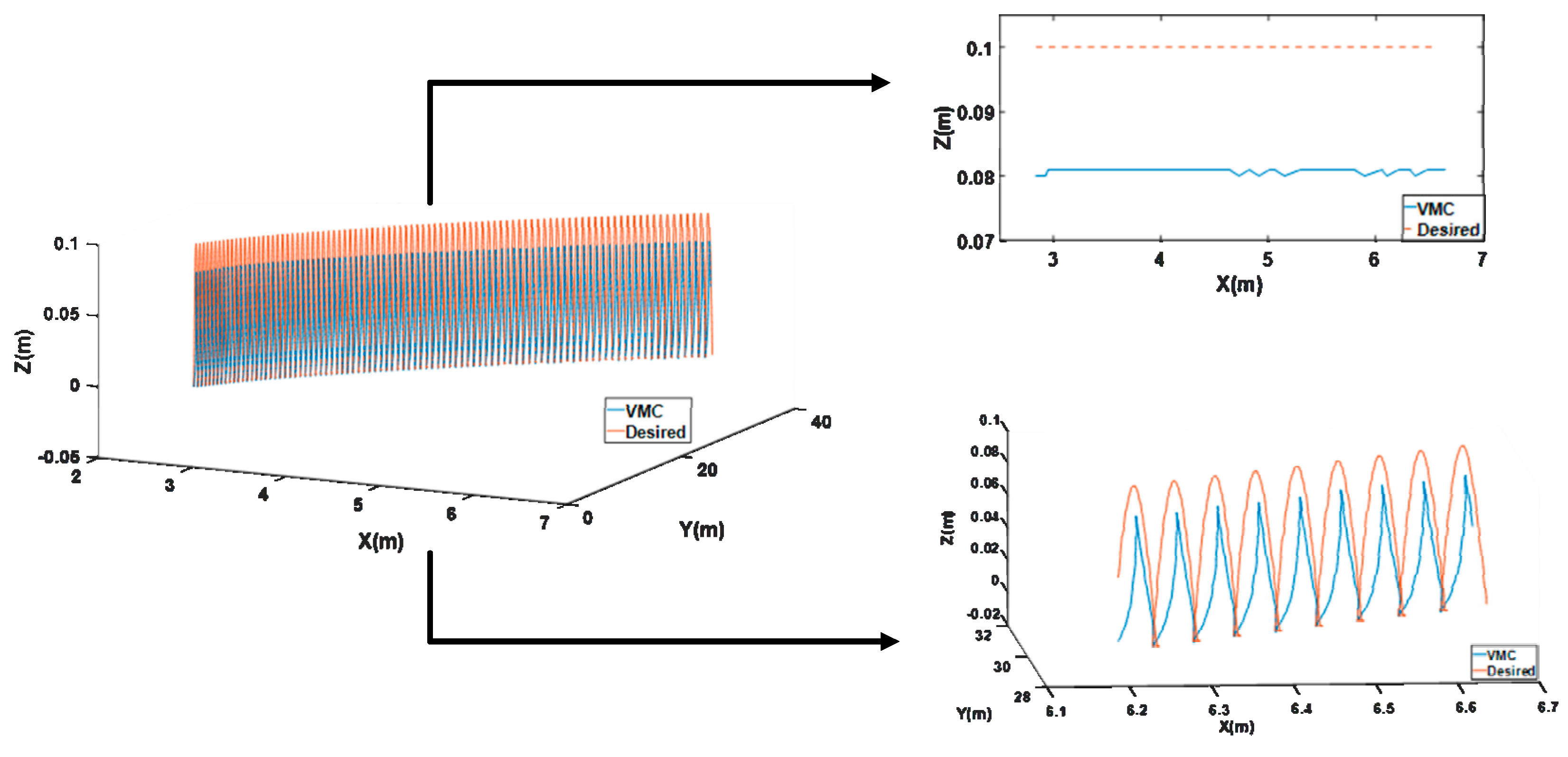
4.3.1. Linear Trajectory Tracking Experiment
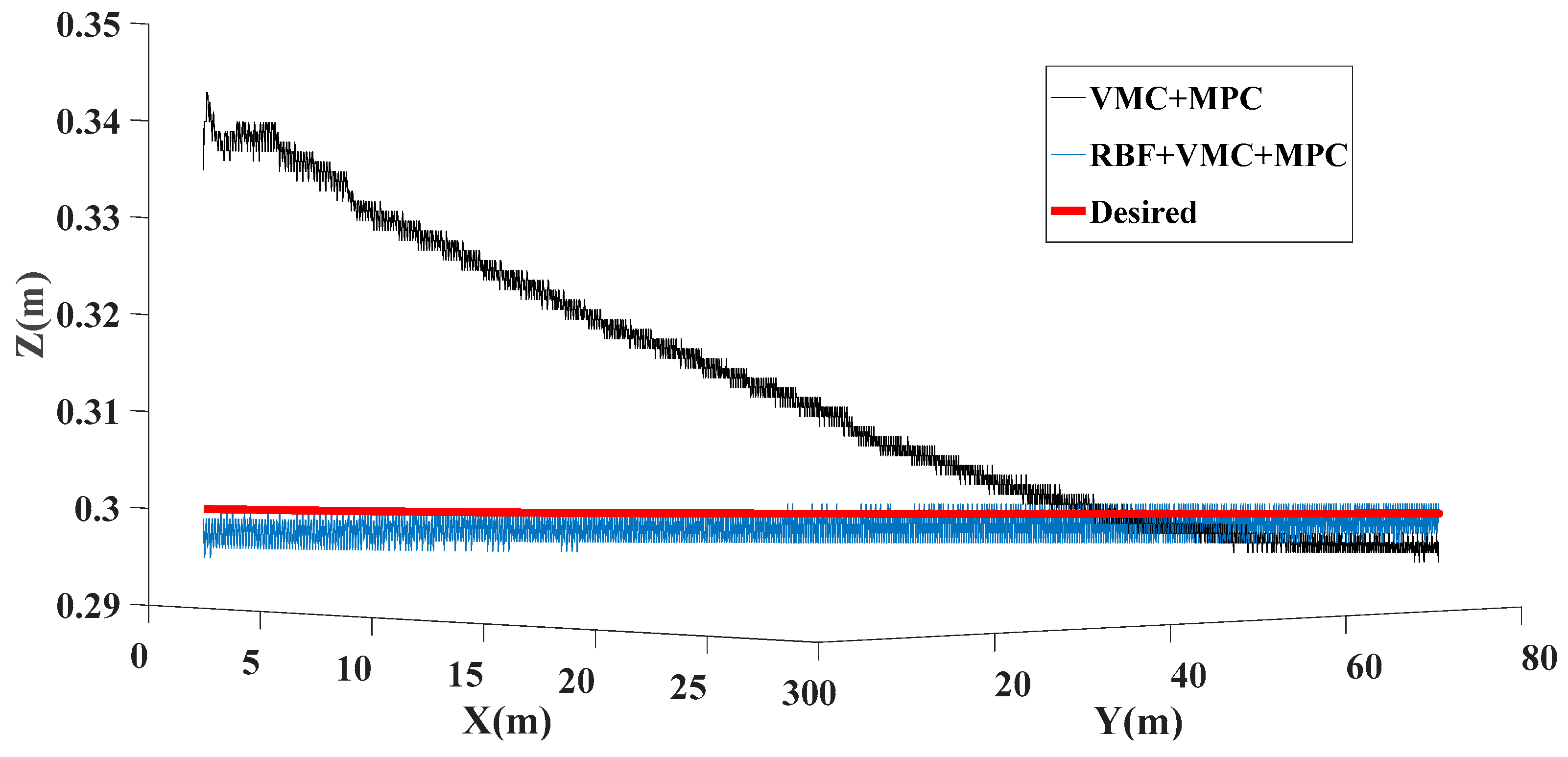
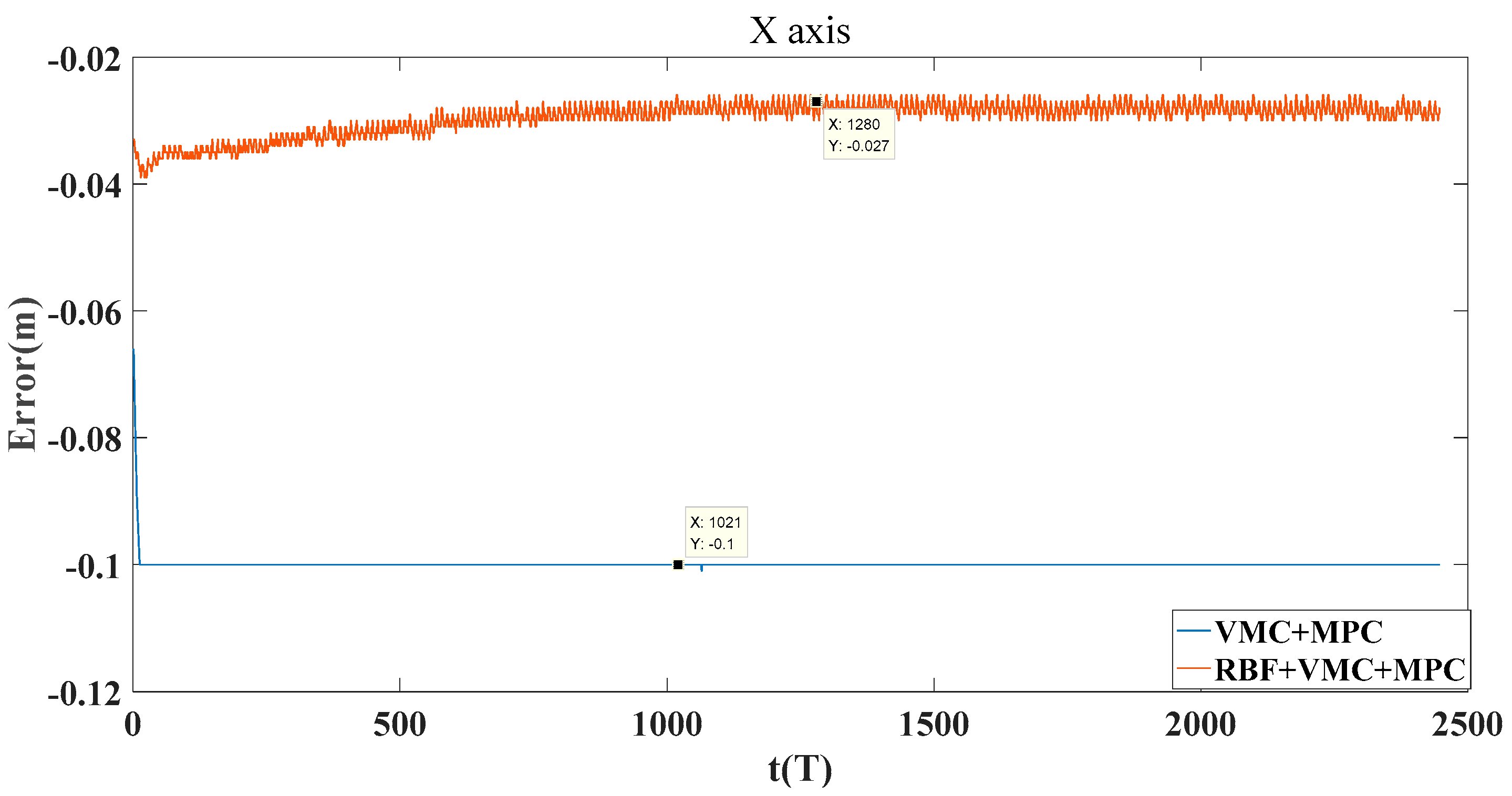
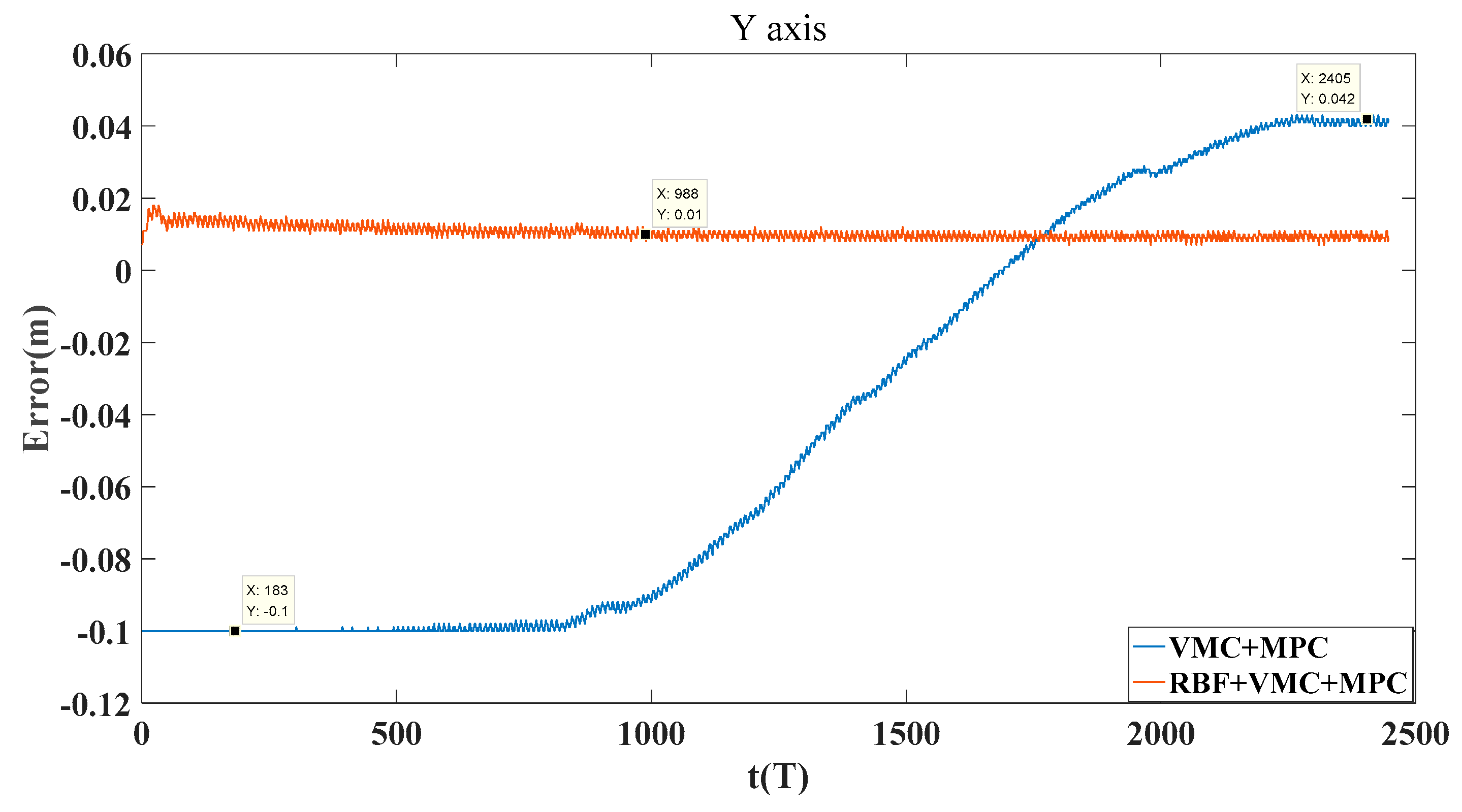
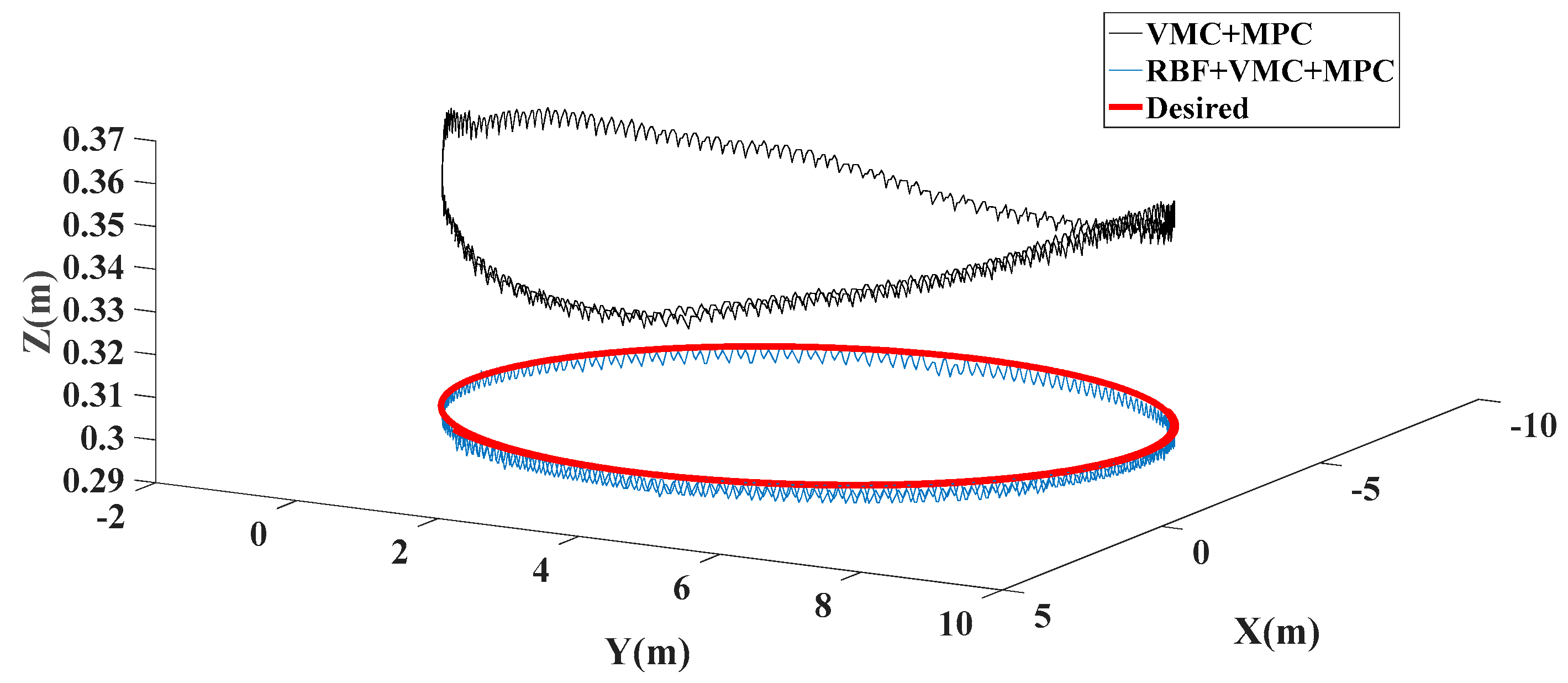
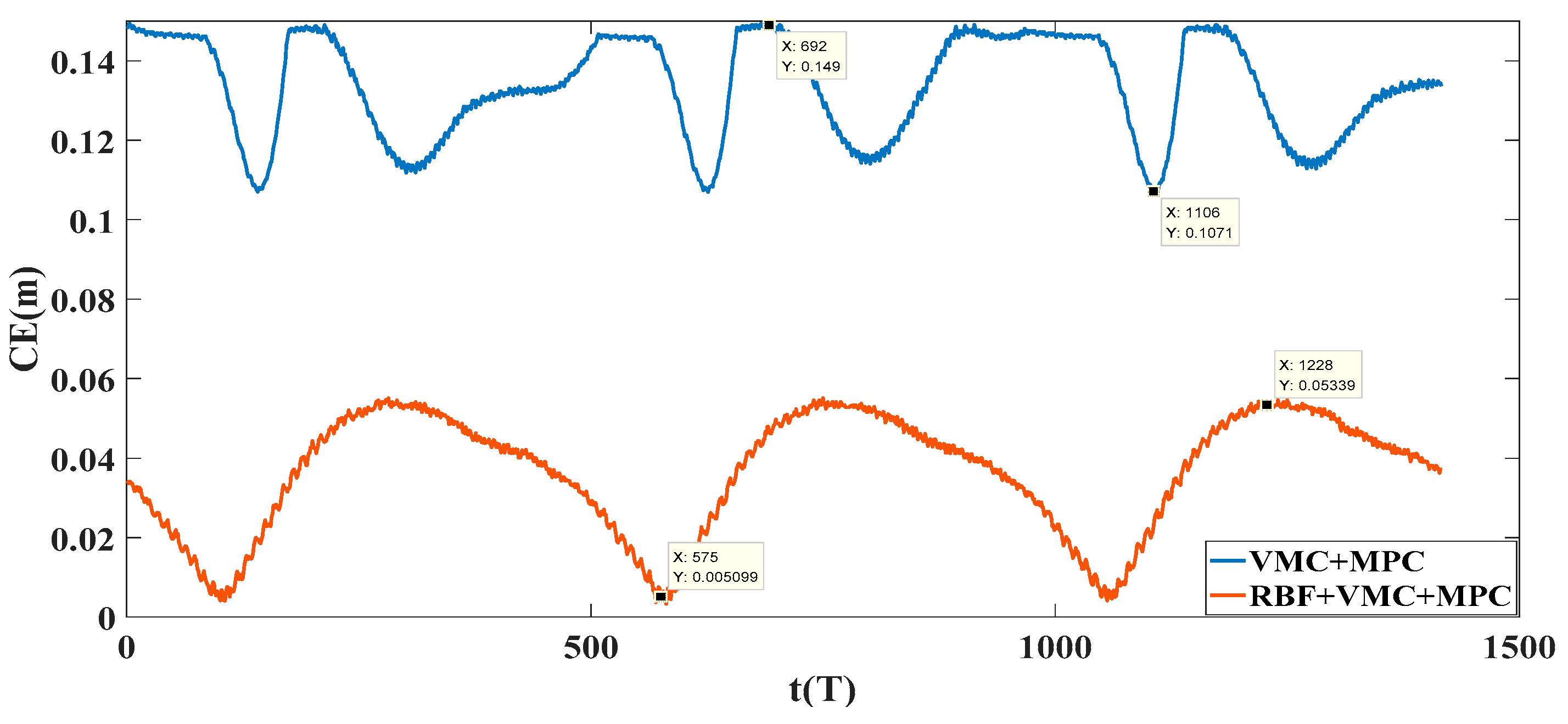
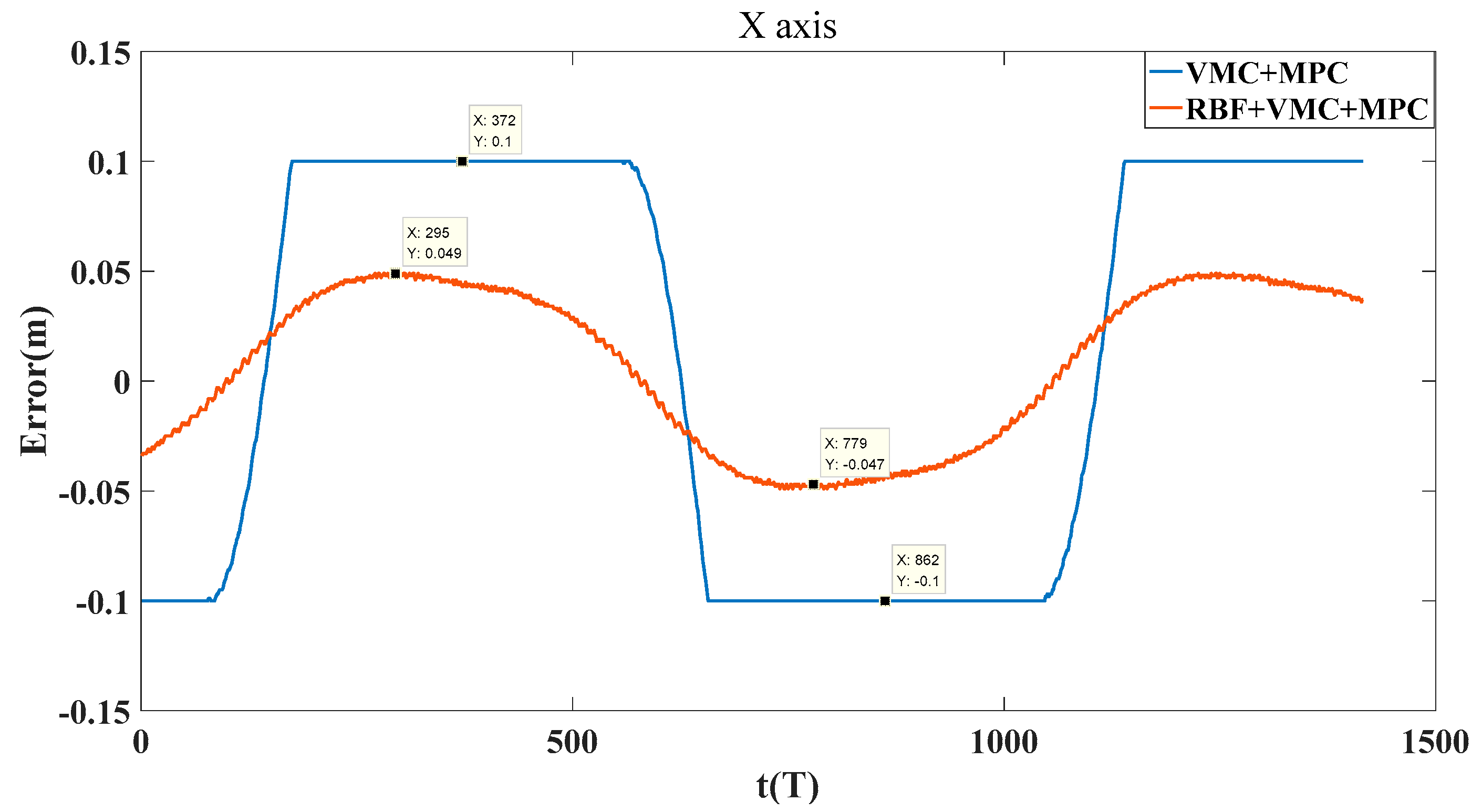
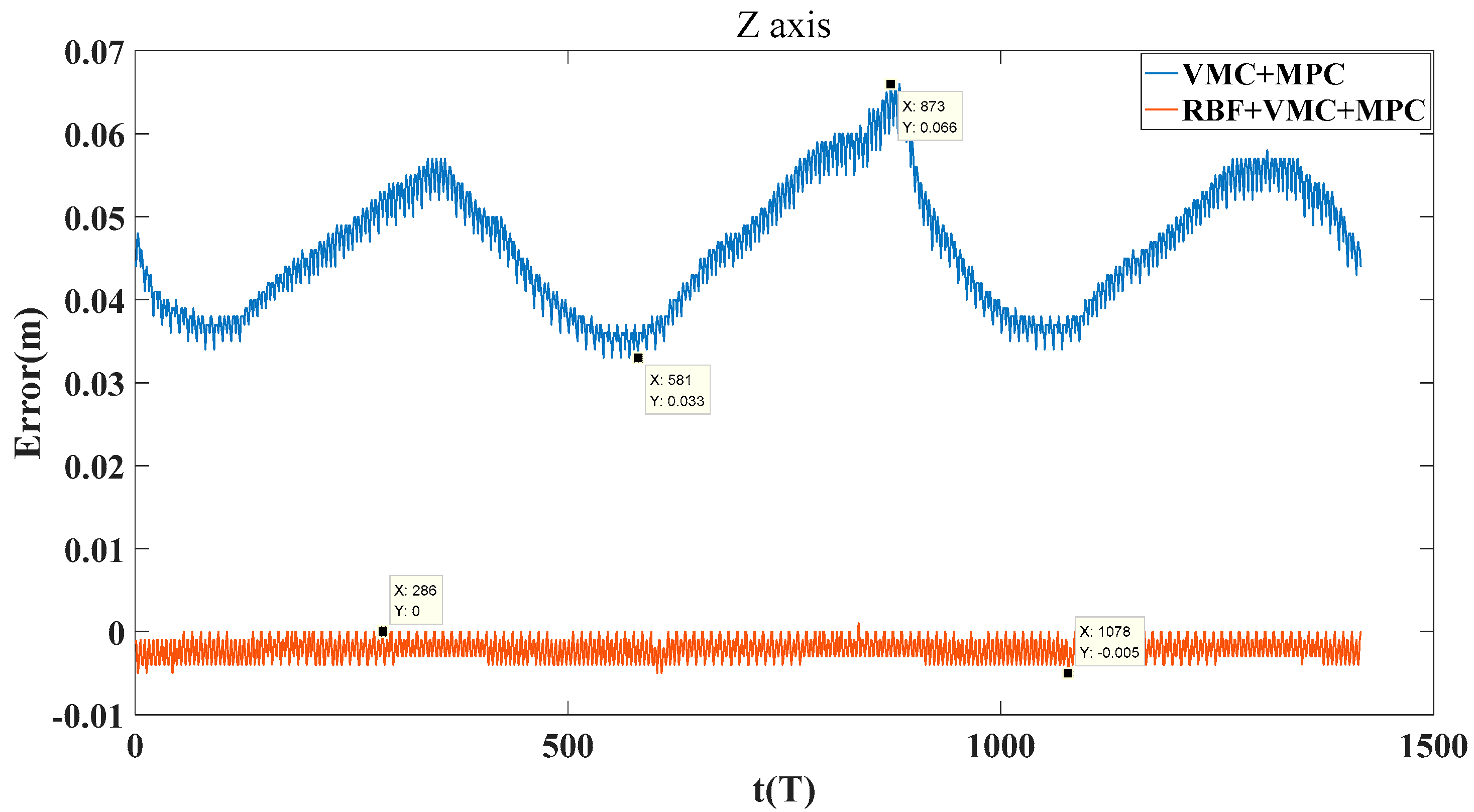
4.3.2. Circular Trajectory Tracking Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, J. Multi-Phase Joint-Angle Trajectory Generation Inspired by Dog Motion for Control of Quadruped Robot. Sensors 2021, 21, 6366. [Google Scholar] [CrossRef] [PubMed]
- Rodino, S.; Matteo Curcio, E.; di Bella, A.; Persampieri, M.; Funaro, M.; Carbone, G. Design, Simulation, and Preliminary Validation of a Four-Legged Robot. Machines 2020, 8, 82. [Google Scholar] [CrossRef]
- Liu, J.; Tan, M.H.; Zhao, X. Legged robots—An overview. Trans. Inst. Meas. Control 2007, 29, 185–202. [Google Scholar] [CrossRef]
- Wang, J.H.; Wen, J.T.; Chen, W.H.; Yue, H.S.; Liu, D. A gait generating algorithm with smooth speed transition for the locomotion of legged robots. Trans. Inst. Meas. Control 2014, 36, 260–275. [Google Scholar] [CrossRef]
- Li, J.; Cong, D.; Yang, Y.; Yang, Z. A new bionic hydraulic actuator system for legged robots with impact buffering, impact energy absorption, impact energy storage, and force burst. Robotica 2021, 56, 1–18. [Google Scholar] [CrossRef]
- Kang, R.; Meng, F.; Wang, L.; Chen, X.; Yu, Z.; Fan, X.; Sato, R.; Ming, A.; Huang, Q. Bio-Inspired Take-Off Maneuver and Control in Vertical Jumping for Quadruped Robot with Manipulator. Micromachines 2021, 12, 1189. [Google Scholar] [CrossRef]
- Chen, X.D.; Watanabe, K.; Kiguchi, K.; Izumi, K. Path tracking based on closed-loop control for a quadruped robot in a cluttered environment. J. Dyn. Syst. Meas. Control 2002, 124, 272–280. [Google Scholar] [CrossRef]
- Oliveira, I.; Barbosa, R.; Silva, M. Modelling, Trajectory Planning and Control of a Quadruped Robot Using Matlab®/Simulink™. In Proceedings of the ROBOT 2017: Third Iberian Robotics Conference, Advances in Intelligent Systems and Computing, Sevilla, Spain, 22–24 November 2017; Volume 694, pp. 757–767. [Google Scholar] [CrossRef]
- Chen, B.; Pei, Z.C.; Tang, Z.Y. Adaptive fuzzy PID control for hydraulic quadruped robot. J. Harbin Inst. Technol. 2016, 48, 140–144. [Google Scholar] [CrossRef]
- Pratt, J.; Dilworth, P.; Pratt, G. Virtual model control of a bipedal walking robot. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; Volume 1, pp. 193–198. [Google Scholar] [CrossRef]
- Liu, B.; Rong, X.; Chai, H. A buffering strategy for quadrupedal robots based on virtual model control. Robot 2016, 38, 659–669. [Google Scholar] [CrossRef]
- Chen, G.; Guo, S.; Hou, B. Virtual model control for quadruped robots. IEEE Access 2020, 8, 140736–140751. [Google Scholar] [CrossRef]
- Boaventura, T.; Buchli, J.; Semini, C.; Caldwell, D.G. Model-based hydraulic impedance control for dynamic robots. IEEE Trans. Robot. 2015, 31, 1324–1336. [Google Scholar] [CrossRef] [Green Version]
- Winkler, A.W.; Mastalli, C.; Havoutis, I.; Focchi, M.; Caldwell, D.G.; Semini, C. Planning and execution of dynamic whole-body locomotion for a hydraulic quadruped on challenging terrain. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation, ICRA, Seattle, WA, USA, 26–30 May 2015; pp. 5148–5154. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.T.; Rong, X.W.; Hui, C.; Li, Y.; Li, B. Torso motion control and toe trajectory generation of a trotting quadruped robot based on virtual model control. Adv. Robot. 2016, 30, 284–297. [Google Scholar] [CrossRef]
- Zhang, G.T.; Rong, X.W.; Li, Y.B.; Cai, H.; Li, B. Gait control method of quadruped robot diagonal trot based on virtual model. Robot 2016, 38, 64–74. [Google Scholar] [CrossRef]
- Luo, B. Balance control based on six-dimensional spatial mechanics and velocity adjustment through region intervention and foot landing for quadruped robot. Robotica 2022, 89, 1–23. [Google Scholar] [CrossRef]
- Kurazume, R.; Byong-Won, A.; Ohta, K.; Hsutomu, H. Experimental study on energy efficiency for quadruped walking vehicles. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Las Vegas, NV, USA, 27–31 October 2003; pp. 613–618. [Google Scholar] [CrossRef]
- Si, Z.; Gao, J.; Duan, X.; Li, H. Trot pattern generation for quadruped robot based on the ZMP stability margin. Int. Conf. Complex Med. Eng. 2013, 32, 603–608. [Google Scholar] [CrossRef]
- Hoang, G.; Kim, H.K.; Kim, S.B. Path tracking controller of quadruped robot for obstacle avoidance using potential functions method. Int. J. Sci. Eng. 2013, 4, 1–5. [Google Scholar] [CrossRef]
- Dini, N.; Majd, V.D. An MPC-based two-dimensional push recovery of a quadruped robot in trotting gait using its reduced virtual model. Mech. Mach. Theory 2019, 146, 1–25. [Google Scholar] [CrossRef]
- Carlo, J.D.; Wensing, P.M.; Katz, B.; Bledt, G.; Kim, S. Dynamic Locomotion in the MIT Cheetah 3 Through Convex Model-Predictive Control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7440–7447. [Google Scholar] [CrossRef]
- Bledt, G.; Powell, M.J.; Katz, B.; Carlo, J.D.; Wensing, P.M.; Kim, S. MIT Cheetah 3: Design and Control of a Robust, Dynamic Quadruped Robot. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2245–2252. [Google Scholar] [CrossRef]
- Luan, F.; Na, J.; Huang, Y.; Gao, G. Adaptive neural network control for robotic manipulators with guaranteed finite-time convergence. Neurocomputing 2019, 337, 153–164. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, Z.; Liao, L.; You, Y.; Sui, Y.; Zhu, T. RPEOD: A Real-Time Pose Estimation and Object Detection System for Aerial Robot Target Tracking. Machines 2022, 10, 181. [Google Scholar] [CrossRef]
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, 831–849. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.Z.; Hou, W.Q.; Wang, J.; Wang, J.W.; Ma, H.X. A strategy for push recovery in quadruped robot based on reinforcement learning. In Proceedings of the 2015 34th Chinese Control Conference, CCC, Hangzhou, China, 28–30 July 2015; pp. 3145–3151. [Google Scholar] [CrossRef]
- Ma, Z.; Liang, Y.; Tian, H. Research on Gait Planning Algorithm of Quadruped Robot Based on Central Pattern Generator. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 3948–3953. [Google Scholar] [CrossRef]
- Ren, D.; Shao, J.; Sun, G. The complex dynamic locomotive control and experimental research of a quadruped-robot based on the robot trunk. Appl. Sci. 2019, 9, 3911. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Dai, J. Trot gait with twisting trunk of a metamorphic quadruped robot. J. Biomim. Eng. Engl. Ed. 2018, 15, 971–981. [Google Scholar] [CrossRef]
- Atique, M.; Sarker, M.; Ahad, M. Development of an 8dof quadruped robot and implementation of inverse kinematics using denavit-hartenberg convention. Heliyon 2018, 4, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, X.; An, H.; Ma, H. Modeling and base parameters identification of legged robots. Robotica 2022, 40, 747–761. [Google Scholar] [CrossRef]
- Zhou, F.L.; You, Y.L.; Li, G. Study on singular trajectory method of inverse kinematics of space 3R manipulator. Mech. Sci. Technol. 2019, 38, 365–372. [Google Scholar] [CrossRef]
- Bledt, G.; Wensing, P.M.; Ingersoll, S.; Ingersoll, S.; Kim, S. Contact Model Fusion for Event-Based Locomotion in Unstructured Terrains. In Proceedings of the 2018 IEEE International Conference on Robotics & Automation, Brisbane, Australia, 21–25 May 2018; pp. 4399–4406. [Google Scholar] [CrossRef] [Green Version]
- Hu, N.; Li, S.; Huang, D.; Gao, F. Trotting gait planning for a quadruped robot with high payload walking on irregular terrain. IFAC Proc. Vol. 2014, 47, 2153–2158. [Google Scholar] [CrossRef] [Green Version]
- Han, B.; Luo, X.; Zhao, R.; Luo, Q.; Liang, G. The optimization algorithm for gait planning and foot trajectory on the quadruped robot. In Proceedings of the International Conference on Geometry and Graphics, Milan, Italy, 3–7 August 2018; pp. 1274–1279. [Google Scholar] [CrossRef]
- Ding, Y.; Pandala, A.; Li, C.; Shin, Y.H.; Park, H.W. Representation-free model predictive control for dynamic motions in quadrupeds. IEEE Trans. Robot. 2020, 37, 1154–1171. [Google Scholar] [CrossRef]
- May, G.; Iacono, F.; Jameson, A. A hybrid multilevel method for high-order discretization of the euler equations on unstructured meshes. J. Comput. Phys. 2010, 229, 3938–3956. [Google Scholar] [CrossRef]
- Trierweiler, J.O.; Farina, L.A. Rpn tuning strategy for model predictive control. J. Process Control 2003, 13, 591–598. [Google Scholar] [CrossRef]
- Shi, Y.; He, X.; Zou, W.; Yu, B.; Yuan, L.; Li, M.; Pan, G.; Ba, K. Multi-Objective Optimal Torque Control with Simultaneous Motion and Force Tracking for Hydraulic Quadruped Robots. Machines 2022, 10, 170. [Google Scholar] [CrossRef]
- Huang, Y.; Wei, Q.; Ma, H.; An, H. Motion planning for a bounding quadruped robot using ilqg based mpc. J. Phys. Conf. Ser. 2021, 1905, 1–12. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Wang, S. Neural Approximation-based Model Predictive Tracking Control of Non-holonomic Wheel-legged Robots. Int. J. Control Autom. Syst. 2021, 19, 372–381. [Google Scholar] [CrossRef]
- Wei, H.; Bo, H.; Dong, Y. Adaptive neural network control for robotic manipulators with unknown deadzone. IEEE Trans. Cybern. 2017, 48, 2670–2682. [Google Scholar] [CrossRef]
- Liu, Q.; Li, D.; Ge, S.S.; Ji, R.; Tee, K.P. Adaptive bias rbf neural network control for a robotic manipulator. Neurocomputing 2021, 447, 213–223. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Taghavifar, H. Mme-ekf-based path-tracking control of autonomous vehicles considering input saturation. IEEE Trans. Veh. Technol. 2019, 68, 5246–5259. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Tang, Z.; Wang, F. Trajectory tracking of distributed driven unmanned vehicle based on variable weight coefficient. Chin. J. Highw. 2019, 32, 36–45. [Google Scholar] [CrossRef]
- Han, Y.Q.; Zhang, K.; Bin, Y. Obstacle avoidance principle based on convex approximation and prediction algorithm of unmanned vehicle path planning model. J. Autom. 2020, 46, 159–173. [Google Scholar] [CrossRef]
- Huang, W.; Xiao, J.; Zeng, F.; Lu, P.; Lin, G.; Hu, W.; Lin, X.; Wu, Y. A Quadruped Robot with Three-Dimensional Flexible Legs. Sensors 2021, 21, 4907. [Google Scholar] [CrossRef]










| Parameters | Symbol | Values | Units |
|---|---|---|---|
| Body mass | m | 3.3 | kg |
| Gravitational acceleration | g | 9.8 | m/s2 |
| Body Inertia | Ixx | 0.35 | kg × m2 |
| Body Inertia | Iyy | 2.1 | kg × m2 |
| Body Inertia | Izz | 2.1 | kg × m2 |
| Body length | Lbody | 0.37 | m |
| Body width | Wbody | 0.11 | m |
| Body height | Hbody | 0.1 | m |
| Ab/Ad link length | L1 | 0.072 | m |
| Upper link length | L2 | 0.211 | m |
| Lower link length | L3 | 0.2 | m |
| Sampling period | T | 15 | ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Y.; Yang, Z.; Zou, T.; Sui, Y.; Xu, C.; Zhang, C.; Xu, H.; Zhang, Z.; Han, J. A New Trajectory Tracking Control Method for Fully Electrically Driven Quadruped Robot. Machines 2022, 10, 292. https://doi.org/10.3390/machines10050292
You Y, Yang Z, Zou T, Sui Y, Xu C, Zhang C, Xu H, Zhang Z, Han J. A New Trajectory Tracking Control Method for Fully Electrically Driven Quadruped Robot. Machines. 2022; 10(5):292. https://doi.org/10.3390/machines10050292
Chicago/Turabian StyleYou, Yulong, Zhong Yang, Teng’an Zou, Yaoyu Sui, Changliang Xu, Chi Zhang, Hao Xu, Zhao Zhang, and Jiaming Han. 2022. "A New Trajectory Tracking Control Method for Fully Electrically Driven Quadruped Robot" Machines 10, no. 5: 292. https://doi.org/10.3390/machines10050292
APA StyleYou, Y., Yang, Z., Zou, T., Sui, Y., Xu, C., Zhang, C., Xu, H., Zhang, Z., & Han, J. (2022). A New Trajectory Tracking Control Method for Fully Electrically Driven Quadruped Robot. Machines, 10(5), 292. https://doi.org/10.3390/machines10050292







