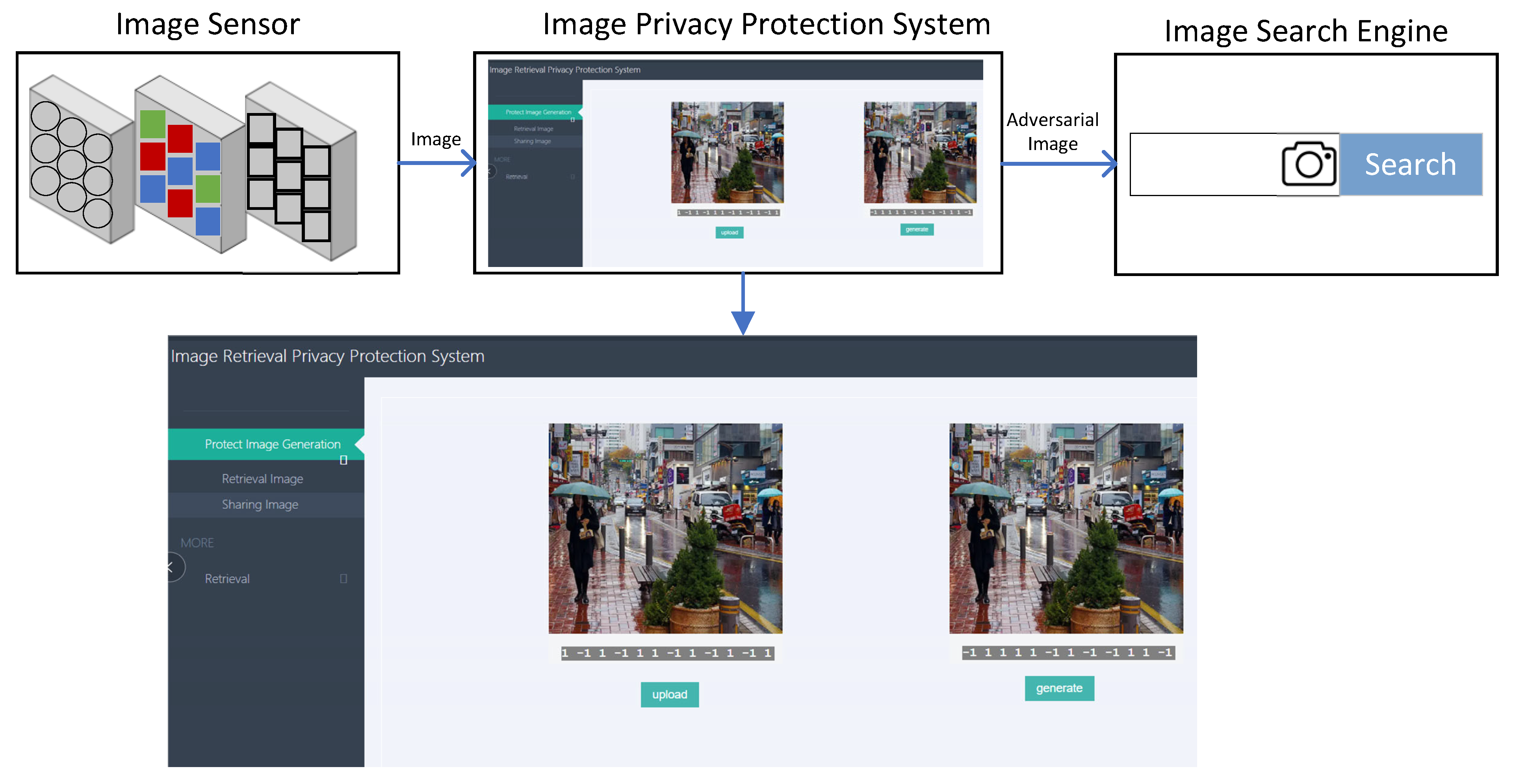
A Fast Method for Protecting Users’ Privacy in Image Hash Retrieval System
Abstract
:1. Introduction
- We reformulate the image hash retrieval system’s targeted attack with the relaxation penalty norm to obtain better performance and convergence speed.
- We introduce a forward–backward strategy to solve the gradient vanishing problem with the relaxation penalty norm for the adversarial attack.
- We propose protecting the privacy of image semantic information and content with an adversarial attack method in an image hash retrieval system.
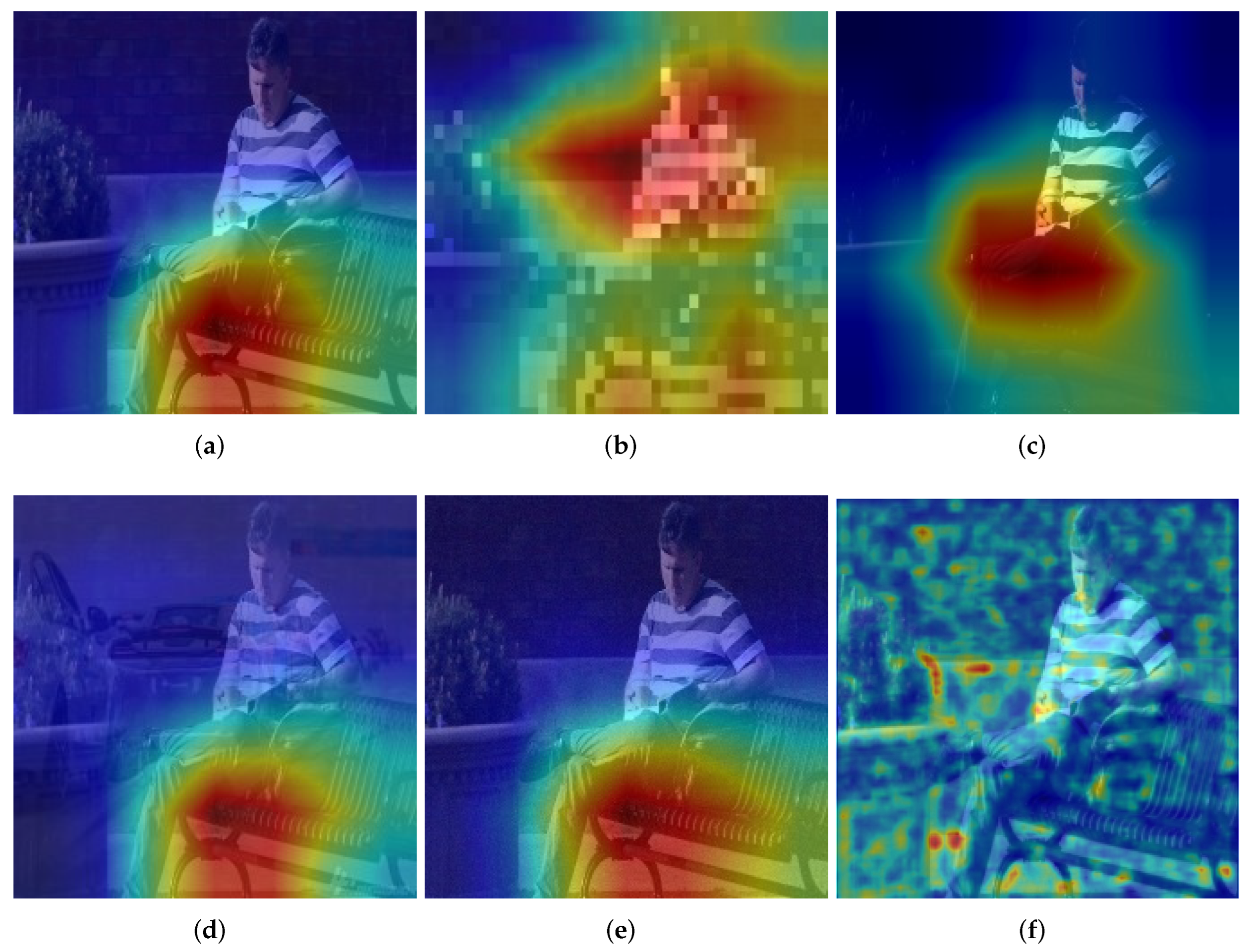
- We exploit the PSNR metric, and gradient-based heatmap [29] to compare the pros and cons of traditional privacy protection methods.
- We conducted experiments on the FLICKER-25K and NUS-WIDE datasets and verified that our method outperforms other adversarial attack methods.
2. Related
2.1. Traditional Method to Image Privacy Protection
2.2. Dnn-Based Image Hash Retrieval System
2.3. Privacy Protection of DNN-Based Image Hash Retrieval System
3. Background
3.1. Image Hash Retrieval System
3.2. Adversarial Attack
4. Approach
4.1. Explore Adversarial Gradient
4.2. Discrete Proximal Linearized Minimization
4.3. Back Propagating with Adversarial Penalty Norm
| Algorithm 1: Optimization Process |
 |
5. Experiment
5.1. Datasets Description
5.2. Baseline and Metrics
5.3. Experiment Settings
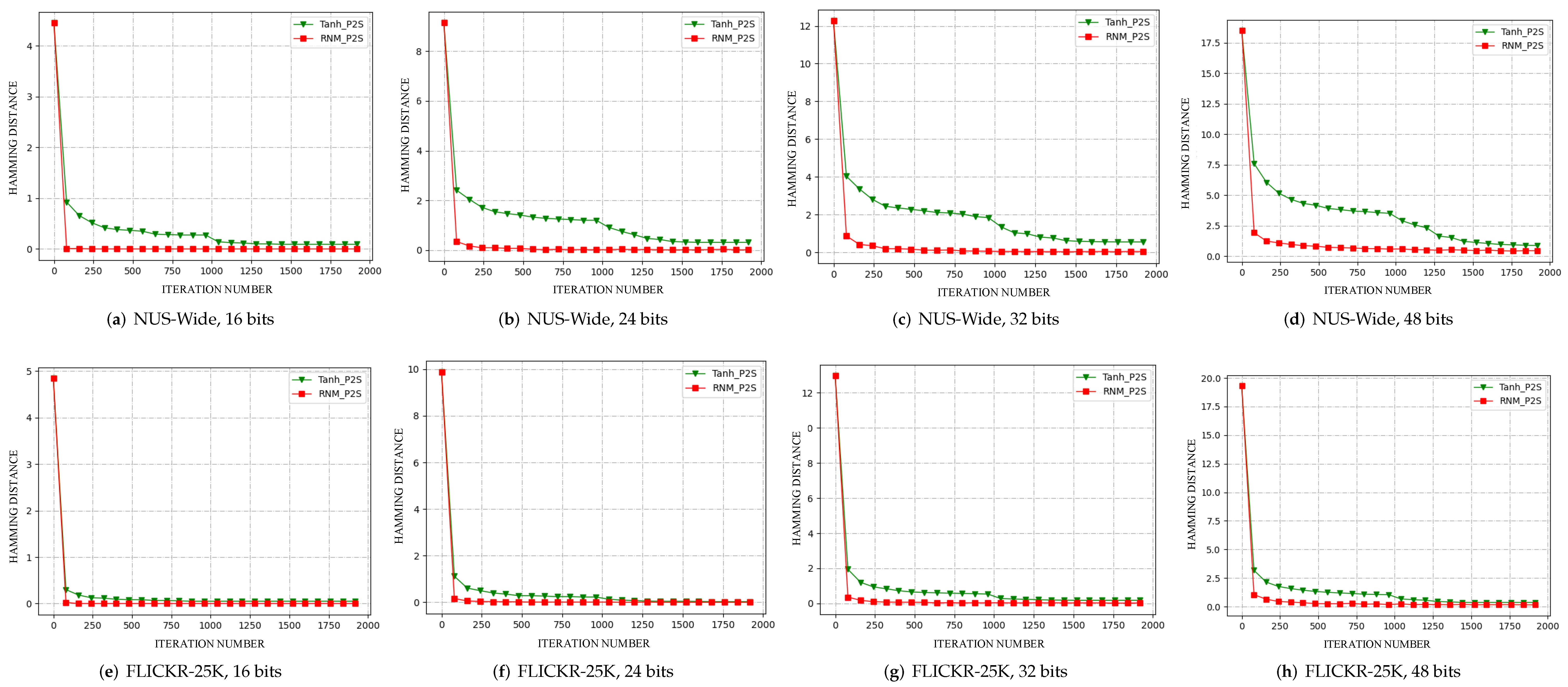
5.4. Results
5.5. Ablation Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Bernardmarr. Available online: https://bernardmarr.com/how-much-data-do-we-create-every-day-the-mind-blowing-stats-everyone-should-read/ (accessed on 11 January 2022).
- Seroundtable. Available online: https://www.seroundtable.com/google-search-by-image-storage-14101.html (accessed on 11 January 2022).
- Theverge. Available online: https://www.theverge.com/2018/12/14/18140771/facebook-photo-exposure-leak-bug-millions-users-disclosed (accessed on 11 January 2022).
- Liu, H.; Wang, R.; Shan, S.; Chen, X. Deep supervised hashing for fast image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2064–2072. [Google Scholar]
- Cao, Z.; Long, M.; Wang, J.; Yu, P.S. Hashnet: Deep learning to hash by continuation. In Proceedings of the IEEE International Conference on Computer Vision(ICCV), Venice, Italy, 22–29 October 2017; pp. 5608–5617. [Google Scholar]
- Lai, Z.; Chen, Y.; Wu, J.; Wong, W.K.; Shen, F. Jointly sparse hashing for image retrieval. IEEE Trans Image Process. 2018, 27, 6147–6158. [Google Scholar] [CrossRef]
- Shen, F.; Xu, Y.; Liu, L.; Yang, Y.; Huang, Z.; Shen, H.T. Unsupervised deep hashing with similarity-adaptive and discrete optimization. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 3034–3044. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, X.; Lu, J.; Tian, Q.; Zhou, J. Deep hashing via discrepancy minimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 6838–6847. [Google Scholar]
- Gu, W.; Gu, X.; Gu, J.; Li, B.; Xiong, Z.; Wang, W. Adversary guided asymmetric hashing for cross-modal retrieval. In Proceedings of the 2019 on International Conference on Multimedia Retrieval(ICMR), Ottawa, ON, Canada, 10–13 June 2019; pp. 159–167. [Google Scholar]
- Wickramasuriya, J.; Alhazzazi, M.; Datt, M.; Mehrotra, S.; Venkatasubramanian, N. Privacy-protecting video surveillance. In Proceedings of the Real-Time Imaging IX, San Jose, CA, USA, 18–20 January 2005; pp. 64–75. [Google Scholar]
- Elkies, N.; Fink, G.; Bärnighausen, T. “Scrambling” geo-referenced data to protect privacy induces bias in distance estimation. Popul. Environ. 2015, 37, 83–98. [Google Scholar] [CrossRef]
- Yang, E.; Liu, T.; Deng, C.; Tao, D. Adversarial examples for hamming space search. IEEE Trans. Cybern. 2018, 50, 1473–1484. [Google Scholar] [CrossRef] [PubMed]
- Tolias, G.; Radenovic, F.; Chum, O. Targeted mismatch adversarial attack: Query with a flower to retrieve the tower. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 5037–5046. [Google Scholar]
- Li, J.; Ji, R.; Liu, H.; Hong, X.; Gao, Y.; Tian, Q. Universal perturbation attack against image retrieval. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 4899–4908. [Google Scholar]
- Xiao, Y.; Wang, C.; Gao, X. Evade Deep Image Retrieval by Stashing Private Images in the Hash Space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Online, 16–18 June 2020; pp. 9651–9660. [Google Scholar]
- Bai, J.; Chen, B.; Li, Y.; Wu, D.; Guo, W.; Xia, S.T.; Yang, E.H. Targeted attack for deep hashing based retrieval. In Proceedings of the European Conference on Computer Vision(ECCV), Glasgow, UK, 23–28 August 2020; pp. 618–634. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial examples in the physical world. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. Deepfool: A simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2574–2582. [Google Scholar]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbruecken, Germany, 21–24 March 2016; pp. 372–387. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1765–1773. [Google Scholar]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Security and Privacy (SP), San Jose, CA, USA, 22–24 May 2017; pp. 39–57. [Google Scholar]
- Xie, C.; Wu, Y.; Maaten, L.V.D.; Yuille, A.L.; He, K. Feature denoising for improving adversarial robustness. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 501–509. [Google Scholar]
- Xu, K.; Liu, S.; Zhao, P.; Chen, P.; Zhang, H.; Fan, Q.; Erdogmus, D.; Wang, Y.; Lin, X. Structured adversarial attack: Towards general implementation and better interpretability. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Fan, Y.; Wu, B.; Li, T.; Zhang, Y.; Li, M.; Li, Z.; Yang, Y. Sparse adversarial attack via perturbation factorization. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 35–50. [Google Scholar]
- Bai, J.; Chen, B.; Wu, D.; Zhang, C.; Xia, S.T. Universal Adversarial Head: Practical Protection against Video Data Leakage. In Proceedings of the ICML 2021 Workshop on Adversarial Machine Learning, Online, 18–24 July 2021. [Google Scholar]
- Wang, X.; Zhang, Z.; Wu, B.; Shen, F.; Lu, G. Prototype-supervised Adversarial Network for Targeted Attack of Deep Hashing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 16357–16366. [Google Scholar]
- Su, S.; Zhang, C.; Han, K.; Tian, Y. Greedy hash: Towards fast optimization for accurate hash coding in cnn. In Proceedings of the 32nd International Conference on Neural Information Processing Systems(NIPS), Montréal, QC, Canada, 4–5 December 2018; pp. 806–815. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A. Grad-cam: Visual explanations from deep networks via gradient-based. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Cao, Y.; Long, M.; Liu, B.; Wang, J. Deep cauchy hashing for hamming space retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1229–1237. [Google Scholar]
- Liu, Z.; Zhao, Z.; Larson, M. Who’s afraid of adversarial queries? The impact of image modifications on content-based image retrieval. In Proceedings of the 2019 on International Conference on Multimedia Retrieval (ICMR), Ottawa, ON, Canada, 10–13 June 2019; pp. 306–314. [Google Scholar]
- Wang, X.; Zhang, Z.; Lu, G.; Xu, Y. Targeted Attack and Defense for Deep Hashing. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGTR), Online, 11–15 July 2021; pp. 2298–2302. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural INF Process Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Gu, Y.; Ma, C.; Yang, J. Supervised recurrent hashing for large scale video retrieval. In Proceedings of the 24th ACM International Conference on Multimedia, Amsterdam, The Netherlands, 15–19 October 2016; pp. 272–276. [Google Scholar]
- Xiao, Y.; Wang, C. You See What I Want You To See: Exploring Targeted Black-Box Transferability Attack for Hash-Based Image Retrieval Systems. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 1934–1943. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Shen, F.; Zhou, X.; Yang, Y.; Song, J.; Shen, H.T.; Tao, D. A fast optimization method for general binary code learning. IEEE Trans. Image Process. 2016, 25, 5610–5621. [Google Scholar] [CrossRef] [PubMed]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Chua, T.S.; Tang, J.; Hong, R.; Li, H.; Luo, Z.; Zheng, Y. Nus-wide: A real-world web image database from national university of singapore. In Proceedings of the ACM International Conference on Image and Video Retrieval (CIVR), Santorini Island, Greece, 8–10 July 2009; pp. 1–9. [Google Scholar]
- Huiskes, M.J.; Lew, M.S. The mir flickr retrieval evaluation. In Proceedings of the 1st ACM International Conference on Multimedia Information Retrieval (MM), Vancouver, BC, Canada, 30–31 October 2008; pp. 39–43. [Google Scholar]
- Li, W.J.; Wang, S.; Kang, W.C. Feature learning based deep supervised hashing with pairwise labels. arXiv 2015, arXiv:1511.03855. [Google Scholar]
- He, K.; Zhang, X.; Ren, S. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, Nevada, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]



| Method | Metric | FLICKER-25k | NUS-Wide | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 16 bits | 24 bits | 32 bits | 48 bits | 16 bits | 24 bits | 32 bits | 48 bits | ||
| Noise | t-MAP | 0.76% | 0.57% | 1.31% | 0.29% | 0.57% | 0.57% | 0.61% | 0.96% |
| Tanh-P2P | t-MAP | 83.22% | 84.39% | 85.25% | 85.92% | 73.97% | 76.10% | 76.66% | 77.49% |
| Tanh-P2S | t-MAP | 85.79% | 88.44% | 88.76% | 89.18% | 78.05% | 79.53% | 80.18% | 81.10% |
| RNM-P2P | t-MAP | 83.95% | 84.32% | 83.22% | 85.26% | 74.02% | 76.03% | 76.93% | 77.25% |
| RNM-P2S | t-MAP | 85.92% | 88.45% | 88.89% | 89.49% | 77.96% | 79.60% | 80.30% | 81.33% |
| Original | MAP | 78.88% | 80.69% | 81.01% | 81.48% | 70.94% | 73.01% | 73.61% | 74.11% |
| Method | Metrics | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 |
|---|---|---|---|---|---|---|
| Noise | t-MAP | 1.24% | 2.78% | 1.31% | 1.25% | 1.14% |
| Tanh-P2P | t-MAP | 54.95% | 63.11% | 75.24% | 75.90% | 77.23% |
| RNM-P2P | t-MAP | 52.44% | 67.03% | 76.19% | 76.13% | 76.95% |
| Method | FLICKER-25k | NUS-WIDE | ||||||
|---|---|---|---|---|---|---|---|---|
| 16 bits | 24 bits | 32 bits | 48 bits | 16 bits | 24 bits | 32 bits | 48 bits | |
| Noise | 74.16% | 76.54% | 78.47% | 80.36% | 70.08% | 70.25% | 71.48% | 72.02% |
| Tanh-P2P | 1.92% | 3.54% | 3.15% | 2.01% | 9.74% | 7.26% | 6.97% | 9.50% |
| RNM-P2P | 1.69% | 2.42% | 3.32% | 1.90% | 9.65% | 6.47% | 5.59% | 9.75% |
| HAG | 1.36% | 2.64% | 4.53% | 1.97% | 3.79% | 3.64% | 3.71% | 3.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Zhan, Y.; Hu, C.; Shi, R. A Fast Method for Protecting Users’ Privacy in Image Hash Retrieval System. Machines 2022, 10, 278. https://doi.org/10.3390/machines10040278
Huang L, Zhan Y, Hu C, Shi R. A Fast Method for Protecting Users’ Privacy in Image Hash Retrieval System. Machines. 2022; 10(4):278. https://doi.org/10.3390/machines10040278
Chicago/Turabian StyleHuang, Liang, Yu Zhan, Chao Hu, and Ronghua Shi. 2022. "A Fast Method for Protecting Users’ Privacy in Image Hash Retrieval System" Machines 10, no. 4: 278. https://doi.org/10.3390/machines10040278
APA StyleHuang, L., Zhan, Y., Hu, C., & Shi, R. (2022). A Fast Method for Protecting Users’ Privacy in Image Hash Retrieval System. Machines, 10(4), 278. https://doi.org/10.3390/machines10040278






