Abstract
The process parameter optimization of laser cladding using a bio-inspired algorithm is a hot issue and attracts the attention of many scholars. The biggest difficulty, at present, is the lack of accurate information regarding the function relationship between objectives and process parameters. In this study, a novel process parameter optimization approach for laser cladding is proposed based on a multiobjective slime mould algorithm (MOSMA) and support vector regression (SVR). In particular, SVR is used as a bridge between target and process parameters for solving the problem of lacking accurate information regarding the function relationship. As a new metaheuristic algorithm, MOSMA is to obtain the Pareto solution sets and fronts. The Pareto solution sets are optimized process parameters, and the Pareto fronts are optimized objectives. Users can select the corresponding optimized process parameters according to their needs for the target. The performance of the proposed approach was evaluated by the TOPSIS method, based on actual laser cladding data and compared with several well known approaches. The results indicate that the optimal process parameters obtained by the proposed approach have better process performance.
1. Introduction
With the growing requirements for the mechanical properties of transmission parts, traditional hardening technology is not remarkable in terms of production cost, benefit and performance improvement. Laser cladding is a new surface hardening technology with great potential application value. Under the irradiation of a high energy laser, the cladding alloy powder is melted and added to the surface of the substrate. The cladding layer has good mechanical properties after cooling [1]. In addition, it also has the advantages of high precision, high quality and the low thermal effect of the substrate [2,3].
Laser power P, laser scanning speed V and powder feeding rate F (voltage ) are the three key process parameters, which are easy to control and have a strong impact on the quality of the cladding layer [4]. Optimal process parameters vary with different substrate materials and laser cladding powders. In order to obtain a high quality cladding layer, it is of great significance to perform parameter optimization for each laser cladding process.
An empirical statistics method has been used to optimize the process parameters of laser cladding. The relationship between cladding geometry (width, height, depth of molten and dilution rate) and process parameters (laser power, powder feeding rate and scanning speed) has been studied to obtain the linear relationship by the regression method [5]. According to simulation results of molten pool temperature distribution, the laser power and scanning speed had a great influence on the temperature field and geometry of the molten pool [6]. There are specific functions that have been proposed to describe the geometry of a laser cladding layer based on the recursive model and experimental results. Thereby, the complete geometry of the laser cladding layer can be predicted from the basic process parameters [7].
In this study, T15 high speed steel powder was deposited on a 42CrMo steel substrate with the laser cladding process. It greatly improved the surface hardness and wear resistance of the substrate and further improved the service life of mechanical parts [8]. On this basis, heuristic algorithms can be used to solve and optimize process parameters. However, there is no accurate formula between the machining objectives (dilution ratio, powder utilization rate, etc.) and process parameters. This causes significant difficulty for the multiobjective optimization of process parameters.
A slime mould algorithm (SMA) is an up to date bio-inspired method, which was presented by Chen et al. [9] in 2020. It simulated the behavior of slime mould and established the distinct mathematic model for an outstanding exploratory capacity and exploitation propensity. SMA was evaluated using various benchmark data and achieved superior results. A multiobjective slime mould algorithm (MOSMA) employed the same underlying SMA mechanisms for convergence, combined with an elitist nondominated sorting approach to estimate Pareto optimal solutions [10].
In this paper, a novel process parameter optimization approach for laser cladding is proposed based on MOSMA and SVR (MOSMA-SVR-POLC). MOSMA is used to optimize the process parameters of laser cladding (Pareto solution set). Support vector regression (SVR) is used to build the relationship between process parameters and machining objectives. The actual laser cladding data are utilized to assess the performance of MOSMA-SVR-POLC. Simultaneously, the data fitting method (DFM) [5], the response surface method (RSM) [11], MODA (multiobjective dragonfly algorithm)-SVR-POLC [12], MOEA/D (multiobjective evolutionary algorithm based on decomposition)-SVR-POLC [13] and other variant methods are compared with the proposed approach.
There are two innovations. First, the ingenious combination of MOSMA and SVR is modeled in the process parameter optimization of laser cladding. SVR is used to predict the optimization objectives based on the past data of laser cladding, and the predicted results are involved in the iteration process of MOSMA. Secondly, the proposed approach is tested using actual machining data, which can well verify the feasibility and effectiveness of the method.
2. MOSMA-SVR-POLC Approach
In this section, the new MOSMA-SVR-POLC hybrid approach is proposed to deal with the problem of the process parameter optimization of laser cladding. The main idea is as follows: (a) carry out the process parameter population representation of laser cladding, (b) obtain the current Pareto solution set and front based on the actual machining data as the training set and SVR as the fitness function, (c) update the population via the Pareto solution set, Pareto front and MOSMA. Steps (b) and (c) are repeated until the cut-off condition is met. The cut-off condition is generally set to reach the maximum iteration. During theorisation, there are two issues that need special attention. The first is how the process parameter population of laser cladding is represented. The second is the membership of the Pareto front. In MOSMA-SVR-POLC, the discussions of these issues are shown in the following.
- The process parameter population representation of laser cladding: The population X is made up of individuals . X = , where n indicates the population size. The attributes of are determined by the process parameters of laser cladding (P, , V).
- The membership of Pareto front: The dilution ratio , powder utilization rate and machining efficiency are usually used to evaluate the effect of laser cladding. Therefore, these indicators can constitute the membership of Pareto front. Thus far, there is no accurate employing these objectives and process parameters; hence, the -SVR is applied to predict the objectives. In addition, and are special (in essence, bigger is better). It is necessary to obtain the reciprocal of and for unifying the characteristics of all the indicators (smaller is better).
In this work, -SVR [14] is used to predict the dilution ratio , powder utilization rate and machining efficiency , because there is no accurate calculation formula employing the objectives (, and ) and the process parameters (P, and V) in the field of laser cladding. The development kit LIBSVM offers the source codes of -SVR [15]. The radial basis function (RBF) kernel is very efficient, especially in the prediction of high dimensional samples [16]. The function is listed below.
where is a coefficient to be set manually, is the prediction result vector, and indicates the actual value vector.
The main process of the MOSMA-SVR-POLC approach is depicted in Figure 1. The specific steps are shown in the following.
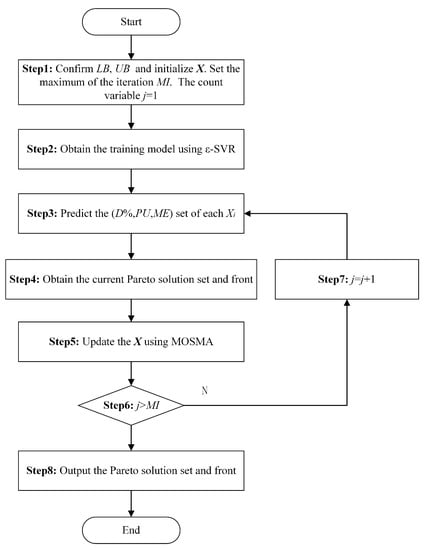
Figure 1.
Flowchart of MOSMA-SVR-POLC.
Step 1 Confirm the lower and upper limits of P, and V to form the lower limit sets and the upper limit sets . Thus, X is initialized randomly within and . The maximum of the iteration is marked as . The iteration count variable j is set to 1.
Step 2 Based on training data, obtain the training model using -SVR.
Step 3 Based on the training model, predict the set of each .
Step 4 Obtain the current Pareto solution set and front with the sets.
Step 5 Update X with the operations of MOSMA.
Step 6 If , go to Step 8; otherwise, go to Step 7.
Step 7 j = j + 1. Go to Step 3.
Step 8 Output the Pareto solution set and front.
Multiobjective Slime Mould Algorithm
SMA was presented by Chen et al. [9] in 2020. It was motivated by the oscillating patterns of slime mould. For forming the optimum path to connect food with outstanding exploratory capacity and exploitation propensity, a distinct mathematic model was presented using accommodative weights to imitate the process of generating positive and negative feedback of the propagation wave supported by a bio-oscillator. MOSMA employed the same underlying SMA mechanisms for convergence, combined with an elitist nondominated sorting approach to estimate Pareto optimal solutions [10]. The operations of MOSMA required for this work are shown in Figure 2.
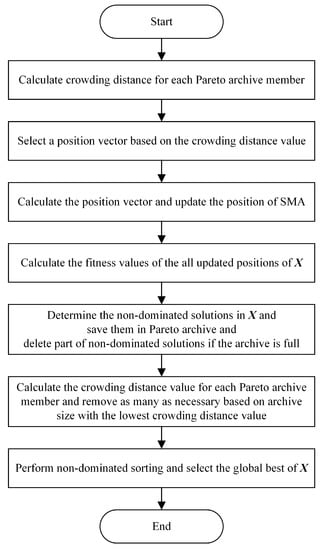
Figure 2.
Flowchart of the required operations of MOSMA.
3. Case Study
3.1. Feasibility Experiment
The experimental conditions involve (i) a PC with Matlab R2018a, (ii) the LIBSVM software package, and (iii) the data sets, which were obtained from the practical laser cladding processing experiment. In this study, 42CrMo steel with dimensions of (100 × 100 × 15) mm was used as the substrate. The steel was treated by quenching and tempering. The cladding powder was T15 high speed steel powder with a particle size of (30–100) m. The chemical compositiosn of the T15 powder and 42CrMo steel are represented in Table 1.

Table 1.
Chemical composition of clad powder and substrate materials.
The laser model was a TruDisk4002, as shown in Figure 3. A single layer cladding layer was prepared by the coaxial powder feeding method with T15 high speed steel as the cladding powder, argon as the powder carrier gas and shielding gas in the cladding process. Experimental process parameters are listed below: laser power (P) selection of 1400 W, 1700 W, 2000 W and 2300 W; the scanning speeds (V) were 6 mm/s, 7 mm/s, 8 mm/s and 9 mm/s; similarly, there were four rates of powder feeding voltage (): 40 V, 50 V, 60 V, 70 V. Other parameters include: defocus: 16 mm, lap rate: 30%, and protective gas flow: 20 L/min. The complete experimental method was adopted. A total of 64 machining experiments were carried out. They were cut with a sample size of (15 × 15 × 15) mm. The inlaying, grinding, polishing and other processes were carried out to make the sample surface show a mirror effect and no obvious scratches. Then, the surface of the samples were etched with a solution with HNO. Lastly, the 64 samples were placed in sequence under an electron microscope for observation and photography. The geometric shape of the cladding layer of each sample was recorded (as shown in Figure 4 and Figure 5, where w is width, h is height, and b is melting depth. is melting height area, and is melting depth area). Figure 5 shows the transverse cross section of the claddings using a scanning electron microscope. The relative geometric dimensions of the cladding layer were measured with AutoCAD software. It was found that there were no obvious cracks, pores, inclusions nor other defects in the cladding layer section.

Figure 3.
Laser cladding system.
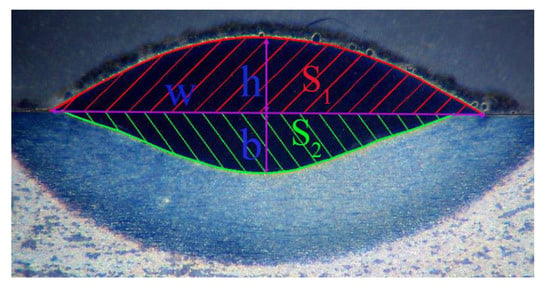
Figure 4.
Geometric shape diagrammatic sketch of the cladding layer.

Figure 5.
Cross section optimal micrographs of the single clad tracks for different process parameters.
The machining data are shown in Table 2, where can be obtained according to Equation (2) [17]. is calculated via Equation (3), and is obtained by Equation (4).

Table 2.
Machining parameters and measurement results for each single clad.
With the machining data in Table 2, the proposed MOSMA-SVR-POLC was used to search the optimized process parameters. The parameter settings of MOSMA-SVR-POLC are shown in Table 3. The machining data is regarded as the training set, and X is taken as the test set. The prediction , and are obtained via these approaches. The final Pareto optimal solution and front of MOSMA-SVR-POLC are revealed in Table 4. The corresponding graphics of MOSMA-SVR-POLC are shown in Figure 6. From the figures, the relationship between , and is extremely complex.

Table 3.
Parameter setting of MOSMA-SVR-POLC and other approaches.

Table 4.
Pareto optimal solutions and fronts of MOSMA-SVR-POLC.
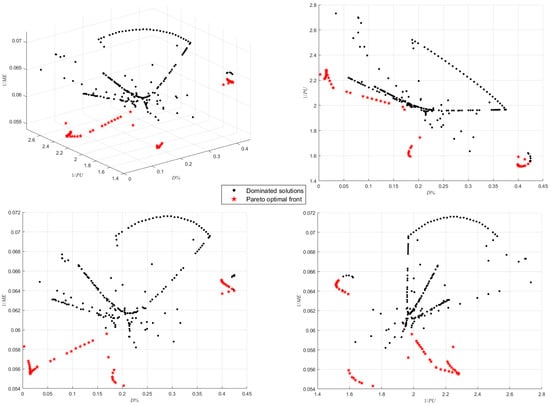
Figure 6.
Pareto front of MOSMA-SVR-POLC (3D and 2D).
Many optimized process parameters were obtained, which is a challenge for practical application: how to select the optimal one for practical machining? The TOPSIS method [18] was used to obtain the best process parameter. The key lies in the weight of the three indicators: , and . The Saaty weight method was used to calculate the weight. The problem becomes to determine how much users value the , and . In this work, is considered to be slightly more important than the other two indicators. Therefore, the weight of , and is 0.6:0.2:0.2 using the Saaty weight method. The optimal process parameters under this weight are shown in Table 5, based on Table 4. The relative error between MOSMA-SVR-POLC and the actual laser cladding is also calculated and shown in Table 5. From Table 5, it can be seen that only the last error of is relatively large, and the others are small. The feasibility of this method is verified to a great extent.

Table 5.
Optimal process parameters and relative errors () of MOSMA-SVR-POLC.
3.2. Comparative Experiment
The experimental conditions are consistent with those in the feasibility experiment. The proposed MOSMA-SVR-POLC is compared with the mainstream methods: DFM [5] and RSM [11], and some variants of MOSMA-SVR-POLC, such as MODA-SVR-POLC [12], MOEA/D-SVR-POLC [13], MOPSO-SVR-POLC [19], NSGAII-SVR-POLC [20], MOGWO-SVR-POLC [21]. The parameter settings of these approaches are also shown in Table 3. The TOPSIS method [18] is also used to obtain the best process parameter. The weight of , and is also set to 0.6:0.2:0.2. The best process parameters and relative errors () of these approaches are shown in Table 6. Figure 7 shows the Pareto optimal front obtained by MOSMA-SVR-POLC and its similar algorithms.

Table 6.
Optimal process parameters and relative errors () of the comparison methods.
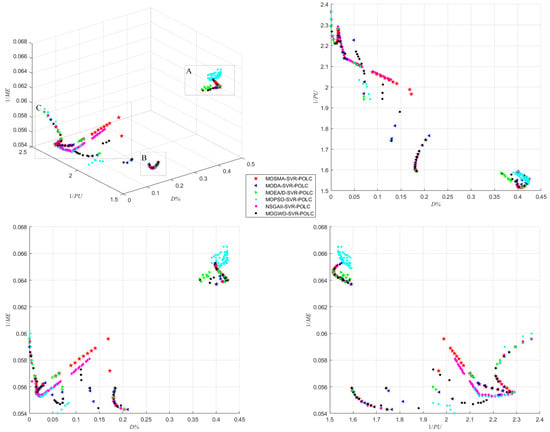
Figure 7.
Pareto optimal front obtained by MOSMA-SVR-POLC and its similar algorithms.
From Table 5 and Table 6, it can be seen that the proposed MOSMA-SVR-POLC had the same optimal process parameters as DFM and MOGWO-SVR-POLC. In terms of , it was much better than DFM and the same as MOPSO-SVR-POLC and MOGWO-SVR-POLC. DFM performed extremely badly in the of . RSM, MODA-SVR-POLC, MOEA/D-SVR-POLC and NSGAII-SVR-POLC obtained different optimal process parameters. RSM lagged behind MOSMA-SVR-POLC. MODA-SVR-POLC and MOEA/D-SVR-POLC also had a good performance, except for the of . NSGAII-SVR-POLC did not perform well in the of D%. From Figure 7, MOPSO-SVR-POLC, NSGAII-SVR-POLC and MOGWO-SVR-POLC had a good performance in area C. MOSMA-SVR-POLC performed well in regions A and B. The above results confirm the capacity of MOSMA-SVR-POLC. The proposed approach proves to be very competitive.
4. Discussion
In the feasibility experiment, the TOPSIS method was used to obtain the optimal process parameters. However, the difference in weight ratios between optimization objectives affects the selection of optimal process parameters. In this section, the different weight ratios were selected to study the output of the optimal process parameters, and the prediction accuracy of the proposed approach will be further discussed. The results are shown in Table 7.

Table 7.
Optimal process parameters and relative errors () of the proposed approach under different weight ratios.
From Table 7, it can be seen that the different weight ratios do define the different optimal process parameters. This meets the needs of different users for objectives. No matter which weight ratio, the prediction accuracy of the first two targets, and , are higher than . Especially in the weight ratios 1/3:1/3:1/3, 0.2:0.6:0.2 and 0.2:0.2:0.6, this situation is more obvious. The improvement ofthe prediction accuracy of may be the next important research topic.
In addition, the big oh notation is used to calculate the computation cost of the proposed approach. The computation cost of MOSMA and SVR is O(()) and O(), respectively, is the consumption time of objective calculation, d is the attribute number of individuals, l represents the sample size, and represents the time consumed for the calculation of the SVR kernel function. The proposed approach is composed of MOSMA and SVR. Therefore, its computation cost is O(()).
5. Conclusions
This work proposed a new hybrid approach for the process parameter optimization of laser cladding using a multiobjective slime mould algorithm and support vector regression. The proposed MOSMA-SVR-POLC realizes objectives prediction and process parameter optimization in laser cladding and provides users with the most valuable parameters for different objectives. Furthermore, -SVR is applied to predict the , and . The training data are from the actual laser cladding. MOSMA is used to obtain the Pareto optimal solutions and fronts. The feasibility experiment and comparative experiment were carried out to test the performance of MOSMA-SVR-POLC. The experimental results reveal that MOSMA-SVR-POLC achieves a competitive predictive performance compared with other well established approaches. The study confirms the feasibility and effectiveness of MOSMA-SVR-POLC in the field of process parameter optimization in laser cladding.
For future work, the improvement of the setting parameters and prediction accuracy of -SVR should be further studied. Secondly, more kinds of laser cladding experiments, such as multichannel laser cladding, should be added to verify and modify the method in this paper.
Author Contributions
Conceptualization, Y.Z. and W.C.; methodology, Y.Z. and W.C.; software, B.G.; validation, B.G. and Z.T.; formal analysis, Z.T.; investigation, B.G.; resources, B.G.; data curation, B.G.; writing—original draft preparation, Y.Z. and B.G.; writing—review and editing, W.C.; visualization, W.C.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition, Y.Z. and W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 51905148) and Fundamental Research Funds for the Central Universities (Grant No. B200202218 and BC210202088).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data is presented in Table 2.
Acknowledgments
The authors want to thank Tsinghua University for providing the laser cladding equipment to support the research of the authors.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Lian, G.; Yao, M.; Liu, Z.; Yang, S.; Chen, C.; Wang, H.; Xiang, Y.; Cong, W. Near-net shaping control of triangular stacking in laser cladding process. Procedia Manuf. 2019, 34, 233–238. [Google Scholar] [CrossRef]
- Carcel, B.; Serrano, A.; Zambrano, J.; Amigo, V.; Carcel, A.C. Laser cladding of TiAl intermetallic alloy on Ti6Al4V—Process optimization and properties. Phys. Procedia 2014, 56, 284–293. [Google Scholar] [CrossRef] [Green Version]
- Nie, Z.; Wang, G.; Mcguffin, J.; Narayanan, B.; Zhang, S.; Schwam, D. Experimental study and modeling of H13 steel deposition using laser hot-wire additive manufacturing. J. Mater. Process. Technol. 2016, 235, 171–186. [Google Scholar] [CrossRef]
- Fatoba, O.S.; Akinlabi, E.T.; Akinlabi, S.A.; Obiegbu, M.C. Data related to optimized process parameters influence on hardness, microstructural evolution and wear resistance performance of Al-Si-Sn-Cu/Ti-6Al-4V composite coatings. Data Brief 2019, 23, 103724. [Google Scholar] [CrossRef]
- Shayanfar, P.; Daneshmanesh, H.; Janghorban, K. Parameters optimization for laser cladding of inconel 625 on ASTM A592 steel. J. Mater. Res. Technol. 2020, 9, 8258–8265. [Google Scholar] [CrossRef]
- Wang, X.J.; Su, S.C. Modeling and parameter calculation for laser cladding silicon films. Opt. Precis. Eng. 2011, 19, 60–63. [Google Scholar]
- Nenadl, O.; Ocelik, V.; Palavra, A.; Hosson, J. The prediction of coating geometry from main processing parameters in laser cladding. Phys. Procedia 2014, 56, 220–227. [Google Scholar] [CrossRef] [Green Version]
- Alouane, C.; Kasser, A. Consolidation by atmospheric pressure of T15 tool steel powder. Powder Technol. 2019, 352, 331–339. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 11, 300–323. [Google Scholar] [CrossRef]
- Manoharan, P.; Jangir, P.; Ravichandran, S.; Alhelou, H.H.; Chen, H. MOSMA: Multi-objective slime mould algorithm based on elitist non-dominated sorting. IEEE Access 2021, 9, 3229–3248. [Google Scholar]
- Alam, M.K.; Urbanic, R.J.; Nazemi, N.; Edrisy, A. Predictive modeling and the effect of process parameters on the hardness and bead characteristics for laser-cladded stainless steel. Int. J. Adv. Manuf. Technol. 2017, 94, 397–413. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Cao, W.; Liu, X.; Ni, J. Parameter optimization of support vector regression using henry gas solubility optimization algorithm. IEEE Access 2020, 8, 88633–88642. [Google Scholar] [CrossRef]
- Reddy, A.L.; Preston, S.P.; Shipway, P.H.; Davis, C.; Hussaina, T. Process parameter optimisation of laser clad iron based alloy: Predictive models of deposition efficiency. Surf. Coat. Technol. 2018, 349, 198–207. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Chu, Z.; Sun, N. Modeling and combined application of orthogonal chaotic NSGA-II and improved TOPSIS to optimize a conceptual hydrological model. Water Resour. Manag. 2018, 32, 3781–3799. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2015, 47, 106–119. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).