Abstract
The first step in the synchronous reluctance machine design is the selection of rotor flux barrier type. The literature provides various barrier construction methods with a common goal of reducing parametric complexity. However, too excessive simplification can lead to decreased performance, while overly complex geometries tend to increase optimization time. This paper presents a set of novel flux barrier construction methods with an increased degree of freedom and minimal geometrical complexity. The paper proposes four topologies based on circular, hyperbolic, and original Zhukovsky lines. When considering parametrization complexity, the original Zhukovsky type is the simplest, but it has barrier depth limitations. Other topologies have equal complexity. The paper proposes a novel Modified Zhukovsky variable depth type based on geometrical conformal mapping of the original Zhukovsky lines. The step-by-step construction of each topology is presented in a form of pseudo-code with detailed comments and illustrations. Overall, the presented research provides a valuable starting point for the designer who wants to investigate different smooth rotor barrier topologies.
1. Introduction
In recent years, the synchronous reluctance machine (SyRM) has become commercially viable as a high-efficiency alternative to induction (IM) and interior permanent magnet machines (IPM). The main benefit of the SyRM is that the rotor has no squirrel cage, windings or magnets, just electric steel plates forming a rotor package.
Due to the highest torque and power density, interior rare earth permanent magnet synchronous machines (IPM) are preferred for automotive traction. On the other hand, the use of rare earth permanent magnet (PM) materials, such as neodymium or dysprosium, has historically been a commercial risk [1,2].
Currently, there is no commercial use of synchronous reluctance machines (SyRM) for automotive traction, but having in mind the market uncertainties and potential production cost reduction, they represent a possible alternative [3,4].
On the other hand, commercial vehicles apart from electric traction, have to actuate additional body systems (usually powered by some sort of hydraulic pump). The interface towards external systems is referred as electric power take-off (e-PTO). Considering that the e-PTO needs to be reliable, robust, and cheap, SyRM is the preferred alternative [5,6,7].
In recent decades, SyRM research has focused on improving the rotor barrier design, minimizing the torque ripple, and increasing the power factor [8]. Literature provides references to several barrier topologies: circular [9,10], hyperbolic [11,12], Zhukovsky fluid type [13,14], segmented, etc. Open-source SyRE project offers more details and instructions on geometry generation [15].
The common goal in barrier construction strategy is the reduction of parametric complexity. However, too simplified rotor topologies can lead to decreased performance, while too complex geometries yield better performance, but also tend to increase optimization time (increase is proportional to the parametric complexity).
By merging both approaches, this paper presents a set of flux barrier construction methods with an increased degree of freedom and minimal parametric complexity, based on non-dimensional rotor parameters.
Considering that sharp edges tend to cause mechanical issues at high rotational speeds, only barrier topologies based on smooth analytical functions have been analyzed (circular, hyperbolic, and Zhukovsky).
By definition, Zhukovsky barrier lines are streamlines and cannot be analytically modified to secure variable barrier depth, in this case, conformal mapping is used to create a novel Modified Zhukovsky barrier type with variable depth lines. The following chapters will demonstrate automated barrier design and related pseudo-code for the following topologies:
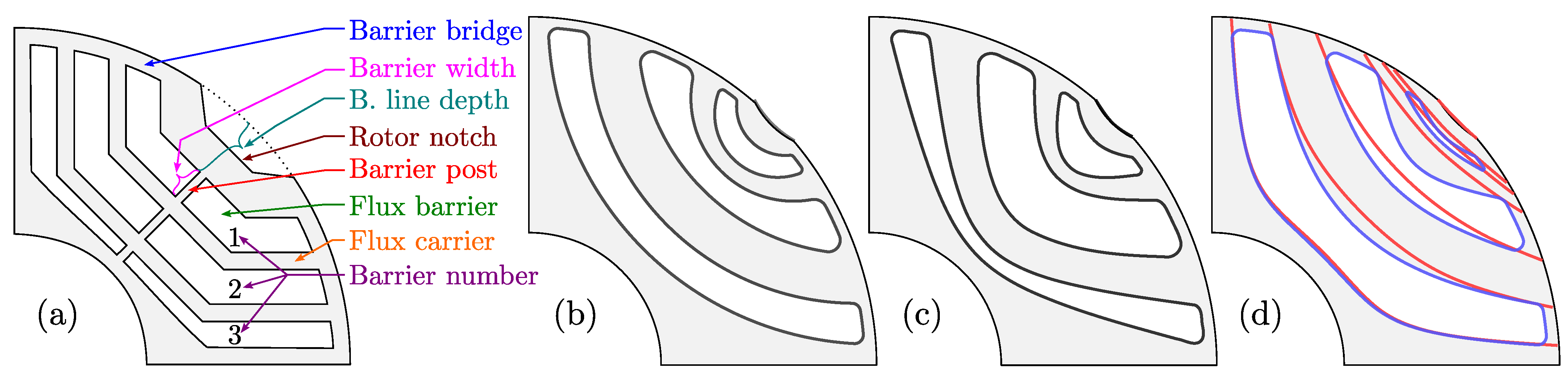
- Circular variable depth (CrVD), Figure 1b
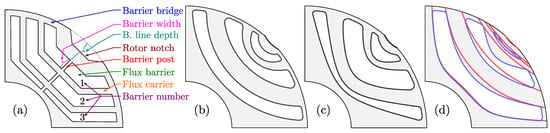 Figure 1. (a) SyRM terminology; SyRM rotor barrier types: (b) Circular variable depth; (c) Hyperbolic variable eccentricity; (d) Modified Zhukovsky (blue), original Zhukovsky (red).
Figure 1. (a) SyRM terminology; SyRM rotor barrier types: (b) Circular variable depth; (c) Hyperbolic variable eccentricity; (d) Modified Zhukovsky (blue), original Zhukovsky (red). - Variable eccentricity hyperbolic (HyVE), Figure 1c
- Original Zhukovsky (Zh), Figure 1d (red)
- Modified Zhukovsky variable depth (MZhVD), Figure 1d (blue).
2. Geometric Feasibility
The term feasibility usually refers to the solution and means that the solution satisfies all the given constraints. There is another type of feasibility called geometric or model feasibility. A geometrically feasible model is valid for solving if: there are no overlapping edges, negative lengths, or non-conventional geometric relations that will inevitably produce issues after optimization starts.
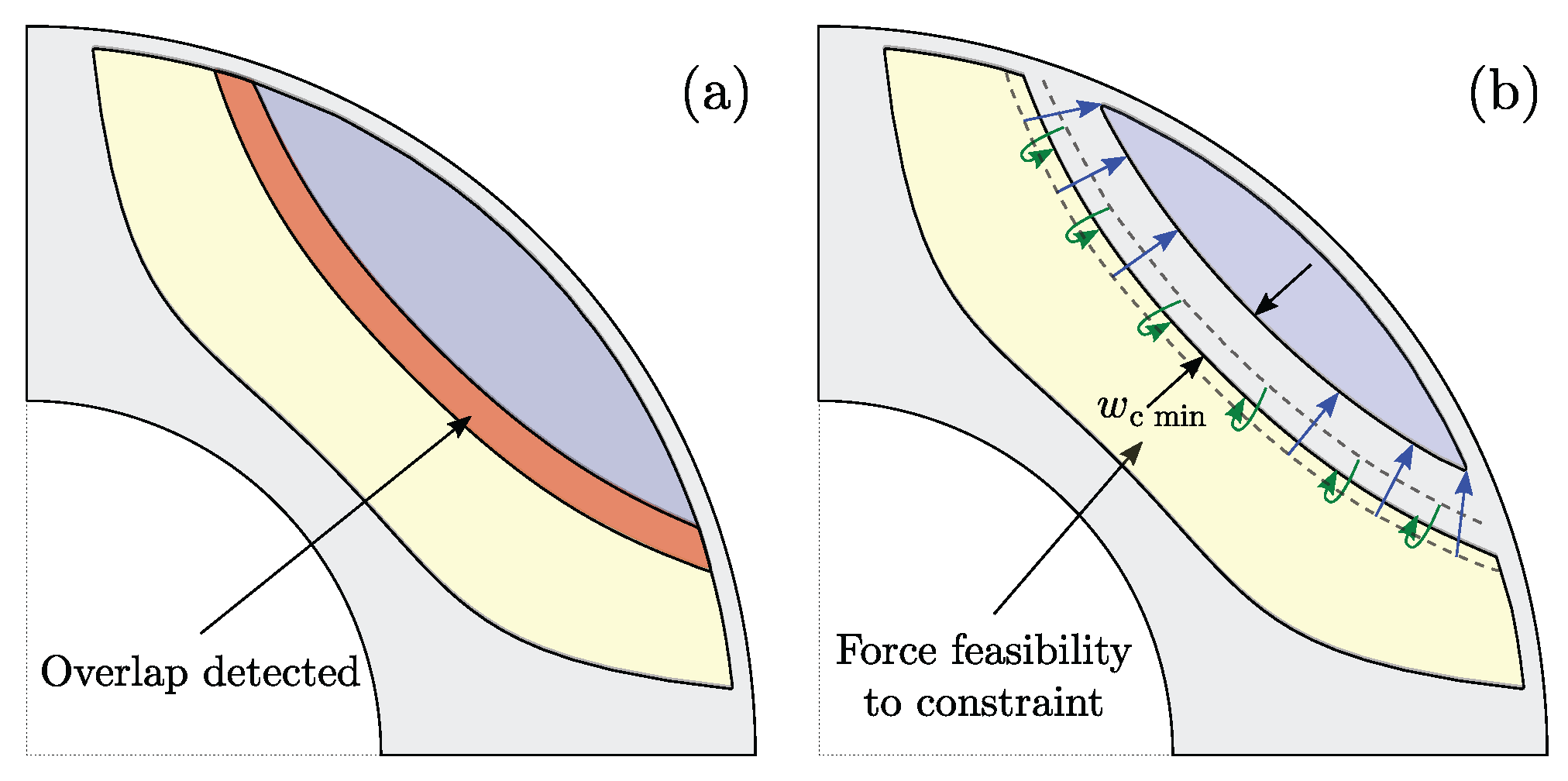
This is especially important when using template-based design software. The generation of such a non-valid model can be avoided in several ways (e.g., barrier 1 (blue) collides with barrier 2 (yellow), the collision is marked in red, Figure 2a). In the first case, the complete set of optimization parameters is initialized until geometric feasibility is achieved [16].
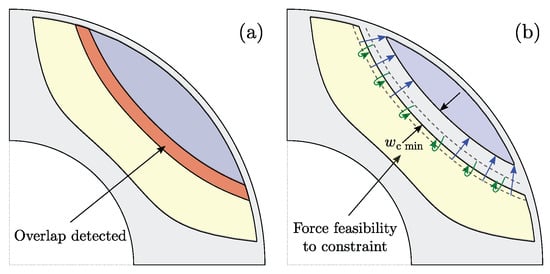
Figure 2.
Infeasible geometry (a) and forced feasibility (b).
The alternative is forced feasibility, where each infeasible design is subjected to parameter modification until feasibility is reached, e.g., barrier 1 (blue) and barrier 2 (yellow) are modified until the minimum flux carrier width is reached, Figure 2b [7].
The final approach is to secure that the design is always feasible.
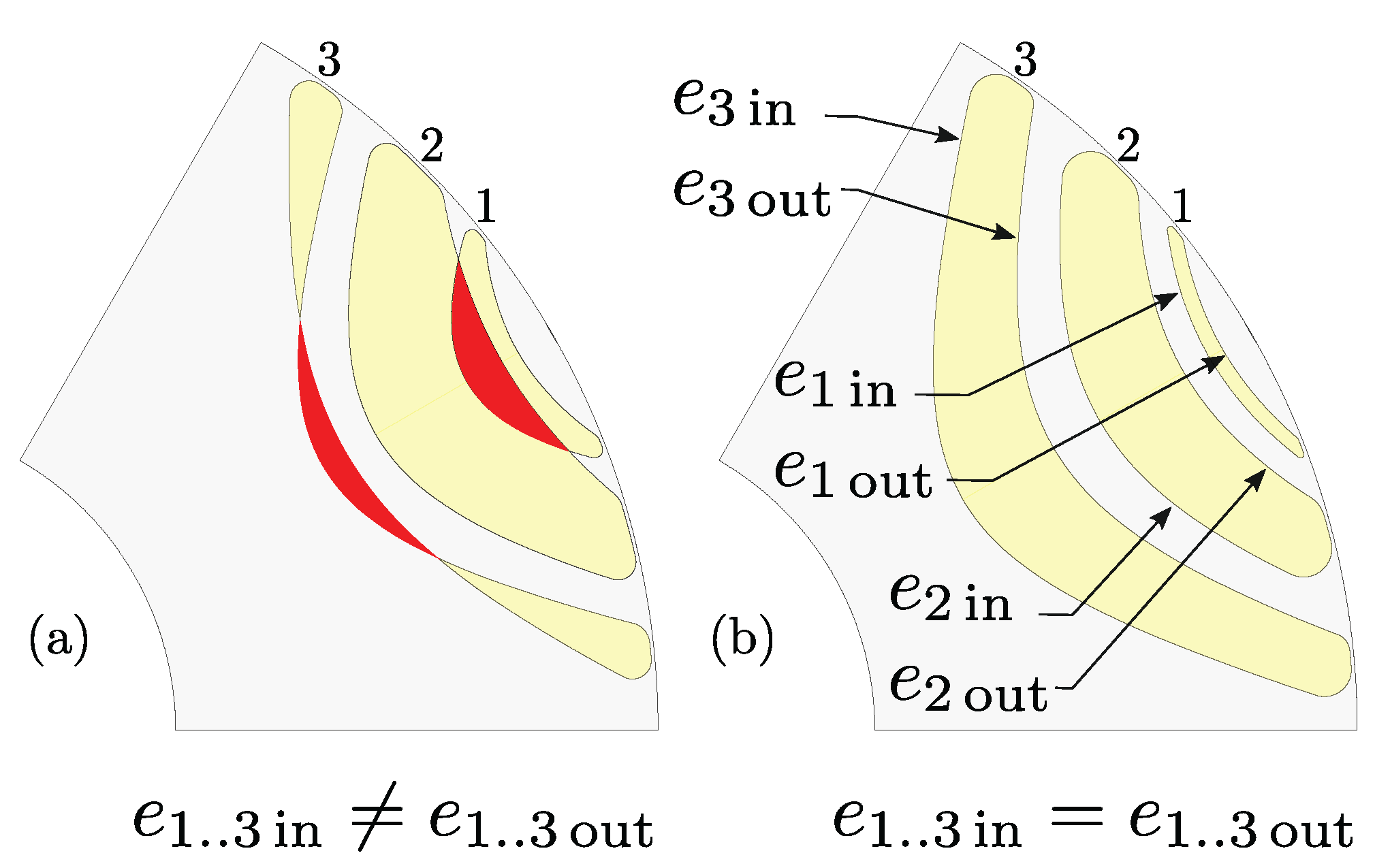
The example is a SyRM with three hyperbolic barriers where barrier depth is varied by hyperbolic eccentricity of each inner and outer barrier line (Figure 3b).
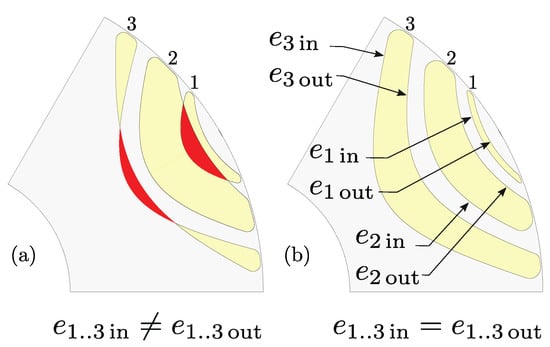
Figure 3.
Illustration of infeasible (a) and feasible geometry (b).
In some cases, the complete freedom in varying the eccentricity causes the inner and outer barrier collision (Figure 3a), which inevitably leads to infeasible designs.
On the other hand, if the designer wants to ensure feasibility, one solution is to parametrize the eccentricity of each outer barrier line relative to the eccentricity of each inner barrier, e.g., (1).
Unfortunately, this option generates constantly changing parameter limits, which can lead to a suboptimal design. Considering the specifics of the SyRM rotor, the rotor geometry can be defined to always yield a feasible design thus achieving absolute feasibility. Instead of directly using eccentricities as parameters, a better approach is to use dimensionless inner and outer barrier depth parameters () for indirect calculation of respective eccentricities. The following text provides detailed instructions on absolutely feasible rotor construction with the corresponding pseudo-code which accepts any pole and barrier number.
3. Design Automation
The following figures are drawn for illustrative purposes and valid for a three barrier rotor (), naming and description of all parameters is explained in Table 1. Vector variables are bolded, e.g., is a variable vector, while R represents a scalar variable.

Table 1.
Example list of design parameters. Color coding is according to Figure 4 variables.
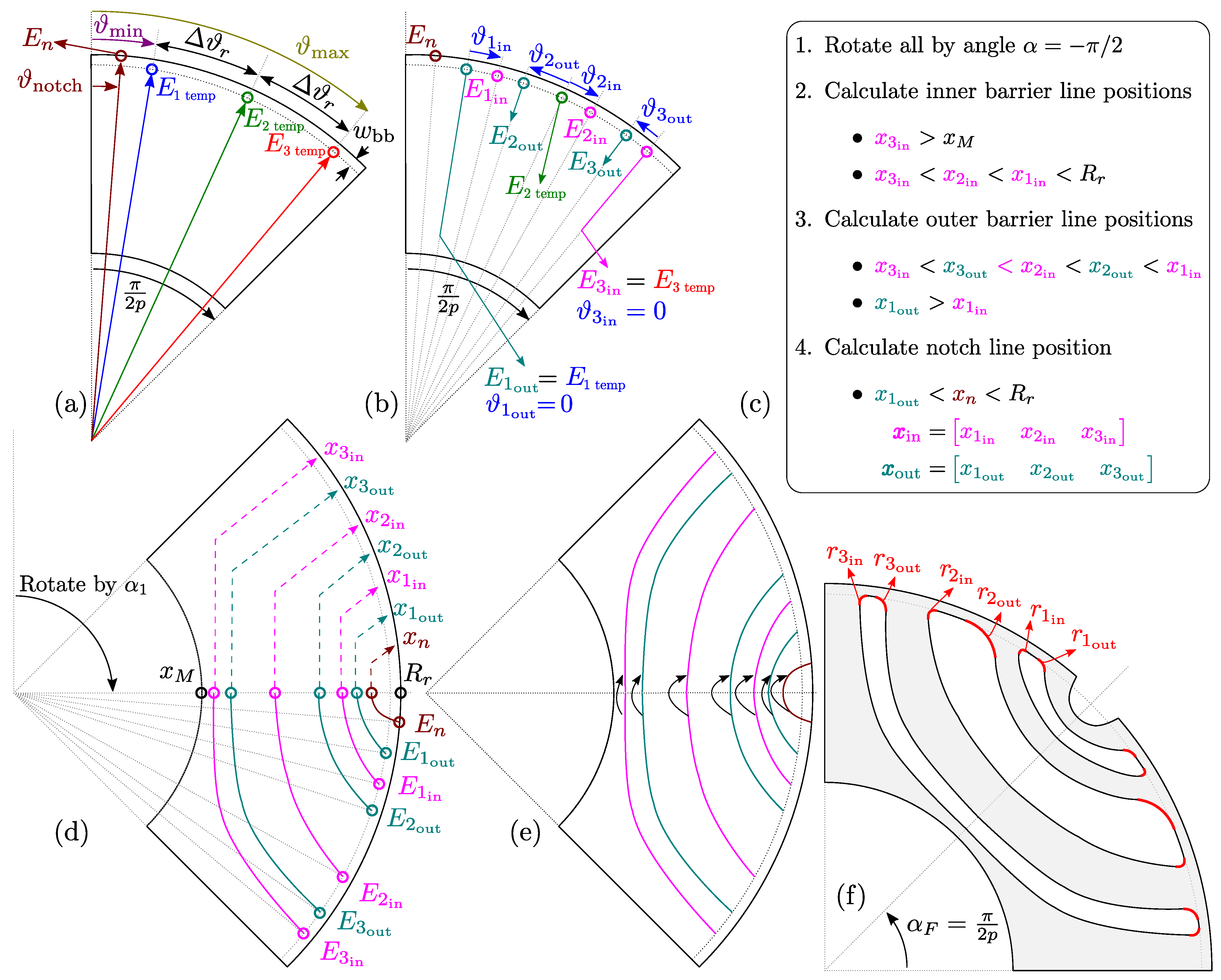
The initial step in rotor construction (Figure 4a) is to specify number of pole pairs (p), rotor barriers (k) and barrier bridge thickness (). The user then specifies dimensionless (Table 1, 18–19). Temporary construction points vector is then created with equidistant angular spacing . Barrier notch point () is defined via additional parameter (Table 1, 20) relative to with radial component equal to rotor radius. Note that the entire geometry is initially constructed in vertical manner (center pole axis is at the angle of ).
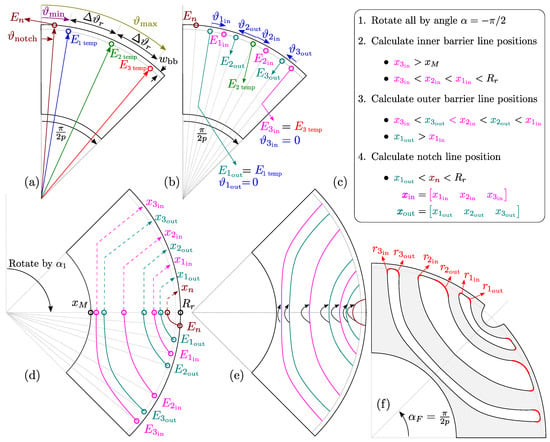
Figure 4.
Rotor barrier construction procedure. Initial rotor construction step (a); Construction of inner and outer barrier line starting points (b); calculation of barrier intersection points (c); calculation of barrier vertices (d); vertex mirroring (e); rotation around center and addition of barrier fillets (f).
The second step (Figure 4b) is the construction of inner and outer barrier line starting points (). The points are calculated relative to , based on additional set of dimensionless parameters (Table 1, 6–11).
The third step is rotation around the center point by the specified angle (in this case ). Barrier line starting points (and additional depth parameters depending of the barrier type) are forwarded to the selected construction function which calculates barrier line intersection points (). The intersection points are calculated based on depth parameters and feasibility conditions listed in Figure 4c. The function returns all inner and outer barrier line vertices (), Figure 4d.
The next step is mirroring line vertices around the horizontal axis (Figure 4e).
The final step is the rotation around the center point by the angle . Barrier fillets (, Table 1, 12–17) responsible for securing mechanical integrity of the rotor are added to the geometry, and final rotor geometry is exported as to the FEA tool (Figure 4f). Adding precise fillets to the discrete lines is a complex problem which is planned to be explained in the future publications. Detail barrier construction steps from Figure 4b–d are discussed in the following sections.
Barrier Depth Variation
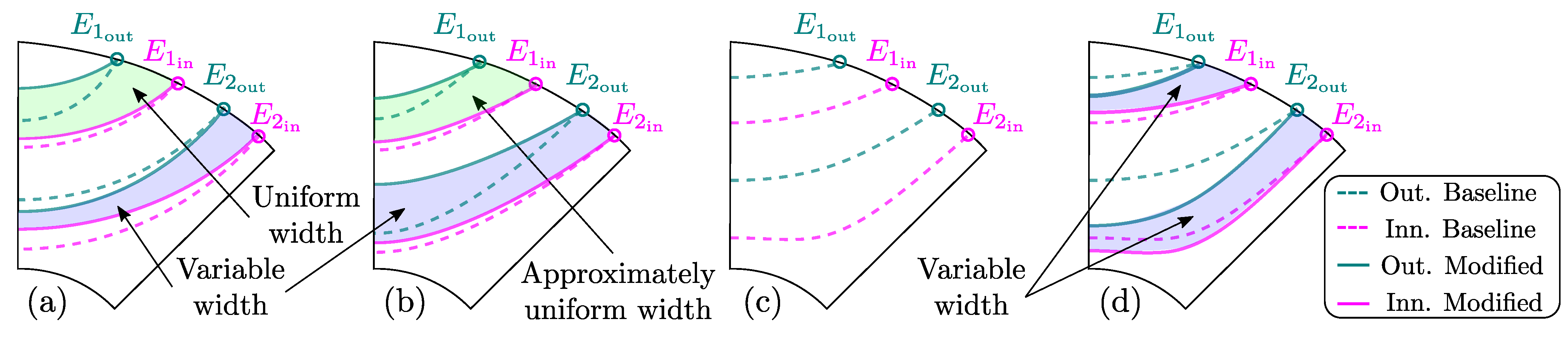
Considering that the barrier width has a substantial impact on the machine performance, this section will explain how inner and outer barrier depth coefficients affect each of the studied topologies, with a simplified presumption of equal line starting points.
Width of the each barrier depends on initial inner and outer line starting points , and depth coefficients . Depending on the depth parameter combination, barrier width can be variable, or uniform. Uniform width is a special case where CrVD barriers are concentric (Figure 5a, green). HyVE barriers can be approximately uniform when they have equal eccentricity (Figure 5b, green). These variants are included in CrVD and HyVE pseudo-code, and will not be studied in detail.
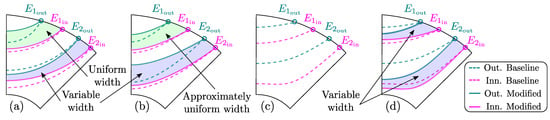
Figure 5.
Barrier depth variation influence on different 2-barrier (k = 2) SyRM topologies. Circular (a); Hyperbolic (b), Zhukovsky (c) and Modified Zhukovsky barrier types (d).
In general, CrVD and HyVE depth variation is unconstrained resulting in variable barrier width (Figure 5a,b, blue).
Zh barrier type (Figure 5c) is a special case because it does not support any depth variation. Barrier line depths are defined directly from starting points and cannot be modified. In order to explore the possible benefits of depth variation, Zh type has been modified as MZhVD where barrier depths have full freedom (Figure 5d).
An example of different barrier line depth parameter combinations is provided in the (Table 2).

Table 2.
Illustrative depth coefficient table for Figure 5.
4. Standard Rotor Barriers
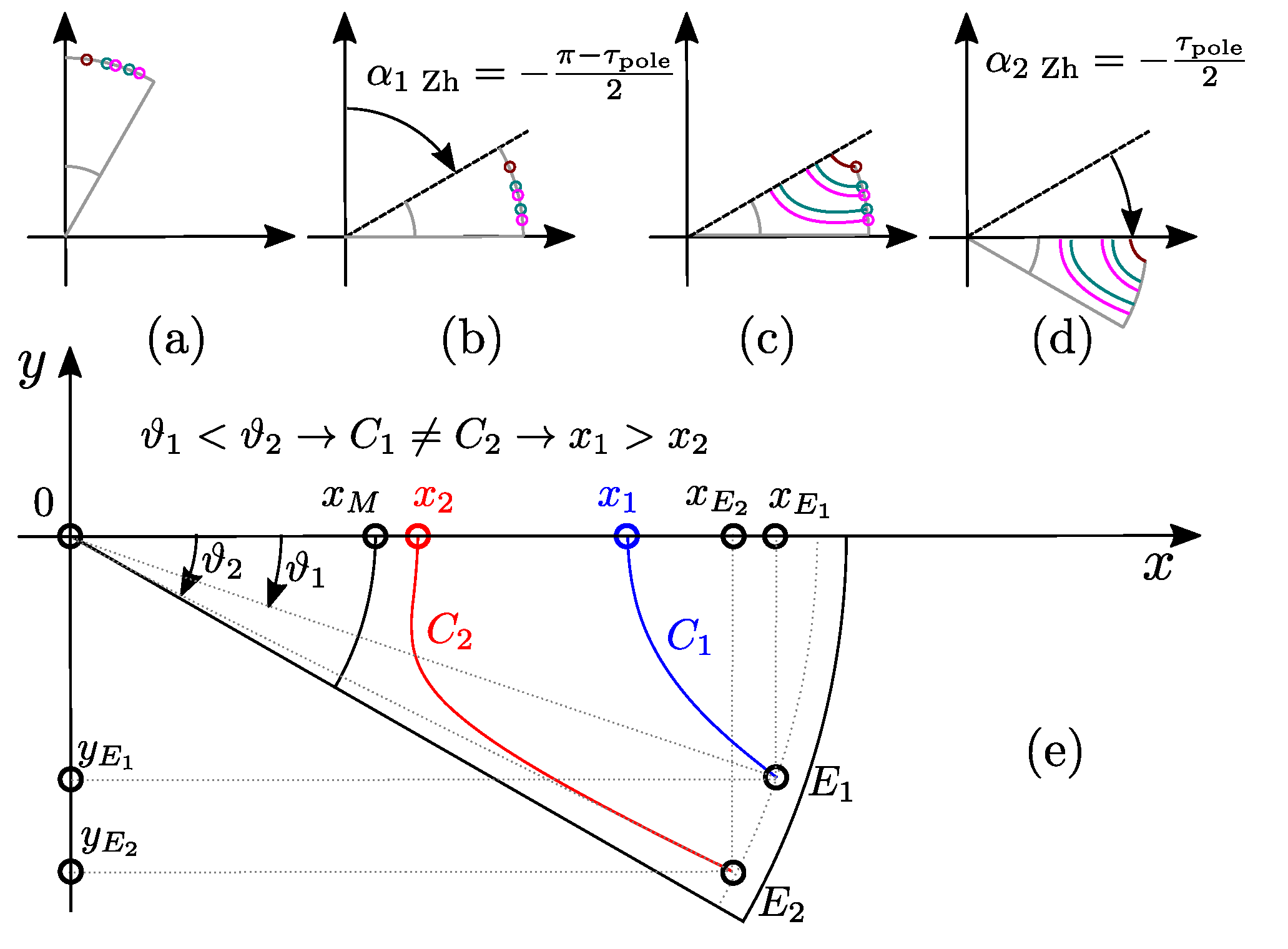
4.1. Zhukovsky Barrier Construction
After definition of all inner and outer barrier line starting points , Figure 6a, the entire geometry is rotated by (Algorithm 1: ln:2, Figure 6b, is the angular pole step.). This partial rotation must be performed because Zhukovsky equations are defined on angular range .
| Algorithm 1 Construction of Zhukovsky barriers |
|
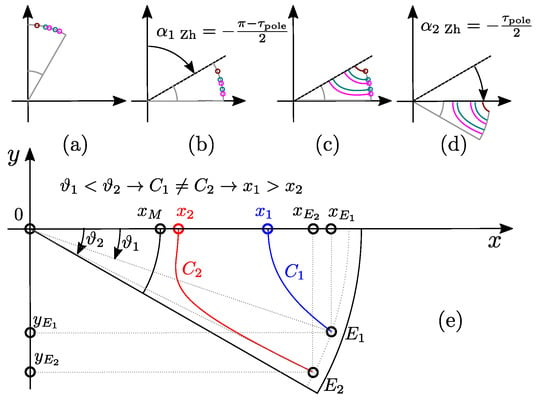
Figure 6.
Zhukovsky barrier construction. Subfigures (a)–(e) are explained in the Section 4.1–Section 4.1.3.
4.1.1. Inner Line Calculation
The first step is the calculation of GetZhukLines barrier line function (Algorithm 1: ln:7) based on and number of barriers k. Note that there are no depth parameters. By definition Zhukovsky barriers are streamlines which cannot mutually intersect. Barrier line profiles (Figure 6e) are derived from conformal mapping theory and the Zhukovsky airflow potential formulation [14,15]. This was originally developed to describe the flow paths of fluids channeled by two infinite plates forming an angle , and a plug centred at the origin of the reference frame. In the solid rotor context, the plug represents the non-magnetic shaft with a radius of . Equations Algorithm 1: ln:12 and Algorithm 1: ln:17 express the magnetic field potential lines in parametric form [7].
Next, polar barrier vertices are calculated based on coefficient vector , starting point polar coordinates and number of barriers k (Algorithm 1: ln:12–19). Finally, GetZhukLines function returns vertices.
4.1.2. Outer Line Calculation
Outer barrier line vertices (Algorithm 1: ln:8) are calculated in the same way as inner lines.
4.1.3. Notch Line Calculation
Notch is specific because it has only one barrier line (Algorithm 1: ln:10). The function GetZhukLines returns which completes the calculation of all barrier lines (Figure 6c). Finally, to be compatible with the rest of the barrier construction procedures, the geometry is rotated by (Algorithm 1: ln:20, Figure 6d).
The next steps (not described within Algorithm 1) are mirroring vertices around horizontal axis (Figure 4e), adding barrier fillets, and geometry rotation around center point (Figure 4f).
Note that Zhukovsky construction pseudo-code is the simplest of all alternatives due to the polar streamline equations (Algorithm 1: ln:12, 17).
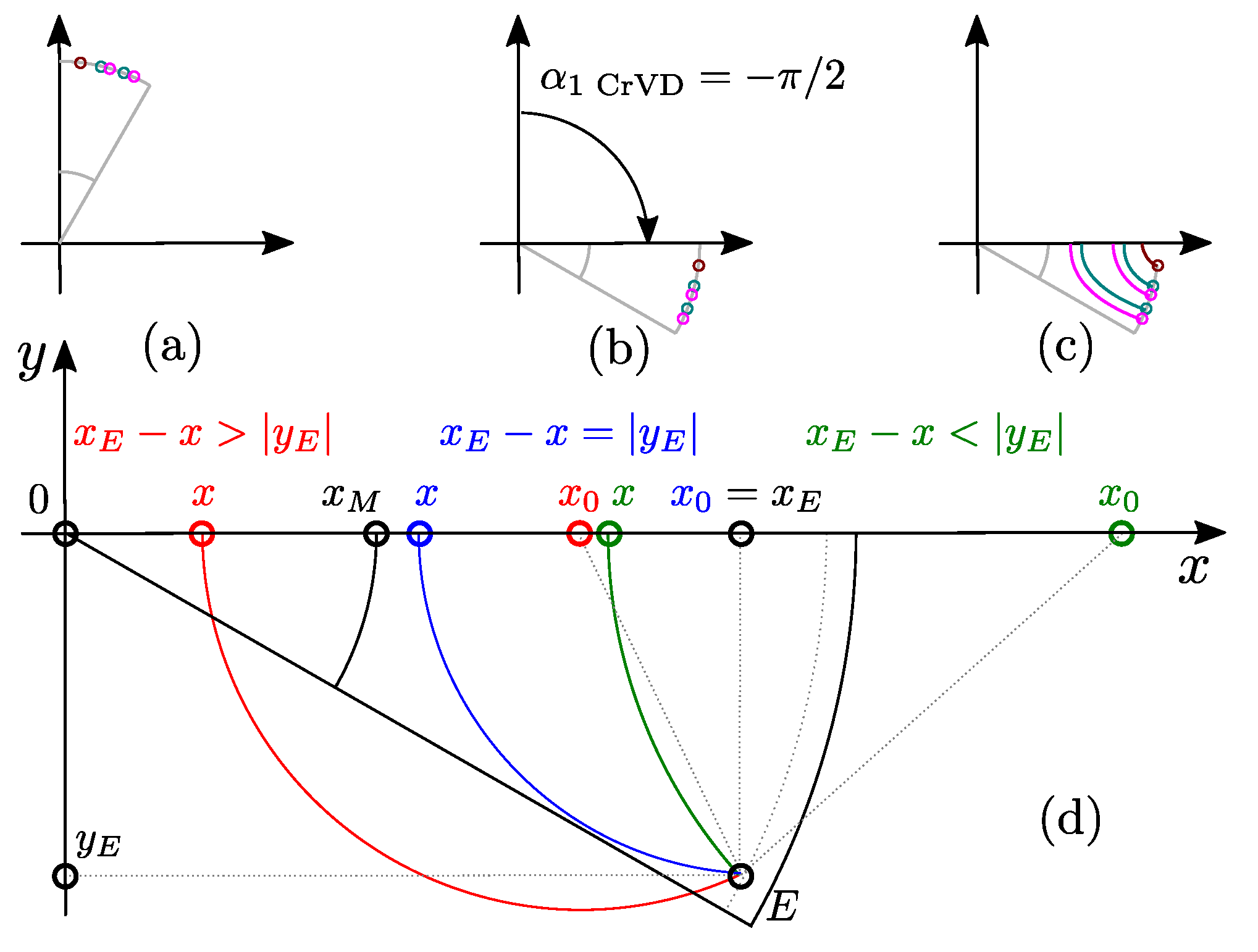
4.2. Circular Barrier Construction
After definition of all inner and outer barrier line starting points and depth parameters , Figure 7a, the entire geometry is rotated by (Algorithm 2: ln:1, Figure 7b).
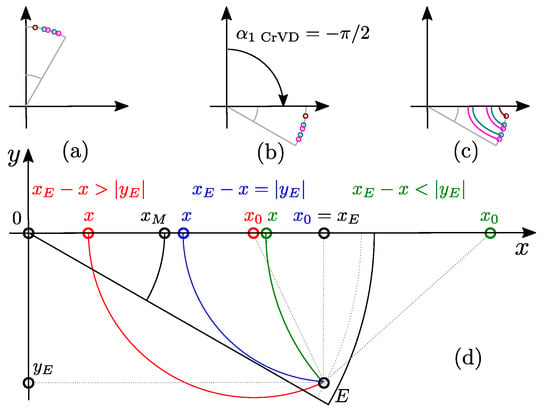
Figure 7.
Circular barrier construction. Subfigures (a)–(d) are explained within the Section 4.2–Section 4.2.3.
4.2.1. Inner Line Calculation
Lets first consider GetInnerLines function which calculates inner line vertices () and intersections () based on and number of barriers k (Algorithm 2: ln:6).
The intersections (Figure 4d) are critical for barrier calculation and in case of circular barriers, they depend on the inequality where x represents the inner or outer intersection. If the condition is fulfilled, the constructed circle is feasible (Figure 7d, green) and the intersection can be calculated based on inner barrier limits (Algorithm 2: ln:15, 21). Otherwise, the circle is infeasible (Figure 7d, red) and the intersection point is calculated from barrier line starting point (Algorithm 2: ln:17, 22).
In case of the most inner line (), the feasibility limit is rotor shaft (), and the intersection is calculated via (Algorithm 2: ln:15). For the second most inner line , feasibility limit is and the intersection is calculated via (Algorithm 2: ln:20). All inner line intersections are then iteratively calculated following the Algorithm 2: ln:12–22 procedure.
Next, GetCrcVtx function (Algorithm 2: ln:23) based on calculated intersections , starting point coordinates and k, calculates the circle origins and radius , and returns barrier vertices (Algorithm 2: ln:39–50). Finally, GetInnerLines returns .
4.2.2. Outer Line Calculation
At this point all inner barrier intersections are defined and now present feasibility limits for outer barrier line construction (Algorithm 2: ln:7). The rest of the GetOuterLines code (Algorithm 2: ln:25–38) is executed in the similar manner as in GetInnerLines. The function in the end returns .
4.2.3. Notch Line Calculation
Notch is specific because it has only one barrier line and depends on the most outer intersection (Algorithm 2: ln:9). Finally, GetOuterLines returns which completes the calculation of all barrier lines (Figure 7c).
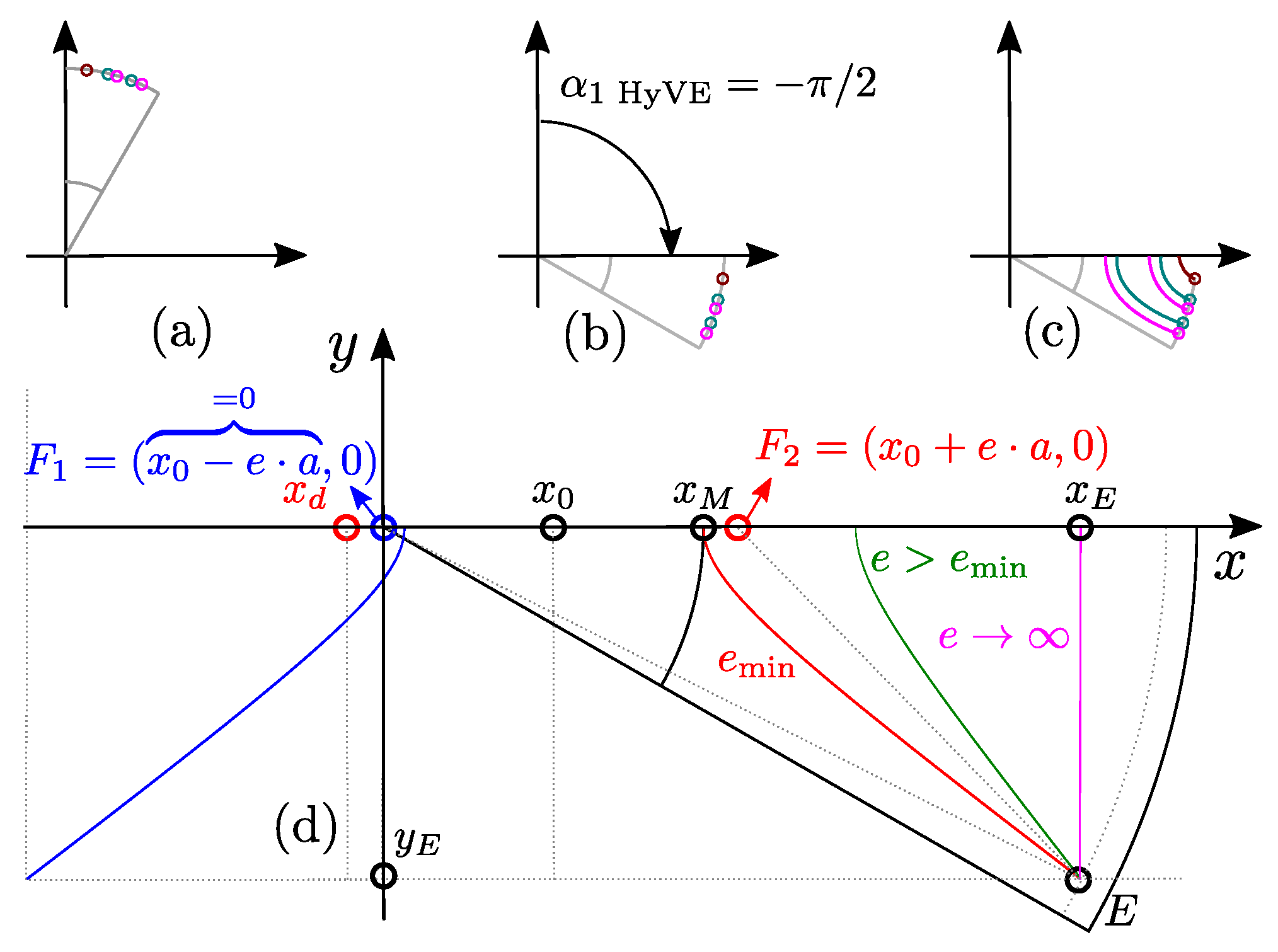
4.3. Hyperbolic Barrier Construction
After definition of all inner and outer barrier line starting points and depth parameters , Figure 8a, the entire geometry is rotated by (Algorithm 3: ln:1, Figure 8b).
| Algorithm 2 Construction of circular barriers |
|
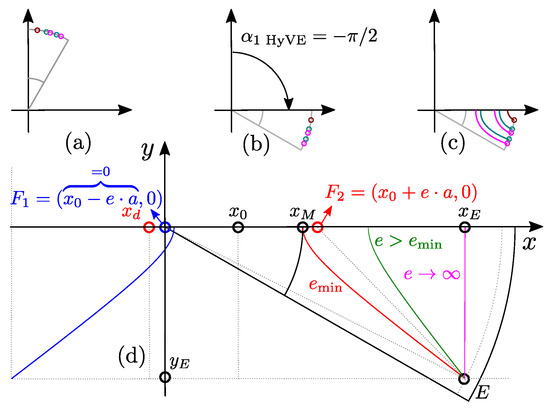
Figure 8.
Hyperbolic barrier construction. Subfigures (a)–(d) are explained in the Section 4.3–Section 4.3.3.
| Algorithm 3 Construction of Hyperbolic barriers |
|
4.3.1. Inner Line Calculation
Lets first consider GetInnerLines function which calculates inner lines vertices () and intersections () based on and number of barriers k (Algorithm 3: ln:7).
To simplify the construction, the left focus is constructed in the origin of the coordinate system (Figure 8d, blue). The intersections with (Figure 4d) are critical for barrier calculation and they depend on the minimum eccentricity Equation , x is the inner or outer intersection limit.
In case of the most inner line (), the feasibility limit is rotor shaft (), the minimum eccentricity is calculated via Algorithm 3: ln:15. For the second most inner line , is calculated via Algorithm 3: ln:17.
If particular barrier has eccentricity within the limits , the construction is feasible (Figure 8d, green). Otherwise the barrier is infeasible (Figure 8d, red, magenta). This is why it is important to limit maximum eccentricity (Algorithm 3: ln:18), where is empirically determined coefficient. The final eccentricity is then calculated depending of the depth parameter (Algorithm 3: ln:19). The next steps are calculation of the left directrix (Algorithm 3: ln:21) and intersection point () based on polar hyperbola Equation (Algorithm 3: ln:21).
All inner line intersections are then iteratively calculated following the described procedure (Algorithm 3: ln:13–21).
Next, GetHypVtx function (Algorithm 3: ln:22) based on calculated directrices , eccentricities , angular starting point coordinates and k, calculates the hyperbolic vertices in polar coordinates , and returns barrier vertices (Algorithm 3: ln:36–41).
Finally, GetInnerLines returns .
4.3.2. Outer line calculation
At this point all inner barrier intersections are defined and now present feasibility limits for outer barrier line construction (Algorithm 3: ln:8). The rest of the GetOuterLines code (Algorithm 3: ln:24–34) is executed in the similar manner as in GetInnerLines. The function returns .
4.3.3. Notch line calculation
Notch is specific because it has only one barrier line and depends on the most outer intersection (Algorithm 3: ln:10). Finally, GetOuterLines returns which completes the calculation of all barrier lines (Figure 7c).
5. Conformal Modifications
5.1. Conformal Mapping
A conformal or angle-preserving transformation also called conformal mapping is a transformation that preserves local angles. An analytic function is conformal at any point where it has a nonzero derivative [17].
Conformal transformations can prove extremely useful in solving physical problems. If the selected complex function satisfies the condition that the real and imaginary parts of w satisfy the Cauchy–Riemann equations and Laplace’s equation, they automatically provide a scalar potential and a so-called stream function [17] (e.g., Zhukovski barrier lines, Figure 1d, red).
FEA is typically used for electromagnetic performance calculations in electric machine design. Depending on the complexity of the calculation and mesh density, it can take several minutes before the calculation is completed. The simulation time can be reduced if a conformal mapping is used for calculation of the analytical airgap magnetic field [16]. The method conformally transforms electric machine cross-section to w-plane thus enabling quick analytic calculations. The w-plane results are then inversely mapped to the real plane. Compared to FEA simulation, this approach yields results within seconds [11,12,16]. On the other hand, the disadvantage is the difficult implementation on complex rotor geometries.
This paper proposes a method for geometrical modification of any SyRM barrier geometry using conformal mapping.
5.2. Mapping Workflow
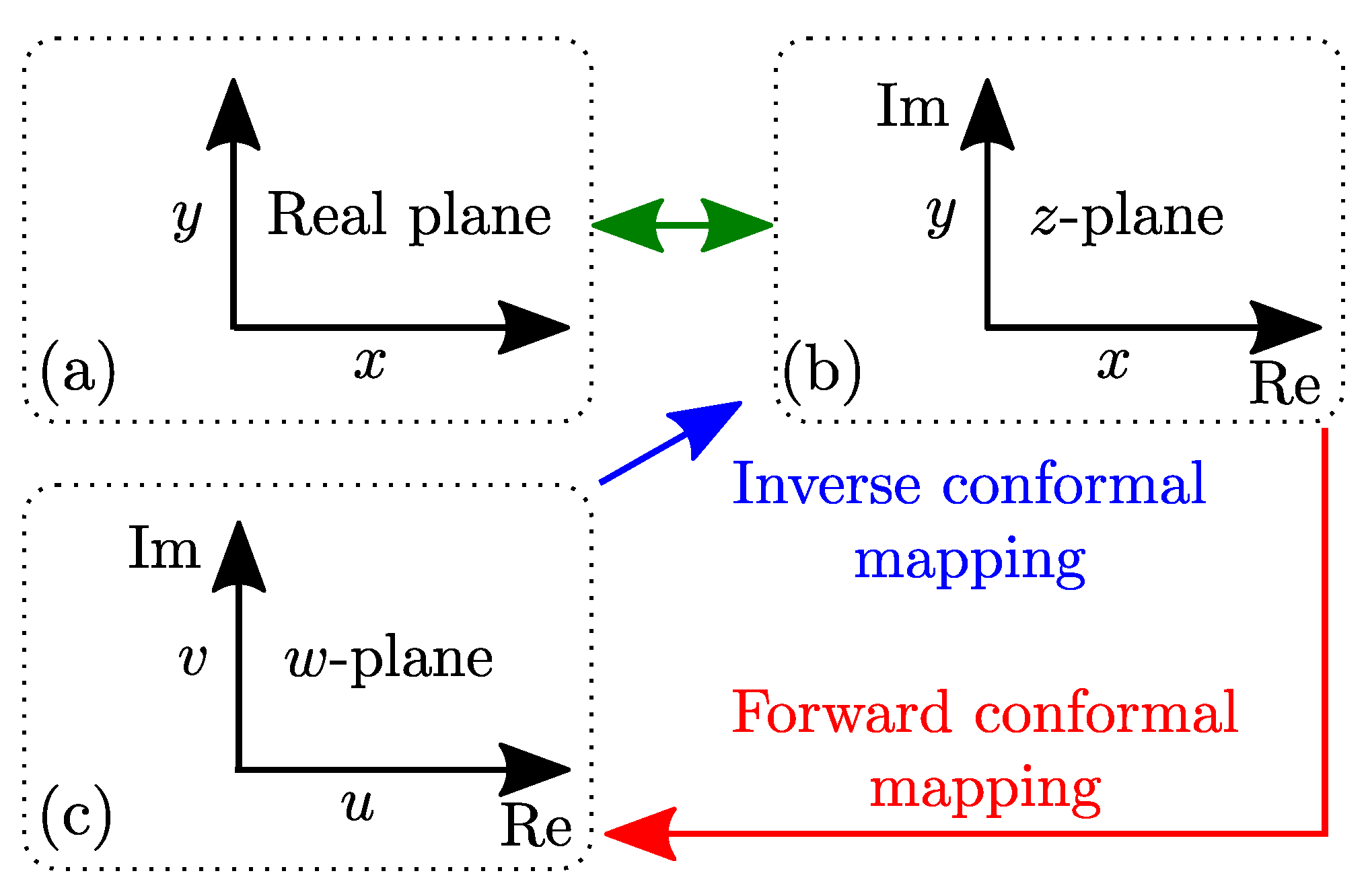
Generated rotor barrier lines are defined by sorted vertices () containing corresponding coordinates which can be drawn on a 2D real Euclidean plane (Figure 9a). For easier manipulation purposes, real plain coordinates are redefined in complex z-plane , Figure 9b. Considering that the vertices are the same in real and complex plane, this is a trivial transformation.
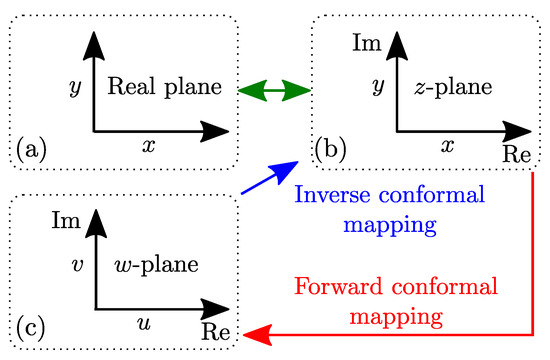
Figure 9.
Mapping workflow, Subfigures (a)–(c) are explained within the Section 5.2.
SyRM rotor has a circular layout which can be exploited by selecting the convenient complex function and applying forward conformal mapping to a complex w-plane , Figure 9c. Geometrical modifications of the barrier geometry are then performed in w-plane and upon completion, returned back to z (and real) plane via inverse conformal mapping. The benefit of the approach is easier barrier modification which leads to simplified software coding.
5.3. Complex Functions
The principal objects of study are complex-valued functions , depending on a single complex variable . In general, the function is defined on an open subdomain, , of the complex plane. Any complex function can be uniquely written as a complex combination [18].
5.3.1. Forward Conformal Mapping
When working with circular shapes, it is useful to use polar form . Considering that electric machines can have an arbitrary number of pole pairs, it is very convenient to select a complex function that somehow ignores angle changes when the number of poles is increased or decreased. This kind of functionality can be achieved by a complex natural logarithm. In terms of polar coordinates, the complex logarithm has the form .
Thus, the logarithm of a complex number has a real part which is a well-defined harmonic function save for a logarithmic singularity at the origin . The imaginary part of the complex logarithm is the polar angle, known in complex analysis as the phase.
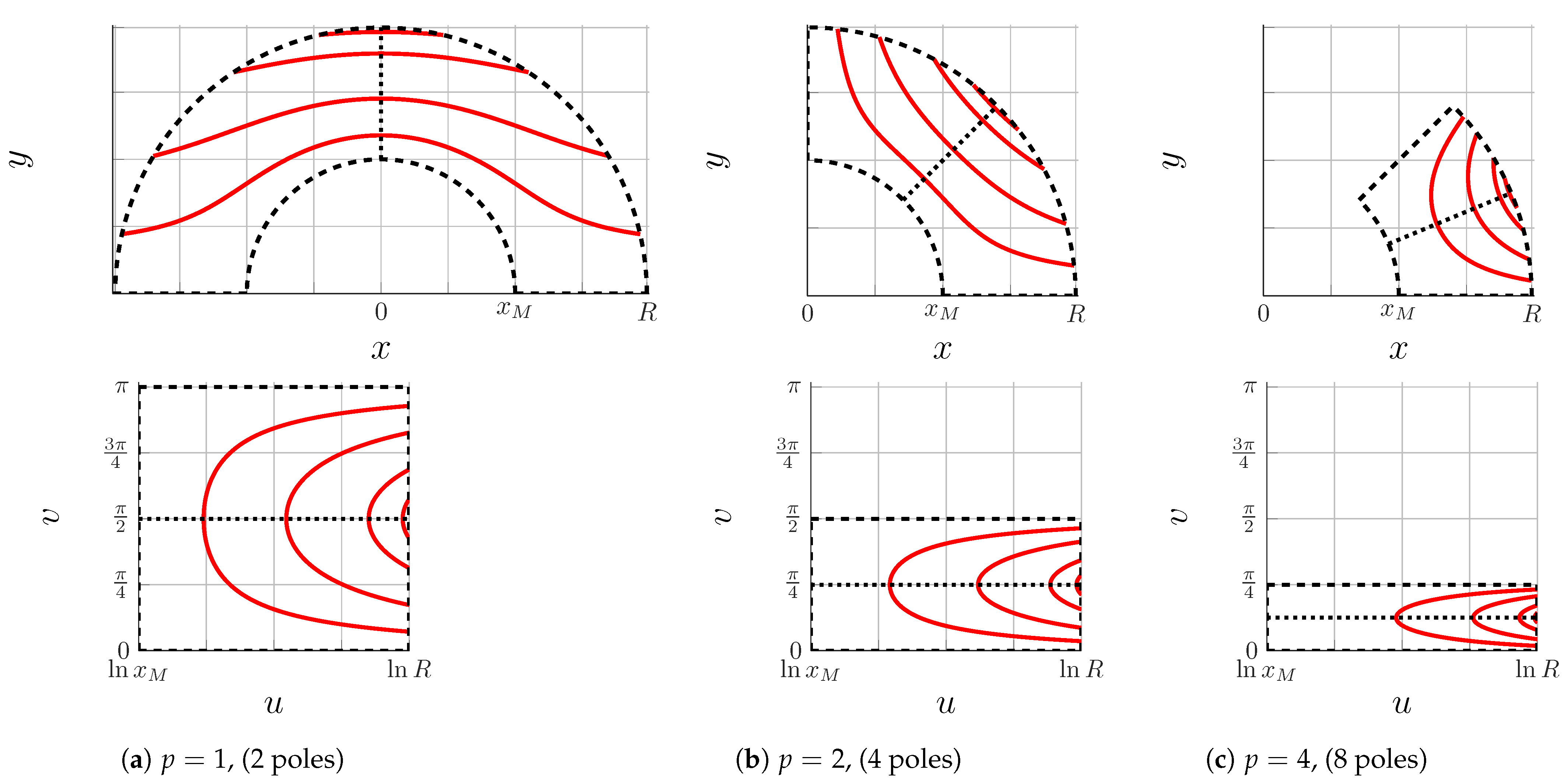
Due to inherent symmetry, it is enough to analyze one electric machine pole. A minimum number of poles is 2, which equals to radian angular span in z-plane, which is mapped to the same vertical span in w-plane. Figure 10 illustrates mapping of different combination of pole geometries. To summarize, always maps z to the upper half-plane with vertical boundaries (p is the number of pole pairs) and horizontal boundaries of .
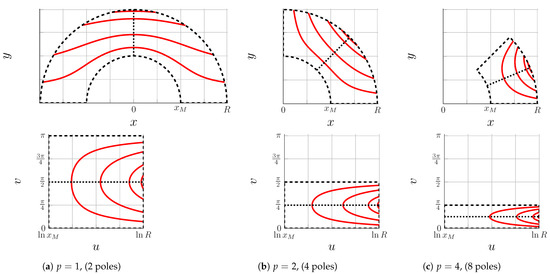
Figure 10.
Real z-plane (upper row); Conformal mapping to plane (bottom row).
Note that always maps SyRM barrier lines horizontally (Figure 10, w-plane), regardless of the number of poles. This feature is exploited for the creation of the Modified Zhukovsky variable depth barrier lines (MZhVD).
5.3.2. Inverse Conformal Mapping
Inverse function for return to z-plane is a complex exponential . Since is a non-zero complex number, the equation can be written as with real and imaginary parts equal to:
5.4. Depth Modification
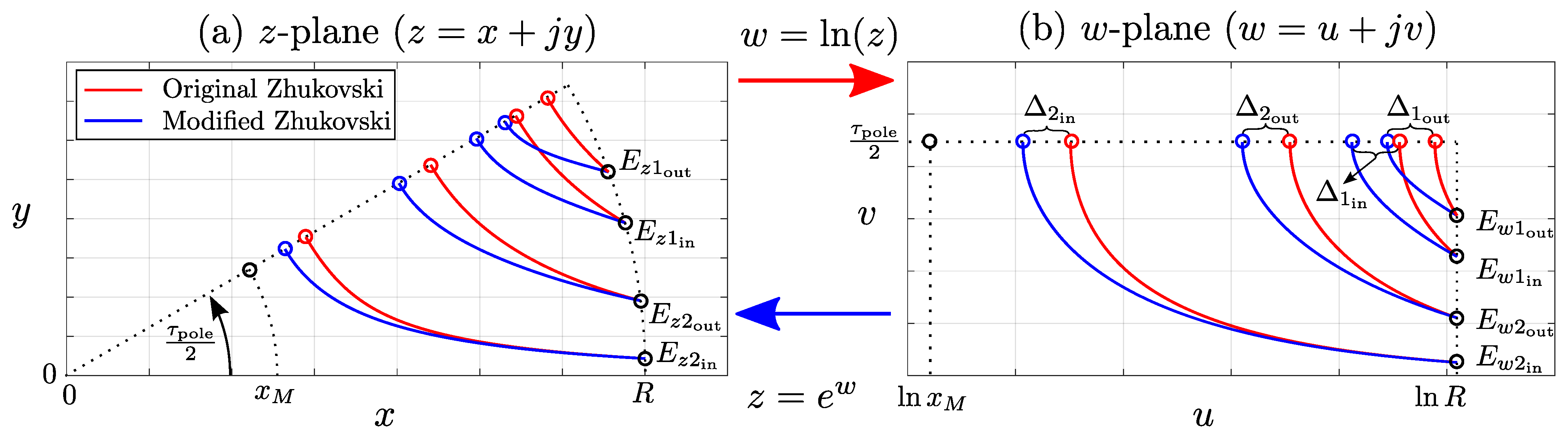
To summarize, original Zhukovsky barrier lines () with corresponding vertices are written as (Figure 11a, red) and conformally transformed to w-plane via as (Figure 11b, red). As previously mentioned, Zhukovsky lines cannot mutually intersect. To secure barrier depth variability and improve machine performance, we are introducing Zhukovsky barrier depth modification (MZhVD) via dimensionless depth parameters .
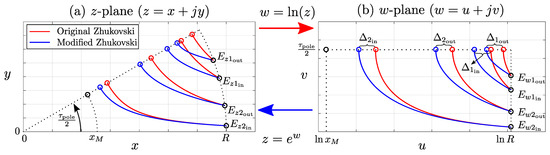
Figure 11.
Modification of Zhukovski lines via conformal mapping. Subfigures (a) and (b) are explained within the Section 5.4 and related subsections.
Depth variability is secured via addition of cosine offsets to the w-plane barrier lines according to Equations (6) and (7). In theory, any even function can be used for generation of offset (7), cosine has been selected due to implementation simplicity.
Upon modification (Figure 11b, blue), barrier lines are inversely mapped to z-plane via function (Figure 11a, blue). The main benefit of the proposed procedure is a simplified modification of SyRM barriers without any influence on simulation time. The following section explains the modification procedure step by step.
5.5. Modified Zh Barrier Construction
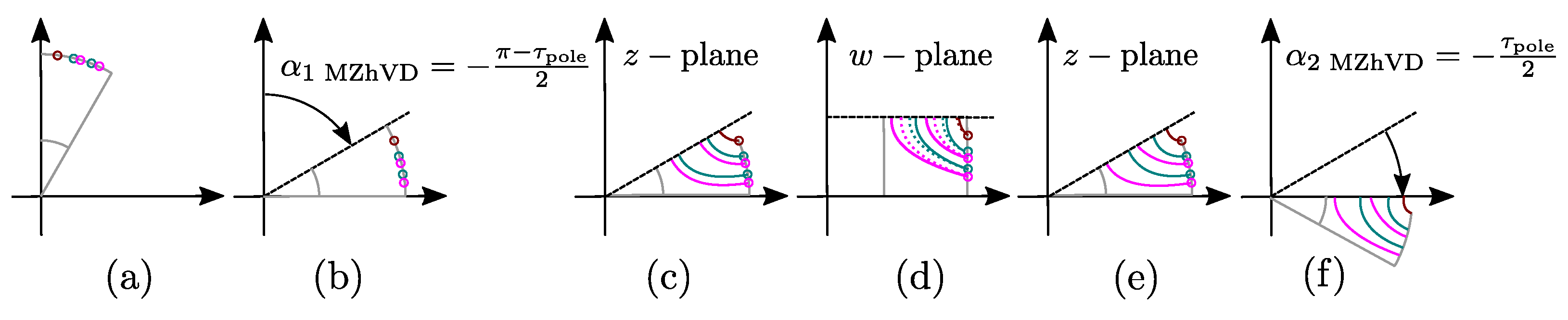
After definition of all inner and outer barrier line starting points , Figure 12a, the entire geometry is rotated by (Algorithm 4: ln:2, Figure 12b).
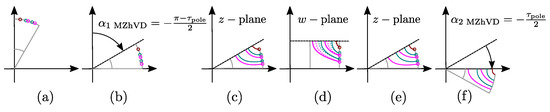
Figure 12.
Modified Zhukovsky barrier construction and rotation steps. Subigures (a)–(f) are explained within the Section 5.5–Section 5.5.3.
5.5.1. Inner Line Calculation
The first step is the calculation of GetInnerLines barrier line function (Algorithm 4: ln:9). Inner line vertices () are calculated based on and number of barriers k.
Next (Algorithm 4: ln:14), original Zhukovsky barrier (Zh) vertices () are calculated in the same way as in Algorithm 1, Figure 12c. Original vertices () and barrier starting points () are then conformally mapped to w-plane as and , Algorithm 4: ln:15, 16, Figure 12d, dotted lines.
Intersections are critical for Modified Zhukovsky barrier variable depth (MZhVD) calculation and they are fully tied to original Zhukovsky intersections (calculated via Algorithm 4: ln:17). As previously mentioned, original Zhukovsky barriers cannot mutually intersect which makes them absolutely feasible, but on the other hand, barrier depth variability cannot be achieved.
Modified Zhukovsky depth variation is secured by iterative recalculation of intersection points in w-plane. In case of the most inner line (), the barrier depth limit is rotor shaft (), and the original Zhukovsky intersection (Algorithm 4: ln:20). For the second most inner line , depth limit is and the intersection is calculated via (Algorithm 4: ln:22). All inner line intersections are then iteratively calculated (Algorithm 4: ln:18–22).
Next, inner line depth offset is calculated based on original Zhukovsky and calculated inner intersections (Algorithm 4: ln:23). ClcDpth function (Algorithm 4: ln:25) calculates modified vertices in w-plain (Figure 12d, full lines), performs inverse conformal mapping, and returns z-plain vertices (Algorithm 4: ln:59–64, Figure 12e).
Finally, GetInnerLines function returns vertices.
5.5.2. Outer Line Calculation
At this point all w-plane inner barrier intersections are defined and now present limits for outer barrier line construction. The rest of the GetOuterLines code (Algorithm 4: ln:27–40) is executed in the similar manner as in GetInnerLines. The function at the end returns .
5.5.3. Notch Line Calculation
Notch is specific because it has only one barrier line and depends on the most outer w-plain intersection (Algorithm 4: ln:12). Finally, GetOuterLines returns which completes the calculation of all barrier lines (Figure 12e). Finally, to be compatible with the rest of the barrier construction procedures, the geometry is rotated by (Algorithm 4: ln:65, Figure 12f).
The next steps (not described within Algorithm 4) are mirroring vertices around horizontal axis (Figure 4e), adding barrier fillets, and geometry rotation around center point (Figure 4f).
| Algorithm 4 Construction of Modified Zhukovsky barriers |
|
6. Parametric Complexity
A high number of optimization variables is associated with a longer optimization time [19,20], so the imperative is to simplify barrier topology parametrization. Gamba et al. [14] state that three parameters per barrier (total complexity of , where k is the number of barriers) are the appropriate number for a fast yet accurate description of multi-barrier SyRM (barrier fillet parameters are not included). In the previous publication, our group of authors has reduced the complexity to per barrier [7].
Table 3 shows the calculation of total number of SyRM parameters for for the demonstrated pseudo-code. Note that the parameters are subtracted from the count because they are constant and equal to zero (Table 1).

Table 3.
Calculation of total parameter number. Color coding is according to Figure 4 variables.
Table 4 lists the complexity comparison of the presented procedures and similar approaches in [7,10,14]. The examples in [7,10,14] do not have a notch feature, so to have a fair comparison, the notch is not included in the complexity calculation (Table 3). Compared to [14], and [7], Zh, respectively, yields smaller complexity (), while CrVD, HyVE, MZhVD have the same complexity as in [10].

Table 4.
Parametric complexity.
Overall, the construction principle explained in Section 3 enables the higher degree of design freedom. Considering that the simple barrier topologies are sub-optimal compared to more complex types, developing the set of different parametrization methods with equal parametric complexity is certainly a novel contribution.
7. Pseudo-Code Validation
After the implementation of the proposed pseudo-code, a set of questions naturally arises. Which barrier topology yields the best performance for the given requirements? Is Modified Zhukovsy barrier type better than alternative topologies? For this reason, we have conducted a detailed optimization study based on meta-modeling (surrogate modeling) approach which compared the different barrier topologies (details are available in [21]).
The optimization process couples automated geometry generation (Matlab), electromagnetic finite element analysis (Ansys Motor-CAD), and metamodel optimization (Ansys OptiSlang). Seven rotor topologies have been derived from circular, hyperbolic, and Zhukovsky barrier types:
- Circular concentric (CrC)
- Circular variable depth (CrVD)
- Hyperbolic with fixed eccentricity (HyFE)
- Hyperbolic with variable eccentricity (HyVE)
- Original Zhukovsky (Zh)
- Modified Zhukovsky variable depth (MZhVD)
- Modified Zhukovsky with equal barrier depth (MZhED)
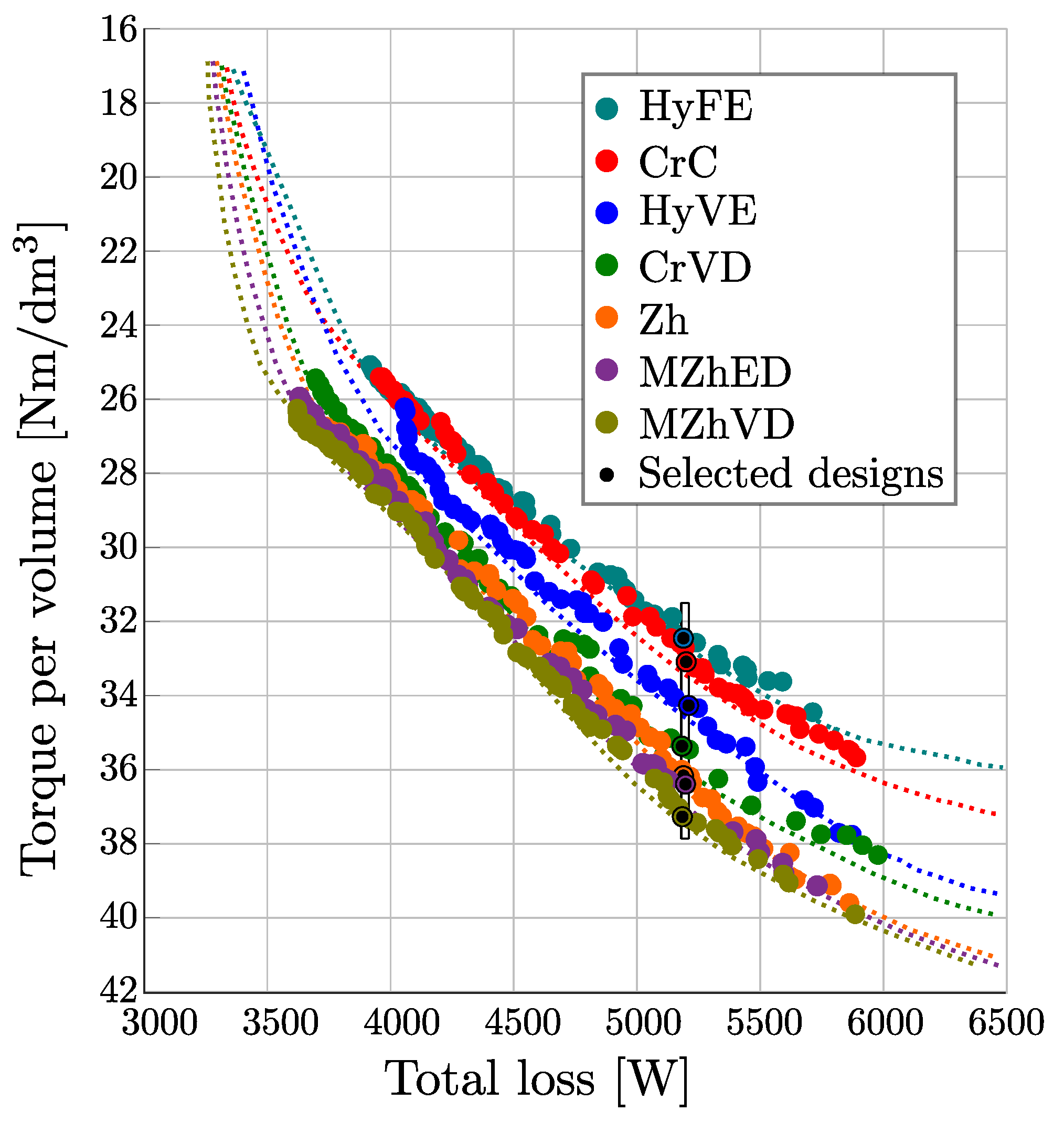
The same optimization strategy (maximize torque per volume (TPV), minimize losses) has been applied to all variants, and results prove that barrier type substantially affects the final machine performance. For easier comparison, seven designs (one per topology) with approximately the same losses (5200 W) have been selected (Figure 13, Table 5).
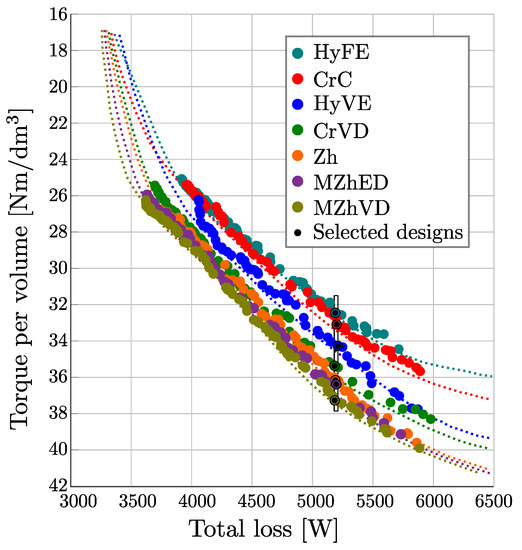
Figure 13.
Validated Pareto fronts for each design variant [21].

Table 5.
Optimization result comparison table [21].
Performance wise, HyFE topology yields the worst results and is considered as baseline design (%). Performance gain is calculated via: . The best results are achieved by MZhVD topology. In relation to the worst (baseline) topology, the performance gain is 14.9% and the power factor is increased from 0.61 to 0.69. It is important to note that these comparisons are valid for design requirements presented in [21]. Other combinations of optimization objectives and requirements might yield a different results.
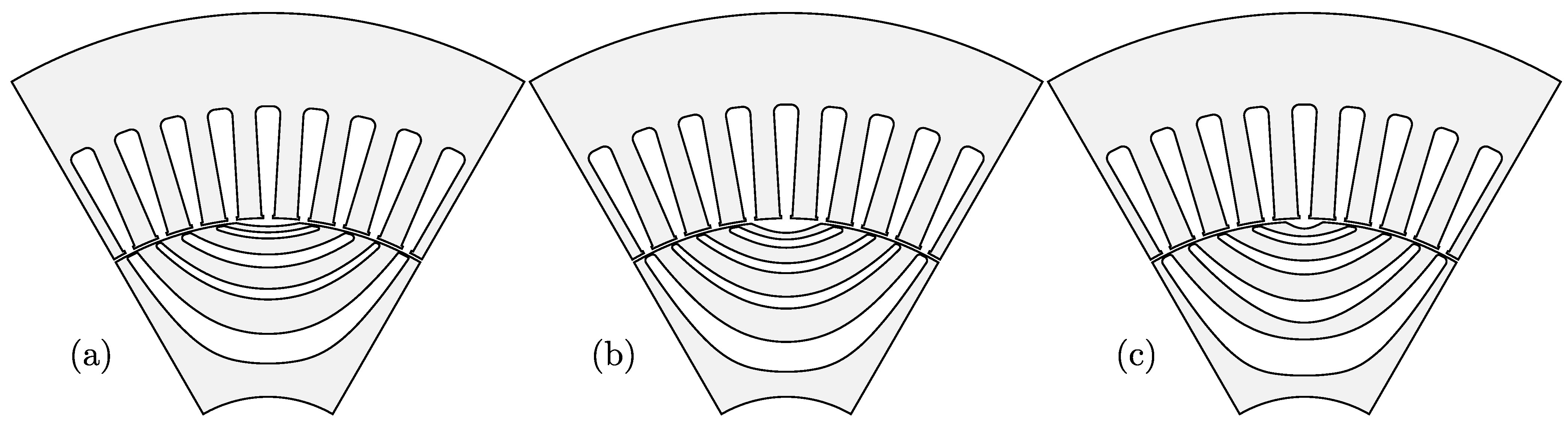
HyFE, CrC and MZhED are special case topologies already covered in CrVD, HyVE and MzVD pseudo-code. Considering that stated topologies can be achieved by appropriate combination of barrier depth parameters, they are not considered in this paper. The summary of three best optimized cross-sections are provided on Figure 14.
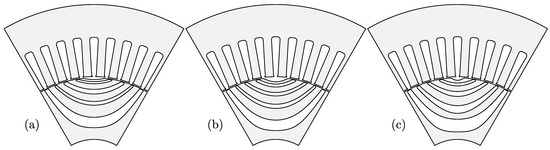
Figure 14.
Optimized cross section of three best topologies: (a) Zh; (b) MZhED; (c) MZhVD [21].
8. Conclusions
SyRM barrier generation procedure was studied in detail. A pseudo-code solution that secures absolute feasibility, barrier topology complexity minimization, and simple implementation is provided. Four smooth barrier types have been presented: circular variable depth (CrVD), hyperbolic with variable eccentricity (HyVE), original Zhukovsky (Zh) and modified Zhukovsky with variable depth (MZhVD). Absolute feasibility is a very important feature because it enables the use of dimensionless parameters which secure code robustness and design scalability to any physical dimension. Barrier topology complexity has been minimized via a systematic approach to design automation (Section 3) and careful analysis of construction features of each topology.
HyVE and CrVD topologies are more complex while Zh has smaller complexity . On the other hand, in its original form, Zh type does not support barrier depth variability which can be a design drawback. Therefore, we introduce a novel MZhVD topology based on geometrical conformal mapping of the original Zh design. This modification provides greater design freedom and sets MZhVD complexity to (same as HyVE and CrVD).
Compared with other referenced topologies, the presented solutions offer higher design freedom with smaller or equal parametric complexity.
It should be noted that construction of barrier fillets (Figure 4f) has not been covered in this paper. Adding a precise fillet between two discrete intersecting lines is a rather complex problem, which deserves a stand-alone publication. A minimum example code with detailed instructions is planned to be published in the near future.
Overall, the presented pseudo-code provides a valuable starting point for the designer who wants to investigate different SyRM smooth barrier topologies.
The description and list of used variables has been added in the Appendix A.
Author Contributions
Conceptualization, B.B.; methodology, B.B.; validation, B.B. and S.S.; original draft preparation, B.B.; review and editing, S.S.; visualization, B.B:; supervision, S.S.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Croatian Science Foundation under the project IP-2018-01-5822-HYDREL.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This paper is an extension of Branko Ban’s Ph.D. research work on Synchronous Reluctance machines menthored by Stjepan Stipetic.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Abbreviation | Description |
| EV | Electric vehicle |
| FEA | Finite element analysis |
| IPM | Interior permanent magnet |
| IM | Induction machine |
| CrC | Circular concentric barrier |
| CrVD | Circular variable depth barrier |
| HyFE | Hyperbolic fixed eccentricity barrier |
| HyVE | Hyperbolic variable eccentricity barrier |
| Zh | Original Zhukovsky barrier |
| MZhED | Modified Zhukovsky equal depth barrier |
| MZhVD | Modified Zhukovsky variable depth barrier |
| PM | Permanent magnet |
| PTO | Power take off |
| e-PTO | Electric power take off |
| SyRM | Synchronous reluctance machine |
| TPV | Torque per volume |
Appendix A. Variable List
All variables have been listed by the order of appearance within text. Vector variables are bolded. e.g., is a variable vector, while R represents a scalar variable.

Table A1.
List of variables.
Table A1.
List of variables.
| No. | Variable | Description | No. | Variable | Description |
|---|---|---|---|---|---|
| 1 | Minimum flux carrier width | 33 | First rotation angle in Zh generation | ||
| 2 | Inner barrier depth parameters | 34 | Second rotation angle in Zh generation | ||
| 3 | Outer barrier depth parameters | 35 | First rotation angle in Zh generation | ||
| 4 | Notch depth parameter | 36 | First rotation angle in Zh generation | ||
| 5 | p | Number of pole pairs | 37 | First rotation angle in MZhVD generation | |
| 6 | k | Number of flux barriers | 38 | Second rotation angle in MZhVD generation | |
| 7 | Minimum angular barrier span | 39 | Radial Zhukovsky line coordinate vector | ||
| 8 | Maximum angular barrier span | 40 | Angular Zhukovsky line coordinate vector | ||
| 9 | Angle of one pole | 41 | Zhukovsky line coefficient | ||
| 10 | First rotation angle in example figure | 42 | Line starting point angular coordinates | ||
| 11 | Initial construction points | 43 | Inner line starting point horizontal coordinates | ||
| 12 | Available angular space | 44 | Inner line starting point vertical coordinates | ||
| 13 | Barrier bridge vector | 45 | Circular barrier center coordinate vector | ||
| 14 | Notch line starting point | 46 | Circular barrier radius vector | ||
| 15 | Notch line starting point angular coordinate | 47 | Minimal eccentricity vector | ||
| 16 | Inner barrier line starting point vector | 48 | Line starting point radial coordinate vector | ||
| 17 | Outer barrier line starting point vector | 49 | Line starting point angular coordinate vector | ||
| 18 | Initial barrier construction angular coord. | 50 | Eccentricity vector | ||
| 19 | Inner barrier line starting point radial coord. | 51 | Left directrix of hyperbola | ||
| 20 | Outer barrier line starting point radial coord. | 52 | Horizontal w-plane coordinate vector | ||
| 21 | Inner barrier line starting point angular coord. | 53 | Vertical w-plane coordinate vector | ||
| 22 | Outer barrier line starting point angular coord. | 54 | z-plane Zh horizontal vertex vector | ||
| 23 | Inner barrier line intersection point vector | 55 | z-plane Zh vertical vertex vector | ||
| 24 | Outer barrier line intersection point vector | 56 | w-plane Zh horizontal vertex vector | ||
| 25 | Inner barrier line horizontal vertex vector | 57 | w-plane Zh vertical vertex vector | ||
| 26 | Inner barrier line vertical vertex vector | 58 | w-plane Zh intersections vector | ||
| 27 | Outer barrier line horizontal vertex vector | 59 | w-plane shaft limit | ||
| 28 | Outer barrier line vertical vertex vector | 60 | w-plane MZhVD inner barrier intersections | ||
| 29 | Notch horizontal vertex vector | 61 | w-plane MZhVD outer barrier intersections | ||
| 30 | Notch vertical vertex vector | 62 | Period vector of MZhVD cosine offset | ||
| 31 | Inner barrier fillet vector | 63 | Frequency vector of MZhVD cosine offset | ||
| 32 | Outer barrier fillet vector | 64 | Barrier depth offset maximum vector | ||
| 33 | Final rotation angle | 65 | MZhVD Barrier depth offset vector |
References
- Bourzac, K. The Rare-Earth Crisis. Technol. Rev. 2011, 114, 58–63. [Google Scholar]
- Justin, R. Rare earths: Neither rare, nor earths. BBC News, 23 March 2014. [Google Scholar]
- Hong, H.S.; Liu, H.C.; Cho, S.Y.; Lee, J.; Jin, C.S. Design of High-End Synchronous Reluctance Motor Using 3-D Printing Technology. IEEE Trans. Magn. 2017, 53, 4–8. [Google Scholar] [CrossRef]
- Yamashita, Y.; Okamoto, Y. Design Optimization of Synchronous Reluctance Motor for Reducing Iron Loss and Improving Torque Characteristics Using Topology Optimization Based on the Level-Set Method. IEEE Trans. Magn. 2020, 56, 36–39. [Google Scholar] [CrossRef]
- Ban, B.; Stipetić, S. Electric Multipurpose Vehicle Power Take-Off: Overview, Load Cycles and Actuation via Synchronous Reluctance Machine. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 27–29 August 2019. [Google Scholar]
- Ban, B.; Stipetic, S. Design and optimization of synchronous reluctance machine for actuation of electric multi-purpose vehicle power take-off. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Göteborg, Sweden, 23–26 August 2020; pp. 1750–1757. [Google Scholar]
- Ban, B.; Stipetic, S.; Jercic, T. Minimum set of rotor parameters for synchronous reluctance machine and improved optimization convergence via forced rotor barrier feasibility. Energies 2021, 14, 2744. [Google Scholar] [CrossRef]
- Hubert, T.; Reinlein, M.; Kremser, A.; Herzog, H.G. Torque ripple minimization of reluctance synchronous machines by continuous and discrete rotor skewing. In Proceedings of the 2015 5th International Electric Drives Production Conference (EDPC), Nürnberg, Germany, 15–16 September 2015. [Google Scholar]
- Ferrari, S. Design, Analysis and Testing Procedures for Synchronous Reluctance and Permanent Magnet Machines. Doctoral Thesis, Politecnico di Torino, Torino, Italy, 2020. [Google Scholar]
- Stipetic, S.; Zarko, D.; Cavar, N. Design Methodology for Series of IE4/IE5 Synchronous Reluctance Motors Based on Radial Scaling. In Proceedings of the 2018 23rd International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 146–151. [Google Scholar]
- Mirazimi, M.S.; Kiyoumarsi, A. Magnetic Field Analysis of Multi-Flux-Barrier Interior Permanent-Magnet Motors Through Conformal Mapping. IEEE Trans. Magn. 2017, 53, 7002512. [Google Scholar] [CrossRef]
- Mirazimi, M.S.; Kiyoumarsi, A. Magnetic Field Analysis of SynRel and PMASynRel Machines with Hyperbolic Flux Barriers Using Conformal Mapping. IEEE Trans. Transp. Electrif. 2020, 6, 52–61. [Google Scholar] [CrossRef]
- Taghavi, S.; Pillay, P. Design aspects of a 50hp 6-pole synchronous reluctance motor for electrified powertrain applications. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 2252–2257. [Google Scholar]
- Gamba, M.; Pellegrino, G.; Cupertino, F. Optimal number of rotor parameters for the automatic design of Synchronous Reluctance machines. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM 2014), Berlin, Germany, 2–5 September 2014; pp. 1334–1340. [Google Scholar]
- Cupertino, F.; Pellegrino, G.; Cagnetta, P.; Ferrari, S.; Perta, M. SyRE: Synchronous Reluctance (Machines)—Evolution. Available online: https://sourceforge.net/projects/syr-e/ (accessed on 11 March 2021).
- Zarko, D. A Systematic Approach To Optimized Design of Permanent Magnet Motors with Reduced Torque Pulsations. Ph.D. Thesis, University Of Wisconsin-Madison, Madison, WI, USA, 2004. [Google Scholar]
- Weisstein, E.W. Conformal Mapping. Available online: https://mathworld.wolfram.com/ConformalMapping.html (accessed on 11 March 2021).
- Olver, P.J. Complex Analysis and Conformal Mapping, Chapter 6. In Complex Analysis and Conformal Mapping; University of Minnesota: Minneapolis, MN, USA, 2011. [Google Scholar]
- Pellegrino, G.; Cupertino, F.; Gerada, C. Automatic Design of Synchronous Reluctance Motors Focusing on Barrier Shape Optimization. IEEE Trans. Ind. Appl. 2015, 51, 1465–1474. [Google Scholar] [CrossRef]
- Lu, C.; Ferrari, S.; Pellegrino, G. Two Design Procedures for PM Synchronous Machines for Electric Powertrains. IEEE Trans. Transp. Electrif. 2017, 3, 98–107. [Google Scholar] [CrossRef] [Green Version]
- Ban, B.; Stipetić, S. Systematic Metamodel-based Optimization Study of Synchronous Reluctance Machine Rotor Barrier Topologies. Struct. Multidiscipl. Optim. 2022. in review. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).