The Effect of Rotating Speeds on the Cavitation Characteristics in Hydraulic Torque Converter
Abstract
:1. Introduction
2. Numerical Method
2.1. Cavitation Model
2.2. Full Three-Dimensional Computational Fluid Dynamics (CFD) Model of the Torque Converter
2.3. CFD Settings
2.4. Mesh Independence Analysis
3. Experiment and Validation
3.1. Hydraulic Torque Converter Test Rig
3.2. Validation of CFD Model
4. Results and Discussion
4.1. Cavitation Characteristics of Hydraulic Torque Converter
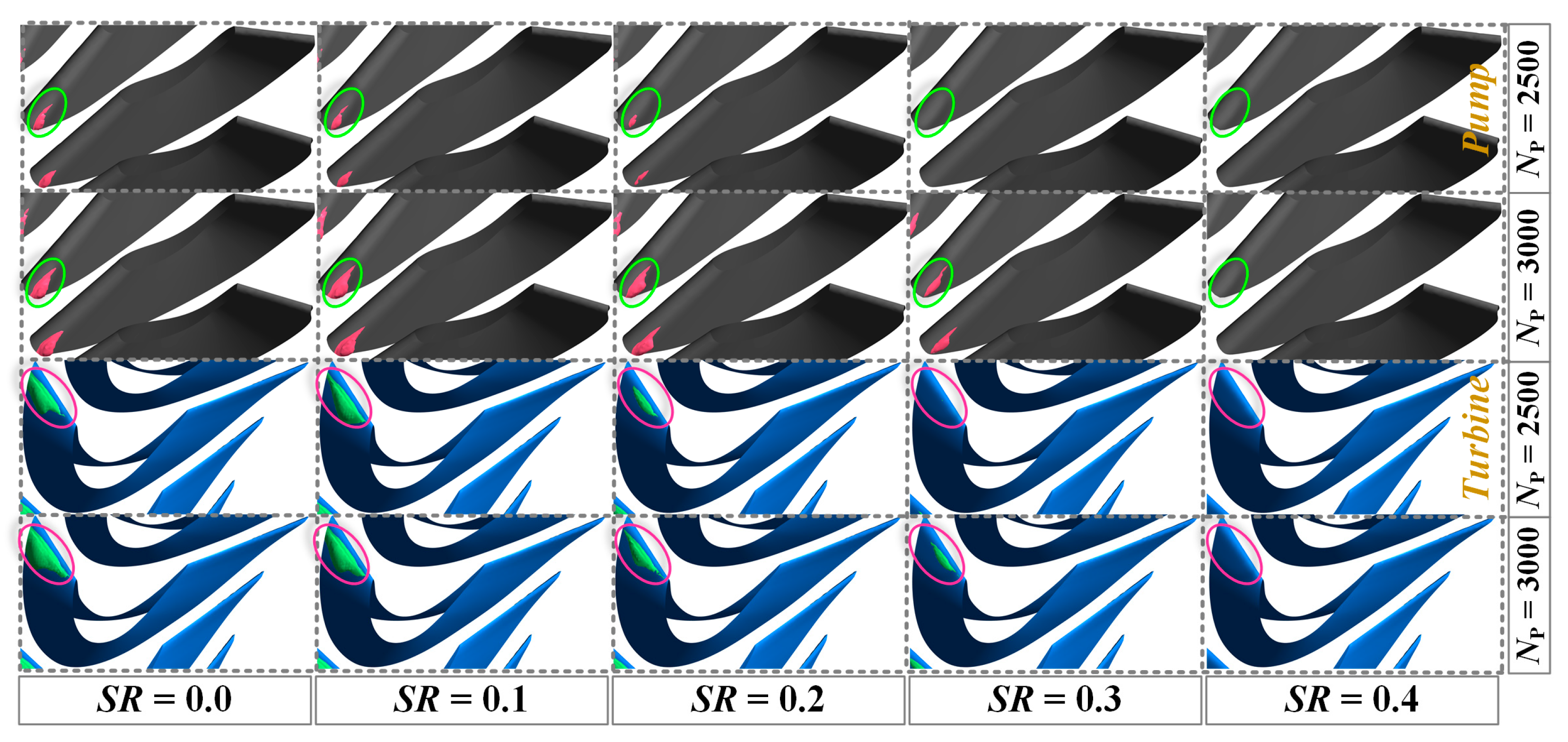
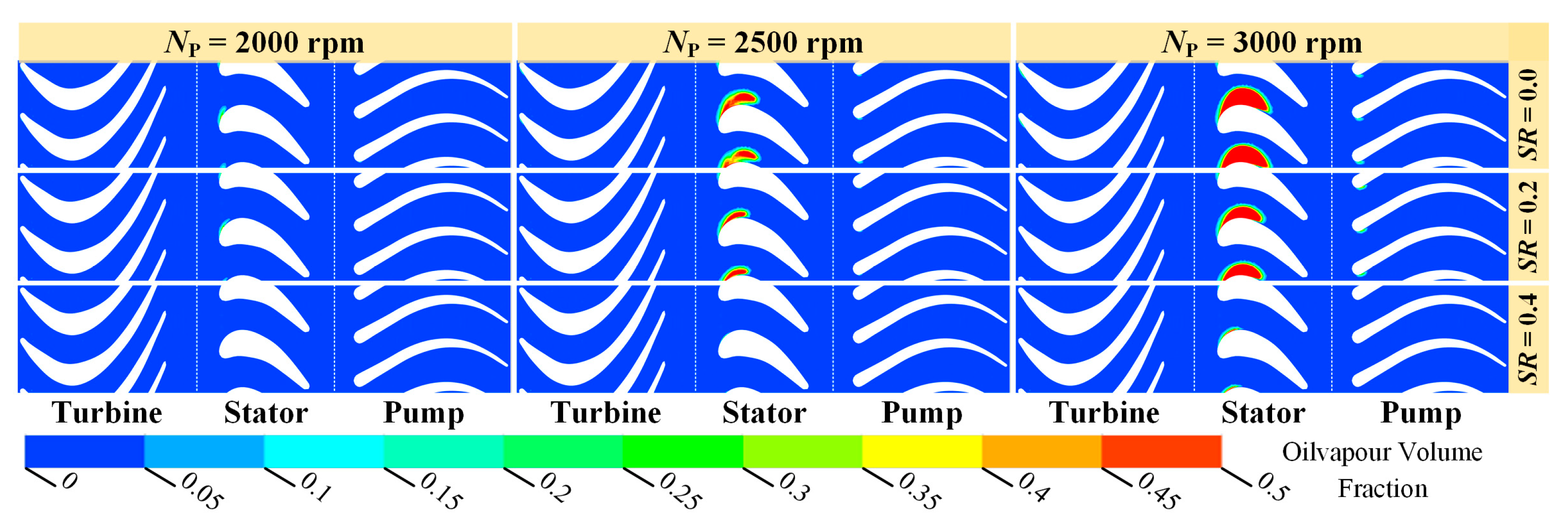
4.2. Cavitating Flow Field in the Torque Converter
4.2.1. Cavitating Flow Field
4.2.2. Cavitation Characteristics under Different Rotating Speeds
4.3. Cavitation Number and Interphase Mass Transfer
5. Conclusions
- (1)
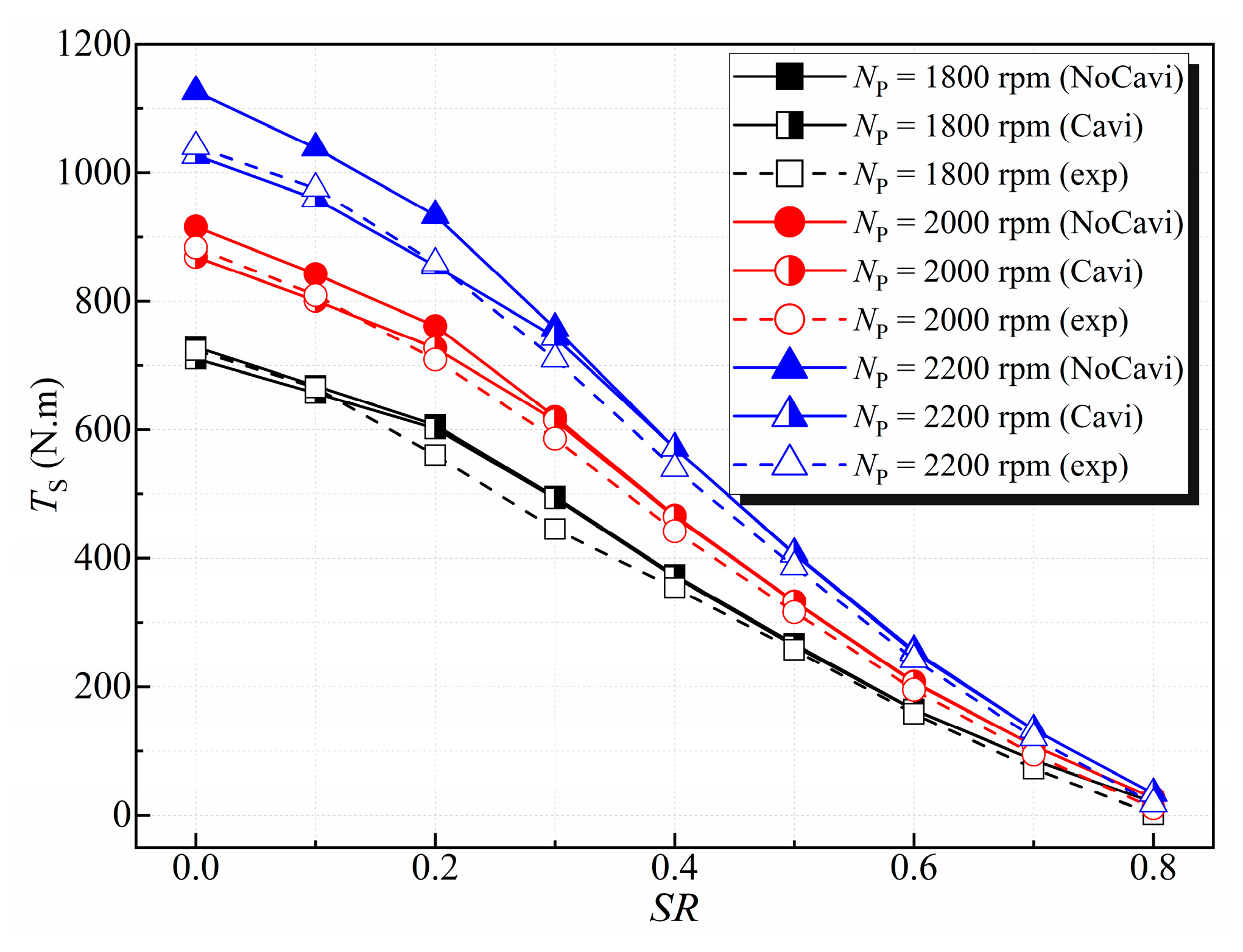
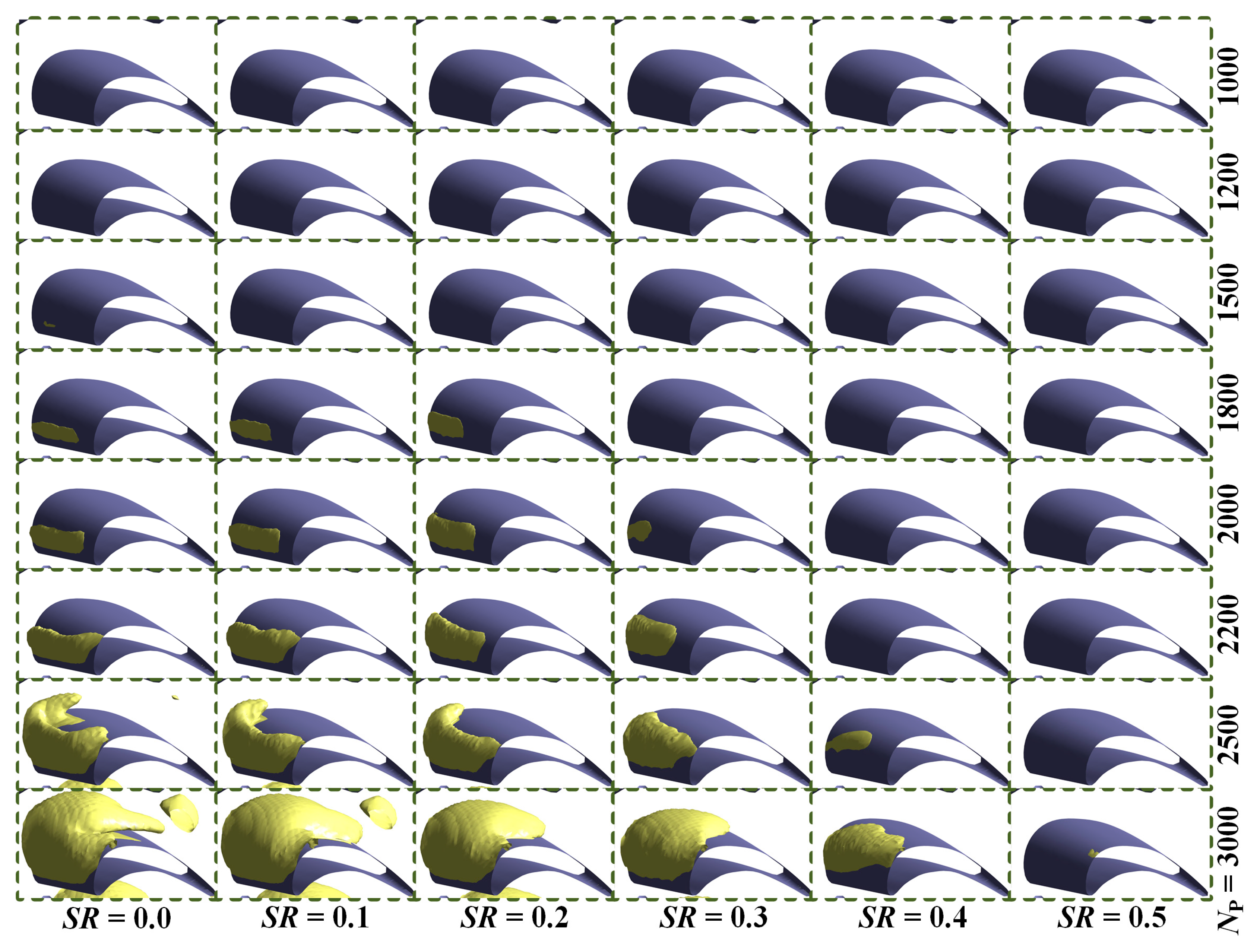
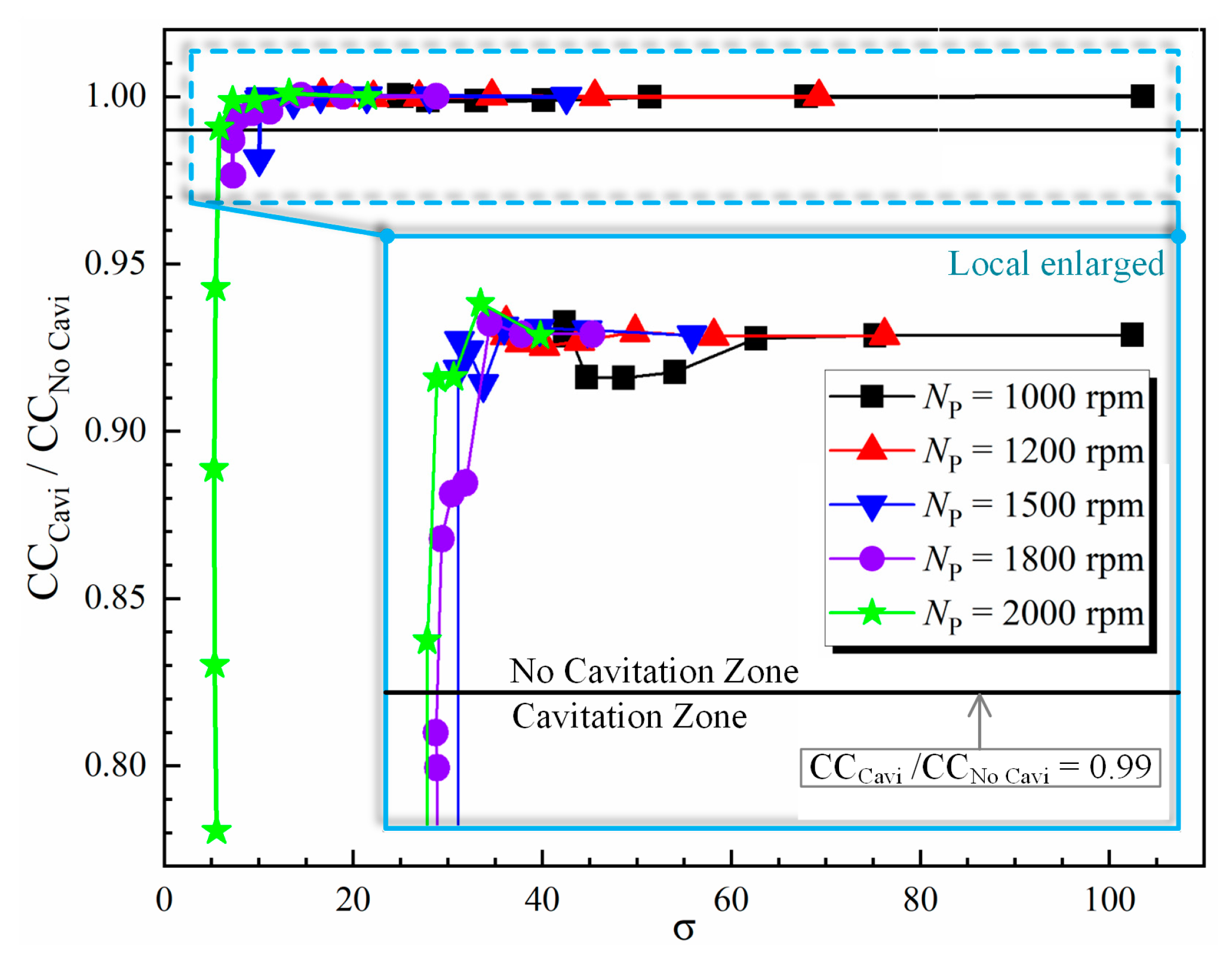
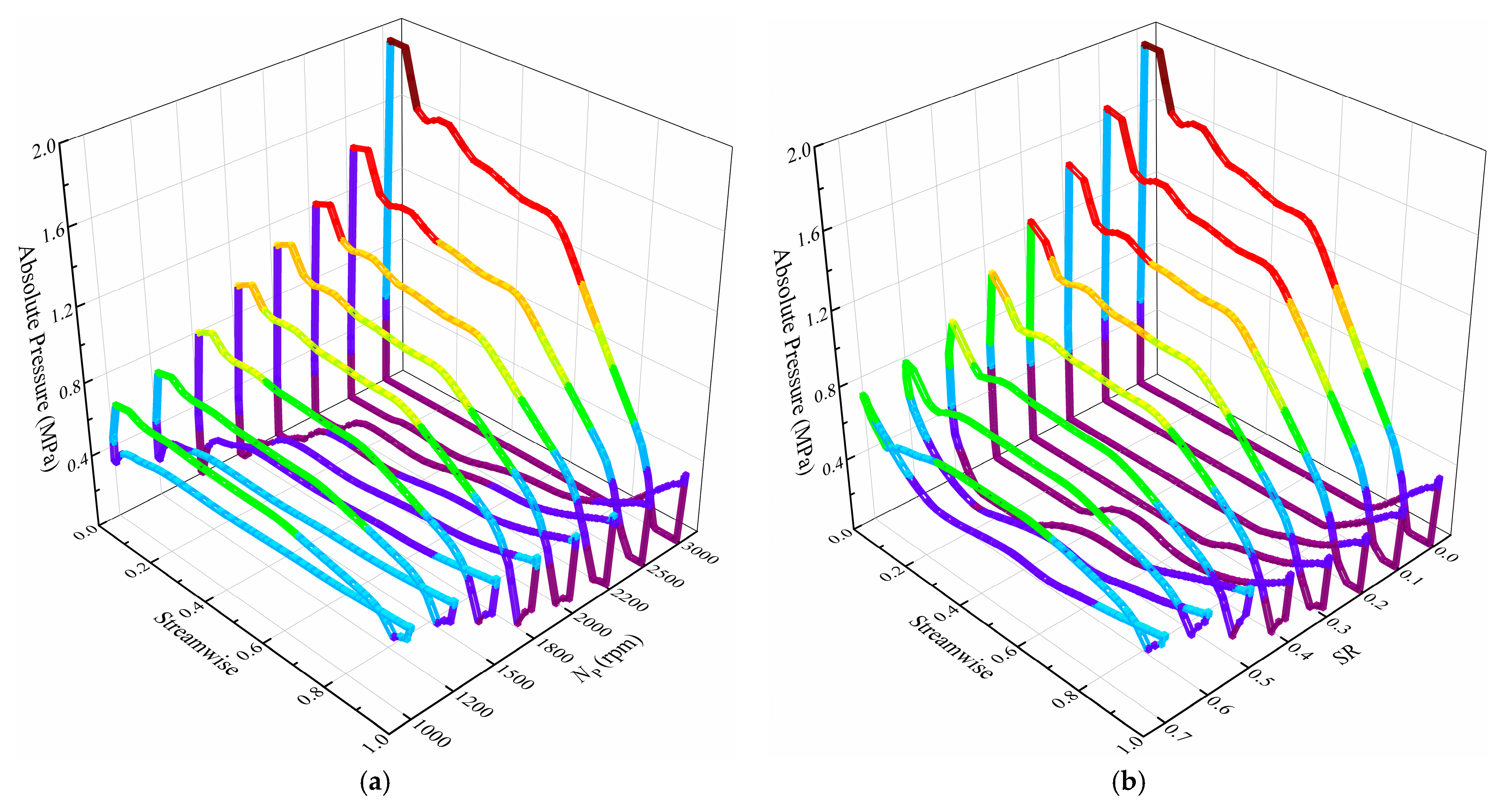
- The pump rotating speed and speed ratio have strong influences on the cavitation characteristics of the torque converter. The cavitation degree demonstrates a positive relationship with the pump rotating speed and a negative relationship with the speed ratio. Higher pump rotating speed and lower speed ratio lead to bigger cavitation regions and more performance degradation. Therefore, one should consider the cavitation effects when designing high capacity and high NP torque converters.
- (2)
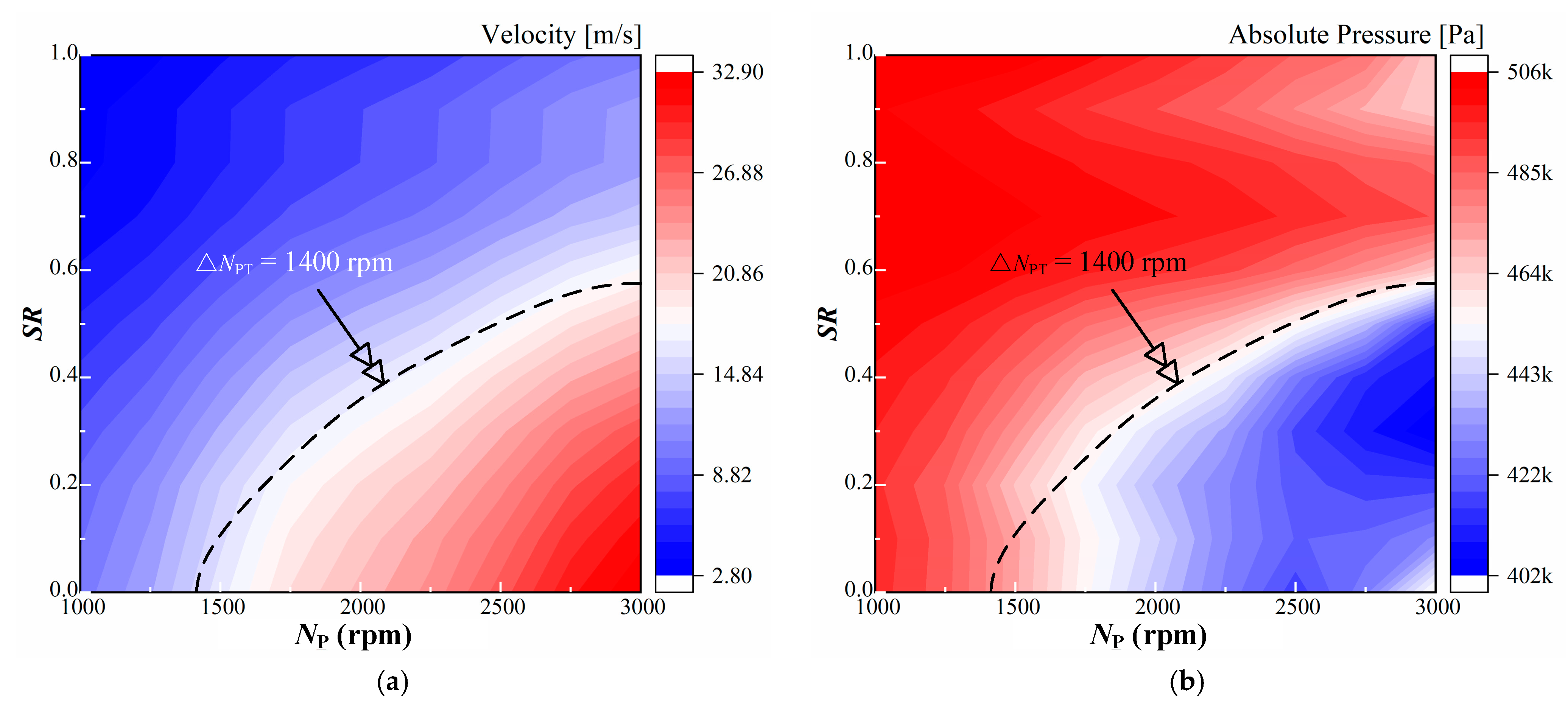
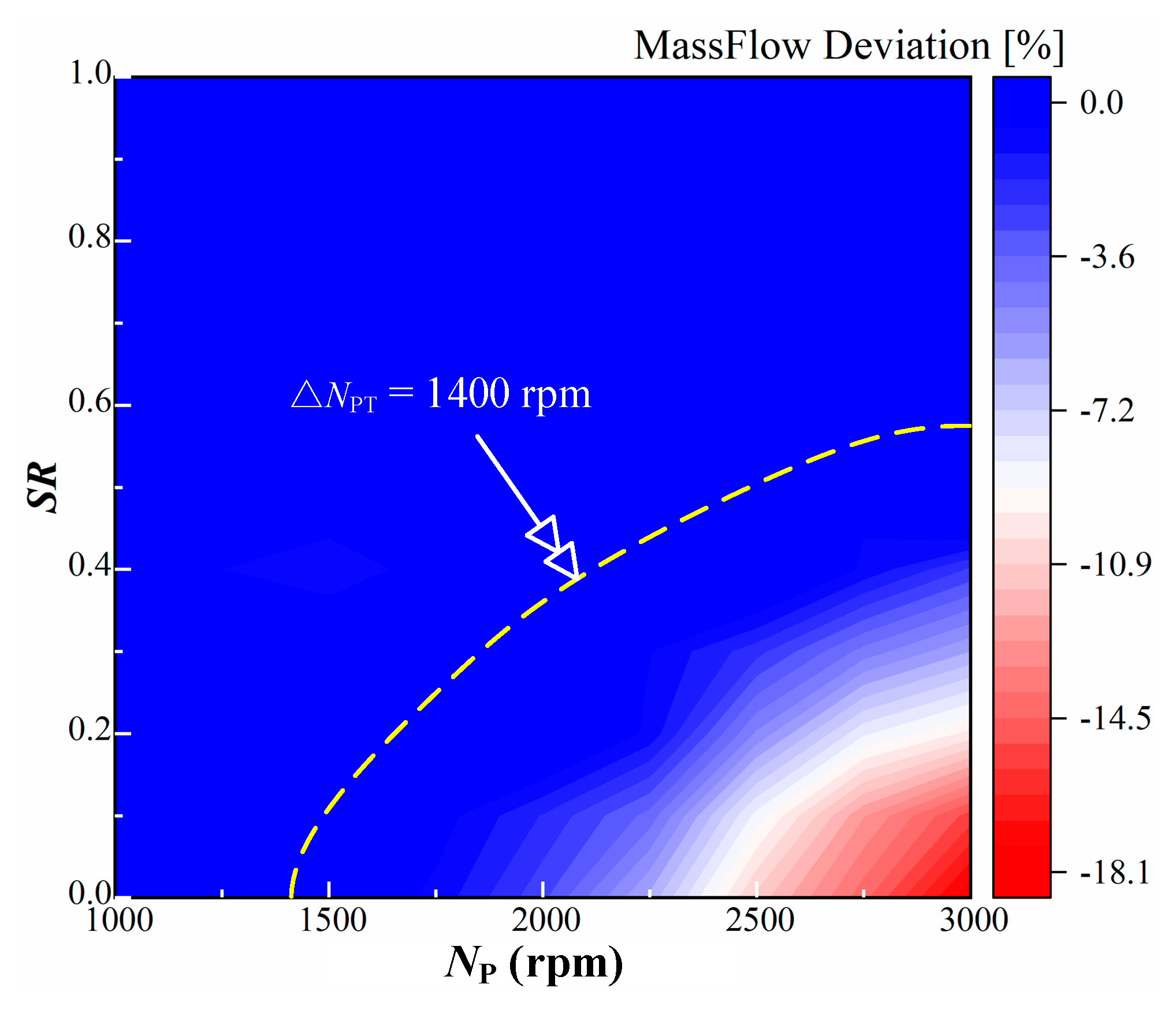
- The difference between NP and NT could be used as a useful indicator for the occurrence and degree of cavitation. We found out that cavitation takes place when △NPT is greater than 1400 rpm regardless of the variations of the pump rotating speed and speed ratio, and the cavitation degree is directly related to △NPT.
- (3)
- Cavitation will not occur if the torque converter runs at low pump rotating speeds (less than 1500 rpm). However, cavity bubbles begin to emerge and the cavitation range expands when pump rotating speed increases, consequently resulting in performance reduction. The stall operating condition is the most critical for cavitation under different pump rotating speeds, and the cavity bubbles may cover as much as 80% of the stator blade suction surface when NP reaches 3000 rpm, which would lead to strong vibration, noise and even cavitation erosion. Moreover, the increase of pump rotating speed also changes the critical cavitation number and extends the cavitation range towards high speed ratio conditions not previously affected.
- (4)
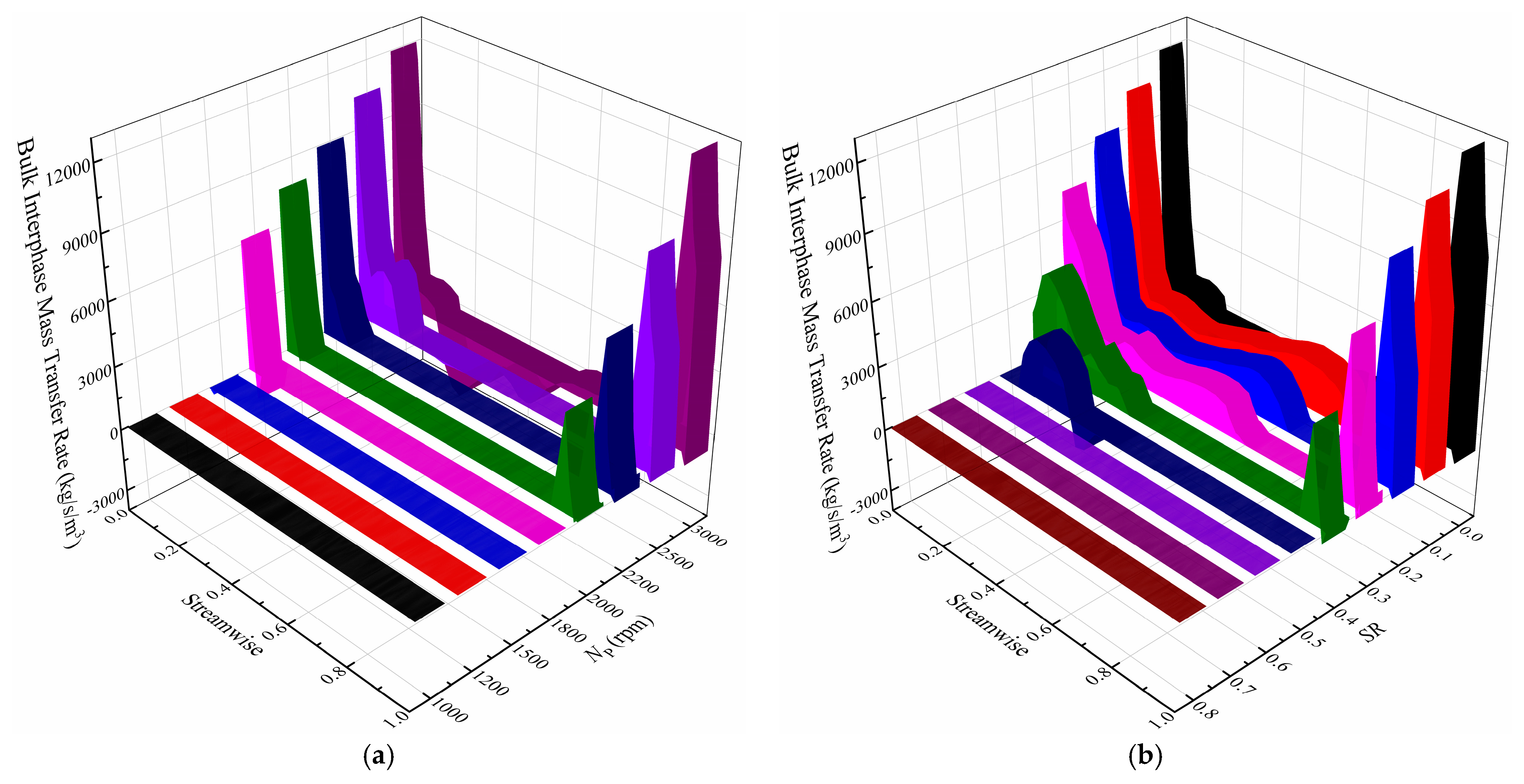
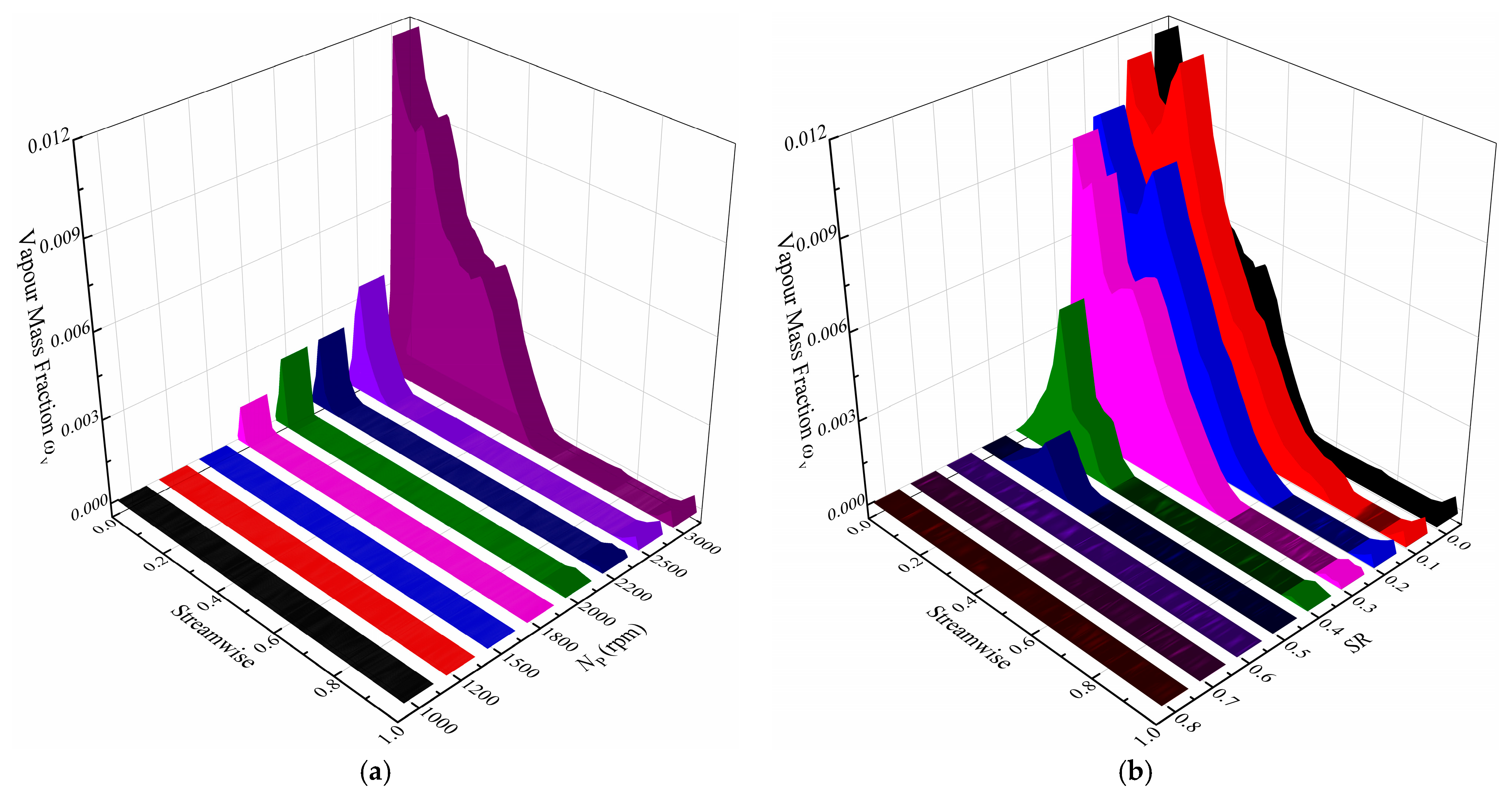
- The results show that the cavitation area, the cavitation extent and the vapor volume fraction increase with the increase of the pump rotating speed and decrease with the increase of the speed ratio. Cavitation bubbles block the flow passage, reduce the mass flow rate and alter the pressure distribution on the blade surface, consequently leading to lower torque and capacity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| △NPT | NP-NT, The speed difference between pump and turbine [rpm] |
| A | Toroidal area [m2] |
| CC | TP*D−5*ωP−2, Capacity constant [kg/rad2/m3] |
| D | Torque converter torus diameter [m] |
| DCC | (CCCavi − CCNoCavi)/CCNoCavi, Capacity constant deviation |
| DT | (TCavi − TNoCavi)/TNoCavi, Torque deviation |
| Dη | (ηCavi − ηNoCavi)/ηNoCavi, Efficiency deviation |
| ECC | (CCCavi − CCexp)/CCexp, Capacity constant error |
| EK | (KCavi − Kexp)/Kexp, Torque ratio error |
| Eη | (ηCavi − ηexp)/ηexp, Efficiency error |
| Fcond | Cavitation Condensation Coefficient |
| Fvap | Cavitation Vaporization Coefficient |
| K | TT/TP, Torque ratio |
| MDR | Maximum Density Ratio |
| MF | Mass flow rate [kg/s] |
| NB | Number of bubbles per unit volume |
| NP | Rotating speed of pump [rpm] |
| NS | Rotating speed of stator [rpm] |
| NT | Rotating speed of turbine [rpm] |
| NVF | Nuclei Volume Fraction |
| p | Liquid pressure [Pa] |
| pref | Reference pressure [Pa] |
| pv | Pressure in the bubble [Pa] |
| Pv | Saturated Vapor Pressure [Pa] |
| RB | Mean Radius [m] |
| rg | Vapor volume fraction |
| SR | NT/NP, Speed ratio |
| TP | Pump torque [N m] |
| TS | Stator torque [N m] |
| TT | Turbine torque [N m] |
| VB | Mass transfer rate of bubble volume |
| vref | Reference velocity [m/s] |
| vref | Equivalent average velocity [m/s] |
| ZP | Pump blade count |
| η | K*SR, Efficiency |
| ρf | Liquid density [kg/m3] |
| ρl | Liquid oil density [kg/m3] |
| ρv | Vapor density [kg/m3] |
| σ | Cavitation number |
| σT | Coefficient of surface tension |
| ωP | Pump rotating speed [rad/s] |
| ωT | Turbine rotating speed [rad/s] |
| ωV | vapor mass fraction |
| Interphase mass transfer per unit [kg/s] | |
| Cavi | Cavitation |
| exp | Experiment |
| NoCavi | No cavitation |
| P | Pump |
| S | Turbine |
| T | Stator |
References
- Yan, Q.D.; Wei, W.; Liu, C.; Liu, S.C.; Li, J.; Liu, B.S. Torque Converter Modern Design Theory and Methodology. Chin. Hydraul. Pneum. 2015, 4, 1–8. [Google Scholar] [CrossRef]
- Zhao, L.L. The Cavitation Research of the Flow Field in the Hydraulic Torque Converter Based on CFD. Ph.D. Thesis, Taiyuan University of Science and Technology, Taiyuan, China, 2016. [Google Scholar]
- Tseng, C.C. Modeling of Turbulent Cavitating Flows. Ph.D. Thesis, Dissertation of The University of Michigan, Ann Arbor, MI, USA, 2010. [Google Scholar]
- Anderson, C.L.; Zeng, L.; Sweger, P.O.; Narain, A. Experimental Investigation of Cavitation Signatures in an Automotive Torque Converter Using a Microwave Telemetry Technique. Int. J. Rotating Mach. 2003, 9, 403–410. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, S.; Otani, R.; Kunimoto, S.; Hara, Y.; Furukawa, A.; Yamaguchi, T. Vibration Characteristics due to Cavitation in Stator Element of Automotive Torque Converter at Stall Condition. In Proceedings of the ASME 2012 Fluids Engineering Summer Meeting Rio Grande, Rio Grande, PR, USA, 8–12 July 2012; pp. 535–541. [Google Scholar] [CrossRef]
- Dong, Y.; Korivi, V.; Attibele, P.; Yuan, Y.Q. Torque converter CFD engineering part 2: Performance improvement through core leakage flow and cavitation control. SAE Int. 2002, 111, 1272–1285. [Google Scholar]
- Tsutsumi, K.; Watanabe, S.; Tsuda, S.; Yamaguchi, T. Cavitation simulation of automotive torque converter using a homogeneous cavitation model. Eur. J. Mech. B/Fluids 2017, 61, 263–270. [Google Scholar] [CrossRef] [Green Version]
- Hayata, R.; Tsutsumi, K.; Watanabe, S.; Tsuda, S.; Yamaguchi, T.; Yoshihide, M. Modeling of Gaseous Cavitation in Torque Converter. In Proceedings of the Japan Mechanical Engineering Congress, Fukuoka, Japan, 11–14 September 2016. [Google Scholar] [CrossRef]
- Ju, J.; Jang, J.; Choi, M.; Baek, J.H. Effects of cavitation on performance of automotive torque converter. Adv. Mech. Eng. 2016, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.L.; Dong, Z.Q.; Lian, J.Y.; Zhao, F.Q. Analysis of Bubble Breakup Motion for Hydrodynamic Torque Converter. Hydraul. Pneum. Seals 2016, 36, 1–4. [Google Scholar] [CrossRef]
- Guo, M.; Liu, C.; Yan, Q.D.; Ke, Z.F.; Wei, W.; Li, J. Evaluation and Validation of Viscous Oil Cavitation Model Used in Torque Converter. Appl. Sci. 2021, 11, 3643. [Google Scholar] [CrossRef]
- Liu, C.; Guo, M.; Yan, Q.D.; Wei, W. Numerical Investigation on the Transient Cavitating Flow Inside a Torque Converter. In Proceedings of the IEEE 8th International Conference on Fluid Power and Mechatronics, Wuhan, China, 10–13 April 2019; pp. 208–216. [Google Scholar] [CrossRef]
- Ran, Z.; Ma, W.; Liu, C. 3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter. Appl. Sci. 2021, 11, 2798. [Google Scholar] [CrossRef]
- Liu, C.; Wei, W.; Yan, Q.D.; Weaver, B.K.; Wood, H.G. Influence of Stator Blade Geometry on Torque Converter Cavitation. ASME J. Fluids Eng. 2018, 140, 041102. [Google Scholar] [CrossRef]
- Liu, C.; Wei, W.; Yan, Q.D.; Weaver, B.K. Torque Converter Capacity Improvement through Cavitation Control by Design. ASME J. Fluids Eng. 2017, 139, 041103. [Google Scholar] [CrossRef]
- Liu, C.; Yan, Q.D.; Li, J.; Li, J.; Zou, B. Investigation on the Cavitation Characteristics of High Power-densityTorque Converter. J. Mech. Eng. 2020, 56, 147–155. [Google Scholar] [CrossRef]
- Kang, C.; Mao, N.; Zhang, G.F. Highly Confined Floes and Cavitation Phenomenon in a Hydraulic Retarder. J. Eng. Thermophys. 2017, 38, 2151–2158. [Google Scholar]
- Dong, L.; Xiao, J.W.; Ming, J.Y.; Liu, H.L. Numerical simulation and experimental study on cavitation behavior of hydraulic retarder model. J. Drain. Irrig. Mach. Eng. 2017, 35, 1–5. [Google Scholar] [CrossRef]
- Liu, H.L.; Liu, D.X.; Wang, Y.; Du, H.; Xu, H. Numerical research status and prospects of cavitating flow in a pump. Fluid Mach. 2011, 39, 38–44. [Google Scholar] [CrossRef]
- Xue, R.; Zhang, M.; Xu, Z.J.; Lin, L.L. Comparison and Study on Different Cavitation Models. Northwest Hydropower 2014, 2, 85–89. [Google Scholar]
- Zwart, P.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the ICMF 2004 International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004; pp. 1–11. [Google Scholar]
- Mejri, I.; Bakir, F.; Rey, R.; Belamri, T. Comparison of computational results obtained from a homogeneous cavitation model with experimental investigations of three inducers. ASME J. Fluids Eng. 2006, 128, 1308–1323. [Google Scholar] [CrossRef]
- Liu, C.; Wei, W.; Yan, Q.D.; Morgan, N.R. Design of Experiments to Investigate Blade Geometric Effects on the Hydrodynamic Performance of Torque Converters. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 276–291. [Google Scholar] [CrossRef]
- Xiong, P.; Sun, H.; Zhong, J.; Zhen, C.; Chen, X.; Gao, H. Analysis of the Influence of the Number of Torque Converter Blades on Working Performance Based on the Response Surface Method. J. Phys. Conf. Ser. 2021, 1748, 1–9. [Google Scholar] [CrossRef]
- Usui, T.; Iga, Y. Prediction Method of Cavitation inside Torque Converter using Gaseous Cavitation Model. Trans. Soc. Automot. Eng. Jpn. 2021, 52, 961–966. [Google Scholar] [CrossRef]
- Ma, W.X.; Liu, H.; Liu, C.B.; Liu, C.S. Measurement and analysis of the internal flow field in the hydrodynamic torque converter with adjustable guide vanes. Adv. Mech. Eng. 2015, 7, 168781401558966. [Google Scholar] [CrossRef]
- Pan, X.; Xinyuan, C.; Hongjun, S.; Jiping, Z.; Lin, W.; Huichao, G. Effect of the blade shaped by Joukowsky airfoil transformation on the characteristics of the torque converter. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 3314–3321. [Google Scholar] [CrossRef]
- Mekkes, J.; Anderson, C.; Narain, A. Static pressure measurements and cavitation signatures on the nose of a torque converters stator blades. In Proceedings of the International Symposium on Rotating Machinery (ISROMAC), Honolulu, HI, USA, 7–11 March 2004. [Google Scholar]
- Liu, B.S.; Tan, L.; Li, J. Influence of Pump Rotation Speed on Hydrodynamic Performance and Stator Blade Surface Pressure Pulsation in Torque Converter. J. Fluids Eng. 2020, 142, 101207. [Google Scholar] [CrossRef]
- Liu, C.; Wei, W.; Yan, Q.; Weaver, B.K.; Wood, H.G. On the application of passive flow control for cavitation suppression in torque converter stator. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 204–222. [Google Scholar] [CrossRef]

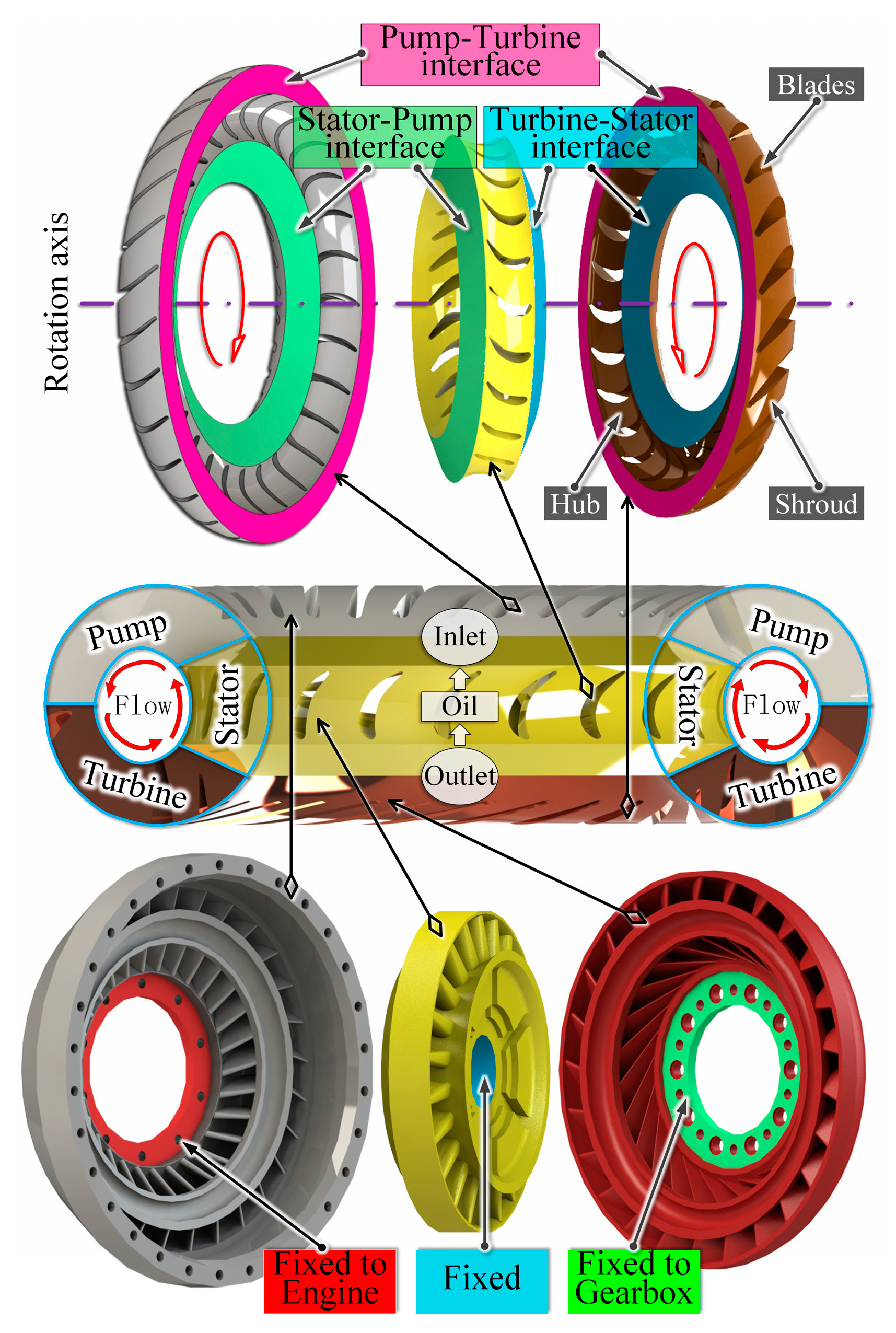
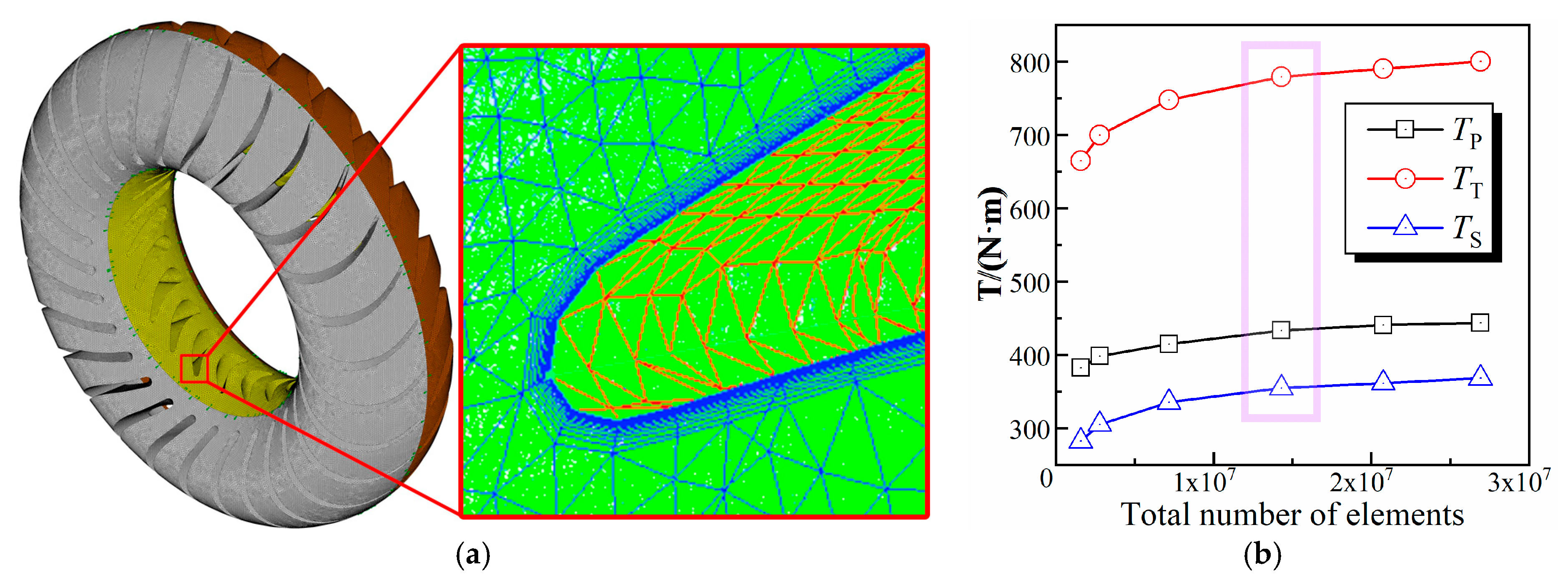

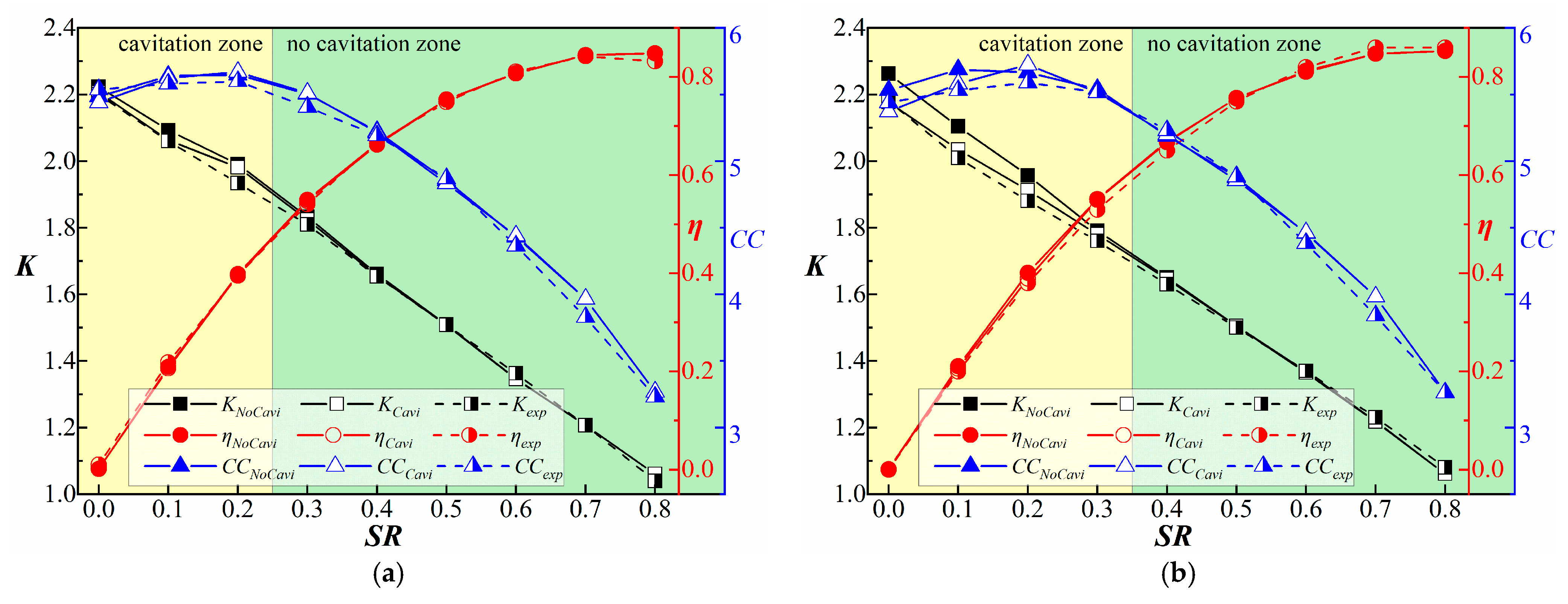
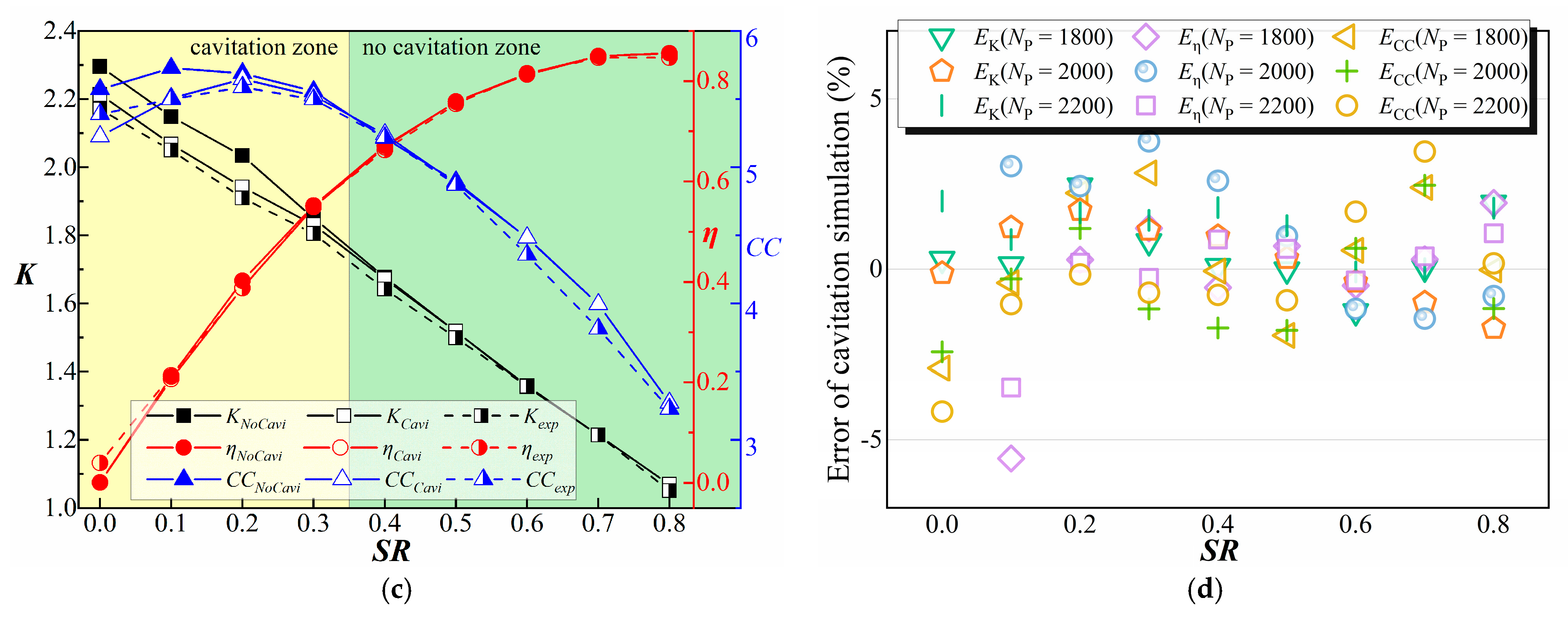


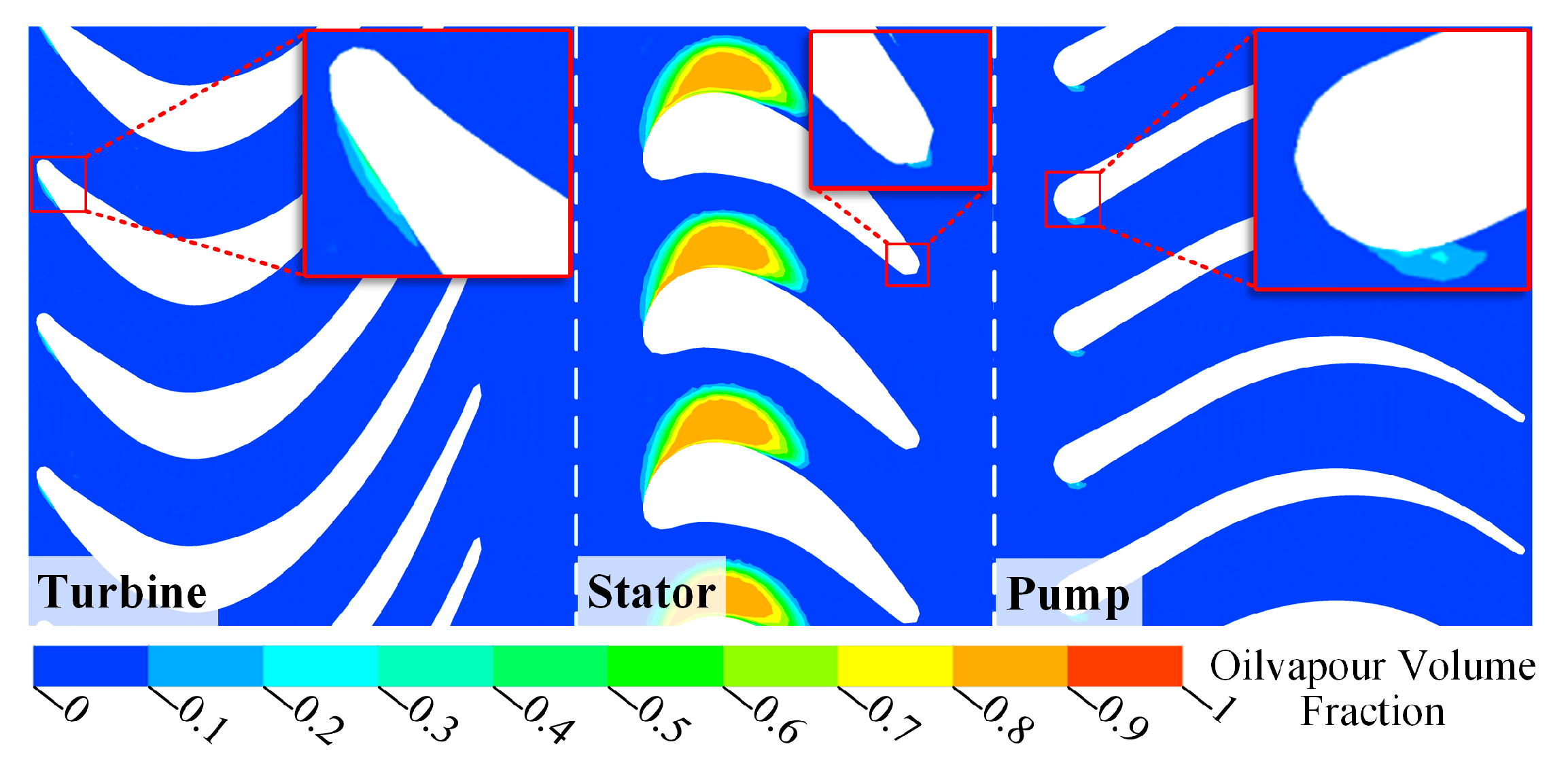
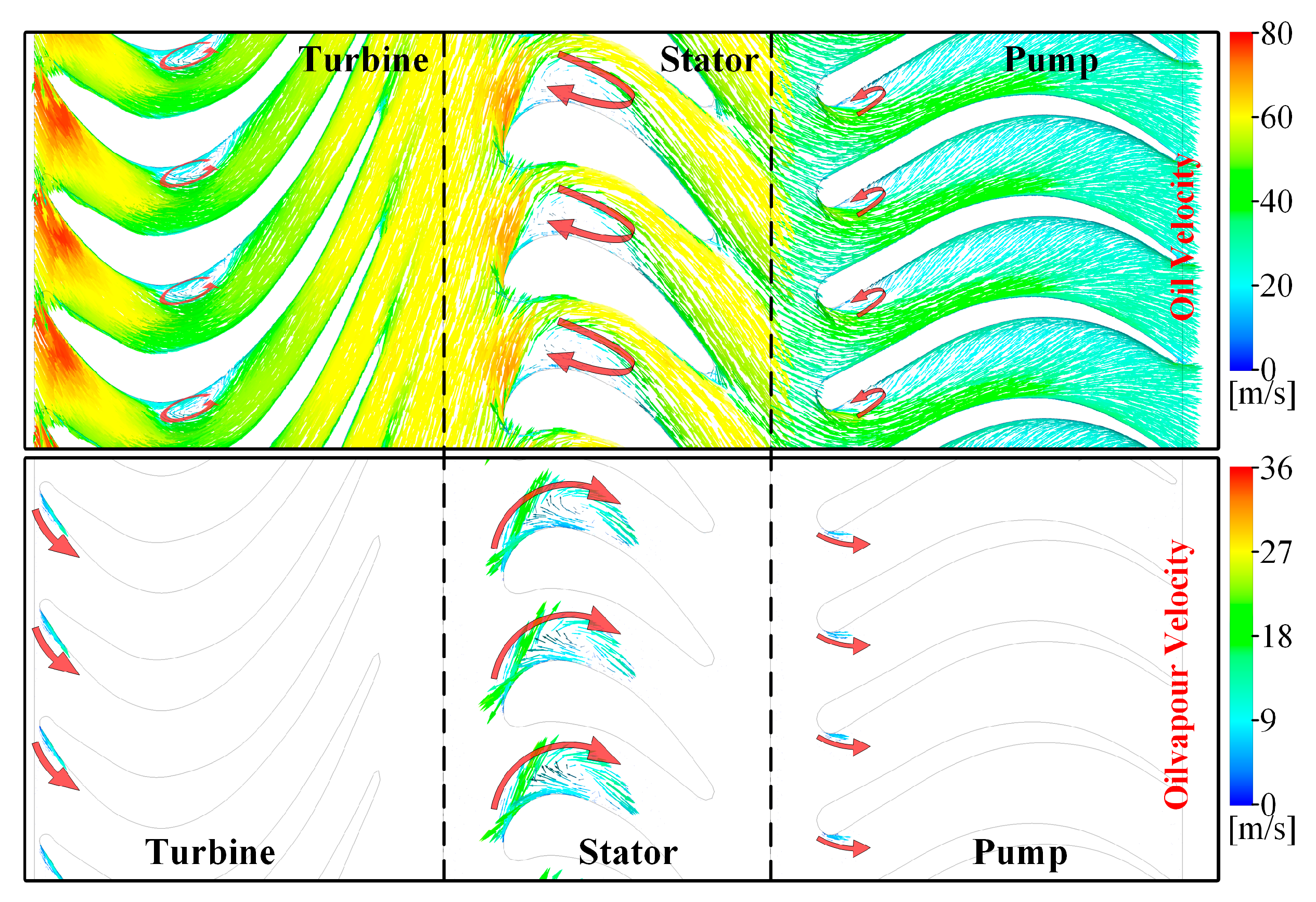
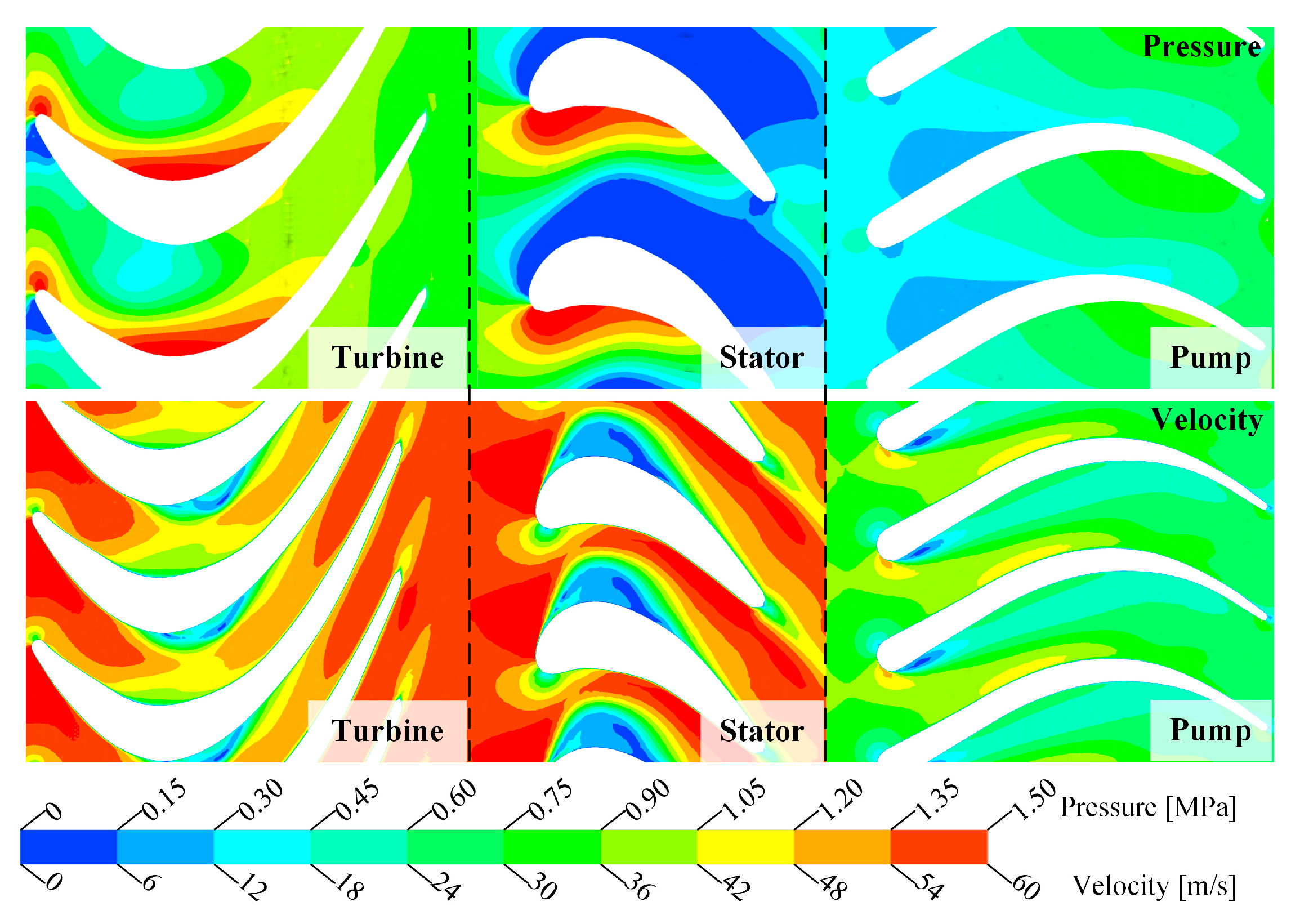
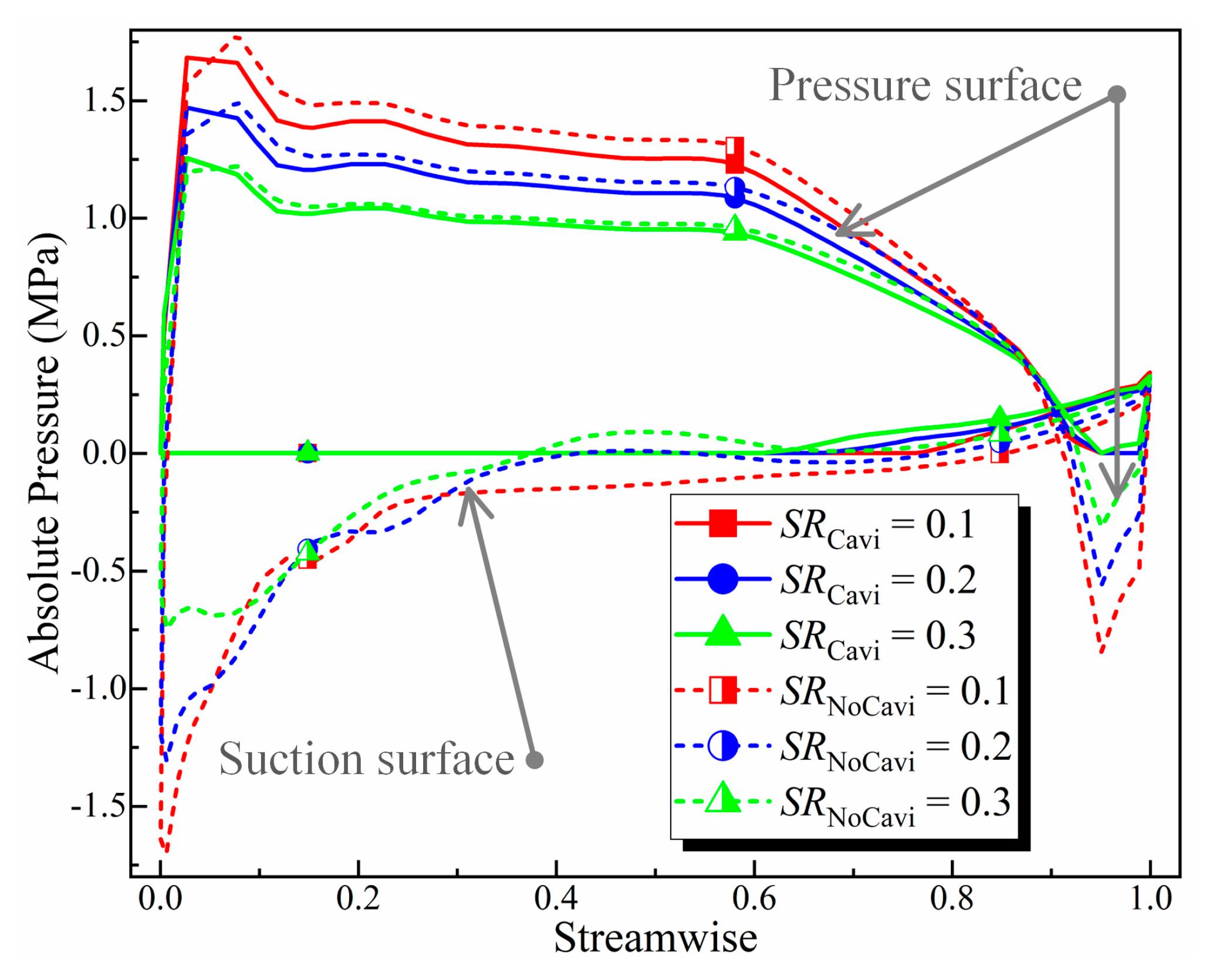


| Analysis Step | No Cavitation Ⅰ | No Cavitation Ⅱ | Cavitation Ⅲ |
|---|---|---|---|
| Analysis type | Steady-state | Steady-state | Steady-state |
| Advection scheme | Upwind | High resolution | High resolution |
| Interface model | Frozen rotor | Frozen rotor | Frozen rotor |
| Cavitation model | None | None | Zwart model |
| Time step | 0.01 s | Auto timescale | Auto timescale |
| Step number | 400 | 300 | 400 |
| Convergence target | RMS 1 × 10−5 | RMS 1 × 10−5 | RMS 1 × 10−5 |
| Turbulence model | SST | SST | SST |
| Fluid properties | ρl = 835.2 kg·m−3, μl = 1.46 × 10−2 Pa·s | ||
| Vapor properties | ρv = 2.1 kg·m−3, μv = 1.2 × 10−5 Pa·s | ||
| Pump status | From 1000 rpm to 3000 rpm | ||
| Turbine status | From 0 rpm to 3000 rpm | ||
| Stator status | Stationary | ||
| Boundary details | No-slip and smooth wall | ||
| NP/rpm | SR = 0 | SR = 0.1 | SR = 0.2 | SR = 0.3 | SR = 0.4 | SR = 0.5 | SR = 0.6 | SR = 0.7 | SR = 0.8 |
|---|---|---|---|---|---|---|---|---|---|
| 1000 | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ |
| 1200 | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ |
| 1500 | □△● | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ |
| 1800 | □▲● | □△● | □△● | □△○ | □△○ | □△○ | □△○ | □△○ | □△○ |
| 2000 | ■▲● | □▲● | □△● | □△● | □△○ | □△○ | □△○ | □△○ | □△○ |
| 2200 | ■▲● | ■▲● | □▲● | □△● | □△○ | □△○ | □△○ | □△○ | □△○ |
| 2500 | ■▲● | ■▲● | ■▲● | □▲● | □△● | □△○ | □△○ | □△○ | □△○ |
| 2800 | ■▲● | ■▲● | ■▲● | □▲● | □△● | □△○ | □△○ | □△○ | □△○ |
| 3000 | ■▲● | ■▲● | ■▲● | ■▲● | □▲● | □△● | □△○ | □△○ | □△○ |
| △NPT/rpm | <1400 | 1400 | 1500 | 1600 | 1700 | 1800 | 1900 | 2000 | >2000 |
|---|---|---|---|---|---|---|---|---|---|
| Cavitation in the pump | □ | □ | □ | □ | □ | □ | □ | ■ | ■ |
| Cavitation in the turbine | △ | △ | △ | △ | ▲ | ▲ | ▲ | ▲ | ▲ |
| Cavitation in the stator | ○ | ● | ● | ● | ● | ● | ● | ● | ● |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Liu, C.; Yan, Q.; Wei, W.; Khoo, B.C. The Effect of Rotating Speeds on the Cavitation Characteristics in Hydraulic Torque Converter. Machines 2022, 10, 80. https://doi.org/10.3390/machines10020080
Guo M, Liu C, Yan Q, Wei W, Khoo BC. The Effect of Rotating Speeds on the Cavitation Characteristics in Hydraulic Torque Converter. Machines. 2022; 10(2):80. https://doi.org/10.3390/machines10020080
Chicago/Turabian StyleGuo, Meng, Cheng Liu, Qingdong Yan, Wei Wei, and Boo Cheong Khoo. 2022. "The Effect of Rotating Speeds on the Cavitation Characteristics in Hydraulic Torque Converter" Machines 10, no. 2: 80. https://doi.org/10.3390/machines10020080
APA StyleGuo, M., Liu, C., Yan, Q., Wei, W., & Khoo, B. C. (2022). The Effect of Rotating Speeds on the Cavitation Characteristics in Hydraulic Torque Converter. Machines, 10(2), 80. https://doi.org/10.3390/machines10020080







