Modeling, Kinematic Characteristics Analysis and Experimental Testing of an Elliptical Rotor Scraper Pump
Abstract
:1. Introduction
1.1. Research Motivation
1.2. Literature Review
1.3. Challenges and Problems
1.4. Contributions of This Work
- This paper proposes a new type of elliptical rotor scraper pump (ERSP) to realize the continuous output of high-pressure fluid.
- The ERSP's structure adopts a swing scraper to divide the pump cavity. This arrangement subverts the design concept of the traditional pump structure.
- Through mathematical modeling, parameter setting and kinematic simulation analysis, the workability of the ERSP is preliminarily verified.
- Based on the current research, the research team developed a prototype to verify the feasibility of the ERSP through practical experiments.
1.5. Organization of the Paper
2. Structure and Working Principle
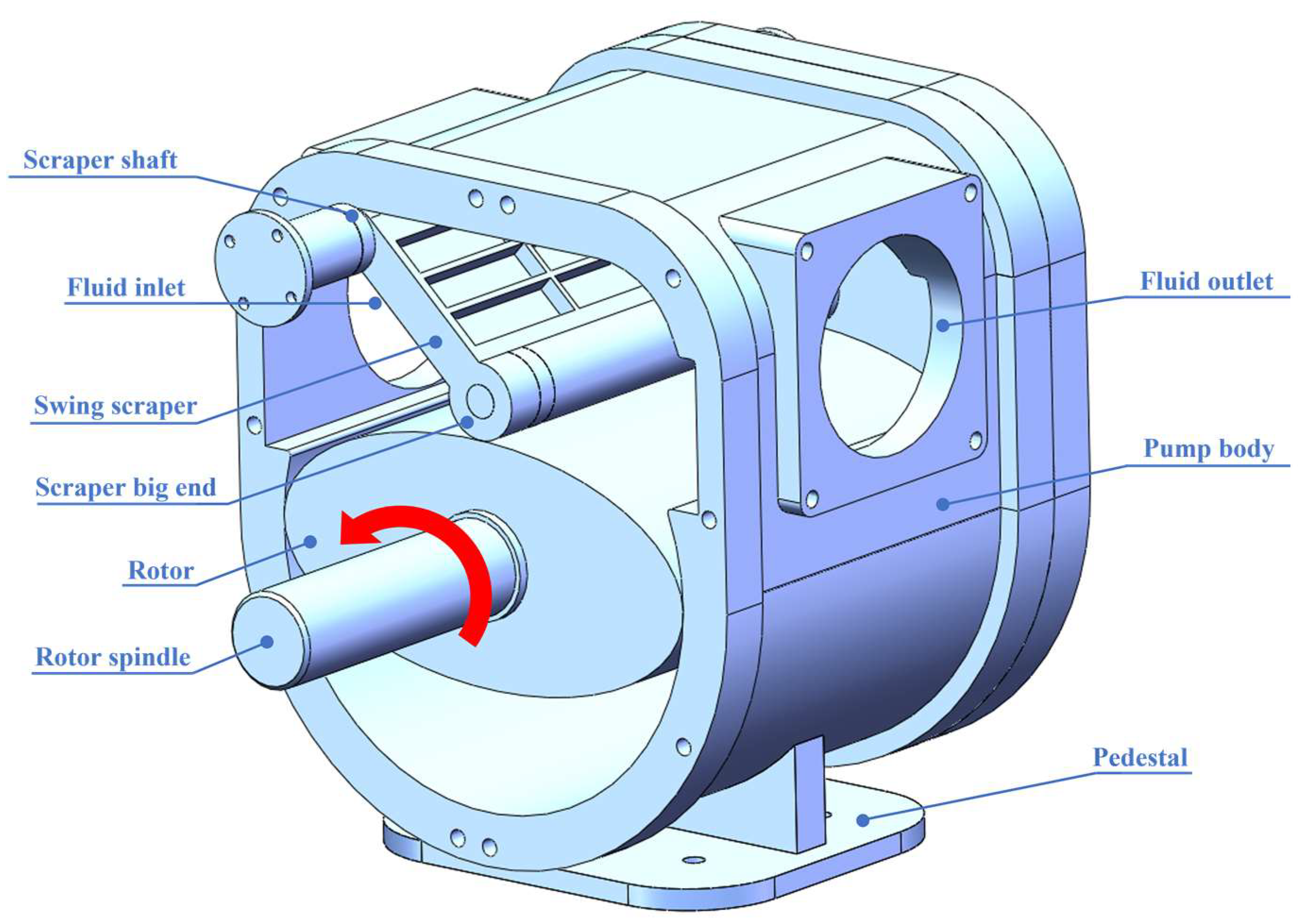
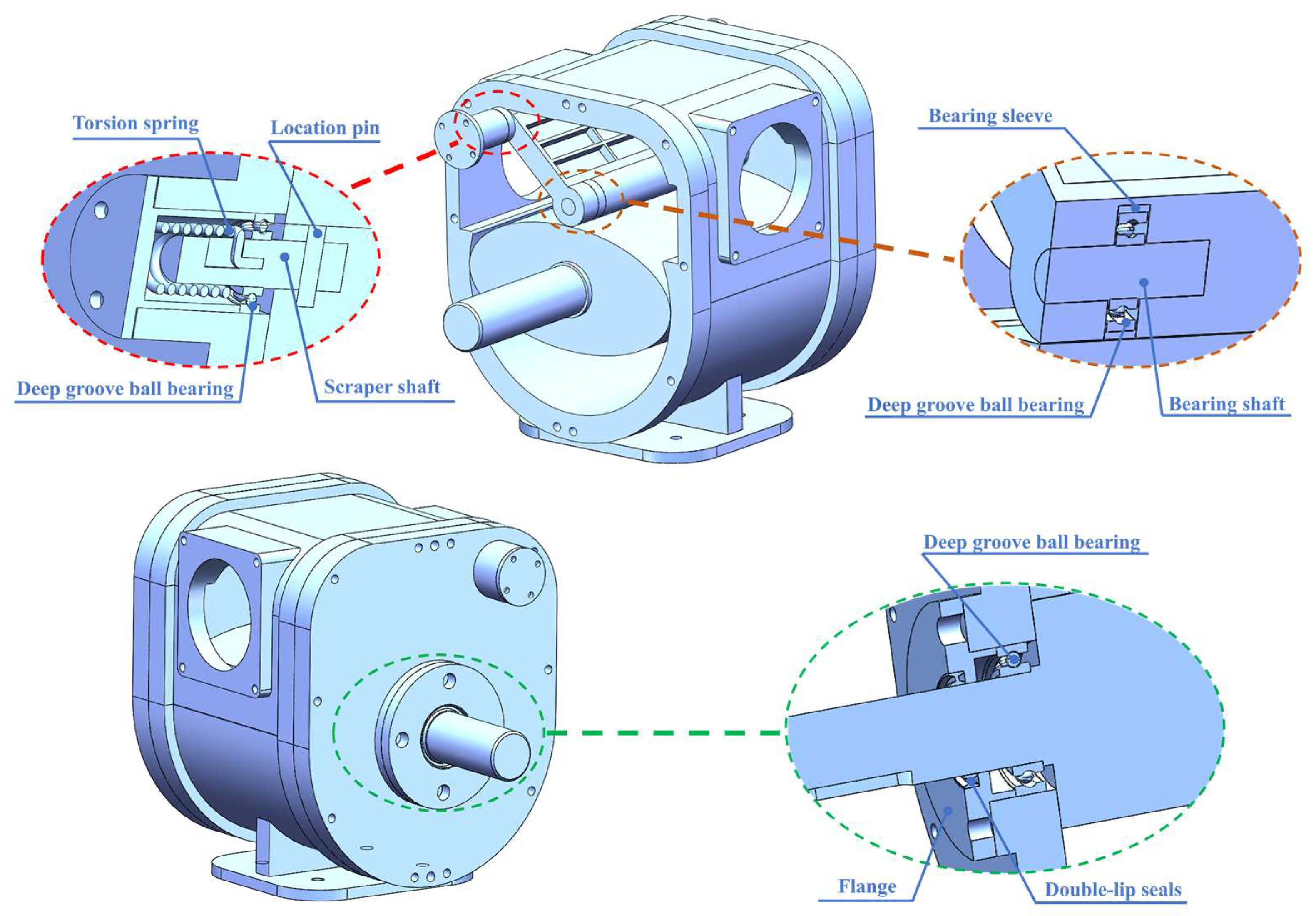
2.1. Pump Structure
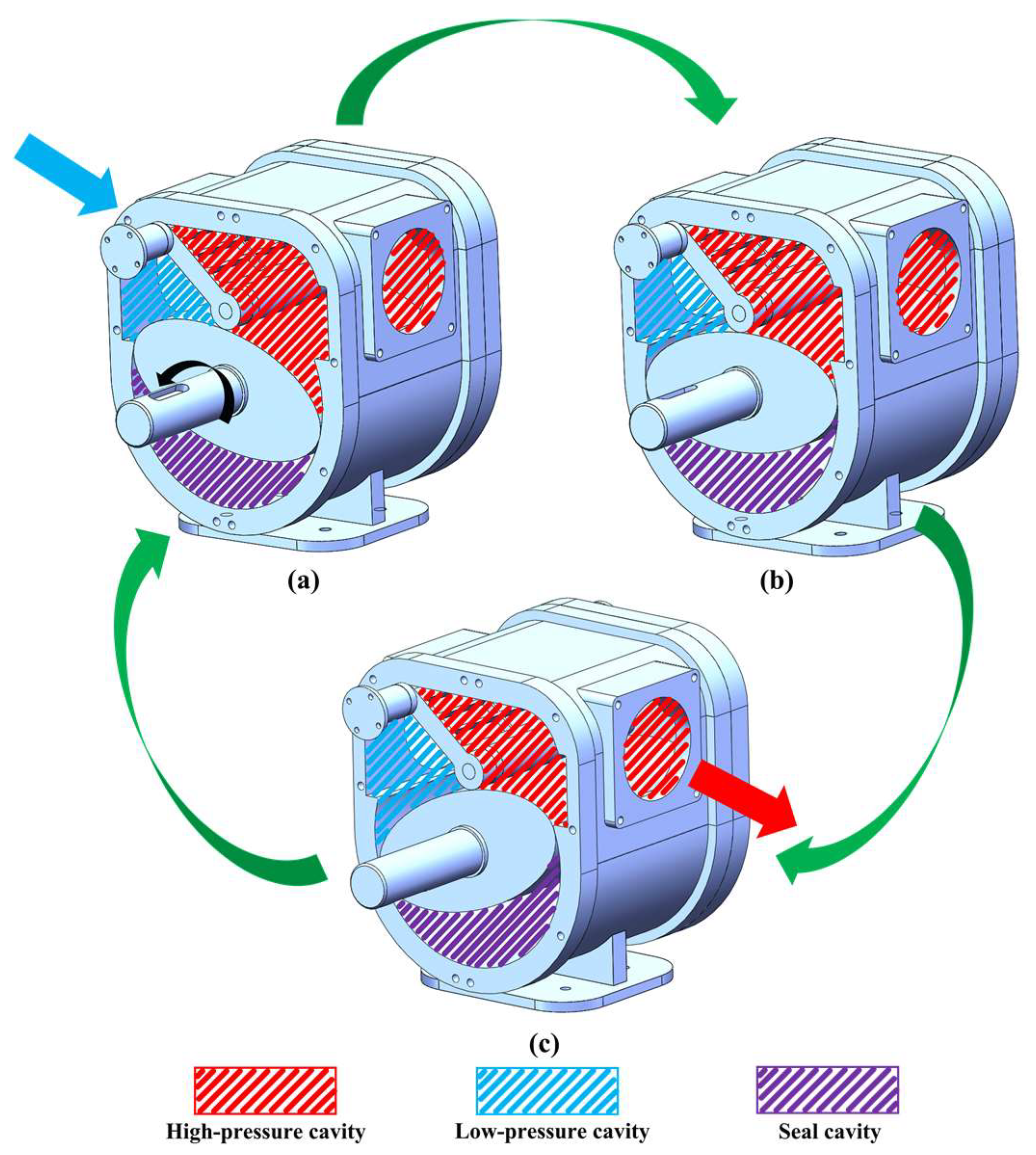
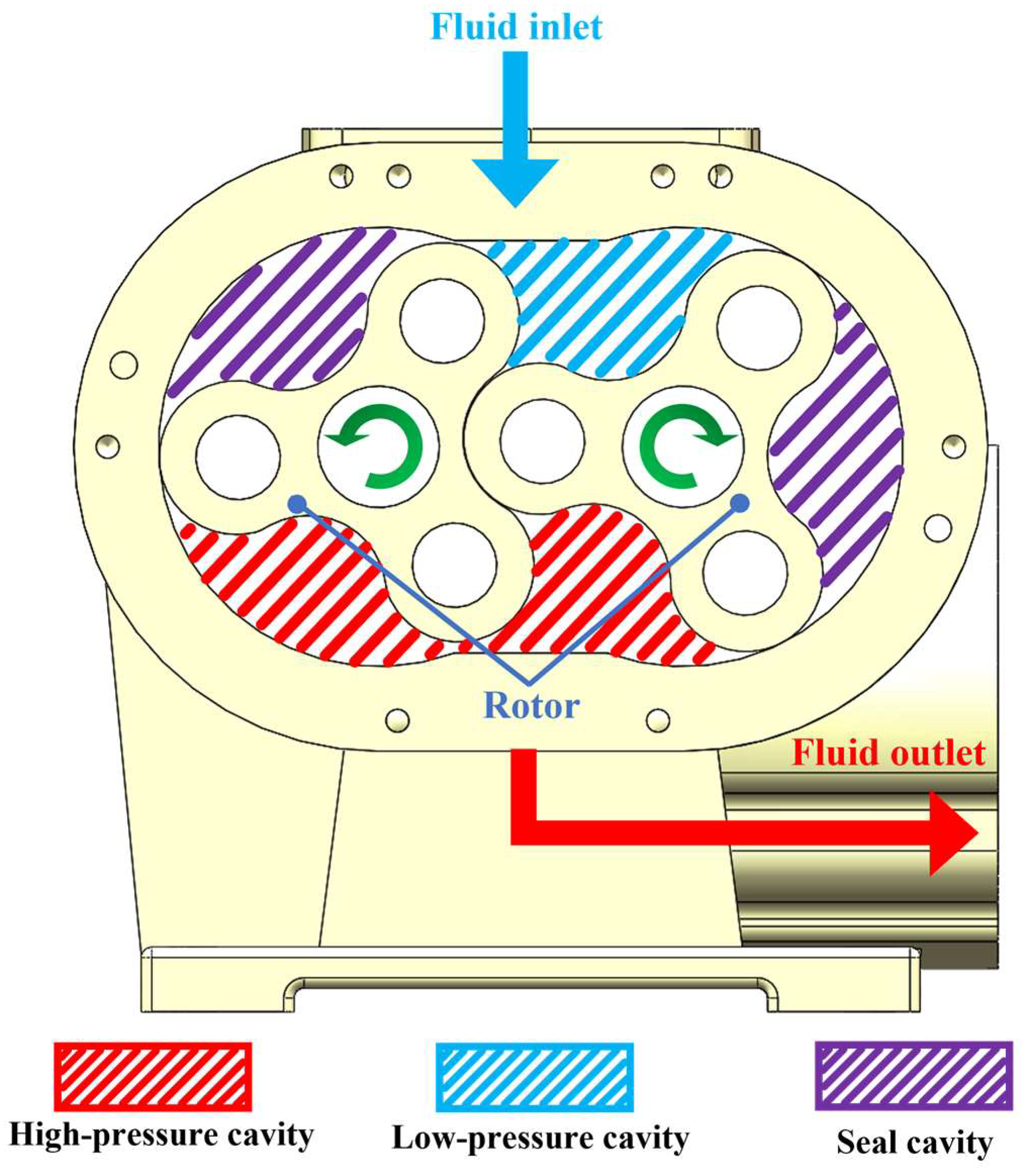
2.2. Working Principles of the ERSP Pump
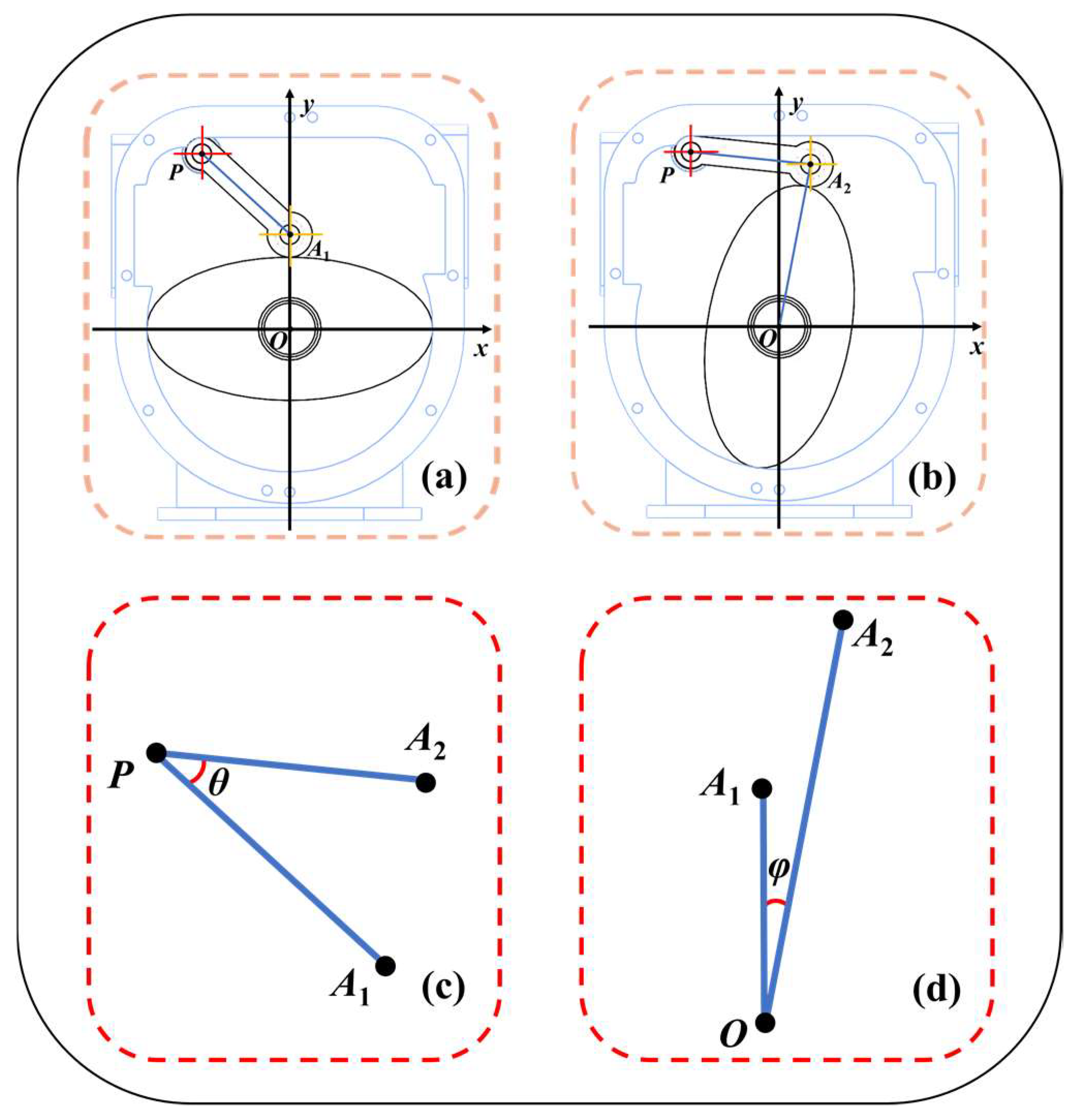
3. Mathematical Model and Related Parameters
3.1. Mathematical Model
3.2. Basic Parameter Setting
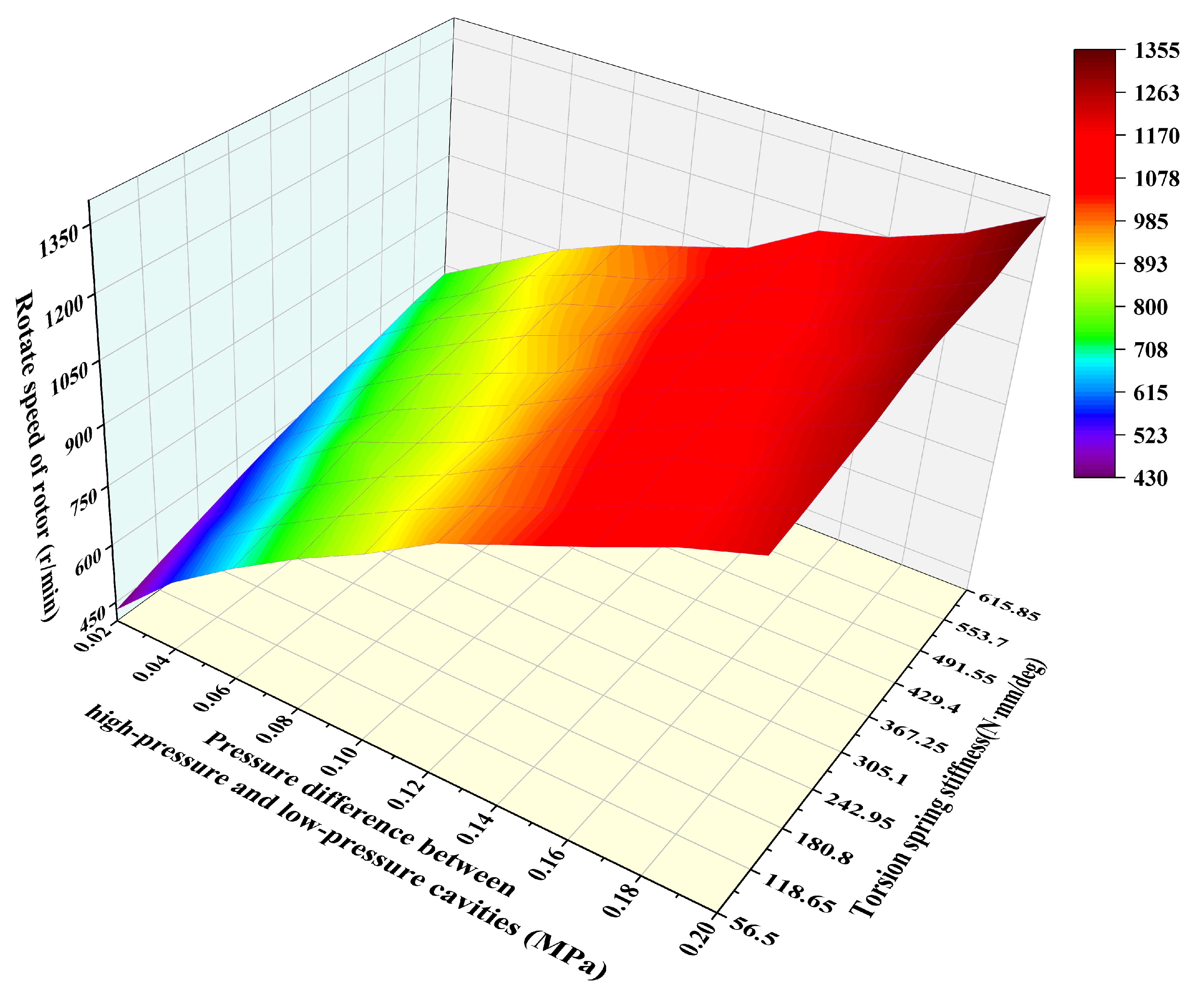
4. Kinematic Characteristics Analysis
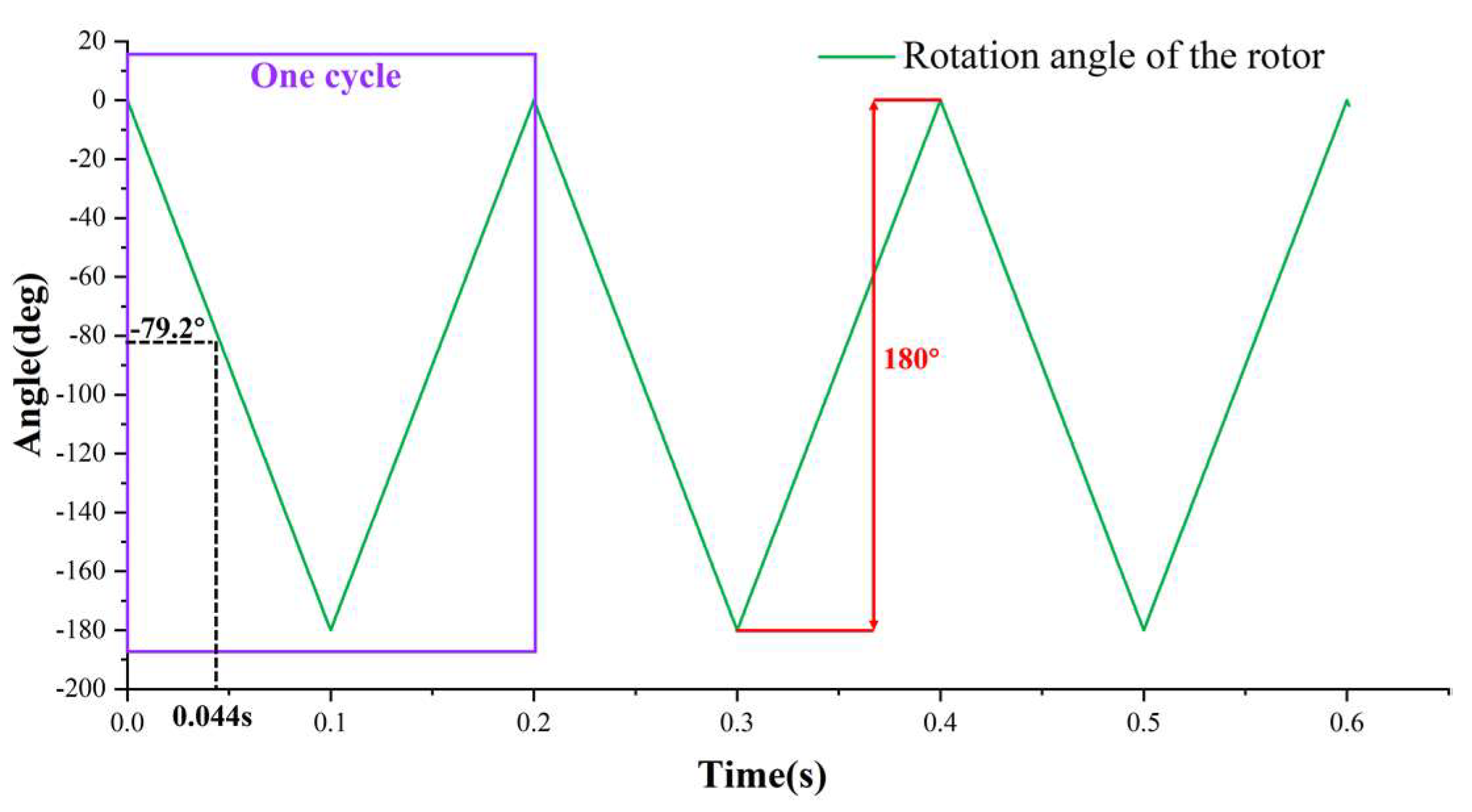
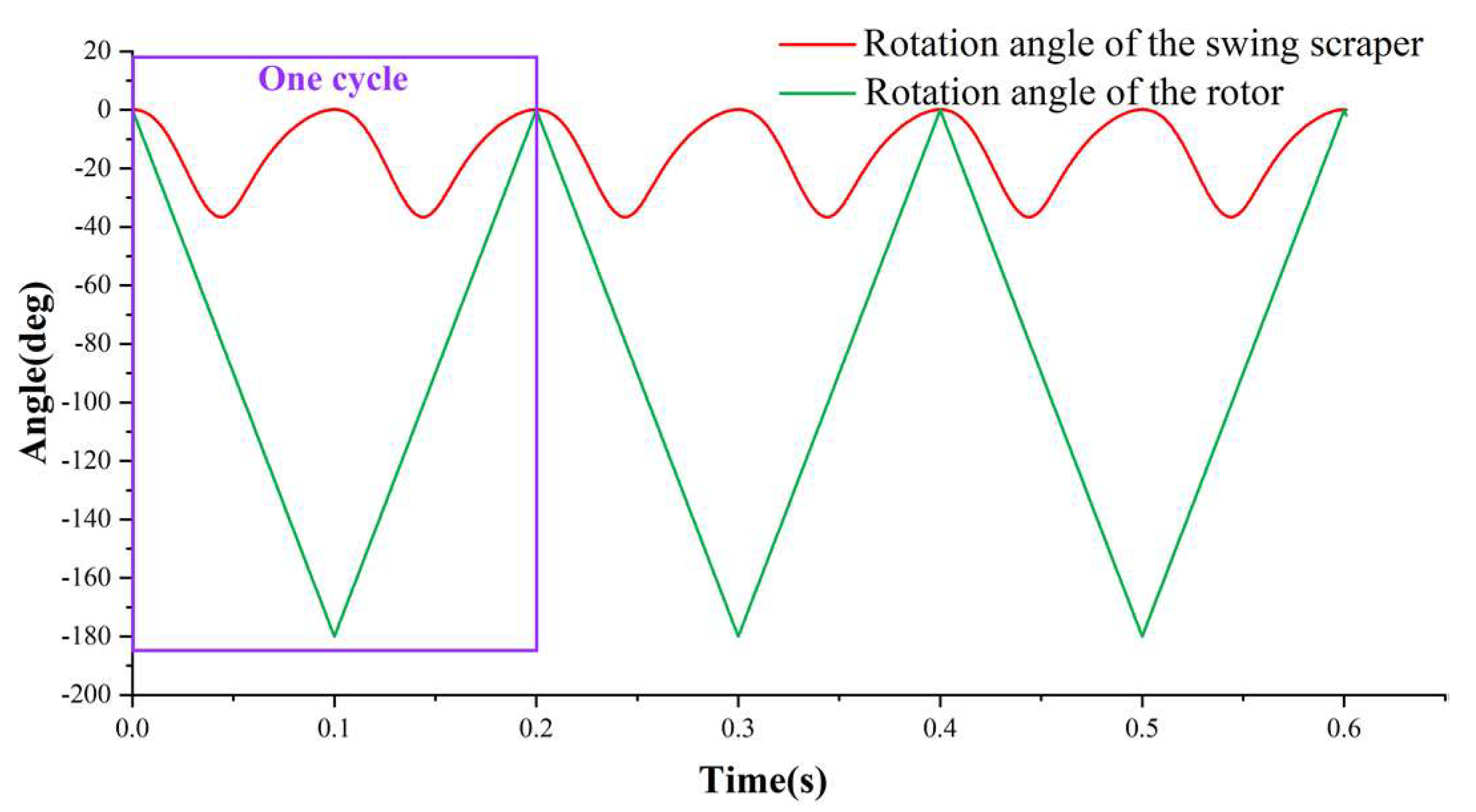
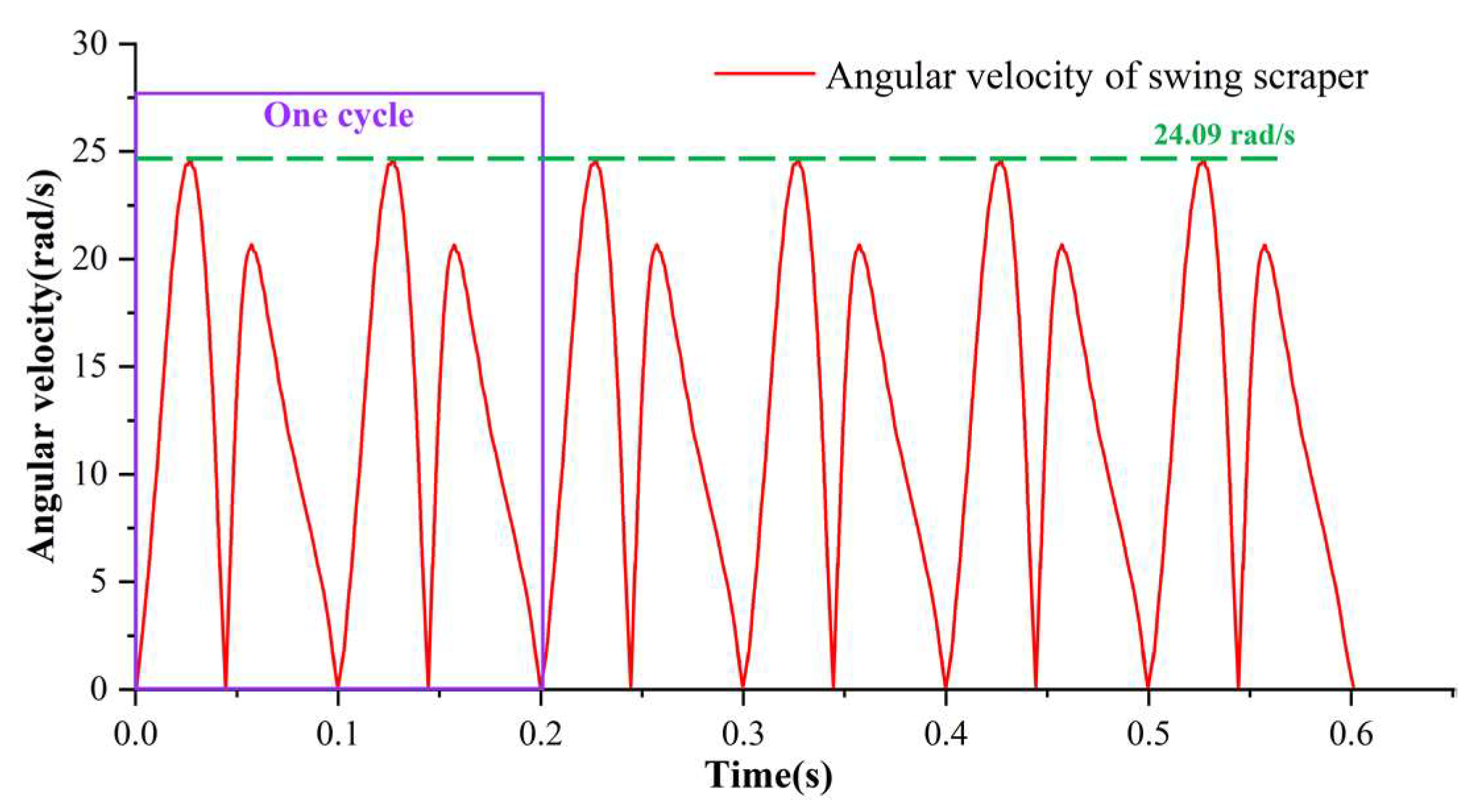
4.1. Steady-State Analysis
4.2. Followability Analysis
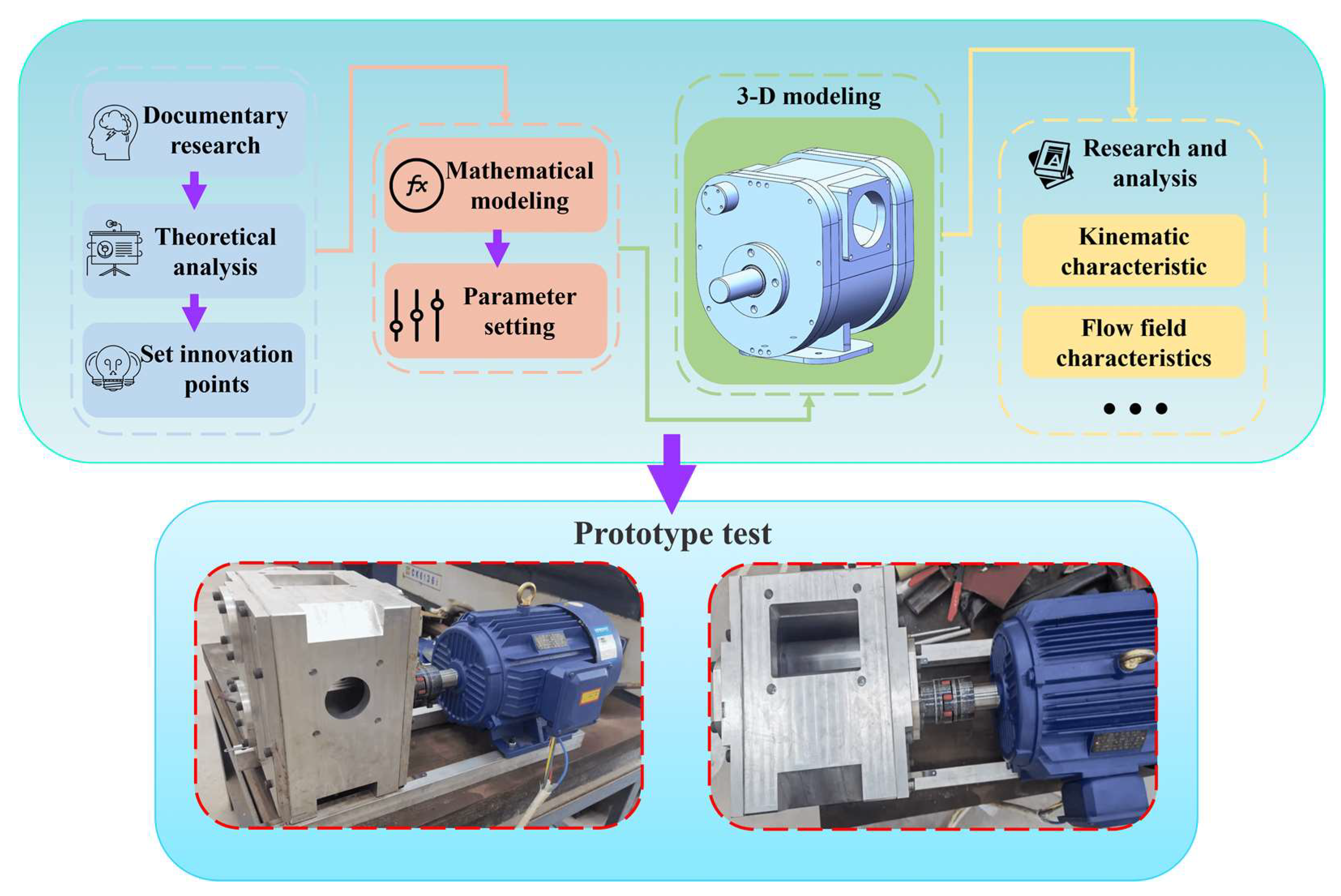
5. Development of Principle Prototype
6. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, L. Development and Application of Soil Coupled Heat Pump; AIP Publishing LLC: Melville, NY, USA, 2017. [Google Scholar]
- Alawadhi, K.; Alzuwayer, B.; Mohammad, T.A.; Buhemdi, M.H. Design and Optimization of a Centrifugal Pump for Slurry Transport Using the Response Surface Method. Machines 2021, 9, 60. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Pu, Q.; Liu, S. Advancement of electroosmotic pump in microflow analysis: A review. Anal. Chim. Acta 2019, 1060, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, J.; Li, K.; Liu, Y. A review of recent studies on piezoelectric pumps and their applications. Mech. Syst. Signal Processing 2021, 151, 107393. [Google Scholar] [CrossRef]
- Miao, L.; Zhang, Y.; Tong, C.; Guo, Q.; Zhang, J.; Yildirim, T. Optimized Energy-Storage Method Based on Deep-Learning Adaptive-Dynamic Programming. J. Energy Eng. 2020, 146, 04020011. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Yao, Y. Fault prognosis of battery system based on accurate voltage abnormity prognosis using long short-term memory neural networks. Appl. Energy 2019, 251, 113381. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.; Lin, P.; Qu, C. Online accurate state of health estimation for battery systems on real-world electric vehicles with variable driving conditions considered. J. Clean. Prod. 2021, 294, 125814. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Ma, F.; Yang, J.; Xu, X.; Qu, C.; Zhang, J.; Shan, T.; Hou, Y.; Zhou, Y. Thermal Runaway Prognosis of Battery Systems Using the Modified Multi-Scale Entropy in Real-World Electric Vehicles. IEEE Trans. Transp. Electrif. 2021, 7, 2269–2278. [Google Scholar] [CrossRef]
- Parlak, Z.; Kemerli, M.; Engin, T.; Ko, Y. Design of a mini double-discharge centrifugal pump under multiphase flow by CFD and experimental verification. J. Appl. Fluid Mech. 2018, 11, 1437–1448. [Google Scholar] [CrossRef]
- Maqsood, M.; Usman, A.; Bodla, M.F.; Ali, J. Evaluation of performance parameters of indigenously developed roots pumping system. IOP Conf. Ser. Mater. Sci. Eng. 2016, 146, 012047. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.M.; Lai, X.D.; Zhang, X.; Zhou, X. Evolutionary Topology Optimization Design of Rotary Lobe of Roots Vacuum Pumps. Adv. Mater. Res. 2013, 798–799, 365–368. [Google Scholar] [CrossRef]
- Szwemin, P.; Fiebig, W. The Influence of Radial and Axial Gaps on Volumetric Efficiency of External Gear Pumps. Energies 2021, 14, 4468. [Google Scholar] [CrossRef]
- Wang, H.; Du, S.S. External Gear Pump Model and Simulation. Appl. Mech. Mater. 2011, 127, 228–232. [Google Scholar] [CrossRef]
- Bai, J.J.; Xu, M.M. Research Status and Development Trend of Vane Pump. Appl. Mech. Mater. 2014, 556, 1143–1146. [Google Scholar] [CrossRef]
- Korkmaz, E.; Glcü, M.; Kurbanolu, C. Effects of blade discharge angle, blade number and splitter blade length on deep well pump performance. J. Appl. Fluid Mech. 2017, 10, 529–540. [Google Scholar] [CrossRef]
- Yang, L.F. Structure Optimization Design of Vane Steering Pump. Appl. Mech. Mater. 2014, 496, 904–907. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, B.; Zhang, Y.; Peng, L.; Liu, M.; Lv, Y. Research on modelling and simulation of a new variable displacement oil pump. J. Eng. 2019, 2019, 350–354. [Google Scholar] [CrossRef]
- Li, Z.; Song, J.; Huang, Y.; Li, Y.; Chen, J. Design and analysis for a new energy-saving hydraulic pumping unit. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 2119–2131. [Google Scholar] [CrossRef]
- Hsieh, C.-F. A new curve for application to the rotor profile of rotary lobe pumps. Mech. Mach. Theory 2015, 87, 70–81. [Google Scholar] [CrossRef]
- Shim, S.-B.; Park, Y.-J.; Nam, J.-S.; Kim, S.-C.; Kim, J.-M.; Kim, K.-U. Development of a rotary clap mechanism for positive-displacement rotary pumps: Experimental verification and optimization. Int. J. Precis. Eng. Manuf. 2017, 18, 587–597. [Google Scholar] [CrossRef]
- Choi, Y.-D.; Kurokawa, J.; Matsui, J. Performance and Internal Flow Characteristics of a Very Low Specific Speed Centrifugal Pump. J. Fluids Eng. 2006, 128, 341. [Google Scholar] [CrossRef]
- Cheng, T.; Jiang, M. Design and Efficiency Analysis of Small Displacement Pump. IOP Conf. Ser. Earth Environ. Sci. 2020, 461, 012052. [Google Scholar] [CrossRef]
- Zhang, C.; Ruan, J.; Xing, T.; Li, S.; Meng, B.; Ding, C. Research on the Volumetric Efficiency of a Novel Stacked Roller 2D Piston Pump. Machines 2021, 9, 128. [Google Scholar] [CrossRef]
- Guan, D.; Wu, J.H.; Jing, L.; Hilton, H.H.; Lu, K. Kinematic modeling, analysis and test on a quiet spherical pump. J. Sound Vib. 2016, 383, 146–155. [Google Scholar] [CrossRef]
- Saputra, O.A.; Syaifudin, M. Design, analysis, and application of solar cell to drive water pump. Int. Conf. Sci. Appl. Sci. 2019, 2202, 020113. [Google Scholar]
- Sun, J.; Shao, L.; Fu, L.; Han, X.; Li, S. Kinematic analysis and optimal design of a novel parallel pointing mechanism. Aerosp. Sci. Technol. 2020, 104, 105931. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J.; Zhang, L.; Wei, Q. Single Stage Horizontal Self-Priming Pump System Assembly and Kinematics Simulation. In Proceedings of the 2015 Seventh International Conference on Advanced Communication and Networking (ACN), Kota Kinabalu, Malaysia, 8–11 July 2015. [Google Scholar]
- Battarra, M.; Blum, A.; Mucchi, E. Kinematics of a balanced vane pump with circular tip vanes. Mech. Mach. Theory 2019, 137, 355–373. [Google Scholar] [CrossRef]
- Chen, R.; Rao, Y.; Yue, H.; Ai, Y.; Zhang, X.; Zhang, L.; Zheng, J. Numerical Simulation of Bed Combustion in Biomass-Briquette Boiler. J. Energy Eng. 2020, 146, 04020031. [Google Scholar] [CrossRef]
- Shcherba, V.; Shalay, V.; Nosov, E.; Pavlyuchenko, E.; Tegzhanov, A.-K. Development and Research of Crosshead-Free Piston Hybrid Power Machine. Machines 2021, 9, 32. [Google Scholar] [CrossRef]

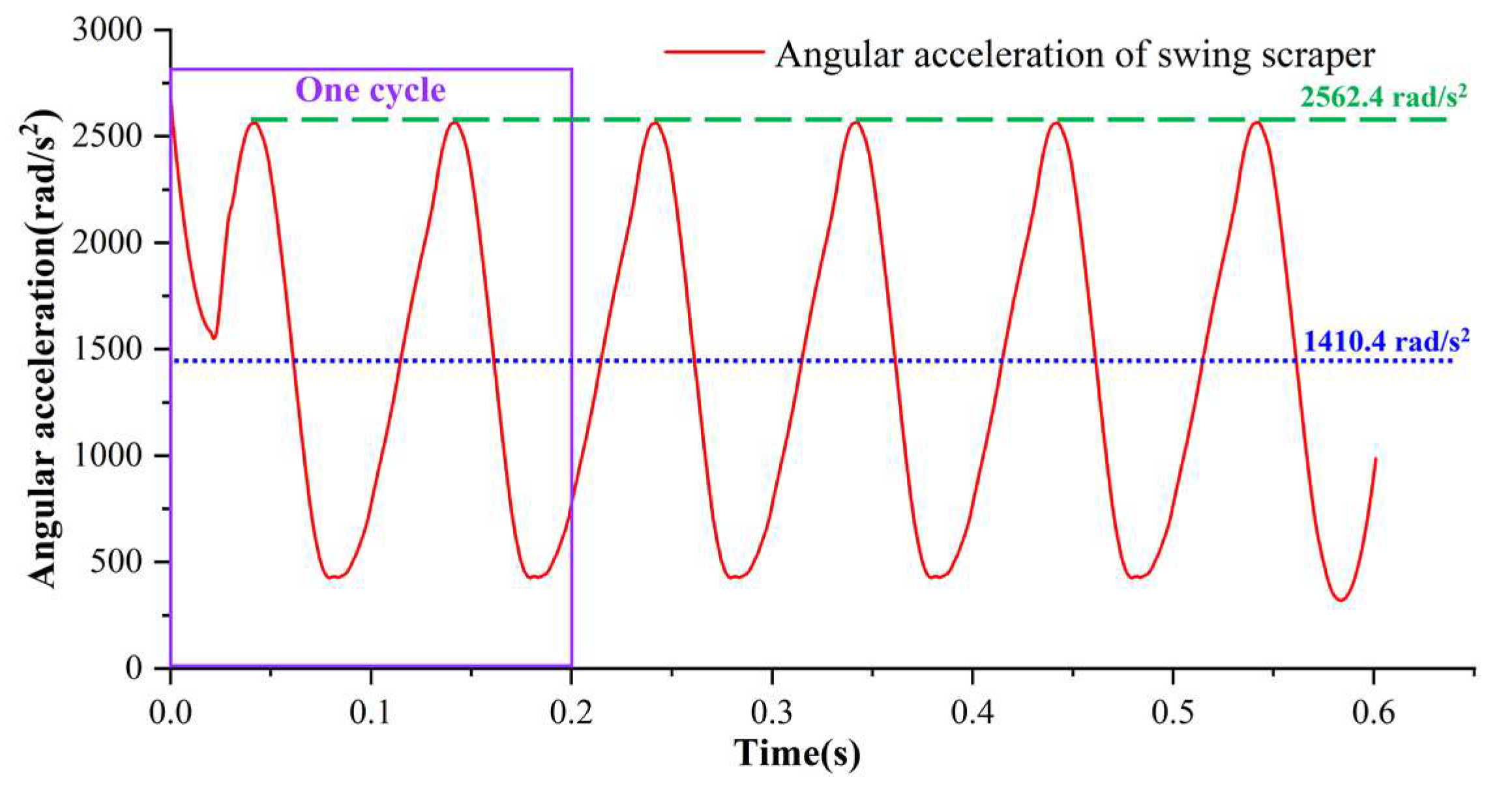
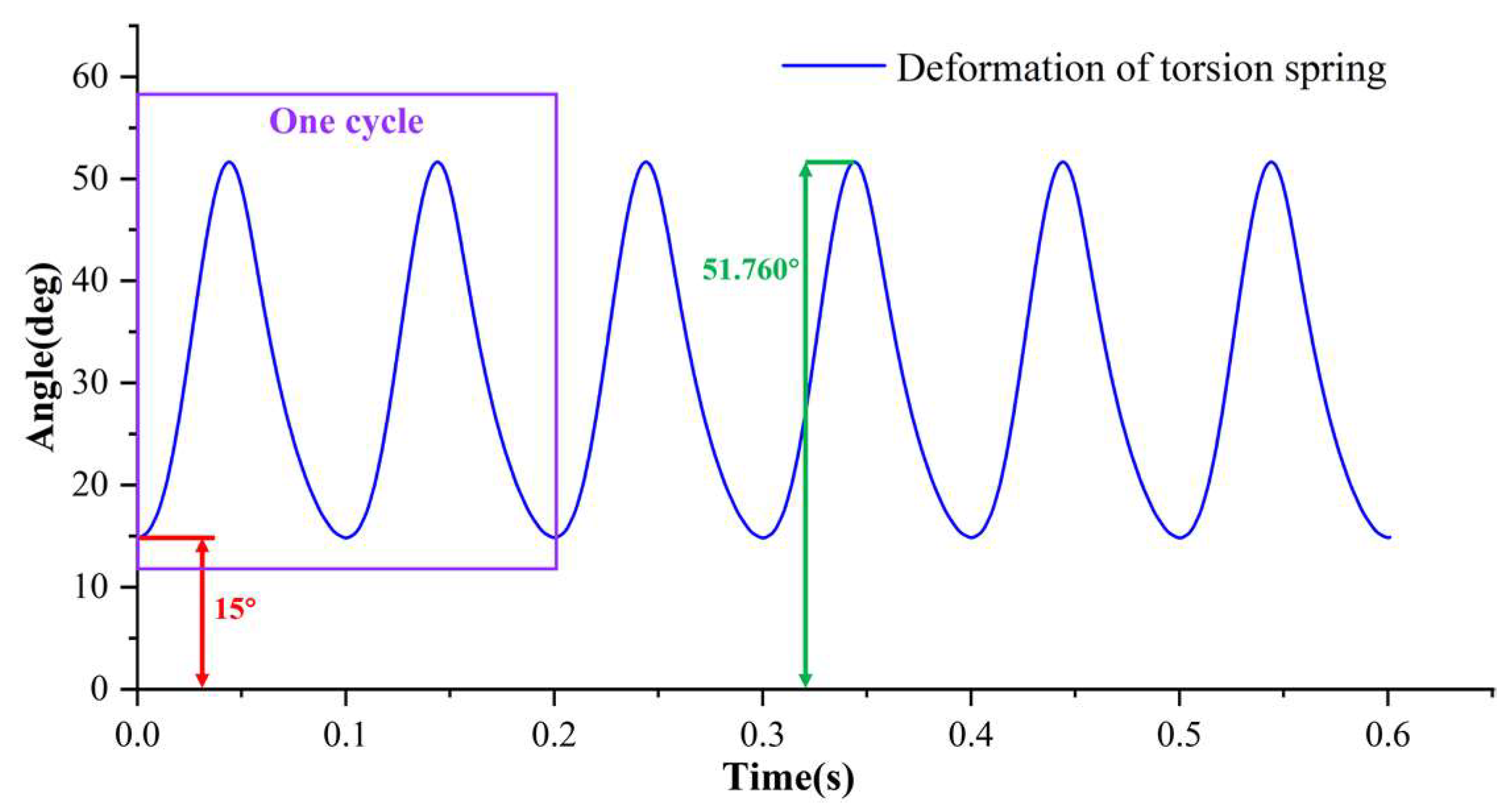
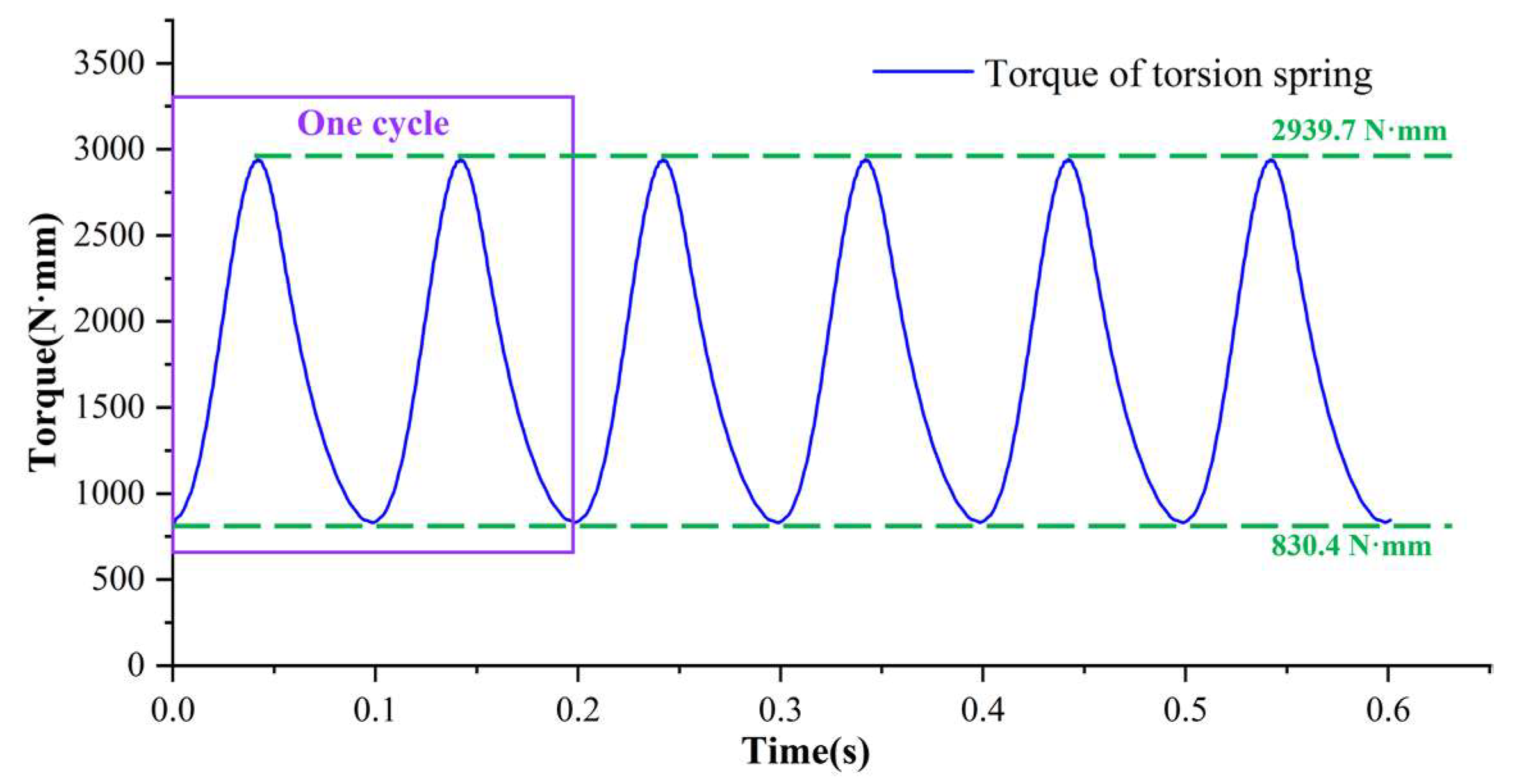
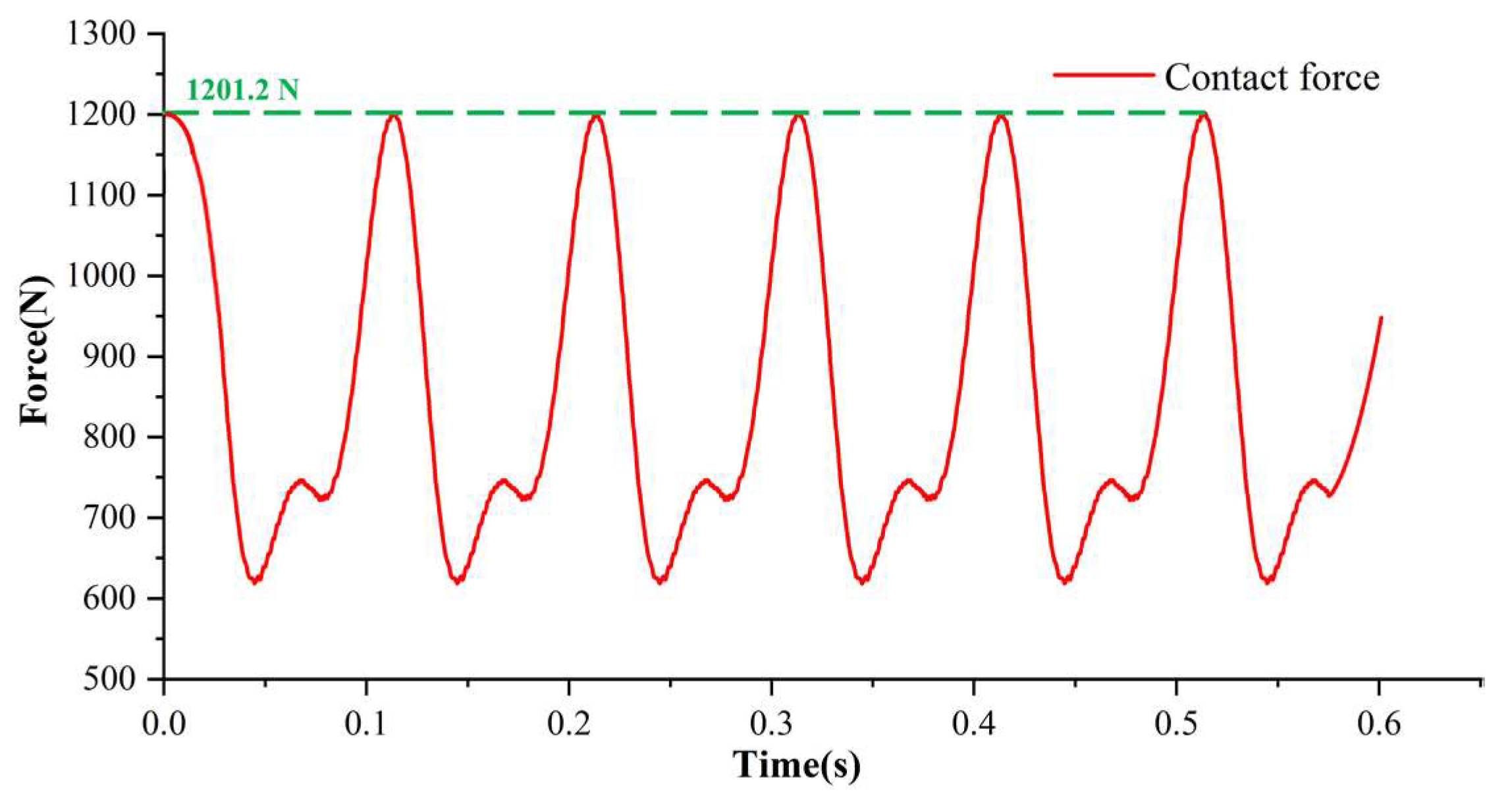
| Parameters | Value |
| Long axis of elliptical line | 228 mm |
| Short axis of elliptical line | 114 mm |
| Length of the PA1 | 95.1804 mm |
| Thickness of swing scraper | 228 mm |
| Thickness of elliptical rotor | 228 mm |
| Diameter of scraper big end section circle | 36 mm |
| Elliptical rotor speed (n) | 300 r/min |
| Torsion spring stiffness | 0.0565 N·m/deg |
| Parameters | Theoretical Calculation Value | Simulation Value |
|---|---|---|
| Maximum angle of scraper (θ) | 36.723° | 36.765° |
| Angle of elliptical rotor (π/2 − φ) | 79.250° | 79.250° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, T.; Zhang, H.; Yang, J.; Cao, Y.; Jiang, Y.; Tian, D. Modeling, Kinematic Characteristics Analysis and Experimental Testing of an Elliptical Rotor Scraper Pump. Machines 2022, 10, 78. https://doi.org/10.3390/machines10020078
Zhang Z, Zhang T, Zhang H, Yang J, Cao Y, Jiang Y, Tian D. Modeling, Kinematic Characteristics Analysis and Experimental Testing of an Elliptical Rotor Scraper Pump. Machines. 2022; 10(2):78. https://doi.org/10.3390/machines10020078
Chicago/Turabian StyleZhang, Zhen, Tiezhu Zhang, Hongxin Zhang, Jian Yang, Yang Cao, Yong Jiang, and Dong Tian. 2022. "Modeling, Kinematic Characteristics Analysis and Experimental Testing of an Elliptical Rotor Scraper Pump" Machines 10, no. 2: 78. https://doi.org/10.3390/machines10020078
APA StyleZhang, Z., Zhang, T., Zhang, H., Yang, J., Cao, Y., Jiang, Y., & Tian, D. (2022). Modeling, Kinematic Characteristics Analysis and Experimental Testing of an Elliptical Rotor Scraper Pump. Machines, 10(2), 78. https://doi.org/10.3390/machines10020078







