Turbine Rotor Dynamics Models Considering Foundation and Stator Effects

Abstract

The paper deals with the modelling of turbine rotors, including a foundation and stator parts, and with their dynamic analysis. The dynamics of turbines can be strongly influenced by the effects of a rotor foundation, and therefore suitable modelling approaches should be developed to obtain proper analysis tools. The standard methods for the modelling of rotating shafts are summarized in the paper, and two approaches to including foundation effects into dynamic models are introduced. The approach based on the dynamic compliance of the foundation with respect to the rotor angular velocity is compared with the approach based on the modal synthesis of rotor and foundation models. The calculation of modal properties is then demonstrated, and the characteristics of both presented methods are discussed. A comparison of the steady-state dynamic response calculated using both methods is shown. It can be concluded that both approaches can be advantageously used for several analyses, and our final recommendations are given in the conclusions.

1. Introduction

Rotor dynamics remain one of the most important mechanical branches of many real industrial problems [1,2]. Although this subject is more than one hundred years old, the development of computational tools in terms of both hardware and numerical methods allows for improving the accuracy and information ability of computational models in rotor dynamics. In particular, the mathematical modelling of turbosets in the case of steam turbines of various power plants is a challenging problem for the sake of growing turbine efficiency and related dynamic problems [3].

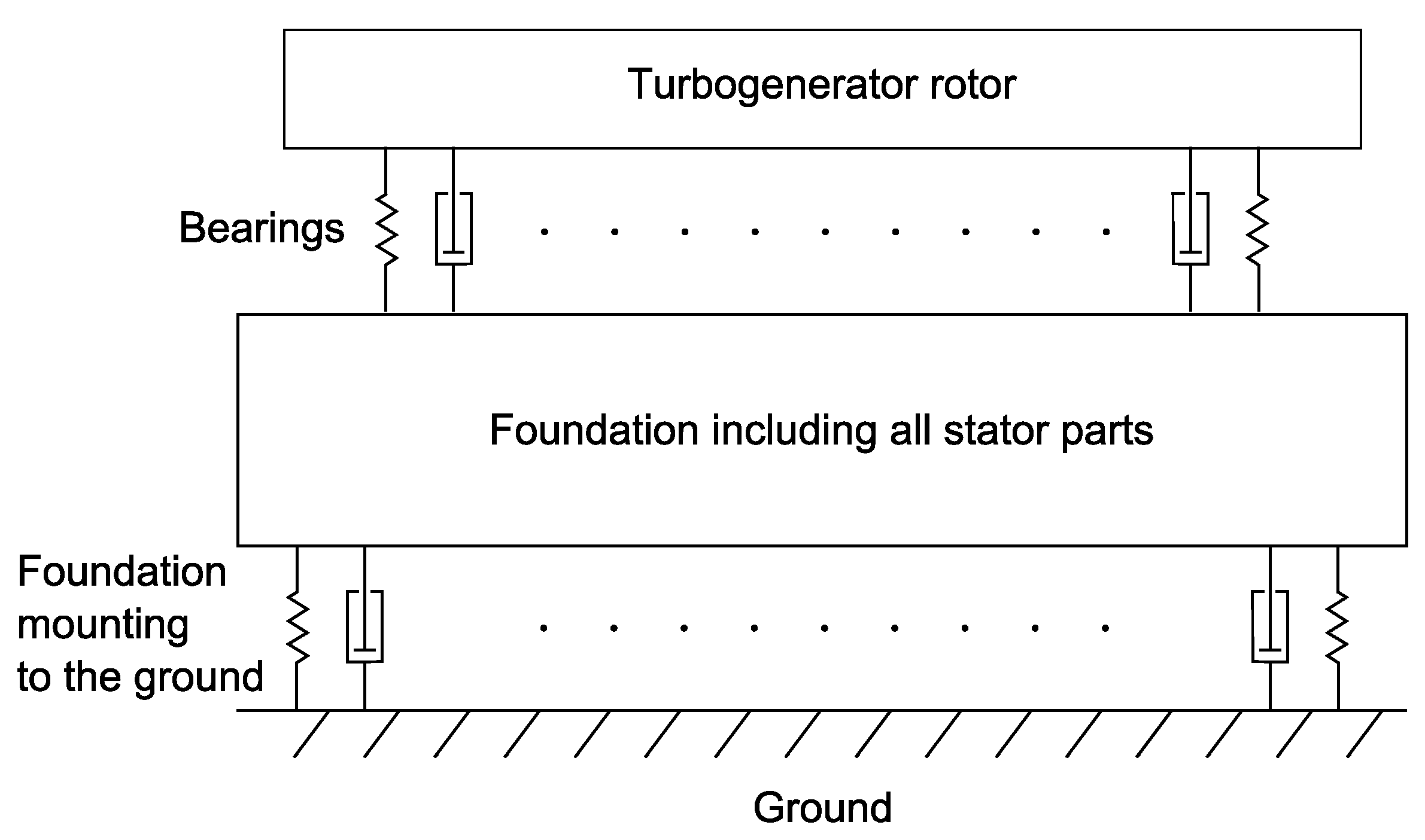
Since rotating systems need to be mounted on the ground using certain special stator parts, a housing or a foundation [4], the method of mounting and the structural design of a foundation can considerably affect the dynamic performance of rotor systems [5]. Therefore, it is important to investigate dynamic characteristics [6] of a foundation, and it is necessary to have suitable tools to create proper mathematical models.

The dynamic effects of a foundation are sometimes neglected in the standard design of rotor systems. Foundation and rotor dynamic analyses are performed nearly independently of each other. However, the mutual interaction of a rotor and a foundation has been investigated by well-known authors. A lumped model of a bearing support was considered in [7], and the whole system stability was analysed. The dynamic stiffness of a foundation is included in the rotor model supported by bearings in [8]. Various design methods of rotor and foundation couplings are summarized in [9]. It was suggested by [10] to consider the foundation effects in models.

Approaches to the incorporation of foundation effects into rotor dynamics have different advantages and drawbacks. A mechanical impedance technique was introduced in [11], where a simple test-rig was used for the experimental validation related to the unbalance response. Dynamical effects of a supporting structure on a rotor were studied in [12] using a frequency response function to find an equivalent support model. The identification of a foundation dynamic stiffness matrix in the case of another simple test-rig is presented in [13].

The authors of [14,15] utilized an identification methodology for the estimation of rotor foundation parameters. More detailed analyses of a modal approach for the supporting structure incorporation in rotor dynamics are discussed in [16,17]. Discussion on the stator properties important for the inclusion in whole models is introduced in [18]. Similarly, a foundation can be described by a state space representation [19], and it can form a complex substructure [20]. A comparison of the substructure method using a transfer function and the creation of the complete dynamic model is shown in [21].

The important issue in the mathematical modelling of complex rotor-foundation systems is model order reduction [22]. A comprehensive explanation of a chosen suitable Krylov-based method to the model order reduction for a system composed of a housing, bearings and a rotor is presented in [23]. The reduced modelling of rotors composed of rotating shafts and disks can be found in [24,25]. Various approaches to the modelling and dynamical analyses of rotors are mentioned in [26,27], while finite element modelling techniques [28] are likely the most common computational tools. Rotor modelling approaches suitable for nonlinear dynamics are summarized in [29].

The work presented in this paper is devoted to the analysis and discussion of the suitability of two fundamental approaches based on dynamic compliance and modal synthesis of turbine foundations. The main and original aim is to compare and to discuss the results of both approaches, which can be used by engineers in industry for a complex example of a real turboset. The novelty of the introduced research is in the detailed description and investigation of used approaches and their application to the real industrial turboset including the result presentation. The original in-house software was created based on the presented methodology.

The paper is structured as follows. The next section deals with the description and summary of the common model for dynamics of rotating shafts with disc suitable for modelling turbine rotors. Two approaches for the consideration of foundation effects in rotor models are introduced in Section 3 and Section 4. The comparison of both approaches and particular results for a real turbine are shown in Section 5.

2. Basic Modelling Procedures of Turboset Rotordynamics

Turbines [30] are generally composed of two main components and their interconnections (see Figure 1). A foundation including all stator parts of a turbine is one large non-rotating component. It can be mounted to the ground by viscous-elastic couplings, whose stiffness and damping properties should be designed to positively influence the overall dynamic behaviour of the whole turbine system.

A rotor train [4] is the second main component of a turbine and can be of different size and complexity depending on the particular type of turbine. The rotor train is coupled to the foundation by bearings, which are fluid-film bearings of different designs in most cases. The interaction between the rotor and stator parts can also be influenced by seals in an operating area.

2.1. Rotor Train

A rotor train of a steam driven turbogenerator consists of several coupled turbine shafts with bladed disks, a generator and other special shafts important for the function of the turbine (e.g., an exciter or various auxiliary engines). The mathematical modelling of such mechanical systems is state-of-the-art of rotor dynamics. Many books [9,26,27,28,29] and journal papers [2] can be found on this topic.

Usually, continuous shafts are discretized using the finite element method into the set of the shaft (rotating beam) finite elements; however, various alternatives, such as [31] or [32] can be used. The shaft element can be formulated on the basis of different theories, while the well-known theories are the so-called Euler–Bernoulli approach and more complex Timoshenko theory [25]. Each element of length l (see Figure 2, rotating with angular frequency ${\omega }_s$) has two nodes with maximally six degrees of freedom in the node depending on the considered motion.

Bending behaviour in two perpendicular planes described by two displacements v, w and two rotations $\vartheta$, $\psi$ is the most important behaviour considered in turbogenerator dynamics. Torsional vibrations described by one torsional rotation $\phi$ in each node can be used mainly in the case of a generator design. The last characteristic is related to the axial motion described by one axial displacement u in each node. The torsional motion and axial motion of the element are approximated using linear polynomials, while the bending behaviour is approximated using cubic polynomials. The generalized coordinate vector for particular node i of the shaft elements is

$${\mathit{q}}_i={\left[u_i{v}_i{w}_i{\phi }_i{\vartheta }_i{\psi }_i\right]}^T,$$

(1)

where the generalized displacements are related to the fixed (non-rotating) coordinate system.

After the derivation of particular matrices of the shaft element, the mathematical model of a stand-alone shaft (rotating at angular velocity $\omega$, without excitation) can be written (e.g., [26]) in the form

$${\mathit{M}}_S{\ddot{\mathit{q}}}_S\left(t\right)+\left({\mathit{B}}_S+\omega {\mathit{G}}_S\right){\dot{\mathit{q}}}_S\left(t\right)+{\mathit{K}}_S{\mathit{q}}_S\left(t\right)=\mathbf{0}$$

(2)

where ${\mathit{M}}_S$ is the shaft mass matrix, ${\mathit{B}}_S$ is the shaft damping matrix, $\omega {\mathit{G}}_S$ represents gyroscopic effects, ${\mathit{K}}_S$ is the shaft stiffness matrix, ${\mathit{q}}_S$ is a vector of shaft generalized coordinates composed of the subvectors ${\mathit{q}}_i$ defined in (1).

2.2. Rotating Rigid Body

Disks, couplings and bladed disks, which can be considered to be rigid bodies with respect to the studied phenomena and considered type of vibration are characterized by mass m and inertia matrix $\mathit{J}$. The components of the inertia matrix are usually simplified using the assumption of symmetry according to the rotation axis and the assumption of the ideal balancing of the body. The spatial motion of the rigid body representing, e.g., bladed disks (see Figure 3, rotating at angular frequency ${\omega }_s$), is described by six coordinates corresponding to the generalized coordinates of shaft nodes

$${\mathit{q}}_D={\left[u_D{v}_D{w}_D{\phi }_D{\vartheta }_D{\psi }_D\right]}^T.$$

(3)

The mathematical model of the rotating body [25,26] consists of mass matrix ${\mathit{M}}_D\in {\mathbb{R}}^{6,6}$ and matrix ${\omega }_s{\mathit{G}}_D\in {\mathbb{R}}^{6,6}$ related to gyroscopic effects. These matrices representing disks and other parts of the rotor train considered rigid bodies can be added to the model (2) of the whole shaft.

2.3. Bearings

Typical interconnections between the rotor and stator parts in turbomachinery rotordynamics are realized using journal bearings, where the elastic and damping properties are strongly influenced by the oil film between a rotor and a stator [33].

For the purpose of motion equations, it is suitable to derive the forces in the oil film [1,34] as

$$\left[\begin{array}{c}{F}_y\\ F_z\end{array}\right]=\left[\begin{array}{cc}{b}_{11}\hfill & b_{12}\hfill \\ b_{21}\hfill & b_{22}\hfill \end{array}\right]\left[\begin{array}{c}\Delta \dot{y}\\ \Delta \dot{z}\end{array}\right]+\left[\begin{array}{cc}{k}_{11}\hfill & k_{12}\hfill \\ k_{21}\hfill & k_{22}\hfill \end{array}\right]\left[\begin{array}{c}\Delta y\\ \Delta z\end{array}\right],$$

(4)

where $\Delta y$ and $\Delta z$ are displacements of a journal centre with respect to a fixed coordinate system (in a plane perpendicular to the rotor axis), $\Delta \dot{y}$ and $\Delta \dot{z}$ are relative velocities of the journal centre. Stiffness and damping coefficients $k_{ij}$ and $b_{ij}$ representing oil-film properties can be calculated using hydrodynamic theory [1,30,33] usually from the Reynolds equation. Each bearing is then characterized by $2\times 2$ matrices of damping ${\mathit{B}}_B^b\left(\omega \right)$ and stiffness ${\mathit{K}}_B^b\left(\omega \right)$ coefficients.

2.4. Model of the Whole Rotor

A mathematical model of the whole rotor (rotating at angular velocity $\omega$, supported by oil-film bearings), which can be composed of several shafts, bladed disks and other wheels, can be written in the form

$${\mathit{M}}_R{\ddot{\mathit{q}}}_R\left(t\right)+\left[{\mathit{B}}_R\left(\omega \right)+\omega {\mathit{G}}_R\right]{\dot{\mathit{q}}}_R\left(t\right)+{\mathit{K}}_R\left(\omega \right){\mathit{q}}_R\left(t\right)={\mathit{f}}_R\left(t\right),$$

(5)

where ${\mathit{M}}_R$ is the rotor mass matrix, ${\mathit{B}}_R$ is the damping matrix, $\omega {\mathit{G}}_R$ represents gyroscopic effects, ${\mathit{K}}_R$ is the stiffness matrix, ${\mathit{f}}_R\left(t\right)$ is the general force excitation vector, and ${\mathit{q}}_R\left(t\right)$ is a vector of generalized coordinates. The continuously distributed mass, damping and stiffness are included in the matrices as well as certain considerations of lumped bodies and frequency-dependant properties of bearings and seals in ${\mathit{B}}_R\left(\omega \right)$ and ${\mathit{K}}_R\left(\omega \right)$.

The damping and stiffness characteristics of bearings are commonly evaluated for the chosen frequencies (rotor angular velocities) and a further (’continuous’) usage of the model is based on a cubic interpolation of the bearing characteristics.

2.5. Model of a Foundation

Since modern computational systems allow the modelling and analysis of very complex and large mechanical systems, models of a foundation are usually created using the finite element method implemented in a certain general-purpose finite element code. Various finite element types can be used in the model; however, the general equation of a foundation motion has the form

$${\mathit{M}}_F{\ddot{\mathit{q}}}_F\left(t\right)+{\mathit{B}}_F{\dot{\mathit{q}}}_F\left(t\right)+{\mathit{K}}_F{\mathit{q}}_F\left(t\right)={\mathit{f}}_F\left(t\right),$$

(6)

where ${\mathit{q}}_F\left(t\right)$ is a vector of foundation (stator) generalized coordinates, ${\mathit{M}}_F$ is the mass matrix, ${\mathit{B}}_F$ is the damping matrix, ${\mathit{K}}_F$ is the stiffness matrix, and ${\mathit{f}}_F\left(t\right)$ is a vector of general excitation forces, which is not commonly important for analysis.

Attention, in connection with the growing complexity of the models, should be paid to a proper consideration of the foundation dynamic effects in turboset models. The description of possible approaches of the consideration of the foundation model (6) in the whole rotor model (5) is the main goal of this paper. Two main methods will be demonstrated in the next sections.

3. Usage of the Dynamic Compliance of a Foundation

The first approach is characterized by the pre-calculation of foundation dynamic compliances for the chosen set of frequencies (with sufficiently small step $\Delta \omega$). It is necessary to create a suitable finite element model (6) of the foundation, including all relevant stator components, and with the complete foundation mounting to the ground.

The dynamic compliances of the foundation are calculated by means of a steady state dynamic response to the single harmonic force with known amplitude $f_0$ in a given principal direction placed in the bearing centre. The mathematical model of this problem has the form

$${\mathit{M}}_F{\ddot{\mathit{q}}}_F\left(t\right)+{\mathit{B}}_F{\dot{\mathit{q}}}_F\left(t\right)+{\mathit{K}}_F{\mathit{q}}_F\left(t\right)={\mathit{f}}_0(t,\omega ),$$

(7)

where the generalized force vector of the given excitation can be written as

$${\mathit{f}}_0(t,\omega )={\mathit{f}}_0{e}^{i\omega t}=\left[\begin{array}{c}0\\ ⋮\\ 0\\ f_0\\ 0\\ ⋮\\ 0\end{array}\right]e^{i\omega t}.$$

(8)

Euler’s number e and imaginary unit i appear in this equation. The position of the nonzero element $f_0$ in vector ${\mathit{f}}_0$ is given by the position of the generalized coordinate, which should be excited. Supposed solution of (7) is

$${\mathit{q}}_F(t,\omega )={\mathit{q}}_F\left(\omega \right)e^{i\omega t}.$$

(9)

After substitution of the supposed solution into (7) and modification, one obtains the final expression for the unknown complex amplitude

$${\mathit{q}}_F\left(\omega \right)={\left[-{\omega }^2{\mathit{M}}_F+i\omega {\mathit{B}}_F+{\mathit{K}}_F\right]}^{-1}{\mathit{f}}_0,$$

(10)

which should be recalculated for every ${\mathit{f}}_0$. Thsi means that, for each radial bearing, it is necessary to perform two calculations (10) for two different vectors ${\mathit{f}}_0$.

Dynamic compliance $d_{yy}^b$ of the foundation for a particular bearing pedestal in the vertical (y) direction can be obtained using the complex amplitude of the bearing centre $q_y^b$ calculated for the excitation in the same point in the same (y) direction (this determines the position of $f_0$ in ${\mathit{f}}_0$)

$$d_{yy}^b\left(\omega \right)=\frac{q_y^b\left(\omega \right)}{f_0},$$

(11)

where $\omega$ is the previously defined excitation frequency. Moreover, cross-compliance $d_{yz}^b$ can be defined for the same excitation in the y-direction as

$$d_{yz}^b\left(\omega \right)=\frac{q_z^b\left(\omega \right)}{f_0},$$

(12)

where $q_z^b$ is the complex amplitude of the bearing centre in the z-direction. Analogously dynamic compliance $d_{zz}^b$ of the foundation for the horizontal (z) direction and the second cross-compliance $d_{zy}^b$ can be obtained using the particular complex amplitudes of the bearing centre calculated for the excitation in the same point in the z-direction

$$d_{zz}^b\left(\omega \right)=\frac{q_z^b\left(\omega \right)}{f_0},d_{zy}^b\left(\omega \right)=\frac{q_y^b\left(\omega \right)}{f_0}.$$

(13)

The repetition of the described approach for all bearing pedestals for the set of angular frequencies ${\omega }_j={\omega }_0,{\omega }_0+\Delta \omega ,{\omega }_0+2\Delta \omega ,\dots$ leads to the set of $2\times 2$ dynamic compliance matrices

$${\mathit{D}}_F^b\left({\omega }_j\right)=\left[\begin{array}{cc}{d}_{yy}^b\left({\omega }_j\right)& d_{yz}^b\left({\omega }_j\right)\\ d_{zy}^b\left({\omega }_j\right)& d_{zz}^b\left({\omega }_j\right)\end{array}\right]\in {\mathbb{C}}^{2,2}.$$

(14)

Damping ${\mathit{B}}_B^b\left(\omega \right)\in {\mathbb{R}}^{2,2}$ and stiffness ${\mathit{K}}_B^b\left(\omega \right)\in {\mathbb{R}}^{2,2}$ matrices introduced in Section 2.3 are known for each bearing of a rotor. The complex dynamic stiffness matrix of a particular bearing, including the influence of the foundation, can be now expressed as

$${\mathit{Z}}^b\left({\omega }_j\right)={\left[{\left({\mathit{K}}_B^b\left({\omega }_j\right)+\mathrm{i}{\omega }_j{\mathit{B}}_B^b\left({\omega }_j\right)\right)}^{-1}+{\mathit{D}}_F^b\left({\omega }_j\right)\right]}^{-1}.$$

(15)

The resulting stiffness and damping matrices, which can be used in model (5) in order to describe the properties of bearings together with the foundation, are

$${\mathit{K}}_{BF}^b\left({\omega }_j\right)=\mathrm{Re}\left\{{\mathit{Z}}^b\left({\omega }_j\right)\right\},{\mathit{B}}_{BF}^b\left({\omega }_j\right)=\frac{\mathrm{Im}\left\{{\mathit{Z}}^b\left({\omega }_j\right)\right\}}{{\omega }_j}.$$

(16)

Thus, the whole dynamic compliance matrix of the foundation can be obtained, and the matrices ${\mathit{B}}_R\left(\omega \right)$ and ${\mathit{K}}_R\left(\omega \right)$ in (5) can be updated by the effects of the foundation including its mounting to the ground. The usage of this methodology will be shown and discussed in the application section. Alternatively, the experimental results [14] can be used for the obtaining of foundation properties.

4. Modal Synthesis of a Foundation

The second approach is based on the consideration of both the rotor train (described by a vector of generalized coordinates ${\mathit{q}}_R$) and the non-rotating foundation part (described by ${\mathit{q}}_F$) in one mathematical model

$$\begin{array}{ll}\hfill \left[\begin{array}{cc}{\mathit{M}}_F& \mathbf{0}\\ \mathbf{0}& {\mathit{M}}_R\end{array}\right]\left[\begin{array}{c}{\ddot{\mathit{q}}}_F\\ {\ddot{\mathit{q}}}_R\end{array}\right]& +\left(\left[\begin{array}{cc}{\mathit{B}}_F+{\mathit{B}}_G\left(\omega \right)& \mathbf{0}\\ \mathbf{0}& {\mathit{B}}_R+\omega {\mathit{G}}_R\end{array}\right]+{\mathit{B}}_B\left(\omega \right)\right)\left[\begin{array}{c}{\dot{\mathit{q}}}_F\\ {\dot{\mathit{q}}}_R\end{array}\right]+\hfill \\ \hfill & +\left(\left[\begin{array}{cc}{\mathit{K}}_F& \mathbf{0}\\ \mathbf{0}& {\mathit{K}}_R\end{array}\right]+{\mathit{K}}_B\left(\omega \right)\right)\left[\begin{array}{c}{\mathit{q}}_F\\ {\mathit{q}}_R\end{array}\right]=\left[\begin{array}{c}{\mathit{f}}_F\\ {\mathit{f}}_R\end{array}\right],\hfill \end{array}$$

(17)

where ${\mathit{M}}_F$ and ${\mathit{M}}_R$ are the mass matrices of the foundation and the rotor, ${\mathit{B}}_F$ and ${\mathit{B}}_R$ are the material damping matrices, ${\mathit{K}}_F$ and ${\mathit{K}}_R$ are the stiffness matrices of the foundation and the rotor, ${\mathit{B}}_G\left(\omega \right)$ is the damping matrix representing viscous-elastic isolators (GERB elements) between the foundation and the ground (generally, the properties of these elements are frequency dependent), $\omega {\mathit{G}}_R$ is the matrix of gyroscopic effects, ${\mathit{B}}_B\left(\omega \right)$ and ${\mathit{K}}_B\left(\omega \right)$ are the damping and stiffness of the bearings (generally dependent on the rotor angular velocity $\omega$) and ${\mathit{f}}_F$ and ${\mathit{f}}_R$ are vectors of possible external excitation. Model (17) can be further improved using suitable modal transformation [25], and the size of the model can be reduced to a reasonable value in order to have an efficient mathematical model of the whole system.

For this purpose, the modal analyses of the foundation and the rotor uncoupled, undamped and non-rotating models of the form

$${\mathit{M}}_F{\ddot{\mathit{q}}}_F\left(t\right)+{\mathit{K}}_F{\mathit{q}}_F\left(t\right)=\mathbf{0}\mathrm{and}{\mathit{M}}_R{\ddot{\mathit{q}}}_R\left(t\right)+{\mathit{K}}_R{\mathit{q}}_R\left(t\right)=\mathbf{0}$$

(18)

can be performed. The results are eigenfrequencies, which can compose diagonal spectral matrices ${\mathsf{\Lambda }}_F$ and ${\mathsf{\Lambda }}_R$, and corresponding eigenvectors (mode shapes), which can compose the modal matrices ${\mathit{V}}_F$ and ${\mathit{V}}_R$. Each subsystem can be represented by the chosen set of eigenvectors and eigenfrequencies ($m_F$ and $m_R$ are the counts of chosen eigenvectors for the foundation and for the rotor model). Then, reduced diagonal spectral matrices and rectangular modal matrices are

$${\mathsf{\Lambda }}_F\in {\mathbb{R}}^{m_F,m_F},{\mathsf{\Lambda }}_R\in {\mathbb{R}}^{m_R,m_R},{\mathit{V}}_F\in {\mathbb{R}}^{n_F,m_F},{\mathit{V}}_R\in {\mathbb{R}}^{n_R,m_R},$$

(19)

where $n_F$ and $n_R$ are the numbers of all eigenvectors of the foundation and the rotor systems.

The transformation between original configuration vector of generalized coordinates $\mathit{q}$ and new vector of modal coordinates $\mathit{x}$ is

$$\mathit{q}=\left[\begin{array}{c}{\mathit{q}}_F\\ {\mathit{q}}_R\end{array}\right]=\left[\begin{array}{cc}{\mathit{V}}_F& \mathbf{0}\\ \mathbf{0}& {\mathit{V}}_R\end{array}\right]\left[\begin{array}{c}{\mathit{x}}_F\\ {\mathit{x}}_R\end{array}\right]=\mathit{V}\mathit{x}.$$

(20)

Using this transformation in the overall model (17), after left multiplication by ${\mathit{V}}^T$ and after consideration of the orthonormal properties of eigenvectors, the final reduced model obtains the form

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\mathit{I}}_F& \mathbf{0}\\ \mathbf{0}& {\mathit{I}}_R\end{array}\right]\left[\begin{array}{c}{\ddot{\mathit{x}}}_F\\ {\ddot{\mathit{x}}}_R\end{array}\right]& +\left(\left[\begin{array}{cc}{\mathit{D}}_F+{\mathit{V}}_F^T{\mathit{B}}_G\left(\omega \right){\mathit{V}}_F& \mathbf{0}\\ \mathbf{0}& {\mathit{D}}_R+{\omega }_0{\mathit{V}}_R^T{\mathit{G}}_R{\mathit{V}}_R\end{array}\right]+{\mathit{V}}^T{\mathit{B}}_B\left(\omega \right)\mathit{V}\right)\left[\begin{array}{c}{\dot{\mathit{x}}}_F\\ {\dot{\mathit{x}}}_R\end{array}\right]+\hfill \\ \hfill & +\left(\left[\begin{array}{cc}{\mathsf{\Lambda }}_F& \mathbf{0}\\ \mathbf{0}& {\mathsf{\Lambda }}_R\end{array}\right]+{\mathit{V}}^T{\mathit{K}}_B\left(\omega \right)\mathit{V}\right)\left[\begin{array}{c}{\mathit{x}}_F\\ {\mathit{x}}_R\end{array}\right]=\left[\begin{array}{c}{\mathit{V}}_F^T{\mathit{f}}_F\\ {\mathit{V}}_R^T{\mathit{f}}_R\end{array}\right],\hfill \end{array}$$

(21)

where ${\mathit{I}}_F$ and ${\mathit{I}}_R$ are unit matrices and ${\mathit{D}}_F$ and ${\mathit{D}}_R$ are diagonal damping matrices composed of damping ratios and eigenfrequencies in the case of weakly damped systems.

Various analyses can be performed using the created model (21), while one of its advantages is a low number of degrees of freedom. The calculated dynamic response in modal coordinates $\mathit{x}$ should be transformed back to the configuration space of generalized coordinates $\mathit{q}$ using transformation (20).

5. Application of the Methodology and Comparison of Different Approaches

This section is aimed at the presentation and discussion of the introduced modelling approaches on the chosen real turbogenerator system including a foundation. The visualization of the rotor train is in Figure 4, and the visualization of the foundation with stator parts (a simplified finite element model) is in Figure 5. The rotor train is composed of several parts—a high pressure section (HP), an intermediate pressure section (MP), two low pressure sections (LP1 and LP2), a generator (G) and an excitor (E).

The rotor supporting system is composed of eleven oil-film bearings with frequency dependent damping and stiffness properties; see Figure 6 for the illustration of damping and stiffness properties. The dynamic characteristics of bearings provided by the bearing producers were used in this model after the necessary post-processing. The foundation was mounted to the ground by GERB isolators (viscous-elastic structural elements).

Three types of dynamical models were created:

(A)

A rotor model with bearings mounted to the rigid ground.

(B)

A rotor model with bearings and the foundation represented using dynamic compliances.

(C)

A whole model composed of the rotor and the foundation using the modal synthesis.

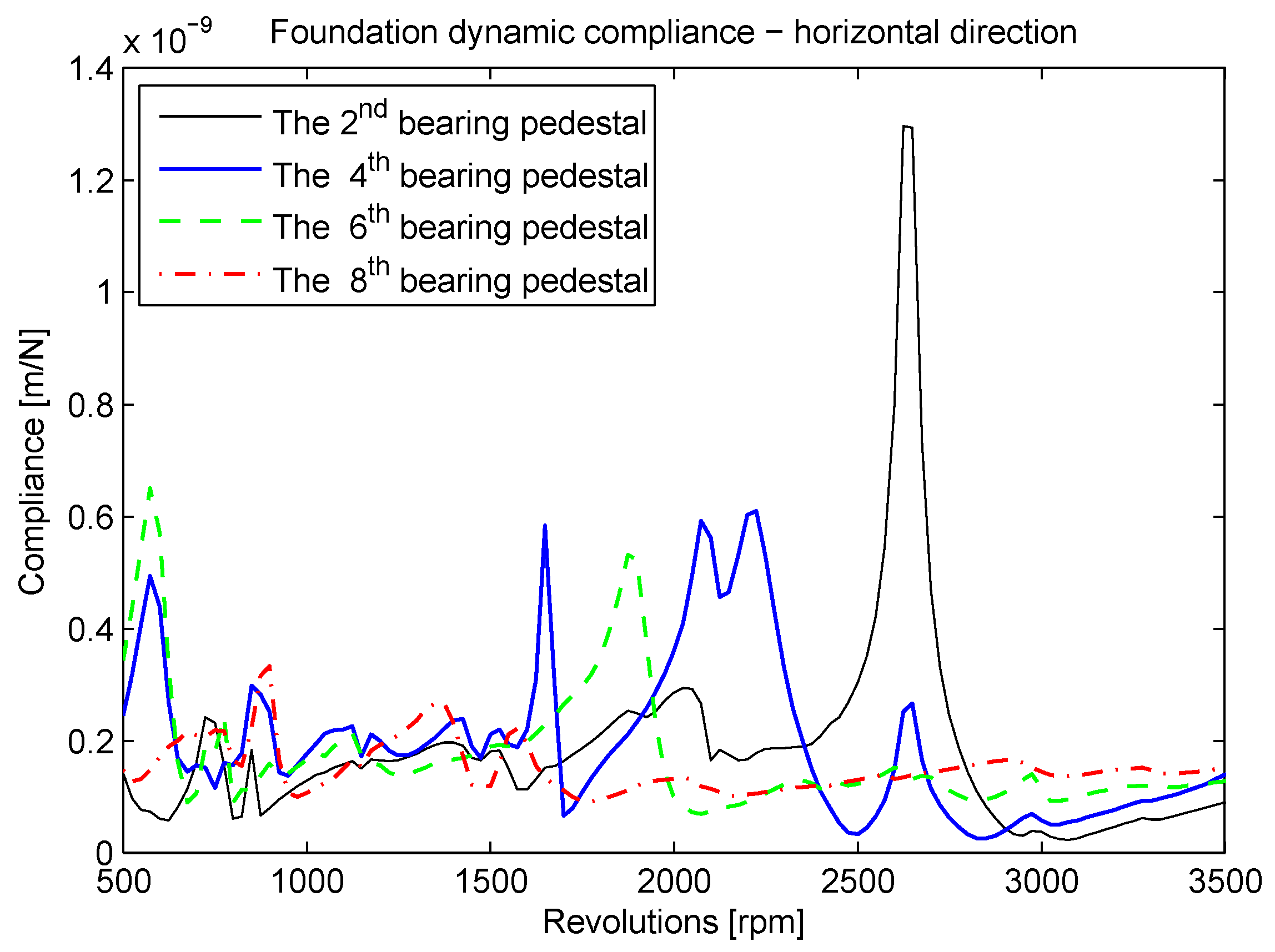
These three cases (models A to C) will be used in the paper. Model A is a standard model without foundation effects according to Equation (5). Model B is based on the same equation but with updated frequency dependent matrices of supporting system concerning expressions (16). Chosen calculated dynamic compliances of the bearing pedestals based on model (7) are shown in Figure 7 and Figure 8. Model C is the most complex reduced model in the form of Equation (21). The number of eigenvectors, which were used for the model creation, was chosen to have a set of mode shapes corresponding to eigenfrequencies with values up to the triple of supposed excitation frequency values (i.e., up to 150 Hz).

The rotor model was created using an in-house computational tool in the MATLAB environment, while the foundation was modelled using the ANSYS software. The characteristics of the bearings were obtained from the bearings producer. All other calculations were performed using the in-house tool in MATLAB.

The created in-house software allows complex combination of rotating and non-rotating subsystems including definition of their various interactions. Moreover, it is possible to define various excitation forces for particular subsystems. Contrary to typical commercial FEM codes (e.g., ANSYS, ABAQUS etc.) the combination of various subsystems is the greatest advantage. It brings more freedom in the definition of the whole model, all operating conditions and setting of numerical simulations. Contrary to dedicated rotor dynamics software, it allows mainly the comprehensive consideration of foundation and stator subsystems.

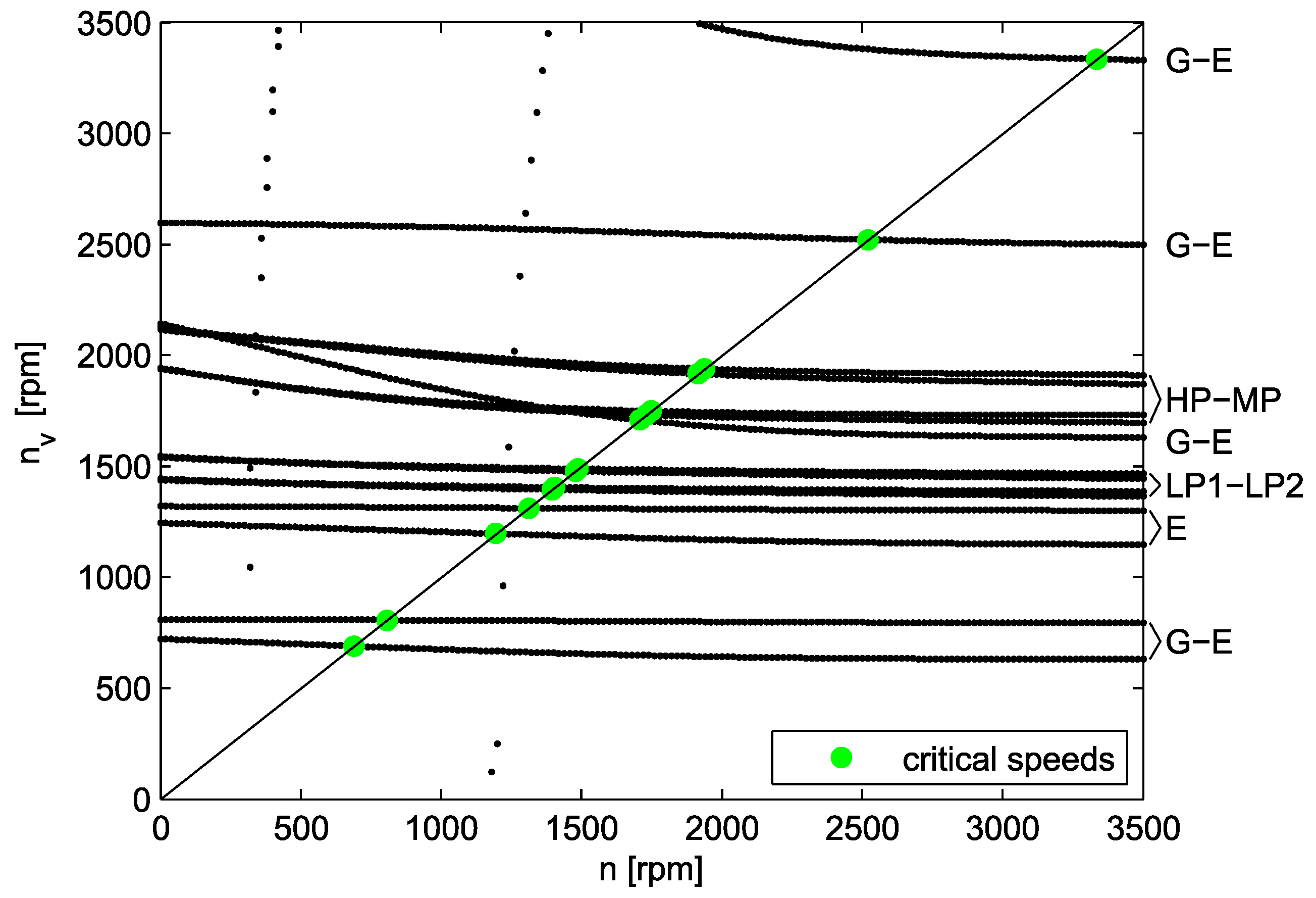
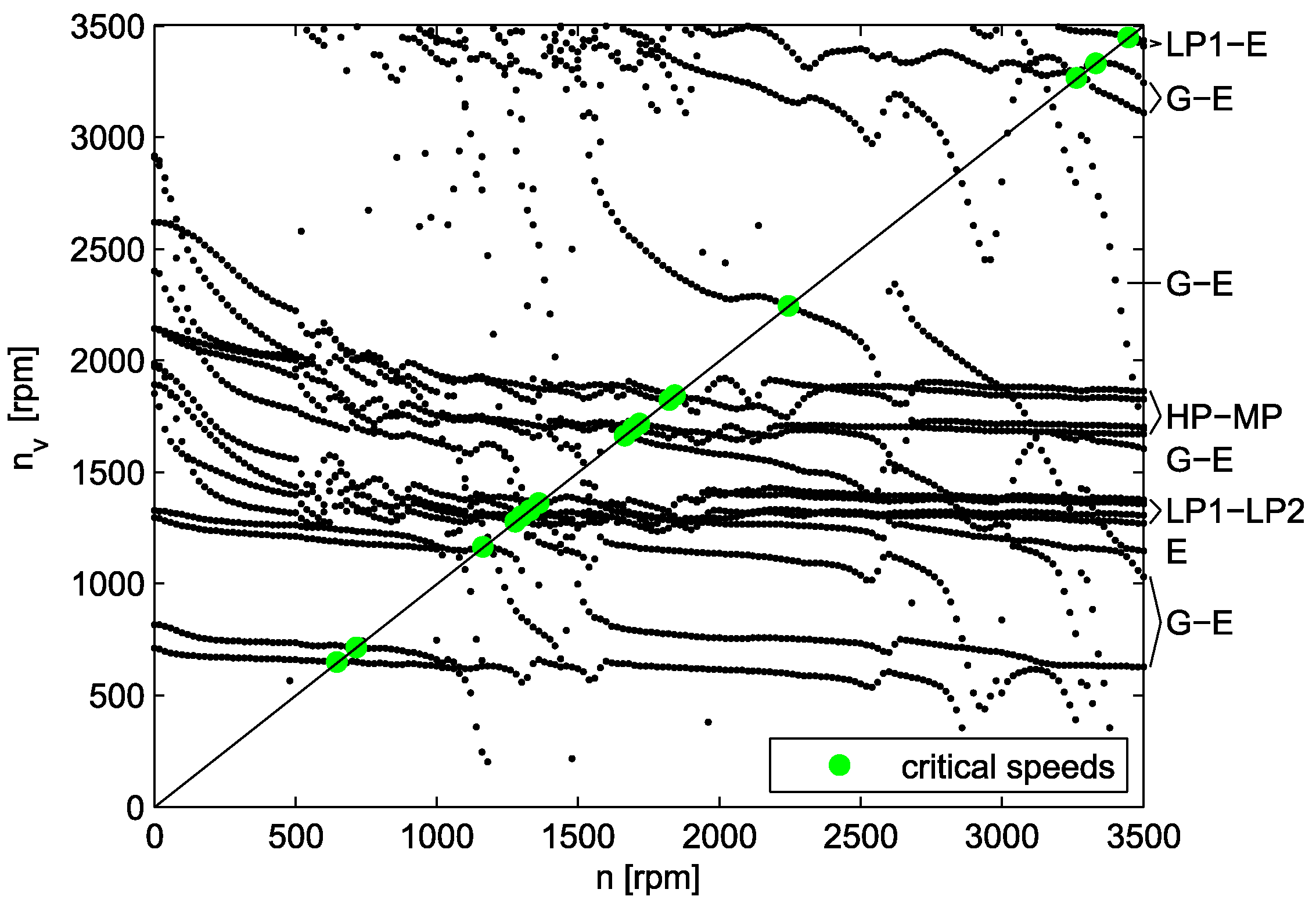
A modal analysis as a basic tool for the evaluation of the proper dynamic design was performed for the models, and the corresponding Campbell diagrams (critical speed maps) were created. The dependancy of particular eigenfrequencies (in revolutions per minute) on the rotor speed (also in revolutions per minute) is demonstrated by the Campbell diagrams. The diagram calculated using model A is shown in Figure 9. The notation on the right border of the picture denotes which parts of the rotor are mainly deformed during a particular mode shape (the eigenvector corresponding to the particular eigenfrequency). The course of eigenfrequencies is relatively smooth for the range of rotor revolutions. It is influenced mainly by the characteristics of the oil-film bearing and by the bending behaviour of the rotor.

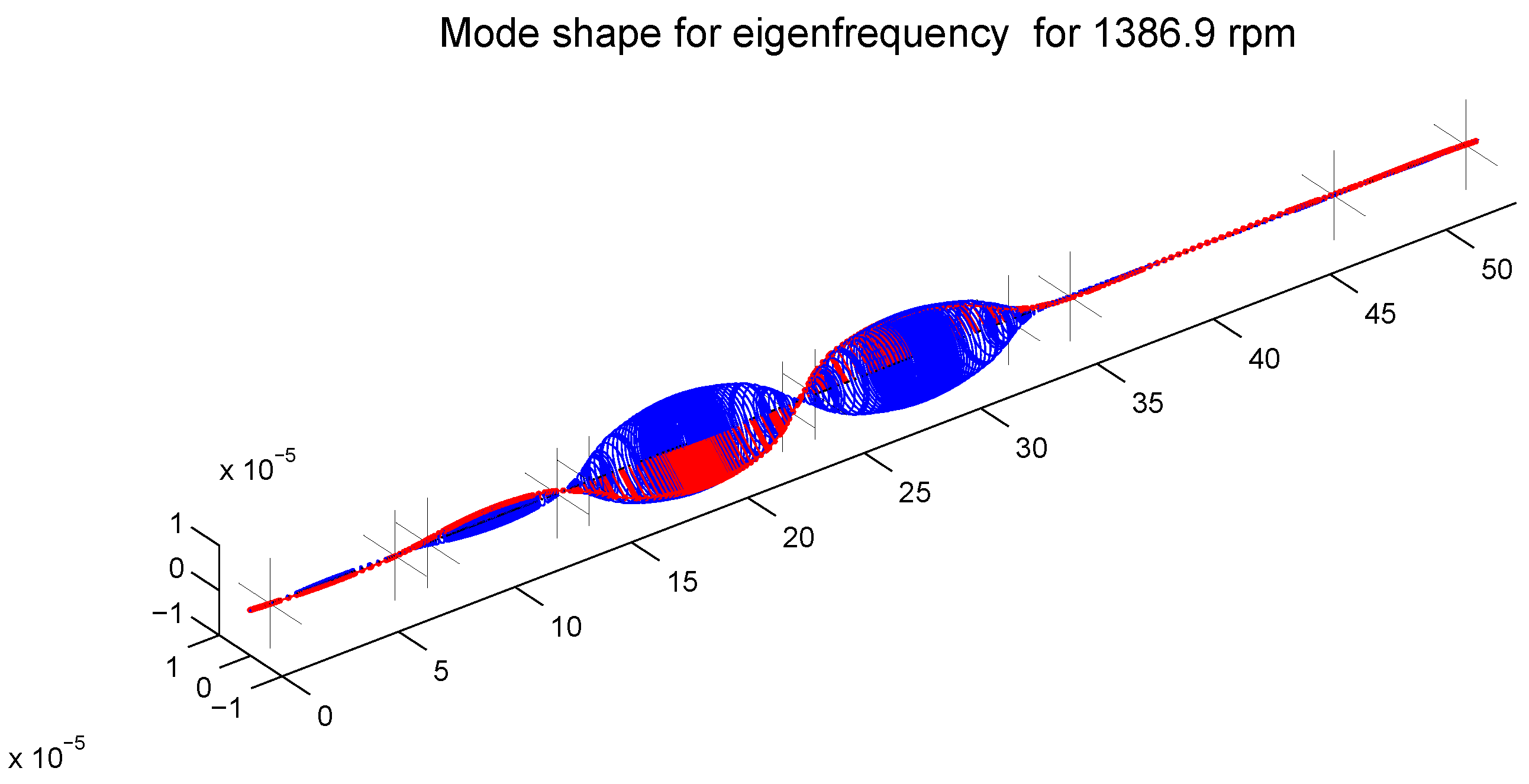
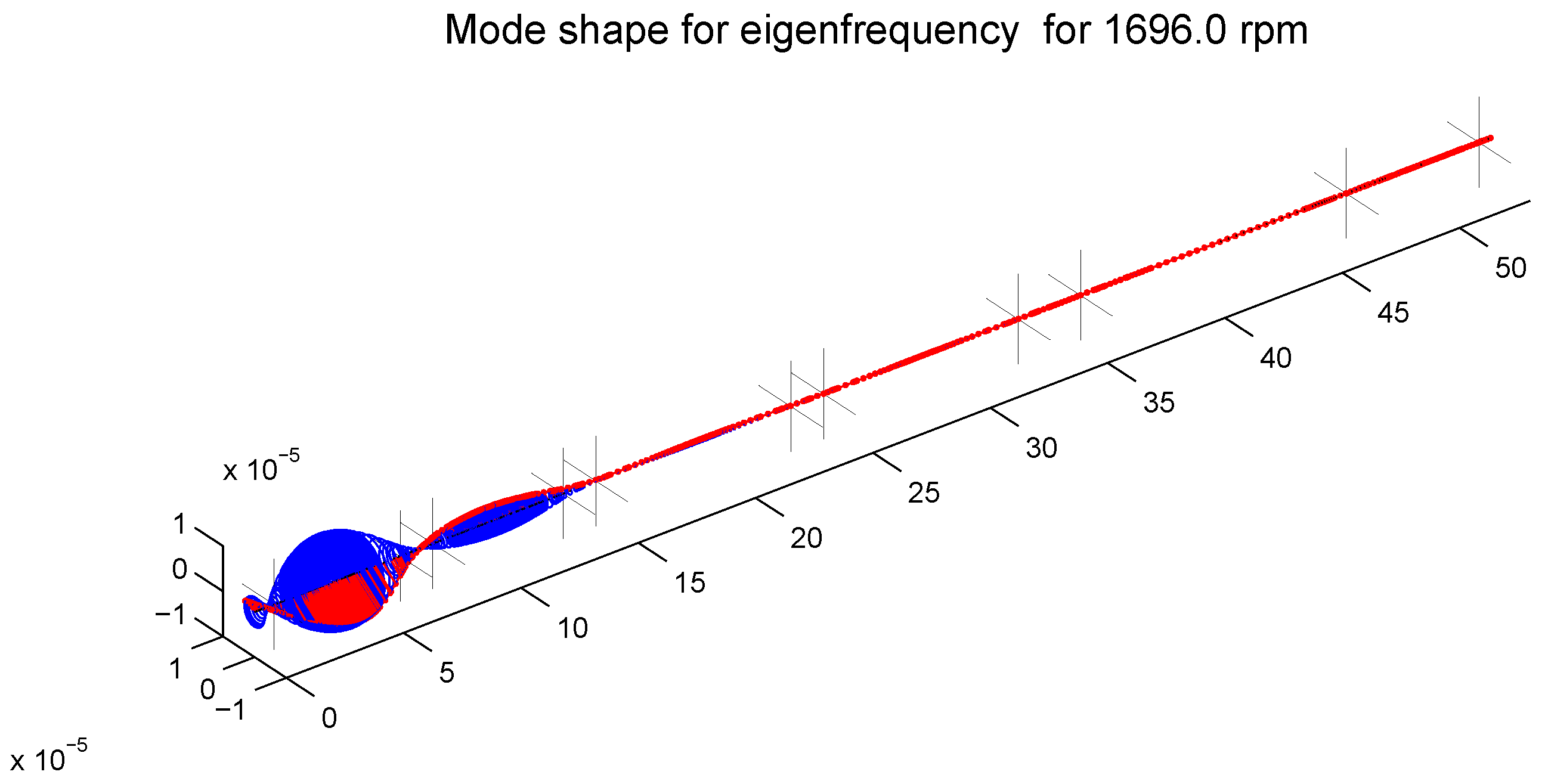
The chosen eigenmodes are shown in Figure 10, Figure 11 and Figure 12. The mode shape characterized by the dominant vibration of the generator and the exciter is depicted in Figure 10. The mode shape with the dominant vibration of the low pressure rotor sections is in Figure 11, and the mode shape with the dominant vibration of the high and intermediate pressure rotor sections is in Figure 12.

On the other hand, Figure 13 represents the Campbell diagram calculated using model B, and it is evident that the added foundation characteristics influence the behaviour of the rotor-bearing system. The Campbell diagram calculated using model C is shown in Figure 14, and it is clear that it is not directly usable due to the presence of many mode shapes related to the combined rotor and foundation vibration. Mode shape tracking [35] can be used for the selection of relevant modes; however, the test calculations show that its contribution is negligible.

Another important task in dynamics of large turbosets is the analysis of a steady state response to rotor unbalance [36]. Clearly, every real rotor has a certain amount of residual unbalance, which should be under the given limit, but it is still the important source of excitation. Therefore, the presented types of turboset models can be used in the analysis of the steady state response to the rotor unbalance.

The calculation of the dynamic response using model A (only bearing damping and stiffness is considered) is based on Equation (5) where the right-hand side vector ${\mathit{f}}_R\left(t\right)={\mathit{f}}_u(\omega ,t)$ is defined as

$${\mathit{f}}_u(\omega ,t)={\mathit{f}}_u\left(\omega \right)e^{i\omega t}$$

(22)

with the complex vector ${\mathit{f}}_u\left(\omega \right)$ composed of the chosen unbalances put in shaft nodes. Particularly, five different combinations of unbalances were selected on the basis of an identification procedure from the measured results of standalone rotor parts. Four combinations of static and dynamic unbalances defined on the high pressure section (HP), the middle (intermediate) pressure section (MP), the first low pressure section (LP1) and the second low pressure section (LP2). One overall combination was given by all unbalances on particular rotor parts. The resulting complex amplitudes of the steady state dynamic response of model A to the given excitation by the chosen unbalance are then

$${\mathit{q}}_A\left(\omega \right)={\left[-{\omega }^2{\mathit{M}}_R+i\omega \left({\mathit{B}}_R\left(\omega \right)+\omega {\mathit{G}}_R\right)+{\mathit{K}}_R\left(\omega \right)\right]}^{-1}{\mathit{f}}_u\left(\omega \right).$$

(23)

The calculation of the corresponding complex amplitudes ${\mathit{q}}_B\left(\omega \right)$ for the model of type B (characteristics of bearings combined with the dynamic properties of the foundation) is analogous to the model of type A with improved damping and stiffness matrices according to (16).

To calculate complex amplitudes ${\mathit{q}}_C\left(\omega \right)$ of model C, it is suitable to rewrite Equation (21) formally into

$$\mathit{M}\ddot{\mathit{x}}\left(t\right)+\mathit{B}\left(\omega \right)\dot{\mathit{x}}\left(t\right)+\mathit{K}\left(\omega \right)\mathit{x}\left(t\right)={\mathit{V}}^T\mathit{f}(\omega ,t),$$

(24)

where

$$\mathit{M}=\left[\begin{array}{cc}{\mathit{I}}_F& \mathbf{0}\\ \mathbf{0}& {\mathit{I}}_R\end{array}\right],$$

$$\mathit{B}\left(\omega \right)=\left[\begin{array}{cc}{\mathit{D}}_F+{\mathit{V}}_F^T{\mathit{B}}_G\left(\omega \right){\mathit{V}}_F& \mathbf{0}\\ \mathbf{0}& {\mathit{D}}_R+\omega {\mathit{V}}_R^T{\mathit{G}}_R{\mathit{V}}_R\end{array}\right]+{\mathit{V}}^T{\mathit{B}}_B\left(\omega \right)\mathit{V},$$

$$\mathit{K}\left(\omega \right)=\left[\begin{array}{cc}{\mathsf{\Lambda }}_F& \mathbf{0}\\ \mathbf{0}& {\mathsf{\Lambda }}_R\end{array}\right]+{\mathit{V}}^T{\mathit{K}}_B\left(\omega \right)\mathit{V},$$

$${\mathit{V}}^T\mathit{f}(\omega ,t)=\left[\begin{array}{c}\mathbf{0}\\ {\mathit{V}}_R^T{\mathit{f}}_u(\omega ,t)\end{array}\right].$$

The supposed solution of (24) with respect to the form of the right-hand side vector can be written as

$$\mathit{x}\left(t\right)=\mathit{x}\left(\omega \right)e^{i\omega t}$$

(25)

and the complex amplitude vector of the steady state response in terms of the reduced model is

$$\mathit{x}\left(\omega \right)={\left[-{\omega }^2\mathit{M}+i\omega \mathit{B}\left(\omega \right)+\mathit{K}\left(\omega \right)\right]}^{-1}{\mathit{V}}^T\mathit{f}\left(\omega \right).$$

(26)

Finally, the complex amplitudes in the original configuration space of generalized coordinates of the whole model C can be obtained by transformation

$${\mathit{q}}_C\left(\omega \right)=\mathit{V}\mathit{x}\left(\omega \right).$$

(27)

It should be noted that vector ${\mathit{q}}_C\left(\omega \right)$ also contains information about the vibration of the foundation.

The selected results are shown in Figure 15, Figure 16 and Figure 17. Each figure contains three plots for the results obtained by the three introduced models (types A, B and C). The plots represent the absolute values of steady state amplitudes of rotor transverse vibration (in all finite element nodes along the rotor length) with respect to the variable excitation frequency (i.e., rotor speed in revolutions per minute).

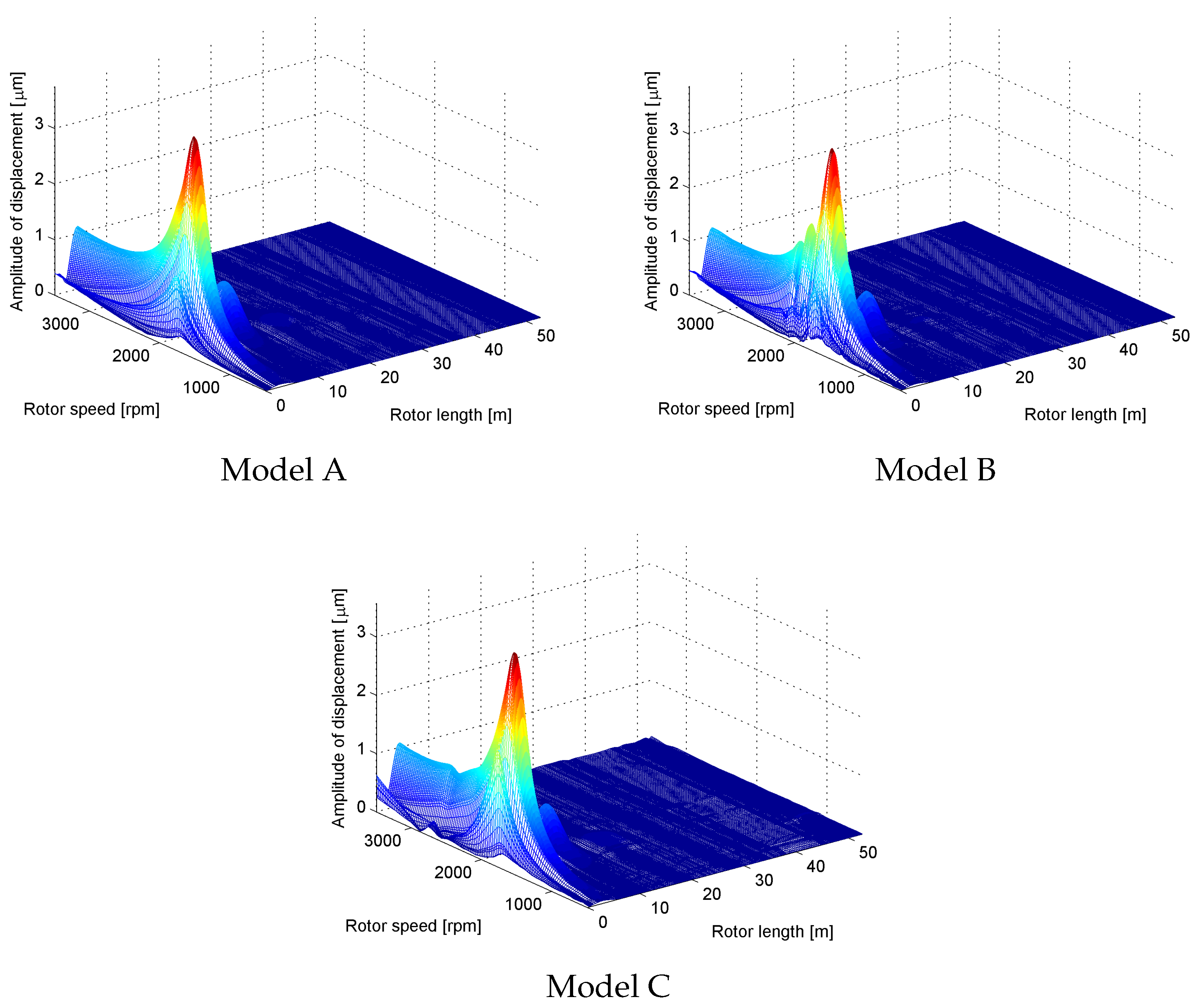
The rotor steady state response to the excitation by the unbalance on the high pressure rotor section can be seen in Figure 15. The resonant peak is related to the first bending mode of the high pressure section (compared with the mode shape in Figure 12 and with the Campbell diagrams in Figure 9 and Figure 13). We concluded that the course of amplitudes for model A was the smoothest, which corresponds to the simplest dynamical model. Concerning the amplitude values, all three model types are comparable.

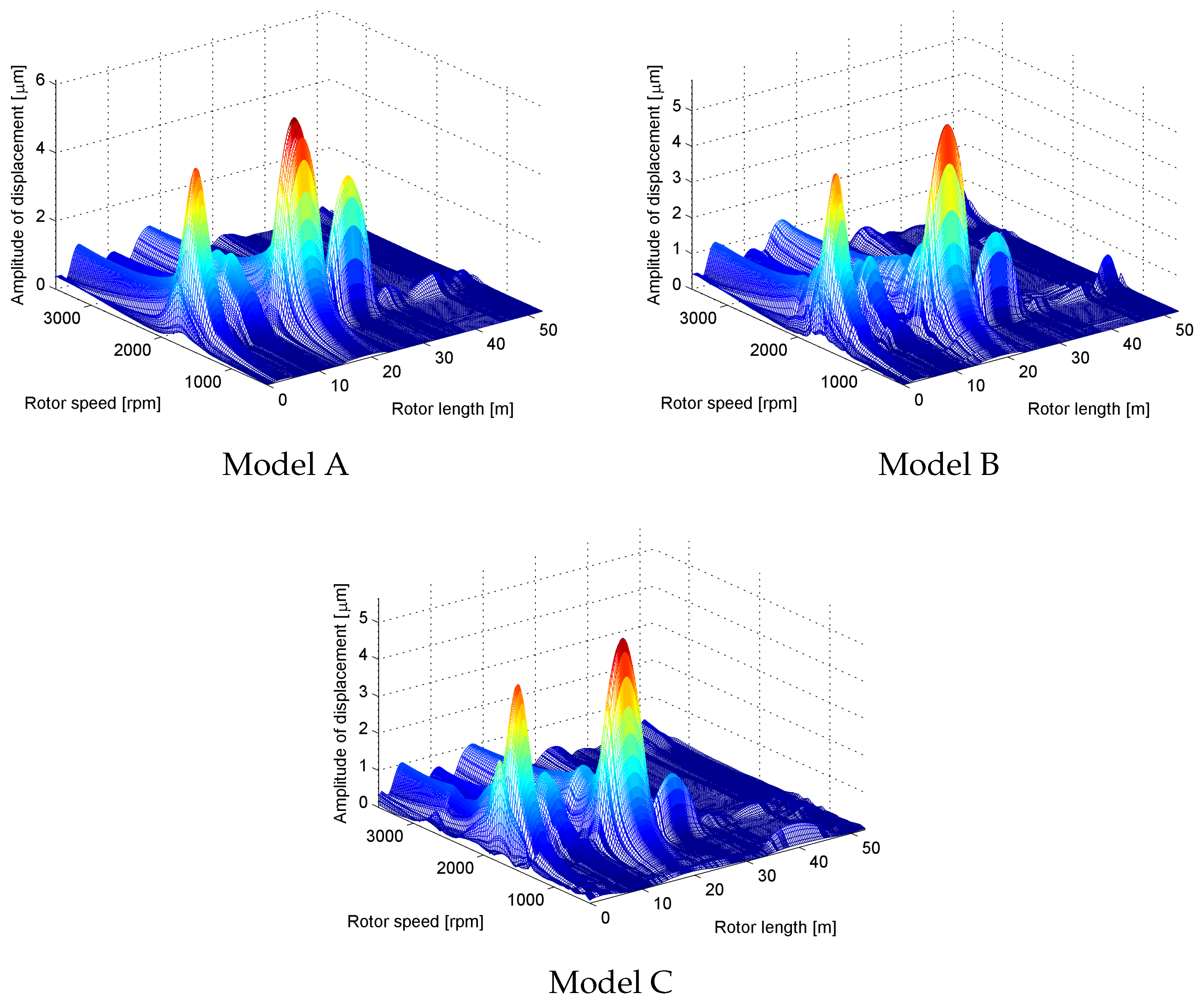
An analogous comparison can be seen in Figure 16, where the rotor steady state response to the excitation by the unbalance on the first low pressure rotor section is shown. The peaks correspond to the first bending mode with the dominant deformation of the low pressure rotor sections (compared with the mode shape in Figure 11 and with the Campbell diagrams in Figure 9 and Figure 13).

The plots of the steady state vibration of the rotor excited by the unbalance of all rotor turbine sections (HP to LP2) are shown in Figure 17.

6. Conclusions

The rotordynamics of large turbosets is a topic that still has importance mainly related to the production of new, highly effective power plants. This paper was aimed at the problem of the foundation incorporation into the model usable in rotor dynamics and general vibration analyses of the whole system. We presented a comprehensive and concise description of possible ways for the combination of rotating and non-rotating subsystems into one computationally efficient mathematical model.

Three different modelling approaches were introduced. The rotor model of type A is the model with bearings mounted to the rigid ground. The rotor model of type B is the model with bearings and the foundation represented using dynamic compliances. The whole model of type C is composed of the rotor and the foundation using the modal synthesis. The results of the modal analyses and the results of the steady state vibration analyses with respect to unbalance were shown and discussed.

The investigation presented in this paper allows evaluation of the usability of the introduced models for the real rotor dynamics applications. The model type A is advantageous mainly for very fast calculations and the first estimations of the rotor behaviour. The models of types B and C are usable for the more realistic calculations.

Models A and B can be used for the Campbell diagram evaluation rather than model C. It can be concluded based on the third modelling approach, that model C is very efficient in the case of possible excitation defined on the stator or foundation, e.g., when another unbalanced rotor is mounted near the turbine or during a seismic excitation [37,38]. This can be used for investigations of rotor-stator rubbing problems [39]. Model C is also suitable for the original evaluation of the foundation vibration together with a turbine for both shaker tests or tests related to stator vibration measurement caused by the excitation on the turbine rotor.