Multi-Sensor Data Driven with PARAFAC-IPSO-PNN for Identification of Mechanical Nonstationary Multi-Fault Mode
Abstract
:1. Introduction
2. PARAFAC for Multi-Dimensional Data Analysis
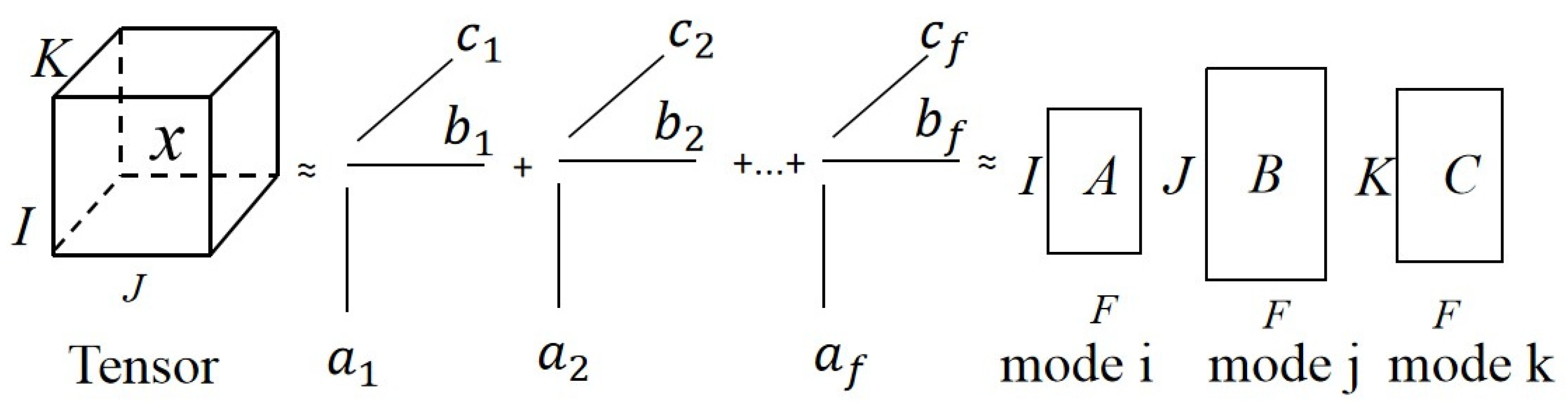
2.1. Principle of PARAFAC
- (1)
- Multi-dimensional analysis of time–frequency signal;
- (2)
- Set the values of component f;
- (3)
- Set the initial loading for two-dimensional arrays and ;
- (4)
- Estimate matrix with the least mean square. The formula is , ;
- (5)
- Calculate B and C;
- (6)
- Return to step (4) and repeat the continuous calculation until convergence is achieved.
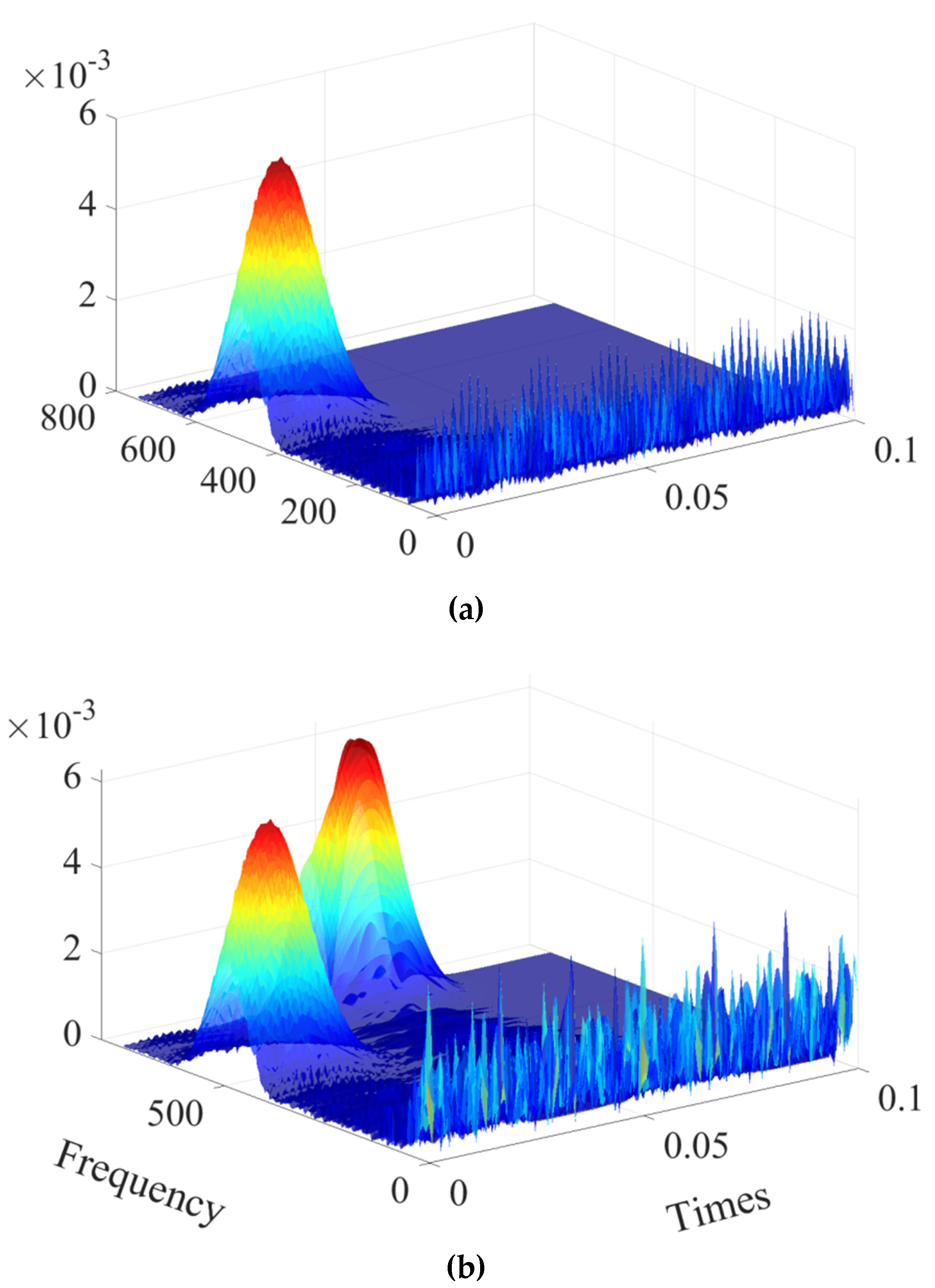
2.2. Algorithm Testing by Numerical Simulation
3. PNN Parameter Optimization with IPSO
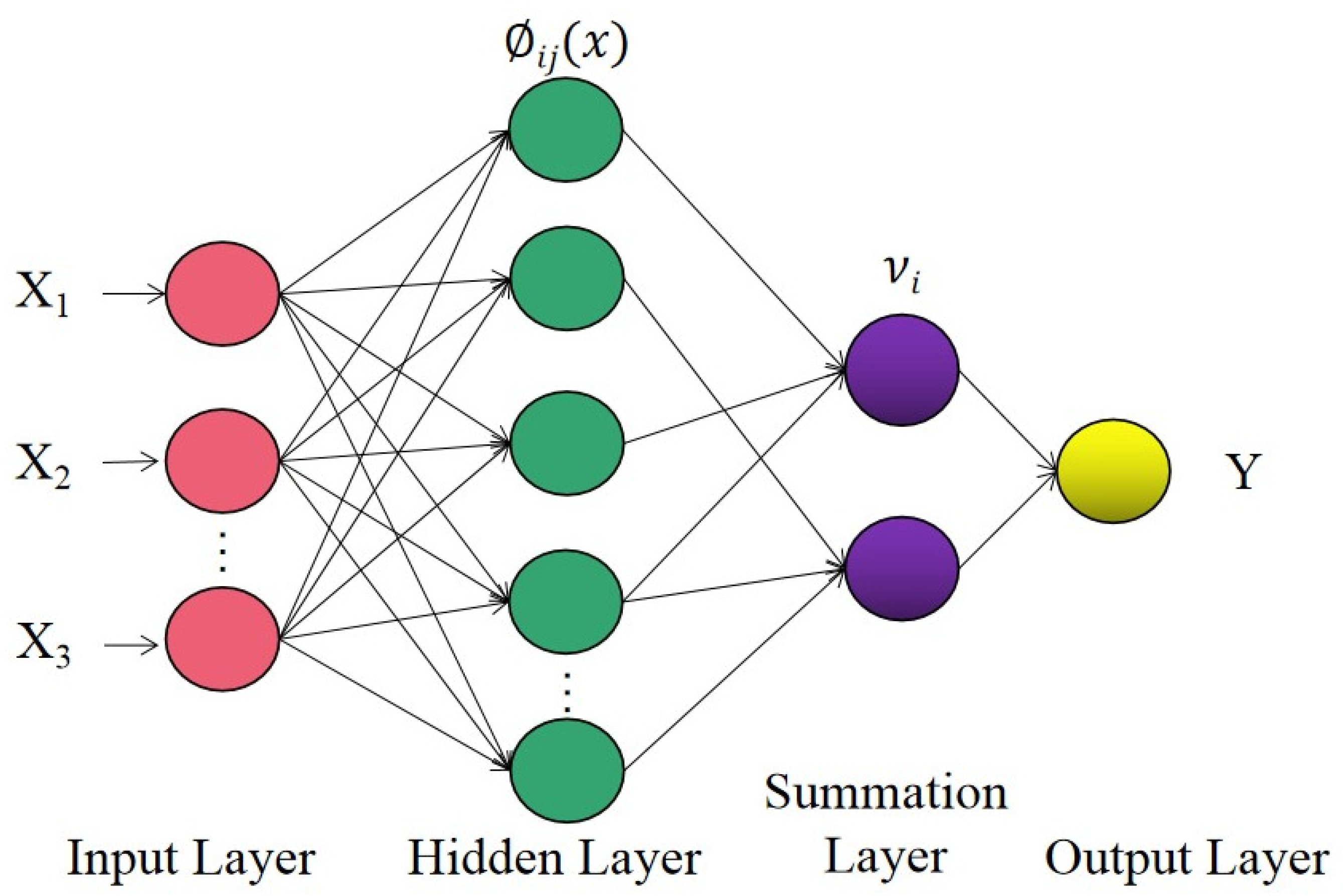
3.1. Principle of PNN
3.2. Improving the Particle Swarm Optimization Algorithm
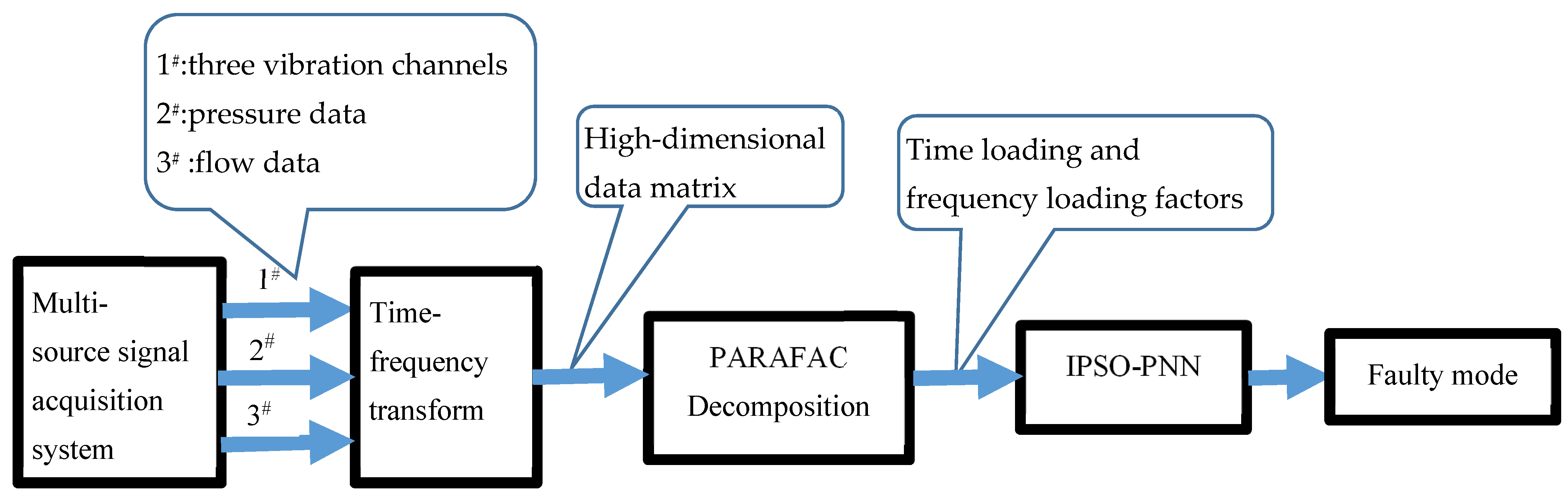
4. Experimental System
5. PARAFAC-IPSO-PNN for Multi-Dimensional Data Analysis
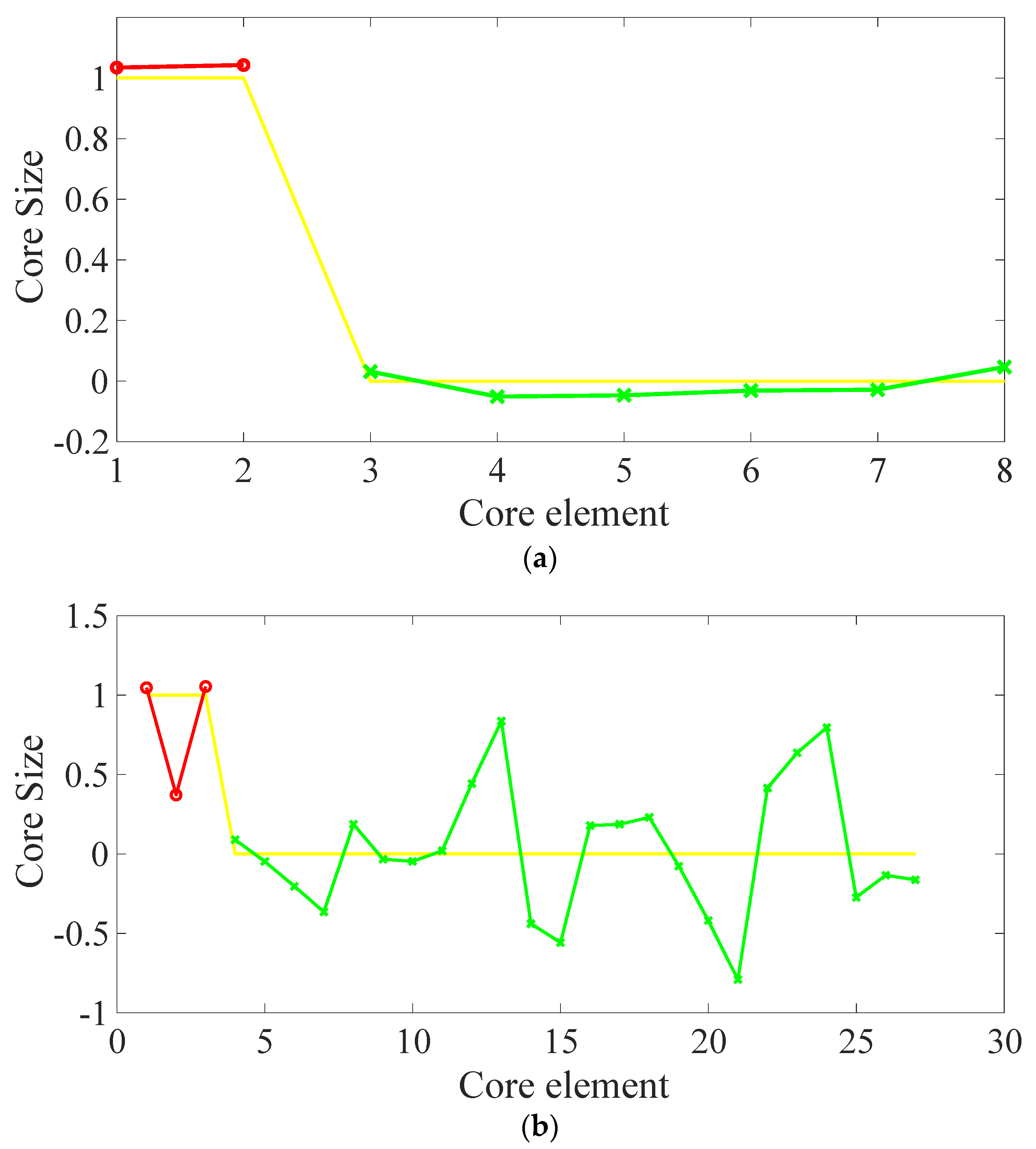
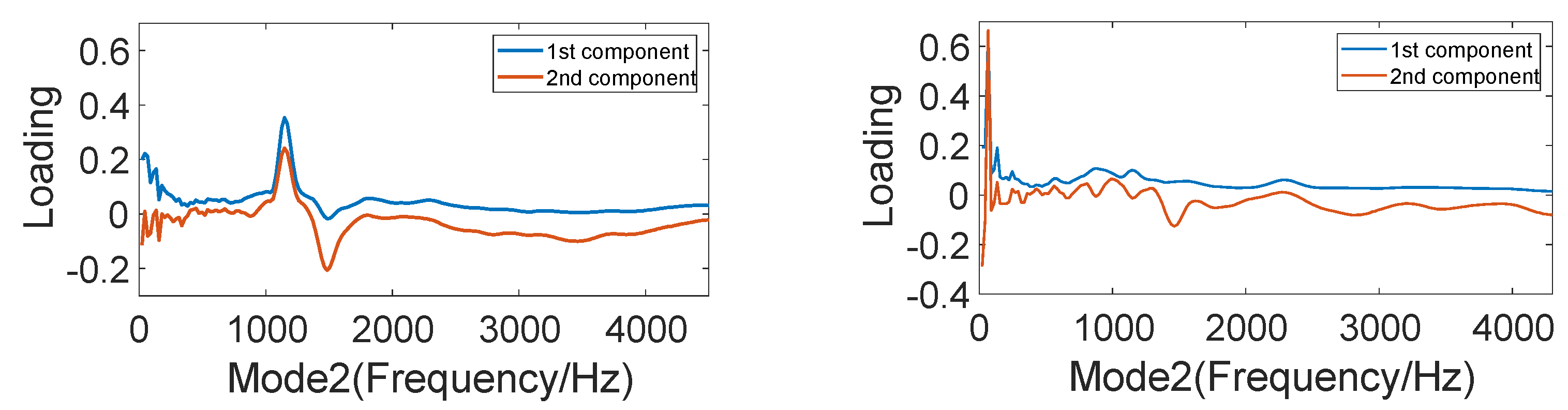
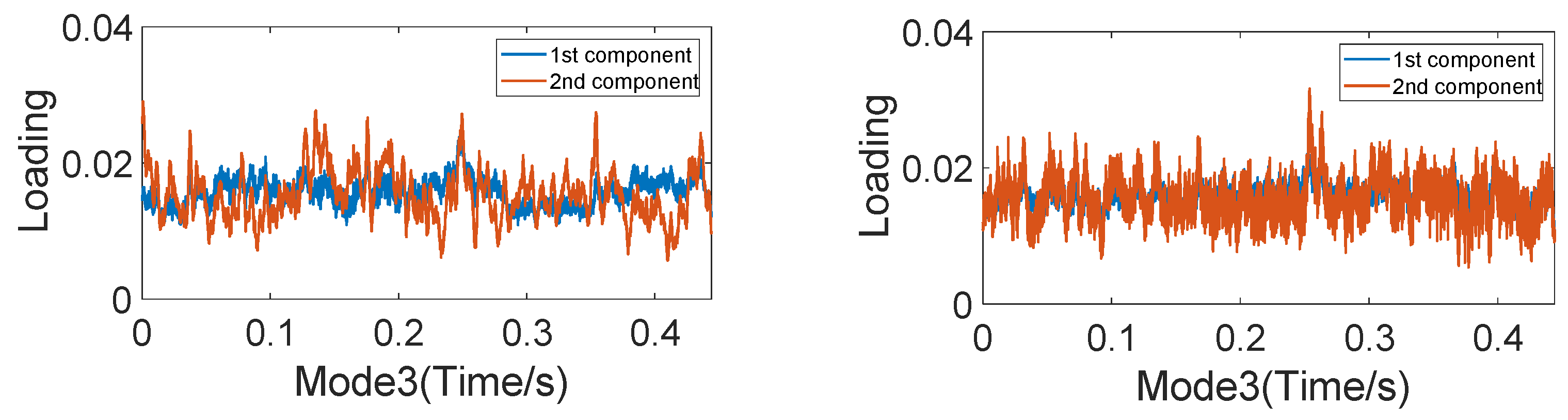
5.1. PARAFAC for Data Decomposition
5.2. IPSO-PNN for Classification
5.3. Multiple-Source Data Analysis for Classification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K. Hierarchical discriminating sparse coding for weak fault feature extraction of rolling bearings. Reliab. Eng. Syst. Saf. 2019, 184, 41–54. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Z.J. Advances in applications of hybrid intelligent fault diagnosis and prognosis technique. J. Vib. Shock. 2011, 30, 129–135. [Google Scholar]
- Shao, H.; Cheng, J.; Jiang, H.; Yang, Y.; Wu, Z. Enhanced deqgated recurrent unit and complex wavelet packet energy momententropy for early fault prognosis of bearing. Knowl.-Bascd Syst. 2020, 188, 105022. [Google Scholar]
- Yang, L.; Chen, H.; Ke, Y.; Li, M.; Huang, L.; Miao, Y. Multi-source and multi-fault condition monitoring based on parallel factor analysis and sequential probability ratio test. EURASIP J. Adv. Signal Process. 2021, 2021, 1–33. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, Y. Development of Mechanical Equipment Fault Diagnosis System Based on Big Data Technology. J. Phys. Conf. Ser. 2020, 1648, 4. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.; Li, K.; Si, C.; Li, L. Survey on Advanced Equipment Fault Diagnosis and Warning Based on Big Data Technique. J. Phys. Conf. Ser. 2020, 1549, 4–5. [Google Scholar] [CrossRef]
- Chen, H.; Shang, Y.; Sun, K. Multiple fault condition recognition of gearbox with sequential hypothesis test. Mech. Syst. Signal Process. 2013, 40, 469–482. [Google Scholar] [CrossRef]
- Yang, L.; Chen, H.; Ke, Y.; Huang, L.; Wang, Q.; Miao, Y.; Zeng, L. A novel time–frequency–space method with parallel factor theory for big data analysis in condition monitoring of complex system. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420916948. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Fan, D.; Huang, J.; Huang, W.; Zhang, G.; Huang, L. Finite element analysis model on ultrasonic phased array technique for material defect time of flight diffraction detection. Sci. Adv. Mater. 2020, 12, 665–675. [Google Scholar] [CrossRef]
- Yang, Z.; Chai, Y. A survey of fault diagnosis for onshore grid-connected converter in wind energy conversion systems. Renew. Sustain. Energy Rev. 2016, 66, 345–359. [Google Scholar] [CrossRef]
- Chen, H.; Fan, D.L.; Fang, L.; Huang, W.; Huang, J.; Cao, C.; Yang, L.; He, Y.; Zeng, L. Particle Swarm Optimization Algorithm with Mutation Operator for Particle Filter Noise Reduction in Mechanical Fault diagnosis. Int. J. Pattern Recognit. Artif. Intell. 2019, 34, 2058012. [Google Scholar] [CrossRef]
- Azamfar, M.; Singh, J.; Bravo-Imaz, I.; Lee, J. Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis. Mech. Syst. Signal Process. 2020, 144, 106861. [Google Scholar] [CrossRef]
- Zhao, P. Research on Vibration Fault Diagnosis Method and System Implementation of Centrifugal Pump. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2011. [Google Scholar]
- Tong, Z.M.; Xin, J.G.; Tong, S.G.; Yang, Z.Q.; Zhao, J.Y.; Mao, J.H. Internal flow structure fault detection, and performance optimization of centrifugal pumps. Appl. Phys. Eng. 2020, 21, 85–117. [Google Scholar] [CrossRef]
- Chen, H.; Miao, Y.; Chen, Y.; Fang, L.; Zeng, L.; Shi, J. Intelligent Model-based Integrity Assessment of Nonstationary Mechanical System. J. Web Eng. 2021, 20, 253–280. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; Zhang, S.; Wang, T.; Zhang, S. Hydraulic Pump Fault Diagnosis Method Based on EWT Decomposition Denoising and Deep Learning on Cloud Platform. Shock Vib. 2021. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Zhang, S.; Sun, Y.; Zhang, S. A Hydraulic Pump Fault Diagnosis Method Based on the Modified Ensemble Empirical Mode Decomposition and Wavelet Kernel Extreme Learning Machine Methods. Sensors 2021, 21, 2599. [Google Scholar] [CrossRef]
- Abdi, A.; Emamian, E.S. Fault diagnosis engineering in molecular signaling networks: An overview and applications in target discovery. Chem. Biodivers. 2010, 7, 1111–1123. [Google Scholar] [CrossRef]
- Guo, X. Research on Online Monitoring and Fault Diagnosis Method of Electric Motor and Centrifugal Pump Set. Ph.D. Thesis, Beijing University of Chemical Technology, Beijing, China, 2020. [Google Scholar]
- Nie, J. Research on Centrifugal Pump Fault Diagnosis Method Based on Support Vector Machine. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- Yang, C. Research on the Application of Parallel Factor Analysis in Blind Separation of Multiple Fault Sources. Ph.D. Thesis, Nanchang University of Aeronautics, Nanchang, China, 2018. [Google Scholar]
- Li, J.F.; Zhang, S.F. Joint angular and Doppler frequency estimation of dual-base MIMO radar based on quadratic linear decomposition. J. Aeronaut. 2012, 33, 1474–1482. [Google Scholar]
- Nion, D.; Sidiropoulos, N.D. A PARAFAC-based technique for detection and localization of multiple targets in a MIMO radar system. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 2077–2080. [Google Scholar] [CrossRef]
- Weis, M.; Romer, F.; Haardt, M.; Jannek, D.; Husar, P. Multi-dimensional space-time-frequency component analysis of event related EEG data using closed-form PARAFAC. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 349–352. [Google Scholar] [CrossRef]
- Ishii Stephanie, K.L.; Boyer Treavor, H. Behavior of reoccurring PARAFAC components in fluorescent dissolved organic matter in natural and engineered systems: A critical review. Environ. Sci. Technol. 2012, 46, 2006–2017. [Google Scholar] [CrossRef]
- Feng, A.A. Research on Fault Diagnosis of Truck Bearings Based on Optimized Probabilistic Neural Network. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Li, K.; Tai, N.; Zhang, S. Fault monitoring of microtempered motor bearings based on wavelet packet entropy and probabilistic neural network. Micro Spec. Mot. 2016, 44, 37–39. [Google Scholar]
- Fang, L.; Fan, D.; Zhang, G.; Chen, H. A particle swarm optimization particle filtering noise reduction algorithm with variational operators. J. Wuhan Univ. Eng. 2019, 41, 392–398. [Google Scholar]



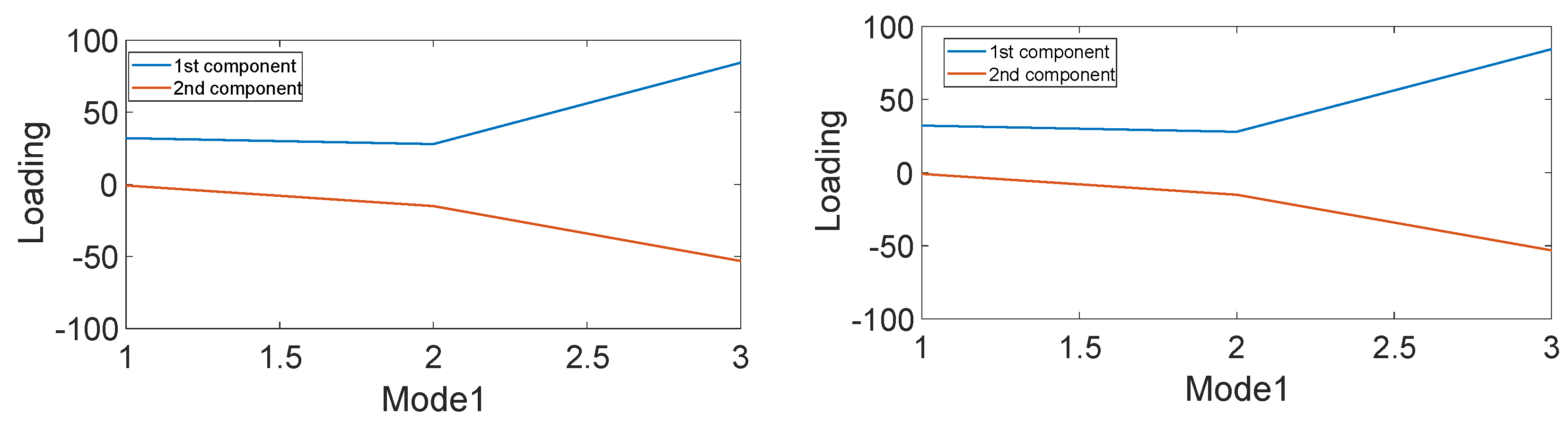
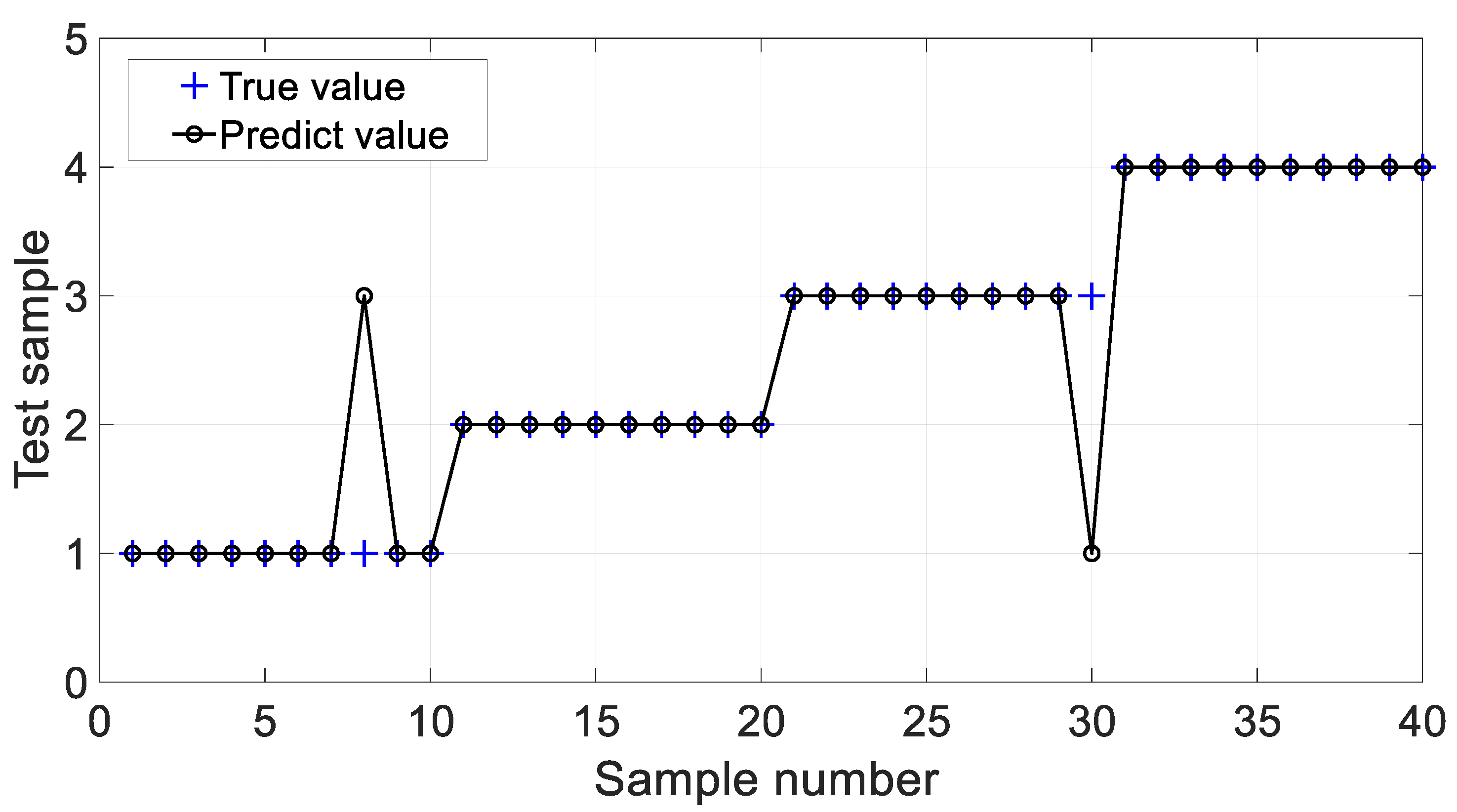
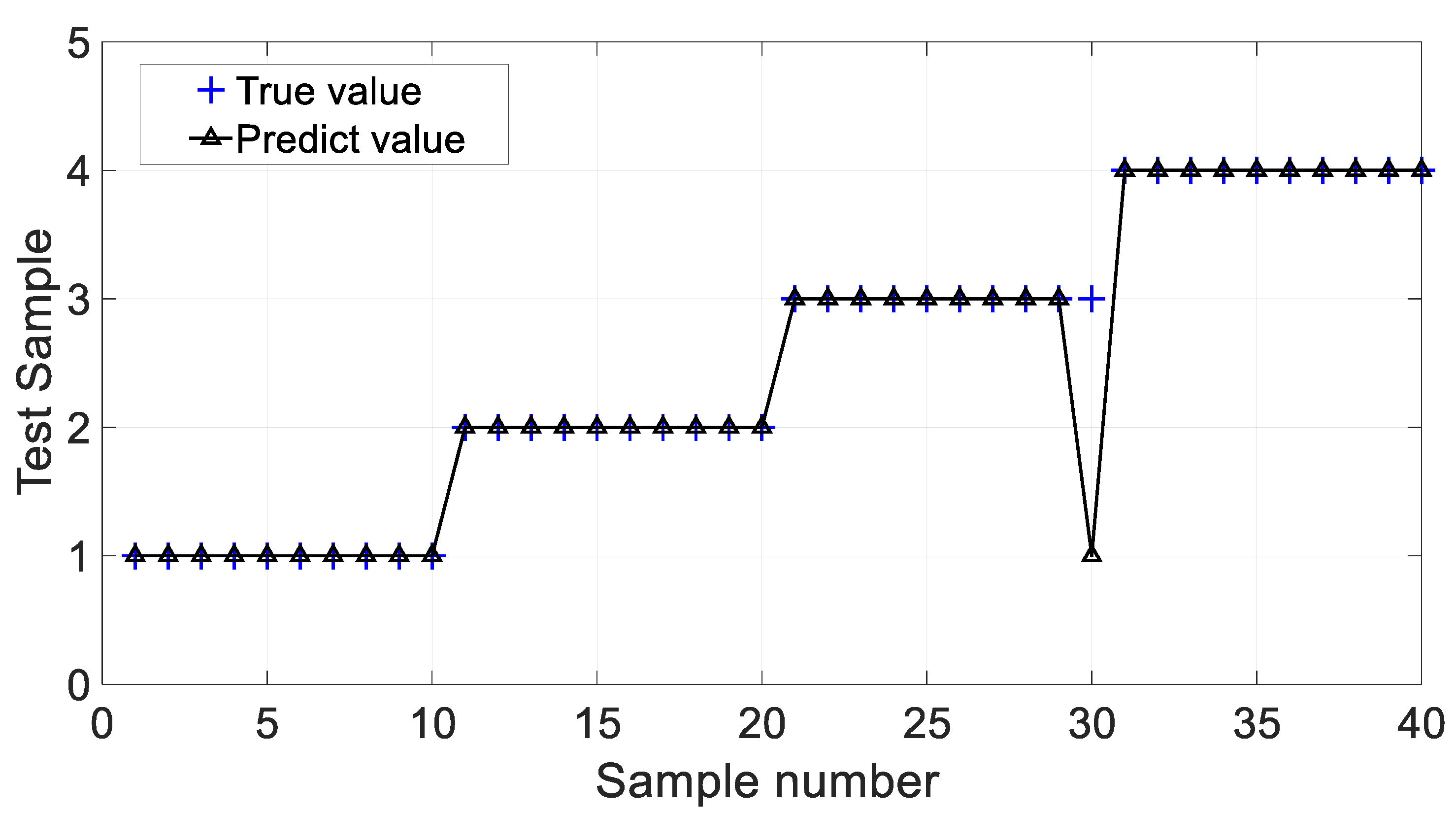
| Pattern | F1 | F2 | F3 | F4 |
|---|---|---|---|---|
| Output of PNN | 1 | 2 | 3 | 4 |
| Test Set Accuracy | Time (s) | |
|---|---|---|
| PNN | 82.5% | 0.125 |
| IPSO-PNN | 85% | 0.026 |
| Test Set Accuracy | Time (s) | |
|---|---|---|
| PNN | 95% | 0.033 |
| IPSO-PNN | 97.5% | 0.025 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Xiong, Y.; Li, S.; Song, Z.; Hu, Z.; Liu, F. Multi-Sensor Data Driven with PARAFAC-IPSO-PNN for Identification of Mechanical Nonstationary Multi-Fault Mode. Machines 2022, 10, 155. https://doi.org/10.3390/machines10020155
Chen H, Xiong Y, Li S, Song Z, Hu Z, Liu F. Multi-Sensor Data Driven with PARAFAC-IPSO-PNN for Identification of Mechanical Nonstationary Multi-Fault Mode. Machines. 2022; 10(2):155. https://doi.org/10.3390/machines10020155
Chicago/Turabian StyleChen, Hanxin, Yunwei Xiong, Shaoyi Li, Ziwei Song, Zhenyu Hu, and Feiyang Liu. 2022. "Multi-Sensor Data Driven with PARAFAC-IPSO-PNN for Identification of Mechanical Nonstationary Multi-Fault Mode" Machines 10, no. 2: 155. https://doi.org/10.3390/machines10020155
APA StyleChen, H., Xiong, Y., Li, S., Song, Z., Hu, Z., & Liu, F. (2022). Multi-Sensor Data Driven with PARAFAC-IPSO-PNN for Identification of Mechanical Nonstationary Multi-Fault Mode. Machines, 10(2), 155. https://doi.org/10.3390/machines10020155





