Influence of Graded Surface Decarburization of Automobile Forging Front Axle on the Bending Behavior Based on a Third-Order Shear Deformation Beam Theory
Abstract
:1. Introduction
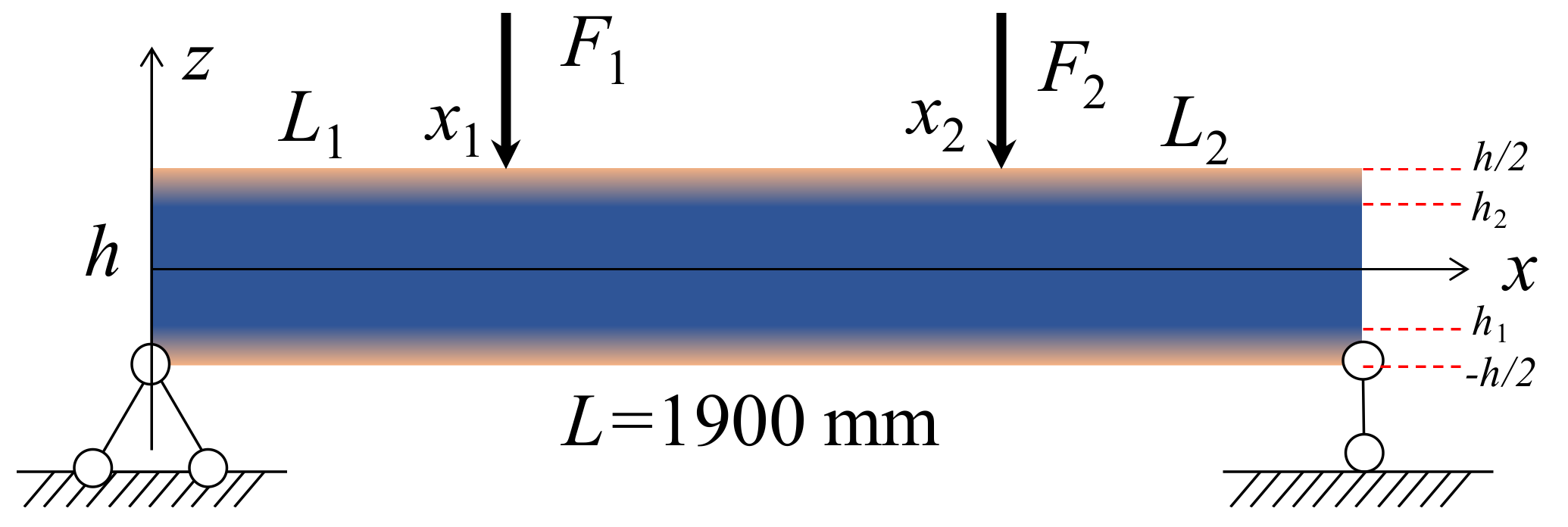
2. Materials and Methods
2.1. Materials
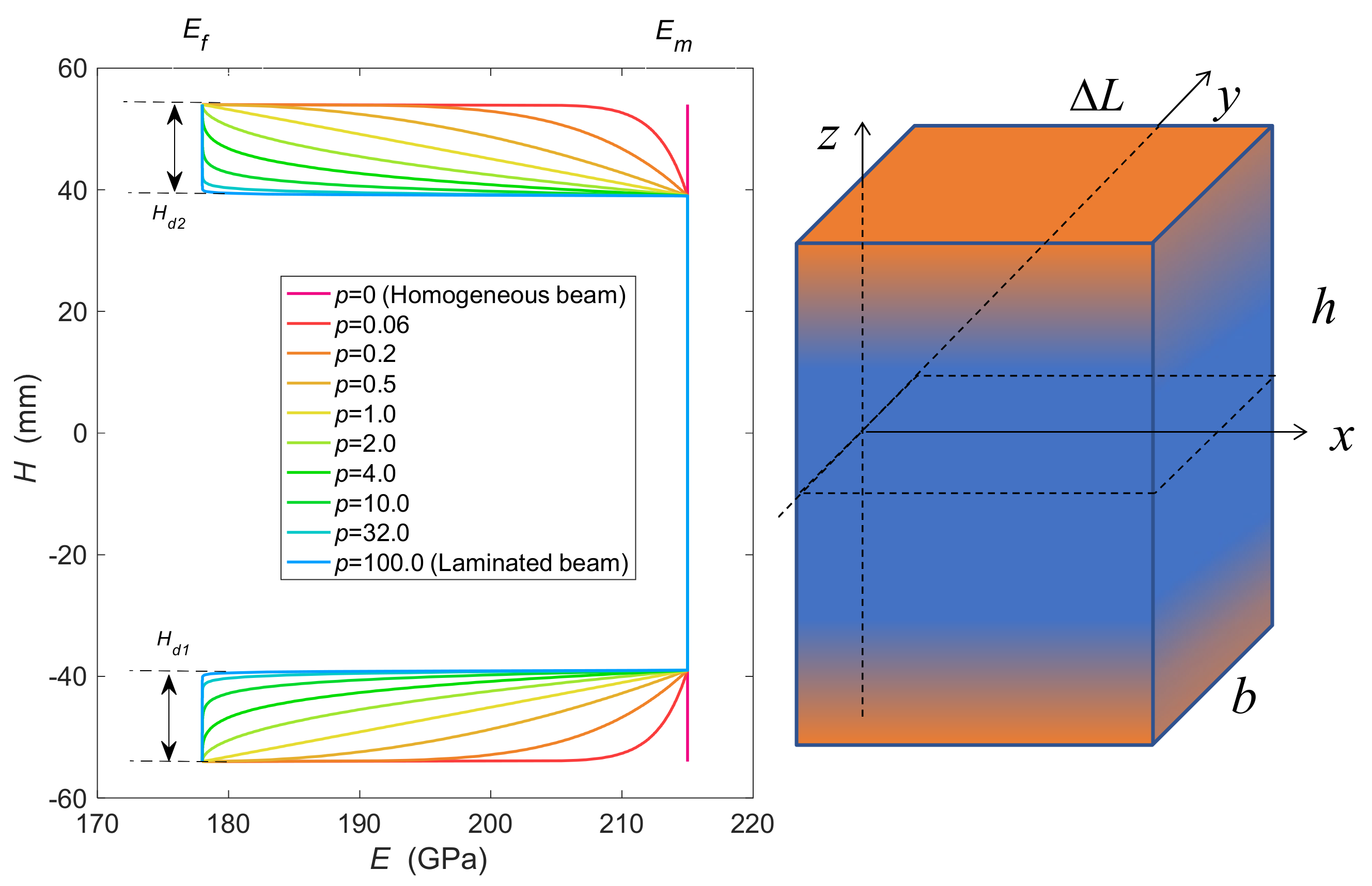
2.2. Mechanical Properties of Beams with Surface Decarburization
2.3. Methods
2.4. Analytical Solution with Navier Method
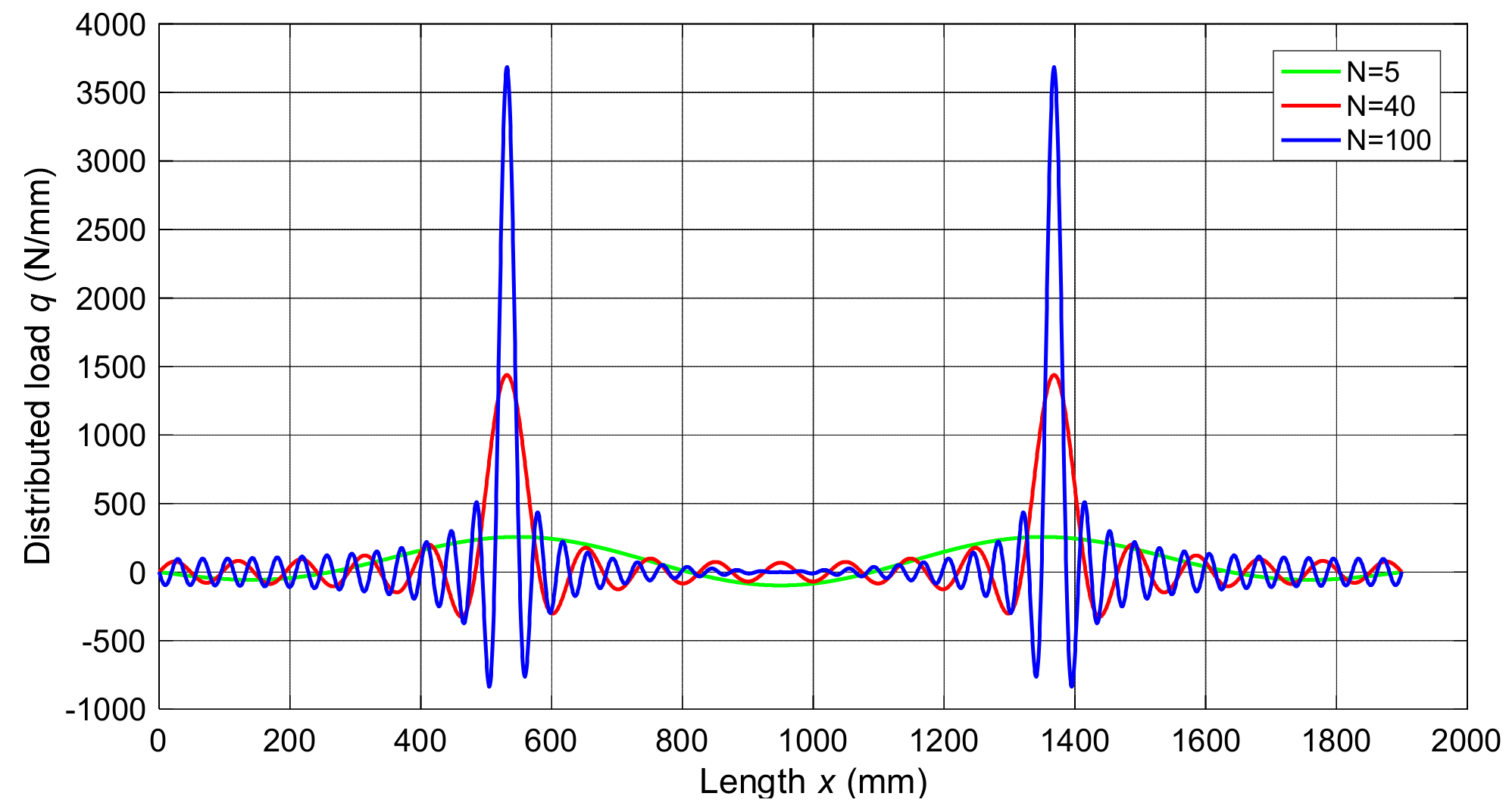
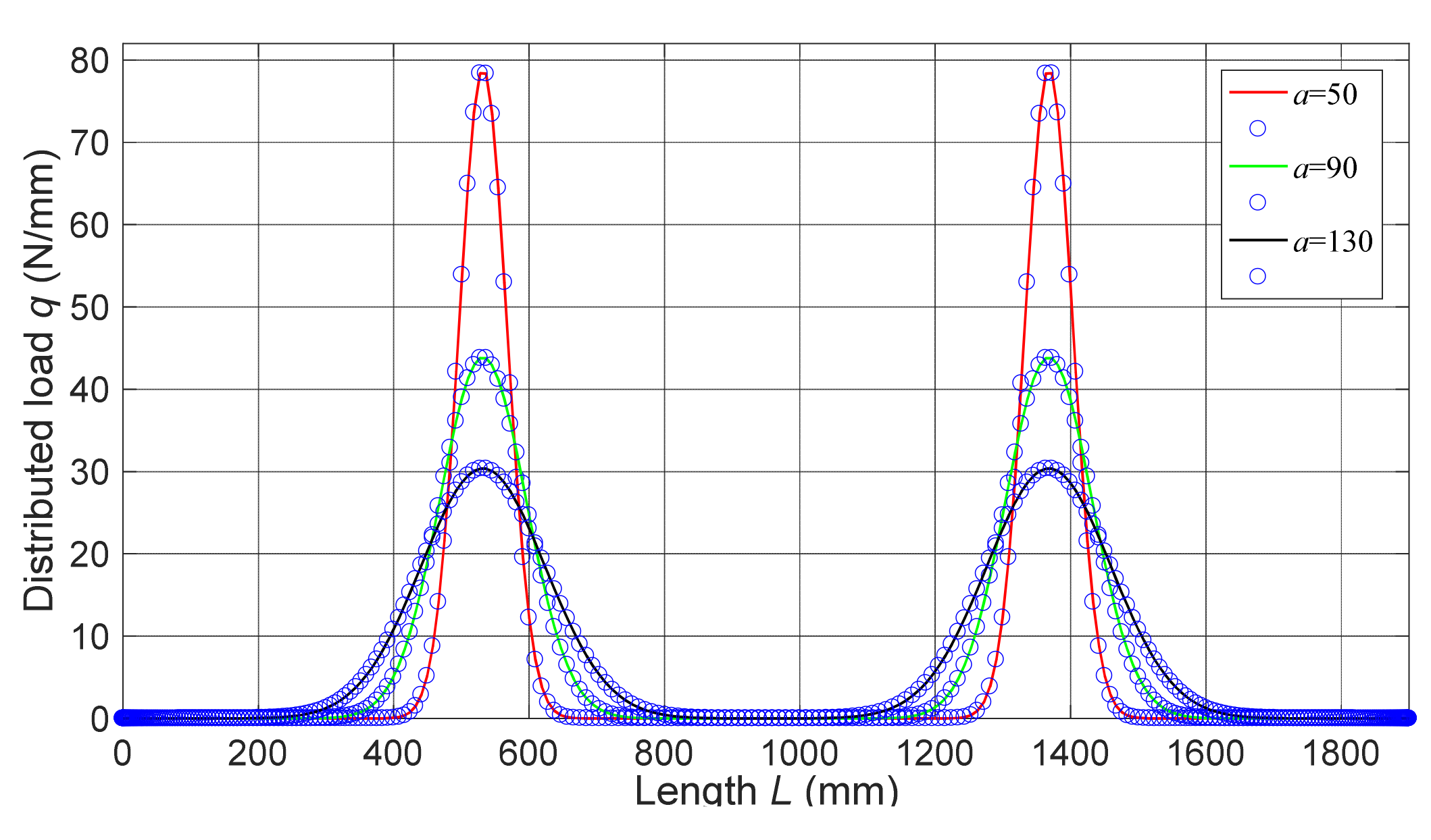
2.5. Differential Quadrature Method (DQM)
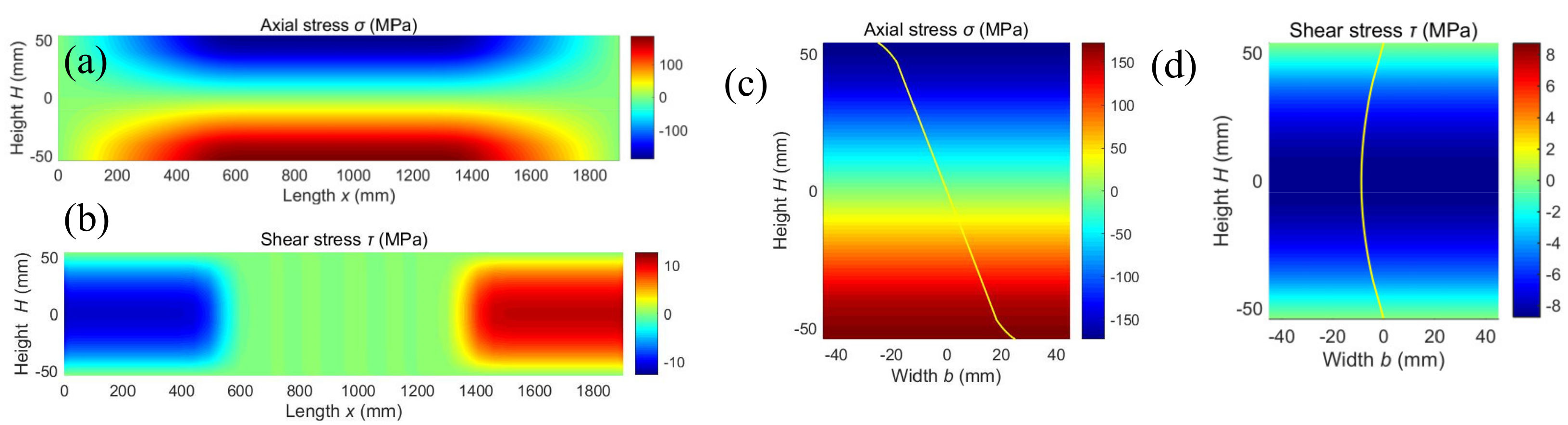
3. Results and Discussion
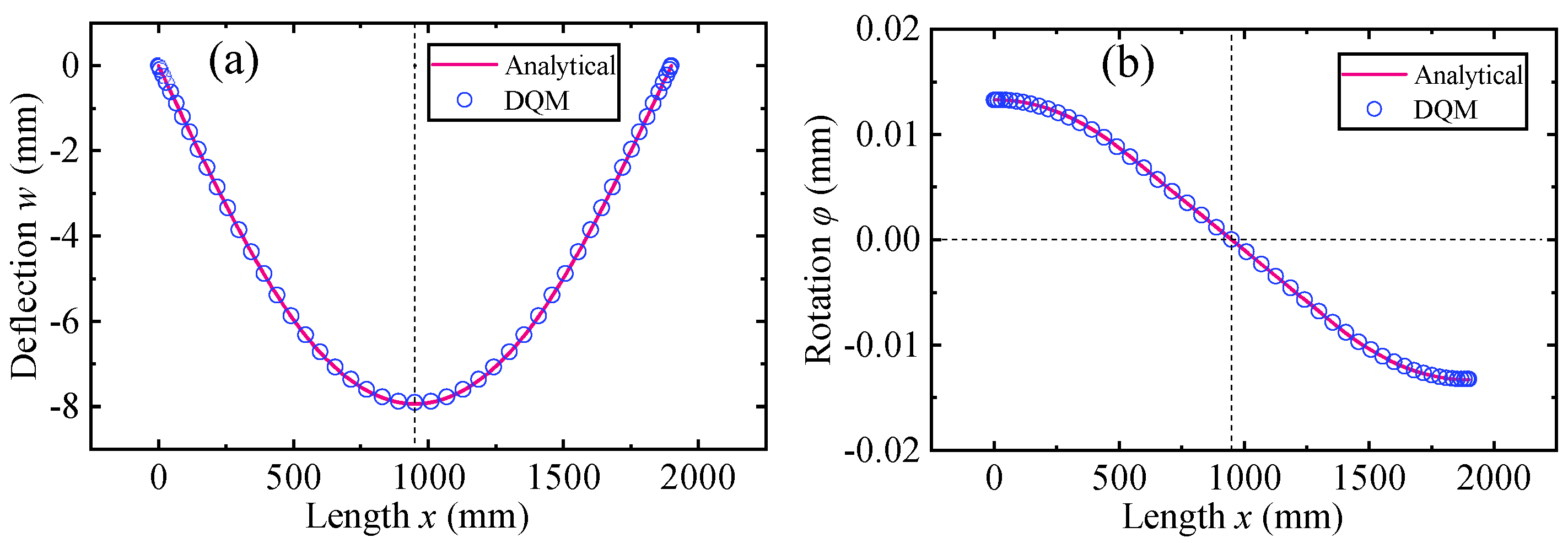
3.1. Numerical Verification
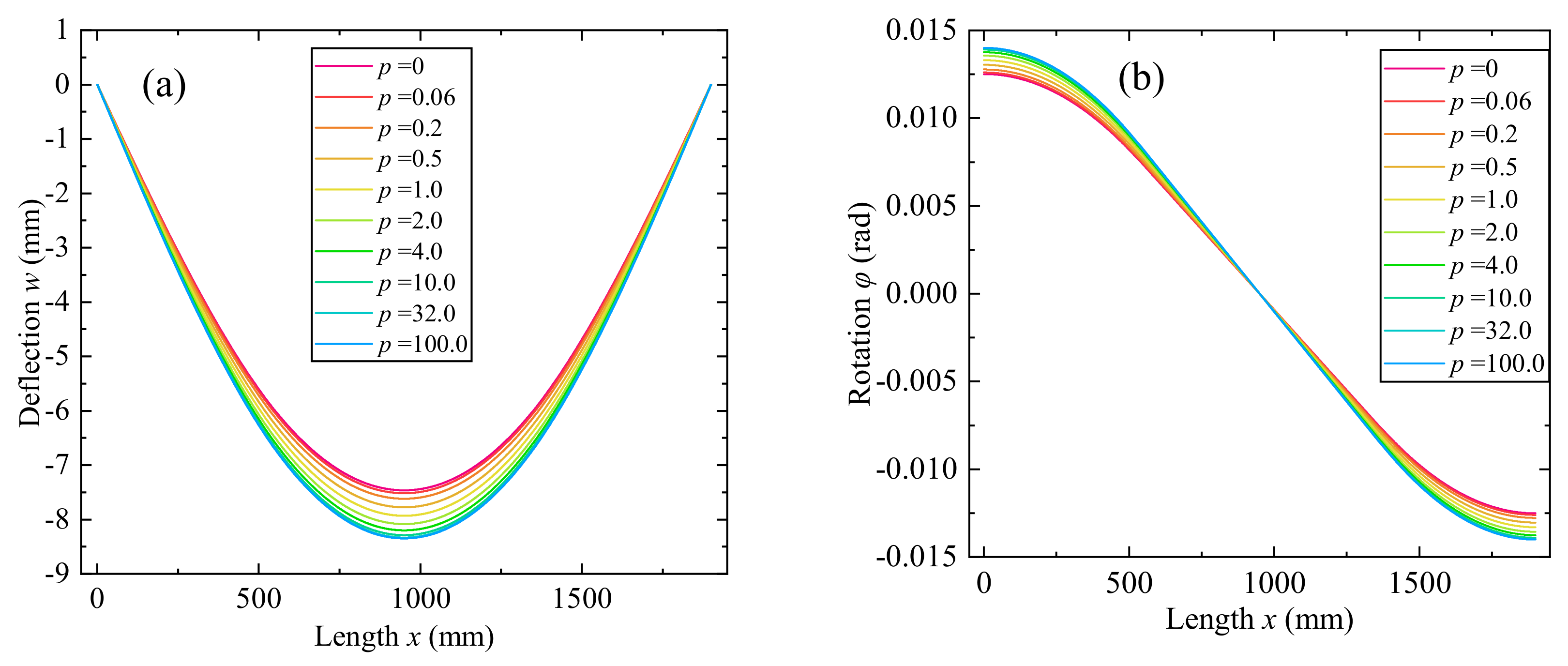
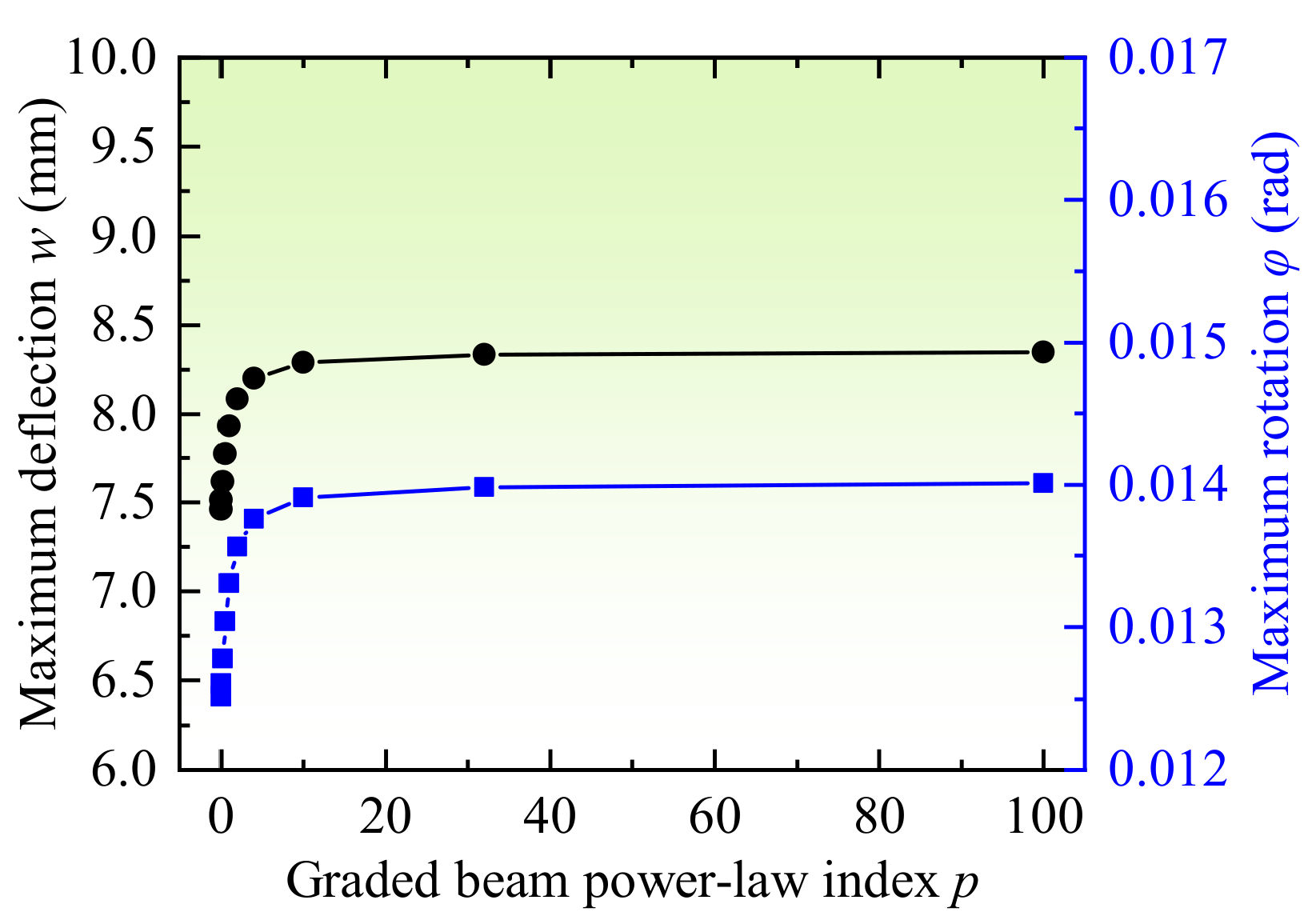
3.2. Effect of Power−Law Index of Graded Decarburization Layer
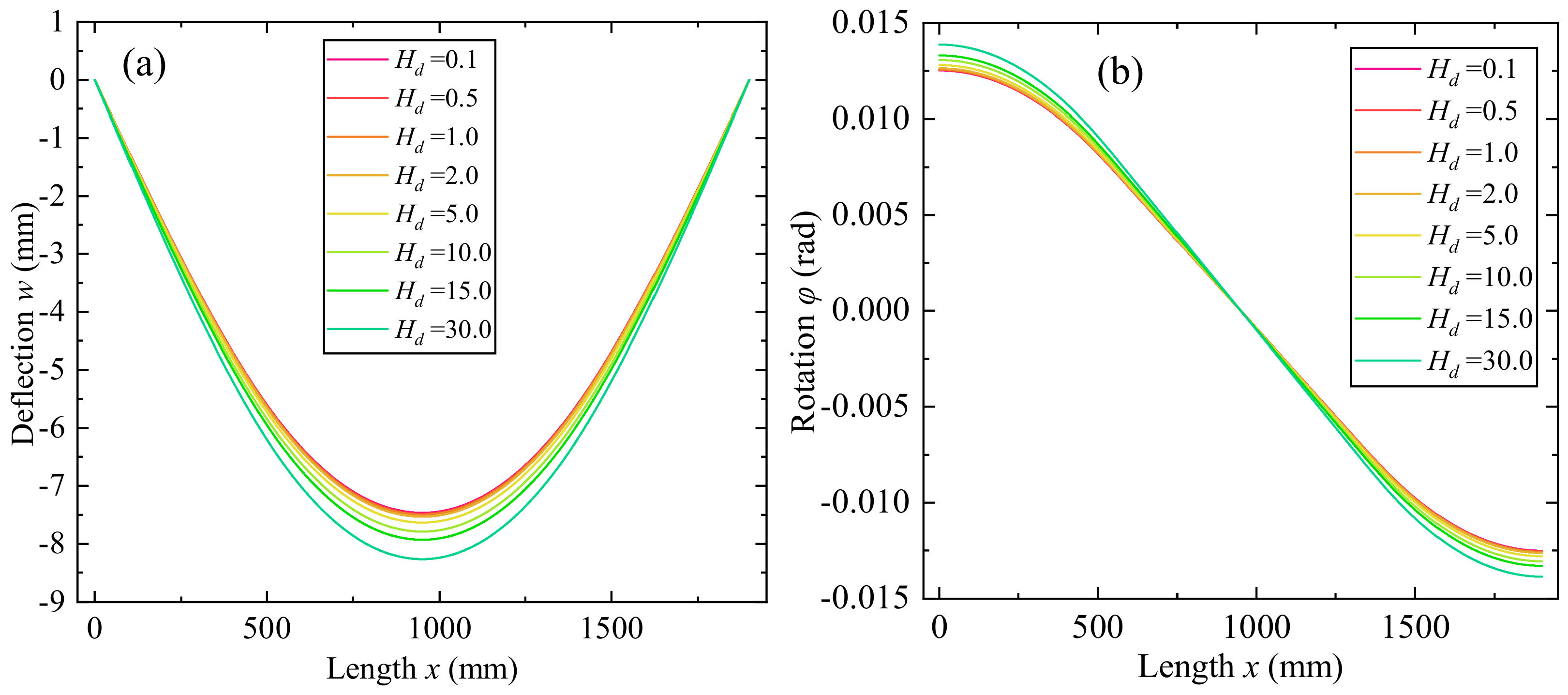
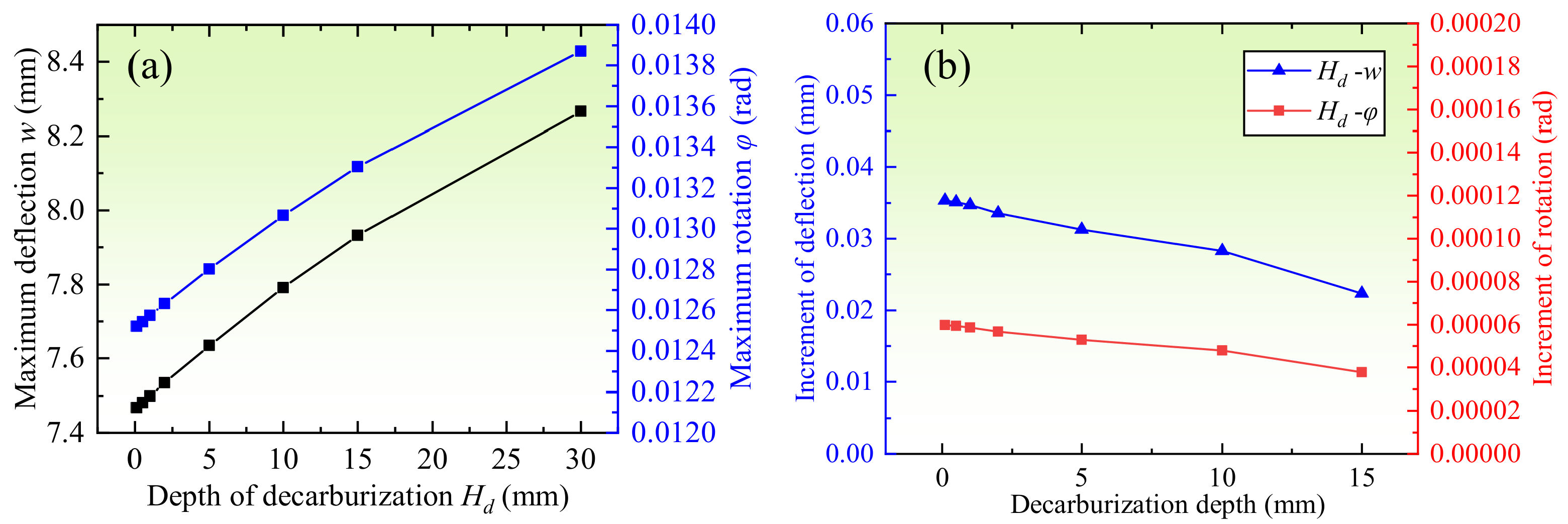
3.3. Effect of Depth of Graded Decarburization Layer
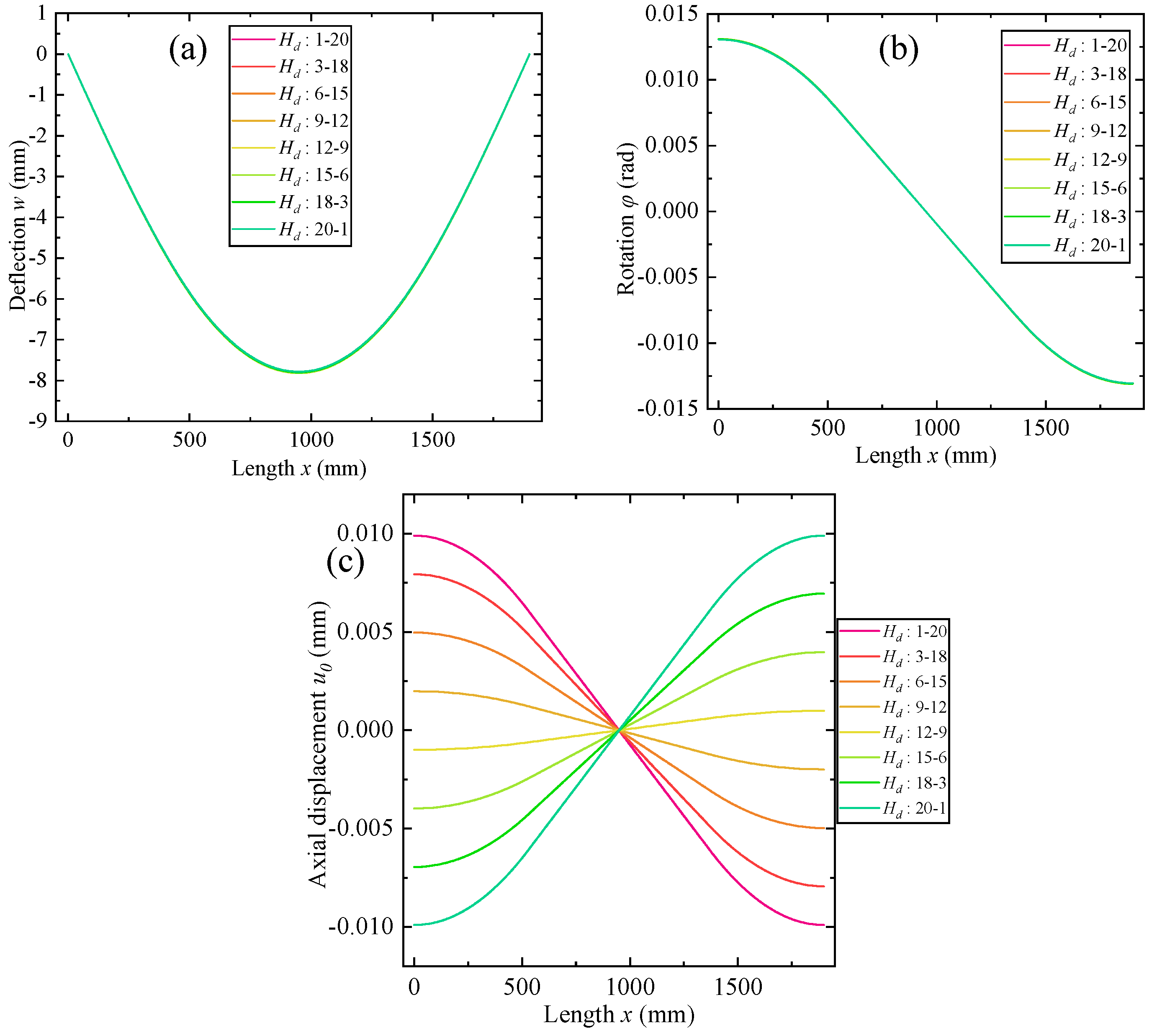
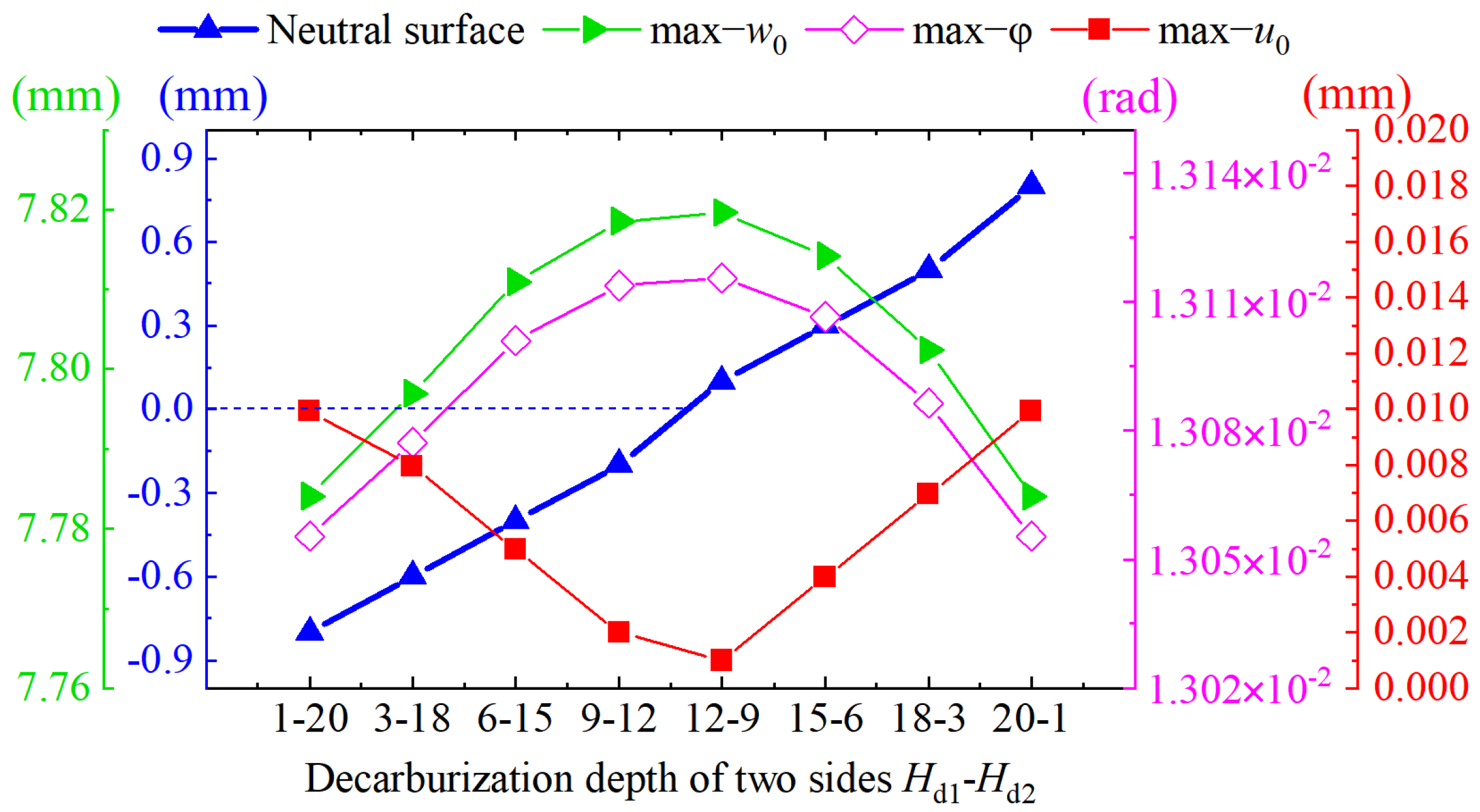
3.4. Effect of Unsymmetrical Decarburization Depth of Two Sides
3.5. Effect of Unbalancing Loading
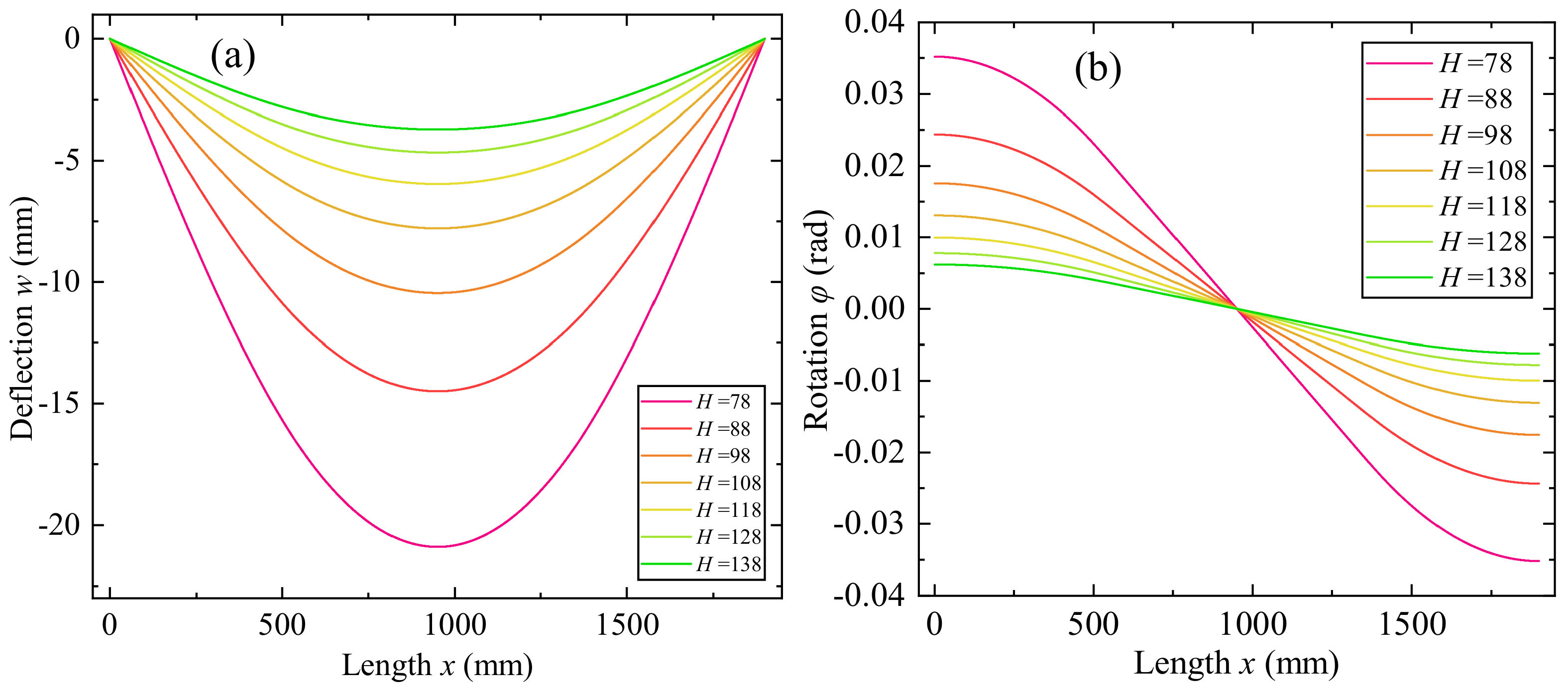
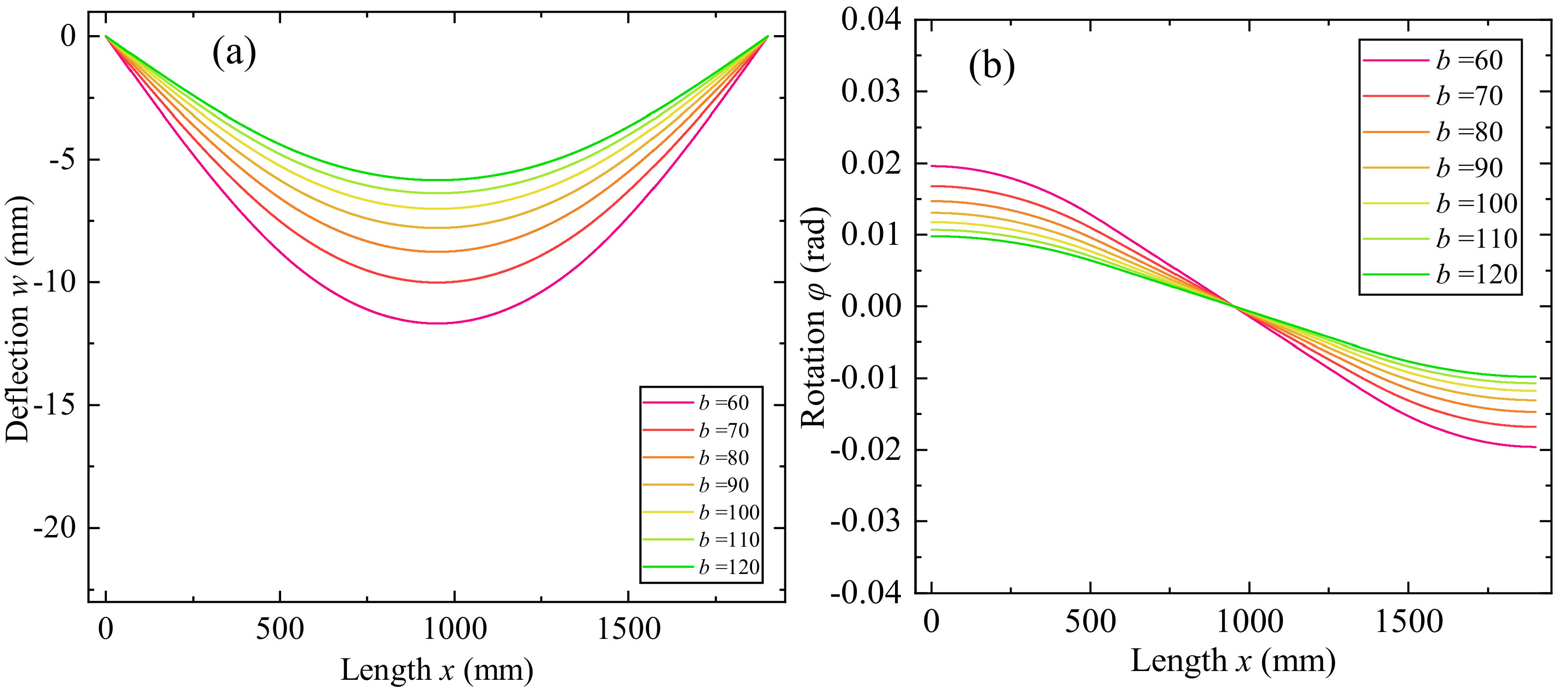
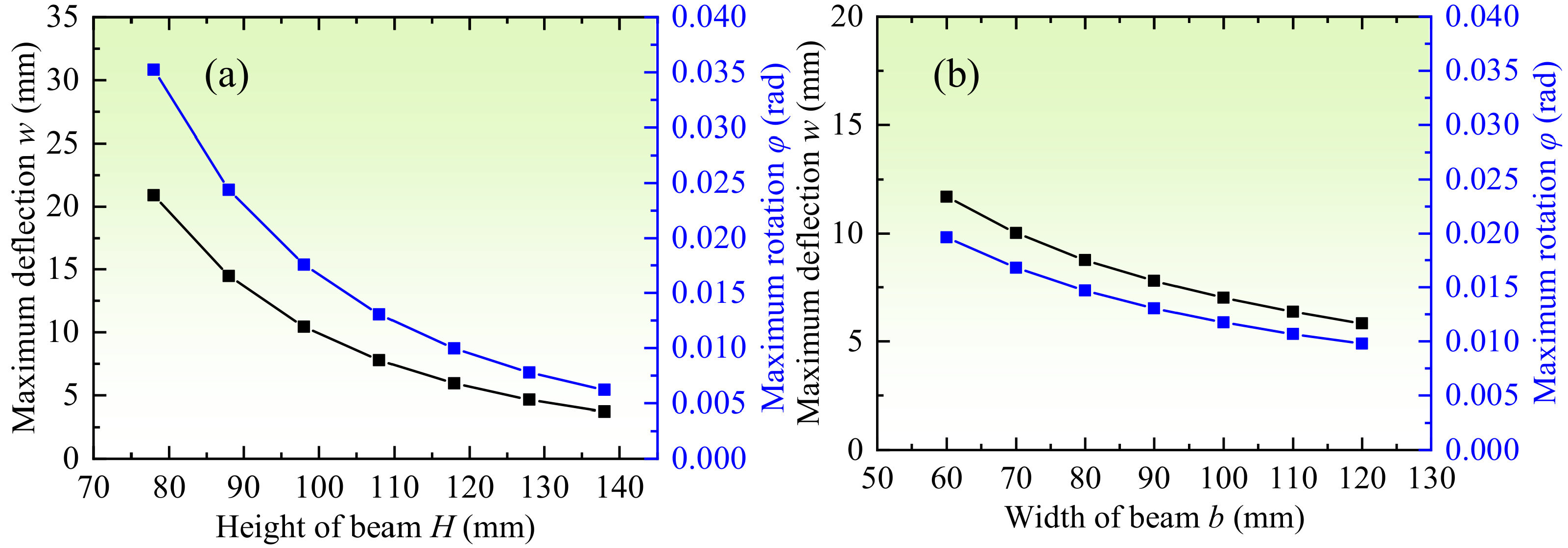
3.6. Effect of Beam Dimension
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.J.; Guo, J.; Wang, H.Y.; Wen, Z.F.; Liu, Q.Y.; Zhao, G.T.; Wang, W.J. Effects of decarburization on the wear resistance and damage mechanisms of rail steels subject to contact fatigue. Wear 2016, 364–365, 130–143. [Google Scholar] [CrossRef]
- Zhan, Q.; Yu, L.; Ye, F.; Xue, Q.; Li, H. Quantitative evaluation of the decarburization and microstructure evolution of WC–Co during plasma spraying. Surf. Coat. Technol. 2012, 206, 4068–4074. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Zhou, L.; Jiang, C.; Xiao, J. Forming condition and control strategy of ferrite decarburization in 60Si2MnA spring steel wires for automotive suspensions. Int. J. Miner. Metall. Mater. 2012, 19, 116–121. [Google Scholar] [CrossRef]
- Grake, H.J. Kinetics and mechanisms of the surace reactions occurring during carburization and decarburizaition and also nitrogenation and dednitrogenation of iron in gases. Arch. Eisenhüttenwesen 1975, 46, 75–81. [Google Scholar]
- Liu, Y.; Zhang, W.; Tong, Q.; Sun, Q. Effects of Si and Cr on Complete Decarburization Behavior of High Carbon Steels in Atmosphere of 2 vol. % O2. J. Iron Steel Res. Int. 2016, 23, 1316–1322. [Google Scholar] [CrossRef]
- Hao, X.J.; Yin, W.; Strangwood, M.; Peyton, A.J.; Morris, P.F.; Davis, C.L. Off-line measurement of decarburization of steels using a multifrequency electromagnetic sensor. Scr. Mater. 2008, 58, 1033–1036. [Google Scholar] [CrossRef]
- Zhao, X.; Song, B.; Zhang, Y.; Zhu, X.; Wei, Q.; Shi, Y. Decarburization of stainless steel during selective laser melting and its influence on Young’s modulus, hardness and tensile strength. Mater. Sci. Eng. A 2015, 647, 58–61. [Google Scholar] [CrossRef]
- Suresh Babu, P.; Basu, B.; Sundararajan, G. Processing–structure–property correlation and decarburization phenomenon in detonation sprayed WC–12Co coatings. Acta Mater. 2008, 56, 5012–5026. [Google Scholar] [CrossRef]
- Kovačič, M. Modeling of Total Decarburization of Spring Steel with Genetic Programming. Mater. Manuf. Process. 2015, 30, 434–443. [Google Scholar] [CrossRef]
- Suresh Babu, P.; Basu, B.; Sundararajan, G. Abrasive wear behavior of detonation sprayed WC–12Co coatings: Influence of decarburization and abrasive characteristics. Wear 2010, 268, 1387–1399. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Liu, Y. Surface decarburization characteristics and relation between decarburized types and heating temperature of spring steel 60Si2MnA. Int. J. Miner. Metall. Mater. 2013, 20, 720–724. [Google Scholar] [CrossRef]
- Heo, N.H.; Jung, Y.C.; Lee, J.K.; Kim, K.T. Decarburization, grain boundary segregation of P and primary water stress corrosion cracking in a low-alloy steel. Scr. Mater. 2008, 59, 1200–1203. [Google Scholar] [CrossRef]
- Leitner, M.; Aigner, R.; Grün, F. Numerical Fatigue Analysis of Induction-Hardened and Mechanically Post-Treated Steel Components. Machines 2019, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- Qiu, C.; Zurob, H.S.; Hutchinson, C.R. The coupled solute drag effect during ferrite growth in Fe–C–Mn–Si alloys using controlled decarburization. Acta Mater. 2015, 100, 333–343. [Google Scholar] [CrossRef]
- Zhuang, W.; Hua, L.; Wang, X.; Liu, Y.; Han, X.; Dong, L. Numerical and experimental investigation of roll-forging of automotive front axle beam. Int. J. Adv. Manuf. Technol. 2015, 79, 1761–1777. [Google Scholar] [CrossRef]
- Ji, H.; Liu, J.; Wang, B.; Fu, X.; Xiao, W.; Hu, Z. A new method for manufacturing hollow valves via cross wedge rolling and forging: Numerical analysis and experiment validation. J. Mater. Process. Technol. 2017, 240, 1–11. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Hong, T.T.; Van Vinh, P.; Van Thom, D. An efficient beam element based on Quasi-3D theory for static bending analysis of functionally graded beams. Materials 2019, 12, 2198. [Google Scholar] [CrossRef] [Green Version]
- Farahmand, S.; Soorgee, M.H.; Monazzah, A.H. Evaluating the elastic properties of Al2O3–Al FGMs by longitudinal and transverse ultrasonic bulk waves velocity features. Ceram. Int. 2021, 47, 24906–24915. [Google Scholar] [CrossRef]
- Cardoso, R.P.R. A new beam element which blends the Euler-Bernoulli beam theory with idealised transverse shear flows for aircraft structural analysis. Thin-Walled Struct. 2020, 157, 107118. [Google Scholar] [CrossRef]
- Qin, X.; Shen, Y.; Chen, W.; Yang, J.; Peng, L.X. Bending and free vibration analyses of circular stiffened plates using the FSDT mesh-free method. Int. J. Mech. Sci. 2021, 202–203, 106498. [Google Scholar] [CrossRef]
- Żur, K.K.; Arefi, M.; Kim, J.; Reddy, J.N. Free vibration and buckling analyses of magneto-electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory. Compos. Part B Eng. 2020, 182, 107601. [Google Scholar] [CrossRef]
- Khorshidi, K.; Fallah, A. Buckling analysis of functionally graded rectangular nano-plate based on nonlocal exponential shear deformation theory. Int. J. Mech. Sci. 2016, 113, 94–104. [Google Scholar] [CrossRef]
- Zheng, X.; Xu, D.; Ni, Z.; Zhou, C.; An, D.; Wang, B.; Li, R. New benchmark free vibration solutions of non-Lévy-type thick rectangular plates based on third-order shear deformation theory. Compos. Struct. 2021, 268, 113955. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. A simple quasi-3D sinusoidal shear deformation theory for functionally graded plates. Compos. Struct. 2013, 99, 172–180. [Google Scholar] [CrossRef]
- Karamanlı, A. Bending behaviour of two directional functionally graded sandwich beams by using a quasi-3d shear deformation theory. Compos. Struct. 2017, 174, 70–86. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Ghugal, Y.M. Bending, buckling and free vibration of laminated composite and sandwich beams: A critical review of literature. Compos. Struct. 2017, 171, 486–504. [Google Scholar] [CrossRef]
- Kadoli, R.; Akhtar, K.; Ganesan, N. Static analysis of functionally graded beams using higher order shear deformation theory. Appl. Math. Model. 2008, 32, 2509–2525. [Google Scholar] [CrossRef]
- Zhang, D.-G. Nonlinear bending analysis of FGM beams based on physical neutral surface and high order shear deformation theory. Compos. Struct. 2013, 100, 121–126. [Google Scholar] [CrossRef]
- Niknam, H.; Fallah, A.; Aghdam, M.M. Nonlinear bending of functionally graded tapered beams subjected to thermal and mechanical loading. Int. J. Non-Linear. Mech. 2014, 65, 141–147. [Google Scholar] [CrossRef]
- Belarbi, M.-O.; Houari, M.S.A.; Hirane, H.; Daikh, A.A.; Bordas, S.P.A. On the finite element analysis of functionally graded sandwich curved beams via a new refined higher order shear deformation theory. Compos. Struct. 2022, 279, 114715. [Google Scholar] [CrossRef]
- Şimşek, M.; Yurtcu, H.H. Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory. Compos. Struct. 2013, 97, 378–386. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Hadi, A. Eringen’s non-local elasticity theory for bending analysis of bi-directional functionally graded Euler–Bernoulli nano-beams. Int. J. Eng. Sci. 2016, 106, 1–9. [Google Scholar] [CrossRef]
- Eftekhari, S.A. Differential quadrature procedure for in-plane vibration analysis of variable thickness circular arches traversed by a moving point load. Appl. Math. Model. 2016, 40, 4640–4663. [Google Scholar] [CrossRef]
- Zhu, X.; Xiong, C.; Yin, J.; Yin, D.; Deng, H. Bending experiment and mechanical properties analysis of composite sandwich laminated box beams. Materials 2019, 12, 2959. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Zhou, L.; Wen, X.; Zhang, C.; Liu, Y. Heat Treatment Properties of 42CrMo Steel for Bearing Ring of Varisized Shield Tunneling Machine. Acta Metall. Sin. 2014, 27, 383–388. [Google Scholar] [CrossRef]
- Olanipekun, A.T.; Nthabiseng, M.; Ayodele, O.O.; Mphahlele, M.R.; Mampuya, B.M.; Olubambi, P.A. Datasets on the measurement of mechanical properties of ferrite and austenite constitutive phases using nanoindentation and micro hardness techniques. Data Br. 2019, 27, 104551. [Google Scholar] [CrossRef]
- Kiefer, D.; Gibmeier, J.; Stark, A. Determination of Temperature-Dependent Elastic Constants of Steel AISI 4140 by Use of In Situ X-ray Dilatometry Experiments. Materials 2020, 13, 2378. [Google Scholar] [CrossRef]
- Hadji, L.; Khelifa, Z.; El Abbes, A.B. A new higher order shear deformation model for functionally graded beams. KSCE J. Civ. Eng. 2016, 20, 1835–1841. [Google Scholar] [CrossRef]
- Ben-Oumrane, S.; Abedlouahed, T.; Ismail, M.; Mohamed, B.B.; Mustapha, M.; El Abbas, A.B. A theoretical analysis of flexional bending of Al/Al2O3 S-FGM thick beams. Comput. Mater. Sci. 2009, 44, 1344–1350. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, H. Nonlinear bending response of functionally graded nanobeams with material uncertainties. Int. J. Mech. Sci. 2017, 134, 123–135. [Google Scholar] [CrossRef]
- Eshraghi, I.; Jalali, S.K.; Pugno, N.M. Imperfection sensitivity of nonlinear vibration of curved single-walled carbon nanotubes based on nonlocal timoshenko beam theory. Materials 2016, 9, 786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Twinkle, C.M.; Jeyaraj, P. A semi-analytical nonlocal elasticity model for static stability and vibration behaviour of agglomerated CNTs reinforced nano cylindrical panel under non-uniform edge loads. Appl. Math. Model. 2022, 103, 68–90. [Google Scholar] [CrossRef]
- Wang, X.; Jin, C. Differential Quadrature Analysis of Moving Load Problems. Adv. Appl. Math. Mech. 2016, 8, 536–555. [Google Scholar] [CrossRef]
- Koutoati, K.; Mohri, F.; Daya, E.M. Finite element approach of axial bending coupling on static and vibration behaviors of functionally graded material sandwich beams. Mech. Adv. Mater. Struct. 2021, 28, 1537–1553. [Google Scholar] [CrossRef]







| Element | Content |
|---|---|
| C | 0.38~0.45 |
| Si | 0.17~0.37 |
| Mn | 0.50~0.80 |
| Cr | 0.9~1.2 |
| Mo | 0.15~0.25 |
| Ni | ≤0.03 |
| Cu | ≤0.03 |
| S | ≤0.03 |
| P | ≤0.03 |
| Method | Koutoati et al. [44] | Present-Navier | Present-DQM |
|---|---|---|---|
| p = 0.0 | 84.29 | 84.29 | 84.29 |
| p = 0.5 | 126.59 | 126.60 | 126.60 |
| p = 1.0 | 162.00 | 162.00 | 162.00 |
| p = 5.0 | 281.12 | 281.12 | 281.12 |
| p = 10.0 | 314.74 | 314.74 | 314.74 |
| Method | Navier | DQM | Deviation | |
|---|---|---|---|---|
| p = 0.2 | ϕ | 0.0127 | 0.0127 | −0.31% |
| w | −7.6190 | −7.5994 | −0.26% | |
| p = 1.0 | ϕ | 0.0133 | 0.0132 | −0.31% |
| w | −7.9319 | −7.9114 | −0.26% | |
| p = 5.0 | ϕ | 0.0138 | 0.0137 | −0.31% |
| w | −8.2277 | −8.2064 | −0.26% | |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Bottom side Hd1 (mm) | 20 | 18 | 15 | 12 | 9 | 6 | 3 | 1 |
| Top side Hd2 (mm) | 1 | 3 | 6 | 9 | 12 | 15 | 18 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Wu, M.; Hua, L.; Qin, X.; Ni, M. Influence of Graded Surface Decarburization of Automobile Forging Front Axle on the Bending Behavior Based on a Third-Order Shear Deformation Beam Theory. Machines 2022, 10, 139. https://doi.org/10.3390/machines10020139
Hu Z, Wu M, Hua L, Qin X, Ni M. Influence of Graded Surface Decarburization of Automobile Forging Front Axle on the Bending Behavior Based on a Third-Order Shear Deformation Beam Theory. Machines. 2022; 10(2):139. https://doi.org/10.3390/machines10020139
Chicago/Turabian StyleHu, Zeqi, Min Wu, Lin Hua, Xunpeng Qin, and Mao Ni. 2022. "Influence of Graded Surface Decarburization of Automobile Forging Front Axle on the Bending Behavior Based on a Third-Order Shear Deformation Beam Theory" Machines 10, no. 2: 139. https://doi.org/10.3390/machines10020139
APA StyleHu, Z., Wu, M., Hua, L., Qin, X., & Ni, M. (2022). Influence of Graded Surface Decarburization of Automobile Forging Front Axle on the Bending Behavior Based on a Third-Order Shear Deformation Beam Theory. Machines, 10(2), 139. https://doi.org/10.3390/machines10020139






