Fuzzy Broad Learning System Combined with Feature-Engineering-Based Fault Diagnosis for Bearings
Abstract
:1. Introduction
2. The Basic Theory of the Model
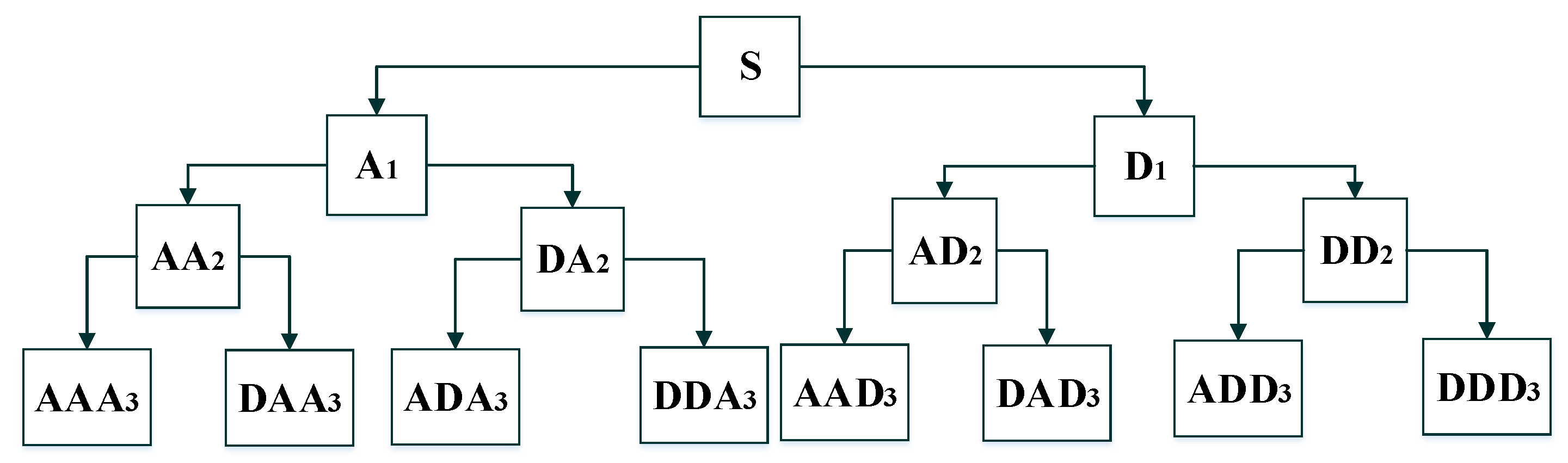
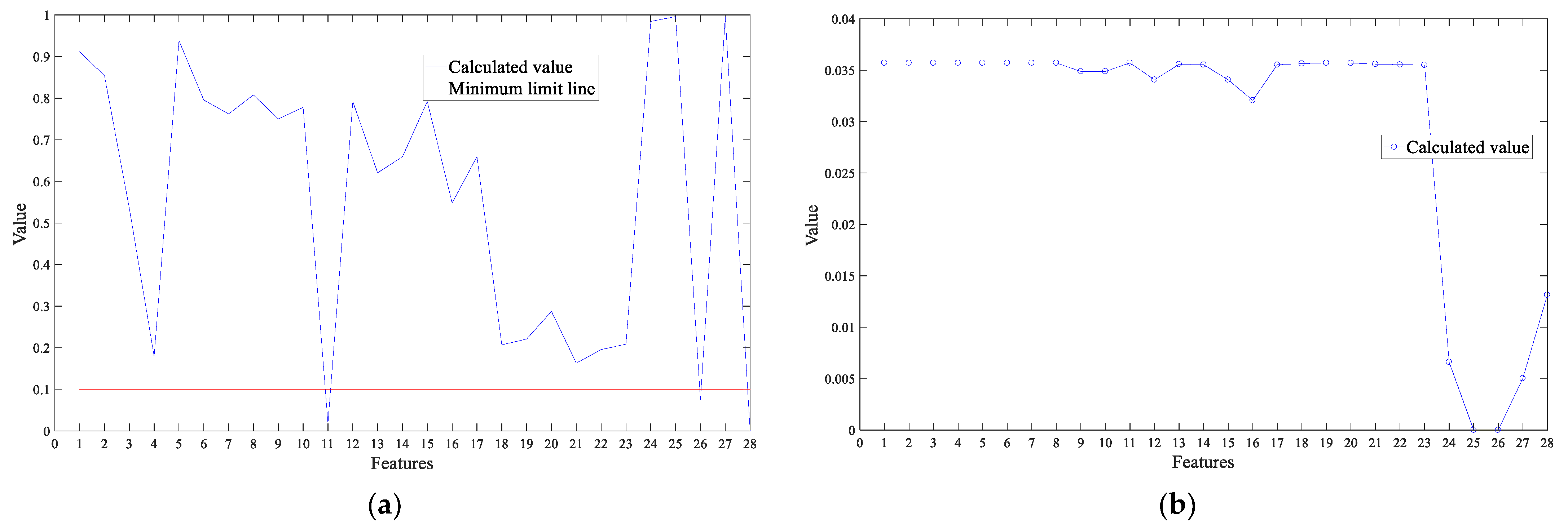
2.1. Feature Engineering
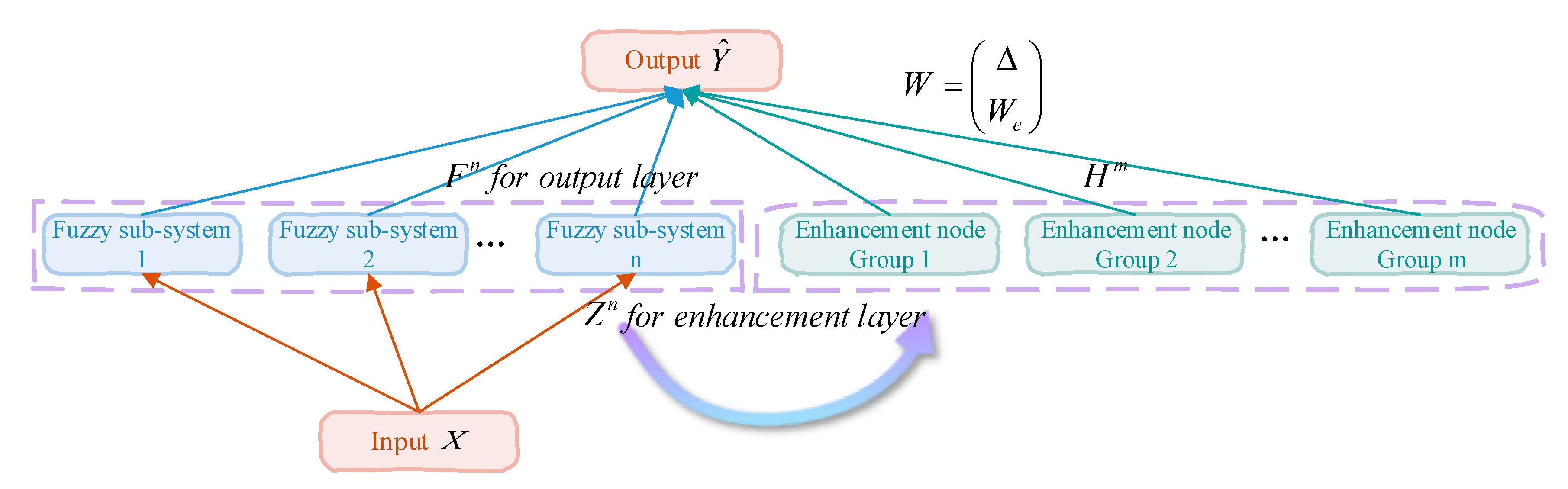
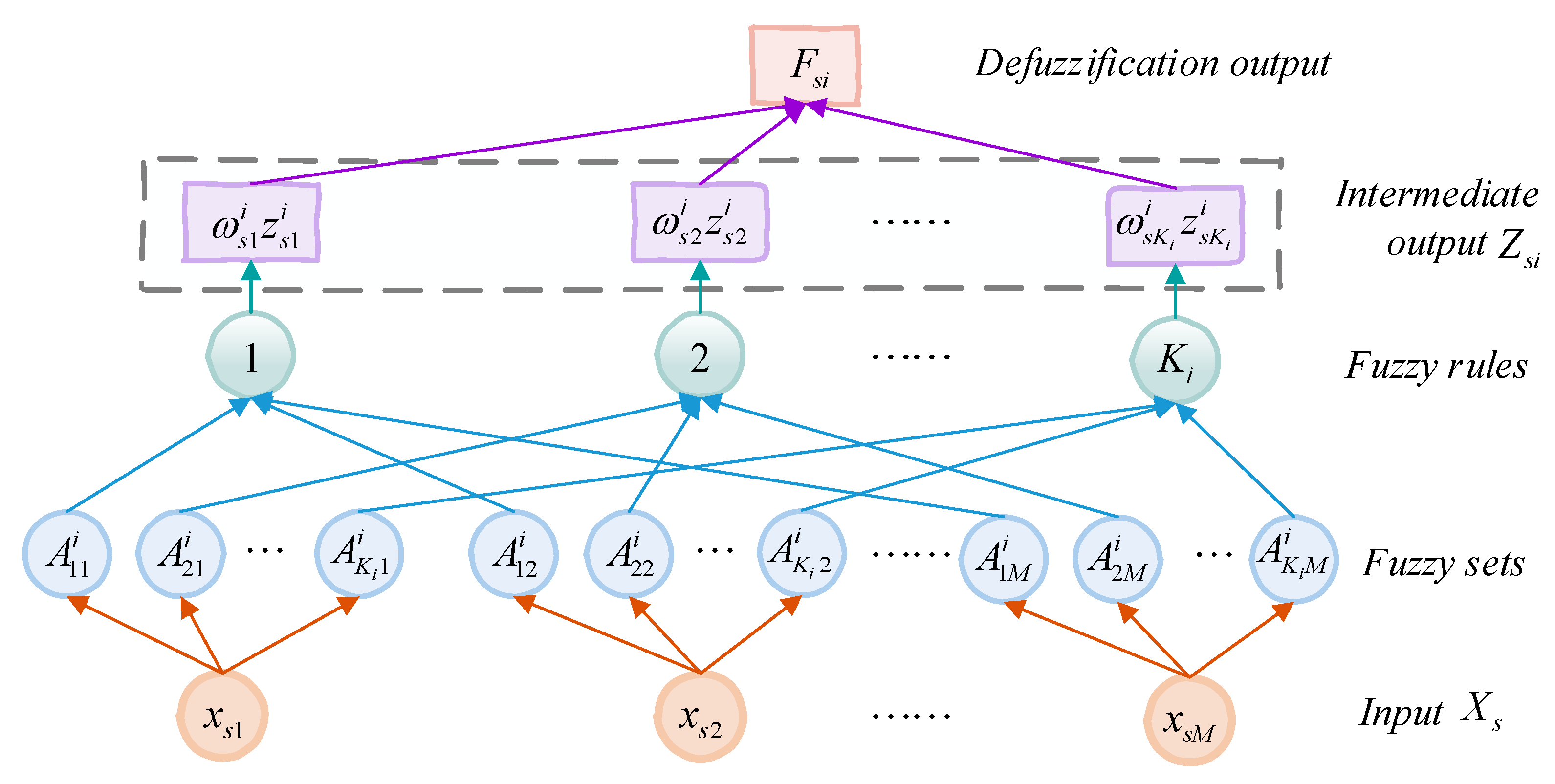
2.2. Fuzzy Broad Learning System
3. Diagnostic Model
4. Experimental
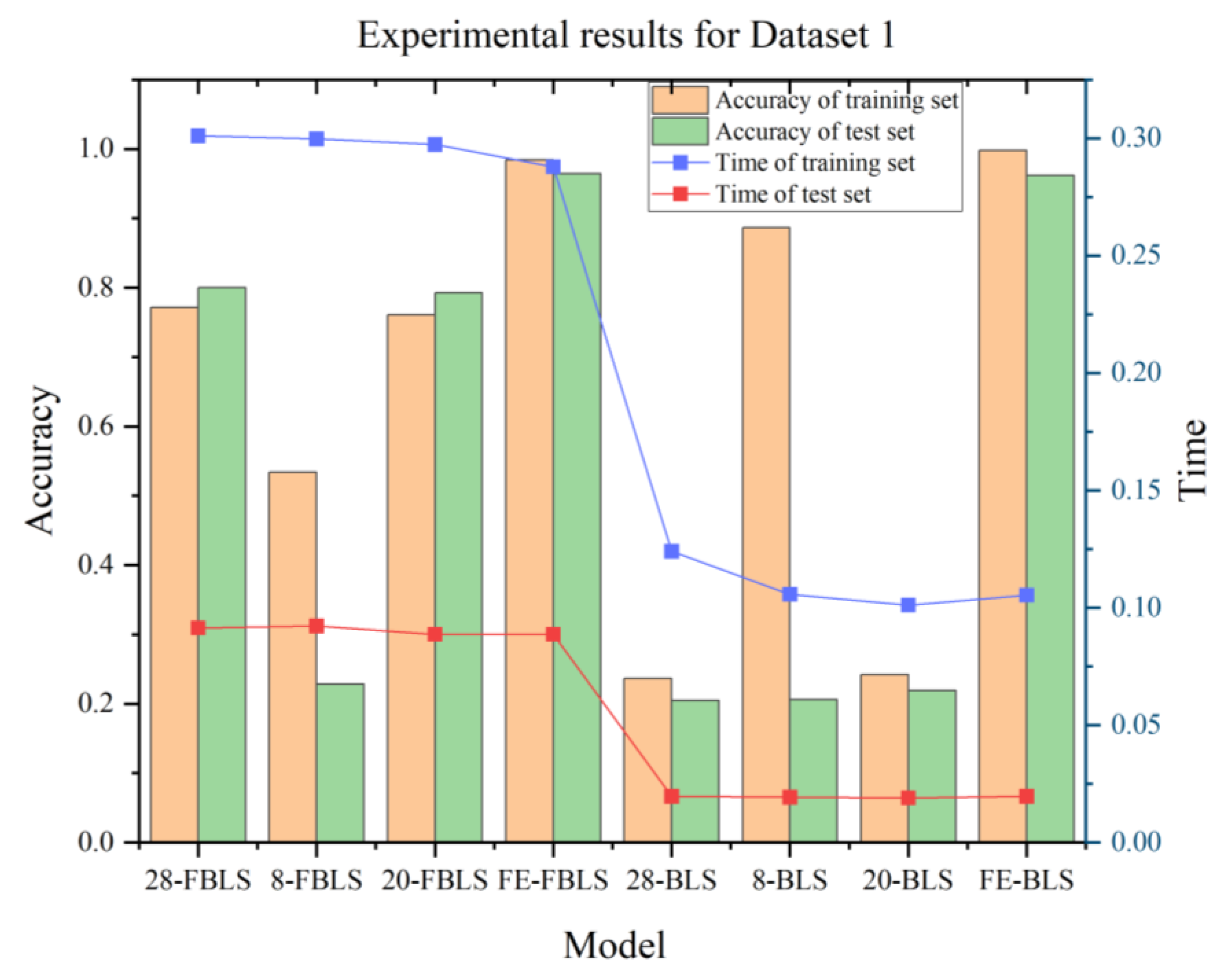
4.1. DATASET 1
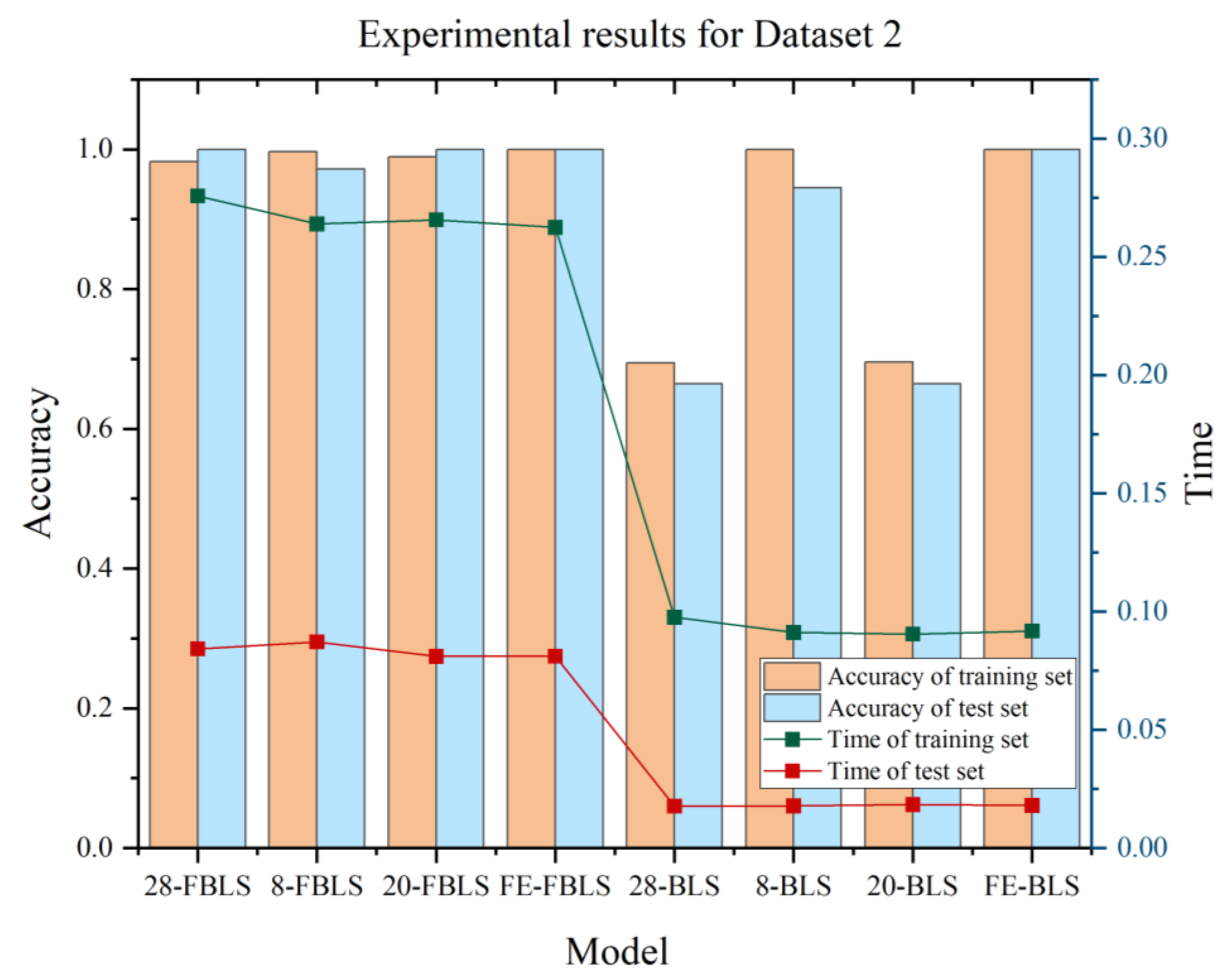
4.2. DATASET 2
4.3. DATASET 3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, J.M.; Zhang, C.C. Rolling Bearing Vibration Data Prediction Based on ARMA. J. East China Jiaotong Univ. 2018, 35, 99–103. [Google Scholar]
- Harlişca, C.; Szabó, L.; Frosini, L. Diagnosis of rolling bearings faults in electric machines through stray magnetic flux monitoring. In Proceedings of the 2013 8th International Symposium on Advanced Topics in Electrical Engineering, Bucharest, Romania, 19 September 2013. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Ramirez-Núñez, J.A. Automatic diagnosis of electromechanical faults in induction motors based on the transient analysis of the stray flux via MUSIC methods. IEEE Trans. Ind. Appl. 2020, 56, 3604–3613. [Google Scholar] [CrossRef]
- Azeez, A.A.; Alkhedher, M.; Gadala, M.S. Thermal imaging fault detection for rolling element bearings. In Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences, Dubai, United Arab Emirates, 6 January 2020. [Google Scholar] [CrossRef]
- Choudhary, A.; Goyal, D. Infrared thermography based fault diagnosis of induction motor bearings using machine learning. IEEE Sens. J. 2020, 21, 1727–1734. [Google Scholar] [CrossRef]
- Pham, M.T.; Kim, J.M. Efficient fault diagnosis of rolling bearings using neural network architecture search and sharing weights. IEEE Access 2021, 9, 98800–98811. [Google Scholar] [CrossRef]
- Chen, R.; Tang, L. Fault diagnosis method of low-speed rolling bearing based on acoustic emission signal and subspace embedded feature distribution alignment. IEEE Trans. Ind. Inform. 2020, 17, 5402–5410. [Google Scholar] [CrossRef]
- Zhou, J.M.; Yin, W.H. Review on performance degradation assessment of rolling bearings based on data-driven. Mod. Manuf. Eng. 2021, 05, 146–153+160. [Google Scholar]
- Lei, Y.G.; Jia, F. Opportunities and Challenges of Machinery Intelligent Fault Diagnosis in Big Data Era. J. Mech. Eng. 2010, 54, 99–104. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H. Aircraft bearing fault diagnosis based on automatic feature engineering. CIESC J. 2021, 72 (Suppl. S1), 430–436. [Google Scholar]
- Peña, M.; Cerrada, M. Feature engineering based on ANOVA, cluster validity assessment and KNN for fault diagnosis in bearings. J. Intell. Fuzzy Syst. 2018, 34, 3451–3462. [Google Scholar] [CrossRef]
- Li, B.; Tang, B. Joint attention feature transfer network for gearbox fault diagnosis with imbalanced data. Mech. Syst. Signal Process. 2022, 176, 109146. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, Y. A novel end-to-end feature selection and diagnosis method for rotating machinery. Sensors 2021, 21, 2056. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Lan, K. Progressive ensemble kernel-based broad learning system for noisy data classification. IEEE Trans. Cybern. 2021, 52, 9656–9669. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Yao, Y. Domain knowledge-based deep-broad learning framework for fault diagnosis. IEEE Trans. Ind. Electron. 2020, 68, 3454–3464. [Google Scholar] [CrossRef]
- Pu, X.; Li, C. Online semisupervised broad learning system for industrial fault diagnosis. IEEE Trans. Ind. Inform. 2021, 17, 6644–6654. [Google Scholar] [CrossRef]
- Feng, S.; Chen, P. Fuzzy broad learning system: A novel neuro-fuzzy model for regression and classification. IEEE Trans. Cybern. 2018, 50, 414–424. [Google Scholar] [CrossRef]
- Yin, C.E.; Yuan, C.; Sun, Y.L. Research of broad learning system. Appl. Res. Comput. 2021, 38, 2258–2267. [Google Scholar] [CrossRef]
- Ekici, S.; Yildirim, S.; Poyraz, M. Energy and entropy-based feature extraction for locating fault on transmission lines by using neural network and wavelet packet decomposition. Expert Syst. Appl. 2008, 34, 2937–2944. [Google Scholar] [CrossRef]
- Chen, P.; Liu, Z.L. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef]
- Dibaj, A.; Ettefagh, M.M.; Hassannejad, R. A hybrid fine-tuned VMD and CNN scheme for untrained compound fault diagnosis of rotating machinery with unequal-severity faults. Expert Syst. Appl. 2021, 167, 114094. [Google Scholar] [CrossRef]
- Chen, L.; Xu, G.; Tao, T. Deep residual network for identifying bearing fault location and fault severity concurrently. IEEE Access 2020, 8, 168026–168035. [Google Scholar] [CrossRef]
- Yu, W.; Lv, P. An end-to-end intelligent fault diagnosis application for rolling bearing based on MobileNet. IEEE Access 2021, 9, 41925–41933. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, X.; Li, J. Deep Residual Network Combined with Transfer Learning Based Fault Diagnosis for Rolling Bearing. Appl. Sci. 2022, 12, 7810. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Oscillatory behavior-based wavelet decomposition for the monitoring of bearing condition in centrifugal pumps. Proceedings of the Institution of Mechanical Engineers. J. Eng. Tribol. 2018, 232, 757–772. [Google Scholar] [CrossRef]
- Kumar, A.; Gandhi, C.P. Improved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images. Appl. Acoust. 2020, 167, 107399. [Google Scholar] [CrossRef]
- Kumbhar, S.G.; Desavale, R.G.; Dharwadkar, N.V. Fault size diagnosis of rolling element bearing using artificial neural network and dimension theory. Neural Comput. Appl. 2021, 33, 16079–16093. [Google Scholar] [CrossRef]
- Truong, N.T.; Seo, T.I.; Nguyen, S.D. Bearing fault online identification based on ANFIS. Int. J. Control. Autom. Syst. 2021, 19, 1703–1714. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Zhu, Y. Intelligent fault diagnosis of rolling element bearing based on SVMs and fractal dimension. Mech. Syst. Signal Process. 2007, 21, 2012–2024. [Google Scholar] [CrossRef]







| Part | Configured Version | |
|---|---|---|
| hardware | CPU | Intel Core i9-10900 |
| GPU | NVIDIA Quadro RTX 4000 | |
| Memory | 32 G | |
| software | Operating System | windows10 64 bit |
| Python | 3.7.11 | |
| Pytorch | 1.7.1 | |
| CUDA | 10.2.89 |
| Model | ResNet34-TL | MobileNet-TL | ResNet34 | MobileNet | CNN | FE-FBLS | FE-BLS |
|---|---|---|---|---|---|---|---|
| Accuracy of the test set | 96.84% | 93.02% | 87.82% | 73.54% | 90.03% | 96.43% | 96.19% |
| Training time/s | 52.2495 | 38.1495 | 50.8465 | 39.1945 | 51.123 | 0.2879 | 0.1054 |
| Model | ResNet34-TL | MobileNet-TL | ResNet34 | MobileNet | CNN | FE-FBLS | FE-BLS |
|---|---|---|---|---|---|---|---|
| Accuracy of the test set | 99.66% | 98.44% | 97.18% | 92.8% | 97.56% | 100.00% | 100.00% |
| Training time/s | 52.744 | 37.6075 | 49.9525 | 37.8175 | 51.865 | 0.2624 | 0.0918 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Yang, X.; Liu, L.; Wang, Y.; Wang, J.; Hou, G. Fuzzy Broad Learning System Combined with Feature-Engineering-Based Fault Diagnosis for Bearings. Machines 2022, 10, 1229. https://doi.org/10.3390/machines10121229
Zhou J, Yang X, Liu L, Wang Y, Wang J, Hou G. Fuzzy Broad Learning System Combined with Feature-Engineering-Based Fault Diagnosis for Bearings. Machines. 2022; 10(12):1229. https://doi.org/10.3390/machines10121229
Chicago/Turabian StyleZhou, Jianmin, Xiaotong Yang, Lulu Liu, Yunqing Wang, Junjie Wang, and Guanghao Hou. 2022. "Fuzzy Broad Learning System Combined with Feature-Engineering-Based Fault Diagnosis for Bearings" Machines 10, no. 12: 1229. https://doi.org/10.3390/machines10121229
APA StyleZhou, J., Yang, X., Liu, L., Wang, Y., Wang, J., & Hou, G. (2022). Fuzzy Broad Learning System Combined with Feature-Engineering-Based Fault Diagnosis for Bearings. Machines, 10(12), 1229. https://doi.org/10.3390/machines10121229






